Exerc´ıcios de Teoria da Computa¸c˜
ao
Rodrigo de Souza
Sum´
ario
1 Conjuntos, rela¸c˜oes, grafos, provas 2
2 Palavras 3
3 Linguagens 5
4 Express˜oes regulares 7
5 Autˆomatos e linguagens reconhec´ıveis 8
6 Linguagens livre de contexto 10
7 M´aquinas de Turing 11
1
Conjuntos, rela¸c˜
oes, grafos, provas
Exerc´ıcio 1 Prove por indu¸c˜ao que para todo inteiro n ≥3, 2n>2n.
Exerc´ıcio 2 Prove que em toda festa com pelo menos duas pessoas h´a no m´ınimo duas pessoas com o mesmo n´umero de conhecidos dentro da festa.
Exerc´ıcio 3 Prove que todo grafo simples tem um n´umero par de v´ertices de grau ´ımpar. Vocˆe pode usar se quiser o fato de que a soma dos graus dos v´ertices ´e o dobro
do nmero de arestas.
Exerc´ıcio 4 Prove que todo grafo simples com dois ou mais v´ertices tem pelo menos dois vrtices de mesmo grau. (O grau de um v´ertice o n´umero de arestas que incidem no mesmo).
Exerc´ıcio 5 O grafo (dirigido) dos prefixos da L´ıngua Portuguesa definido assim: os vrtices so palavras e h um arco de uma palavrau a uma palavra distinta v exatamente quando u um prefixo de v (recorde que u prefixo de v quando v comea com u; por exemplo abra prefixo de abradacabra).
1. Desenhe o grafo dos prefixos para as seguintes palavras: amoroso, amo, ramo, amorosamente, amorosos. Escreva a defini¸c˜ao formal desse grafo, designando o conjunto de v´ertices e o conjunto de arcos (vocˆe vai notar que n˜ao h´a arcos par-alelos, ent˜ao vocˆe pode descrever os arcos simplesmente como pares de v´ertices).
2. Dizemos que um grafo ac´ıclico se no tem passeios fechados. O grafo que vocˆe acabou de desenhar acclico? O grafo de todas as palavras da L´ıngua Portuguesa ac´ıclico? Justifique.
2
Palavras
Exerc´ıcio 6 Prove que para palavras u e v quaisquer, se uv = vu, ent˜ao existe uma palavra w e inteiros k e l tais que u = wk e v = wl (ou seja, u e v s˜ao potˆencias de
uma mesma palavra).
Exerc´ıcio 7 Prove que para palavrasuev e um inteiro k quaisquer,(uv)ku=u(vu)k.
Exerc´ıcio 8 Para toda palavra u = a1. . . an, onde cada ai ´e uma letra, o reverso de
u, denotado por (u)̺, ´e a palavra u escrita de tr´as para frente: an. . . a1.
a) Defina de forma indutiva a opera¸c˜ao reverso.
b) Prove que para palavrasu e v quaisquer vale ((uv))̺= (v)̺(u)̺.
Exerc´ıcio 9 Dizemos que uma palavra u ´e pal´ındromo se u = (u)̺. Um exemplo:
u=madamimadam.
a) Escreva todos os pal´ındromos de comprimento no m´aximo 4 sobre {a, b}.
b) Prove que se u ´e um pal´ındromo de comprimento par, ent˜ao u ´e da forma w(w)̺.
c) Prove que se u ´e um pal´ındromo, ent˜ao para todon > 0, un tamb´em ´e.
d) Prove que se un ´e pal´ındromo, onde u ´e uma palavra e n > 0, ent˜ao u tamb´em ´e.
Exerc´ıcio 10 Dizemos que uma palavra sobre o alfabetoA ={(,)}´e balanceada se ´e poss´ıvel parear os s´ımbolos de abertura e fechamento de parˆentesis (nessa ordem). Por exemplo, as palavras seguintes n˜ao s˜ao balanceadas:
)(, (, ,())
As seguintes s˜ao balanceadas:
ǫ, ()(), (()((())))()
Formalmente, podemos definir as palavras balanceadas de forma indutiva:
• a palavra vazia ´e balanceada;
• se u e v s˜ao palavras balanceadas, ent˜ao (u)v s˜ao palavras balanceadas.
a) Escreva todas as palavras balanceadas de comprimento no m´aximo 6.
c) Prove, por indu¸c˜ao no comprimento da palavra e usando a defini¸c˜ao indutiva de palavra balanceada, que o comprimento de uma palavra balanceada ´e par (vocˆe provavelmente dir´a que isso ´e evidente, mas o objetivo desse exerc´ıcio ´e fazˆe-lo entender bem uma defini¸c˜ao indutiva e saber trabalhar com ela).
Exerc´ıcio 11 Sejam A={a, b, c} e k >0 um inteiro.
a) Encontre uma f´ormula fechada para o n´umero de palavras sobre A de comprimento exatamente k.
b) Liste todas as palavras de comprimento no m´aximo 3 sobre A.
c) Encontre uma f´ormula fechada para o n´umero de palavras de comprimento no m´aximo k.
d) Repita para um alfabeto de tamanho arbitr´ario n.
Exerc´ıcio 12 SejamAum alfabeto comnletras e auma letra deA. Quantas palavras sobre A de comprimento k onde a aparece uma ´unica vez existem?
Exerc´ıcio 13 Uma fator de uma palavra u ´e um segmento de u. Por exemplo, a palavra abab tem trˆes fatores de comprimento 2, que come¸cam, respectivamente, na primeira, na segunda e na terceira posi¸c˜oes (note que ab aparece em duas posi¸c˜oes distintas).
a) Quantos fatores tem uma palavra de comprimenton?
b) Quantos fatores de comprimento k tem uma palavra de comprimenton?
c) Quantos fatores de comprimento no m´aximo k tem uma palavra de comprimento
n?
3
Linguagens
Exerc´ıcio 14 Prove ou dˆe um contra-exemplo: para linguagens X, Y e Z quaisquer,
a) XY =Y X
b) X+
⊆X∗∪X
c) (XY)∗ ⊆X∗Y∗
d) (XY)∗ =X∗Y∗
e) (X∪Y)∗ ⊆(XY)∗
f ) (X∪Y)∗ =X∗Y∗
g) (X∪Y)Z =XZ∪Y Z
h) (X∩Y)Z =XZ∩Y Z
i) XY ∩XZ ⊆X(Y ∪Z)
Exerc´ıcio 15 Prove ou dˆe um contra-exemplo: para linguagens finitasX, Y eZ quais-quer,
a) |X(Y ∩Z)|=|XY ∩XZ|
b) |X(Y ∪Z)|=|XY ∪XZ|
Exerc´ıcio 16 Prove que para uma linguagem X qualquer,
a) (X+
)∗ =X∗
b) (X+
)+
=X+
c) (X∗)+
= (X+
)∗
Exerc´ıcio 17 Seja X a linguagem sobre o alfabeto {0,1} das palavras que come¸cam com0, e seja Y a linguagem das palavras que come¸cam com 1. Descreva em Portuguˆes as linguagens seguintes, e justifique brevemente sua resposta.
a) X∪Y
b) (X∪ {ǫ})Y
a) X∪Y
b) XX
c) XY
d) Y X
e) Y Y
Exerc´ıcio 19 Considere a seguinte linguagem sobre o alfabeto A={a, b}:
L={u∈A∗ : |u|
a=|u|b}
Determine as seguintes linguagens:
a) LA∗
b) L∗
Exerc´ıcio 20 Considere a linguagem X = {a, ba} sobre o alfabeto {a, b}. Descreva em Portuguˆes a linguagem X∗.
4
Express˜
oes regulares
Exerc´ıcio 21 Descreva em Portuguˆes as linguagens representadas pelas express˜oes regulares seguintes sobre o alfabeto {a, b}.
a) ((a+b)∗a(a+b)∗a(a+b)∗)∗
b) b∗(a+ǫ)b∗
c) (a+b)∗a(a+b)(a+b)
d) b∗ab∗(a+ǫ)b∗
e) (b+ǫ)(ab)∗(a+ǫ)
Exerc´ıcio 22 Escreva uma express˜ao regular que representa a linguagem descrita em Portuguˆes (pode assumir o alfabeto A={a, b}).
a) Palavras onde toda ocorrˆencia de b ´e seguida por um a.
b) Palavras sem nenhuma ocorrˆencia de bb.
c) Palavras que possuem pelo menos uma ocorrˆencia de ab.
d) Palavras onde nenhuma ocorrˆencia de a ´e seguida por um b.
e) Palavras de comprimento maior ou igual a 2 cuja pen´ultima letra ´e a.
f ) Palavras com pelo menos um b.
g) Palavras com no m´aximo duas ocorrˆencias de a.
h) Palavras cujo n´umero de ocorrˆencias da letra a ´e divis´ıvel por 3.
i) Palavras onde toda ocorrˆencia de a ´e seguida por um b e toda ocorrˆencia de b ´e seguida por um a.
j) Palavras onde toca ocorrˆencia de b ´e seguida e precedida por um a.
5
Autˆ
omatos e linguagens reconhec´ıveis
Exerc´ıcio 23 Apresente um autˆomado finito determin´ıstico realizando cada uma das linguagens a seguir sobre o alfabeto {a, b}.
a) Todas as palavras onde toda ocorrˆencia de a ´e seguida por um b.
b) Todas as palavras formadas apenas dea’s ou de b’s.
c) Todas as palavras onde o n´umero de ocorrˆencias de a ´e par.
d) Todas as palavras que possuem uma ocorrˆencia deabaa.
e) Todas as palavras que n˜ao possuem nenhuma ocorrˆencia de aa nem de bb.
f ) Todas as palavras formadas por zero ou mais concatena¸c˜oes de blocos ab ou ba.
g) Todas as palavras nas quais todo bloco de cinco letras consecutivas tem pelo menos duas ocorrˆencias de a (dica: use os estados para codificar as posi¸c˜oes dos ´ultimos doisa’s lidos no ´ultimo bloco de cinco letras).
Exerc´ıcio 24 Prove que o complemento de uma linguagem reconhec´ıvel tamb´em ´e uma linguagem reconhecivel. (Dica: prove que todo autˆomato determin´ıstico ´e equivalente a um autˆomato completo e manipule esse autˆomato completo convenientemente)
Exerc´ıcio 25 O prefixo de uma palavra u ´e um segmento inicial de u, ou seja, uma palavra v tal que u=vz. O fecho prefixo de uma linguagem X ´e a linguagem formada por todos os prefixos das palavras emX.
a) Diga quem ´e o fecho prefixo da linguagem {u∈ {a, b} | |u|a=|u|b}.
b) Prove que se X ´e reconhec´ıvel, ent˜ao seu fecho prefixo tamb´em ´e.
Exerc´ıcio 26 Prove que as seguintes linguagens sobre o alfabeto {a, b, c} n˜ao s˜ao re-conhec´ıveis:
a) {a2nb2n | n≥0}.
b) {ambn | m≥n2
}.
c) {ambn | m+n≥5}.
d) {u∈ {a, b}∗ | |u|
a= 2|u|b}.
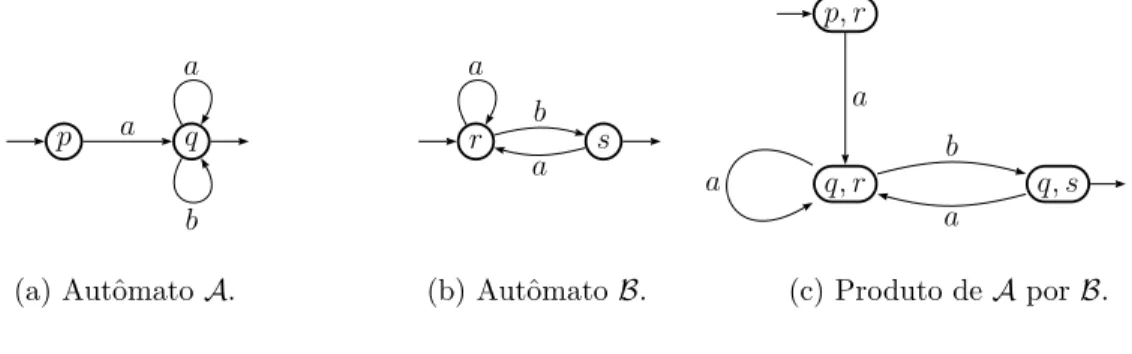
Exerc´ıcio 27 (Produto de autˆomatos) O produtode dois autˆomatos determin´ısticos
A = (Q, A, δ, i, F) e B = (R, A, δ′, j, G)
(ambos sobre o mesmo alfabetoA) ´e um novo autˆomato
C = (Q×R, A, γ,(i, j), F×G)
onde a fun¸c˜ao de transi¸c˜aoγ ´e definida como segue:
∀a∈A γ((p, q), a) = (δ(p, a), δ(q, a))
Ou seja: os estados de C s˜ao o produto cartesiano dos estados de A e B, e a fun¸c˜ao de transi¸c˜ao γ “executa”as fun¸c˜oes δ e δ′ ao mesmo tempo, uma em cada coordenada
(assim, essa fun¸c˜ao s´o est´a definida quando ambas as coordenadas est˜ao). Exemplo:
p a q
a
b
(a) Autˆomato A.
r s
a
a b
(b) AutˆomatoB.
p, r
q, r q, s
a a
b a
(c) Produto deAporB.
Figura 1: Produto de autˆomatos
a) Diga qual ´e a linguagem reconhecida por cada um dos autˆomatos no exemplo.
b) Descreva qual ´e a linguagem reconhecida pelo produto de dois autˆomatos.
c) Modifique essa constru¸c˜ao para demonstrar que a diferen¸ca entre duas linguagens reconhec´ıveis ´e uma linguagem reconhec´ıvel.
d) Usando essa constru¸c˜ao, apresente um autˆomato para a linguagem das palavras sobre {a, b} onde o n´umero dea’s ´e par e o n´umero de b’s ´e ´ımpar.
Exerc´ıcio 28 O reverso de uma linguagem X ´e a linguagem formada pelos reversos das palavras de X. Prove que se X ´e reconhec´ıvel ent˜ao o reverso de X tamb´em ´e.
Exerc´ıcio 29 Construa um autˆomato que reconhece a linguagem representada por cada uma das express˜oes seguintes:
a) (a+b∗)+
+ (ba)∗
b) (a+bb+ba(b+aa)∗ab)∗
6
Linguagens livre de contexto
Exerc´ıcio 31 Determine uma gram´atica e um autˆomato `a pilha para cada uma das linguagens a seguir sobre o alfabeto {a, b, c}:
a) {anbn | n≥ 0} (refa¸ca para n >0)
b) {a3nb2n | n≥0}
c)
aknbℓn | n≥0 , onde k e ℓ s˜ao dois inteiros positivos fixos
d)
a2nbnck | k, n≥0
e) {u∈ {a, b}∗ | |u|
a=|u|b}
f ) {u∈ {a, b}∗ | |u|
a= 2|u|b}
g) {u∈ {a, b}∗ | |u|
a6=|u|b}
h) {u∈ {a, b, c}∗ | |u|
a=|u|b}
i) A linguagem das palavras balanceadas sobre “(”e “)”(´e a linguagem descrita no Exerc´ıcio 10, mas n˜ao inclua a palavra vazia).
7
M´
aquinas de Turing
Exerc´ıcio 32 Determine uma m´aquina de Turing para cada uma das linguagens des-critas no Exerc´ıcio 31.
Exerc´ıcio 33 Determine uma m´aquina de Turing para cada uma das linguagens a seguir sobre o alfabeto {a, b, c}:
a) {anbncn | n >0}
b) {anbn+1cn+2
| n >0}
Exerc´ıcio 34 Prove que a uni˜ao de duas linguagens recursivamente enumer´aveis ´e uma linguagem recursivamente enumer´avel. Para isso, mostre como construir uma m´aquina de Turing que “simula”a m´aquina para uma dessas linguagens, e para cada palavra que ´e aceita, executa em seguida a m´aquina para a outra linguagem, na mesma palavra. Cuidado com o fato de que a palavra pode ser alterada pela m´aquina. Como vocˆe resolve esse problema? (Para facilitar, pode considerar m´aquinas de Turing cuja fita ´e infinita apenas para a direita).
Exerc´ıcio 35 Prove que a intersec¸c˜ao de duas linguagens recursivamente enumer´aveis ´e uma linguagem recursivamente enumer´avel.
Exerc´ıcio 36 Prove que a estrela de uma linguagem recursivamente enumer´avel ´e uma linguagem recursivamente enumer´avel.
8
Computabilidade
Exerc´ıcio 38 Prove que n˜ao ´e decid´ıvel se um programa na linguagem C imprime alguma coisa durante sua execu¸c˜ao (pode assumir que toda impress˜ao ´e feita com o printf). Para isso, reduza a este problema outro problema que vocˆe j´a sabe que ´e indecid´ıvel.
Exerc´ıcio 39 Explique em linhas gerais por qual raz˜ao existem linguagens que n˜ao podem ser reconhecidas por uma m´aquina de Turing.