UNIVERSIDADE ESTADUAL DE CAMPINAS
INSTITUTO DE MATEMÁTICA, ESTATÍSTICA E COMPUTAÇÃO CIENTÍFICA DEPARTAMENTO DE MATEMÁTICA DE MATEMÁTICA APLICADA
Relatório Final
Notas de Aula.
Disciplina: MT 624 - Biomatemática I Prof. Dr. Laécio Carvalho de Barros
Deccy Yaneth Trejos Angel Marta Maria Mucacho Macufa Miguel Tadayuki Koga
Sumário
Seção 1 - Introdução . . . 4
1.1 - Modelos Matemáticos . . . 4
Seção 2 - Equações de Diferença Lineares . . . 5
2.1 - Equações de Diferença Lineares . . . 5
2.2 - Equações de Diferença Lineares Homogêneas de Ordemk . . . 7
2.3 - Equações de Diferença de Segunda Ordem . . . 8
Seção 3 - Sistema de Equações de Diferenças Lineares . . . 14
3.1 - Autovalores Complexos . . . 16
3.2 - Raízes Complexas . . . 17
3.3 - Comportamento Qualitativo das Soluções para a Equação de Diferença Linear 19 Seção 4 - Equações de Diferença Não Lineares . . . 21
4.1 - Equações de Diferença Não Lineares . . . 21
4.2 - Modelo Logístico de Diferença . . . 22
4.3 - Sistema de equações de Diferença Não Lineares . . . 24
Seção 5 - Aplicação de Equações de Diferença Não Linear . . . 26
5.1 - Sistemas não Lineares . . . 26
Seção 6 Modelos Contínuos . . . 32
6.1 - Modelos Contínuos . . . 32
6.2 - Modelos Matemáticos com de Equações Diferenciais . . . 32
6.3 - Equilíbrio e Estabilidade . . . 40
6.3.1 - Análise de Estabilidade dos Pontos de Equilíbrio. . . 40
Seção 7 - Sistemas de Equações Diferenciais Lineares . . . 43
7.1 - Sistemas de Equações Diferenciais Lineares Bidimensionais . . . 43
7.2 - Sistema de Equações Lineares n Dimensional . . . 48
7.3 - Sistemas Autônomos (quase-linear) . . . 50
Seção 8 - Modelos em Biomatemáticas . . . 52
8.1 - Modelos em Biomatemáticas . . . 52
8.1.1 - Modelos de Competição entre duas Espécies. . . 52
8.1.2 - Modelo Presa-Predador . . . 55
8.2 - Modelos Epidemíológicos . . . 61
Seção 9 - Equações Diferenciais Parciais . . . 71
9.1 - Populações Distribuidas no Espaço . . . 71
Seção 1
Introdução
Definição 1 Biomatemática: A Biomatemática é compreendida como a aplicação de modelos matemáticos para a resolução e compreensão de fenômenos biológicos.
1.1 - Modelos Matemáticos
Os Modelos Matemáticos surgem com o objetivo de buscar a interação entre a teoria matemática e outras ciências. De acordo com a história da matemática, a matemática surge da necessidade de um processo de organização e controle. Na Babilônia por volta de 2000 a.c., através escavações arqueológicas, foram encontrados tabletes cuneiformes que mostram uma aritmética utilizada para o cálculo de comprimentos, áreas, volumes, pesos, estoques de mercadoria, etc.
Nesses tabletes encontraram registrados símbolos e regras bem definidas, que utilizavam para resolver problemas reais. A resolução destes problemas propiciava a motivação e estrutura para a construção de uma teoria matemática, além da sua aplicação.
Dentro deste contexto tem se mostrado através dos tempos que a matemática tem se tornado uma ferramenta importante para o desenvolvimento de uma sociedade, contribuindo para a solução de várias situações problemas. NEWMANN (apud Bassanezi, Ferreira - 1988) "Eu penso que seria uma aproximação relativamente boa da realidade (que é demasiadamente complexa para permitir qualquer coisa melhor do que uma aproximação), dizer que as idéias matemáticas tem a sua origem em situações empíricas".
Historicamente ocorreram o desenvolvimento de vários campos da matemática, em nossa situação, estaremos construíndo modelos matemáticos de situações problema que pressupõe a existência de um dicionário que interpréta símbolos e operações de uma teoria matemática de acordo com a linguagem utilizada para a descrição do problema estudado, transpondo o problema para a matemática, sendo estudado com toda teoria matemática já desenvolvida e através desta teoria objetiva-se encontrar resultados que visam solucionar o problema original, em alguns modelos pode ocorrer de não existir uma teoria adequada para analisar o problema, cabe então ao matemático, desenvolver um novo campo da matemática.
A matemática aplicada assume uma função importante no desenvolvimento dessa teoria, pois cabe a ela estruturar modelos e atacá-lo com uma teoria matemática já desenvolvida, almejando resultados que visam solucioná-lo.
Seção 2
Equações de Diferença Lineares
2.1 - Equações de Diferença Lineares
Definição 2 Equações de diferenças lineares são equações de recorrência. Uma equação geral de diferença de ordem n, tem a seguinte forma:
yt+1−yt =f(yt, yt−1, yt−2, ..., yt−n), (1)
onde f :D ⊂ ℜn =⇒ ℜ.
2.1.1 - Equações de Diferença Autônomas
Definição 3 Equações de diferença autônomas são equações em que a função f não depende
de t, mas depende apenas dos estágio.
yt+1−yt =f(yt, yt−1, yt−2, ..., yt−n) (2)
Ou
yt+1=g(yt, yt−1, yt−2, ..., yt−n) (3)
ondef é linear nas variáveis yt, yt−1, ..., yt−n, isto é, se (2) puder ser escrito na formag(t) = yt+1+atyt+at−1y t −1+...+at−nyt−n, temos uma equação de diferença linear e não homogênea.
A equação de diferença linear será homogênea seg(t) = 0, caso contrário diz-se equação de diferença linear não homogênea.
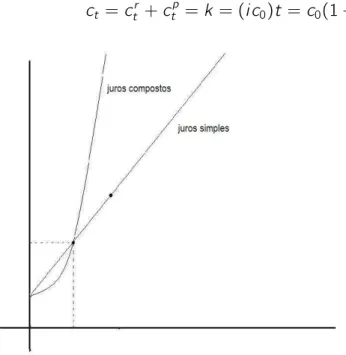
Exemplo 1 Economia:
Suponha que um capital C0 é aplicado a uma taxa i. Qual é o montante após t periódo, se
o regime for:
a) de juros simples b) de juros composto
Solução
a) ct+1−ct =i c0 é uma equação não homogénea.
Solução geral para a equação homogênea: Seja ct =kλt
Substituindo no item (b) teremos:
ct+1−(1+i)ct = 0 ⇒kλt+1−(1+i)kλt = 0 ⇒λtk[λ−(1+i)] = 0⇒
λtk = 0 λ−(1 +i) = 0
Paraλtk = 0 ⇒λ= 0, temos uma solução trivial.
Paraλ−(1 +i) = 0 ⇒λ= 1 +i, e substituido em ct =kλt, temos: ct =k(1 +i)t e se t = 0 ⇒c0=k(1 +i)0=k ⇒ct =c0(1 +i)t.
Portanto a solução ct =kλ t
, onde λ é solução da equação λ−(1 +i) = 0. A solução do item (b) também pode ser calculada por recorrência:
ct+1 = (1 +i)ct t = 0 ⇒ c1 = (1 +i)c0 t = 1 ⇒ c2 = (1 +i)2c0
t = 2 ⇒ c3 = (1 +i)3c 0
... ...
t = n ⇒ cn = (1 +i)nc0
Para solução do item (a) ct+1−ct =i c0, se i c0= 0, então ct+1−ct = 0 ⇒λ−1 = 0⇒ λ= 1.
Note quech
t =k×1t =k, é solução da equação homogênea. Supondo quet = 0 ⇒k =c0,
é fácil de ver que ctp= (i c0)t é uma solução particular.
A solução geral é:
ct =ctr +c p
t =k = (i c0)t =c0(1 +i +t)
2.2 - Equações de Diferença Lineares Homogêneas de Ordem
k
Dada uma equação de diferença linear:
yt+k +αt+k−1yt+k−1+αt+k−2yt+k−2+...+αt+1yt+1+αtyt = 0 (4)
Seja yt = Cλt uma solução de (4) e substituindo yt, temos: Cλt+k +α
t+k−1Cλt+k−1+αt+k−2Cλt+k−2+...+αt+1Cλt+1+αtCλt = 0⇒
⇒Cλt(λk+α
t+k−1λk−1+...+αt+1λ+αt) = 0 ⇒
Cλt = 0 λk +α
t+k−1λk−1+...+αt+1λ+αt = 0
Dessa equação tiramos que:
Cλt = 0 ⇒λ= 0 pk(λ) = 0
Portanto: λt é uma solução de (4) ⇔ λ é uma solução de p
k(λ) e pk(λ) é chamado de
polinômio característico.
Teorema 1 O conjunto solução da equação (4) é um espaço de dimensão k.
Demontração:
Seja yt e xt ∈ ℜk e solução da equação (4) e β
i ∈ ℜ, tal que,
yt+k +αt+k−1yt+k−1+αt+k−2yt+k−2+...+αt+1yt+1+αtyt = 0
e
xt+k +αt+k−1xt+k−1+αt+k−2xt+k−2+...+αt+1xt+1+αtxt = 0
então, para (yt +βtxt), teremos que:
(yt+k+βt+kxt+k) +αt+k−1(yt+k−1+βt+k−1xt+k−1) +αt+k−2(yt+k−2+βt+k−2xt+k−2) +...+ αt+1(yt+1+βt+1xt+1)t+ 1 +αt(yt +βtxt) =
= yt+k+βt+kxt+k+αt+k−1yt+k−1+αt+k−1βt+k−1xt+k−1+αt+k−2yt+k−2+αt+k−2βt+k−2xt+k−2+
...+αt+1yt+1+αt+1βt+1xt+1+αtyt+αtβtxt =
= (yt+k +αt+k−1yt+k−1+αt+k−2yt+k−2+...+αt+1yt+1+αtyt) +
(βt+kxt+k +αt+k−1βt+k−1xt+k−1+αt+k−2βt+k−2xt+k−2+...+αt+1βt+1xt+1+αtβtxt) = = 0 + 0 = 0
logo, (yt+βtxt) é solução da equação (4).
seyt = 0, entãoyt também é solução da equação (4), portanto o espaço solução da equação
(4) é um espaço vetorial de dimensão k
Corolário 1 Se o polinômiopk(λ)só tiver raízesλi simples, como sãokraízes, entãoλt1, λt2, ..., λtk
formam uma base do conjunto solução.
Proposição 1 Se α for uma raíz depk(λ) com multiplicidade m então αt, tαt, t2αt, ..., tm−1λt
são solução linearmente independente.
Assim a solução geral da equação (4) tem a forma:
yt =c11λt+c21tλt +. . .+cm(i)tm1−1λt1+c12λt2+. . .+cm2tm2−1λt2c1nλt1+. . .+cmnt
mn−1λt
n
Em quem1+m2+. . .+mn=k.
Exemplo 2 yt+1=ayt ⇔yt−1−ayt = 0⇒p(λ) =λ−a⇒λ=a
Figura 2: Solução
2.2.1 - Equilíbrio de uma Equação de Diferença
Definição 4 Dizemos que há equilíbrio quando a geração atual é igual a geração seguinte, isto é, yt+1=yt ∀t
Neste caso teremos, ayt =yt ⇒
yt = 0 ∀t a= 1
2.3 - Equações de Diferença de Segunda Ordem
Definição 5 Equações de diferença de segunda ordem são equações que depedem de duas ger-ações anteriores.
Fórmula geral de uma equação de segunda ordem:
yt+2+byt+1+cyt = 0 (5)
ou
yt+byt−1+cyt−2= 0
Suponha que yt = kλt seja uma solução geral para a equação (5). Substituindo yt = kλt
em (5), teremos:
p2(λ) =λ2+bλ+c = 0
2.3.1 - Tipos de Soluções para Equações de Segunda Ordem
• se λ16=λ2; a solução de p2(λ) é dada pela forma yt =c1λt
1+c2λt2
• seλi, comi = 1,2, forem complexos, teremosλ1=a+b1, λ2 =a−bi, a solução complexa
vem sempre em par conjugado.
No caso de soluções complexas podemos transformá-las na forma trigonomérica, ou seja,
yt = C1(a+bi)t + C2(a−bi)t, onde (a−bi)t = rt(cosθt+i senθt), rt = √a2+b2,
θ =ar ctga b
; a6= 0 e θ = π
2 sea = 0
Portanto teremos que yt =rt(Acos(θt) +Bi sen(θt)), ondeA=c1+c2 e B =c1−c2.
Exercício 1 Resolva as seguintes equações: a) yt+2−5yt+1+ 6yt = 0
b)
xt+1−5xt + 4xt−1= 0
x1= 9
x2= 23
c)
xt−4xt−1+ 4xt−2= 0
x0= 9 x1= 2
d)
xt+2+xt = 0 x0 =x1= 4
Solução
(a) yt+2−5yt+1+ 6yt = 0
Seja yt =λt substituindo na equação acima, encontrmosλ2−5λ+ 6 = 0
Obtemos um polinômio do segundo grau e usando a fórmula de Baskara:
∆ =b2−4ac
λ1,2= −b±
√
∆
2a ⇒λ1,2= 5±1
2 ⇒
(
λ1 = 2 λ2 = 3.
Como λ16=λ2 então a solução é da forma:
yt =C1λt
1+C2λt2⇔yt =C12t +C23t
b)
xt+1−5xt+ 4xt−1 = 0
x1 = 9
x2 = 23.
λ2−5λ+ 4 = 0 ⇒ λ
1= 1 e λ2= 4
λ1 6= λ2
xt = C1λt1+C2λt2
Parax1 = 9 e para x2 = 23temos o seguinte sistema:
9 = C1+ 4C2
23 = C1+ 16C2
Resolvendo o sistema acima temos:
C1 =
26
6 e C2=
7 6
Então temos:
xt = 26 6 +
7 6
4t
Representação gráfica da equação solução:
Os outros "items"resovem-se da mesma maneira
2.3.2 - Exemplos de Modelos Biológicos com Equações de Diferença Lineares Exemplo 3 Insetos(Leah, ano 1988).
Insetos geralmente tem mais que um estágio no seu ciclo de vida. Um ciclo completo pode levar semanas, meses ou mesmo anos. No entanto é costume usar uma única geração como unidade básica de tempo quando tentamos escrever um modelo para o crescimento da população de insetos. Os vários estágios do seu ciclo de vida podem ser representados por escrever várias equações de diferença.
Por exemplo, consideremos a reprodução do choupo gall afídio. As fêmas afídios adultas produzem galls. Todos os progênios de afídios simples estão contidas em um gall. Uma fração destas emergirão e sobreviverão até a fase adulta. Geralmente a capacidade de produzir den-cendêcia e a probabilidade de sobreviver para a fase adulta depende das condições de seu meio ambiente, na qualidade da sua alimentação e do tamanho da população. Vamos ignorar esses efeitos momentaneos e fazer o um estudo ingênuo no qual os parâmentros são constantes.
at - insetos adultos na geração t (fêmeas) pt - número de descendentes em t
r - fração de fêmeas pt+1=f at
at+1=r(1−m)f at
Observação 1 para fazer o controle da população estuda-se o parâmetro a diminuição ou cresci-mento da população.
Exemplo 4 Sequência de Fibonacci.
Quantos coelhos haverá em um ano, começando com um casal adulto e casal adulto e um casal jovem, se em cada més cada adulto gerou um novo casal, o qual se torna adulto apóis dois meses.
at é o número de casais adultos na geração t.
Tabela 1:
Mês casais adultos casais jovens total de casais
1 1 1 2
2 1 2 3
3 2 3 5
4 3 5 8
... ... ... ...
onde a0= 1, a1 = 1, a2= 2 . . .at+2=at+1+at
Temos então uma equação de diferença de segunda ordem:
Seat =kλt, for uma solução da equação (6), então: p(λ) =λ2−λ−1 sep(λ) = 0⇒λ2−λ−1 = 0
Usando a fomúla de Baskara para resolver a equação de segundo grau, temos:
∆ =b2−4ac = 1−4.1.(−1) = 5 e substituindo obteremos,
λ1,2= −
b±√∆
2a ⇒λ1,2 =
1±√5
2 ⇒
λ1 =
1 +√5 2
λ2 =
1−√5
2 .
A solução geral da equação (6) é:
at =A
1
−√5 2
t
+B
1 +√5
2
t
⇒
t = 0 ⇒ A+B = 1
t = 1 ⇒ A
1 +√5 2
+B
1−√5 2
= 1
Resolvendo o sistema, teremos:
B =
√
5−1
2√5 e A=
√
5 + 1 2√5
Então:
at = 1
√
5
"
1 + 5
2
t+1
−
1
−√5 2
t+1#
Exemplo 5 Modelo de propagação anual de plantas sazonais(Leah, ano 1988).
Determinadas plantas produzem sementes no final do verão, quando então morrem. Parte das sementes sobrevivem no inverno e algumas germinam dando origem a uma nova geração de plantas. A fração que germina depende da idade da semente que sobrevive no máximo dois invernos.
Onde:
γ é o número de sementes por plantas.
σ é a fração de sementes que sobrevivem a cada inverno. α é a fração de sementes que germinam no primeiro ano.
β é a fração de sementes que germinam no segundo ano.
Pt é o número de plantas no período t.
Pt =ασγPt−1+β(1−α)σγPt−2 ⇒Pt −ασγPt−1−βσ(1−α)σγPt−2= 0
onde:
ασγ =b e βσ(1−α)σγ=c, e teremos
Pt−bPt−1−cPt−2= 0 (7)
Seja Pt = cλt a solução da equação (7), e substituindo encontramos a equação na forma
(5), ou seja :
Pt−bPt−1−cPt−2 =cλt−bcλt−1−ccλt−2=cλt−2(λ2−bλ−c) = 0⇒
(
cλt−2 = 0
λ2−bλ−c = 0
ou sejaλ2−bλ−c = 0, onde λ 1=
b+√b2+ 4c
2 e λ2=
b−√b2+ 4c
2
E a solução geral da equação (7), conforme 2.3.1 será dada por:
• Se λ16=λ2, então Pt =c1λt
1+c2λt2. neste sentido se λ1 ≥1 e λ2 ≥1, a população
de plantas cresce e se |λ1|<1 e |λ2|<1 a população descresce;
• Se λ1 = λ2 = α; então pt = c1αt +c2tαt. Se α ≥ 1 a população cresce e se α < |1| a
população decresce.
• Se ∆ =b2+ 4c <0, então λ
Seção 3
Sistema de Equações de Diferenças Lineares
O problema anual de reprodução de plantas leva a um sistema de equações de diferenças de primeira ordem ou equivalentes a equações de diferenças de segunda ordem.
Para enteder tais equações vamos momentaneamente voltar a nossa atenção para o sistema na forma:
xt+1 = a11xt+a12yt
yt+1 = a21xt+a22yt,ondeaij são constantes.
(8) O sistema de equações de diferença (8) pode ser escrito na seguinte forma matricial:
xt+1
yt+1
=
a11 a12
a21 a22
xt yt
.
A solução do sistema (8)faremos por meio de equações de diferenças de segunda ordem. Considerando a geração seguinte e da primeira equação do sistema (8), temos:
xt+2 =a11xt+1+a12yt+1.
Utilizando yt+1 da segunda equação e substituindo na equação anterior, teremos:
xt+2 = a11xt+1+a12a21xt +a12a22yt
xt+2 = a11xt+1+a12a21xt +a22(xt+1−a11xt) xt+2 = a11xt+1+a12a21xt +a22xt+1−a22a11xt xt+2 = (a11+a22)xt+1−(a11a22−a12a21)xt
0 = xt+2−(a11+a22)xt+1+ (a11a22−a12a21)xt
ou
0 =xt+2−(tr M)xt+1+ (detM)xt (9)
onde, M=
a11 a12
a21 a22
Outra forma de resolver o sistema (8) é através do seguinte teorema:
Teorema 2 Seλ for um autovalor de M associada ao autovetorv =
v1
v2
entãoXt =v λt =
v1 v2
λt
1 e yt =uλt =
u1 u2
λt
2 é uma solução do sistema (8).
Seja λ autovalor de M e v =
v1
v2
, autovetor associado a λ. Então temos que:
Mv =λv ⇐⇒
a11 a12
a21 a22
v1
v2
=λ
v1
v2
.
Desse sistema temos que:
comoλ é autovalor deM, temos que se p(λ) = 0 ⇒λ2−(tr M)λ+detM = 0e comparando
(9) e (10), temos que xt+2 =λé solução do sistema (8). Portanto, a solução do sistema (8) é
dado por:
xt yt
=C1
v1
v2
λt
1+c2
u1 u2 λt 2
Proposição 2 O conjunto solução do sistema (8) é um espaço vetorial de dimensão 2.
Proposição 3 Se λ1 6= λ2 forem autovetores associados a v e u, então v e u são linearmente
independentes. Demonstração:
Suponha que v e u sejam vetores linearmente dependentes, isto é,v =αu com α∈ ℜ, logo temos:
λ1v =Mv =M(αu) =αMu =αλ2u =λ2αu =λ2v
Portanto, podemos ver que λ1v = λ2v ⇒ λ1v −λ2v = (λ1− λ2)v = 0 como v é um
autovetor, então v 6= 0, e λ1−λ2 = 0 ⇒ λ1 = λ2, mas por hipótese temos que λ1 6= λ2.
Portanto, v e u são vetores linearmente independentes.
Observação 2 Podemos ter autovalores iguais, isto é, λ=λ1 =λ2, neste caso é fácil verificar que tλt é também solução do sistema (8), que tem como solução geral X
t =C1λt+C2tλt.
Exemplo 6 Resolver os seguintes sistemas de equações de diferença: a)
xt+1=xt +yt yt+1=xt + 2yt
solução
xt+1= 2xt+1+yt+1
xt+2= 2xt+1+xt + 2yt
xt+2= 2xt+1+xt + 2xt+1−4xt xt+2= 4xt+1−3xt
xt+2−4xt+1+ 3xt = 0
Seja xt =λt, então λ2−4λ+ 3 = 0 ⇒λ
1 = 1 e λ2 = 3
Usando a matriz M =
2 1 1 2
para achar a solução, determinamos os seus autovalores e encontraremos a mesma equação ou mesmo polinômio caraterístico p(λ) =λ2−4λ+ 3.
Para λ1= 1, temos:
(M−λI)v = 0 ⇔
1 1 1 1 v1 v2 = 0 0 ⇒
v1+v2= 0
v1+v2= 0 ⇒v1=−v2.
Assumindo v2= 1, então V =
−v2
Para λ2= 3
(M−λI)v = 0 ⇔
−1 1 1 −1
u1 u2 = 0 0 ⇒
−u1+u2 = 0
u1−u2 = 0 ⇒
⇒u1 =u2
Assumindo u2= 1, então U =
u1 u1 = 1 1
A solução geral do sistema é dada por:
xt yt
=C1
−1 1
+C2
1 1
3t
Note que quando t aumenta, a solução irá crescer, isto é,xt ou yt aumentará.
b)
xt+1 = xt −yt yt+1 = xt + 3yt
Para resolver este sistema começaremos pelo calculo dos autovalores da matrizM:
p(λ) =det(M−λI) = 0 ⇒det
1−λ −1
1 3−λ
= (1−λ) (3−λ) + 1 = 0
logo temos os autovalores deM são raízes da equação λ2−4λ+ 4 = 0 ⇒λ
1=λ2 = 2
Como λ1=λ2 = 2, temos que:
(M−λI)v = 0⇔
−1 −1
1 1 v1 v2 = 0 0 ⇒
−v1−v2 = 0
v1+v2 = 0 ⇒v1 =−v2
Assumindo v1= 1, temos V =
v1
−v1
= 1 −1
A solução geral do sistema será:
xt yt
=C1
1
−1
2t+C
2
t+ 1
−t−3
2t
Quando t aumenta,xt aumenta enquanto yt diminui, isto é aumenta negativamente.
3.1 - Autovalores Complexos
O polinômio característico (10) pode apresentar autovalores complexos, quando ∆ < 0 ou seja, β2<4γ, ocorrendo portanto, um par conjulgado.
λ1=a+bi e λ2 =a−bi
Como os autovalores são complexos uma solução é dada por:
porém temos que se
xt yt
é uma solução, então
x1 t y1 t e x2 t y2 t
, também são soluções, pois temos que:
xt+1
yt+1
=M xt yt =M x1 t y1 t +M x2 t y2 t i x1 t+1 y1 t+1 + x2 t+1 y2 t+1 i =
a11 a12 a21 a22
x1 t y1 t +
a11 a12 a21 a22
x2 t y2 t i =
a11xt1+a12yt1 a21xt1+a22yt1
+
a11xt2+a12yt2 a21xt2+a22yt2
i
Portanto, se Xt =Xt1+Xt2i for solução, então Xt1 e Xt2 também são soluções e são reais.
3.2 - Raízes Complexas
Sejamλ1 =α+βi e λ1=α−βi autovalores complexos
A solução geral é dada por:
xt yt
=C1
v11
v21
(α+βi)t +C2
v12
v22
(α−βi)t (11)
Seja:
(α+βi)t = |r|t(cosθt+i senθt) (α−βi)t = |r|t(cosθt−i senθt)
Substituindo na equação (11), teremos:
xt yt
= C1
v11 v21
|r|t(cosθt+i senθt) +C2
v12 v22
|r|t(cosθt−i senθt)
= |r|t
C1
v11cosθt+v11i senθt
v21cosθt+v21i senθt
+C2
v12cosθt −v12i senθt
v22cosθt +v22i senθt
= |r|t
(C1v11+C2v12)cosθt + (C1v12−C2v12)i senθt
(C1v21+C2v22)cosθt + (C1v21−C2v22)i senθt
Seja:
A = (C1v11+C2v12)
B = (C1v11−C2v12) C = (C1v21+C2v22)
D = (C1v21−C2v22).
Então:
xt yt
=|r|t
Acosθt Bcosθt
+|r|t
Csenθt Dsenθt
ou
xt yt
=|r|t E1cosθt
+|r|t E2senθt
i, onde E1 =
A B
e E2 =
C D
Exemplo 7 Resolva o sistema:
(
xt+1 = xt+ 2yt yt+1 = −2xt +yt
onde:
p(λ) =det(M−λI) =
1 2
−2 1
= (1−λ)2+ 4 = 0⇒1−λ=±2i ⇒λ= 1±2i
Paraλ= 1−2i, o autovetor associado é dados por: M−λI = 0⇒
2i 2
−2 2i
v1 v2 = 0 0 ⇒
2i v1+ 2v2 = 0
−2v1+ 2i v2 = 0 ⇔
i v1 = v2
−v1 = i v2
Multiplicada a segunda equação por i, temos:
i v1=−v2
i v1=−v2 ⇒ v =
v1 v2 = v1
−i v1
= 1 −i v1
Paraλ= 1 + 2i, temos:
−2i 2
−2 −2i
u1 u2 = 0 0 ⇒
−2i u1+ 2u2 = 0
−2u1−2i u2 = 0 ⇔
i u1 =u2
u1 =−i u2
Multiplicada a segunda equação por i, temos:
i u1=u2 i u1=u2 ⇒
u = u1 u2 = u1 i u1
= 1 i
u1.
A solução do sistema é:
xt yt
= C1
1 i
(1 + 2i)t +C
2
1
−i
(1−2i)t
= (√5)t
C1 1 i
(cosθt +i senθt) +C2
1
−i
(cosθt−i senθt)
= (√5)t
C1
cosθt+i senθt
−senθt +i cosθt
+C2
cosθ−i senθt senθt −i cosθt
= (√5)t
C1
C1cosθt+i C1senθt +C2cosθt −i C2senθt
−C1senθt +i C1cosθt+C2senθt −i C2cosθt
= (√5)t
C1cosθt+C2cosθt
−C1senθt −C2senθt
+
i C1cosθ−i C2senθt i C1senθt −i C2cosθt
= (√5)t
cosθt −senθt + senθt cosθt i
xt yt
=C1
cosθt
−senθt
(√5)t+C
2
senθt cosθt
i(√5)t
3.3 - Comportamento Qualitativo das Soluções para a Equação Linear de
Diferença
As equações de diferença lineares são caraterizadas pelas seguintes propriedades. 1) Uma equação de diferença tem a seguinte forma:
a0xn+a1xn−1+· · ·+amxn−m
2) A ordem da equação é o número de gerações prévias que influenciam directamente o valor de x numa dada geração.
3) Quando a0, a1· · · , am são constantes e bn = 0, o problema é um coeficiente constante
da equação de diferença linear homogênea; o método estabelecido neste capítulo pode ser usado para resolver tais equaçãoes. As soluções são compostas por combinações lineares de expressões básicas da forma:
Xn=Cλn (12)
4) Os valores de λ que aparece em (12) são obtidos por determinar as raízes do polinômio
caraterístico P(λ) =a0λm+a
1λm−1+· · ·+am.
5) O número de soluções básicas (distintas) é determinada pela ordem da equação caraterís-tica. Por exemplo uma equação de primeira ordem tem uma solução básica, a equação de ordem 2 tem duas soluções básicas em geral a equação de m-ésima ordem pode ter m
soluções básicas.
6) A solução geral é uma superposição linear dem soluções básicas da equação (que vem de todos os valores de λ que são distintos).
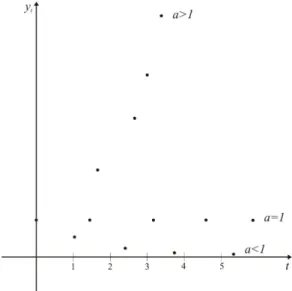
7) Para o valor real de λ o comportamento qualitativo de uma solução básica de ((1),(2))
depende se λ cai numa das quatro possibilidades.
λ≥1, λ≤ −1, 0< λ <1 e −1 < λ <0
Uma solução básica é caraterizada pela seguintes classificações: a) Para λ >1, λn Cresce quando n aumenta, assim X
n =Cλn cresce sem limite.
b) Para 0< λ <1, λn decresce para zero quandon aumenta, assimX
n =Cλn decresce para
zero.
c) −1 < λ < 0, λn oscila entre o valor positivo e negativo, porém X
n = Cλn decresce para
d) λ <−1, λn oscila como no item c) mas com diminuição de magnitude.
No caso em que λ = 1, λ = 0 ou λ = −1 que são pontos marginais da demarcação entre
o domínio do comportamento, corresponde respetivamente para a (1) solução estática, onde
x =C, (2) x = 0 e (3) uma oscilação entre o valor de x =C e x =−C.
As figuras abaixo representam o comportamento de Xn =Cλn nos quarto casos
Seção 4
Equações de Diferença Não Lineares
4.1 - Equações de Diferença Não Lineares
Nesta seção desenvolveremos a equação de diferença não linear de primeira ordem na forma
yn+1 =f(yn) (13)
onde f : I ⊂ ℜ −→ ℜ é o valor de y na n-ésima iteração e f é uma função dependente das combinações não lineares de yn. Dado um valor inicial y0, então
{y0, f(y0), f2(yn), ..., fn(yn)}
as sequências de iterações sobre a funçãof, é a solução ou órbitas dey0, isto é,yn=fn(yn)
é a solução de (13).
O estudos deste tipo de equação (13) se faz qualitativamente encontrando um ponto de equilíbrio, isto é, definindo um ponto fixo y tal que f(y) =y então
yn+1=yn =y
A estabilidade do ponto de equilíbrio de uma equação de diferença não linear pode ser definida do seguinte modo:
Definição 6 Seja y um ponto de equlibrio para (13), então y é dito estável se,
∀ε >0,∃δ >0,|y0−y|< δ ⇔ |fn(y
0)−y|< ε
y é dito instável se não é estável.
y é assintóticamente estável se for estável e existeγ >0 tal que
|y0−y|< γ =⇒ lim
n→∝f
n(y
0) −→y
Teorema 3 Critério de estabilidade
Seja f de classe C1 e y ponto de equlibrio, então, f é assintoticamente estável se
|dfdy(y)|<1
e é instável se
|dfdy(y)|>1
Prova:
Sey é um ponto de equilíbrio de (13) se e somente se
yn+1 =g(yn) (14)
Portanto, as propriedades de estabilidade para y são as mesmas que para o ponto origem (0,0) então para (14) temos queg′(y) =f′(y+y), logog′(0) =f′(y), supondo que zero é um equilíbrio e fazendo a expansão através da série de Taylor obtemos que
g(yn) +g(0) +g′(0)y
n+O((yn)2)
então o sistema (14) é linearizadoyn+1=g′(0)yn portanto a solução é yn+1 =C1(λ)n
onde λ=g′(0).
Se|g′(0)|<1, o equilíbrio nulo é assintoticamente estável, e instável se |g′(0)|>1.
A solução yn da equação (13) pode ser constituída por um número finito de valores, isto é, y∗
n =yn+T, T = 0,1,2, ... e yn∗+j 6=yn∗ para j = 1,2, ..., T −1 tal solução é chamada ciclo limite
ou ciclo de período T.
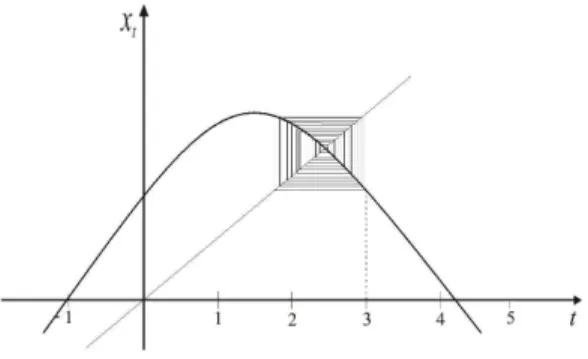
O ponto de equilíbrioy pode ser encontrado fazendo a interseção da bissetriz comf(y). Isto significa que yn = y e portanto, satisfaz y = f(y). Usando o diagrama de Lamery podemos
garantir a existência do ponto de equilíbrio de acordo com o gráfico seguinte.
Figura 5: Lamery
4.2 - Modelo Logístico de Diferença
Quando os recursos são limitados, o crescimiento da população num intervalo do tempo unitário é reduzido de uma quantidade proporcional ao quadrado da população existente no início do intervalo. De fato, se existe uma competição entre elementos de uma mesma especie, o termo de inibição do crescimento populacional é proporcional ao produto destes elementos.
Na forma de recorrência, para tal modelo é dado por:
yt+1 =yt(r −dyt)
Seja xt = d
r yt sustituindo na equação temos que
o termoK = r
d é a capacidade do suporte no ambiente da população.
Análise de estabilidade.
Seja x o ponto de equilíbrio para (15) pela definição do ponto de equilíbrio, temos que
x =f(x) então
x =r x(1−x)
logo os pontos de equilíbrio são, x0= 0 e x2= 1−
1 r
Suponhamos que r > 1, então o ponto fixo x ∈ (0,1), e f′(x
0) = r e f′(x1) = 2−r pelo
critério de estabilidade o ponto de equilíbrio x0, se r <1, então o ponto é estável e se r = 1 o
critério não decide se o ponto é instável ou não.
Se1< r <4 dada uma condição inicialx0∈(0,1), entãof(x0)∈(0,1)portanto,|f′(x
1)|<
1 ⇔1< r <3 logo, x1 é assintoticamente estável, e se r > 3, x1 é instável.
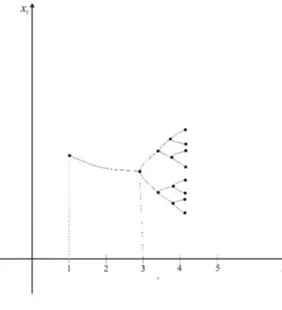
Ser = 3 existe um ponto de bifurcação(6), isto é, o valor do parâmetro muda de estado ou de equilíbrio.
Se1 < r <2, x1 é assintoticamente estável monotonicamente.
Se2 < r <3, x1 é assintoticamente estável oscilante.
Se3< r < 1 +√6,x1 possui duas órbitas de período 2, para achar os pontos fixos def2(x)
ou seja f2(x) =x, então
f(f(x)) =x ⇔r2x2−r(r + 1)x +r + 1 = 0
portanto x3,4 =
r + 1
2r ±
p
(r −3)(r + 1)
2r . Para analizar a estabilidade dos pontos x3, x4,
devemos aplicar o critério de estabilidade em |(f2(x
i))′| < 1 ou |(f2(xi))′| > 1 para i = 3,4,
isto é,|(f2(x
i))′|=|(f(f(x3)))′|=|f′(f(x3))f′(x3)|como as órbitas são de periodo 2, temos que
f(x3) =x4 então |f′(x4)f′(x3)|<1 tal que3 < r <1 +
√
6
Figura 6: bifurcação
No modelo de população (inibido) a função f deve ser descrecente a partir de um valor de
Seja a equação
Nt+1 =Nte γ(1−N
k) (16)
onde f(N) = Nte γ(1−N
k) então a função é decrecente a partir do valor N = k
γ e os pontos
de equilíbrio estão definidos em N = 0 e N =k
4.3 - Sistema de equações de Diferença Não Lineares
Seja o sistema de n equações de diferença não lineares dada na formaXt+1=F(Xt)
onde F : D ⊂ ℜn −→ ℜ, consideremos primeiro um sistema de duas equações de diferença,
isto é, n = 2, então o sistema é
xt+1 = f(xt, yt) yt+1 = g(xt, yt)
com f , g : D ⊂ ℜ2 −→ ℜ. Os pontos de equilíbrio ou pontos fixos estão definidos por
f(x, y) =x e g(x, y) =y
Agora analisaremos a estabilidade local destes pontos de equilíbrio, isto é, dado um valor
(xt, yt) próximo ao ponto (x, y). Potanto, teremos xt = x +xt′ e yt = y +yt′ e desenvolvendo
encontraremos,
x′
t+1=xt+1−x =f(xt)−x =f(x +xt′)−x y′
t+1=yt+1−y =g(yt)−y =g(y +yt′)−y
Fazendo expansão pela série de Taylor def na vizinhança deste ponto, temos que;
• f(x +x′
t, y +yt′) =f(x, y) +fx(x, y)xt′ +fy(x, y)yt′ +O(xt′2, yt′2)
• g(x +x′
t, y +yt′) = g(x, y) +gx(x, y)xt′+gy(x, y)yt′+O(xt′2, yt′2)
O novo sistema linearizado é
x′
t+1 = a11xt′ +a12yt′ y′
t+1 = a21xt′ +a22yt′
(17) Podemos escrever este sistema na forma matricial do tipo X′
t+1=AXt′, onde A=
fx(x, y) fy(x, y) gx(x, y) gy(x, y)
e X′
t =
x′
t y′
t
A matriz A é chamada Jacobiana do sistema.
Para analizar a estabilidade do sistema linearizado obtemos o polinômio caracteristico, fazendo
Então teremos que λ2−β+γ = 0, com
β =tr aA=fx +gy e γ =detA=fxgy −gxfy
Por último determinamos as raízes desta equação (os autovalores), são em magnitude menores que a unidade.
O seguinte critério é suficiente e necessário para o estabilidade do sistema. Portanto, como critério de estabilidade, podemos dizer que (x, y) é estável se e somente se
2 >1 +γ >|β| (18)
Prova:
Seja γ um ponto estável, isto é, γ <1 e temos que: P(λ) =λ2−βλ+γ = 0 ⇒ λ
1,2=
β 2 ±
p
(−β)2−4γ
2 ,
como|β|<2 ⇒ |β| 2 <1
1− |β| 2 >
p
(−β)2−4γ
2 ⇒
1− |β| 2
2
>
p
(−β)2−4γ
2
!2
⇒ 1 − |β|+ |β
2|
4 > β2
4 − 4γ
4 ⇒1− |β|>−γ ⇒ γ >|β| −1
Seção 5
Aplicação de Equações de Diferença Não Linear
5.1 - Sistemas não Lineares
Sejam as funções f , g :D ⊂ ℜ2→ ℜ e o sistema
S =
xt+1 = f(xt, yt)
yt+1 = g(xt, yt) (19)
Vamos realizar um estudo qualitativo de(S), seu equilíbrio e sua estabilidade. Dizemos que(x, y) é ponto de equilíbrio do sistema (19) se e somente se:
S =
x = f(x, y) y = g(x , y).
E a estabilidade do sistema (19) do ponto (x, y)é dado por: f(x +x′, y +y′) =f(x, y) +f
x(x , y)x′+fy(x, y)y′ +R1(x, y).
g(x +x′, y +y′) =g(x, y) +g
x(x, y)x′+gy(x, y)y′+R2(x, y).
Portanto o sistema (19) pode ser escrito como:
S =
xt+1 = f(xt, yt) yt+1 = g(xt, yt).
ou
S =
x′
t+1 = a11xt′−a12yt′ y′
t+1 = a21xt′−a22yt′.
Também sobre a forma matricial seria
S =
x′
t+1
y′
t+1
=
a11 a12
a21 a22
xt yt
.
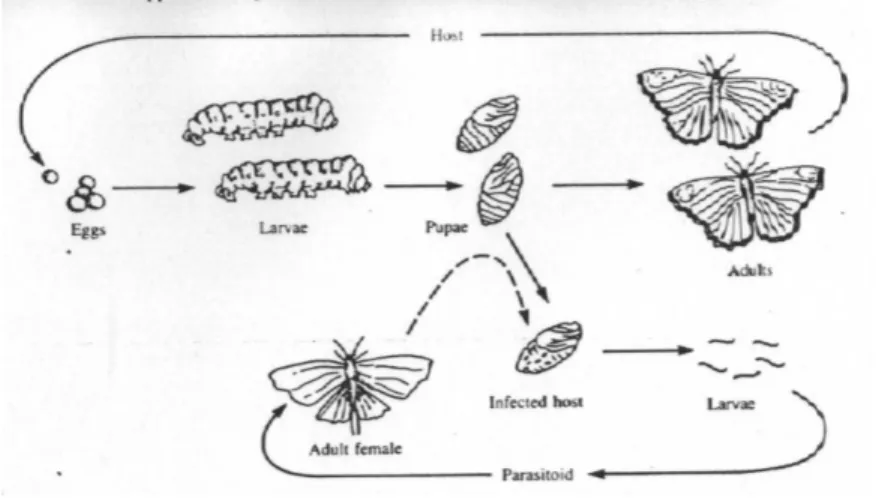
Encontrado quase exclusivamente no mundo dos insetos, na qual o sistemas de duas espécies têm várias características distintas. Essa espécie têm um número de fases no seu ciclo de vida que inclui as fases de ovos, Larvas, Pupa e adultos. Uma delas é chamada de parasita, explora a segunda da seguinte forma: Uma fêmea adulta parasita estuda o hospedeiro na qual a oviposita (depositar seus ovos). Em alguns casos, os ovos são anexados à superfície exterior do hospedeiro durante seu estágio de pupa ou larva. Em outros casos, os ovos são injetados no corpo (na carne) do hospedeiro. As larvas do parasita se desenvolve e cresce à custa do seu hospedeiro, consumindo-o e eventualmente acaba matando. Os ciclos de vida das duas espécies, mostrado na figura abaixo, são, portanto, intimamente interligadas.
Figura 7: hospedeiro-parasita
Um modelo simples para este sistema tem o seguinte conjunto de restrições: 1. Hospedeiros que foram parasitados darão origem à próxima geração de parasitas;
2. Hospedeiros que não foram parasitados darão origem à sua própria prole;
3. A fração dos hospedeiros que são parasitados depende da taxa de encontro das duas espécies em geral, esta fração pode depender da densidade de uma ou de ambas as espécies. Enquanto outros efeitos provocam mortalidade encontrada em todo o sistema natural, é instrutivo considerar apenas este conjunto mínimo de primeiros encontros e examinar as suas conseqüências. Estamos, portanto, definindo o seguinte:
Nt = quantidade de hospedeiros na geração t; Pt = quantidade de parasitas na geraçãot;
c = número médio de ovos depositados por um parasita em um único hospedeiro.
Esses três pressupostos conduz a:
Nt+1=número de hospedeiros na anterior geração x fração não parasitados x taxa reprodutiva(λ).
Pt+1=número de hospedeiros parasitados na anterior geração X fecundidade de parasitóides
(c).
Observando que 1−f é a fração de hospedeiros que são parasitados, obtemos:
S =
Nt+1 = λNtf(Nt, Pt)
Pt+1 = cNt(1−f(Nt, Pt)) (20)
Essas equações esboçam um quadro geral do modelo hospedeiro-parasita. Para prosseguir, é necessário especificar em termos de f(Nt, Pt) e como ela depende das duas populações. Na
próxima seção examinaremos uma determinada forma sugerida pelo Nicholson E Bailey (1935).
5.1.1 - O Modelo de Nicholson-Bailey
A.J. Nicholson foi um dos primeiros biólogos a sugerir o sitema hospedeiro-parasita que poderia ser entendida utilizando um modelo teórico, embora apenas com a ajuda do físico V.A. Bailey que seus argumentos foram desenvolvidos com o rigor matemático.
Nicholson e Bailey estruturaram mais duas hipóteses sobre o número de encontros e a taxa de parasitismo de um hospedeiro:
• 4. Encontros ocorrem aleatoriamente. O número médio de encontros Ne dos hospedeiros
com os parasitas é, portanto, proporcional ao produto da sua densidade.
Ne =aNtPt,
onde a é uma constante, que representa a busca da eficiência dos parasitas.
• 5. Apenas o primeiro encontro entre o hospedeiro e o parasita é levado em conta.
A distribuição de Poisson é a que descreve a probabilidade de ocorrência de eventos discretos, aleatoriamente (como o encontro entre um predador e suas presas). A probabilidade de que um certo número de eventos irá ocorrer em algum intervalo de tempo (como o tempo de vida do hospedeiro) é dado pelos sucessivos termos nesta distribuição. Por exemplo, a probabilidade de
r eventos é
Pr = e− uµr
r!
Onde µ é o número médio de eventos de um determinado intervalo de tempo.
No caso de encontros entre hospedeiro-parasita, o número médio de encontros por hospedeiro por unidade de tempo é
µ= Ne Nt
Assim, por exemplo, a probabilidade de exatamente dois encontros seria dada por
P2=
e−aPt(−aP
t)2 2!
A probabilidade de um parasita escapar é a mesma que a probabilidade de zero encontros durante o acolhimento da vida, ou seja p(0). Assim,
f(Nt, Pt) =p(0) = e−
aPt(−aP
t)0
0! =e−
aPt
Portanto, substituíndo no sistema (20) teremos
S =
Nt+1 = λNte−aPt Pt+1 = cNt(1−e−aPt)
Vamos agora analisar esse modelo, os passos incluem:
• 1. Encontrar os coeficientes da matriz Jacobiana (para o sistema linearizado);
• 2. Analisar a estabilidade do sistema.
Modelo Nicholson-Bailey: Equilíbrio e Estabilidade Seja
F(Nt, Pt) =λNte−aPt G(Nt, Pt) =cNt(l−e−aPt).
Ao estudar os estágios estáveis, obtemos a solução triviaisP =N = 0, para outro ponto de equilíbrio, pelo ponto fixo, teremos que,
F(Nt, Pt) = Nt G(Nt, Pt) = Pt ⇔
λe−aPt = 1
cNt(1−e−aPt) = P
t.
Desenvolvendo este sistema encontramos:
λe−aPt = 1 ⇒e−aPt = 1
λ ⇒ −aPt =ln
1
λ
⇒ −aPt =−ln(λ) ⇒Pt =
ln(λ)
a
e
cNt
1− 1 λ
=Pt ⇒cNt
1− 1 λ
=
ln(λ) a
⇒ Nt =
λln(λ) ac(λ−1)
.
Nt =
λln(λ)
ac(λ−1)
.
Pt =
ln(λ)
a
.
Portanto temos dois ponto de equilíbrio P1 = (0,0) e P2 = (N, P), para analisarmos
1. ∂F
∂N =λe
−aP
2. ∂F
∂P =−aλNe− aP
3. ∂G
∂N =c(1−e
−aP)
4. ∂G
∂P =acNe
−aP.
Para o primeiro pontoP1= (0,0), encontraremos:
∂F
∂N(0,0) =λ , ∂F
∂P(0,0) = 0 ∂G
∂N(0,0) = 0 , ∂G
∂P(0,0) = 0
A matriz Jacobiana é,
J1=
λ 0 0 0
(21) desta matriz temos que:
det(J1) =γ1= 0
e
tr(J1) =β1 =λ
Portanto temos queP1 é estável ⇔ |λ| ≤1, masλ <1⇒P < 0.
Para o segundo ponto P2(N, P), encontraremos:
∂F
∂N(N, P) = 1 , ∂F
∂P(N, P) = −aN ∂G
∂N(N, P) =c
1− 1 λ
, ∂G
∂P(N, P) = caN
λ
A matriz Jacobiana é,
J2 =
1 −aN
c
1− 1 λ
caN λ
(22)
desta matriz temos que:
det(J2) =γ2=
caN
λ − −aN
c
1− 1 λ
(23) e
tr(J2) =β2= 1 + caN
Podemos desenvolver a equação 23 para verificar a estabilidade,γ2 será:
γ2 =
caN
λ − −aN
c
1− 1 λ
γ2 =
ca
λln(λ)
ac(λ−1)
λ −
−a
λln(λ)
ac(λ−1) c
1− 1 λ
γ2 =
ln(λ) λ−1 +
λln(λ) (λ−1)
λ−1 λ
γ2 =
ln(λ)
λ−1 +ln(λ)
γ2 = ln(λ) + (λ−1)ln(λ) λ−1
γ2 =
ln(λ) + (λln(λ)−ln(λ) λ−1
γ2 =
λln(λ) λ−1
e β2 temos,
β2= 1 +
caN λ
β2= 1 +
ca
λln(λ)
ac(λ−1)
λ β2= 1 +
ln(λ) λ−1
Vamos mostrar que γ2 > 1, para isto precisamos mostrar que
λln(λ)
λ−1 >1, ou seja H(λ) = λ−1−λln(λ) <0
Observe ainda queH(1) = 1−1−1ln(1) = 0e queH′(λ) = 1−ln(λ)−λ
1
λ
=−ln(λ)<0,
para λ ≥ 1, portanto a função H(λ) é decrescente e H(λ) < 0 para λ ≥ 1, mas por γ2 e β2
λ6= 1, entãoλ >1.
Pelo critério de estabilidade 18, temos que2 >1 +γ >|β|, mas λ≥1, logo o ponto P2não
é estável.
Seção 6
Modelos Contínuos
6.1 - Modelos Contínuos
OS modelos contínuos são problemas matemáticos no qual estaremos dando um tratamento diferencial, portanto são problemas escritos sob a forma de equações diferenciais. Uma equação diferencial linear de primeira ordem é apresentada na forma
dx
dt =f(x) (25)
Exemplo 9 Modelo Populacional.
Seja x(t) o tamanho de uma população, então, a taxa de crescimento é proporcional ao
tamanho na população em um tempo t portanto dx
dt = γx onde γ > 0 e sua solução é dada
pela equação x(t) = x0eγt e o ponto de equilíbrio é em x = 0
6.2 - Modelos Matemáticos com Equações Diferenciais
Os primeros modelos matemáticos que apareceram envolvendo equações diferenciais ordinar-ias foram:
• Decaimento radioativo • Dinâmica de populacional
• Resfriamento térmico
• Difusão através de uma menbrana 6.2.1 - Decaimento Radioativo
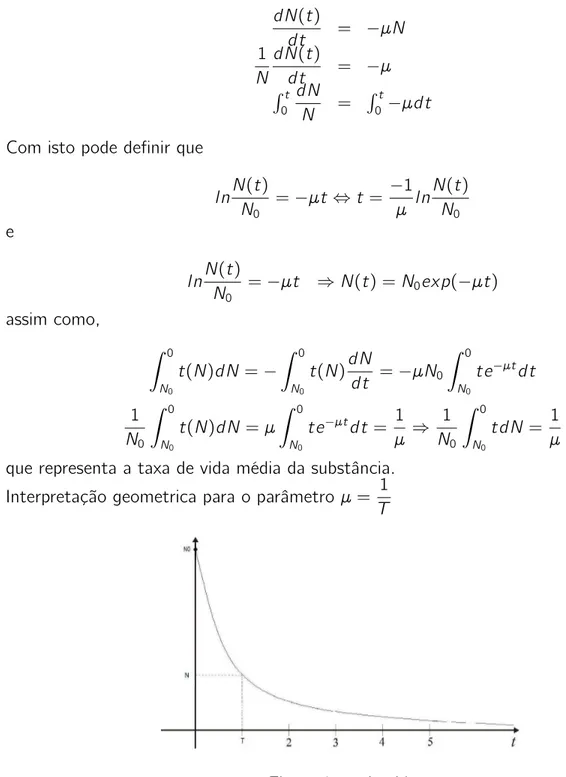
Uma substância radiotiva desintegra-se proporcionalmente da sua quantidade presente. Seja
N(t) a quantidade da substância, então dN(t)
dt = −µN, µ > 0 e 1 N
dN(t)
dt = −µ é a taxa de
variação especifica. O estudo da unidade é importante para o parâmetro µ. Analise dimensional
[N] =P ⇒População
[t] =T ⇒Tempo
dN dt
= P T
[µ] = 1 P
P T =T
−1 ou
1 µ
=T
A vida média de uma substância é dada pela razão 1
dN(t)
dt = −µN
1 N
dN(t)
dt = −µ
Rt
0
dN
N =
Rt
0 −µdt
Com isto pode definir que
lnN(t)
N0 =−µt ⇔t =
−1 µ ln
N(t) N0
e
lnN(t)
N0 =−µt ⇒N(t) =N0exp(−µt)
assim como,
Z 0
N0
t(N)dN =−
Z 0
N0
t(N)dN
dt =−µN0
Z 0
N0
te−µtdt
1 N0
Z 0
N0
t(N)dN =µ
Z 0
N0
te−µtdt = 1
µ ⇒
1 N0
Z 0
N0
tdN = 1 µ
que representa a taxa de vida média da substância. Interpretação geometrica para o parâmetroµ = 1
T
Figura 8: meia vida
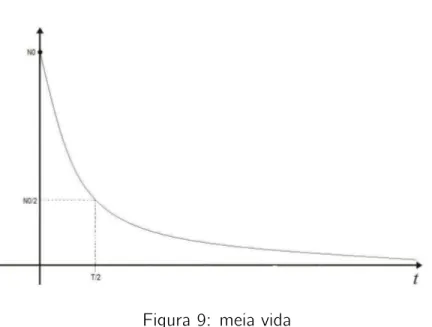
Meia vida (T1/2): O tempo necessário para que a radiação de uma amostra se reduza a
metade N0
2 é dada por:
N(t) = N0exp(−µt)
N0
2 = N0e
−µT1/2
Figura 9: meia vida
Exercício 2 Nas ecavações arqueológicas da cidade de Nipur (Antiga Babilónia) foi encontrada uma viga carbonizada com uma atividade de 4,09 dpm/g. Usando para o carvão recente de 6,7 dpm/g. Calcule quando se de tal incêndio na antiga cidade.
Solução Usando t1
2 = 5,730 anos para c
14 temos:
λ= 0,12×10−3 anos
m(t) = 4,09 dpm/g m0 = 6,7 dpm/g
λ= 0,000121
m(t) =m0e−λt substituíndo, teremos:
4,09 = 6,7×e−0,000121t 4,06
6,7 =e−
1,21·10−4
t
ln
4,06 6,7
=−1.21·10−4t
ln(0,606) = 0,000121·t =⇒t ∼= 4139,5 anos
Exercício 3 Távola Redonda
A enorme mesa redonda presa as paredes do castelo de wincherster - e que é mostrada aos crédulos turistas como sendo famosa "Távola redonda"do rei Artur - apresentou em 1977 uma atividade de 6,08dpm/g. Sabendo que a atividade da madeira viva da região é de6,68dpm/g,
verifique se esta mesa serviu de fato para os cotovelos do Rei e dos seus ledáiros cavaleiros Lancelot, Galahad, Gwain, Percival etc. Do pouco que se sabe dessa famosa confraria, uma coisa é certa: viveram no século V.
Usando t1
2 = 5,730anos para c
14 temos:
λ= 0,12×10−3 anos
m(t) = 6,08 dpm/g m0 = 6,68 dpm/g λ= 0,000121
m(t) =m0e−λt substituíndo, teremos:
6,08 = 6,68×e1,21·10−4t 6,08
6,68 =e
1,21·10−4
t
ln
4,
06 6,7
=−1.21·10−4t
ln(0,6910176) =−0,000121·t =⇒t ∼= 777,8 anos
Exercício 4 Um indivíduo é encontrado morto em seu escritório pele sua secretária que liga imediatamente para a polícia. Quando a polícia chega, duas horas depois da chamada, examina o cadáver. Uma hora depois o detetive prende a secretária, porquê?
Solução A temperetura do escretório era de20o
c. Quando a polícia chegou, mediu o defunto, achando 35oc. Uma hora depois mediu novamente,34,2oc. Supondo que a temperatura normal
de uma pessoa viva seja constante e igual a 36,5o
c, temos: T(0) = 36,5
T(t∗) = 35 t∗ tempo decorrido desde o instante da morte
T(t∗+ 1) = 34 é a temperatura da vítima mais uma hora depois que a polícia chegou. A questão de resfriamento para esse caso é:
Equação do resfriamento do corpo
T(t) = (T0−Ta)e−λt+Ta T(t) = (36,5−20)e−λt+ 20
35 = 16,5e−λt∗ + 20 34,2 = 16,5e−λ(t∗+1)
+ 20
15 16,5 =e
−λt∗ 14,2
16,5 = 16,5e
−λ(t∗+1)
Resolvendo o sistema, temos: 15
14,2 = 1
e−λ =⇒e
λ = 1×0,056338
dondeλ= 0,05481
Portanto,t∗ =
−ln
15 16,5
λ = 1,73898h
Quais seriam as medidas corretas obtidas pelo logista para termos uma melhor aproximação da realidade?
t− ∞= 6 horas 6 = 1
λln
100 (20
−36,5) 20
Ou seja
λ= 1,36 =⇒t∗ = 1,7389, fazemos
T(t∗) = 16,5e−1,36·1,7389+ 20≈21,55o
c T(t∗+ 1) = 16,5e−1,36+2,7389+ 2 ≈20,39o
c
Suponha que o indivíduo assassinado estivesse com febre quando morreu, ainda possível descobrir o instante da sua morte?
Solução Supondo:
T(0) = 36,5
T(t∗) = 38t∗ tempo decorrido desde o instante da morte
T(t∗+ 1) = 37,2 é a temperatura da vítima mais 1 hora depois que a polícia chegou.
T(t) = (36,5−20)e−λt+ 20
38 = 16,5e−λt∗ + 20 34,2 = 16,5e−λ(t∗+1)
+ 20
18 16,5 =e
−λt∗ 14,2
16,5 = 16,5e− λ(t∗+1)
1,09 =e−λt∗
0,86 = 16,5e−λ(t∗+1)
⇐⇒ 1,0,0986 =e−λt∗
·eλt∗ eλ
=⇒1,26744186 =eλ
λ= 1,16744186 = 0,2370006 =⇒ 18
16,5 =e− λt∗
=⇒ln 18
16,5 =−λt∗ =⇒ 0,087011376
0,2370006 = 36,71
Método de Separação de Variáveis Seja dy
dt =g(y)h(t), desejamos:
1. Achar as soluções constantes: g(y) = 0
2. Achar as soluções não constantes: g(y)6= 0
Temos dy
dt =g(y)h(t)⇔
R dy
g(y) =
R
h(t)dt
Exemplo 10 Para a equação dN
dt =−µN+K, ondeg(N) =−µN +K e h(t) = 1,∀t ≥0.
1. soluções constantes: g(N) = 0⇔ −µN+K = 0⇒N = K
µ,∀t ≥0
2. soluções não constantes: g(y)6= 0 dN
K−µN =dt ⇒
R dN
K−µN =
R
dt ⇒ln(K−µN) =−µt−µC ⇔K−µN =e−µtC ⇒
⇒N(t) = K µ +
A µe−
µt
Se N(0) =N0⇒N(t) =
1
µ(K−(K−µN0)e
−µt)
6.2.2 - Dinâmica Populacional
Seja P(t) o tamanho da população de um país num instante t. Num intervalo de tempo ∆t, a Lei de Malthus (1789) pressupõe que os nascimentos e as mortes são proporcionais ao tamanho da população e ao tamanho do intervalo.
Seja:
N =γP(t)∆t número de nascimentos;
M =µP(t)∆tnúmero de mortes; γ é o coeficiente de natalidade; µ o de mortalidade;
1
µ é o tempo meia-vida de um individuo pertenecente a esta população; γ
µ é o número meio de nascimentos sobre o tempo de vida de um individuo.
Assim,
∆P = P(t+ ∆t)−P(t) ∆P = γP(t)∆t−µP(t)∆t ∆P = (γ−µ)P(t)∆t ∆P
∆t = (γ−µ)P(t)
Fazendo com que ∆t →0, obtemos, da equação de diferença, a equação diferencial dP dt = (γ−µ)P(t) que nos diz que a taxa de variação de uma população é proporcional a população
em cada instante.
A solução desta é dada pela equação
P(t) = P0e(γ−µ)t
P(0) = P0
1. Se γ =µ, então a população não varia.
2. Se γ > µ, então a população cresce exponencialmente com o tempo.
3. Se γ < µ, então a população diminui e tende à extinção à medida que t cresce.
γ =µ γ > µ γ < µ
Se consideramos que os recursos da população são limitados, o crescimento da população num intervalo de tempo é reduzido de uma quantidade proporcional ao quadrado da população existente no início do intervalo. De fato, se existe uma competição entre elementos de uma mesma espécie, o termo de inibição do crescimento populacional é proporcional ao produto destes elementos. Então a equação de Malthus modificada é a equação logística,
dP
dt = (λ−aP(t))P(t)
Introduzido pela primeira vez por Verhulst (1838) e estudada por Pearl e L. J. Redd (1920). Pode-se escrever a equação da seguinte forma:
dP
dt =γP(t)
1− P(t) K
Os parâmetros γ = λ, K = λ
a com γ > 0 é dito taxa de crescimento intrinsico por que
representa a taxa per capita e K >0 onde K é a capacidade do suporte da população. Desenvolvendo o processo de separação de variáveis teremos, e observando que
1
P(K−P) = 1 K
1 P +
1 K−P
:
R dP
P(K−P) = γ K
R
dt
R 1
KPdP +
R 1
K(K−P)dP = γ K
R
dt 1
KlnP − 1
Kln(K−P) = γ Kt+C 1
Kln
P K−P
= γ
Kt+C
onde C é uma constante de integração.
P(t) = KP0
P0+ (K−P0)e−γt
A solução é valida no sentido biológico para 0 < P0 < K, e o tamanho da população Pt → K
quando t → ∞.
6.2.3 - Resfriamento de um Corpo - Propagação de Calor
Um corpo que não possui internamente nenhuma fonte de calor, quando deixado em um meio ambiente na temperatura T, tende áquela do meio que o cerca Ta. Assim, se a temperatura T < Ta, este corpo se aquecerá e, caso contrário, se resfriará.
A temperatura do corpo, considerada uniforme, será pois uma função do tempo T = T(t).
Verifica-se experimentalmente que quanto maior for o valor |T−Ta|mais rápida será a variação
de T(t).
Isto é evidenciado de forma precisa pela chamadaLei de resfriamento enunciada por I. New-ton: A taxa de variação da temperatura de um corpo é proporcional à diferença entre sua temperatura e a do meio ambiente.
Então colocando em termos matemáticos temos que
dT
dt =µ(Ta−T) =f(T)
onde µ >0 pois se T < Ta então dT
dt >0 e se T > Ta, dT
dt <0.
Observe que T = Ta é solução da equação f(T) = 0 e significa que se a temperatura do
corpo for igual à temperatura ambiente, então ela não variará. A solução geral da equação diferencial é dada por:
T(t) =Ta+Ce−µt
Usando T(0) =T0, obtemos a equação T(t) = (T0−Ta)e−µt+T a
Neste modelo matemático, a temperatura do corpo só atinge a temperaturaTa no limite em
que t →+∞; entretanto, na realidade, a temperatura ambiente é atingida num tempo finito.
No exemplo, podemos chamar det∞ o tempo necessário para queT atinja 0,99 deTa. Em
termos numéricos, isto significa que se o erro relativo de 0,01 ou menos, podemos considerar
T(t) como sendo praticamente Ta. Assim,
±10099 Ta = (T0−T a)e−µt∞+Ta
e−µt∞ =
Ta 100(Ta −T0)
−µt∞ = ln
Ta 100(Ta−T0)
t∞ = 1 µln
100(Ta−T0) Ta
6.3 - Equilíbrio e Estabilidade
Definição 7 x é um ponto de equilíbrio para (25) sef(x) = 0.
Exemplo 11 Se uma população inicialx0=x então a solução da equação diferencial é dada por
x(t) =x ∀t.
6.3.1 - Análise de Estabilidade dos Pontos de Equilíbrio.
Um equilíbrio x de (25) é dito estável se para todo ǫ > 0, existe δ > 0 tal que, para todo
|x0−x|< δ, a solução,x(t, x0) obedece |x(t, x0)−x|< ǫ∀t ≥t0, caso contrário, x é chamado
de instável.
x é assintoticamente estável se for estável elimt→∝|x(t, x0)−x|= 0 se|x0−x|< γ
Para determinar se um ponto de equilíbrio é estável ou não, podemos usar o seguinte teorema. Teorema 4 Suponhamos que f ∈C1 e x é um ponto de equilíbrio de (25). Então x é
assimtot-icamente estável se f′(x) <0 e instável se f′(x)>0 .
Seja y =x −x e y′ =x′ onde x é constante. Considere dx
dt = f(x) ⇔ dy
dt = f(x +y) ≡ f(x) +f
′(x)y = f′(x)y ⇒ dy
y = f
′(x)dt, temos que o equilíbrio def(x) = x ⇔equilíbrio def(x+y) = 0⇒equilíbrio def′(x)y portanto
dy
dt = f′(x)y ⇒ y(t) = Ae f′(x)t
como dy
dt = dx
dt = f(x) se fizermos x = y +x temos que o
equilíbrio de f(x +y) é também de f′(x)y
Observação 3 dx
dt =f(x) ⇒ dx
dt =f(x)x esta segunda equação é chamada de linearização de
Exemplo 12 Seja a equação de Verhulst
dy
dt =ay(K−y)
os pontos de equilíbrio sãoy = 0 ou y =K⇒f(y) =aKy−ay2, onde a e K são positivos,
logo temos que:
f′(y) = aK −2ay = 0 e f′(0) = aK > 0 ⇒ y = 0 portanto o ponto é instável e para
f′(K) = aK−2aK =−aK <0 ⇒y =K é assimtóticamente estável. A Equação de Gompertz dada por
dy
dt =−ay
lny K
com a >0 e y > K, os pontos de equilíbrio da equação sãoy 6= 0 ouy =K, então temos que: f(y) =−aylny
K
f′(y) =−alny
K
−ayK y
1 K f′(y) =−alny
K
−a
temos que, para y = K então f′(y) = f′(K) = −a
lnK K
− a = −a < 0 portanto, f′(y) =−alny
K
−a logo f′(K) = −a é estável.
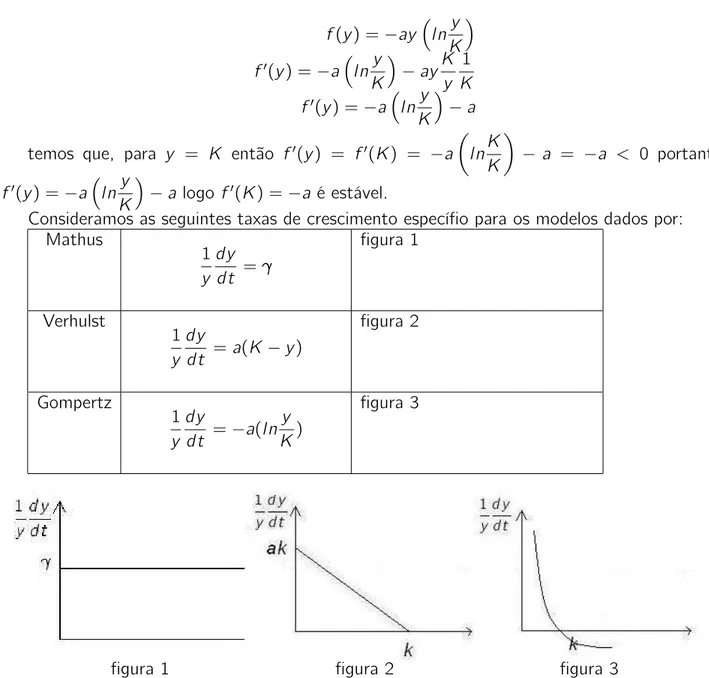
Consideramos as seguintes taxas de crescimento específio para os modelos dados por: Mathus
1 y
dy dt =γ
figura 1
Verhulst
1 y
dy
dt =a(K−y)
figura 2
Gompertz
1 y
dy
dt =−a(ln y K)
figura 3
6.3.1 - Crescimento Específico ou Lei da Alometria
Nem todas as partes do corpo de um inivíduo têm em cada instante um desenvolvimento proporcional. A cabeça de uma criança cresce mais lentamente que seu corpo. O rápido cresci-mento dos pés de um adolescente, comparado com o resto de seu corpo, causa muitas vezes alguns transtornos. A alometria estuda estes diferentes padrões de crescimento. O tamanho de um orgão pode ser a medida do seu volume, peso, comprimento ou área lateral.
Sejam x = x(t) e y = y(t) os tamanhos de órgãos ou partes do corpo distintos de um
mesmo individuo, num instante t.
A Lei da Alometria establece que, no mesmo indivíduo, os crescimentos específicos de seus órgãos são proporcionais. Logo o modelo matmático é:
1 x
dx dt =α
1 y
dy dt
Separando as variáveis e integrando, obtemos
lnx =αlny +lnC
com C >0 ou x =Cyα
Exemplo 13 Crescimento de peixes
O peso de um peixe cresce proporcionalmente à sua áreaA(t) e descrece proporcionalmente
ao próprio peso. Seja P(t) o peso do peixe em um tempo t, então a equação metemática é:
dP
dt =αA(t)−βP(t)
onde α e β são as taxa de anabolismo e cotabolismo, respectivamente.
Equação de Vor Bertalanffy
1 A
dA dt =C
1 P
dP dt
integrando, obtemos A(t) = K(P(t))C e portanto dP
dt = a(P(t))
C −βP(t), onde a= αK
e o valor de C ∼= 2
3 logo a equação diferencial não linear é: dP
dt =a(P(t)) 2
3 −βP(t)
e os pontos de equilíbrio são P1 = 0 ouP2= (
a β)
3 ef′(P) = 2
3aP
−1
3 −β ⇒f′(P
2) =−
1 3β < 0