Estudo Sobre a Escolha Estatística de Modelos Extremais na Metodologia POT

(1)

António Miguel Nunes Gomes

MESTRADO EM MATEMÁTICA

Estudo Sobre a Escolha Estatística

de Modelos Extremais na Metodologia POT

DISSERTAÇÃO DE MESTRADO

fevereiro_|2017

DM

(2)

António Miguel Nunes Gomes

MESTRADO EM MATEMÁTICA

Estudo Sobre a Escolha Estatística

de Modelos Extremais na Metodologia POT

DISSERTAÇÃO DE MESTRADO

ORIENTADORA

(3)

❏úr✐✿

❉♦✉t♦r❛ ❆♥❛ ▼❛r✐❛ ❈♦rt❡sã♦ P❛✐s ❋✐❣✉❡✐r❛ ❞❛ ❙✐❧✈❛ ❆❜r❡✉

✕ Pr♦❢❡ss♦r❛ ❆✉①✐❧✐❛r ❞❛ ❯♥✐✈❡rs✐❞❛❞❡ ❞❛ ▼❛❞❡✐r❛

❉♦✉t♦r❛ ❙❛♥❞r❛ ▼❛r✐❛ ❋r❡✐t❛s ▼❡♥❞♦♥ç❛

✕ Pr♦❢❡ss♦r ❆✉①✐❧✐❛r ❞❛ ❯♥✐✈❡rs✐❞❛❞❡ ❞❛ ▼❛❞❡✐r❛

❉♦✉t♦r❛ ❉é❧✐❛ ❈❛♥❤❛ ●♦✉✈❡✐❛ ❘❡✐s

(4)

❆❣r❛❞❡❝✐♠❡♥t♦s

❆ ❡❧❛❜♦r❛çã♦ ❞❡st❛ ❞✐ss❡rt❛çã♦ ❞❡ ▼❡str❛❞♦ ❝♦♥t♦✉ ❝♦♠ ♦ ❛♣♦✐♦ ❡ ✐♥❝❡♥t✐✈♦s ❝r✉❝✐❛✐s ❞❛s ♣❡ss♦❛s q✉❡ s❡♠♣r❡ ❛❝r❡❞✐t❛r❛♠ ❡♠ ♠✐♠ ❞❡s❞❡ ❛ ♠✐♥❤❛ ❡♥tr❛❞❛ ♥♦ ▼❡str❛❞♦ ❡♠ ▼❛t❡♠át✐❝❛ ❛té ❛♦s ❞✐❛s ❞❡ ❤♦❥❡✳ ❆ss✐♠✱ ❞❡✈♦ ❞✐③❡r q✉❡ s❡♠ ♦ ✈♦ss♦ ❛♣♦✐♦ ♥ã♦ t❡r✐❛ ❝♦♥s❡❣✉✐❞♦ ❝♦♥❝r❡t✐③❛r ❡st❛ ✐♠♣♦rt❛♥t❡ ❡t❛♣❛ ❞❛ ♠✐♥❤❛ ✈✐❞❛✳

❉❡st❛ ❢♦r♠❛✱ q✉❡r♦ ❛❣r❛❞❡❝❡r✿

❼ ❆♦s ♣r♦❢❡ss♦r❡s ♣❡❧♦s ❝♦♥❤❡❝✐♠❡♥t♦s tr❛♥s♠✐t✐❞♦s ❛♦ ❧♦❣♦ ❞♦ ▼❡str❛❞♦ ❡ q✉❡ ❡♠ ♠✉✐t♦ ❝♦♥tr✐❜✉ír❛♠ ♣❛r❛ ♦ ♠❡✉ ❡♥r✐q✉❡❝✐♠❡♥t♦ ✐♥t❡❧❡❝t✉❛❧ ❡ ♣❡ss♦❛❧❀

❼ ❆♦s ♠❡✉s ❢❛♠✐❧✐❛r❡s q✉❡ s❡♠♣r❡ s❡ ♠♦str❛r❛♠ ♦r❣✉❧❤♦s♦s ❝♦♠ ♦s ❢❡✐t♦s ❛❝❛❞é♠✐❝♦s ♣♦r ♠✐♠ ❛❧❝❛♥ç❛❞♦s✱ ♥♦♠❡❛❞❛♠❡♥t❡ ♦s ♠❡✉s ♣❛✐s ❡ ✐r♠ã♦s ♣❡❧❛ tr❛♥s♠✐ssã♦ ❞❡ ❝♦♥✜❛♥ç❛ ❡ ♠♦t✐✈❛çã♦ ♣❛r❛ ✜♥❛❧✐③❛r ❡st❡ ❝✉rs♦❀

❼ ❆♦s ♠❡✉s ❣r❛♥❞❡s ❛♠✐❣♦s ❡ ❝♦❧❡❣❛s ❞❡ ❝✉rs♦ ■✈♦ ❋❡rr❡✐r❛✱ ❉✉❛rt❡ ❙♦✉s❛ ❡ ❱ít♦r ❏❡s✉s q✉❡ s❡ ♠♦str❛r❛♠ ❞❡ ✈✐t❛❧ ✐♠♣♦rtâ♥❝✐❛ t❛♥t♦ ♣❡❧♦ ❛♣♦✐♦ ❝✉rr✐❝✉❧❛r q✉❡ ♠❡ ❞❡r❛♠ q✉❡r ♣❡❧♦ ❝♦♠♣❛♥❤❡✐r✐s♠♦✳ ❚❡♥❤♦ ❛ ❞✐③❡r q✉❡ ❢♦✐ ✉♠ ❡♥♦r♠❡ ♣r❛③❡r t❡r ❢❡✐t♦ ❡st❡ ❝✉rs♦ ❝♦♠ ✈♦❝ês❀

❼ ➚ ♠✐♥❤❛ ❛♠✐❣❛ ❉❡✐s❡ ❋❛r✐❛ q✉❡ ♠❡s♠♦ ♥ã♦ t❡♥❞♦ ❢❡✐t♦ ♦ ❝✉rs♦ ❝♦♠✐❣♦ s❡♠♣r❡ s❡ ❞✐s♣♦♥✐❜✐❧✐③♦✉ ❛ ❛❥✉❞❛r✱ ♥♦♠❡❛❞❛♠❡♥t❡ ❝♦♠ ❛ ❧í♥❣✉❛ ✐♥❣❧❡s❛✱ ❡ ❛ q✉❡♠ ♠✉✐t♦ ❞❡✈♦ ❛❣r❛❞❡❝❡r ♣♦✐s ❛ s✉❛ ❛❥✉❞❛ ❢♦✐ ❢✉♥❞❛♠❡♥t❛❧❀

❼ ➚ ♠✐♥❤❛ ❛♠✐❣❛ ❡ ❝♦♠♣❛♥❤❡✐r❛ ❞❡ ❡st✉❞♦ ♥❛ r❡t❛ ✜♥❛❧ ❞❡st❛ ❞✐ss❡rt❛çã♦ ❚â♥✐❛ P✐♥t♦ ♣❡❧♦ s❡✉ ❛♣♦✐♦ ❡ tr❛♥s♠✐ssã♦ ❞❡ ♠♦t✐✈❛çã♦ ♣❛r❛ ♦s ❡st✉❞♦s ❛♣ós ✉♠ ❞✐❛ ❞❡ tr❛❜❛❧❤♦✱ ♠✉✐t❛s ✈❡③❡s ❝❛♥s❛t✐✈♦❀

❼ ➚ ❈❛t❛r✐♥❛ ❘❡❜♦❧♦ ❡ ❈❧❡♦❞✐❝❡ ❋❡r♥❛♥❞❡s✱ ❛♠✐❣❛s ❞❡ ❧♦♥❣❛ ❞❛t❛✱ q✉❡ s❡♠♣r❡ ♠❡ ♠♦t✐✈❛r❛♠ ❡ ✐♥❝❡♥t✐✈❛r❛♠ ❛♦ ❧♦♥❣♦ ❞❡st❡ ❝✉rs♦❀

❼ ❆♦s ♠❡✉s ✈❡r❞❛❞❡✐r♦s ❛♠✐❣♦s q✉❡ ❞❡ ♠❛♥❡✐r❛ ❛❧❣✉♠❛ ❞❡✐①❛r❛♠ ❞❡ s❡ ♠♦str❛r ❞✐s♣♦♥í✈❡✐s ♣❛r❛ ❛❥✉❞❛r ❡ s❡♠♣r❡ ❞❡♣♦s✐t❛r❛♠ ❡♠ ♠✐♠ ♠✉✐t❛ ❝♦♥✜❛♥ç❛ ❡ ♦r❣✉❧❤♦✳

(5)

✐✈

◗✉❛♥t♦ ❛ ♠✐♥❤❛ ♦r✐❡♥t❛❞♦r❛✱ ❛ Pr♦❢❡ss♦r❛ ❉r✳➟ ❉é❧✐❛ ❈❛♥❤❛ ●♦✉✈❡✐❛ ❘❡✐s✱ t❡♥❤♦ ❛ ❞❛r✲❧❤❡ ♦ ♠❡✉ ♠❛✐♦r ❛❣r❛❞❡❝✐♠❡♥t♦ ♣♦✐s s❡♠ s✐ ♥❛❞❛ ❞✐st♦ s❡r✐❛ ♣♦ssí✈❡❧✳ ❆ Pr♦❢❡ss♦r❛ r❡✈❡❧♦✉✲s❡ ✉♠ ❛♣♦✐♦ ❢✉♥❞❛♠❡♥t❛❧ ♣❛r❛ r❡❛❧✐③❛çã♦ ❞❡st❡ tr❛❜❛❧❤♦ q✉❡ ♠❡ ❞❡✐①❛ ❝❤❡✐♦ ❞❡ ♦r❣✉❧❤♦✳ ❆ s✉❛ ❢♦r♠❛ ❞❡ ✐♥❝❡♥t✐✈❛r✱ ♠♦t✐✈❛r✱ ❡♥s✐♥❛r ❡ tr❛♥s♠✐t✐r ❝♦♥❤❡❝✐♠❡♥t♦✱ ❛❧✐❛❞♦ s✉❛ s✐♠♣❛t✐❛ ❡ ♣❛❝✐ê♥❝✐❛ ❢❛③❡♠ ❞❡ s✐ ✉♠❛ ❢♦r♠✐❞á✈❡❧ Pr♦❢❡ss♦r❛ ♣❛r❛ ❛❧é♠ ❞❡ ✉♠❛ ót✐♠❛ ♣❡ss♦❛✳ ❋✐❝♦ ✐♠❡♥s❛♠❡♥t❡ ❣r❛t♦ ♣♦r t✉❞♦ ♦ q✉❡ ❢❡③ ♣♦r ♠✐♠ ❡ ❡s♣❡r♦ ✉♠ ❞✐❛ ✈♦❧t❛r ❛ tr❛❜❛❧❤❛r ❝♦♥s✐❣♦✳

(6)

❘❡s✉♠♦

❆ ♥❡❝❡ss✐❞❛❞❡ ❞❡ ❡st✉❞❛r ❡ ❝♦♠♣r❡❡♥❞❡r ♦s ❡✈❡♥t♦s ❡①tr❡♠♦s q✉❡ s✉r❣❡♠ ♥❛s ♠❛✐s ❞✐✈❡rs❛s ár❡❛s ❞♦ ♥♦ss♦ q✉♦t✐❞✐❛♥♦ ❧❡✈♦✉ ❛♦ ❛♣❛r❡❝✐♠❡♥t♦ ❞❡ ❞✐❢❡r❡♥t❡s ♠❡t♦❞♦❧♦❣✐❛s ❞❡ ❡st✉❞♦ ❞❡ t❛✐s ❛❝♦♥t❡❝✐♠❡♥t♦s✳ ❯♠❛ ❞❡ss❛s ♠❡t♦❞♦❧♦❣✐❛s é ❛ ❞❡♥♦♠✐♥❛❞❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚✱ ♥❛ q✉❛❧ sã♦ ❛♥❛❧✐s❛❞♦s ♦s ✈❛❧♦r❡s q✉❡ ❡①❝❡❞❡♠ ✉♠ ❞❡t❡r♠✐♥❛❞♦ ♥í✈❡❧ ❡❧❡✈❛❞♦✳ ◆❡st❡ ❝♦♥t❡①t♦✱ ✉♠ ❞♦s ♣r♦❜❧❡♠❛s ❞❡ ❣r❛♥❞❡ ✐♠♣♦rtâ♥❝✐❛ ♥❛ ♣rát✐❝❛ é ❛ ❡s❝♦❧❤❛ ❞❛ ❞✐str✐❜✉✐çã♦ ❛ ✉t✐❧✐③❛r ♥❛ ♠♦❞❡❧❛çã♦ ❞❡ss❡s ✈❛❧♦r❡s ❡①tr❡♠♦s✳

❖ ♣r✐♥❝✐♣❛❧ ♦❜❥❡t✐✈♦ ❞❡st❛ ❞✐ss❡rt❛çã♦ é ❛ ❡❧❛❜♦r❛çã♦ ❞❡ ✉♠❛ ❝♦❧❡tâ♥❡❛ ❞❡ ♠ét♦❞♦s ❡st❛tíst✐❝♦s ❡①✐st❡♥t❡s ♥❛ ❧✐t❡r❛t✉r❛ ❝✐❡♥tí✜❝❛ r❡❧❛t✐✈❛ ❛♦ ♣r♦❜❧❡♠❛ ❞❛ ❡s❝♦❧❤❛ ❡♥tr❡ ❛ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ❡ ❛ ❞✐str✐❜✉✐çã♦ ❣❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❡①♣♦♥❡♥❝✐❛❧✳ ❆ r❡❛❧✐③❛çã♦ ❞❡ ✉♠❛ ❜r❡✈❡ ❛♥á❧✐s❡ ❞❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ é t❛♠❜é♠ ✉♠ ❞♦s ♦❜❥❡t✐✈♦s ❞❡st❡ ❡st✉❞♦✱ ❛ss✐♠ ❝♦♠♦ ❛ ❡①❡♠♣❧✐✜❝❛çã♦✱ ❝♦♠ r❡❝✉rs♦ ❛♦ s♦❢t✇❛r❡ ❡st❛tíst✐❝♦ ❘✱ ❞♦s ♣r♦❝❡❞✐♠❡♥t♦s ♥❡❝❡ssár✐♦s ♣❛r❛ ❛ r❡❛❧✐③❛çã♦ ❞♦s ♠ét♦❞♦s ❡st❛tíst✐❝♦s ❛♥❛❧✐s❛❞♦s✳

◆❡st❛ ❞✐ss❡rt❛çã♦ é r❡❛❧✐③❛❞❛ ✉♠❛ ❜r❡✈❡ ✐♥tr♦❞✉çã♦ à ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s✱ ❝♦♠ ♣r✐♥❝✐♣❛❧ ✐♥❝✐❞ê♥❝✐❛ ♥❛s ♠❡t♦❞♦❧♦❣✐❛s ❞❡ ●✉♠❜❡❧ ❡ P❖❚✳ ❆ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ é ❡st✉❞❛❞❛ ❝♦♠ ♠❛✐s ♣♦r♠❡♥♦r✱ s❡♥❞♦ ❞❛❞❛ ❛ ♠❡r❡❝✐❞❛ ✐♠♣♦rtâ♥❝✐❛ à ❡st✐♠❛çã♦ ❞♦s ♣❛râ♠❡tr♦s ❞❛s ❞✐str✐❜✉✐çõ❡s ❡①♣♦♥❡♥❝✐❛❧ ❡ ❣❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❡①♣♦♥❡♥❝✐❛❧✳ ❆ ♣❛r ❞❛ ❡st✐♠❛çã♦ ❞❡ ♣❛râ♠❡tr♦s✱ ❛ ❡st✐♠❛çã♦ ❞❡ q✉❛♥t✐s ❡①tr❡♠❛✐s é t❛♠❜é♠ ❛❜♦r❞❛❞❛ ❞❛❞❛ ❛ s✉❛ r❡❧❡✈â♥❝✐❛ ♥❛ ❣❡stã♦ ❞♦ r✐s❝♦✳ ❉❡ ❢♦r♠❛ ❛ s❡r r❡❛❧✐③❛❞❛ ✉♠❛ ❡s❝♦❧❤❛ ❡♥tr❡ ❛s ❞✐str✐❜✉✐çõ❡s ❡①♣♦♥❡♥❝✐❛❧ ❡ ❣❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❡①♣♦♥❡♥❝✐❛❧ sã♦ s✉❣❡r✐❞♦s ❛❧❣✉♥s ♠ét♦❞♦s ❡st❛tíst✐❝♦s q✉❡ ❛ss❡♥t❛♠ ❡♠ t❡st❡s ❞❡ ❤✐♣ót❡s❡s✱ ❡♠ ✐♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ❡ ❡♠ ♠ét♦❞♦s ❣rá✜❝♦s✳ ❉❡ ♠♦❞♦ ❛ ❡①❡♠♣❧✐✜❝❛r ❛ ❛♣❧✐❝❛çã♦ ❞❡st❡s ♠ét♦❞♦s ❡st❛tíst✐❝♦s✱ ❛ss✐♠ ❝♦♠♦ ❞♦s ❝♦♥❝❡✐t♦s ❡st✉❞❛❞♦s✱ é r❡❛❧✐③❛❞❛ ✉♠❛ ✐❧✉str❛çã♦ ♣rát✐❝❛ ♥❛ q✉❛❧ é ✉t✐❧✐③❛❞❛ ✉♠❛ ❜❛s❡ ❞❡ ❞❛❞♦s ❞❛ ár❡❛ ❞❛s ❋✐♥❛♥ç❛s✳

P❛❧❛✈r❛s✲❈❤❛✈❡✿ ▼❡t♦❞♦❧♦❣✐❛ P❖❚✱ ❉✐str✐❜✉✐çã♦ ❊①♣♦♥❡♥❝✐❛❧✱

❉✐str✐❜✉✐çã♦ ●❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❊①♣♦♥❡♥❝✐❛❧✱ ❚❡st❡s ❞❡ ❍✐♣ót❡s❡s✱ ■♥t❡r✈❛❧♦s ❞❡ ❈♦♥✜❛♥ç❛✱ ▼ét♦❞♦s ●rá✜❝♦s✳

(7)

(8)

❆❜str❛❝t

❚❤❡ ♥❡❡❞ t♦ st✉❞② ❛♥❞ ✉♥❞❡rst❛♥❞ t❤❡ ❡①tr❡♠❡ ❡✈❡♥ts t❤❛t ❛r✐s❡ ✐♥ t❤❡ ♠♦st ❞✐✈❡rs❡ ❛r❡❛s ♦❢ ♦✉r ❞❛✐❧② ❧✐❢❡ ❧❡❞ t♦ t❤❡ ❛♣♣❡❛r❛♥❝❡ ♦❢ ❞✐✛❡r❡♥t ❛♣♣r♦❛❝❤❡s ❢♦r t❤❡ st✉❞② ♦❢ s✉❝❤ ❡✈❡♥ts✳ ❖♥❡ ♦❢ t❤❡s❡ ❛♣♣r♦❛❝❤❡s ✐s t❤❡ P❖❚ ❛♣♣r♦❛❝❤✱ ✐♥ ✇❤✐❝❤ t❤❡ ✈❛❧✉❡s t❤❛t ❡①❝❡❡❞ ❛ ❤✐❣❤ t❤r❡s❤♦❧❞ ❛r❡ ❛♥❛❧②③❡❞✳ ■♥ t❤✐s ❝♦♥t❡①t✱ ♦♥❡ ♦❢ t❤❡ ♣r♦❜❧❡♠s ♦❢ ❣r❡❛t ✐♠♣♦rt❛♥❝❡ ✐♥ ♣r❛❝t✐❝❡ ✐s t❤❡ ❝❤♦✐❝❡ ♦❢ t❤❡ ❞✐str✐❜✉t✐♦♥ t♦ ❜❡ ✉s❡❞ ✐♥ t❤❡ ♠♦❞❡❧✐♥❣ ♦❢ t❤❡s❡ ❡①tr❡♠❡ ✈❛❧✉❡s✳

❚❤❡ ♠❛✐♥ ♦❜❥❡❝t✐✈❡ ♦❢ t❤✐s ❞✐ss❡rt❛t✐♦♥ ✐s t❤❡ ❡❧❛❜♦r❛t✐♦♥ ♦❢ ❛ ❝♦❧❧❡❝t✐♦♥ ♦❢ st❛t✐st✐❝❛❧ ♠❡t❤♦❞s ❢♦r t❤❡ ♣r♦❜❧❡♠ ♦❢ st❛t✐st✐❝❛❧ ❝❤♦✐❝❡ ❜❡t✇❡❡♥ ❡①♣♦♥❡♥t✐❛❧ ❛♥❞ ♥♦♥✲❡①♣♦♥❡♥t✐❛❧ ❣❡♥❡r❛❧✐③❡❞ P❛r❡t♦ ❞✐str✐❜✉t✐♦♥s✳ ❆ ❜r✐❡❢ ❛♥❛❧②s✐s ♦❢ t❤❡ P❖❚ ❛♣♣r♦❛❝❤ ✐s ❛❧s♦ ♦♥❡ ♦❢ t❤❡ ♦❜❥❡❝t✐✈❡s ♦❢ t❤✐s st✉❞②✱ ❛s ✇❡❧❧ ❛s t❤❡ ❡①❡♠♣❧✐✜❝❛t✐♦♥✱ ❜② ♠❡❛♥s ♦❢ t❤❡ st❛t✐st✐❝❛❧ s♦❢t✇❛r❡ ❘✱ ♦❢ t❤❡ ♣r♦❝❡❞✉r❡s r❡q✉✐r❡❞ t♦ ♣❡r❢♦r♠ t❤❡ st❛t✐st✐❝❛❧ ♠❡t❤♦❞s ❛♥❛❧②s❡❞✳

■♥ t❤✐s ❞✐ss❡rt❛t✐♦♥✱ ❛ ❜r✐❡❢ ✐♥tr♦❞✉❝t✐♦♥ t♦ t❤❡ ❊①tr❡♠❡ ❱❛❧✉❡ ❚❤❡♦r② ✐s ❝❛rr✐❡❞ ♦✉t ✇❤✐❝❤ ❢♦❝✉s❡s ♠❛✐♥❧② ♦♥ ●✉♠❜❡❧✬s ❛♥❞ P❖❚ ❛♣♣r♦❛❝❤❡s✳ ❚❤❡ P❖❚ ❛♣♣r♦❛❝❤ ✐s st✉❞✐❡❞ ✐♥ ♠♦r❡ ❞❡t❛✐❧✱ ✇✐t❤ t❤❡ ❞❡s❡r✈❡❞ ✐♠♣♦rt❛♥❝❡ ❜❡✐♥❣ ❣✐✈❡♥ t♦ t❤❡ ❡st✐♠❛t✐♦♥ ♦❢ ❡①♣♦♥❡♥t✐❛❧ ❛♥❞ ❣❡♥❡r❛❧✐③❡❞ P❛r❡t♦ ❞✐str✐❜✉t✐♦♥s ♣❛r❛♠❡t❡rs✳ ■♥ ❛❞❞✐t✐♦♥ t♦ ♣❛r❛♠❡t❡r ❡st✐♠❛t✐♦♥✱ t❤❡ ❡st✐♠❛t✐♦♥ ♦❢ ❡①tr❡♠❡ q✉❛♥t✐❧❡s ✐s ❛❧s♦ ❛❞❞r❡ss❡❞ ❣✐✈❡♥ t❤❡✐r r❡❧❡✈❛♥❝❡ ✐♥ r✐s❦ ♠❛♥❛❣❡♠❡♥t✳ ■♥ ♦r❞❡r t♦ ♠❛❦❡ ❛ st❛t✐st✐❝❛❧ ❝❤♦✐❝❡ ❜❡t✇❡❡♥ t❤❡ ❡①♣♦♥❡♥t✐❛❧ ❛♥❞ t❤❡ ●❡♥❡r❛❧✐③❡❞ P❛r❡t♦ ❞✐str✐❜✉t✐♦♥s✱ s♦♠❡ st❛t✐st✐❝❛❧ ♠❡t❤♦❞s ❜❛s❡❞ ♦♥ ❤②♣♦t❤❡s✐s t❡sts✱ ❝♦♥✜❞❡♥❝❡ ✐♥t❡r✈❛❧s ❛♥❞ ❣r❛♣❤✐❝❛❧ ♠❡t❤♦❞s ❛r❡ s✉❣❣❡st❡❞✳ ■♥ ♦r❞❡r t♦ ❡①❡♠♣❧✐❢② t❤❡ ❛♣♣❧✐❝❛t✐♦♥ ♦❢ t❤❡s❡ st❛t✐st✐❝❛❧ ♠❡t❤♦❞s✱ ❛s ✇❡❧❧ ❛s t❤❡ st✉❞✐❡❞ ❝♦♥❝❡♣ts✱ ❛ ♣r❛❝t✐❝❛❧ ✐❧❧✉str❛t✐♦♥ ✐s ♣❡r❢♦r♠❡❞ ✉s✐♥❣ ❛ ❞❛t❛❜❛s❡ ❢r♦♠ t❤❡ ❋✐♥❛♥❝❡ ✜❡❧❞✳

❑❡②✇♦r❞s✿ P❖❚ ❆♣♣r♦❛❝❤✱ ❊①♣♦♥❡♥t✐❛❧ ❉✐str✐❜✉t✐♦♥✱ ◆♦♥✲❡①♣♦♥❡♥t✐❛❧ ●❡♥❡r❛❧✐③❡❞ P❛r❡t♦ ❉✐str✐❜✉t✐♦♥s✱ ❙t❛t✐st✐❝❛❧ ❚❡sts✱ ❈♦♥✜❞❡♥❝❡ ■♥t❡r✈❛❧s✱ ●r❛♣❤✐❝❛❧ ▼❡t❤♦❞s✳

(9)

(10)

❮♥❞✐❝❡

▲✐st❛ ❞❡ ❋✐❣✉r❛s ①✐

▲✐st❛ ❞❡ ❚❛❜❡❧❛s ①✐✐✐

◆♦t❛çã♦ ①✈

✶ ■♥tr♦❞✉çã♦ ✶

✷ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✺

✷✳✶ ▼á①✐♠♦s ♣♦r ❜❧♦❝♦s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺

✷✳✷ ❊①❝❡ss♦s ❛❝✐♠❛ ❞❡ ✉♠ ♥í✈❡❧ ❡❧❡✈❛❞♦ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✶✵

✸ ▼❡t♦❞♦❧♦❣✐❛ P❖❚ ✶✼

✸✳✶ ❊st✐♠❛çã♦ ❞❡ ♣❛râ♠❡tr♦s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✷✵ ✸✳✷ ❊st✐♠❛çã♦ ❞❡ q✉❛♥t✐s ❡①tr❡♠❛✐s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✷✽

✹ ❊s❝♦❧❤❛ ❡st❛tíst✐❝❛ ❞❡ ♠♦❞❡❧♦s ❡①tr❡♠❛✐s ✸✶

✹✳✶ ❚❡st❡ ❞❡ ❤✐♣ót❡s❡s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✶

✹✳✶✳✶ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T1 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✸

✹✳✶✳✷ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T2 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✺

✹✳✶✳✸ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T3 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✻

✹✳✶✳✹ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T4 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✼

✹✳✶✳✺ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T5 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✽

✹✳✶✳✻ ❊st❛tíst✐❝❛ ❞❡ t❡st❡ T6 ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✸✽

✹✳✷ ■♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ❡ ♠ét♦❞♦s ❣rá✜❝♦s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✵

✺ ■❧✉str❛çã♦ ♣rát✐❝❛ ✹✺

✺✳✶ ❘❡s✉❧t❛❞♦s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✼ ✺✳✶✳✶ ❚❡st❡s ❞❡ ❤✐♣ót❡s❡s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✶ ✺✳✶✳✷ ■♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ❡ ♠ét♦❞♦s ❣rá✜❝♦s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✻✵ ✺✳✶✳✸ ❊st✐♠❛çã♦ ❞♦s q✉❛♥t✐s ❡①tr❡♠❛✐s ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✻✹

✻ ❈♦♥❝❧✉sã♦ ✻✼

(11)

① ❮♥❞✐❝❡

❇✐❜❧✐♦❣r❛✜❛ ✼✶

(12)

▲✐st❛ ❞❡ ❋✐❣✉r❛s

✷✳✶ ❆ ❢✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ λ ❡ ❛s ❢✉♥çõ❡s ❞❡♥s✐❞❛❞❡

♣r♦❜❛❜✐❧✐❞❛❞❡ ψ ❡ ϕ ♣❛r❛ α = 1✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✾

✷✳✷ ❋✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ F ❡ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❝♦♥❞✐❝✐♦♥❛❧Fu✳ ✶✶

✷✳✸ ❋✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ hγ,1 ♣❛r❛ γ = 0.5, 0 ❡ −0.25✳ ✶✹

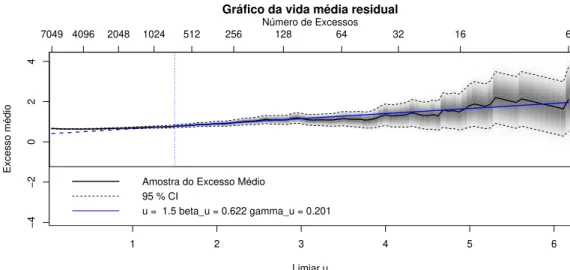
✹✳✶ ●rá✜❝♦s ❞❡ ❞✐❛❣♥óst✐❝♦ ❞❛ ❜✐❜❧✐♦t❡❝❛ ✐s♠❡✈✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✸ ✺✳✶ ●rá✜❝♦s ❞❛s ❜✐❜❧✐♦t❡❝❛s ❡✈❞✱ ❡✈✐r ❡ ✐s♠❡✈✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✽ ✺✳✷ ●rá✜❝♦ ▼❘▲ ❞❛ ❜✐❜❧✐♦t❡❝❛ ❡✈♠✐①✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✾

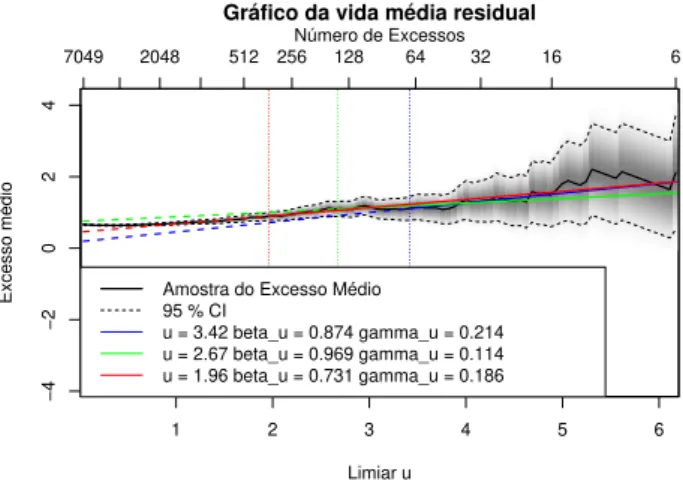
✺✳✸ ●rá✜❝♦s ▼❘▲ ❝♦♥s✐❞❡r❛♥❞♦ 0.5%✱ 1% ❡ 2.5% ❞♦s ✈❛❧♦r❡s ❡①tr❡♠♦s✳ ✺✵

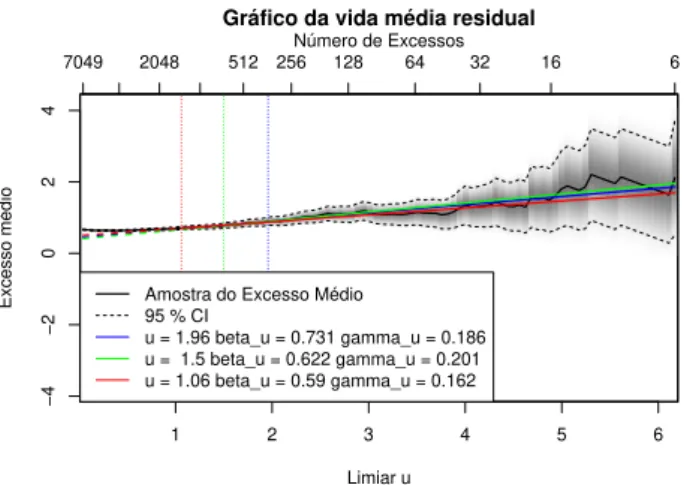
✺✳✹ ●rá✜❝♦s ▼❘▲ ❝♦♥s✐❞❡r❛♥❞♦ 2.5%✱ 5% ❡ 10% ❞♦s ✈❛❧♦r❡s ❡①tr❡♠♦s✳ ✺✶

✺✳✺ ❊st✐♠❛t✐✈❛s ❡ ✐♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ♣❛r❛ γ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✻✷

✺✳✻ ●rá✜❝♦s ❞❡ ❞✐❛❣♥óst✐❝♦ ❞❛ ❜✐❜❧✐♦t❡❝❛ ✐s♠❡✈ ♣❛r❛ u0.05 = 1.499139✳ ✻✸

✺✳✼ ●rá✜❝♦s ❞❡ ❞✐❛❣♥óst✐❝♦ ❞❛ ❜✐❜❧✐♦t❡❝❛ ✐s♠❡✈ ♣❛r❛ u0.10 = 1.059779✳ ✻✸

(13)

(14)

▲✐st❛ ❞❡ ❚❛❜❡❧❛s

✹✳✶ ❊st❛tíst✐❝❛s ❞❡ t❡st❡ ✲ ❞✐str✐❜✉✐çõ❡s✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✵ ✺✳✶ ❉❡s❝r✐çã♦ ❞♦s ❞❛❞♦s ❙✫P✺✵✵✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✻ ✺✳✷ ▲✐♠✐❛r❡s ❡ ♥ú♠❡r♦ ❞❡ ❡①❝❡❞ê♥❝✐❛s✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✹✾ ✺✳✸ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✼✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✷ ✺✳✹ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✾✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✸ ✺✳✺ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✵✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✹ ✺✳✻ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✶✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✺ ✺✳✼ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✷✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✻ ✺✳✽ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✸✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✼ ✺✳✾ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✹✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✼ ✺✳✶✵ ▲✐♠✐❛r❡s ❡ ✈❛❧♦r❡s r❡s✉❧t❛♥t❡s ❞♦ ♣r♦❝❡❞✐♠❡♥t♦ ✶✺✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✺✽

✺✳✶✶ ❉❡❝✐sã♦ ❞❡ r❡❥❡✐t❛r ♦✉ ♥ã♦ ❛ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ✭α= 0.05✮✳ ✳ ✺✾

✺✳✶✷ ❊st✐♠❛t✐✈❛s ♣❛r❛ γ ❡ ✐♥t❡r✈❛❧♦s ❞❡ 95% ❝♦♥✜❛♥ç❛ r❡s✉❧t❛♥t❡s ❞♦

♣r♦❝❡❞✐♠❡♥t♦ ✶✻✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✻✶ ✺✳✶✸ ❊st✐♠❛çã♦ ❞♦ ❱❛❘ ❡ ❈❚❊ ♣❛r❛ ♦s ❞✐❢❡r❡♥t❡s ❧✐♠✐❛r❡s✳ ✳ ✳ ✳ ✳ ✳ ✳ ✳ ✻✺

(15)

(16)

◆♦t❛çã♦

❊❱❚ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s✳

P❖❚ P❡❛❦s ❖✈❡r ❚❤r❡s❤♦❧❞✳

●P ●❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❡①♣♦♥❡♥❝✐❛❧✳

●❊❱ ●❡♥❡r❛❧✐③❛❞❛ ❞❡ ✈❛❧♦r❡s ❡①tr❡♠♦s

u ▲✐♠✐❛r✳

▼ét♦❞♦ ▼❖▼ ▼ét♦❞♦ ❞♦s ♠♦♠❡♥t♦s✳

▼ét♦❞♦ P❲▼ ▼ét♦❞♦ ❞♦s ♠♦♠❡♥t♦s ♣♦♥❞❡r❛❞♦s ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡✳

▼ét♦❞♦ ▼▲ ▼ét♦❞♦ ❞❡ ♠á①✐♠❛ ✈❡r♦s✐♠✐❧❤❛♥ç❛✳

❱❛❘ ❱❛❧✉❡✲❛t✲❘✐s❦✳

❈❚❊ ❱❛❧♦r ❡s♣❡r❛❞♦ ❞❡ ❝❛✉❞❛ ❝♦♥❞✐❝✐♦♥❛❧✳

Xi =d X ❚ê♠ ❛ ♠❡s♠❛ ❞✐str✐❜✉✐çã♦ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡s✳

Nu =m ◆ú♠❡r♦ ❞❡ ♦❜s❡r✈❛çõ❡s q✉❡ ❡①❝❡❞❡♠ ✉♠ ❧✐♠✐❛ru✳

{·} ❆rr❡❞♦♥❞❛♠❡♥t♦ ♣❛r❛ ♦ ♥ú♠❡r♦ ✐♥t❡✐r♦ ♠❛✐s ♣ró①✐♠♦✳

(17)

(18)

❈❛♣ít✉❧♦ ✶

■♥tr♦❞✉çã♦

❆ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✭❊❱❚ ❞♦ ✐♥❣❧ês ❊①tr❡♠❡ ❱❛❧✉❡ ❚❤❡♦r②✮ ❡♠❡r❣✐✉ ❝♦♠♦ ✉♠❛ ❞❛s ❞✐s❝✐♣❧✐♥❛s ❡st❛tíst✐❝❛s ♠❛✐s ✐♠♣♦rt❛♥t❡s ♣❛r❛ ❛ ❝✐ê♥❝✐❛ ❛♣❧✐❝❛❞❛ ♥♦s ú❧t✐♠♦s ✻✵ ❛♥♦s✳ ❈♦♠♦ ♦ ♣ró♣r✐♦ ♥♦♠❡ s✉❣❡r❡✱ ♦ ❢♦❝♦ ❞❛ ❊❱❚ é ♦ ❡st✉❞♦ ❞♦s ✈❛❧♦r❡s ❡①tr❡♠♦s✱ ✈❛❧♦r❡s ❡ss❡s q✉❡✱ ❛♣❡s❛r ❞❡ ♥ã♦ s❡r❡♠ ♠✉✐t♦ ❢r❡q✉❡♥t❡s✱ tê♠ ❝♦♥s❡q✉ê♥❝✐❛s ✐♠♣r❡✈✐sí✈❡✐s q✉❛♥❞♦ s✉r❣❡♠✳ ❆ss✐♠✱ ❛ ❊❱❚ ❝♦♥té♠ ❢❡rr❛♠❡♥t❛s q✉❡ sã♦ ✉s❛❞❛s ♣❛r❛ ❝♦♥s✐❞❡r❛r ♣r♦❜❛❜✐❧✐❞❛❞❡s ❛ss♦❝✐❛❞❛s ❛ ❡✈❡♥t♦s r❛r♦s ♠❛s ❞❡ ❣r❛♥❞❡ ✐♠♣❛❝t♦ ♥❛s ♠❛✐s ❞✐✈❡rs❛s ár❡❛s ❞❡ ❛♣❧✐❝❛çã♦✱ t❛✐s ❝♦♠♦ ❍✐❞r♦❧♦❣✐❛✱ ❖❝❡❛♥♦❣r❛✜❛✱ ▼❡t❡♦r♦❧♦❣✐❛✱ P♦❧✉✐çã♦✱ ❙❡❣✉r♦s✱ ❚❡❧❡❝♦♠✉♥✐❝❛çõ❡s ♦✉ ❋✐♥❛♥ç❛s✳

❆ ár❡❛ ❞❛s ❋✐♥❛♥ç❛s t❡♠ s✐❞♦ ❛❧✈♦ ❞❡ ✐♥ú♠❡r♦s ❡st✉❞♦s ♣♦r ♣❛rt❡ ❞❛ ❊❱❚✱ ✉♠❛ ✈❡③ q✉❡ ♦s ❛❝♦♥t❡❝✐♠❡♥t♦s ❡①tr❡♠♦s q✉❡ ♣♦r ✈❡③❡s ♦❝♦rr❡♠ ♥♦s ♠❡r❝❛❞♦s ✜♥❛♥❝❡✐r♦s sã♦ ❞❡ ❣r❛♥❞❡ ✐♠♣♦rtâ♥❝✐❛ ♣❛r❛ ♦s ✐♥✈❡st✐❞♦r❡s ❡♠ ♣❛rt✐❝✉❧❛r ❡ ♣❛r❛ t♦❞❛ ❛ ❡❝♦♥♦♠✐❛ ❡♠ ❣❡r❛❧✳ ❊ss❡s ❛❝♦♥t❡❝✐♠❡♥t♦s ❛✐♥❞❛ ♥ã♦ sã♦ ❜❡♠ ❝♦♠♣r❡❡♥❞✐❞♦s ♣❡❧♦s ❡st✉❞✐♦s♦s ❞❛ ár❡❛✱ ❞❡ t❛❧ ❢♦r♠❛ q✉❡ ♠❡s♠♦ ❞❡♣♦✐s ❞❡ ♣❛ss❛❞♦s ✈ár✐♦s ❛♥♦s ❞❡s❞❡ ♦ ❞✐❛ ✶✾ ❞❡ ♦✉t✉❜r♦ ❞❡ ✶✾✽✼✱ ❛ ✏❇❧❛❝❦ ▼♦♥❞❛②✑✱ ❛✐♥❞❛ s❡ ❡stá ❛ t❡♥t❛r ♣❡r❝❡❜❡r ♦ q✉❡ ❝❛✉s♦✉ ♦ ❝♦❧❛♣s♦ ❞♦ ♠❡r❝❛❞♦ ❞❡ ❛çõ❡s✳ ❖ ❞❡s❡♥✈♦❧✈✐♠❡♥t♦ ❞❛ ❊❱❚ ❛♦ ❧♦♥❣♦ ❞♦ t❡♠♣♦ ❢♦r♥❡❝❡ ❛ss✐♠ ✉♠❛ ❜❛s❡ t❡ór✐❝❛ ♠❛✐s só❧✐❞❛ s♦❜r❡ ❛ q✉❛❧ sã♦ ❝♦♥str✉í❞♦s ♠♦❞❡❧♦s ❡st❛tíst✐❝♦s ❝♦♠ ♦ ✐♥t✉✐t♦ ❞❡ ♠❡❧❤♦r ❝♦♠♣r❡❡♥❞❡r ❡ss❡s ❡✈❡♥t♦s ❡①tr❡♠♦s✳

❆ ❊❱❚ t❛❧ ❝♦♠♦ ❛ ❝♦♥❤❡❝❡♠♦s ❤♦❥❡✱ t❡✈❡ ❝♦♠♦ ✉♠ ❞♦s s❡✉s ♣r✐♠❡✐r♦s ❛rt✐❣♦s ♦ tr❛❜❛❧❤♦ r❡❛❧✐③❛❞♦ ♣♦r ❋✐s❤❡r ❬✶✾❪ ♥♦s ❛♥♦s ✷✵ ❞♦ sé❝✉❧♦ ♣❛ss❛❞♦✳ P❛r❛ ❛❧é♠ ❞❡ ❋✐s❤❡r✱ ❚✐♣♣❡t ❡ ●♥❡❞❡♥❦♦ ♠✉✐t♦ ✜③❡r❛♠ ♣❛r❛ t❡r❡♠ ✉♠ ❧✉❣❛r ♥❛ ❤✐stór✐❛ ❞❛ ❊❱❚✱ ❝❤❡❣❛♥❞♦ ❛ t❡r ♦s s❡✉s ♥♦♠❡s ❛tr✐❜✉í❞♦s ❛ ✉♠ ❞♦s t❡♦r❡♠❛s ❢✉♥❞❛♠❡♥t❛✐s ❞❛ ❊❱❚✱ ♦ ❚❡♦r❡♠❛ ❞❡ ❋✐s❤❡r✲❚✐♣♣❡t✲●♥❡❞❡♥❦♦✳ ❖✉tr❛s ♣❡rs♦♥❛❧✐❞❛❞❡s ❞❛ ár❡❛ ❝♦♠♦ ❲❡✐❜✉❧❧✱ ●✉♠❜❡❧✱ ❡st❡ t❡♥❞♦ s✐❞♦ ✉♠ ❞♦s ♣✐♦♥❡✐r♦s ❡ ♠❛✐s s♦♥❛♥t❡s ♥♦♠❡s

(19)

✷ ✶✳ ■♥tr♦❞✉çã♦

❞❛ ❊❱❚✱ ♦✉ ❋ré❝❤❡t t❛♠❜é♠ s❡ r❡✈❡❧❛r❛♠ ❞❡ ✈✐t❛❧ ✐♠♣♦rtâ♥❝✐❛✱ ❞❡ t❛❧ ❢♦r♠❛ q✉❡ t❡♠♦s três ✐♠♣♦rt❛♥t❡s ❞✐str✐❜✉✐çõ❡s ❞❛ ❊❱❚ ❝♦♠ ♦s s❡✉s ♥♦♠❡s✱ ❛ ❉✐str✐❜✉✐çã♦ ❞❡ ❲❡✐❜✉❧❧✱ ❛ ❉✐str✐❜✉✐çã♦ ❞❡ ●✉♠❜❡❧ ❡ ❛ ❉✐str✐❜✉✐çã♦ ❞❡ ❋ré❝❤❡t✳

❆ ♠❡t♦❞♦❧♦❣✐❛ ❞❡ ●✉♠❜❡❧ ✭♦✉ ❞♦s ❜❧♦❝♦s ♦✉ ❞♦s ♠á①✐♠♦s ❛♥✉❛✐s✮ ❡ ❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚✱ ❞❡s✐❣♥❛çã♦ q✉❡ ❛❞✈é♠ ❞♦ ✐♥❣❧ês P❡❛❦s ❖✈❡r ❚❤r❡s❤♦❧❞✱ sã♦ ❞✉❛s ❞❛s ♠❡t♦❞♦❧♦❣✐❛s ❞❛ ❊❱❚✳ ◆❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚✱ q✉❡ t❛♠❜é♠ é ❞❡♥♦♠✐♥❛❞❛ ❞❡ ♠❡t♦❞♦❧♦❣✐❛ ❞♦s ❊①❝❡ss♦s ❆❝✐♠❛ ❞❡ ✉♠ ◆í✈❡❧ ❊❧❡✈❛❞♦✱ sã♦ ❝♦♥s✐❞❡r❛❞♦s r❡❧❡✈❛♥t❡s ♦s ♠❛✐♦r❡s ✈❛❧♦r❡s ♦❜s❡r✈❛❞♦s q✉❡ s❡ ❡♥❝♦♥tr❛♠ ❛❝✐♠❛

❞♦ ♥í✈❡❧ ♦✉ ❧✐♠✐❛r ❡❧❡✈❛❞♦ u✳ ■st♦ ❝♦♥st✐t✉✐ ✉♠❛ ✈❛♥t❛❣❡♠ r❡❧❛t✐✈❛♠❡♥t❡ à

♠❡t♦❞♦❧♦❣✐❛ ❞❡ ●✉♠❜❡❧ ♥❛ q✉❛❧ é ❛♣❡♥❛s ❝♦♥s✐❞❡r❛❞♦ ♦ ✈❛❧♦r ♠á①✐♠♦ ❞❡ ❝❛❞❛ ♣❡rí♦❞♦ ❡♠ ❡st✉❞♦✱ ❝♦♠♦ ♣♦r ❡①❡♠♣❧♦ ♦ ♠á①✐♠♦ ♣♦r ❝❛❞❛ ❛♥♦✳ ❆ss✐♠✱ ❛♦ ❝♦♥trár✐♦ ❞❛ ♠❡t♦❞♦❧♦❣✐❛ ❞❡ ●✉♠❜❡❧✱ ♥❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ ♥ã♦ ❝♦rr❡♠♦s ♦ r✐s❝♦ ❞❡ ♣❡r❞❡r ♦❜s❡r✈❛çõ❡s ❡❧❡✈❛❞❛s ♦✉ ❞❡ ❝♦♥s✐❞❡r❛r ♦❜s❡r✈❛çõ❡s ❜❛✐①❛s ❬✶✼❪✳ ❯♠❛ ❜r❡✈❡ ❛♥á❧✐s❡ ❞❡st❛s ♠❡t♦❞♦❧♦❣✐❛s é ❛♣r❡s❡♥t❛❞❛ ♥♦ ❈❛♣ít✉❧♦ ✷ ❞❡st❛ ❞✐ss❡rt❛çã♦✱ s❡♥❞♦ ❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ ❡st✉❞❛❞❛ ❝♦♠ ♠❛✐s ♣♦r♠❡♥♦r ♥♦ ❈❛♣ít✉❧♦ ✸✳

❉❛✈✐s♦♥ ❡ ❙♠✐t❤✱ ❞✉❛s ♣❡rs♦♥❛❧✐❞❛❞❡s ❞❛ ár❡❛ q✉❡ ❡♠ ♠✉✐t♦ ❝♦♥tr✐❜✉ír❛♠ ♣❛r❛ ♦ ❞❡s❡♥✈♦❧✈✐♠❡♥t♦ ❞❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚✱ ❛✜r♠❛r❛♠ ❡♠ ❬✶✺❪ q✉❡ ❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ ❝♦♠❡ç♦✉ ❛ s❡r ❞❡s❡♥✈♦❧✈✐❞❛ ❞❡ ❢♦r♠❛ s✐st❡♠át✐❝❛ ♥♦s tr❛❜❛❧❤♦s r❡❛❧✐③❛❞♦s ♣♦r ❚♦❞♦r♦✈✐❝ ❡ ❘♦✉ss❡❧❧❡ ❡♠ ❬✹✷❪ ❡ ❚♦❞♦r♦✈✐❝ ❡ ❩❡❧❡♥❤❛s✐❝ ❡♠ ❬✹✸❪✳ P♦r s✉❛ ✈❡③✱ ❉❛✈✐s♦♥ ❡ ❙♠✐t❤ t❛♠❜é♠ ❡❧❛❜♦r❛♠✱ ❡♥tr❡ ♦✉tr♦s tr❛❜❛❧❤♦s ❞❡ ❣r❛♥❞❡ ✐♠♣♦rtâ♥❝✐❛ ♣❛r❛ ❡st❛ ♠❡t♦❞♦❧♦❣✐❛✱ ♦s ❡st✉❞♦s ❡♠ ❬✶✹❪✱ ❬✶✺❪ ❡ ❬✹✵❪✳ ❖✉tr♦ ♠❛r❝♦ ✐♠♣♦rt❛♥t❡ ♣❛r❛ ❛ ❛♥á❧✐s❡ ❞♦s ❡①❝❡ss♦s ✭❞✐❢❡r❡♥ç❛s ❡♥tr❡ ♦s ✈❛❧♦r❡s ❛❝✐♠❛ ❞♦ ❧✐♠✐❛r ❡ ❡st❡ ✈❛❧♦r✮ ❢♦✐ ❡st❛❜❡❧❡❝✐❞♦ ♣♦r P✐❝❦❛♥❞s ❡♠ ❬✸✻❪ ❡ ❇❛❧❦❡♠❛ ❡ ❞❡ ❍❛❛♥ ❡♠ ❬✸❪✳ ❊st❡s ❛✉t♦r❡s ❡st❛❜❡❧❡❝❡r❛♠ q✉❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❝♦♥❞✐❝✐♦♥❛❧

❞♦s ❡①❝❡ss♦s ❛❝✐♠❛ ❞♦ ❧✐♠✐❛r u ♣♦❞❡ s❡r ❜❡♠ ❛♣r♦①✐♠❛❞❛ ♣♦r ✉♠❛ ❢✉♥çã♦ ❞❡

❞✐str✐❜✉✐çã♦ ❣❡♥❡r❛❧✐③❛❞❛ ❞❡ P❛r❡t♦ ♥ã♦ ❡①♣♦♥❡♥❝✐❛❧ ✭●P✮✳

(20)

✶✳ ■♥tr♦❞✉çã♦ ✸

❞♦s ♣❛râ♠❡tr♦s ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P ♣❛r❛ ✉♠❛ ✈❛r✐❡❞❛❞❡ ❞❡ ❞✐❢❡r❡♥t❡s ❧✐♠✐❛r❡s ♣❡r♠✐t❡ ❡st❛❜❡❧❡❝❡r ✉♠ ♠ét♦❞♦ ❣rá✜❝♦ ❛ ✉t✐❧✐③❛r ♥❡ss❛ ❡s❝♦❧❤❛✳ ❊st❛s ❡st✐♠❛t✐✈❛s ♣♦❞❡♠ s❡r ♦❜t✐❞❛s ♣♦r ✐♥ú♠❡r♦s ♠ét♦❞♦s ❞❡ ❡st✐♠❛çã♦✱ t❛✐s ❝♦♠♦ ♦ ♠ét♦❞♦ ❞♦s ♠♦♠❡♥t♦s ✭♠ét♦❞♦ ▼❖▼✮✱ ♦ ♠ét♦❞♦ ❞♦s ♠♦♠❡♥t♦s ♣♦♥❞❡r❛❞♦s ♣❡❧❛ ♣r♦❜❛❜✐❧✐❞❛❞❡ ✭♠ét♦❞♦ P❲▼✮ ♦✉ ♦ ♠ét♦❞♦ ❞❡ ♠á①✐♠❛ ✈❡r♦s✐♠✐❧❤❛♥ç❛ ✭♠ét♦❞♦ ▼▲✮✱ s❡♥❞♦ ❡st❡ ú❧t✐♠♦ ♦ ♠❛✐s ✉t✐❧✐③❛❞♦ ♥❛ ❜✐❜❧✐♦❣r❛✜❛ ❡①✐st❡♥t❡✳ P❛r❛ ❛❧é♠ ❞❛ ❡st✐♠❛çã♦ ❞❡ ♣❛râ♠❡tr♦s t❡♠♦s t❛♠❜é♠ ❛ ❡st✐♠❛çã♦ ❞❡ q✉❛♥t✐s ❡①tr❡♠❛✐s✱ ❛ q✉❛❧ s❡ r❡✈❡❧❛ ❞❡ ✈✐t❛❧ ✐♠♣♦rtâ♥❝✐❛ ♣❛r❛ ❛ ❣❡stã♦ ❞♦ r✐s❝♦✳ ❯♠❛ ♠❡❞✐❞❛ ❞❡ r✐s❝♦ ♠✉✐t❛ ✉t✐❧✐③❛❞❛ ♥❡st❡ t✐♣♦ ❞❡ ❣❡stã♦ é ♦ ✈❛❧♦r ❞❡♥♦♠✐♥❛❞♦ ❱❛❧✉❡✲❛t✲❘✐s❦ ✭❱❛❘✮✱ ✈❛❧♦r q✉❡ é s✐♠♣❧❡s♠❡♥t❡ ✉♠ q✉❛♥t✐❧ ❡①tr❡♠♦✳ ❖✉tr❛ ♠❡❞✐❞❛ ❞❡ r✐s❝♦ ♠✉✐t♦ ✉t✐❧✐③❛❞❛ ♥❛ ár❡❛ ❞❛s ❋✐♥❛♥ç❛s é ♦ ❞❡♥♦♠✐♥❛❞♦ ✈❛❧♦r ❡s♣❡r❛❞♦ ❞❡ ❝❛✉❞❛ ❝♦♥❞✐❝✐♦♥❛❧ q✉❡ ❞❡♥♦t❛r❡♠♦s ♣♦r ❈❚❊ ❞♦ ✐♥❣❧ês ❈♦♥❞✐❝✐♦♥❛❧ ❚❛✐❧ ❊①♣❡❝t❛t✐♦♥✳ ▲❡✈❛♥❞♦ ❡♠ ❝♦♥t❛ ❡st❛s ❞✉❛s ♠❡❞✐❞❛s ❞❡ r✐s❝♦ ♦❜t❡♠♦s✱ r❡s♣❡t✐✈❛♠❡♥t❡✱ ❛tr❛✈és ❞❡ ✉♠❛ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❛ss♦❝✐❛❞❛ ♠✉✐t♦ ❜❛✐①❛✱ ✉♠ ✈❛❧♦r ❛ ♣❛rt✐r ❞♦ q✉❛❧ s❡ ❡s♣❡r❛ q✉❡ ❤❛❥❛ ✉♠ ❛❝♦♥t❡❝✐♠❡♥t♦ ❡①tr❡♠♦ ❡ q✉❛♥t✐✜❝❛r ❡♠ ♠é❞✐❛ q✉❡ ✈❛❧♦r ❞❡❝♦rr❡rá ❞❡ss❡ ❛❝♦♥t❡❝✐♠❡♥t♦✳

❆ ♦❜t❡♥çã♦ ❞❡ t❛✐s ✈❛❧♦r❡s ❛ss♦❝✐❛❞♦s ❛ ✉♠ ❛❝♦♥t❡❝✐♠❡♥t♦ ❡①tr❡♠♦ ❡stá ❛ss♦❝✐❛❞❛ à ❡s❝♦❧❤❛ ❞❡ ✉♠❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦✳ ◆❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚✱ ❡ss❛ ❡s❝♦❧❤❛ ♣♦❞❡ r❡❝❛✐r ❡♥tr❡ ❛ ❡s❝♦❧❤❛ ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ♦✉ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P✳ ❆ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ é ❛ ❢❛✈♦r✐t❛ ♠✉✐t♦ ♣♦r ❝♦♥t❛ ❞❛ s✉❛ s✐♠♣❧✐❝✐❞❛❞❡ ♥❛ ❡st✐♠❛çã♦ t❛♥t♦ ❞♦s q✉❛♥t✐s ❡①tr❡♠❛✐s q✉❛♥t♦ ❞♦s ♣❛râ♠❡tr♦s✳ ❆ss✐♠✱ ❛ ❡s❝♦❧❤❛ ❡♥tr❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P é ✉♠ ♣r♦❜❧❡♠❛ ❡st❛tíst✐❝♦ ✐♠♣♦rt❛♥t❡✱ s❡♥❞♦ ❡st❛ t❡♠át✐❝❛ ❛ ♠♦t✐✈❛çã♦ ♣r✐♥❝✐♣❛❧ ❞❡st❛ ❞✐ss❡rt❛çã♦✳

(21)

✹ ✶✳ ■♥tr♦❞✉çã♦

❛♥❛❧✐s❛❞❛ ♣♦r ●♦♠❡s ❡ ✈❛♥ ▼♦♥t❢♦rt ❡♠ ❬✷✺❪✳ ❊st❛ q✉❛rt❛ ❡st❛tíst✐❝❛ ❞❡ t❡st❡ ❢♦✐ ♣r♦♣♦st❛ ♣♦r ✈❛♥ ▼♦♥t❢♦rt ❡ ❲✐tt❡r ♥♦ tr❛❜❛❧❤♦ r❡❛❧✐③❛❞♦ ❡♠ ❬✹✹❪✳ ❆ q✉✐♥t❛ ❡st❛tíst✐❝❛ ❞❡ t❡st❡ s✉❣❡r✐❞❛ ♣♦❞❡ s❡r ❡♥❝♦♥tr❛❞❛ ❡♠ ❬✷✸❪✱ ❛ q✉❛❧ é ❞❛❞❛ ♣❡❧❛ r❛③ã♦ ❡♥tr❡ ❛ ❞✐❢❡r❡♥ç❛ ❞♦ ♠á①✐♠♦ ❡ ❛ ♠❡❞✐❛♥❛ ❡ ❛ ❞✐❢❡r❡♥ç❛ ❞❡st❛ ❡ ♦ ♠í♥✐♠♦✳ ❇❛s❡❛❞❛ ♥❡st❛ ❡st❛tíst✐❝❛ ❞❡ t❡st❡✱ ❇r✐❧❤❛♥t❡ ❡♠ ❬✽❪ ❛♣r❡s❡♥t♦✉ ❛ s❡①t❛ ❡st❛tíst✐❝❛ ❞❡ t❡st❡ s✉❣❡r✐❞❛ ♥❡st❛ ❞✐ss❡rt❛çã♦✱ ❞❡✜♥✐❞❛ ♣❡❧❛ r❛③ã♦ ❡♥tr❡ ❛ ❞✐❢❡r❡♥ç❛ ❞♦ q✉❛rt♦ s✉♣❡r✐♦r ❡ ❛ ♠❡❞✐❛♥❛ ❡ ❛ ❞✐❢❡r❡♥ç❛ ❞❡st❛ ❡ ♦ q✉❛rt♦ ✐♥❢❡r✐♦r✳ ❚❡♥❞♦ ❡♠ ❝♦♥t❛ ❛s ❡st✐♠❛t✐✈❛s ❞♦s ♣❛râ♠❡tr♦s ❞❡ ❢♦r♠❛ q✉❡ ♣♦❞❡♠ s❡r ♦❜t✐❞❛s ♣❡❧♦s ♠ét♦❞♦s ❞❡ ❡st✐♠❛çã♦ ❞❡ ♣❛râ♠❡tr♦s ❛♥t❡r✐♦r♠❡♥t❡ r❡❢❡r✐❞♦s✱ é ❞❡ ❡s♣❡❝✐❛❧ ✐♥t❡r❡ss❡ ❝♦♥str✉✐r ♦s r❡s♣❡t✐✈♦s ✐♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ♣❛r❛ ♦ ♣❛râ♠❡tr♦ ❞❡ ❢♦r♠❛✳ ❆ ❡s❝♦❧❤❛ ❡♥tr❡ ❛ ❢✉♥çã♦ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P ♠❡♥❝✐♦♥❛❞❛ ♥❛ ❙❡❝çã♦ ✹✳✷ ❛ss❡♥t❛ ♥❛ ♦❜s❡r✈❛çã♦ ❞❛ ✐♥❝❧✉sã♦ ♦✉ ♥ã♦ ❞♦ ✈❛❧♦r ③❡r♦ ♥♦s ✐♥t❡r✈❛❧♦s ❞❡ ❝♦♥✜❛♥ç❛ ♦❜t✐❞♦s✱ r❡s♣❡t✐✈❛♠❡♥t❡✳ ◆❛ ♠❡s♠❛ s❡❝çã♦✱ ❡♥❝♦♥tr❛♠♦s t❛♠❜é♠ ✉♠ ♠ét♦❞♦ ✐♥❢♦r♠❛❧ ♣❛r❛ ❛ ✈❛❧✐❞❛çã♦ ❞❡ ♠♦❞❡❧♦s ❛tr❛✈és ❞❡ ♠ét♦❞♦s ❣rá✜❝♦s q✉❡ ♣♦❞❡♠♦s ❛♣❧✐❝❛r ❝♦♠♦ ♠ét♦❞♦ ❞❡ ❡s❝♦❧❤❛ ❡♥tr❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧ ❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P✳

❈♦♠ ♦ ♦❜❥❡t✐✈♦ ❞❡ ❝♦❧♦❝❛r ❡♠ ♣rát✐❝❛ ♦s t❡♠❛s ❛❜♦r❞❛❞♦s✱ ❢♦✐ r❡❛❧✐③❛❞❛ ✉♠❛ ✐❧✉str❛çã♦ ♣rát✐❝❛ ♥♦ ❈❛♣ít✉❧♦ ✺✳ ❉❛❞❛ ❛ ❢r❛♥❝❛ ❡①♣❛♥sã♦ ❞❛ ❊❱❚ ♥❛s ú❧t✐♠❛s ❞é❝❛❞❛s✱ ♦❜s❡r✈❛♠♦s q✉❡ ♦ s♦❢t✇❛r❡ ❡st❛tíst✐❝♦ ❘✱ ❞❡ ❡♥tr❡ ❛❧❣✉♥s s♦❢t✇❛r❡s ❡st❛tíst✐❝♦s✱ t❡♠ ❛❝♦♠♣❛♥❤❛❞♦ ❡ss❡ ❞❡s❡♥✈♦❧✈✐♠❡♥t♦✳ ❊st❡ s♦❢t✇❛r❡✱ ♣❛r❛ ❛❧é♠ ❞❡ s❡r ❞❡ ✉t✐❧✐③❛çã♦ ❣r❛t✉✐t❛✱ ❝♦♥té♠ ✉♠❛ ❣r❛♥❞❡ ✈❛r✐❡❞❛❞❡ ❞❡ ❜✐❜❧✐♦t❡❝❛s q✉❡ ♣♦❞❡♠ s❡r ❡♥❝♦♥tr❛❞❛s ♥❛ t❛s❦ ✈✐❡✇ ❞❡♥♦♠✐♥❛❞❛ ❊①tr❡♠❡ ❱❛❧✉❡ ❆♥❛❧②s✐s✳

(22)

❈❛♣ít✉❧♦ ✷

❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s

❊①tr❡♠♦s

❆ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s t❡♠ ❝♦♠♦ ❢♦❝♦ ♣r✐♥❝✐♣❛❧ ♦ ❡st✉❞♦ ❞♦ ❝♦♠♣♦rt❛♠❡♥t♦ ❞❡ ✈❛❧♦r❡s ✐♥✈✉❧❣❛r♠❡♥t❡ ❣r❛♥❞❡s ♦✉ ♣❡q✉❡♥♦s✳ ❉✐❢❡r❡♥t❡s ❢♦r♠❛s ❞❡ ❞❡✜♥✐r ❡st❡s ✈❛❧♦r❡s✱ ❞❡♥♦♠✐♥❛❞♦s ❞❡ ❡①tr❡♠♦s✱ ♦r✐❣✐♥❛r❛♠ ❞✐❢❡r❡♥t❡s ♠❡t♦❞♦❧♦❣✐❛s✳ ◆❛ ♠❡t♦❞♦❧♦❣✐❛ ❞❡ ●✉♠❜❡❧ é ❝♦♥s✐❞❡r❛❞♦ ✉♠ ♠á①✐♠♦ ♣♦r ❜❧♦❝♦✱ ❢❛❝t♦ q✉❡ ♣♦❞❡ ❧✐♠✐t❛r ♦ ❡st✉❞♦ ❬✶✷❪✳ ◆❛ ♠❡t♦❞♦❧♦❣✐❛ P❖❚ sã♦ ✐♥t❡❣r❛❞❛s ♥❛ ❛♥á❧✐s❡ t♦❞❛s ❛s ♦❜s❡r✈❛çõ❡s ❛❝✐♠❛ ❞❡ ✉♠ ❝❡rt♦ ❧✐♠✐❛r✱ ♦ q✉❡ ♣♦ss✐❜✐❧✐t❛ ✉♠❛ ✉t✐❧✐③❛çã♦ ♠❛✐s ❡✜❝✐❡♥t❡ ❞♦s ❞❛❞♦s ❬✷✶❪✳ ❆♣❡s❛r ❞❛ ❡①✐stê♥❝✐❛ ❞❡ ♦✉tr❛s ♠❡t♦❞♦❧♦❣✐❛s✱ ❢❛r❡♠♦s ♥❛s s❡❝çõ❡s s❡❣✉✐♥t❡s ❛♣❡♥❛s ✉♠❛ ❜r❡✈❡ ❛♥á❧✐s❡ ❞❡st❛s ❞✉❛s ♠❡t♦❞♦❧♦❣✐❛s ❞✐t❛s ♠❛✐s ❝❧áss✐❝❛s✳

✷✳✶ ▼á①✐♠♦s ♣♦r ❜❧♦❝♦s

❙❡❥❛ x = (x1, . . . , xn) ✉♠❛ r❡❛❧✐③❛çã♦ ❞♦ ✈❡t♦r ❛❧❡❛tór✐♦ (X1, . . . , Xn)✳

❉❡♥♦t❛♠♦s ❛ ♦r❞❡♥❛çã♦ ❛s❝❡♥❞❡♥t❡ ❞♦s ❡❧❡♠❡♥t♦s ❞❡ x ♣♦r x1:n, . . . , xn:n✱ ♦♥❞❡

x1:n ≤ . . . ≤ xn:n✳ ❖ ✈❡t♦r q✉❡ ♣❛r❛ ❛ r❡❛❧✐③❛çã♦ (x1, . . . , xn) ❞❡ (X1, . . . , Xn)

t❡♠ ❝♦♠♦ r❡❛❧✐③❛çã♦x1:n, . . . , xn:né ❞❡♥♦♠✐♥❛❞♦ ❞❡ ✈❡t♦r ❞❛s ❡st❛tíst✐❝❛s ♦r❞✐♥❛✐s

❛ss♦❝✐❛❞♦ ❛♦ ✈❡t♦r ❛❧❡❛tór✐♦ (X1, . . . , Xn)✳ ❚♦♠❛♠♦s

X1:n := min 1≤i≤nXi

❡

Xn:n := max

1≤i≤nXi. ✭✷✳✶✮

(23)

✻ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

❈❛❞❛ ❝♦♠♣♦♥❡♥t❡ ✉♥✐✈❛r✐❛❞❛ Xi:n ❞♦ ✈❡t♦r ❞❛s ❡st❛tíst✐❝❛s ♦r❞✐♥❛✐s

(X1:n, . . . , Xn:n) é ❞❡♥♦♠✐♥❛❞❛ i✲és✐♠❛ ❡st❛tíst✐❝❛ ♦r❞✐♥❛❧ ❛s❝❡♥❞❡♥t❡ ❞♦ ✈❡t♦r

❛❧❡❛tór✐♦ (X1, . . . , Xn) ❬✹✺❪✳ ❈♦♥s✐❞❡r❡♠♦s ❛✐♥❞❛ q✉❡ ❛s ♠❛r❣✐♥❛✐s ❞♦ ✈❡t♦r

✭X1, . . . , Xn✮ sã♦ ✈❛r✐á✈❡✐s ❛❧❡❛tór✐❛s ✐♥❞❡♣❡♥❞❡♥t❡s ❡ ✐❞❡♥t✐❝❛♠❡♥t❡ ❞✐str✐❜✉í❞❛s

❛ ✉♠❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ X ✭Xi

d

=X✮ ❝♦♠ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦F ❞❡✜♥✐❞❛ ♣♦r

F(x) :=P(X _≤x). ✭✷✳✷✮

❆ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡♠♣ír✐❝❛ é ❞❛❞❛ ♣♦r

ˆ

Fn(x) =     

0, s❡ x < x1:n; i

n, s❡ x∈[x1:n, xi+1:n[, i= 1. . . n−1;

1, s❡ x_≥xn:n,

✭✷✳✸✮

♦♥❞❡ xi:n é ♦ ✐✲és✐♠♦ ✈❛❧♦r ❛♠♦str❛❧ ❬✹❪✳

❉❡♥♦t❛♠♦s Xn:n ♣♦r Mn✳ ❆ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❞❡ Mn é ❞❛❞❛ ♣♦r

F(x) =P[Mn≤x] = P h

max

1≤i≤nXi ≤x i

= P[X1 ≤x, X2 ≤x, . . . , Xn≤x]

=

n Y

i=1

P[Xi ≤x]

= P[X _≤x]n

= Fn(x) ✭✷✳✹✮

◆♦ ❡♥t❛♥t♦✱ ❝♦♠♦ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦F é ❞❡s❝♦♥❤❡❝✐❞❛✱ ❛ ✐❣✉❛❧❞❛❞❡ ✭✷✳✹✮

♥ã♦ t❡♠ ❣r❛♥❞❡ ✉t✐❧✐❞❛❞❡ ♥❛ ♣rát✐❝❛✳ ❯♠❛ ♣♦ssí✈❡❧ ❛❜♦r❞❛❣❡♠ ❞❡ r❡s♦❧✉çã♦ ❞❡st❡

♣r♦❜❧❡♠❛ s❡r✐❛ ❡st✐♠❛r ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ F ❛ ♣❛rt✐r ❞❡ ❞❛❞♦s ♦❜s❡r✈❛❞♦s✱

♥❛ q✉❛❧ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❡♠♣ír✐❝❛✱ _Fˆ_n_{✱ t❡r✐❛ ✉♠ ♣❛♣❡❧ ✐♠♣♦rt❛♥t❡✳ ◆♦}

❡♥t❛♥t♦✱ ♥ã♦ é ❡st❛ ❛ ❛❜♦r❞❛❣❡♠ ♠❛✐s ❛♣❧✐❝❛❞❛ ♣♦rq✉❡ ♣❡q✉❡♥❛s ❞✐s❝r❡♣â♥❝✐❛s

♥❛ ❢✉♥çã♦ ❡st✐♠❛t✐✈❛ ♣❛r❛F ♣♦❞❡♠ ♦r✐❣✐♥❛r ❣r❛♥❞❡s ❞✐s❝r❡♣â♥❝✐❛s ♣❛r❛Fn_{❬✶✷❪✳}

❆ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦F é ❛ss✐♠ ❝♦♥s✐❞❡r❛❞❛ ❞❡s❝♦♥❤❡❝✐❞❛ ❡ ♦ ❡st✉❞♦ é ❢♦❝❛❞♦

♥♦ ❝♦♠♣♦rt❛♠❡♥t♦ ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦Fn q✉❛♥❞♦n_→+_∞✳ ❆ss✐♠✱ s✉r❣❡

♥❛t✉r❛❧♠❡♥t❡ ❛ q✉❡stã♦ s♦❜r❡ q✉❛✐s ❞✐str✐❜✉✐çõ❡s ♣♦❞❡♠ s✉r❣✐r ♣❛r❛ ❛ ✈❛r✐á✈❡❧

❧✐♠✐t❡ ❞❡ Mn✳

❆♥t❡s ❞❡ ❡♥✉♥❝✐❛r ❛ r❡s♣♦st❛ ❞❡st❛ q✉❡stã♦✱ r❡❧❡♠❜r❡♠♦s ❛s ❞❡✜♥✐çõ❡s ❞❡ ❝♦♥✈❡r❣ê♥❝✐❛ ❡♠ ❞✐str✐❜✉✐çã♦ ❡ ❡♠ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❬✹✺❪✿

(24)

✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✼

❼ ❈♦♥✈❡r❣ê♥❝✐❛ ❡♠ ❞✐str✐❜✉✐çã♦

❉✐③❡♠♦s q✉❡ Xn ❝♦♥✈❡r❣❡ ❡♠ ❞✐str✐❜✉✐çã♦ ♣❛r❛ ❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ Y s❡ ❡

só s❡

lim

n→∞FXn(x) =FY(x),

♣❛r❛ t♦❞♦ ♦ x q✉❡ s❡❥❛ ♣♦♥t♦ ❞❡ ❝♦♥t✐♥✉✐❞❛❞❡ ❞❡ FY✱ ❡ ❞❡♥♦t❛♠♦s t❛❧

♣r♦♣r✐❡❞❛❞❡ ♣♦r Xn

d −→ n→∞ Y✳

❼ ❈♦♥✈❡r❣ê♥❝✐❛ ❡♠ ♣r♦❜❛❜✐❧✐❞❛❞❡

❉✐③❡♠♦s q✉❡ Xn ❝♦♥✈❡r❣❡ ❡♠ ♣r♦❜❛❜✐❧✐❞❛❞❡ ♣❛r❛ ❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ Y

✭❡✈❡♥t✉❛❧♠❡♥t❡ ❞❡❣❡♥❡r❛❞❛✮ s❡ ∀ε >0✱

P_[_|_X_n₋_Y_|_{> ε}_] _−→ n→∞ 0

❡ ❡s❝r❡✈❡♠♦s Xn

P −→ n→∞Y✳

❖r❛✱ q✉❛♥❞♦ n_{→ ∞} ♦❜t❡♠♦s✿

lim

n→∞FMn(x) =

(

0, se F(x)<1;

1, se F(x) = 1, ✭✷✳✺✮

♣❡❧♦ q✉❡ Mn

d −→ n→∞ x

F_{✱ ♦♥❞❡} _xF _{é ♦ ❧✐♠✐t❡ s✉♣❡r✐♦r ❞❡ s✉♣♦rt❡ ❞❡}

F (xF _{:= sup}_{_F₍_x₎ _< ₁_{} ≤ ∞}₎_{✳ ❊st❛ ❝♦♥✈❡r❣ê♥❝✐❛ ❡♠ ❞✐str✐❜✉✐çã♦ ✐♠♣❧✐❝❛} ❛ ❝♦♥✈❡r❣ê♥❝✐❛ ❡♠ ♣r♦❜❛❜✐❧✐❞❛❞❡ ♣❛r❛ ❛ ♠❡s♠❛ ❝♦♥st❛♥t❡✱ ♦✉ s❡❥❛✱ t❡♠♦s

Mn

P −→ n→∞ x

F_{✱ ♠❡s♠♦ q✉❡} _xF ₌ _∞ _{❬✷✹❪ ❡✱ ❛ss✐♠ ♦❜s❡r✈❛♠♦s q✉❡ ❛ ❞✐str✐❜✉✐çã♦}

❧✐♠✐t❡ ❞❡ Mn é ❞❡❣❡♥❡r❛❞❛✳ ◆♦ ❡♥t❛♥t♦✱ ❛ ❞✐✜❝✉❧❞❛❞❡ ❞❡ t❡r♠♦s ❝♦♠♦

❞✐str✐❜✉✐çã♦ ❧✐♠✐t❡ ✉♠❛ ❞✐str✐❜✉✐çã♦ ❞❡❣❡♥❡r❛❞❛ é ❡✈✐t❛❞❛ s❡ ❢♦r ♣♦ssí✈❡❧

❡♥❝♦♥tr❛r s✉❝❡ssõ❡s ❞❡ ❝♦♥st❛♥t❡s r❡❛✐s {an}n≥1(an >0) ❡{bn}n≥1 t❛✐s q✉❡

Mn−bn

an d −→

n→∞ Y ✭✷✳✻✮

❝♦♠ Y ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ ♥ã♦ ❞❡❣❡♥❡r❛❞❛✱ ♦✉ s❡❥❛✱ t❛✐s q✉❡

Fn(anx+bn)−→

n→∞G(x), ∀x∈C(G),

❝♦♠ G❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❞❡ ✉♠❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ ♥ã♦ ❞❡❣❡♥❡r❛❞❛ ❡ C(G)

♦ ❝♦♥❥✉♥t♦ ❞♦s ♣♦♥t♦s ❞❡ ❝♦♥t✐♥✉✐❞❛❞❡ ❞❡ ●✳ ◆❡st❛s ❝♦♥❞✐çõ❡s✱ ❞✐③❡♠♦s q✉❡ F

(25)

✽ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

s✉❝❡ssõ❡s ❞❡ ❝♦♥st❛♥t❡s {an}n≥1 (a >0) ❡ {bn}n≥1 ❞❡ ❝♦❡✜❝✐❡♥t❡s ❞❡ ❛tr❛çã♦ ❞❡

F ♣❛r❛ G✳ ❆ r❡s♣♦st❛ à q✉❡stã♦ r❡❛❧✐③❛❞❛ ❢♦✐ ♦❜t✐❞❛ ♣♦r ●♥❡❞❡♥❦♦ ♥♦ tr❛❜❛❧❤♦

r❡❛❧✐③❛❞♦ ❡♠ ❬✷✷❪✱ ♥❛ s❡q✉ê♥❝✐❛ ❞♦s ❡st✉❞♦s ❞❡ ❋✐s❤❡r ❡ ❚✐♣♣❡t ❡♠ ❬✶✽❪ ❡ ❞❡ ✈♦♥ ▼✐s❡s ❡♠ ❬✹✼❪✳ ❖ ❡♥✉♥❝✐❛❞♦ ❞♦ t❡♦r❡♠❛ ❞❡ t✐♣♦s ❡①tr❡♠❛✐s ✭❝❢✳ ❬✶✻❪✮✱ t❛♠❜é♠ ❞❡♥♦♠✐♥❛❞♦ ❞❡ t❡♦r❡♠❛ ❞❡ ●♥❡❞❡♥❦♦ ♦✉ t❡♦r❡♠❛ ❞❡ ❋✐s❤❡r✲❚✐♣♣❡t✲●♥❡❞❡♥❦♦✱ é ❛♣r❡s❡♥t❛❞♦ ❡♠ s❡❣✉✐❞❛✿

❚❡♦r❡♠❛ ✷✳✶ ✭❚❡♦r❡♠❛ ❞❡ t✐♣♦s ❡①tr❡♠❛✐s✮ ❙❡❥❛ {Xn}n≥1 ✉♠❛ s✉❝❡ssã♦

❞❡ ✈❛r✐á✈❡✐s ❛❧❡❛tór✐❛s✳ ❙❡ ❡①✐st❡♠ s✉❝❡ssõ❡s ❞❡ ❝♦♥st❛♥t❡s {an}n≥1 (an ≥ 0)✱

{bn}n≥1 ❡ ✉♠❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ♥ã♦ ❞❡❣❡♥❡r❛❞❛G t❛✐s q✉❡

lim

n→∞P

Mn−bn

an ≤

x

= lim

n→∞F

n₍_a

nx+bn) = G(x), ∀x∈C(G), ✭✷✳✼✮

❡♥tã♦✱ G ♣❡rt❡♥❝❡ ❛ ✉♠ ❞♦s três t✐♣♦s ❞❡ ❞✐str✐❜✉✐çã♦ ❞❡ ✈❛❧♦r❡s ❡①tr❡♠♦s✿

❋ré❝❤❡t: Φα(x) =

  

0, x_≤0

α >0

exp(₋x−α₎_{, x >} ₀ ✭✷✳✽✮

❲❡✐❜✉❧❧: Ψα(x) =

  

exp(₋(₋x)α₎_{, x}_≤₀

α >0

1, x >0

✭✷✳✾✮

●✉♠❜❡❧: Λ(x) = exp(₋exp(₋x)), x_∈R_. _{✭✷✳✶✵✮}

❆s ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ ❞❡✜♥✐❞❛s ❡♠ ✭✷✳✽✮✱ ✭✷✳✾✮ ❡ ✭✷✳✶✵✮ tê♠✱ r❡s♣❡t✐✈❛♠❡♥t❡✱ ❝♦♠♦ ❢✉♥çã♦ ❞❡ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❛s s❡❣✉✐♥t❡s ❢✉♥çõ❡s✿

ψ(x, α) = α_·x−α−1_·exp(₋x−α), x >0 ✭✷✳✶✶✮

ϕ(x, α) = ₋(₋1)α_·xα−1_·α_·exp[₋(₋1)αxα] x <0 ✭✷✳✶✷✮

λ(x) = exp(₋x₋exp(₋x)) ✭✷✳✶✸✮

◆❛ ❋✐❣✉r❛ ✷✳✶ t❡♠♦s ❛ r❡♣r❡s❡♥t❛çã♦ ❞❛ ❢✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡

❡♠ ✭✷✳✶✸✮ ❝♦♠♦ t❛♠❜é♠ ❞❛s ❢✉♥çõ❡s ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ ψ ❡ ϕ ♣❛r❛

α= 1✳

❆s ❞✐str✐❜✉✐çõ❡s ❞❡ ✈❛❧♦r❡s ❡①tr❡♠♦s ♣♦❞❡♠ s❡r r❡♣r❡s❡♥t❛❞❛s ♣♦r ♠❡✐♦ ❞❡ ✉♠❛ ú♥✐❝❛ ❢❛♠í❧✐❛ ❞❡ ❢✉♥çõ❡s ❞❡♥♦♠✐♥❛❞❛ ❞❡ ❞✐str✐❜✉✐çã♦ ❣❡♥❡r❛❧✐③❛❞❛ ❞❡ ✈❛❧♦r❡s ❡①tr❡♠♦s ✭●❊❱✱ ❞♦ ✐♥❣❧ês ❣❡♥❡r❛❧✐③❡❞ ❡①tr❡♠❡ ✈❛❧✉❡✮✱ ❞❡✜♥✐❞❛ ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦

Gγ(x) =     

exp(₋(1 +γx)−1/γ₎_, _♣❛r❛ _{1 +}_{γx >}₀_, _s❡ _γ ₆_{= 0}_,

exp(₋exp(₋x)), ♣❛r❛ x_∈R _s❡ _γ _{= 0}_.

(26)

✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✾

−4 ₋2 0 2 4

0 0.5 1 1.5

x

y

❢✳❞✳♣✳ ❋ré❝❤❡t ❢✳❞✳♣✳ ❲❡✐❜✉❧❧ ❢✳❞✳♣✳ ●✉♠❜❡❧

❋✐❣✉r❛ ✷✳✶✿ ❆ ❢✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ λ ❡ ❛s ❢✉♥çõ❡s ❞❡♥s✐❞❛❞❡

♣r♦❜❛❜✐❧✐❞❛❞❡ ψ ❡ϕ ♣❛r❛ α= 1✳

❆ ❢✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❝♦rr❡s♣♦♥❞❡♥t❡ ❛ ✭✷✳✶✹✮ é ❞❛❞❛ ♣♦r ✭❝❢✳ ❬✷✾❪✮

gγ(z) =             

exph₋ 1 +γx−

1 γ

i

·h1 +γxi−

1 γ−1

, ♣❛r❛ 1 +γx >0,

s❡γ ₆= 0,

exp(₋exp(₋x))_·exp(₋x) , ♣❛r❛ x_∈R _s❡_γ _{= 0}_. ✭✷✳✶✺✮

❖ ♣❛râ♠❡tr♦ ❞❡ ❢♦r♠❛γ é ❞❡♥♦♠✐♥❛❞♦ ❞❡ í♥❞✐❝❡ ❞❡ ✈❛❧♦r❡s ❡①tr❡♠♦s ✭❊❱■✮✳

❆ ✉♥✐✜❝❛çã♦ ❞❛s três ❢❛♠í❧✐❛s✱ ❋ré❝❤❡t✱ ❲❡✐❜✉❧❧ ❡ ●✉♠❜❡❧✱ ♣❡❧❛ ❞✐str✐❜✉✐çã♦ ●❊❱ é ❛tr✐❜✉í❞❛ ❛ ✈♦♥ ▼✐s❡s ❬✹✼❪ ❡ ❏❡♥❦✐♥s♦♥ ❬✷✽❪✱ s❡♥❞♦ ♣♦r t❛❧ ❞❡♥♦♠✐♥❛❞❛ ❞❡ ♣❛r❛♠❡tr✐③❛çã♦ ❞❡ ✈♦♥ ▼✐s❡s✲❏❡♥❦✐♥s♦♥✳ ❊st❛ ♣❛r❛♠❡tr✐③❛çã♦ ♣♦❞❡ s❡r ❡s❝r✐t❛ ❡♠ ❢✉♥çã♦ ❞❛s ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ ❡♠ ✭✷✳✽✮✱ ✭✷✳✾✮ ❡ ✭✷✳✶✵✮ ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦ ✭❝❢✳ ❬✸✾❪✮

Gγ(x) =        Φ1

γ(1 +γx) s❡ γ >0,

Ψ₋1

γ(−(1 +γx) s❡ γ <0,

Λ(x) s❡ γ = 0.

◆♦t❡♠♦s q✉❡ limγ→0Gγ(x) = G0(x) ♦♥❞❡ G0 é ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦

(27)

✶✵ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

r❡s✉❧t❛ ♥❛ ❢❛♠í❧✐❛ ❝♦♠♣❧❡t❛ ❞❡ ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ ●❊❱ ❞❡✜♥✐❞❛ ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦

Gγ,σ,µ(z) = exp

−

1 +γ

z₋µ σ

−1/γ

✭✷✳✶✻✮

❞❡✜♥✐❞❛ ❡♠ {z : 1 + γ(z ₋ µ)/σ > 0_}✱ ♦♥❞❡ _−∞ < µ < +_∞✱ σ > 0 ❡

−∞< γ <+_∞ ❬✶✷❪✳

■st♦ ♣❡r♠✐t❡ r❡❡s❝r❡✈❡r ♦ ❚❡♦r❡♠❛ ✷✳✶ ✭❝❢✳✱ ❡✳❣✳ ❬✷✹❪✮ ❞❡ ♦✉tr❛ ❢♦r♠❛✿

❚❡♦r❡♠❛ ✷✳✷ ✭❚❡♦r❡♠❛ ❯♥✐✜❝❛❞♦ ❞♦s ❚✐♣♦s ❊①tr❡♠❛✐s✮ ❙❡ ❡①✐st❡♠ ❛s

s✉❝❡ssõ❡s {an}n≥1 (an >0) ❡ {bn}n≥1✱ t❛✐s q✉❡✱ q✉❛♥❞♦ n → ∞

P

Mn−bn

an ≤

z

−→G(z)

♣❛r❛ ❛❧❣✉♠❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦G ♥ã♦✲❞❡❣❡♥❡r❛❞❛✱ ❡♥tã♦Gé ❞♦ ♠❡s♠♦ t✐♣♦

❞❛ ❞✐str✐❜✉✐çã♦ ●❊❱✱ ❞❡✜♥✐❞❛ ❡♠ ✭✷✳✶✻✮✱ ♣❛r❛ ❛❧❣✉♠ γ _∈R_✳

✷✳✷ ❊①❝❡ss♦s ❛❝✐♠❛ ❞❡ ✉♠ ♥í✈❡❧ ❡❧❡✈❛❞♦

❙❡❥❛X✉♠❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ ❝♦♠ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦F ❡xF _{♦ ❧✐♠✐t❡ s✉♣❡r✐♦r}

❞❡F✳ P❛r❛u < xF _{✜①♦✱ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❞❡✜♥✐❞❛ ♣♦r}

Fu(y) = P[X−u≤y|X > u], 0≤y≤xF −u ✭✷✳✶✼✮

é ❞❡♥♦♠✐♥❛❞❛ ❞❡ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❝♦♥❞✐❝✐♦♥❛❧ ❞♦s ❡①❝❡ss♦s ❛❝✐♠❛ ❞❡ u

❬❝❢✳✱ ❬✷✶✱ ✷✹❪❪✳ ❖ ✈❛❧♦r ❞❡ u é ❞❡♥♦♠✐♥❛❞♦ ❞❡ ♥í✈❡❧ ♦✉ ❧✐♠✐❛r ❡❧❡✈❛❞♦ ❡ ♦s ✈❛❧♦r❡s

y=x₋usã♦ ❞❡s✐❣♥❛❞♦s ❞❡ ❡①❝❡ss♦s✳

❖❜s❡r✈❡♠♦s q✉❡

Fu(y) = P[X−u≤y|X > u]

= P[X−u≤y, X > u]

P[X > u]

= P[u < X ≤u+y]

P[X > u]

= F(u+y)−F(u)

1₋F(u) ✭✷✳✶✽✮

❆ss✐♠✱ ❛s ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ Fu ❡F✱ r❡♣r❡s❡♥t❛❞❛s ♥❛ ❋✐❣✉r❛ ✷✳✷✱ ❡stã♦

(28)

✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✶✶

x

u xF

Fu

F(x)

1

0 y

xF −u

Fu(y) 1

0

❋✐❣✉r❛ ✷✳✷✿ ❋✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ F ❡ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ❝♦♥❞✐❝✐♦♥❛❧Fu✳

❙❡❣✉♥❞♦ P✐❝❦❛♥❞s ❡♠ ❬✸✻❪ ❡ ❇❛❧❦❡♠❛ ❡ ❞❡ ❍❛❛♥ ❡♠ ❬✸❪✱ ❛ ❢✉♥çã♦ ❞❡

❞✐str✐❜✉✐çã♦ Fu ♣♦❞❡ s❡r ❜❡♠ ❛♣r♦①✐♠❛❞❛ ♣♦r ✉♠❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P✱

✐✳❡✳ ∃y_∈R_, _∃_σ_u _>₀_✿

Fu(y)≈Wγ,σu(y) :=

          

1₋ 1 + _σγy

u

−1/γ

, ♣❛r❛ y_≥0, s❡γ >0,

1₋exp ₋ _σy

u

, ♣❛r❛ y_≥0, s❡γ = 0,

1₋ 1 + _σγy

u

−1/γ

, ♣❛r❛ 0_≤y_{≤ −}σu

γ , s❡γ <0. ✭✷✳✶✾✮ ■st♦ é✱ ♣♦❞❡♠♦s ❝♦♥s✐❞❡r❛r

Fu(y)≈Wγ,σu(y)

♣❛r❛ y _∈ [0, xF ₋_u_]_{✱ s❡} _γ _≥ ₀_{✱ ❡ ♣❛r❛} _y _∈ _[0_,₋σu

γ ] s❡ γ < 0✳ ❖ t❡♦r❡♠❛ ❞❡♠♦♥str❛❞♦ ♣♦r P✐❝❦❛♥❞s✱ ❇❛❧❦❡♠❛ ❡ ❞❡ ❍❛❛♥ é ♦ s❡❣✉✐♥t❡✿

❚❡♦r❡♠❛ ✷✳✸ ✭❚❡♦r❡♠❛ P✐❝❦❛♥❞s✲❇❛❧❦❡♠❛✲❞❡ ❍❛❛♥✮

F _{∈ D}(Gγ), γ ∈R⇐⇒ lim

u→xF sup

0<y<xF₋_u|

Fu(y)−Wγ,σu(y)|= 0.

➱ ❞❡ s❛❧✐❡♥t❛r q✉❡ ❡①✐st❡ ✉♠❛ ❢♦rt❡ ❞✉❛❧✐❞❛❞❡ ❡♥tr❡ ❛ ❞✐str✐❜✉✐çã♦ ●P ❡ ❛ ❞✐str✐❜✉✐çã♦ ●❊❱✳ ❆♥❛❧✐s❡♠♦s ❝♦♠ ♠❛✐s ♣♦r♠❡♥♦r ❡ss❛ ❞✉❛❧✐❞❛❞❡ ❬✶✷✱ ✸✵❪✳

❙❡❥❛ ♥♦✈❛♠❡♥t❡ X ✉♠❛ ✈❛r✐á✈❡❧ ❛❧❡❛tór✐❛ ❝♦♠ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ F✳ ◆❛s

❝♦♥❞✐çõ❡s ❞♦ ❚❡♦r❡♠❛ ✷✳✷✱ ♣❛r❛ n s✉✜❝✐❡♥t❡♠❡♥t❡ ❣r❛♥❞❡✱ t❡♠♦s

Fn(z)_≈exp

−

1 +γ

z₋µ σ

−1/γ

♣❛r❛ ❛❧❣✉♠ µ, γ _∈R _❡ _{σ >}₀_{✳ ❈♦♥s❡q✉❡♥t❡♠❡♥t❡}

nlogF(z)_{≈ −}

1 +γ

z₋µ σ

−1/γ

(29)

✶✷ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

P❛r❛ ✈❛❧♦r❡s ❣r❛♥❞❡s ❞❡ z✱ ❛ ❡①♣❛♥sã♦ ❡♠ sér✐❡ ❞❡ ❚❛②❧♦r ✐♠♣❧✐❝❛ q✉❡

logF(z)_{≈ −{}1₋F(z)_}.

❙✉❜st✐t✉✐♥❞♦ ❡♠ ✭✷✳✷✵✮✱ ♦❜t❡♠♦s

n(_−{1₋F(z)_})_{≈ −}

1 +γ

z₋µ σ

−1/γ

,

❞❛ q✉❛❧ ❞❡❝♦rr❡

1₋F(u)_≈ 1

n

1 +γ

u₋µ σ

−1/γ

,

s❡ t♦♠❛r♠♦s ♣❛r❛z ✉♠ ✈❛❧♦r u ❡❧❡✈❛❞♦✳ ❆♥❛❧♦❣❛♠❡♥t❡✱ t♦♠❛♥❞♦ y >0✱

P(X > u+y) = 1₋F(u+y)_≈ 1

n

1 +γ

u+y₋µ σ

−1/γ

. ✭✷✳✷✶✮

❈♦♥s❡q✉❡♥t❡♠❡♥t❡✱

P r(X > u+y_|X > u) _≈ n

−1_{[1 +}_γ₍_u₊_y₋_µ₎_/σ_]−1/γ

n−1_{[1 +}_γ₍_u₋_µ₎_/σ_]−1/γ

=

1 + γy/σ 1 +γ(u₋µ)/σ

−1/γ

=

1 + γy

σu

−1/γ

,

♦♥❞❡ σu =σ+γ(u−µ)✳

❊♠ r❡s✉♠♦✱ t❡♠♦s ♦ s❡❣✉✐♥t❡ t❡♦r❡♠❛ ✭❝❢✳ ❬✶✷❪✮✳

❚❡♦r❡♠❛ ✷✳✹ ❙❡❥❛ Xi ✉♠ t❡r♠♦ ❛r❜✐trár✐♦ ❞❛ s✉❝❡ssã♦ ❞❡ ✈❛r✐á✈❡✐s ❛❧❡❛tór✐❛s

✐♥❞❡♣❡♥❞❡♥t❡s ❡ ✐❞❡♥t✐❝❛♠❡♥t❡ ❞✐str✐❜✉í❞❛s {Xn}n≥1 ❝♦♠ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦

❝♦♠✉♠ ❋✳ ❙✉♣♦♥❤❛♠♦s q✉❡ ❋ s❛t✐s❢❛③ ❛s ❝♦♥❞✐çõ❡s ❞♦ ❚❡♦r❡♠❛ ✷✳✷✱ ♣❛r❛ ✉♠ n

❣r❛♥❞❡✱

P r_{Mn ≤z} ≈G(z), ♦♥❞❡

G(z) = exp

−

1 +γ

z₋µ σ

−1/γ

♣❛r❛ ❛❧❣✉♠ µ, γ _∈R _❡ _{σ >} ₀_{✳ ❊♥tã♦✱ ♣❛r❛ ✉♠ ✈❛❧♦r} _u _{s✉✜❝✐❡♥t❡♠❡♥t❡ ❣r❛♥❞❡✱}

❛ ❢✉♥çã♦ ❞✐str✐❜✉✐çã♦ ❞❡ (X₋u) ❝♦♥❞✐❝✐♦♥❛❧ ❛ X > u✱ é ❛♣r♦①✐♠❛❞❛♠❡♥t❡

H(y) = 1₋

1 + γy

σu

−1/γ

(30)

✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✶✸

❝♦♠ {y: y >0 ❡ (1 +γy/σu)>0}

σu =σ+γ(u−µ). ✭✷✳✷✸✮

❖❜s❡r✈❛♠♦s ❛ss✐♠ q✉❡ ♦s ♣❛râ♠❡tr♦s ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦Wγ,σu ♣♦❞❡♠

s❡r ♦❜t✐❞♦s ❡①❝❧✉s✐✈❛♠❡♥t❡ ❞♦s ♣❛râ♠❡tr♦s ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ Gγ,σ,µ

❝♦♥s✐❞❡r❛❞❛✳ ➱ ❞❡ s❛❧✐❡♥t❛r q✉❡ ❛s ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ Gγ,σ,µ ❡ Wγ,σu

♣❛rt✐❧❤❛♠ ♦ ♠❡s♠♦ ♣❛râ♠❡tr♦ ❞❡ ❢♦r♠❛γ✱ ❡ q✉❡ ♦ ♣❛râ♠❡tr♦ ❞❡ ❡s❝❛❧❛ ❞❡Wγ,σu✱

σu✱ é ❡s❝r✐t♦ à ❝✉st❛ ❞♦s três ♣❛râ♠❡tr♦s ❞❡Gγ,σ,µ ❡ ❞♦ ❧✐♠✐❛r ❡❧❡✈❛❞♦ u✳

❖❜s❡r✈❡♠♦s q✉❡✱ s❡♥❞♦ y = x₋u✱ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P ❡♠ ✭✷✳✶✾✮

t❛♠❜é♠ ♣♦❞❡ s❡r ❡①♣r❡ss❛ ❡♠ t❡r♠♦s ❞❡ três ♣❛râ♠❡tr♦s ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦

Wγ,σu,u(x|u) :=

          

1₋ 1 + γ(x_σ−u)

u

−1/γ

, ♣❛r❛ x_≥u, s❡ γ >0,

1₋exp(₋x_σ−u

u ), ♣❛r❛ x≥u, s❡ γ = 0,

1₋ 1 + γ(x_σ−u)

u

−1/γ

, ♣❛r❛ u_≤x_≤1₋ σu

γ , s❡γ <0, ✭✷✳✷✹✮

❝♦♠ ♣❛râ♠❡tr♦ ❞❡ ❢♦r♠❛ γ✱ ♣❛râ♠❡tr♦ ❞❡ ❡s❝❛❧❛ σu ❡ ♣❛râ♠❡tr♦ ❞❡ ❧♦❝❛❧✐③❛çã♦

u✳

❆ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P✱ Hγ✱ ♣♦❞❡ t❛♠❜é♠ s❡r ❡s❝r✐t❛ ❡♠ ❢✉♥çã♦ ❞❛

♣❛r❛♠❡tr✐③❛çã♦ ❞❡ ✈♦♥ ▼✐s❡s✲❏❡♥❦✐♥s♦♥ ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦

Hγ(x) = 1 + lnGγ(x) =   

1₋(1 +γx)−1/γ_, _{1 +}_{γx >}₀_{, x >} ₀_s❡ _γ ₆_{= 0}_,

1₋exp(₋x), x >0 s❡γ = 0.

✭✷✳✷✺✮ ❆❧é♠ ❞✐ss♦✱ ♣♦❞❡ s❡r ❡s❝r✐t❛ à ❝✉st❛ ❞❛s s❡❣✉✐♥t❡s ❢✉♥çõ❡s ❞❡ ❞✐str✐❜✉✐çã♦ ✭❡✳❣✳✱ ❝❢✳✱ ❬✷✹✱ ✸✾❪✮

❊①♣♦♥❡♥❝✐❛❧ : F1(x) = 1−e−x, x >0

P❛r❡t♦ : F2,α(x) = 1−x−α, x >1, α >0

❇❡t❛ s✐♠étr✐❝❛ : F3,α(x) = 1−(−x)−α, −1< x <0, α >0

❞❛ s❡❣✉✐♥t❡ ❢♦r♠❛✿

Hγ(x) =       

F_2,1

γ(1 +γx) s❡ γ >0,

F_3,₋1

γ(−(1 +γx)) s❡ γ <0,

(31)

✶✹ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

◆♦t❡♠♦s q✉❡ limγ→0Hγ(x) = H0(x)✱ ♦♥❞❡ H0 r❡♣r❡s❡♥t❛ ❛ ❢✉♥çã♦ ❞❡

❞✐str✐❜✉✐çã♦ ❡①♣♦♥❡♥❝✐❛❧✱ ❡ q✉❡ ♣♦❞❡♠♦s t❛♠❜é♠ ❞❡✜♥✐r s✉❝✐♥t❛♠❡♥t❡ ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P ❞♦ s❡❣✉✐♥t❡ ♠♦❞♦

Hγ,β(x) = 1−

1 +γx β

−1/γ

, ♣❛r❛ x_∈D(γ, β) ✭✷✳✷✻✮

❝♦♠ D(γ, β) = [0,+_∞[ s❡ γ _≥0 ❡ D(γ, β) = [0,₋β/γ] s❡ γ < 0 ❬✶✻❪✳ ❆ ❢✉♥çã♦

❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❝♦rr❡s♣♦♥❞❡♥t❡ é ❞❛❞❛ ♣♦r

hγ,β(x) =

1

β

1 +γx β

−1

γ−1

, x_∈D(γ, β). ✭✷✳✷✼✮

◆❛ ❋✐❣✉r❛ ✷✳✸ t❡♠♦s ❛s r❡♣r❡s❡♥t❛çõ❡s ❣rá✜❝❛s ❞❛s ❢✉♥çõ❡s ❞❡♥s✐❞❛❞❡ ❞❡

♣r♦❜❛❜✐❧✐❞❛❞❡ hγ,β ♣❛r❛ β = 1 ❡ ♣❛r❛ γ ✐❣✉❛❧ ❛ 0.5✱ 0❡ −0.25✳

0 1 2 3 4 5

0 0.2 0.4 0.6 0.8 1

x

y

γ = 0.5

γ = 0

γ =₋0.25

❋✐❣✉r❛ ✷✳✸✿ ❋✉♥çã♦ ❞❡♥s✐❞❛❞❡ ❞❡ ♣r♦❜❛❜✐❧✐❞❛❞❡ hγ,1 ♣❛r❛ γ = 0.5, 0 ❡ −0.25✳

❉❡ ❡♥tr❡ ❛s ♣r♦♣r✐❡❞❛❞❡s ❞❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P ❡♥✉♥❝✐❛❞❛s ♣♦r ❊♠❜r❡❝❤❡ts ❡t ❛❧✳ ❡♠ ❬✶✻❪✱ s❛❧✐❡♥t❛♠♦s ❛ ♣r♦♣r✐❡❞❛❞❡ ✈❡r✐✜❝❛❞❛ ❡♠ s❡❣✉✐❞❛✳

❙❡❥❛ xi ∈ D(γ, β)✱ i ∈ {1,2}✳ ❈♦♥s✐❞❡r❛♥❞♦ H¯γ,β = 1−Hγ,β ❝♦♠ ❛ ❢✉♥çã♦

(32)

✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s ✶✺

¯

Hγ,β(x1+x2)

¯

Hγ,β(x1)

=

1₋1 +

1 +γx1+x2 β

−1/γ

1₋1 +

1 +γx1 β

−1/γ

= β+γ(x1+x2)

β+γx1

!−1/γ

=

_β₊_γx

1+γx2

β+γx1

−1/γ

=

1 + γx2

β+γx1

−1/γ

= 1₋

"

1₋

1 + γx2

β+γx1

−1/γ#

= 1₋Hγ,β+γx1(x2) ❉❡ ♦♥❞❡ ✈❡♠ q✉❡

¯

Hγ,β(x1+x2)

¯

Hγ,β(x1)

= 1₋Hγ,β+γx1(x2) = ¯Hγ,β+γx1(x2). ✭✷✳✷✽✮

❆ ✐❣✉❛❧❞❛❞❡ ✭✷✳✷✽✮ ♣❡r♠✐t❡ ❝♦♥st❛t❛r q✉❡ ❛ ♣r♦❜❛❜✐❧✐❞❛❞❡ ❞❛ ✈❛r✐á✈❡❧ X

❡①❝❡❞❡r ♦ ❧✐♠✐❛r x1+x2 ❞❛❞♦ q✉❡ ❡①❝❡❞❡ x1 ♣♦❞❡ s❡r ♦❜t✐❞❛ ♣♦r ✉♠❛ ❢✉♥çã♦ ❞❡

❞✐str✐❜✉✐çã♦ ●P✳ ❙❡ t♦♠❛r♠♦s ❛ ❢✉♥çã♦ ❞❡ ❞✐str✐❜✉✐çã♦ ●P Wγ,σu ❡xi ∈D(γ, β)✱

i_{∈ {}1,2_} ❝♦♠ β =σu t❡♠♦s

¯

Wγ,σu(x1+x2)

¯

Wγ,σu(x1)

≈ 1−₁Fu(x1+x2) −Fu(x1)

= 1−P[X−u≤x1 +x2|X > u] 1₋P[X₋u_≤x1|X > u]

= P[X−u > x1 +x2|X > u]

P[X₋u > x1|X > u]

= P[X > x1+x2+u|X > u]

P[X > x1+u|X > u]

= P[X > x1+x2]

P[X > x1]

,

❡ s❡ ❝♦♥s✐❞❡r❛r♠♦sx1 ≤x2✱ ❡♥tã♦ ♦❜t❡♠♦s

¯

Wγ,σu(x1+x2)

¯

Wγ,σu(x1)

(33)

✶✻ ✷✳ ❙♦❜r❡ ❛ ❚❡♦r✐❛ ❞♦s ❱❛❧♦r❡s ❊①tr❡♠♦s

❉❡ ✭✷✳✷✽✮ ❡ ✭✷✳✷✾✮✱ ✈❡♠ q✉❡

P[X > x1+x2|X > x1] = ¯Wγ,σu+γx1(x2).