Repositório Institucional UFC: Leis de potência no regime estacionário do escoamento bifásico em meios porosos

(1)

DEPARTAMENTO DE F´ISICA

PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

JONATHAN M ´ARCIO AM ˆANCIO SALES

LEIS DE POT ÊNCIA NO REGIME ESTACION ÁRIO DO ESCOAMENTO BIF ÁSICO EM MEIO POROSOS

(2)

Dissertação de Mestrado apresentada ao Pro-grama de Pós-Graduação em F´ısica da Univer-sidade Federal do Ceará, como requisito parcial para a obtenção do T´ıtulo de Mestre em F´ısica.

´

Area de Concentração: F´ısica da Matéria Con-densada.

Orientador: Prof. Dr. Claudio Lucas Nunes de Oliveira.

(3)

Dissertação de Mestrado apresentada ao Pro-grama de Pós-Graduação em F´ısica da Univer-sidade Federal do Ceará, como requisito parcial para a obtenção do T´ıtulo de Mestre em F´ısica.

´

Area de Concentração: F´ısica da Matéria Con-densada.

Aprovada em 14/09/2017.

BANCA EXAMINADORA

Prof. Dr. Claudio Lucas Nunes de Oliveira (Orientador) Universidade Federal do Cear´a (UFC)

Prof. Dr. José Soares de Andrade Júnior Universidade Federal do Ceará (UFC)

(4)

S155l Sales, Jonathan Márcio Amâncio.

Leis de potência no regime estacionário do escoamento bifásico em meio porosos / Jonathan Márcio Amâncio Sales. – 2017.

58 f. : il. color.

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Programa de Pós-Graduação em Física, Fortaleza, 2017.

Orientação: Prof. Dr. Claudio Lucas Nunes de Oliveira.

1. Escoamento Bifásico. 2. Meios Porosos. 3. Leis de Potência. 4. Fluidos. I. Título.

(5)

(6)

Agradeço, acima de tudo, a Cristo, meu Senhor, a quem devo toda a minha vida. Agradeço a minha esposa e melhor amiga Juliana Monteiro da Costa Sales por todo seu amor, sua dedicação, sua compreensão e por sempre estar ao meu lado.

Agradeço aos meus pais Márcio Moreira Sales e Vânia Amâncio Sales por todo apoio que me deram, pelos incentivos e por todos os seus conselhos; e também às minhas irmãs Mylena Amâncio Sales Silva e Amanda Caroline Amâncio Sales.

Agradeço ao meu orientador, Professor Dr. Claudio Lucas Nunes de Oliveira, por todo apoio e pela excelente orientação neste trabalho.

Agradeço também aos meus amigos e colegas do Grupo de Sistemas Complexos, a saber, Wagner Sena, Aurélio Wildson, Emanuel Fontelles, Samuel Morais, João Paulo Nou-gueira, William Mesquita, César Menezes e Rilder Pires.

Agradeço também aos professores, amigos e colegas do Departamento de F´ısica da Universidade Federal do Ceará.

(7)

O escoamento de dois fluidos imisc´ıveis em meios porosos ocorre espontaneamente na natureza mas também pode ser induzido por ações humanas. O exemplo mais óbvio deste último caso é a injeção de um fluido (normalmente água ou gás) em um reservatório de petróleo. De fato, devido à sua aplicação tecnológica, tal tema tem sido objeto de pesquisa há décadas. Entretanto, a maioria destes estudos se concentra no deslocamento de uma fase por outra, onde a interface entre elas se move em um regime transiente até atingir uma dada região (usualmente, o poço produtor). Essa perspectiva é importante em uma abordagem macroscópica onde o interesse é retardar o tempo debreakthrough, ou seja, o tempo que o fluido injetado leva até alcançar o poço produtor. Por outro lado, em uma abordagem mesoscópica, na escala do tamanho dos poros, a interface não é abrupta e os canais porosos são alimentados por ambos os fluidos. Isto produz uma competição desorganizada no escoamento, mas que durante um curto intervalo de tempo pode levar a um escoamento estacionário onde a velocidade de cada fluido, e portanto, a permeabilidade relativa de cada fase, não muda com o tempo. Esse tipo de escoamento es-tacionário e sua influência na propagação macroscópica da frente de invasão ainda são pouco conhecidos. Neste trabalho, nós estamos interessados em investigar o deslocamento de dois fluidos no regime estacionário de escoamento bifásico em meios porosos. Para obter o regime estacionário nós consideramos um meio poroso bidimensional com condições periódicas de contorno em ambas as direções. Por isso, nosso sistema pode ser compreendido como duas fa-ses se movendo na superf´ıcie de um toro poroso. O regime estacionário é então definido quando a velocidade (que está relacionada com a permeabilidade relativa) de ambas as fases oscila em torno de um valor médio, que não muda com o tempo. Nós, então, mostramos que, neste regime, as oscilações na série temporal da velocidade apresentam leis de potência caracter´ısticas cujos expoentes dependem da quantidade (saturação) e das propriedades dos fluidos. Por exemplo, a distribuição de avalanches das velocidades, que ocorrem devido a formação de bolhas de fluido, de diferentes tamanhos, que ficam presas nos canais porosos durante um tempo e são libera-das repentinamente no fluxo alterando assim a velocidade e a permeabilidade relativa da fase, depende da saturação das fases fluidas envolvidas e, também, do valor da tensão interfacial.

(8)

be induced by human actions. The most obvious example of this latter case is the injection of a fluid (usually water or gas) into an oil reservoir. In fact, due to its technological application, this theme has been the object of research for decades. However, most of those studies focus on the displacement of a phase due to another, where the interface between them moves in a transient regime until it reaches a given region (usually the producing well). This perspective is important in a macroscopic approach where the interest is delaying the breakthrough time, that is, the time that the injected fluid takes until reaching the producing well. On the other hand, in a mesoscopic approach, in the pore size scale, the interface is not abrupt and the porous channels are fed by both fluids. This produces a disorganized competition in the flow, but which for a short time can lead to a steady flow where the velocity of each fluid, and hence the relative permeability of each phase, does not change with time. This type of steady flow and its influence on the macroscopic spread of the invasion front is still not well known. In this paper, we are interested in investigating the displacement of two fluids in the steady state biphasic flow regime in porous media. To obtain the steady state we consider a two dimensional porous medium with periodic boundary conditions in both directions. Therefore, our system can be understood as two phases moving on the surface of a porous torus. The steady state is then defined when the velocity (which is related to the relative permeability) of both phases oscillates around an average value, which does not change with time. We then show that in this regime the oscillations in the time series of velocity have characteristic power laws whose exponent depends on the quantity (saturation) and properties of the fluids. For example, the avalanche distribution of velocities occurring due to the formation of fluid bubbles of different sizes that become trapped in the porous channels for a time and are suddenly released into the stream thereby altering the velocity and the relative permeability of the phase, depends on the saturation of the fluid phases involved and also on the value of the interfacial tension.

(9)

Figura 1 – Experiˆencia cl´assica das duas placas. . . 17

Figura 2 – Molhabilidade e ˆangulo de contato. . . 25

Figura 3 – O meio poroso. . . 34

Figura 4 – A malha de discretizac¸˜ao do meio poroso. . . 34

Figura 5 – Configurac¸˜ao inicial do escoamento de duas fases newtonianas. . . 35

Figura 6 – Escoamento bifásico após 50.000 iterações. . . 38

Figura 7 – Mapa da magnitude da velocidade após50.000iterações. . . 39

Figura 8 – Avalanches (bursts) em uma s´erie temporal. . . 42

(10)

Gráfico 1 – Tensão de cisalhamento em função da taxa de deformação. . . 21

Gráfico 2 – Comparação da área da interface entre os fluidos. . . 36

Gráfico 3 – Velocidade média (componente na direçãox),hVxi, em função do número de iterações. . . 37

Gráfico 4 – Análise das séries temporais da velocidade através do método DFA. . . 41

Gráfico 5 – Análise da distribuição dos tamanhos das avalanches nas séries temporais da velocidade. . . 43

Gráfico 6 – Saltos de velocidade (∆v) em função do número de iterações. . . 44

Gráfico 7 – Análise das distribuições dos valores absolutos dos saltos de velocidade,|∆v(t)|, nas séries temporais da velocidade médiahVx(t)i, paraγ = 0.0001N/m. . . 45

Gráfico 8 – Análise das distribuições dos valores absolutos dos saltos de velocidade,|∆v(t)|, nas séries temporais da velocidade médiahVx(t)i, paraγ = 0.010e0.030N/m. 46 Gráfico 9 – Viscosidade aparente em função da taxa de deformação de um fluido não-newtoniano com duas viscosidades. . . 47

Gráfico 10 –Saturação em função da taxa de deformação cr´ıtica. . . 48

Gráfico 11 –Velocidade média (na direçãox) em função da taxa de deformação cr´ıtica. .ˆ 49 Gráfico 12 –Permeabilidade efetiva em função da taxa de deformação cr´ıtica. . . 49

Gr´afico 13 –Primeiro passo do m´etodo DFA. . . 52

Gr´afico 14 –Segundo passo do m´etodo DFA. . . 53

(11)

Tabela 1 – Comparação dos expoentes obtidos a partir do método DFA. . . 40 Tabela 2 – Comparação dos expoentes das distribuições dos tamanhos das avalanches. . 42 Tabela 3 – Comparação dos expoentes obtidos das distribuições dos valores absolutos

(12)

m Massa

ρ Massa espec´ıfica ou densidade ~g Acelerac¸˜ao local da gravidade

~

P Momento linear

~

V ou~u Velocidade

Vx Componente da velocidade na direc¸˜aoxˆ VT Velocidade terminal ou limite

hVx(t)i M´edia volum´etrica deVx no instante de tempot

Q Vaz˜ao

p Press˜ao

pcap Press˜ao capilar

T Temperatura

µ Coeficiente de viscosidade dinˆamica ou absoluta η Coeficiente de viscosidade aparente ou efetiva

φ Porosidade

k Coeficiente de permeabilidade absoluta kef Coeficiente de permeabilidade efetiva

S Saturac¸˜ao

S1 Saturação do fluido de viscosidadeµ= 0.1 M Razão da viscosidade

~

F Forc¸a

γ Tens˜ao superficial

σ Tens˜ao normal

τ Tens˜ao de cisalhamento ˙

γ Taxa de deformac¸˜ao ˙

(13)

1 INTRODUC¸ ˜AO . . . 13

1.1 Descric¸˜ao do problema f´ısico e objetivo . . . 13

1.2 Organização da dissertação . . . 14

2 ESCOAMENTO MULTIF ´ASICO EM MEIOS POROSOS . . . 15

2.1 Fluidos . . . 15

2.1.1 Viscosidade . . . 17

2.2 Meios Porosos . . . 21

2.2.1 Porosidade e Permeabilidade . . . 22

2.3 Escoamento multif´asico . . . 22

2.3.1 Tens˜ao superficial e Molhabilidade . . . 23

2.3.2 Press˜ao Capilar . . . 25

2.3.3 Lei de Darcy . . . 26

2.3.4 Escoamento em um Tubo Capilar . . . 26

2.4 Equações básicas da dinâmica de fluidos . . . 27

2.4.1 Conservac¸˜ao da massa . . . 27

2.4.2 Equac¸˜ao do momento linear . . . 28

2.4.3 Equac¸˜oes de Navier-Stokes . . . 29

3 FORMULAÇ ÃO DO PROBLEMA, RESULTADOS E DISCUSS ÕES . . . 33

3.1 Formulação do Problema e da Solução . . . 33

3.2 Resultados e Discuss˜oes . . . 35

3.2.1 An´alise das s´eries temporais da velocidade . . . 40

3.2.1.1 Método de análise de flutuações sem tendências . . . 40

3.2.1.2 Avalanches . . . 41

3.2.1.3 Saltos . . . 44

3.3 Fluido N˜ao-Newtoniano com duas viscosidades . . . 47

4 CONCLUS ˜AO . . . 51

AP ˆENDICE A -- M ´ETODO DFA . . . 52

(14)

1 INTRODUC¸ ˜AO

O escoamento de dois fluidos imisc´ıveis em meios porosos pode ocorrer esponta-neamente na natureza, como também pode ser induzido por ações humanas. Considerando este último caso, certamente o primeiro exemplo que nos vem a mente é a recuperação de petróleo através da injeção de um fluido (normalmente água ou gás) em um reservatório de petróleo. De fato, devido à sua grande aplicação tecnológica, o escoamento em meios porosos tem sido, há décadas, objeto de pesquisa de diversos campos das Ciências e Engenharias. Entretanto, muitos desses estudos se concentram no deslocamento de uma fase por outra, onde a interface entre elas se move em um regime transiente até atingir uma dada região (usualmente, o poço produtor).

Essa perspectiva é importante em uma abordagem macroscópica onde o interesse é retardar o tempo debreakthrough, ou seja, o tempo que o fluido injetado leva até alcançar o poço produtor. Por outro lado, em uma abordagem mesoscópica, na escala do tamanho dos poros, a interface não é abrupta e os canais porosos são alimentados por ambos os fluidos. Isto produz uma competição desorganizada no escoamento, mas que durante um curto intervalo de tempo pode levar a um escoamento estacionário onde a velocidade de cada fluido, e portanto, a permeabilidade relativa de cada fase, não muda com o tempo. Esse tipo de escoamento es-tacionário e sua influência na propagação macroscópica da frente de invasão ainda são pouco conhecidos.

1.1 Descric¸˜ao do problema f´ısico e objetivo

O comportamento dos fluidos pode ser descrito pelas equações de Navier-Stokes, que consistem em um conjunto de equações diferenciais parciais não-lineares que se baseiam em leis de conservação, tais como as conservações de massa (equação da continuidade), de mo-mento linear, de momo-mento angular e de energia. A partir dessas equações, pode-se determinar os campos de velocidade e de pressão em um escoamento, porém, na prática, devido a alta comple-xidade matemática presente nessas equações, apenas casos mais simples podem ser resolvidos analiticamente [1]. Além disso, as condições iniciais e as condições de contorno fazem com que as soluções, para a maioria das situações, sejam dif´ıceis ou até mesmo imposs´ıveis de se obter. No entanto, as equações de Navier-Stokes podem ser simplificadas de modo significativo dependendo das propriedades dos fluidos envolvidos e do tipo de escoamento, possibilitando assim uma solução numérica [2].

(15)

e isotérmico. Para tanto, nós consideramos um meio poroso bidimensional com condições periódicas de contorno em ambas as direções. Por isso, nosso sistema pode ser compreen-dido como duas fases newtonianas movendo-se na superf´ıcie de um toro poroso. O regime estacionário é definido quando a velocidade (que, como veremos no próximo cap´ıtulo, está re-lacionada com a permeabilidade relativa por meio da lei de Darcy) de ambas as fases oscila em torno de um valor médio, que não muda com o tempo.

1.2 Organização da dissertação

Essa dissertação está organizada da seguinte forma. O Cap´ıtulo 1 é uma introdução geral aos assuntos que serão abordados nesta dissertação. O Cap´ıtulo 2 é uma introdução à alguns conceitos fundamentais relacionados à Mecânica dos fluidos, no que diz respeito ao escoamento em meios porosos. Nessa parte falaremos sobre as definições de fluido e de vis-cosidade, como também, sobre a caracterização dos fluidos chamados de newtonianos e não-newtonianos. Apresentaremos os conceitos de porosidade e permeabilidade que caracterizam, respectivamente, o meio poroso e como se dá o escoamento de um fluido nesse meio. Também abordaremos questões como tensão superficial, molhabilidade, pressão capilar, lei de Darcy, escoamentos multifásicos, equação de continuidade e as equações de Navier-Stokes.

(16)

2 ESCOAMENTO MULTIF ´ASICO EM MEIOS POROSOS

Neste cap´ıtulo serão discutidos alguns dos conceitos fundamentais do escoamento de fluidos em meios porosos. Primeiramente, abordaremos sobre as propriedades básicas dos fluidos e definiremos o meio poroso, depois discutiremos sobre as equações que descrevem o escoamento dos fluidos através dos canais porosos.

2.1 Fluidos

Fluidos são substâncias que se deformam continuamente quando um esforço de cisalhamento é aplicado [3, 4]. Eles são um subconjunto das fases da matéria que incluem l´ıquidos, gases, plasmas e, até certo ponto, sólidos plásticos. Em termos mais simples, um fluido é uma substância que não consegue resistir a uma força de cisalhamento, por menor que seja a intensidade desta força. Apesar de o termo “fluido” incluir as fases l´ıquida e gasosa, no cotidiano, entretanto, fluido é frequentemente usado como sinônimo de l´ıquido. Por exemplo, o “fluido de freio” em um motor de carro é um óleo incompress´ıvel que não irá funcionar corretamente se houver gás nele. Podemos diferenciar l´ıquidos e gases com base na resistência que o material apresenta quando submetido à compressão: enquanto os l´ıquidos resistem às forças de compressão, os gases apresentam pouca resistência. Essa diferença está relacionada às forças de coesão entre as moléculas dessas substâncias.

A distinção entre sólidos e fluidos, por outro lado, tende a ser mais clara. Entre-tanto, como veremos mais adiante, em alguns casos especiais, como os sólidos plásticos, essa distinção é bem mais confusa. Como já foi dito, os fluidos são incapazes de suportar um esforço de cisalhamento, e em equil´ıbrio estático não resistem à deformação permanente, resistindo ape-nas a taxas relativas de deformação de forma dissipadora, mas podem responder com forças de restauração a tensões normais. Em contraste, os sólidos respondem às ações externas, sejam elas cisalhantes ou normais, com uma força de restauração semelhante a de uma mola, o que significa que pequenas deformações são revers´ıveis. Em um sólido, o esforço de cisalhamento é uma função da tensão, mas em um fluido, o esforço de cisalhamento é uma função da taxa de deformação. Uma consequência desse comportamento é a lei de Pascal, que descreve o papel da pressão na caracterização do estado de um fluido.

(17)

porém, ambos tentarão minimizar sua energia superficial: os l´ıquidos tendem a formar gotas arredondadas, enquanto que os sólidos puros tendem a formar cristais. Os gases, por outro lado, não possuem superf´ıcies livres e difundem-se livremente. Como veremos nos próximos cap´ıtulos, a tensão superficial é uma propriedade de grande relevância no escoamento dos flui-dos.

A estrutura molecular de um fluido é importante para caracterizá-lo, porém não é poss´ıvel descrever seu comportamento, seja em equil´ıbrio ou em movimento, a partir da dinâmica individual das moléculas que o constituem [3]. Em outras palavras, é praticamente imposs´ıvel, seja analitica ou numericamente, estudar os fluidos pela abordagem Lagrangiana. Ao invés disso, o comportamento dos fluidos é descrito com base na hipótese do cont´ınuo, isto é, considerando um fluido como um meio cont´ınuo. Tal abordagem é chamada de Euleriana, onde as propriedades, como massa espec´ıfica, temperatura e velocidade dos fluidos são consi-deradas como tendo um valor definido em cada ponto do espaço e por isso são consiconsi-deradas funções cont´ınuas da posição e do tempo [4].

A hipótese do cont´ınuo é válida quando, para um dado volume de uma substância, este pode ser dividido em elementos de volume, considerados muito pequenos do ponto de vista macroscópico, que contenham um número suficiente de moléculas para que os efeitos médios de suas propriedades dentro de cada elemento de volume sejam constantes ou variem continuamente com o tempo e com a posição [2, 5]. Por exemplo, embora a distribuição das velocidades das moléculas em um fluido seja extremamente não-uniforme [6], a distribuição das velocidades médias dos elementos de fluido não o é. Entretanto, essa hipótese falha sempre que a trajetória média livre das moléculas torna-se da mesma ordem de grandeza que a menor dimensão caracter´ıstica significativa do problema [2, 4]. A esses elementos de volume m´ınimo para os quais a hipótese do cont´ınuo é válida chamaremos de part´ıculas fluidas. Vale destacar que o conceito de um meio cont´ınuo constitui a base da mecânica dos fluidos clássica [4].

Os tipos de forças que agem sobre as part´ıculas fluidas são asforças de superf´ıcie ouforças de contato (e.g., forças de atrito e normal), que são geradas pelo contato com outras part´ıculas ou com superf´ıcies sólidas, e asforças de campo(e.g., forças gravitacional e eletro-magnética), que agem através das part´ıculas [4]. O módulo da força gravitacional, por exemplo, atuando sobre um elemento de fluido de volume dV é dado por ρgdV, onde ρ é a densidade (massa espec´ıfica) do fluido eg é o módulo da aceleração local da gravidade. Já, as forças de superf´ıcie agindo sobre part´ıculas fluidas geram o que chamamos de tensões [4], e podem ser descritas da seguinte forma.

(18)

normalσe uma tensão de cisalhamentoτ são, então, definidas como [4]:

σ = lim δAn→0

δFn δAn =

dFn

dAn, (2.1)

τ = lim δAn→0

δFt δAn =

dFt

dAn. (2.2)

Como veremos mais adiante, dependendo da relação entre a tensão de cisalhamento e a taxa de deformação por cisalhamento e seus derivados, os fluidos podem ser caracterizados como “fluidos newtonianos” ou “fluidos não-newtonianos”. No primeiro, a tensão de cisalha-mento é diretamente proporcional à taxa de deformação, mas no segundo isso não é verdade.

2.1.1 Viscosidade

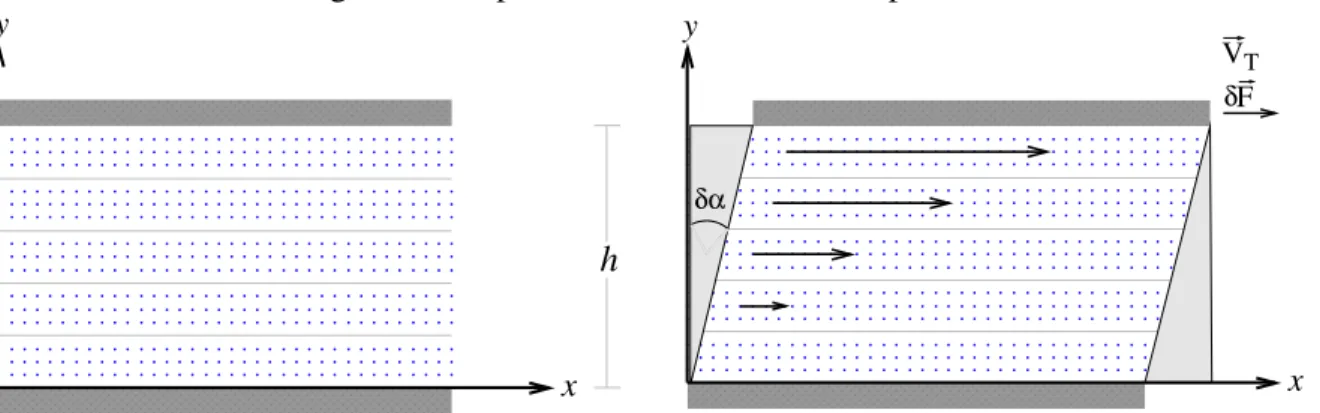
Considere a experiência clássica das duas placas, que consiste em duas placas sólidas paralelas separadas por uma distânciahcom uma porção de fluido incompress´ıvel entre elas, como mostra a Figura 1a. Suponha que o sistema está inicialmente em repouso. Fixando o referencial, em coordenadas cartesianas, na placa inferior e aplicando uma força constante para a direita,δ ~F =δFxx, na placa superior, a experiência mostra que esta última move-se com umaˆ aceleração não nula durante um certo intervalo de tempo, e depois, se move com velocidade constante~u =VTx, chamada velocidade limite ou velocidade terminal [7].ˆ

Figura 1 – Experiˆencia cl´assica das duas placas.

x y

h

(a) Duas placas sólidas paralelas separadas por uma distânciahcom uma porção de fluido entre elas, inicialmente em repouso.

δF

V_T

x y

δα

(b) Uma forc¸a constante,δ ~F, atuando na placa superior faz com que esta se mova a uma velocidade constanteV~T.

A experiência das duas placas é utilizada para calcular a deformação angularδα. Fonte: Elaborado pelo autor.

(19)

cisalhamento,γ, ´e dada por [4]:˙

˙

γ = lim δt→0

δα δt =

dα

dt. (2.3)

Pela Figura 1b, temos que o ˆanguloδα´e dado por:

tanδα= δx

h , (2.4)

mas, para ângulos pequenos,tanδα≈δα. Assim a Equação 2.4 pode ser escrita como:

δα= δx

h . (2.5)

Como a velocidade ´e constante podemos escrever:

VT = δx

δt ⇒δx=VTδt. (2.6)

Combinando as Equações 2.5 e 2.6, teremos que a taxa de deformação será:

dα dt =

VT

h . (2.7)

Devido à ação cisalhante da placa sobre o fluido, este separa-se em lâminas ou camadas paralelas entre si e também paralelas em relação às placas, e que movem-se com velocidades de módulos diferentes [7]. Esse tipo de escoamento em que as part´ıculas fluidas se movem em camadas lisas ou lâminas é chamado deescoamento laminar [4]. Sabe-se, no entanto, que um fluido em contato com uma superf´ıcie sólida não desliza sobre a mesma, pois, o fluido adquire a mesma velocidade da superf´ıcie devido à condição de não deslizamento, que é um fato experimental [4]. Portanto, a lâmina de fluido adjacente à placa móvel se move com a mesma velocidade da placa,VT; e a lâmina de fluido adjacente à placa imóvel permanece com velocidade nula. Os módulos das velocidades das demais lâminas variam linearmente entre os dois extremos, zero e VT [7]. Esse fato experimental pode ser expresso através da seguinte equação:

u(y) =yVT

h . (2.8)

em quey é uma distância genérica em relação à placa inferior. Observe que no escoamento entre as placas existe um gradiente de velocidade dado por [3]:

du dy =

VT

h . (2.9)

Das equações 2.7 e 2.9 teremos que a taxa de deformação será:

dα dt =

du

(20)

cisalhamento,τ, aplicada ao fluido que é dada pela Equação 2.2. Uma tensão de cisalhamento aplicada em um fluido gera, por sua vez, uma taxa de deformação dada pela Equação 2.10. Assim, podemos escrever a tensão de cisalhamento como uma função da taxa de deformação:

τ =τ

du dy

=τ( ˙γ). (2.11)

Os fluidos para os quais a tensão de cisalhamento segue uma relação linear, ou diretamente proporcional, com a taxa de deformação são chamados defluidos newtonianos. Já, os fluidos em que a tensão de cisalhamento não é diretamente proporcional à taxa de cisalhamento são denominadosfluidos não-newtonianos.

Para o escoamento unidimensional de fluidos newtonianos, a relação entre a tensão de cisalhamento e a taxa de deformação é do tipo:

τ ∝ du

dy. (2.12)

Inserindo uma constante de proporcionalidade na Equac¸˜ao 2.12 obtemos a famosa lei de Newton da viscosidade [3, 4, 8]:

τ =µdu

dy, (2.13)

ondeµé o coeficiente de viscosidade dinâmica ou absoluta. A Equação 2.13 é conhecida como lei de Newton da viscosidade (como já foi citado) pelo fato de expressar matematicamente as ideias básicas apontadas na Seção IX “The circular motion of fluids” da obra seminal Philo-sophiae Naturalis Principia Mathematicade Isaac Newton [8, 9, 10].

A viscosidade é definida como a propriedade f´ısica que mede a resistência de um fluido ao escoamento. Assim, quanto maior for a viscosidade de um fluido, maior será sua resistência ao escoamento. A viscosidade dos fluidos se origina do atrito interno [7, 9, 11]. Nos l´ıquidos, esse atrito interno está associado às forças de coesão entre as moléculas; já nos gases, está relacionado à transferência de momento [3, 7]. Da definição de viscosidade como resistência ao escoamento, percebe-se que a taxa de deformação de um fluido depende de sua viscosidade; em comparação com um sólido, a deformação sofrida por este, devido a uma tensão de cisalhamento, depende do seu módulo de rigidez. Assim, os sólidos são ditos elásticos e os fluidos, viscosos [4].

´

E interessante destacar que a viscosidade dos fluidos newtonianos é função da tem-peratura e da pressão [9, 12], isto é:

µ=µ(T, p). (2.14)

(21)

gases a viscosidade aumenta com o aumento da temperatura [3, 7, 9]. Essa dependência da viscosidade em relação à temperatura pode ser percebida a partir de duas equações emp´ıricas [3]. A primeira equação é a equação de Andrade [13, 14], que mostra que a viscosidade dos l´ıquidos decai exponencialmente com a temperatura:

µ(T) = AeB/T. (2.15)

onde A e B são constantes emp´ıricas positivas e T é a temperatura absoluta [3, 9, 15]. A equação 2.15 foi originalmente proposta por Guzman [15], mas ficou popularmente conhe-cida como equação de Andrade, sendo também referida por alguns autores como equação de Guzman-Andrade. A segunda equação emp´ırica é a equação de Sutherland [16], que mostra que a viscosidade dos gases cresce com a temperatura:

µ(T) = C T 3/2

T +S. (2.16)

ondeC e S são constantes e T é a temperatura absoluta [3]. Com relação à dependência da pressão, a viscosidade de um fluido, em muitos casos, aumenta com o aumento da pressão [17]. Segundo Partal [9], a expressão mais usada para avaliar os efeitos da pressão na viscosidade de um l´ıquido é a equação de Barus [18, 19]:

µ(p) = µ0 eα

∆p_. _(2.17)

ondeµ0 é a viscosidade nas condições atmosféricas,αé o coeficiente de piezoviscosidade e∆p é a diferença de pressão em relação à pressão atmosférica.

Como já foi dito, os fluidos não-newtonianos são aqueles em que a tensão de ci-salhamento não segue uma relação linear com a taxa de deformação. Um modelo bastante utilizado para modelar a relação entre a tensão e a taxa de cisalhamento de muitos fluidos não-newtonianos cujo comportamento é independente do tempo é o modelo exponencial, também conhecido como relação de Ostwald-Waele [20], que, para o escoamento unidimensional, é dado por [4]:

τ =k

du dy

n

=k( ˙γ)n, (2.18)

(22)

Gráfico 1 – Tensão de cisalhamento em função da taxa de deformação.

.

Fluido ne

wtoniano

Fluido pseudoplás

tico (n < 1)

Fluido dilatante (n > 1)

τ

γ

Gráfico da tensão de cisalhamento em função da taxa de deformação para fluidos newtonianos (Equação 2.13) e não-newtonianos (Equação 2.18). Fonte: Elaborado pelo autor.

A Equação 2.18 é comumente reescrita na forma

τ =k

du dy

n−1 du dy =η

du

dy =ηγ,˙ (2.19)

de formato idêntico ao da equação de Newton (Equação 2.13), onde η = k|du/dy|n−1 = k|γ˙|n−1

é chamado deviscosidade aparenteouefetiva. Em alguns fluidos não-newtonianos, a viscosidade aparente é também dependente do tempo,η=η( ˙γ, t). Esse é o caso dos fluidos ti-xotrópicos, cuja viscosidade aparente diminui com o passar do tempo, e dos fluidosreopéticos, cuja viscosidade aparente aumenta com o tempo. Há ainda substâncias que, dependendo da tensão de cisalhamento aplicada, comportam-se ora como fluidos, ora como sólidos. Esse é o caso dos plásticos de Binghamou plásticos ideais, que para tensões de cisalhamento abaixo de um determinado valor,τ0, comportam-se como sólidos, resistindo à tensão aplicada; entre-tanto, para tensões maiores que esse valor limite, essas substâncias comportam-se como fluidos, apresentando uma relação linear entre a tensão de cisalhamento e a taxa de deformação [3]:

τ =τ0+η du

dy. (2.20)

Mais informações quanto as propriedades de fluidos não-newtonianos podem ser encontradas nas referências [3, 4, 21].

2.2 Meios Porosos

(23)

Quando os poros estão conectados, formam-se canais por onde os fluidos podem escoar. Os meios porosos podem ser classificados de diversas maneiras de acordo com vários critérios. Três desses critérios são a conectividade do poros, a estabilidade da estrutura porosa e a distribuição espacial dos poros. Quanto à conectividade do poros, o meio poroso pode ser classificado como permeável, quando permite o escoamento de um fluido, ou impermeável, em caso contrário. Com relação à estabilidade da estrutura porosa, o meio poroso é dito consolidado, quando a estrutura é rigida o suficiente para manter a configuração dos poros (como em ossos e pedra-pomes, por exemplo) ou não-consolidado, quando a estrutura não mantém a configuração dos poros (como em esponjas e areia, por exemplo) [2]. Finalmente, quanto à distribuição espacial dos poros, o meio poroso pode ser classificado como ordenados ou desordenados, dependendo da forma como os poros estão distribu´ıdos ao longo do meio poroso.

A simulação de escoamentos em meios porosos é, em geral, bastante dif´ıcil devido a complexa natureza da geometria do meio poroso e também devido a heterogeneidade presente na composição qu´ımica de suas paredes internas [2]. Duas propriedades fundamentais com respeito aos meios porosos são a porosidade,φ, e a permeabilidade absoluta,k, que veremos a seguir.

2.2.1 Porosidade e Permeabilidade

A porosidade, φ, é o parâmetro f´ısico que mede a fração de poros em um meio poroso e é definida como a razão entre o volume dos poros (espaços vazios) e o volume total do meio poroso:

φ= volume total dos poros

volume total do meio poroso. (2.21) Assim, como fica claro da Equação 2.21, a porosidade varia entre0e1. Em queφ = 0significa que não há espaços vazios, isto é, o material é totalmente maciço, e φ = 1 significa que o material é oco. Dependendo da conectividade dos poros, pode-se ter dois tipos de porosidades, a saber, a porosidade absoluta ou total, definida na Equação 2.21, que considera todos os poros, e a porosidade efetiva que considera apenas os poros interconectados [23].

Já a permeabilidade, k, é o parâmetro f´ısico que mostra como os poros estão co-nectados. Essa quantidade descreve a habilidade de uma determinada fase escoar pelos canais entre os poros e depende somente da geometria do meio poroso, sendo, por isso, chamada frequentemente de permeabilidade absoluta [22, 24].

2.3 Escoamento multif´asico

(24)

temos então o escoamento bifásico, que é simplesmente um caso particular do escoamento mul-tifásico. Cabe aqui definir o conceito de saturação. Em um escoamento multifásico em meios porosos, a saturação, S, de uma determinada fase é a fração do volume do meio poroso que é ocupada por essa fase. É interessante destacar que diferentes valores de algumas proprie-dades, como tensão superficial e viscosidade, por exemplo, formam diferentes estruturas de escoamento [5, 22].

2.3.1 Tens˜ao superficial e Molhabilidade

Na interface entre dois fluidos (l´ıquido e gás ou dois l´ıquidos imisc´ıveis) é poss´ıvel observar a existência de forças superficiais que fazem com que a superf´ıcie do l´ıquido se com-porte como uma espécie de membrana fict´ıcia [3]. Essas forças superficiais atuam tangencial-mente na superf´ıcie fazendo com que a interface entre os fluidos esteja em um estado de tensão [25]. Essa tensão surge então nos l´ıquidos como resultado do desequil´ıbrio entre as forças co-esivas que atuam nas moléculas próximas à superf´ıcie do fluido [3, 26]. Tal desequil´ıbrio se deve ao fato de que as moléculas, que estão no interior do fluido, interagem com as moléculas vizinhas atraindo-se igualmente, de modo que a força resultante que age sobre elas é nula, enquanto que as moléculas situadas próximas à superf´ıcie estão sujeitas a forças l´ıquidas que apontam para o interior do fluido [3]. A intensidade da força de atração molecular por uni-dade de comprimento ao longo de qualquer linha na superf´ıcie do fluido é chamada de tensão superficial [3, 25], sendo frequentemente representada porγ.

A tensão superficial é a responsável por fazer com que os sistemas f´ısicos tendam a minimizar as áreas das interfaces entre os fluidos [25, 27], razão pela qual é poss´ıvel observar pequenas quantidades de l´ıquido formarem gotas esféricas e, também, a formação de bolhas de gás em um l´ıquido. Por esta razão, uma interpretação f´ısica alternativa de tensão superficial está relacionada ao trabalho (energia) necessário para alterar a área superficial de um fluido [25, 26, 27]. Assim, podemos escrever que o trabalho, dW, necessário para aumentar a superf´ıcie de um fluido por uma área infinitesimal,dA, é:

dW =γdA. (2.22)

Por esse motivo, a tensão superficial é também chamada deenergia de superf´ıcie.

Vale destacar que a tensão superficial é uma propriedade do l´ıquido e que também depende da temperatura e do outro fluido que está em contato com o l´ıquido [3]. Quanto à dependência da temperatura, em geral, o valor da tensão superficial decresce com o aumento da temperatura [3, 27].

(25)

positiva entre as partes interna e externa da superf´ıcie [4, 25]. Como um exemplo desse fato, vamos calcular a diferença de pressão na interface de uma gota esférica de um fluido incom-press´ıvel. Para isso, vamos considerar uma gota, de raioR, formada na extremidade de uma seringa devido ao deslocamento do êmbolo. O êmbolo, ao deslocar-se, realiza um trabalho so-bre o l´ıquido dado pordW = p dV, ondep é a pressão exercida pelo êmbolo sobre o l´ıquido eV é o volume da gota. Entretanto, a gota, ao aumentar seu volume, também realiza trabalho, dW =pextdV, ao deslocar o ar a sua volta. Portanto, o trabalho total realizado sobre o fluido é:

dW = (p−pext)dV, (2.23)

ondepext é a pressão externa à gota. Por outro lado, o trabalho necessário para formar a su-perf´ıcie de uma gota é dado pela Equação 2.22. Combinando essas duas equações (2.22 e 2.23), obtemos:

dW =γdA= (p−pext)dV. (2.24)

Sabendo que a ´area e o volume de uma esfera s˜ao, respectivamente,A = 4πR2

eV = 4 3πR

3 , podemos escrever a Equac¸˜ao 2.24 como:

γ d(4πR2) = (p−pext)d(4πR3/3) (2.25)

γ8πRdr = (p−pext)4πR2dr (2.26)

2γ = (p−pext)R. (2.27)

Portanto, a diferença de pressão,∆p= p−pext, na interface de uma gota esférica é dada pela lei de Laplace ou também chamada de lei Young-Laplace:

∆p= 2γ

R. (2.28)

(26)

(Figura 2). Assim, θ = 0o _{indica a completa molhabilidade da fase mais densa [28], o que}

significa que essa fase ir´a espalhar-se completamente sobre a superf´ıcie. Paraθ= 90o_{, temos a}

molhabilidade neutra, significando que ambas as fases molhar˜ao igualmente a superf´ıcie s´olida, e paraθ = 180o_{, temos a completa molhabilidade da fase menos densa. Dessa forma, quando}

θ <90o_{, o fluido mais denso será a fase molhante, e quando}_{θ >}₉₀o_{, será a fase não-molhante.}

A molhabilidade pode ser explicada levando em consideração os conceitos de forças de coesão e adesão: no caso de uma fase molhante, a força de adesão (atração entre moléculas diferentes) será maior do que a força de coesão (atração entre moléculas do mesmo tipo), fa-zendo com que a fase molhe a superf´ıcie; já para a fase não-molhante ocorre justamente o contrário, isto é, a força de coesão será superior a força de adesão, fazendo com que a fase não se espalhe sobre a superf´ıcie.

Figura 2 – Molhabilidade e ˆangulo de contato.

θ=0_° θ<90_° θ=90_° θ>90_° θ=180_°

θ θ

Ilustração da quantificação da molhabilidade por meio do ângulo de contato, θ. Para θ = 0o_{, temos}

a completa molhabilidade da fase mais densa, enquantoθ = 90o _{representa uma molhabilidade neutra}

para ambas as fases eθ = 180o _{indica que a fase mais densa ´e completamente n˜ao-molhante. Fonte:}

Elaborado pelo autor.

2.3.2 Press˜ao Capilar

Considere uma interface curva em equil´ıbrio entre dois fluidos imisc´ıveis, um fluido molhante e outro não-molhante, nos canais que ligam os poros do meio poroso [22]. A diferença de pressão na interface entre esses dois fluidos é chamada de pressão capilar,pcap, e pode ser escrita como

pcap=pnm−pm, (2.29)

ondepnm é a pressão na interface do lado do fluido não-molhante epm, é a pressão no lado do fluido molhante.

(27)

conhecida como lei de Young-Laplace [5, 22]:

pcap = 2γ cosθ

r . (2.30)

2.3.3 Lei de Darcy

Em seus estudos sobre o escoamento de fluidos em meios porosos, o engenheiro francês Henry Darcy, em 1856, observou que a velocidade da água, ao passar por um meio poroso, seguia uma relação linear com gradiente de pressão, ao qual estava submetida a amos-tra [22, 24]. Depois de vários experimentos, Darcy concluiu que a velocidade de um fluido escoando em um meio poroso dependia, não apenas do gradiente de pressão, mas também da permeabilidade do meio e do inverso do coeficiente de viscosidade do fluido, deduzindo a se-guinte lei que carrega seu nome:

~v =−k

µ(∇p−ρ~g), (2.31)

ondeρ~g é a densidade de força gravitacional, o primeiro sinal negativo significa que o esco-amento segue para regiões de menor pressão e a velocidade é definida em uma região muito maior do que o tamanho dos poros. Portanto, a lei de Darcy, dada pela equação 2.31, é válida para meios porosos macroscópicos.

No escoamento simultâneo de várias fases fluidas em meios porosos, há uma espécie de competição no escoamento dessas fases. Surge então, uma nova permeabilidade, a permeabi-lidade efetiva,kef, que não depende apenas das propriedades do meio poroso, mas também das propriedades dos fluidos e de suas respectivas saturações. A lei de Darcy para um escoamento bifásico, desprezando o efeito gravitacional, é dada por [22]

~vf =−k

f ef µf

∇p, (2.32)

ondek_eff ´e a permeabilidade efetiva de cada fase eµf ´e o coeficiente de viscosidade da fase.

2.3.4 Escoamento em um Tubo Capilar

Sabe-se que em um escoamento laminar e estacionário, através de um tubo cil´ındrico, o fluido se divide em camadas cil´ındricas coaxiais, que se movem com velocidades de diferentes magnitudes, dadas pela seguinte equação [7]:

V(r) = ∆p 4µL(R

2

−r2), (2.33)

(28)

por isso, tem velocidade nula,V(R) = 0; enquanto a camada central (r = 0) tem velocidade de magnitude máxima dada porV(0) = ∆pR2_/₍₄_µL₎_{[7]. A equação 2.33 mostra, então, que} a magnitude da velocidade de uma dada camada cil´ındrica do fluido, em um referencial fixo no tubo, é diretamente proporcional a diferença de pressão e ao quadrado do raio do tubo e, também, inversamente proporcional a viscosidade do fluido e ao comprimento do tubo.

De posse da equação 2.33, podemos então calcular a vazão,Q, desse escoamento, isto é, o volume de fluido que atravessa uma seção reta do tubo por unidade de tempo:

dQ(r) = V(r)·2πrdr. (2.34)

Utilizando a equac¸˜ao 2.33, obtemos

dQ(r) = ∆p 4µL(R

2

−r2

)·2πrdr. (2.35)

Integrando a equac¸˜ao 2.35, obtemos

Q=

Z R

0

dQ(r) = π∆p 2µL

Z R

0 (R2

−r2

)rdr. (2.36)

Finalmente, temos que o fluxo laminar através de um tubo cil´ındrico é dado pela equação de Hagen-Poiseuille [22, 29]:

Q= πR 4

8µL∆p. (2.37)

Portanto, a vazão em um tubo cil´ındrico é diretamente proporcional a diferença de pressão e ao raio do tubo elevado à quarta potência e, também, inversamente proporcional a viscosidade do fluido e ao comprimento do tubo.

2.4 Equações básicas da dinâmica de fluidos

A derivação das equações que governam a dinâmica de fluidos é baseada em três princ´ıpios básicos, a saber, a conservação da massa, a conservação da energia, e a segunda lei de Newton [6]. Dois desse princ´ıpios serão discutidos a seguir e logo depois introduziremos as equações de Navier-Stokes.

2.4.1 Conservac¸˜ao da massa

(29)

massa,m, do sistema permanece constante, o que significa que a taxa de variação temporal de massa do sistema é nula, assim podemos escrever

dm dt = d dt Z sistema

ρ(~r, t)dτ = 0, (2.38)

ondeρ(~r, t) é a massa espec´ıfica em função da posição~r e do tempot, e dτ é um elemento infinitesimal de volume. Entretanto, a taxa de variação de massa do sistema pode ser escrita, em termos do volume de controle, utilizando o teorema de transporte de Reynolds [3], da seguinte forma: dm dt = ∂ ∂t Z Ω

ρ(~r, t)dτ+

Z

∂Ω

ρ(~r, t)(~u·d ~A), (2.39)

onde~u é velocidade de escoamento do fluido medida com relação ao volume de controle ed ~A é o elemento infinitesimal de área direcionado para fora da superf´ıcie, além disso, o primeiro termo do lado direito dessa equação corresponde à taxa de variação da quantidade de massa dentro do volume de controle e o segundo termo corresponde à a taxa de variação de massa que atravessa a superf´ıcie de controle [4]. Das equações 2.38 e 2.39 temos então a lei de conservação de massa na forma integral:

∂ ∂t

Z

Ω

ρ dτ +

Z

∂Ω

ρ(~u·d ~A) = 0. (2.40)

Utilizando o teorema da divergência no segundo termo do lado esquerdo da equação 2.40 e escrevendo os dois termos sob o mesmo sinal de integral, obtemos

Z

Ω

∂ρ

∂t +∇·(ρ~u)

dτ = 0, (2.41)

de onde obtemos então a lei de conservação de massa na forma diferencial, que também é conhecida comoequação de continuidade:

∂ρ

∂t +∇·(ρ~u) = 0. (2.42)

2.4.2 Equac¸˜ao do momento linear

A segunda lei Newton, para sistemas movendo-se em relac¸˜ao a um referencial iner-cial, estabelece que

~

F =XFext~ = d ~P

dt , (2.43)

(30)

~ P =

Z

sistema

~u ρ(~r, t)dτ. (2.44)

Utilizando o teorema de transporte de Reynolds e a equação 2.44, podemos reescrever a segunda lei de Newton para um sistema, dada pela equação 2.43, na seguinte forma

~ F = ∂

∂t

Z

Ω

~u ρ dτ +

Z

∂Ω

~u ρ(~u·d ~A). (2.45)

Portanto, a força resultante sobre um sistema ou a taxa de variação do momento linear de um sistema corresponde à taxa de variação do momento linear dentro do volume de controle mais o fluxo l´ıquido de momento através da superf´ıcie de controle [3].

2.4.3 Equac¸˜oes de Navier-Stokes

O comportamento dos fluidos pode ser descrito pelas equações de Navier-Stokes, que consistem em um conjunto de equações diferenciais parciais não-lineares que se baseiam em leis de conservação, tais como as conservações de massa (equação da continuidade), de momento linear e de energia. A partir dessas equações, pode-se determinar os campos de velocidade e de pressão em um escoamento, porém, na prática, devido a alta complexidade matemática presente nessas equações, apenas casos mais simples podem ser resolvidos analiti-camente [1]. Além disso, as condições iniciais e as condições de contorno fazem com que as soluções, para a maioria das situações, sejam dif´ıceis ou até mesmo imposs´ıveis de se obter. No entanto, as equações de Navier-Stokes podem ser simplificadas de modo significativo depen-dendo das propriedades dos fluidos envolvidos e do tipo de escoamento, possibilitando assim uma solução numérica [2].

As equações de Navier-Stokes são largamente utilizadas em diversas áreas para resolver os mais variados problemas, inclusive, são usadas, segundo Souza [1], no estudo do clima e para modelar as correntes oceânicas, o fluxo de ar ao redor de aerofólios de automóveis e de aviões, a propagação de fumaça em incêndios e em chaminés industriais, além disso, são utilizadas nos estudos do fluxo sangu´ıneo, no projeto de usinas hidrelétricas, na análise dos efeitos das poluições h´ıdrica e atmosférica, entre outros.

(31)

uma part´ıcula ser´a dada, de acordo com a regra da cadeia, por

~a= d

dt~u(~r, t) = ∂~u ∂xx˙ +

∂~u ∂yy˙+

∂~u ∂zz˙+

∂~u

∂t, (2.46)

onde~r(t) =x(t)î+y(t)ˆj+z(t)ˆk é a posição no tempot, em coordenadas cartesianas, dentro do volume de controle ex˙ representa a derivada temporal da variável indicada. De forma mais compacta, podemos escrever a aceleração de uma part´ıcula fluida como

~a = D~u

Dt = (~u· ∇)~u+ ∂~u

∂t, (2.47)

onde o operador

D

Dt = (~u· ∇) + ∂

∂t (2.48)

é chamado dederivada material, uma vez que essa derivada é calculada para uma part´ıcula de matéria fluida [4]. Utilizando a definição de derivada material e a segunda lei de Newton, a força resultante que atua sobre uma part´ıcula fluida é dada por

~

F = D ~P Dt =

∂ ~P

∂t + (~u· ∇)P ,~ (2.49)

ou ainda, ~ F = Z Ω ρ∂~u

∂t + (~u· ∇)ρ~u

dτ. (2.50)

A forc¸a resultante sobre o fluido pode ser escrita em termos das forc¸as de superf´ıcieFS~ e de campoFB~ , como

~

F =FS~ +FB~ =

Z

Ω

∇ ·Tdτ +

Z

Ω

ρ ~f dτ, (2.51)

ondef~é a força de campo por unidade de massa eTé um tensor de tensões dado por

T=



  

σxx τxy τxz τyx σyy τyz τzx τzy σzz



  

, (2.52)

onde σij representa as tensões normais e τij, as tensões de cisalhamento. Combinando as equações 2.50 e 2.51 obtemos

ρ∂~u

∂t + (~u· ∇)ρ~u=∇ ·T+ρ ~f . (2.53)

Para um fluido newtoniano, as tensões de cisalhamento, em notação indicial, são dadas por [3, 4]

τij =τji =µ

(32)

σii=−p+λ(∇ · ~u) + 2µ∂ui

∂xi, (2.55)

ondexirepresentam as coordenadasx, yez;pé a pressão termodinâmica local, e o coeficienteλ é aviscosidade volumétricaque está relacionado à variação de volume devido ao efeito viscoso [30] e que, de acordo com a hipótese de Stokes, é dado por λ = −2µ/3 [4, 30]. Note que a equação 2.54 é uma generalização da equação 2.13. Utilizando as equações 2.54 e 2.55, podemos escrever os elementos do tensorTcomo

Tij = [−p+λ(∇ · ~u)]δij +µ

∂uj ∂i +

∂ui ∂j

, (2.56)

ondeδij ´e o delta de Kronecker, dado por

δij =

(

1, se i=j

0, se i6=j . (2.57)

Ou ainda, de forma mais compacta,

T= [−p+λ(∇ · ~u)]I+µ(∇~u+ (∇~u)t), (2.58)

onde I é a matriz identidade e sobrescrito t indica a transposta da matriz. Aplicando a di-vergência ao tensorT, dado pela equação 2.58, obtemos

∇ ·T=−∇p+∇[λ(∇ · ~u)] +∇·[µ(∇~u+ (∇~u)t)], (2.59)

onde

∇[λ(∇ · ~u)] =λ∇(∇ · ~u) + (∇·~u)∇λ, (2.60)

e

∇·[µ(∇~u+ (∇~u)t_{)] =} _µ_∇·₍_∇_~u_{+ (}_∇_~u₎t_{) + (}_∇_~u_{+ (}_∇_~u₎t₎_{· ∇}_µ = µ∇2

~u+µ∇(∇ ·~u) + (∇~u+ (∇~u)t₎_{· ∇}_µ. (2.61) Finalmente, substituindo as expressões 2.60, 2.61 e 2.59 na equação 2.53 obtemos então as equações de movimento de um fluido newtoniano, as chamadas equações de Navier-Stokes:

ρ∂~u

∂t +ρ(~u· ∇)~u=−∇p+ (λ+µ)∇(∇·~u) +µ∇ 2

~u+ρ ~f+ (∇·~u)∇λ+ (∇~u+ (∇~u)t)· ∇µ. (2.62) Considerando a viscosidade (µeλ) constante, as equac¸˜oes de Navier-Stokes se tornam:

ρ∂~u

∂t +ρ(~u· ∇)~u =−∇p+ (λ+µ)∇(∇·~u) +µ∇ 2

~u+ρ ~f . (2.63)

(33)

constante (∂ρ/∂t= 0), a equação da continuidade (equação 2.42) se reduz a:

∇·~u = 0, (2.64)

por conseguinte, as equações de Navier-Stokes são simplificadas para:

ρ∂~u

∂t +ρ(~u· ∇)~u=−∇p+µ∇ 2

~u+ρ ~f . (2.65)

Para o caso de escoamento sem atrito, isto é, com viscosidade nula (µ= 0), e fazendof~=~g, a equação 2.65 se reduz a

ρ∂~u

(34)

3 FORMULAÇ ÃO DO PROBLEMA, RESULTADOS E DISCUSS ÕES

3.1 Formulação do Problema e da Solução

Neste trabalho, nós estamos interessados em investigar o escoamento bifásico, em meios porosos, de fluidos newtonianos imisc´ıveis e incompress´ıveis, no regime estacionário e isotérmico. Para tanto, nós simulamos o escoamento de duas fases newtonianas, com viscosida-desµ1 = 0.1P a·seµ2 = 1.0P a·s, e iguais massas espec´ıficasρ1 =ρ2 =ρ= 1.0Kg/m3, em um meio poroso bidimensional com condições periódicas de contorno em ambas as direções, onde um gradiente de pressão constante de1000P a/m, aplicado na direçãox, provoca o escoa-ˆ mento. Por isso, nosso sistema pode ser compreendido como duas fases newtonianas movendo-se na superf´ıcie de um toro poroso. Conforme está apremovendo-sentado na Figura 3, o meio poroso é do tipoModelo do Queijo Suiço[6, 31] e consiste em uma caixa quadrada de50mm×50mm que é preenchida aleatoriamente com discos de1mmde diâmetro, onde a sobreposição desses discos é permitida. Esse preenchimento aleatório é feito até obter-se a porosidade desejada, que no nosso caso foiφ= 0.8.

Como se sabe, a solução das equações de Navier-Stokes mediante os métodos tra-dicionais de diferenças finitas e elementos finitos requer a discretização do meio poroso sobre uma malha regular [2]. Assim, a malha de discretização (oumesh, em inglês) do meio poroso utilizado em nossas simulações está representado na Figura 4. Chamaremos defase 1o fluido de menor viscosidade (µ1 = 0.1P a·s), e defase 2o fluido de maior viscosidade (µ2 = 1.0P a·s), e suas respectivas saturações denotaremos porS1 e S2, em queS1 +S2 = 1. Os valores das saturações utilizados nas simulações como parâmetros de entrada foramS1 = 0.20eS1 = 0.40 (Figura 5, a fase 1 está representada na cor azul e a fase 2, na cor vermelha). Já, os valores de tensão superficial utilizados foramγ = 0.0001, γ = 0.010 e γ = 0.030 N/m. O regime es-tacionário é definido quando a velocidade (que está relacionada com a permeabilidade relativa por meio da lei de Darcy) de ambas as fases oscila em torno de um valor médio que não muda com o tempo.

(35)

Figura 3 – O meio poroso.

O meio poroso ultilizado nas simulações consiste em uma caixa quadrada de50mm×50mmpreenchida aleatoriamente com discos de1mmde diâmetro, e possui uma porosidade deφ = 0.8. Fonte: Obtida através do software ParaView.

Figura 4 – A malha de discretizac¸˜ao do meio poroso.

(a) Visão completa da malha de discretização utili-zada nas simulações.

(b) Visão ampliada da região superior à direita da malha de discretização.

(36)

(a)S1 = 0.20. (b)S1 = 0.40.

Fase 1 (µ1 = 0.1P a·s), em azul; e fase 2 (µ2 = 1.0P a·s), em vermelho. Fonte: Obtida atrav´es do software Fluent da ANSYS.

e temperaturas em uma dada regi˜ao do escoamento [2].

3.2 Resultados e Discuss˜oes

Foram realizadas várias simulações, até atingir o regime estacionário, variando-se os valores da tensão superficial e das saturações dos fluidos. Em cada uma dessas simulações, o valor médio da componente da velocidade na direçãox, calculado sobre todo o volume,ˆ hVxi, foi registrado, a cada passo de tempo, para ambas as fases. O tempo total das simulações foi de250 segundos, com um intervalo de tempo,dt, de5×10−3

s, at´e que o estado estacion´ario

fosse obtido. Na Figura 6 temos os instantâneos do escoamento após50.000 passos de tempo para cada um dos casos estudados, isto é, para cada parâmetro utilizado nas simulações, a saber, a saturação e a tensão superficial.

(37)

Gráfico 2 – Comparação da área da interface entre os fluidos.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

0 10000 20000 30000 40000 50000

Ár

ea da Int

er

face

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(a)S1 = 0.20.

0 0.05 0.1 0.15 0.2

0 10000 20000 30000 40000 50000

Ár

ea da Int

er

face

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(b)S1 = 0.40.

Gráfico da área da interface entre os fluidos em função do número de iterações. Fonte: Elaborado pelo autor.

a área da interface entre os fluidos vai aumentando, com o passar do tempo, até estabilizar-se em torno de um determinado valor. Na Figura 7 temos o contorno (ou mapa) da magnitude das velocidades, após50.000 iterações, para cada uma dos casos estudados. E as séries temporais do valor médio da componente da velocidade na direção x, calculado sobre todo o volume,ˆ

(38)

Gráfico 3 – Velocidade média (componente na direçãox),hVxi, em função do número de iterações. 0 1 2 3 4 5

0 10000 20000 30000 40000 50000

Vx

(10

-4 m/s)

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(a) Fase 1;S1= 0.20.

2 3 4 5 6 7 8

0 10000 20000 30000 40000 50000 Vx

(10

-4 m/s)

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(b) Fase 2;S1 = 0.20.

0 5 10 15 20 25

0 10000 20000 30000 40000 50000

Vx

(10

-4 m/s)

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(c) Fase 1;S1= 0.40.

1 2 3 4 5 6 7 8

0 10000 20000 30000 40000 50000

Vx

(10

-4 m/s)

Iterações

γ = 0.0001 γ = 0.010 γ = 0.030

(d) Fase 2;S1 = 0.40.

(39)

Figura 6 – Escoamento bifásico após 50.000 iterações.

(a)S1= 0.20;γ = 0.0001N/m. (b)S1= 0.40;γ = 0.0001N/m.

(c)S1 = 0.20;γ= 0.010N/m. (d)S1 = 0.40;γ = 0.010N/m.

(e)S1 = 0.20;γ= 0.030N/m. (f)S1= 0.40;γ = 0.030N/m.

(40)

(a)S1= 0.20;γ = 0.0001N/m. (b)S1= 0.40;γ = 0.0001N/m.

(c)S1 = 0.20;γ= 0.010N/m. (d)S1 = 0.40;γ = 0.010N/m.

(41)

3.2.1 An´alise das s´eries temporais da velocidade

Vamos analisar as séries temporais da velocidade média (componente na direção ˆ

x),hVx(t)i, utilizando três métodos. O primeiro método utilizado será ométodo de análise de flutuações sem tendências. O segundo método será uma análise da distribuição dos tamanhos das avalanchespresentes na série temporal das velocidades. E o terceiro, será uma análise da distribuição dos saltosde velocidade.

3.2.1.1 Método de análise de flutuações sem tendências

O método de análise de flutuações sem tendências ou método DFA (do inglês De-trended Fluctuations Analysis), é amplamente utilizado para detectar correlações de longo al-cance em séries temporais, particularmente em séries não-estacionárias [33, 34]. Este método é descrito com mais detalhes no Apêndice A. A ideia básica desse método consiste em subtrair poss´ıveis tendências da série original e analisar a flutuação dos dados destendenciados. Nessa análise, constrói-se uma funçãoF(n), chamada de função de flutuação (veja a Equação A.3), onden é o tamanho dos blocos de tempo, em que a série temporal é divida, para que seja rea-lizada a análise. Em seguida, um gráfico deF(n) contran é esboçado e o comportamento de F(n) é analisado. Se os dados a serem analisados, possu´ırem correlações de longo alcance, a

função de flutuação apresentará um comportamento do tipo lei de potência [33]: F(n) ∝ nα (Equação A.4). Os Gráficos 4, a seguir, mostram a função de flutuação para cada uma das séries temporais das velocidades médias,hVx(t)i, das duas fases fluidas para cada caso estudado; e como é poss´ıvel observar, as funções de flutuação das séries temporais analisadas apresentam um comportamento do tipo lei de potência. A Tabela 1 apresenta um resumo dos expoentes obtidos a partir do método DFA para cada caso estudado.

Tabela 1 – Comparação dos expoentes obtidos a partir do método DFA.

Tens˜ao superficial (N/m) S1 = 0.2 S1 = 0.4

Fase 1 Fase 2 Fase 1 Fase 2

0.0001 1.744 ± 0.004 1.666 ± 0.006 1.656 ± 0.008 1.677 ± 0.010 0.010 1.610 ± 0.009 1.404 ± 0.017 1.632 ± 0.014 1.555 ± 0.011 0.030 1.394 ± 0.014 1.426 ± 0.013 1.489 ± 0.011 1.392 ± 0.011

(42)

100 101 102 103 104 105 n 10-8 10-6 10-4 10-2 100 10 F(n)

γ = 0.0001; α = 1.744 ± 0.004 γ = 0.010; α = 1.610 ± 0.009 γ = 0.030; α = 1.394 ± 0.014

(a) Fase 1;S1 = 0.20.

100 101 102 103 104 105

n 10-8 10-6 10-4 10-2 100 10 F(n)

γ = 0.0001; α = 1.666 ± 0.006 γ = 0.010; α = 1.404 ± 0.017 γ = 0.030; α = 1.426 ± 0.013

(b) Fase 2;S1= 0.20.

100 101 102 103 104 105

n 10-8 10-6 10-4 10-2 100 102 F(n)

γ = 0.0001; α = 1.656 ± 0.008 γ = 0.010; α = 1.632 ± 0.014 γ = 0.030; α = 1.489 ± 0.011

(c) Fase 1;S1 = 0.40.

100 101 102 103 104 105

n 10-8 10-6 10-4 10-2 100 102 F(n)

γ = 0.0001; α = 1.677 ± 0.010 γ = 0.010; α = 1.555 ± 0.011 γ = 0.030; α = 1.392 ± 0.011

(d) Fase 2;S1= 0.40.

Método DFA: Gráfico, em escala logar´ıtmica, da função de flutuação em função do tamanho dos inter-valos. Fonte: Elaborado pelo autor.

3.2.1.2 Avalanches

Asavalanches (ouburst [35], em inglês) podem ser calculadas em qualquer série temporal, da forma como se segue. Considerando uma série temporalX(t), pode-se definir o tamanho∆t de uma avalanche como um intervalo de tempo (ou número de passos de tempo) deX(t)que inicia-se em um pontot = ta, de valor (ou altura) X(ta) = H e termina em um pontot =tb, de altura igual ou superior àH, isto é,X(tb)≥ H, tal queta < tb eX(t) < H,

∀t∈(ta, tb). Assim, tendo em vista essas considerações, o tamanho da avalanche que inicia-se no pontota é o número de passos de tempo entre ta etb, isto é, no intervalo aberto(ta, tb); e pode ser escrito como

∆t(ta) = 1

δt(tb −ta)−1, (3.1)

(43)

(ou valor) da série temporal. A avalanche, do modo como foi definida acima, é chamada de avalanche ‘progressiva’ (em inglês, forward bursts), uma vez que a avalanche em um dado pontot é calculada levando em conta os pontos posteriores. Para uma melhor compreensão, a Figura 8 ilustra como é calculado o tamanho das avalanches, onde as setas mostram onde ocorrem as avalanches e indicam seus respectivos tamanhos.

Figura 8 – Avalanches (bursts) em uma s´erie temporal.

0 0.1 0.2 0.3 0.4 0.5 0.6

0 5 10 15 20 25 30

Sér

ie temporal

X(t)

Passos de tempo

t

Fonte: Elaborado pelo autor.

Para o cálculo das avalanches, tomamos como a nossa série temporal a média da componente da velocidade na direção x,ˆ hVx(t)i, para cada fase fluida. As distribuições dos tamanhos das avalanches, nos casos estudados neste trabalho, apresentaram um comportamento do tipo lei de potência,P(∆t) ∝ (∆t)α, comα < 0. Os Gráficos 5, a seguir, apresentam os histogramas logar´ıtmicos dos tamanhos das avalanches e seus respectivos expoentes para cada caso estudado. E a Tabela 2 apresenta um resumo dos expoentes das distribuições dos tamanhos das avalanches para os casos apresentados nos Gráficos 5.

Tabela 2 – Comparação dos expoentes das distribuições dos tamanhos das avalanches.

Tens˜ao superficial (N/m) S1 = 0.2 S1= 0.4

0.0001 −1.334±0.335 −1.257±0.037 −1.253±0.039 −1.235±0.031 0.010 −1.556±0.055 −1.654±0.029 −1.606±0.039 −1.646±0.030 0.030 −1.582±0.039 −1.613±0.032 −1.561±0.040 −1.629±0.024

(44)

velocidade.

100 101 102 103 104

∆t 10-6 10-4 10-2 100 Frequência

γ = 0.0001; α = −1.334 ± 0.335 γ = 0.010; α = −1.556 ± 0.055 γ = 0.030; α = −1.582 ± 0.039

(a) Fase 1;S1 = 0.20.

100 101 102 103 104

∆t 10-6 10-4 10-2 100 Frequência

γ = 0.0001; α = −1.257 ± 0.037 γ = 0.010; α = −1.654 ± 0.029 γ = 0.030; α = −1.613 ± 0.032

(b) Fase 2;S1= 0.20.

100 101 102 103 104

∆t 10-6 10-4 10-2 100 Frequência

γ = 0.0001; α = −1.253 ± 0.039 γ = 0.010; α = −1.606 ± 0.039 γ = 0.030; α = −1.561 ± 0.040

(c) Fase 1;S1 = 0.40.

100 101 102 103 104

∆t 10-6 10-4 10-2 100 Frequência

γ = 0.0001; α = −1.235 ± 0.031 γ = 0.010; α = −1.646 ± 0.030 γ = 0.030; α = −1.629 ± 0.024

(d) Fase 2;S1= 0.40.

Histograma logar´ıtmico dos tamanhos das avalanches nas s´eries temporais da velocidade m´edia,hVx(t)i. Fonte: Elaborado pelo autor.

(45)

3.2.1.3 Saltos

Vamos definir ossaltos(oujumps, em inglês),∆v, da série temporal da velocidade média,hVx(t)i, como simplesmente:

∆v(t) = hVx(t+δt)i − hVx(t)i. (3.2)

ondeδt é o tamanho do passo de tempo. Dessa forma, construimos uma nova série temporal, ∆v(t), a partir da série da velocidade média,hVx(t)i. O Gráfico 6 apresenta as séries temporais dos saltos de velocidade, ∆v(t), para cada um dos casos estudados. Os saltos de velocidade, da maneira como foram definidos, nada mais são do que variações na velocidade; e como se pode observar, a partir do Gráfico 6, essas variações são bem maiores nos casos onde a tensão superficial é maior.

Gráfico 6 – Saltos de velocidade (∆v) em função do número de iterações.

-10 -5 0 5 10 15

0 10000 20000 30000 40000 50000

Δ

V (10

-5 m/s)

Iterações

γ = 0.030 γ = 0.010 γ = 0.0001

(a) Fase 1;S1= 0.20.

-10 -5 0 5 10 15 20

0 10000 20000 30000 40000 50000

Δ

V (10

-5 m/s)

Iterações

γ = 0.030 γ = 0.010 γ = 0.0001

(b) Fase 2;S1 = 0.20.

-20 -10 0 10 20 30

0 10000 20000 30000 40000 50000

Δ

V (10

-5 m/s)

Iterações

γ = 0.030 γ = 0.010 γ = 0.0001

(c) Fase 1;S1= 0.40.

-10 -5 0 5 10 15 20

0 10000 20000 30000 40000 50000

Δ

V (10

-5 m/s)

Iterações

γ = 0.030 γ = 0.010 γ = 0.0001

(d) Fase 2;S1 = 0.40.

Gráfico dos saltos de velocidade (∆v) em função do número de iterações, para cada fase fluida e para vários valores de tensão superficial e saturação. Fonte: Elaborado pelo autor.

(46)

Tabela 3 – Comparação dos expoentes obtidos das distribuições dos valores absolutos dos saltos de velocidade|∆v|.

Tens˜ao superficial (N/m) S1 = 0.2 S1= 0.4

0.0001 −0.620±0.015 −0.541±0.009 −1.822±0.026 −0.390±0.007 0.010 −2.058±0.049 −1.467±0.035 −0.761±0.019 −0.345±0.028 0.030 −1.140±0.024 −0.933±0.026 −0.388±0.009 −0.816±0.020

Gráfico 7 – Análise das distribuições dos valores absolutos dos saltos de velocidade,|∆v(t)|, nas séries temporais da velocidade médiahVx(t)i, paraγ = 0.0001N/m.

0 5 10 15

|∆v| ×10-7 100 101 102 103 104 Frequência

γ = 0.0001; α = −0.620 ± 0.015

(a) Fase 1;S1 = 0.20.

0 5 10 15

|∆v| ×10-7 100 101 102 103 104 Frequência

γ = 0.0001; α = −0.541 ± 0.009

(b) Fase 2;S1= 0.20.

0 1 2 3 4 5

|∆v| ×10-6 100 101 102 103 104 Frequência

γ = 0.0001; α = −1.822 ± 0.026

(c) Fase 1;S1 = 0.40.

0 5 10 15 20

|∆v| ×10-7 100 101 102 103 104 Frequência

γ = 0.0001; α = −0.390 ± 0.007

(d) Fase 2;S1= 0.40.

(47)

Gráfico 8 – Análise das distribuições dos valores absolutos dos saltos de velocidade,|∆v(t)|, nas séries temporais da velocidade médiahVx(t)i, paraγ = 0.010e0.030N/m.

0 1 2 3 4 5 6 7

|∆v| ×10-5

100

101

102

103

104

Frequência

γ = 0.010; α = −2.058 ± 0.049 γ = 0.030; α = −1.140 ± 0.024

(a) Fase 1;S1 = 0.20.

0 1 2 3 4 5 6

|∆v| ×10-5

100

101

102

103

104

Frequência

γ = 0.010; α = −1.467 ± 0.035 γ = 0.030; α = −0.933 ± 0.026

(b) Fase 2;S1= 0.20.

0 5 10 15

|∆v| ×10-5

100

101

102

103

104

Frequência

γ = 0.010; α = −0.671 ± 0.019 γ = 0.030; α = −0.388 ± 0.009

(c) Fase 1;S1 = 0.40.

0 1 2 3 4 5 6 7

|∆v| ×10-5

100

101

102

103

104

Frequência

γ = 0.010; α = −1.345 ± 0.028 γ = 0.030; α = −0.816 ± 0.020

(d) Fase 2;S1= 0.40.

(48)

Um caso à parte, também estudado nessa dissertação, é o escoamento, em um meio poroso, de um fluido não-newtoniano incompress´ıvel, no regime estacionário e isotérmico. Como vimos no cap´ıtulo anterior, a viscosidade aparente de um fluido não-newtoniano depende da sua taxa de deformação, isto é,η = η( ˙γ). Suponha, entretanto, um fluido não-newtoniano cuja dependência com a taxa de deformação seja dada pela seguinte equação:

η( ˙γ,γ˙0) =

(

η1, γ˙ ≥γ˙0

η2, γ <˙ γ˙0

, (3.3)

ondeη1 eη2são valores constantes de viscosidade aparente eγ˙0 é a taxa de deformação cr´ıtica, isto é, o valor da taxa de deformação em que ocorre a transição da viscosidade. Assim, de acordo com a Equação 3.3, tal fluido não-newtoniano apresenta duas viscosidades aparentes (veja o Gráfico 9): η( ˙γ,γ˙0) = η1, para altas tensões de deformação, isto é, para γ˙ ≥ γ˙0, e η( ˙γ,γ˙0) = η2, para baixas tensões de deformação, quandoγ <˙ γ˙0. Nesta parte do trabalho,

estamos interessados em saber como certos parâmetros, como saturação, velocidade média e permeabilidade efetiva, variam em função da taxa de deformação cr´ıtica.

Gráfico 9 – Viscosidade aparente em função da taxa de deformação de um fluido não-newtoniano com duas viscosidades.

η₁ η₂

γ₀

.

η

γ

Gráfico da viscosidade aparente em função da taxa de deformação para um fluido não-newtoniano cujo comportamento obedece a Equação 3.3. Para baixas tensões de deformação, isto é, paraγ <˙ γ˙0, o coeficiente de viscosidade éη( ˙γ,γ˙0) = η2, e para altas tensões,γ˙ ≥γ˙0, a viscosidade éη( ˙γ,γ˙0) = η1. Fonte: Elaborado pelo autor.

Um fluido não-newtoniano com essas caracter´ısticas pode ser modelado, no soft-ware Fluent, por uma lei definida pelo usuário, que alterna o valor da viscosidade entreη1 e η2, de acordo com a Equação 3.3. O modelo de meio poroso utilizado nessas simulações é o