Universidade de Trás-os-Montes e
Alto Douro
Sintonia do controlador PID, com
Algoritmo de Optimização por
Grupo de Partículas.
Dissertação de Mestrado
Engenharia Electrotécnica e de Computadores
Joaquim Jesus Pereira
ii
Sintonia do controlador PID, com Algoritmo de
Optimização por Grupo de Partículas
Joaquim Jesus Pereira
Licenciado em Engenharia Electrotécnica e de Computadores pelo Departamento de
Engenharias da Universidade Trás-os-Montes e Alto Douro.
Dissertação submetida para satisfação parcial dos requisitos do programa do curso de
Mestrado em Engenharia Electrotécnica e de Computadores
Orientador Científico:
Professor Doutor José Paulo Barroso de Moura Oliveira
Professor auxiliar do Departamento Engenharias
Universidade Trás-os-Montes e Alto Douro
Co-orientador Científico:
Professor Doutor José Boaventura Ribeiro da Cunha
Professor auxiliar do Departamento Engenharias
iii
Agradecimentos
Chegado a este momento é minha intenção expressar os mais sinceros agradecimentos às várias pessoas que, em diferentes momentos, deram o seu contributo para a concretização deste projecto.
Ao Professor Paulo Oliveira, orientador desta dissertação que desde o início, depositou toda a confiança em mim e sempre me apoiou durante a execução deste trabalho. Gostaria de manifestar o meu reconhecimento pela forma como delineou as linhas deste trabalho e pelos ensinamentos prestados durante a sua realização. Quero ainda agradecer o constante incentivo e pela serenidade que sempre me transmitiu, um muito e reconhecido obrigado.
Ao Professor José Boaventura, agradeço todo o apoio prestado na escrita desta dissertação e a cooperação ao longo do percurso académico.
Agradeço em especial ao Professor Eduardo Pires, pela ajuda prestada na implementação dos algoritmos multi-objectivos, assim como pelos esclarecimentos de alguns conceitos mais específicos desta área.
A todos os professores e colegas que directa ou indirectamente contribuíram para a realização deste trabalho.
Aos meus Amigos, em quem tantas vezes pensei ao longo destes anos, que sempre me apoiaram e entusiasmaram, compreendendo sempre a minha indisponibilidade.
À minha família, em especial à minha mãe e ao meu irmão, pelo apoio, compreensão e paciência que me têm sempre dedicado.
A Todos, Muito Obrigado.
iv
Dedicatória
Á minha mãe Maria Almeida e Irmão Agostinho Pereira.
v
Resumo
A maior parte das malhas industriais de controlo utilizam um controlador com acção proporcional, integrativa e derivativa (PID). É de muita utilidade desenvolver ferramentas informáticas de suporte ao projecto deste tipo de controladores, particularmente utilizando técnicas de optimização inspiradas em comportamentos biológicos e naturais. O desenvolvimento de uma ferramenta de simulação que permita projectar controladores do tipo PID é o objectivo global desta dissertação. O conjunto de teste deve conter modelos que representam as dinâmicas mais comuns na indústria de controlo de processos.
O algoritmo evolutivo seleccionado é o “Algoritmo de Optimização com Grupo de Partículas” (PSO), por ter demonstrado ter bom desempenho num leque alargado de aplicações. O PSO é um algoritmo simples, capaz de solucionar problemas bastantes complexos. O algoritmo PSO implementado é testado na optimização de um conjunto de funções uni-objectivo padrão, seguindo-se a optimização do controlador PID. O objectivo de projecto é a optimização da resposta a um degrau aplicado à entrada de referência do sistema ou na entrada de perturbação da saída controlada. Os resultados obtidos são comparados com técnicas clássicas de sintonia.
Uma implementação do algoritmo de optimização multi-objectivo por grupo de partículas (MOPSO) é testada num conjunto de funções padrão, seguindo-se a optimização multi-objectivo do controlador PID. Dois objectivos de projecto foram considerados simultaneamente: i) a optimização da resposta a um degrau aplicado na entrada da referência; ii) a optimização da resposta a uma perturbação em degrau aplicada na saída controlada.
Palavras-chave: Controlador PID, Algoritmos evolutivos, Sistema por Grupo de
vi
Abstract
The great majority of industrial control loops are controlled by using a controller with proportional, integral and derivative (PID) controllers. The development of software tools to design this type of controllers is very useful, namely by using optimization techniques inspired in biological and natural behaviours. The global objective of this dissertation is to develop a simulation tool which allows the Project of PID controllers. The plant test set should include models which represent some of the most usual dynamics within the process control industry.
The evolutionary algorithm selected is the Particle Swarm Optimization (PSO), due to the good performance shown in a broad application set. The PSO algorithm is simple and capable of solving complex problems. The PSO algorithm implemented is tested in optimization a set of standard functions, followed by the PID controller’s optimization. The design objective is the set-point-tracking. The results are compared with the ones archived with classics tuning techniques.
An implementation of the multi-objective particle swarm optimization algorithm (MOPSO) is tested in a set of standard functions followed by the multi-objective optimization of PID controllers. Two design objectives were considered simultaneously: i) the set-point tracking response; ii) the output disturbance rejection.
Keywords: PID control, Evolutionary algorithms, Particle Swarm Systems, Multi-Objective Optimization.
vii
Índice
Capítulo 1 Introdução... 1 1.1 Motivação ... 1 1.2 Objectivos da Dissertação ... 2 1.3 Organização da Dissertação ... 3Capítulo 2 Algoritmo de Optimização por Grupo de Partículas ... 5
2.1 Algoritmos Evolutivos ... 5
2.2 Introdução ao Algoritmo de Optimização por Grupo de Partículas ... 6
2.3 Algoritmo PSO Padrão ... 8
2.3 Topologias ... 13
2.4 Aplicações ... 16
2.5 Variantes do algoritmo PSO ... 17
Capítulo 3 Algoritmos de Optimização Multi-Objectivo por Grupo de Partículas ... 19
3.1 Conceitos Básicos ... 19
3.2 Formulação ... 20
3.2.1 Frente de Pareto ... 21
3.2.2 Metas na Optimização Multi-objectivo ... 23
3.3 Optimização Uni-Objectivo vs Multi-objectivo ... 24
3.4 Operador de dominância Pareto ... 25
3.4.1 Propriedades da relação de dominância ... 25
3.4.2 Optimalidade de Pareto ... 26
3.5 MOPSO ... 29
3.5.1 Estrutura típica do MOPSO ... 29
3.5.2 Selecção e actualização das partículas guias ... 33
3.5.3 Promoção da diversidade ... 35
3.5.4 Algoritmos Evolutivos com preservação da elite. ... 36
3.6 Diferentes métodos de Implementação do MOPSO ... 37
3.6.1 Ordenação Lexicográfica ... 38
3.6.2 Aproximação com Subpopulações. ... 39
viii
3.7 MOPSO implementado ... 49
3.7.1 Algoritmo MaxiMin ... 49
Capítulo 4 Optimização de Funções Uni-Objectivo ... 52
4.1.1 Função Esférica ... 52
4.2.1 Função de Ackley ... 55
4.3.1 Função de Shaffer ... 57
Capítulo 5 Optimização de Funções Multi-objectivo ... 59
5.1 Função 1 ... 59 5.2 Função 2 ... 61 5.3 Função 3 ... 63 5.4 Função 4 ... 64 5.5 Função 5 ... 66 5.6 Notas finais ... 67
Capítulo 6 Controlador Proporcional Integrativo e Derivativo ... 68
6.1 Enquadramento histórico do controlador PID ... 68
6.2 Controlador PID ... 72
6.3 Estrutura de Controlo Utilizado ... 73
6.3.1 Estrutura com Ruído ... 74
6.4 Rejeições de Perturbações ... 75
Capítulo 7 Optimização Uni-objectivo do PID com o PSO ... 76
7.1 Processo I ... 76
7.1.1 Simulação com perturbações aleatórias na saída do sistema. ... 80
7.2 Processo II ... 82
7.2.1 Simulação com perturbações aleatórias na saída do sistema. ... 85
7.3 Processo III ... 87
7.3.1 Simulação com perturbações aleatórias na saída do sistema. ... 90
7.4 Processo IV ... 92
7.4.1 Simulação com perturbações aleatórias na saída do sistema. ... 96
7.5 Sistema com perturbação na saída controlada ... 98
7.5.1 Processo I ... 98
7.5.2 Processo II ... 99
7.5.3 Processo III ... 101
ix
7.6 Notas finais ... 103
Capítulo 8 Comparação da sintonia PSO vs outros Métodos. ... 105
8.1 Processo I ... 105
8.2 Processo II ... 107
8.3 Processo III ... 108
8.4 Processo IV ... 109
Capítulo 9 Optimização Multi-objectivo do PID com MOPSO ... 111
9.1 Processo I ... 111
9.2 Processo II ... 115
9.3 Processo III ... 118
9.4 Processo IV ... 120
Capítulo 10 Conclusão e Trabalho Futuro ... 123
Referências ... 125
x
Índice de Figuras
FIGURA 2.1-UM CARDUME E UM BANDO DE PÁSSAROS, QUE SE DESLOCAM EM GRUPO. ... 6
FIGURA 2.2ALGORITMO DE OPTIMIZAÇÃO COM GRUPO DE PARTÍCULAS. ... 8
FIGURA 2.3-FLUXOGRAMA DO ALGORITMO PSO,(COELHO,2003). ... 9
FIGURA 2.4–TOPOLOGIA EM ANEL (CÍRCULO REPRESENTA UMA PARTÍCULA). ... 14
FIGURA 2.5-TOPOLOGIA COMPLETAMENTE LIGADA (FULL CONNECTED). ... 14
FIGURA 2.6–TOPOLOGIA EM ESTRELA. ... 15
FIGURA 2.7-TOPOLOGIA ÁRVORE. ... 15
FIGURA 2.8-ARTIGOS RELACIONADOS COM O ALGORITMO PSO,(RICARDO POLI,2007). ... 16
FIGURA 3.1-OPÇÕES NA COMPRA DE UM AUTOMÓVEL. ... 22
FIGURA 3.2-DISTRIBUIÇÃO DE SOLUÇÕES NA FRENTE DE PARETO. ... 23
FIGURA 3.3-CONJUNTOS ÓPTIMOS DE PARETO ... 27
FIGURA 3.4-SOLUÇÕES LOCAIS E GLOBAIS DE PARETO. ... 28
FIGURA 3.5-FLUXOGRAMA GENÉRICO DO MOPSO ... 31
FIGURA 3.6-CÁLCULO DA DENSIDADE NO MÉTODO CROWDING DISTANCE (DEB ET AL.,2002). ... 34
FIGURA 3.7-EXEMPLO DE NICHOS ... 35
FIGURA 3.8-ESQUEMA DO MODELO NSGAII,(DEB,2001) ... 37
FIGURA 3.9-MÉTODO MOPSO EM HU E EBERHART,(2002). ... 39
FIGURA 3.10-MOPSO MODELO PARSOPOULOS E VRAHATIS (2002) ... 40
FIGURA 3.11-PROCESSO DE SELECÇÃO UTILIZADO EM HANNE (1999), COM A APTIDÃO NA POPULAÇÃO DO HIPERCUBO. ... 42
FIGURA 3.12-MOPSO DE COELLO E LECHUNGA (2002). ... 43
FIGURA 3.13-MÉTODO SIGMA PARA DOIS OBJECTIVOS. ... 45
FIGURA 3.14-SELECÇÃO DO LOCAL GBEST PARA CADA PARTÍCULA DO GRUPO ... 46
FIGURA 3.15–SOLUÇÕES NÃO-DOMINADAS NO ALGORITMO MAXIMIN ... 50
FIGURA 4.1-ESPAÇO DE PESQUISA DEFINIDO PELA FUNÇÃO ESFÉRICA (4.1) ... 52
FIGURA 4.2-DESEMPENHO DA FUNÇÃO (4.1) PARA UMA POPULAÇÃO COM 10 PARTÍCULAS... 53
FIGURA 4.3-DESEMPENHO DA FUNÇÃO (4.1), PARA UMA POPULAÇÃO COM 30 PARTÍCULAS. ... 53
FIGURA 4.4-DESEMPENHO DA FUNÇÃO (4.1) PARA UMA POPULAÇÃO COM 50 PARTÍCULAS... 54
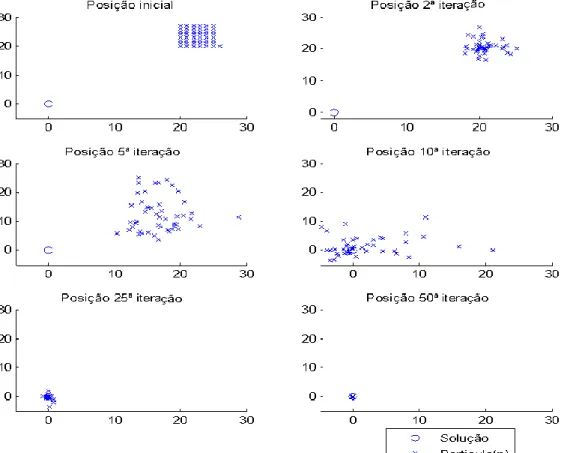
FIGURA 4.5-EVOLUÇÃO DE UMA POPULAÇÃO DE 50 PARTÍCULAS AO LONGO DAS ITERAÇÕES. ... 54
FIGURA 4.6-ESPAÇO DE PESQUISA DEFINIDO PARA A FUNÇÃO DE ACKELY (4.2). ... 55
FIGURA 4.7-DESEMPENHO PARA UMA POPULAÇÃO DE 50 PARTÍCULAS. ... 56
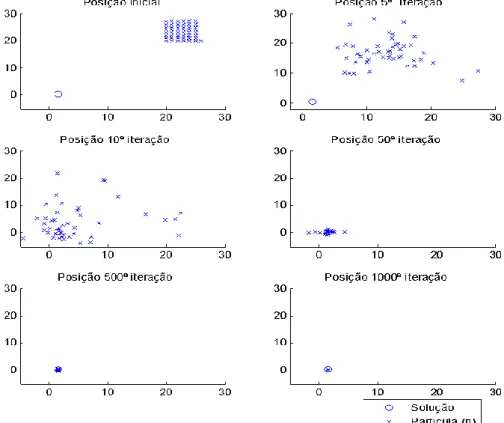
FIGURA 4.8-EVOLUÇÃO DAS PARTÍCULAS AO LONGO DAS ITERAÇÕES. ... 56
FIGURA 4.9-ESPAÇO DE PESQUISA DEFINIDO PARA A FUNÇÃO SHAFFER. ... 57
FIGURA 4.10-EVOLUÇÃO DAS PARTÍCULAS AO LONGO DAS ITERAÇÕES. ... 58
FIGURA 5.1-OPTIMIZAÇÃO DA FUNÇÃO F1, UMA SIMULAÇÃO... 60
FIGURA 5.2-OPTIMIZAÇÃO DA FUNÇÃO F1, MELHOR DE CEM SIMULAÇÕES. ... 61
FIGURA 5.3-OPTIMIZAÇÃO DA FUNÇÃO F2, UMA SIMULAÇÃO ... 62
FIGURA 5.4-OPTIMIZAÇÃO DA FUNÇÃO F2, MELHOR DE 100 SIMULAÇÕES. ... 62
FIGURA 5.5-OPTIMIZAÇÃO DA FUNÇÃO F3, PARA UMA SIMULAÇÃO. ... 63
FIGURA 5.6-OPTIMIZAÇÃO DA FUNÇÃO F3, O MELHOR DE CEM SIMULAÇÕES. ... 64
FIGURA 5.7-OPTIMIZAÇÃO DA FUNÇÃO F4, PARA UMA SIMULAÇÃO. ... 65
FIGURA 5.8-OPTIMIZAÇÃO DA FUNÇÃO F4, O MELHOR DE CEM SIMULAÇÕES. ... 65
FIGURA 5.9-OPTIMIZAÇÃO DA FUNÇÃO F5, UMA SIMULAÇÃO COM 100 ITERAÇÕES. ... 66
FIGURA 5.10-OPTIMIZAÇÃO DA FUNÇÃO F5, O MELHOR DE 100 ITERAÇÕES... 67
FIGURA 6.1-SISTEMA DE CONTROLO COM O CONTROLADOR PID ... 72
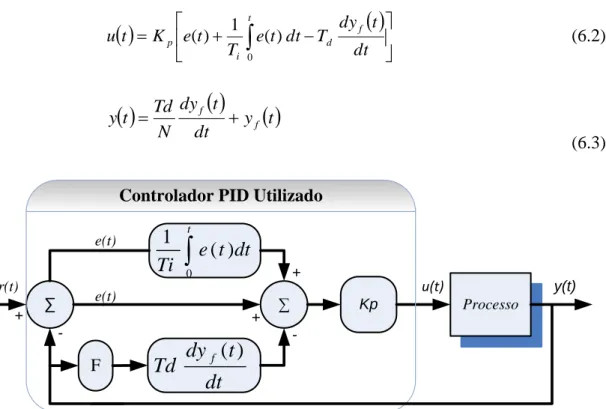
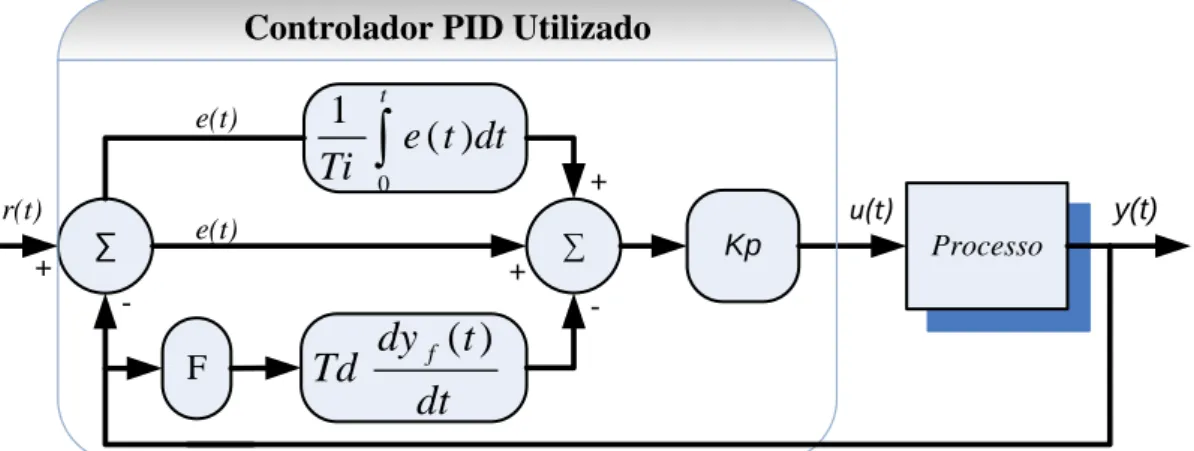
FIGURA 6.2-CONTROLADOR PID COM ACÇÃO DERIVATIVA SOBRE O SINAL DE SAÍDA ... 73
FIGURA 6.3-CONTROLADOR PID COM ADIÇÃO DE RUÍDO ALEATÓRIO NA SAÍDA. ... 74
xi
FIGURA 6.5-CONTROLADOR PID COM PERTURBAÇÃO. ... 75 FIGURA 7.1-RESPOSTA AO DEGRAU PARA O MODELO (7.1),EN=2 E POP=30... 78 FIGURA 7.2-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES MODELO (7.1),EN=2 E
POP=30. ... 78 FIGURA 7.3-RESPOSTA AO DEGRAU PARA O MODELO (7.1),EN=3 E POP=30... 79 FIGURA 7.4-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES, MODELO (7.1),EN=3 E
POP=30. ... 79 FIGURA 7.5-SINAL DE SAÍDA IDEAL (Y) E SINAL DE SAÍDA COM ADIÇÃO DE RUÍDO (Y*), MODELO (7.1),
EN=2 E POP=30. ... 81 FIGURA 7.6-SINAL DE CONTROLO IDEAL (U) E COM ADIÇÃO DE RUÍDO (U*) REFERENTES À FIGURA
ANTERIOR. ... 81 FIGURA 7.7-RESPOSTA AO DEGRAU PARA O MODELO (7.2),T=1 E POP=90. ... 83 FIGURA 7.8-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES, MODELO (7.2),T=1 E
POP=90. ... 84 FIGURA 7.9-RESPOSTA AO DEGRAU PARA O MODELO (7.2),T=10 E POP=90. ... 84 FIGURA 7.10-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS 50 ITERAÇÕES, MODELO (7.2), ... 85 FIGURA 7.11-SINAL DE SAÍDA IDEAL (Y) E SINAL DE SAÍDA COM ADIÇÃO DE RUÍDO (Y*), MODELO (7.2),T=
10 E POP=90. ... 86 FIGURA 7.12-SINAL DE CONTROLO IDEAL U E COM ADIÇÃO DE RUÍDO REFERENTES U* FIGURA ANTERIOR.
... 87 FIGURA 7.13-RESPOSTA AO DEGRAU PARA O MODELO (7.3), N =2 E POP=90. ... 88 FIGURA 7.14-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES, MODELO (7.3), N =2 E
POP=90. ... 89 FIGURA 7.15-RESPOSTA AO DEGRAU PARA O MODELO (7.3), N =8 E POP=90. ... 89 FIGURA 7.16-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS 50 ITERAÇÕES, MODELO (7.3), N =8 E
POP=90. ... 90 FIGURA 7.17-RESPOSTA AO DEGRAU PARA O MODELO (7.3), N =2 E POP=90. ... 91 FIGURA 7.18-SINAL DE CONTROLO IDEAL U E COM ADIÇÃO DE RUÍDO U* REFERENTE À FIGURA ANTERIOR.
... 92 FIGURA 7.19-RESPOSTA AO DEGRAU PARA O MODELO (7.4), Α=2 E POP=90. ... 94 FIGURA 7.20-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES, MODELO (7.4), Α=2 E
POP=90. ... 94 FIGURA 7.21-RESPOSTA AO DEGRAU PARA O MODELO (7.4), Α=5 E POP=90. ... 95 FIGURA 7.22-EVOLUÇÃO DO VALOR ITAE COM O DECORRER DAS ITERAÇÕES, MODELO (7.4), =5 E
POP=90. ... 95 FIGURA 7.23-SINAL DE SAÍDA IDEAL (Y) E SINAL DE SAÍDA COM ADIÇÃO DE RUÍDO (Y*), MODELO (7.4),
=5 E POP=90. ... 97 FIGURA 7.24-SINAL DE CONTROLO IDEAL (U) E COM ADIÇÃO DE RUÍDO (U*), MODELO (7.4),=5 E
POP=90. ... 97 FIGURA 7.25-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.1),EN=2 E POP=90.
... 98 FIGURA 7.26-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.1),EN=2 E POP=90.
... 99 FIGURA 7.27-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.2),T=2 E POP=90.
... 100 FIGURA 7.28-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.2),T=2 E POP=90.
... 100 FIGURA 7.29-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.3), N=2 E POP=90.
... 101 FIGURA 7.30-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.3), N=2 E POP=90.
xii
FIGURA 7.31-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.4), Α=2 E POP=90.
... 102
FIGURA 7.32-SINAL DE CONTROLO (U) E RESPECTIVO SINAL DE SAÍDA (Y), MODELO (7.4), Α=2 E POP=90. ... 103
FIGURA 8.1-COMPARAÇÃO DE VÁRIOS MÉTODOS DE SINTONIA DO PROCESSO I. ... 106
FIGURA 8.2-COMPARAÇÃO DE VÁRIOS MÉTODOS DE SINTONIA DO PROCESSO II. ... 107
FIGURA 8.3-COMPARAÇÃO DE VÁRIOS MÉTODOS DE SINTONIA DO PROCESSO III. ... 109
FIGURA 8.4-COMPARAÇÃO DE VÁRIOS MÉTODOS DE SINTONIA DO PROCESSO IV. ... 110
FIGURA 9.1-FRENTE NÃO DOMINADA PARA OS DOIS OBJECTIVOS ... 112
FIGURA 9.2-FRENTE DE PARETO E RESPECTIVAS SAÍDAS DO SISTEMA. ... 113
FIGURA 9.3-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA O SEGUIMENTO DA REFERÊNCIA. ... 114
FIGURA 9.4-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA A REJEIÇÃO DE PERTURBAÇÕES. ... 114
FIGURA 9.5-FRENTE NÃO DOMINADA OBTIDA PARA O PROCESSO II ... 115
FIGURA 9.6-RESPOSTA A UM DEGRAU APLICADA A ENTRADA DE REFERENCIA yE A UM DEGRAU APLICADO PERTURBAÇÃOy*, PARA AS TRÊS SOLUÇÕES NÃO DOMINADAS NA TABELA 9.1. ... 116
FIGURA 9.7-RESPOSTA A UM DEGRAU UNITÁRIO PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO REPRESENTADA NA FIGURA 9.5 ... 117
FIGURA 9.8-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA A REJEIÇÃO DE PERTURBAÇÕES ... 117
FIGURA 9.9-FRENTE NÃO DOMINADA OBTIDA PARA O PROCESSO III, COM N=1 ... 118
FIGURA 9.10-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA A REJEIÇÃO DE PERTURBAÇÕES (Y*) E SEGUIMENTO DA REFERÊNCIA (Y). ... 119
FIGURA 9.11-FRENTE NÃO DOMINADA OBTIDA PARA O PROCESSO III, COM N=2 ... 119
FIGURA 9.12-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA A REJEIÇÃO DE PERTURBAÇÕES (Y*) E SEGUIMENTO DA REFERÊNCIA (Y). ... 120
FIGURA 9.13-FRENTE NÃO DOMINADA OBTIDA PARA O PROCESSO II ... 121
FIGURA 9.14-RESPOSTA A UM DEGRAU APLICADA NA ENTRADA yE A UM DEGRAU APLICADO PERTURBAÇÃOy*. ... 121
FIGURA 9.15-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA A REJEIÇÃO DE PERTURBAÇÕES (Y*). ... 122
FIGURA 9.16-RESPOSTA PARA TODAS AS SOLUÇÕES DA FRENTE DE PARETO, PARA O SEGUIMENTO DA REFERÊNCIA (Y). ... 122
xiii
Índice de Tabelas
TABELA 7.1-RESULTADOS DE SIMULAÇÃO PARA VÁRIOS ENSAIOS PARA O PROCESSO I. ... 77
TABELA 7.2-RESULTADO DA SIMULAÇÃO PARA O PROCESSO (I), COM RUÍDO INJECTADO NA SAÍDA DO SISTEMA. ... 80
TABELA 7.3-RESULTADOS DA SIMULAÇÃO PARA O PROCESSO II. ... 82
TABELA 7.4-RESULTADO DA SIMULAÇÃO PARA O PROCESSO (II), COM RUÍDO INJECTADO NA SAÍDA DO SISTEMA. ... 86
TABELA 7.5-RESULTADOS DA SIMULAÇÃO PARA O PROCESSO III. ... 88
TABELA 7.6-RESULTADO DA SIMULAÇÃO PARA O PROCESSO III, COM RUÍDO INJECTADO NA SAÍDA DO SISTEMA. ... 91
TABELA 7.7-RESULTADOS DA SIMULAÇÃO PARA O PROCESSO IV. ... 93
TABELA 7.8-RESULTADO DA SIMULAÇÃO PARA O PROCESSO (IV), COM RUÍDO INJECTADO NA SAÍDA DO SISTEMA. ... 96
TABELA 8.1-MÉTODOS DE SINTONIA DO CONTROLADOR PID ... 105
TABELA 8.2-RESULTADOS OBTIDOS PARA OS VÁRIOS MÉTODOS DE SINTONIA ... 106
TABELA 8.3-RESULTADOS OBTIDOS COM OS VÁRIOS MÉTODOS DE SINTONIA ... 107
TABELA 8.4-RESULTADOS OBTIDOS COM VÁRIOS MÉTODOS DE SINTONIA. ... 108
TABELA 8.5-RESULTADOS OBTIDOS COM VÁRIOS MÉTODOS DE SINTONIA ... 109
Capítulo 1 2008
Capítulo 1
Introdução
1.1
Motivação
A grande maioria das malhas industriais é controlada pelo controlador Proporcional, Integral e Derivativo (PID). Isto deve-se a vários factores, entre os quais a sua simplicidade conceptual, o seu bom desempenho numa larga gama de sistemas e a sua robustez. Devido ao seu uso generalizado no controlo de processos industriais, múltiplas técnicas têm sido propostas para ajustar os seus parâmetros. Este problema é conhecido como o problema da sintonia. As primeiras regras de sintonia de controladores do tipo PID foram propostas pelos investigadores Ziegler e Nichols (1942). Estas regras foram importantes pelo pioneirismo e pela sua simplicidade de aplicação, embora com limitações no âmbito do desempenho conseguido. Desde então muitas outras regras de sintonia e projecto foram propostas (Cohen e Coon, 1953), (Kiong et al., 1999).
O uso de algoritmos evolutivos (AEs) tem despertado muito interesse por ser uma teoria que na prática permite encontrar soluções para problemas de uma forma relativamente fácil. Os algoritmos evolutivos, são algoritmos de optimização e pesquisa inspirados na evolução natural dos seres vivos, que permitem encontrar soluções de problemas.
Os problemas com objectivos múltiplos são frequentes em muitos problemas de optimização e constituem uma área científica que tem adquirido grande relevância em diversas aplicações da Engenharia. Na optimização multi-objectivo pretende-se encontrar uma família de soluções óptimas e não uma só solução. As famílias de soluções são obtidas no final de cada simulação e constituem um conjunto de soluções não-dominadas entre todas as funções objectivo do problema. O conjunto de soluções óptimas, também conhecido como soluções não dominadas, pertencem a um conjunto óptimo chamado de Pareto.
Um dos problemas inerente à utilização de regras de sintonia é a sua multiplicidade, ou seja existir uma tabela de sintonia para cada tipo de dinâmica de processo. Assim, regras de sintonia foram desenvolvidas para sistemas de primeira ou segunda ordem com tempo morto. Em alguns casos chegavam a não funcionar para sistemas com fase não
Introdução
2
mínima, ou para sistemas de ordem superior. Também o aumento significativo do tempo morto implicava uma deterioração significativa do desempenho dos sistemas controlados com controladores do tipo PID. O ideal seria obter um método de sintonia que funcionasse bem independentemente da dinâmica dos sistemas a controlar. A utilização de algoritmos evolutivos como ferramenta de optimização do controlador PID é uma alternativa às técnicas clássicas de sintonia.
Nesta dissertação o algoritmo de optimização por Grupo Partículas (De Moura Oliveira, 2002), é aplicado na optimização do controlador PID considerando um único objectivo de projecto e dois objectivos de projecto. No último caso é utilizado um algoritmo de optimização multi-objectivo por grupo de partículas multi-objectivo.
1.2
Objectivos da Dissertação
Os objectivos deste trabalho estão sumariados nos seguintes pontos, que também constituíram as fases de execução do mesmo:
Estudo dos algoritmos PSO e MOPSO.
Projecto de controladores PID com algoritmos evolutivos. Neste projecto serão apenas considerados os algoritmos PSO e MOPSO.
Desenvolvimento de uma ferramenta de projecto utilizando o Matlab®, e o
Simulink®.
Realização de testes de simulação, utilizando PSO, para determinar os parâmetros de sintonia do controlador PID. Realização de comparações com outras técnicas de sintonia do controlador PID. Execução de testes utilizando o MOPSO para a situação de optimização multi-objectivo.
Introdução
3
1.3
Organização da Dissertação
Para além deste capítulo introdutório, esta dissertação está organizado em 9 capítulos.
O Capítulo 2 apresenta uma revisão do Algoritmo de Optimização por Grupo de Partículas (PSO).
No Capítulo 3 descreve-se a metodologia da optimização multi-objectivo. Neste capítulo é ainda apresentado o Algoritmo Evolutivo multi-objectivo MOPSO seleccionado para optimização dos problemas multi-objectivo do controlador PID.
No Capítulo 4 são apresentados testes efectuados a algumas funções padrão uni-objectivo com o PSO. Os resultados apresentados pertencem à resolução de funções de um só problema de optimização com o algoritmo PSO.
No Capítulo 5 mostram-se os resultados obtidos com a optimização multi-objectivo referentes a funções multi-objectivo citadas como adequadas a este tipo de estudo. Na optimização das funções é utilizado o algoritmo MOPSO.
O Capítulo 6 trata do estudo de alguns conceitos do controlador PID, especialmente a dificuldade existente na sintonia dos parâmetros do controlador PID. São apresentados os esquemas dos sistemas a serem optimizados, em pesquisa da solução óptima e no caso dos problemas multi-objectivo no grupo de soluções não-dominadas.
A implementação do algoritmo PSO na optimização do controlador PID é descrita no Capítulo 7. É objectivo do algoritmo de optimização encontrar os valores dos parâmetros do controlador do PID para um processo específico, esperando-se obter a resposta óptima do sistema.
No Capítulo 8 é realizada uma comparação dos resultados obtidos no capítulo 7, com os resultados obtidos com os métodos clássicos de sintonia do controlador PID. Referem-se ainda as respectivas conclusões desta comparação.
Introdução
4
O Capítulo 9 trata da implementação do algoritmo multi-objectivo MOPSO para a optimização do controlador PID, visando optimizar mais do que um objectivo simultaneamente.
Por último, no capítulo 10 é apresentada a síntese com as conclusões da dissertação. São ainda apontadas as principais contribuições feitas por este trabalho para à área de controlo de processos e feitas sugestões para a realização de trabalhos futuros, que possam dar continuidade ao que foi desenvolvido.
Capitulo 2
5
2008
Capítulo 2 Algoritmo
de Optimização por Grupo de
Partículas
2.1 Algoritmos Evolutivos
Algoritmos evolutivos (AEs) compreendem todos os métodos de pesquisa que têm a sua inspiração em processos naturais, tais como: comportamento social de grupos de animais, reprodução de animais, entre outros. Esses algoritmos baseiam-se na selecção natural como processo de pesquisa da solução óptima, apoiados na teoria de que na natureza os mais aptos prevalecem sobre os menos aptos. Os algoritmos evolutivos possuem características que os tornam mais eficazes do que outros algoritmos na pesquisa de soluções óptimas, das quais se destacam:
A capacidade de trabalhar com uma população de soluções simultaneamente, introduzindo assim uma perspectiva global e uma maior diversidade de pesquisa (possibilita uma avaliação mais abrangente do espaço de pesquisa em cada iteração). Tal característica proporciona uma grande capacidade de encontrar óptimos globais em problemas que possuem diversos óptimos locais.
Os algoritmos evolutivos trabalham com soluções aleatórias e operadores probabilísticos, o que possibilita uma maior capacidade de fuga de óptimos locais, além de também manter uma maior diversidade da população.
A funcionalidade com qualquer tipo de função objectivo, ao contrário de outros algoritmos baseados no cálculo diferencial ou noutro procedimento específico, que geralmente requerem características específicas da função objectivo para funcionarem de forma adequada, como por exemplo, que as mesmas sejam côncavas, convexas ou contínuas.
Quanto ao domínio da pesquisa, não é necessário um conhecimento prévio, podendo este ser multidimensional, com ou sem restrições, lineares ou não lineares.
Algoritmo de Optimização por Grupo de Partículas
6
2.2 Introdução ao Algoritmo de Optimização por Grupo de Partículas
Quando grupos de seres vivos resolvem problemas na natureza essa capacidade costuma ser atribuída à inteligência do grupo. Os melhores exemplos dessa inteligência são as colónias sociais de insectos como as térmitas, formigas e as abelhas. Desde que foi possível descrever os princípios computacionais desses grupos inteligentes nos meios científicos têm sido desenvolvidas novas técnicas. Uma das melhores técnicas desenvolvidas intitula-se Algoritmo de Optimização por Grupo de Partículas (Particle Swarm Optimization, PSO) proposto por Eberhart e Kennedy, (1995).
Este método consiste na optimização de uma função objectivo através da troca de informação entre elementos (partículas), como é o caso dum grupo de organismos da mesma espécie: bando de aves e cardumes de peixes (Figura 2.1).
Figura 2.1 - Um cardume e um bando de pássaros, que se deslocam em grupo.
.
A capacidade de alguns animais para se deslocarem de uma forma organizada, resultando numa movimentação colectiva de visualização muito estética, despertou a curiosidade de cientistas acerca das regras que regem o seu comportamento. A sincronização do movimento de bando de pássaros motivou o estudo de modelos que permitam simular o seu comportamento. Um dos estudos pioneiros para desenvolver um modelo comportamental distribuído para bandos de pássaros, rebanhos e cardumes foi proposto por Reynolds (1987). Utilizando três regras simples para evitar a colisão entre os pássaros, sincronizar a velocidade do movimento e promover o agrupamento em
Algoritmo de Optimização por Grupo de Partículas
7
redor do centro do bando, Reynolds desenvolveu um programa, conhecido por BOIDS, que simula o movimento sincronizado de um bando. Reynolds comparou o seu modelo com um sistema de partículas criado por Reeves (1983), muito utilizado na computação gráfica para modelar fogo, fumo, nuvens e espuma das ondas oceânicas.
Wilson (1991), escreve que a vantagem da partilha da informação social supera a desvantagem da competitividade e da localização imprevisível dos recursos alimentares. Foi essa hipótese da vantagem evolutiva, da partilha social de informação, que motivou Kennedy e Eberhart (1995) a desenvolverem um algoritmo evolutivo que chamaram de
Particle Swarm Optimization Algorithm, (PSO). É um algoritmo de optimização não
determinístico, eficiente, robusto e de simples implementação computacional. Cada elemento desloca-se no hiperespaço atraído por posições que ele considera promissoras.
A expressão Swarm Intelligence (SI) refere-se a uma técnica de inteligência artificial baseada no estudo colectivo de sistemas descentralizados, tendo sido introduzida por Beni e Bang (1989) no contexto de sistemas robóticos celulares. Embora o termo swarm tenha como tradução corrente para o português o termo Enxame, neste trabalho será utilizado o termo Grupo (por o algoritmo PSO se basear no movimento de aves e peixes). Uma definição de swarm foi apresentada por Hoffmeyer (1991) como “um
conjunto de agentes (móveis) que são capazes de comunicar entre si, directamente ou indirectamente (agindo no seu meio ambiente), resolvendo colectivamente um problema distribuído”.
A optimização por bandos de partículas é um método baseado na simulação, no relacionamento social entre os indivíduos de uma população. Nela, cada elemento desloca-se no hiperespaço atraído por posições que ele considera promissoras. Essas posições consideradas promissoras são o resultado da melhor posição que ele obteve e da melhor posição observada na sua vizinhança. Existem contudo outras formas de considerar posições promissoras, sempre baseadas na interacção entre os indivíduos.
Algoritmo de Optimização por Grupo de Partículas
8
2.3 Algoritmo PSO Padrão
No PSO as partículas são geradas aleatoriamente, iniciando o seu movimento pelo espaço de pesquisa com uma velocidade inicial também gerada aleatoriamente. Numa determinada iteração t, cada partícula move-se através de um espaço de pesquisa n-dimensional estando associada a dois conjuntos de vectores:
Posição, X ti
xi1
t ,xi2
t ,,xin
t
Velocidade, V ti
vi1
t v, i2 t ,,vin
t
A posição de cada partícula é actualizada de acordo com a velocidade actual, o conhecimento adquirido pela partícula e o conhecimento adquirido pelo bando. Neste algoritmo, os ajustes da velocidade e da posição são efectuados por equações algébricas simples. O algoritmo apresentado na Figura 2.2 e o fluxograma apresentado na Figura 2.3, ilustram o princípio de funcionamento deste algoritmo com alguns aperfeiçoamentos relativamente à sua forma original (Shi e Eberhart, 1998).
t=0
Inicia o grupo de partículas X (t) Enquanto (! (critério de paragem)) Avalia X (t)
t=t+1
Enquanto (i ≤ tamanho do grupo) Calcular o vector velocidade vi(t1)
Calcular o vector solução xi(t1)
i i1
Fim
Substituir X (t) por X (t+1) Fim
Algoritmo de Optimização por Grupo de Partículas
9
Figura 2.3 - Fluxograma do algoritmo PSO, (Coelho, 2003).
Ao longo das iterações, as partículas modificam a sua posição até que um estado relativamente estacionário seja atingido ou até que os limites definidos pelo utilizador sejam excedidos. As velocidades das partículas em cada dimensão são limitadas a um valor máximo Vmáx.
A escolha da partícula que exerce a influência social é um ponto fundamental neste algoritmo. Quando o paradigma foi apresentado pela primeira vez em 1995, a partícula que exercia a influência social era sempre a mais bem sucedida do grupo. Quando se começaram a considerar topologias, a partícula que exerce a influência social é a mais bem sucedida entre os vizinhos do indivíduo.
O algoritmo original integra dois tipos de aquisição de conhecimento por parte da partícula. Através da sua experiência e através de partilha social com outros membros da população. O primeiro caso foi designado como modelo de conhecimento cognitivoe o último de modelo de conhecimento social (Kennedy, 1997). O comportamento de cada partícula é baseado nestes dois tipos de conhecimento e nas suas posições actuais com respeito à pesquisa. Kennedy modelou o comportamento das partículas através das seguintes equações:
Algoritmo de Optimização por Grupo de Partículas
10 ) ( ) ( ) ( t id x t id p t id co (2.1) ) ( ) ( t id x t gd p id so (2.2) ) ( * 2 ) ( * 1 ) ( ) 1 ( t id so t id co t id v t id v (2.3) ) 1 ( ) ( ) 1 ( t id v t id x t id x (2.4)Onde: d representa o índice da dimensão, 1 d n, pid
t define a melhor posição dapartícula i na presente iteração t, pgd
t representa a melhor partícula na correnteiteração para um tipo de vizinhança pré definida, coid
t e soid
t referem-se aomodelo cognitivo e social, respectivamente, para cada partícula i na presente iteração. Os vectores xid
t e vid
t representam a posição e a velocidade de cada partícula i naépoca t. O parâmetro 1 é conhecido por constante cognitiva e 2 como constante social, representando números aleatórios uniformemente distribuídos num determinado intervalo.
O parâmetro , define um factor de peso, chamado de inércia, que foi incorporado na equação anterior (2.3) por Shi e Eberhart (1999), resultando na equação:
* ( ) 2 ) ( * 1 ) ( * ) ( ) 1 ( t id so t id co t id v t t id v (2.5)
Um valor elevado de orienta o algoritmo para uma pesquisa global enquanto que um valor baixo direcciona-o para uma pesquisa local. Por esta razão, normalmente faz-se variar linearmente o factor de inércia a partir de um valor elevado para um mais baixo de forma a conduzir uma pesquisa global no início da pesquisa e local no fim. As três parcelas da equação (2.5) podem ser interpretadas como a confiança que cada partícula tem na sua posição corrente, na sua experiência e na experiência dos seus pares, respectivamente.
Algoritmo de Optimização por Grupo de Partículas
11
A vizinhança entre partículas pode ser definida por diferentes tamanhos e topologias. Cada partícula pode ter em conta:
1. A informação social a partir de uma lista de partículas predefinidas no início da evolução. Esta lista pode incorporar todos os indivíduos da população, estando cada indivíduo habilitado a usar a melhor solução encontrada por todos os outros membros. Esta estrutura social ligada em rede é denominada de estrela. É possível definir outras propriedades da lista, onde um indivíduo usa apenas os k vizinhos adjacentes organizados em círculo Kennedy e Eberhart,( 2001).
2. A informação física que considera a distância entre indivíduos vizinhos avaliada recorrendo a uma definição métrica.
Uma versão simplificada da equação (2.3) foi proposta por Clerc e Kennedy, (2001) considerando 1 2 e definindo uma posição intermédia:
2 ) ( ) ( * ) ( ) ( t gd p t id p t igd p t igd p (2.6)
entre a melhor posição anterior pi e a melhor posição global pg, resultando numa velocidade regida pela equação:
)] ( ) ( [ ) ( ) 1 ( t id x t igd p t id v t id v (2.7)
Clerc (1999) propôs a utilização de um coeficiente de restrição incorporado na equação simplificada da velocidade como:
Algoritmo de Optimização por Grupo de Partículas
12 )]} ( ) ( [ ) ( { * ) 1 ( t id x t igd p t id v x t id v (2.8)com 4. O coeficiente de constrição pode ser avaliado utilizando a seguinte equação: 1 0 4 2 2 * 2 k k x (2.9)
O efeito deste coeficiente é o de promover a convergência ao logo do tempo. Parâmetros k1 e 4.1 são sugeridos em (Keneddy e Eberhart, 2001) como valores razoáveis a usar. Outra versão do coeficiente de constrição resulta na seguinte modificação da equação da velocidade:
)] ( * 2 ) ( * 1 ) ( * ) ( [ ) ( t id so t id co t id v t w x t id v (2.10)
Como já foi referido, a velocidade é limitada a um máximo Vmax, significando o máximo salto que a velocidade de cada partícula pode dar em cada iteração. O valor seleccionado para esta variável não deve ser muito elevado de forma a evitar oscilações, ou demasiado baixo de forma a ser possível escapar de mínimos locais. O factor de peso de inércia assim como a velocidade máxima foram estudados e relatados por Shi e Eberhart (1998). Adicionalmente, a posição de cada partícula pode também ser limitada
pela sua gama dinâmica
max , min x
x de forma a impedir o posicionamento de
Algoritmo de Optimização por Grupo de Partículas
13
Para facilitar o entendimento de futuros conceitos serão descritas duas expressões. A do deslocamento de cada partícula, a equação (2.11), e a respectiva equação (2.12) da actualização da velocidade de cada partícula.
t xi
t 1 vi(t) i x (2.11)
t vi(t-1) c1r1
pbest xi
t
c2r2(gbest xi
t ) i v (2.12)Na equação (2.12) c1 e c2 representam as constantes cognitivas e sociais, respectivamente.
2.3 Topologias
As partículas tendem a ser influenciadas pelo sucesso de outras a que estão ligadas. Esses vizinhos não são necessariamente partículas que se encontram próximas umas das outras no espaço dos parâmetros. São partículas que estão próximas umas das outras segundo uma determinada topologia que define a estrutura social do Grupo.
As partículas podem ser ligadas a outras, conforme um tipo específico de vizinhança, representada com um gráfico. Algumas das topologias de vizinhanças mais comuns são (Kennedy e Eberhart, 2001):
Gráfico vazio: Nesta topologia, as partículas estão isoladas de qualquer tipo de vizinhança. Cada partícula isolada compara a sua actual posição com a sua melhor posição encontrada até ao momento (pbest). Neste caso, c2=0 na equação 2.12. Esta topologia corresponde ao modelo cognitivo.
Melhor local: Nesta topologia, cada partícula é afectada com o melhor desempenho dos seus k vizinhos imediatos. As partículas são influenciadas pela melhor posição na sua vizinhança (lbest), bem como pela própria experiência
Algoritmo de Optimização por Grupo de Partículas
14
passada (pbest). Quando k=2, esta estrutura é equivalente a uma topologia de anel, tal como representado na Figura 2.4.
Figura 2.4 – Topologia em anel (círculo representa uma partícula).
Gráfico totalmente ligado (full connected): Esta topologia é o oposto do gráfico vazio. Nas topologias totalmente ligadas, todas as partículas do grupo estão ligadas às restantes partículas do grupo. Cada partícula usa a sua experiência, com a sua melhor solução até ao momento, pbest, mas, além disso, estas partículas usam o melhor posicionamento da partícula grupo gbest. Esta estrutura é também conhecida por topologia estrela e está ilustrada na Figura 2.5.
Figura 2.5 - Topologia completamente ligada (full connected).
Rede estrela: Nesta topologia, uma única partícula está ligada a todas as outras e é chamada de partícula focal (Figura 2.6). As restantes partículas estão isoladas umas das outras e toda a informação tem de ser comunicada através da partícula
Algoritmo de Optimização por Grupo de Partículas
15
focal. A partícula focal compara o desempenho de todas as partículas do grupo e ajusta a sua trajectória no sentido do melhor resultado obtido no grupo. Este desempenho é comunicado ao resto do grupo. A esta estrutura pode-se chamar também topologia roda.
Figura 2.6 – Topologia em estrela.
Rede árvore: Nesta topologia (Figura 2.7)., todas as partículas são dispostas segundo uma arquitectura semelhante a uma árvore em que cada nó da árvore contém uma partícula. A partícula é influenciada pela sua melhor posição até ao momento pbest e pela melhor posição da partícula que está directamente acima na árvore (progenitor). Se uma partícula descendente encontrar uma solução que seja melhor do que a melhor solução encontrada até ao momento a partícula nó
progenitor, passa a ser a solução da partícula descendente. Desta forma, esta
topologia oferece uma vizinhança dinâmica. Esta estrutura é também chamada topologia hierárquica.
Algoritmo de Optimização por Grupo de Partículas
16
A topologia e a respectiva vizinhança são susceptíveis de afectar a taxa de convergência, influenciando significativamente o tempo necessário para que as partículas encontrem a localização da melhor região do espaço de pesquisa. Por exemplo, com a topologia totalmente ligada, todas as partículas recebem a informação da melhor solução a partir de qualquer parte do grupo ao mesmo tempo. Assim, quando se utiliza essa topologia, o grupo tende a convergir mais rapidamente do que quando utiliza outras topologias locais. Nas últimas topologias da lista anterior, as informações da melhor posição do grupo levam um tempo superior a serem transferidas no grupo. A topologia totalmente ligada, mais rápida na partilha da informação, é também mais susceptível de sofrer uma prematura convergência (ou seja, a convergir para um local óptimo).
2.4 Aplicações
Existe um número muito significativo de aplicações do PSO, como se pode ver pelo número de artigos publicados (Figura 2.8 extraída do estudo efectuado por (Ricardo Poli, 2007)). Estando dispersas por diversas fontes, entre as quais, destacamos a basede dados IEEE com aproximadamente 1100 artigos.
Algoritmo de Optimização por Grupo de Partículas
17
No artigo referenciado, foram estudados apenas documentos presentes da base de dados do IEEE Xplore, aproximadamente 700 artigos tratando o algoritmo PSO, divididos por 26 categorias distintas. Os temas, para além de incluírem o algoritmo PSO, abordam diversas áreas de estudo tais como: Biologia, Medicina, Electrónica, Electrotécnica, Electromagnetismo, Inteligência artificial, Processamento de imagem, entre outras.
O sucesso deste algoritmo deve-se sobretudo à sua simplicidade e adaptabilidade a diferentes problemas. A maioria da resolução destes problemas, no presente momento é dominada, por resoluções de difícil implementação. Sendo por isso o algoritmo PSO, a alternativa escolhida por diversas pessoas que encontram neste algoritmo um meio mais prático de resolver os seus problemas.
2.5
Variantes do algoritmo PSO
Com o decorrer do tempo, novas variantes do algoritmo PSO canónico foram desenvolvidas. O algoritmo PSO na sua forma canónica apresenta aspectos importantes relacionados com a actualização da velocidade. Se a posição actual de uma partícula coincidir com a melhor posição global a partícula só se moverá afastando-se desse ponto se o seu valor de inércia e a sua velocidade anterior da partícula forem diferentes de zero. Se a velocidade anterior da partícula for próxima de zero, todas as partículas ficam paradas, uma vez que alcançaram a melhor posição global (até ao momento). Isto pode conduzir o algoritmo a uma convergência prematura. Mas na realidade isto não garante que o algoritmo tenha atingido um mínimo global, apenas significa que todas as partículas convergiram para a melhor posição encontrada até ao momento pelo grupo de partículas. Este fenómeno é conhecido pela estagnação, (Van et
al. 2002).
Løvbjerg et al. (2001), apresentam um novo método HPSOBS (Hybrid Particle Swarm
Optimiser with Breeding and Subpopulations) que combina o PSO com técnicas dos
Algoritmo de Optimização por Grupo de Partículas
18
(subpopulations). O método é comparado com o PSO canónico e AGs, obtendo-se resultados promissores.
Van et al. (2002) desenvolvem uma solução GCPSO (Guaranteed Convergence
Particle Swarm Optimiser), baseada em acrescentar um novo parâmetro e adicionar
novas equações ao PSO. Esta variante converge mais rapidamente para a solução especialmente quando se trabalha com grupos de partículas pequenos.
No seguimento dos trabalhos anteriores Esmin et al. (2005), propuseram outro algoritmo híbrido, HPSOM (Optimização por Grupo de Partícula Híbrido com Mutação) que incorpora no PSO um processo típico dos algoritmos genéticos: a mutação da população. Este processo vai permitir que as partículas possam evitar óptimos locais se realizar a pesquisa em diferentes áreas no espaço. Este processo inicia-se pela escolha aleatória da partícula do grupo para a mover para uma posição diferente no espaço de pesquisa. No artigo (Esmin et al., 2005), são realizados testes com funções padrão e os resultados são comparados com o PSO tendo o MPSOM atingido uma melhor taxa de convergência e solucionado problemas de estagnação.
O algoritmo PSO completamente informado foi proposto por Mendes et al. (2004), (Fully Informed Particle Swarm) FIPS. Na variante FIPS, cada indivíduo é atraído para o centro de gravidade das melhores posições obtidas pelas partículas na sua vizinhança. Estudos efectuados (Mendes et al., 2004) da comparação entre FIPS e PSO canónico demonstram, que esta variante apresenta resultados muito promissores. Com certas topologias, os resultados obtidos eram muito melhores que os obtidos pelo PSO canónico. Concluiu-se deste estudo que a forma clássica de pensar na criação de novas soluções pode ser posta em causa, e que os comportamentos normativos podem resultar em formas bastantes sofisticadas de resolver problemas.
Capítulo 3
19
2008
Capítulo 3
Algoritmos de Optimização
Multi-Objectivo por Grupo de Partículas
Neste capítulo é abordada a problemática da optimização multi-objectivo. É efectuado um estudo do estado da arte sobre os métodos de tornar o algoritmo PSO, desenvolvido para um problema uni-objectivo, num algoritmo multi-objectivo, MOPSO, mantendo as principais características do algoritmo de optimização por grupo de partículas.
3.1 Conceitos Básicos
Um problema de optimização multi-objectivo (Multi-Objective Optimization Problem,
MOOP), trabalha com mais de uma função objectivo. Muitos problemas implicam
tomar decisões. Decidir é escolher ou optar entre alternativas praticáveis. A maioria das situações da vida real consiste na resolução de problemas com múltiplos critérios, geralmente conflituosos. No entanto, em situações em que a pressão do tempo é elevada, como sejam as situações de crise, resvala-se com facilidade para modelos muito simples, em que apenas um dos critérios de decisão assume particular relevância, levando a pôr de parte outros aspectos do problema. Consequentemente, reduz-se o problema mais complexo a um problema de optimização (minimização ou maximização) do objectivo associado ao critério relevante. Todavia, cada vez mais, a entidade que decide é forçada a considerar uma grande variedade de critérios para avaliação das diferentes alternativas que se lhes oferecem. Pode-se tornar difícil a modelação e a formulação do problema à custa de apenas um critério, devido à complexidade, heterogeneidade, natureza conflituosa e aos compromissos presentes na situação de escolha.
Muitos problemas de tomada de decisão implicam considerar vários critérios. Técnicas tradicionais de optimização têm sido usadas para solucionar estes problemas no passado. Estas técnicas originalmente foram formuladas para trabalhar com uma única função objectivo e encontrar uma solução óptima. Assim os vários objectivos são
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
20
formulados numa só função, chamada função agregada. Contudo, existem diferenças fundamentais entre a optimização multi-objectivo e de objectivo simples, que serão explicadas neste capítulo.
3.2
Formulação
Um MOOP possui um número de funções objectivo a serem optimizadas (a maximizar ou a minimizar). Os MOOP’s referem-se aos casos em que as alternativas são definidas indirectamente por um conjunto de restrições matemáticas. Um exemplo clássico de um problema multi-objectivo é determinar a trajectória mais económica para efectuar a entrega/recolha de produtos a um conjunto de clientes duma determinada empresa, em que os critérios de optimização poderiam ser: o tempo, a distância, o consumo energético, etc..
Um MOOP possui um número de funções objectivo a serem optimizadas que podem possuir restrições, que devem ser satisfeitas por qualquer solução, baseado da seguinte descrição (Deb, 2001): n i x x x K k x h J j M m x fm U i i L i k ,..., 2 , 1 , ,..., 2 , 1 , 0 ) ( ,..., 2 , 1 , 0 g a restrita ,..., 2 , 1 ), ( minimizar maximizar/ j (3.1)
Onde xé o vector de nvariáveis de decisão x
x1,x2,x3,...,xn
T. Os valores xiLe xUi , representam o valor mínimo e máximo, respectivamente, para a variável xi. Esteslimites definem o espaço de decisão D ou espaço das variáveis de decisão. O vector xi será referido como solução.
As desigualdades gje as igualdades hk são chamadas de funções de restrição. Uma
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
21
igualdades) e os 2 limites. Em situação contrária a solução não será viável. O conjunto n
de todas as soluções praticáveis forma a região viável ou espaço de pesquisa S.
Cada uma das M funções objectivo: f1(x), f2(x),f3(x),..., fM(x), pode ser maximizada ou minimizada. Contudo, para trabalhar com os algoritmos de optimização, é necessário converter todas as funções para serem maximizadas ou minimizadas. O vector funções objectivo f(x) adequa um espaço multi-dimensional chamado espaço objectivo Z. Então para cada solução x no espaço de decisão, existe um f(x) no espaço de objectivos. Esta é uma diferença fundamental em relação à optimização de objectivos simples, cujo espaço de objectivos é unidimensional.
3.2.1 Frente de Pareto
Uma decisão implica ter em conta vários factores, com o objectivo de se encontrar a solução que melhor se adequa ao nosso problema. Em alguns casos, podem aparecer várias soluções boas, das quais nenhuma é quantitativamente melhor que a outra. Para exemplificar, apresenta-se o caso da compra de um automóvel. Como critério de compra consideram-se apenas dois objectivos a satisfazer: o conforto e o preço, esquecendo todos os outros critérios que podiam ser considerados.
A Figura 3.1 ilustra algumas alternativas disponíveis na aquisição de um automóvel, com uma relação estabelecida entre a despesa financeira e um determinado nível de conforto.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
22 4 20% 40% 60% 80% 100% 25.000€ 50.000€ 75.000€ 100.000€ 125.000€ Custo Conforto 1 5 3 2 Soluções PossíveisFigura 3.1 - Opções na compra de um automóvel.
O objectivo de todo o cliente será minimizar o custo e maximizar o conforto do seu veículo. Nesta situação tem-se cinco possíveis opções de compra. Eliminam-se duas delas: a solução 1, uma vez que está pelo mesmo nível de conforto da solução 5 e é mais onerosa. A solução 2 é eliminada pelo motivo, de por uma despesa superior temos menos conforto. Fica-se com as soluções (3, 5 e 4) como alternativas de compra. Em termos quantitativos nenhuma é melhor que a outra, pois uma é mais confortável que a outra mas a despesa é superior. Encontram-se então um compromisso entre os objectivos. Quanto maior for o conforto do automóvel mais dispendioso será o seu custo ou vice-versa. Pode-se então afirmar que uma solução domina outra se os seus valores são melhores em pelo menos um de todos os objectivos. Por exemplo a solução 5 domina a solução 1. Não conhecendo à priori a importância relativa de cada objectivo pode-se dizer que as soluções 3, 4 e 5 são igualmente satisfatórias, sendo o conjunto de soluções óptimas. Esse grupo de soluções é chamado conjunto não dominado. As restantes partículas serão o conjunto de soluções dominadas. Os conjuntos referidos têm as seguintes propriedades:
As soluções de qualquer par do conjunto não dominado, devem ser não dominadas uma em relação à outra.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
23
Quaisquer soluções contidas no conjunto dominado, devem ser dominadas por um mínimo de uma solução do grupo não dominado.
Com os pontos não dominados representados num espaço contínuo pode-se desenhar uma curva. Esta curva é conhecida como a Frente de Pareto ou Frente não dominada.
3.2.2 Metas na Optimização Multi-objectivo
Nesta secção são abordadas as metas a atingir quando resolvemos um problema multi-objectivo, (Deb, 2001). A optimização multi-objectivo tenta obter um conjunto de soluções:
1. O mais próximo possível da Frente de Pareto.
2. Com maior diversidade possível.
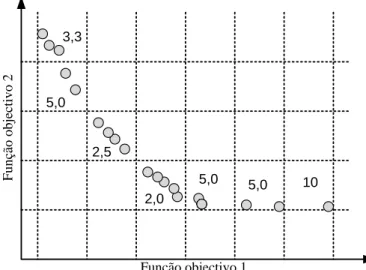
A primeira meta a atingir é habitual para qualquer processo de optimização. As soluções distantes da Frente de Pareto não são desejáveis. Encontrar uma boa diversidade nas soluções dos problemas multi-objectivo é uma especificidade deste tipo de optimização. Na Figura 3.2 são apresentados exemplos de uma boa diversidade de soluções (A) e uma fraca diversidade nas soluções (B).
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
24
Uma fraca diversidade significa um conjunto de soluções que estabelecem um fraco compromisso entre os vários objectivos. Como o MOOP trabalha no espaço de decisões e no espaço dos objectivos, é desejável que as soluções tenham uma boa diversidade nestes espaços. Normalmente uma boa diversidade num local implica uma diversidade semelhante noutro local.
3.3
Optimização Uni-Objectivo vs Multi-objectivo
Três pontos relevantes que diferenciam os dois tipos de optimização foram identificados por (Deb, 2001):
Os problemas de optimização mais comuns têm um só objectivo, e a finalidade é encontrar uma solução óptima global (mínimo ou máximo). Nos problemas multi-objectivo normalmente existe mais do que um óptimo global. A finalidade passa a ser encontrar o conjunto de soluções da Frente de Pareto, bem como preservar a diversidade do mesmo grupo de soluções.
Ao resolver um MOOP estamos a trabalhar com dois espaços (variáveis e objectivos). Os problemas simples trabalham unicamente no espaço de variáveis uma vez que pesquisam apenas uma solução no espaço dos objectivos. É importante voltar a referir que a necessidade de manter a diversidade em ambos os espaços complica mais o processo de encontrar as soluções desejadas, pois a proximidade de duas soluções no espaço de variáveis não implica a proximidade no espaço dos objectivos.
Os métodos tradicionais de optimização multi-objectivo são baseados em funções simples que ponderam cada objectivo separadamente, utilizando cada objectivo separadamente como restrição. Logo um MOOP pode ser convertido num problema de optimização simples, embora este processo seja mais complexo.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
25
3.4
Operador de dominância Pareto
A maioria dos algoritmos de optimização multi-objectivo usa o conceito de dominância. Se existem M funções objectivo fj o operador entre duas soluções, x y, significa que a solução x é melhor do que y em um objectivo particular. Reciprocamente x y, indica que a solução xé pior que y para algum objectivo. Este operador define-se da seguinte forma (Deb, 2001):
Definição 1: uma solução x 1 domina uma outra solução x 2 (apresentado como 1
x x 2 ) se as seguintes condições forem satisfeitas:
1. A solução x não é pior que 1 x 2 em todos os objectivos, ou seja
1
2 x f x fj j para todo j1,2,3,...,M.2. A solução x é estritamente melhor que 1 x 2 em pelo menos um objectivo ou seja, fj
x 1 fj
x 2 , pelo menos em um j1,2,3,...,M.Se ambas as condições são satisfeitas, pode-se dizer:
2
x é dominada por x 1
1
x é não dominada por x 2
1
x é não inferior que x 2
3.4.1 Propriedades da relação de dominância
A relação de dominância satisfaz as seguintes propriedades:
Não é reflexiva, pois de acordo com a definição 1 uma solução não pode ser dominada por si própria.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
26
Não é simétrica, porque se p não implica que, q q p. Transitiva, dado que se p e q q então r p . r
Estas propriedades caracterizam a relação de dominância como uma relação de ordem parcial restrita.
3.4.2 Optimalidade de Pareto
Quando um conjunto de soluções é finito, é possível fazer comparação de soluções duas a duas e pode-se dividir o conjunto em soluções dominadas e não dominadas. Portanto tem-se um conjunto não dominado e um conjunto dominado.
Definição 2: dado um conjunto de soluções P, o conjunto não dominado P'é formado por aquelas soluções que não são dominadas por qualquer elemento P.
Quando o conjunto Pé um espaço completo de pesquisa (PS), o conjunto não dominado P'é chamado de conjunto Pareto Óptimo. Na Figura 3.3 são mostrados vários exemplos de conjuntos Pareto Óptimo, conforme varias combinações de objectivos para as funções f e 1 f . A curva indica onde está localizado o conjunto. É 2
possível ter conjuntos Pareto Óptimo formados, por uma região contínua ou pela união de regiões descontínuas.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
27
Figura 3.3 - Conjuntos Óptimos de Pareto
Definição 3: O conjunto não dominado para a totalidade do espaço de pesquisa S é
chamado de conjunto óptimo Pareto global.
As soluções contidas nesses conjuntos são as soluções óptimas de um problema multi-objectivo. Então os óptimos locais são definidos na Figura 3.3, para diversas situações de optimização.
Definição 4: se cada elemento x do conjunto P não é dominado por alguma solução yna vizinhança de x tal que yx , ondeé um número positivo arbitrariamente pequeno, então o conjunto Pé chamado de conjunto Pareto local.
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
28
A Figura 3.4 ilustra duas frentes Pareto locais que são não dominadas assim como a sua vizinhança do seu espaço de objectivos (A) e espaço de variáveis (B).
Figura 3.4 - Soluções locais e globais de Pareto.
Definição 5: A Frente de Pareto está formada pelo conjunto de vectores de funções
objectivo f(x)
f1(x),f2(x),..., fM(x)
T, para cada solução x que está no conjunto de Pareto.A Frente de Pareto é formada então por valores das funções objectivos (ponto no espaço de objectivos) correspondentes a cada solução no espaço de pesquisa. A relação de dominância também pode ser classificada em dominância forte e fraca. A dominância forte é definida da seguinte forma.
Definição 6: uma solução x 1 domina fortemente uma outra solução x 2 (apresentado como 1
Algoritmos de Optimização Multi-objectivo por Grupo de Partículas
29
3.5
MOPSO
O sucesso do algoritmo PSO na optimização de problemas uni-objectivo, motivou investigadores a fazer o desenvolvimento desta técnica heurística a outras áreas. Umas dessas áreas é a optimização multi-objectivo. A primeira proposta de implementação Multi-Objectivo do Particle Swarm Optimization (MOPSO), surge em (Moore e Chapman, 1999). A partir desta publicação surgem muitas outras (Deb (2001), Hu e Eberhart (2002), Zitzler et al. (2002)), algumas das quais irão ser abordadas neste capítulo. A título de curiosidade existe um intervalo de tempo entre a primeira publicação neste tópico e as seguintes de cerca de dois anos.
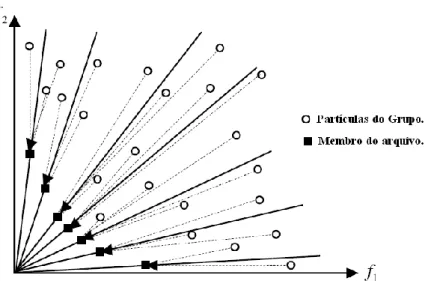
Serão abordadas algumas formas do MOPSO, que se distinguem pelo método aplicado, para descobrir o melhor guia local, no grupo de partículas.
3.5.1 Estrutura típica do MOPSO
Com o objectivo de tornar o Algoritmo de Optimização por Grupo de Partículas (PSO) numa estratégia capaz de resolver problemas multi-objectivo, é necessário efectuar algumas alterações no esquema original do PSO. Como já foi referido neste trabalho, encontrar a solução multi-objectivo não consiste em encontrar uma solução que no global optimiza o nosso problema. O que se pretende é encontrar um conjunto de soluções que optimize o problema com uma relação compromisso entre todos os objectivos (frente de Pareto). Quando estamos a solucionar um problema multi-objectivo temos que ter em conta três princípios essenciais:
Maximizar o número de elementos da frente Pareto encontrada.
Minimizar a distância da frente de Pareto produzida pelo nosso algoritmo, à frente de Pareto real do problema (assumindo que a mesma é conhecida).
Maximizar a credibilidade das soluções encontradas, com um bom resultado, nos valores dos parâmetros de avaliação.