CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA
DEPARTAMENTO DE FÍSICA
CURSO DE BACHARELADO EMFÍSICA DAUFPE
Solução do Exercício Escolar 3
10 de dezembro de 2015, 9h. Tempo de duração: 2h30m
Questão 1: Série Hipergeométrica
Considere a equação de Gauss
z(1−z)w′′
(z) + [γ−(1 +α+β)z]w′
(z)−αβ w(z) = 0
comγ 6= 0 eγ 6=inteiro negativo.
(a) (2 pontos) Mostre a função hipergeométrica2F1(α, β;γ;z)é a primeira solução, em série em torno dez = 0 para raizκ= 0de equação indicial, e é dada por
2F1(α, β;γ;z) =
Γ(γ) Γ(α)Γ(β)
∞
X
j=0
Γ(α+j)Γ(β+j) Γ(j+ 1)Γ(γ+j)z
j
(b) (1 ponto ) Considere γ /∈ I e obtenha a segunda solução pelo método de Frobenius através da segunda solução da equação indicial (κ= 1−γ), e mostre que esta solução em série corresponde a
z1−γ
2F1(α+ 1−γ, β+ 1−γ; 2−γ;z)
Solução:
(a) Tomar a EDO z(1−z)w′′
(z) + [γ−(1 +α+β)
| {z }
µ
z]w′
e aplica o método de Frobenius supondo a solução na forma geralw(z) =zκP∞
j=0ajzj,
donde
w′
(z) =
∞
X
j=0
aj(κ+j)zκ+j
−1
∴
(γ−µz)w′
(z) =
∞
X
j=0
ajγ(κ+j)zκ+j
−1 −
∞
X
j=0
ajµ(κ+j)zκ+j
w′′
(z) =
∞
X
j=0
aj(κ+j)(κ+j −1)zκ+j
−2
∴
z(1−z)w′′
(z) =
∞
X
j=0
aj(κ+j)(κ+j −1)zκ+j
−1 −
∞
X
j=0
aj(κ+j)(κ+j−1)zκ+j ∴
∞
X
j=0
[aj(κ+j)(κ+j+γ−1)zκ+j
−1 −
∞
X
j=0
aj[(κ+j)(κ+j+µ−1)−αβ]zκ+j = 0 ∴
Rearrumando,
a0κ(κ+γ−1)zκ
−1 −
∞
X
j=0
[aj((κ+j)(κ+j+µ−1)+αβ)−aj+1(κ+j+1)(κ+j+γ)]zκ+j = 0
Igualando a zero os coeficientes dos termos de mesma potência emz resulta a0κ(κ+γ−1) = 0, equação indicial ∴
aj((κ+j)(κ+j+γ−1) +αβ)−aj+1(κ+j+ 1)(κ+j+γ) = 0 ∴
aj+1 =
(κ+j)(κ+j+α+β) +αβ
(κ+j+ 1)(κ+j+γ) aj (1) Se
a0 6= 0 → κ1 = 0 e κ2 = 1−γ
Para a primeira solução comκ1 = 0teremos para a equação 1
aj+1 =
j(j+α+β) +αβ
(j+ 1)(j+γ) aj, j = 0,1, . . .
que é a equação de recorrência entre os coeficientes. Iterando obtemos
a1 =
αβ
1.γa0
a2 =
(α+β+ 1) +αβ
2.(γ+ 1) a1 =
(α+ 1)(β+ 1) 2.(γ+ 1) ×
αβ
1.γa0
a3 =
2(2 +α+β) +αβ
3.(γ+ 2) a2 =
(α+ 2)(α+ 1)α(β+ 2)(β+ 1)β
Por indução, escrevemos
aj =
Γ(α+j)Γ(β+ 1) Γ(α)Γ(β)
Γ(γ)
j!Γ(γ+ 1)a0 Finalmente substituindo na solução proposta,
w(z) =a0
Γ(γ) Γ(α)Γ(β)
∞
X
j=0
Γ(α+j)Γ(β+ 1) Γ(γ+j)Γ(j+ 1)z
j
que é a expressão da função hipergeométrica2F1(α, β;γ;z).
(b) Paraκ=κ2 = 1−γ podemos ter para a equação (1) a expressão
aj+1 =
(1−γ+j)(1−γ+j +α+β) +αβ
(2−γ+j)(1 +j) aj ou
aj =
(j −γ+α)(j−γ+β)
(1−γ+j)(j) aj−1 ou (2) Iterando termos a termo resulta por indução
aj =
(α−γ +j)(β−γ+j) (1−γ+j)(j) ×
(α−γ+j−1)(β−γ+j−1)
(j−γ)(j−1) aj−2 ou
aj =
(α−γ+j)(β−γ+j) (1−γ+j)(j) ×
(α−γ+j −1)(β−γ+j−1) (j−γ)(j−1) ×. . .
(α−γ+ 1)(β−γ+ 1) (2−γ)1 a0
(3) ou
aj =
(α−γ+ 1)j(β−γ+ 1)j
j!(2−γ)j
Substituindo na solução resulta
w(z) =z1−γ
∞
X
j=0
(α+γ+ 1)j(β+γ+ 1)j
(2−γ)j
zj
j!
que corresponde à expressão
z1−γ
2F1(α+ 1−γ, β+ 1−γ; 2−γ;z)
Questão 2: Funções hipergeométricas confluentes
(a) (1,5 pontos) Obtenha a expressão da função hipergeométrica confluente
1F1(−n;ℓ+ 1;x)
a partir da sua expressão das Funções Hipergeométricas Generalizadas, dada nas In-formações Gerais. (2,0 pontos)
(b) (1,5 ponto) Compare1F1(−n;ℓ+ 1;x) com a expressão das Funções de Laguerre As-sociadas e encontre a relação entre ambas. Obtenha a função hipergeométrica que representa os Polinômios de Laguerre.
Solução:
(a) Usar a expressão da definição geral das funções hipergeométricas dada nas informações
e escrever para o caso1F1(−n;ℓ+ 1;x)
1F1(−n;ℓ+ 1;x) =
∞
X
j=0
(−n)jxj
(ℓ+ 1)jj!
Usar a definição do símbolo de Pochhammer e escrever (−n)j = (−n)(−n+ 1)(−n+ 2). . .(−n+j−1) ∴
= (−1)jn(n−1)(n−2). . .(n−(j −1))
= (−1)j n!
(n−j)!
que se anula quandoj ≥n+ 1. De maneira análoga,
(ℓ+ 1)j = (ℓ+ 1)(ℓ+ 2). . .(ℓ+j) =
(ℓ+j)!
ℓ! Logo, a expressão para1F1(−n;ℓ+ 1;x)ficará
1F1(−n;ℓ+ 1;x) =
n
X
j=0
(−1)j n!
(n−j)!
ℓ! (ℓ+j)!
xj
j!
(b) A expressão das Funções de Laguerre Associadas está dada por
Lk
n=
n
X
j=0
(−1)j (n+k)!
(n−j)!(k+j)!j! x
A expressão para1F1(−n;ℓ+ 1;x)pode ser rearrumada
1F1(−n;ℓ+1;x) =
n
X
j=0
(−1)j n!
(n−j)!
ℓ! (ℓ+j)!
xj
j! =
n!ℓ! (n+ℓ)!
n
X
j=0
(−1)j (n+ℓ)!
(n−j)!(ℓ+j)!
xj
j!
Identificandok=ℓresulta:
(n+k)!
n!k! 1F1(−n;k+ 1;x) =
n
X
j=0
(−1)j (n+k)!
(n−j)!(k+j)!j! x
j =
Lkn ou
Lkn=
(n+k)!
n!k! 1F1(−n;k+ 1;x)
O caso particulark = 0, i.e. L0
n(x) = Ln(x)representa os polinômios de Laguerre, ou
seja:
Ln=F1(−n; 1;x) = n
X
j=0
(−1)jn!
(n−j)!(j!)2 x
j
Questão 3: Função de Green em 1-d
Resolva a equação de diferencial ordinária (EDO)Dˆy(x) =f(x)ou seja
x2y′′
(x) + 6xy(x) + 6y(x) =f(x), x∈[1,2]
sujeita às condições de contorno
y(1) =y(2) = 0
(a) (2,0 pontos) Analise a natureza do operador diferencialDˆe obtenha a função de GreenG(x, x′
) associada a esta equação, i.e. DGˆ (x, x′
) = δ(x−x′).
(b) (bônus - 1,0 pontos) Calcule a solução da EDO para o caso em quef(x) = 1/x.
Solução:
(a) A EDO de segunda ordem dada não está no formato Sturm-Liouville porqued/dx(x2)6= 5x, mas as c.c são homogêneas.
Logo, podemos desenvolver a solução da equação para a função de Green ˆ
DG(x, x′
) =δ(x−x′
)
a partir das soluções da EDO homogênea correspondente, que está no formato da EDO de Cauchy, i.e.
x2y′′
Supory(x) =xm, então, substituindo na EDO vem:
x2m(m−1)xm−2
+ 6xmxm−1
+ 6xm = 0
∴ m(m−1) + 6m+ 6 = 0 →
m2+ 5m+ 6 = 0 → (m+ 2)(m+ 3) = 0 ∴ m1 =−2 e m2 =−3
Portanto as soluções linearmente independentes serãoy1(x) =x−2 e
y2(x) =x−3, e a
solução geral:
y(x) = Ax−2
+Bx−3
Subdividir o intervalo[1,2]em[1, x′
)e (x′
,2]e obter as soluções em cada subintervalo com as c.c apropriadas, i.e.
Para[1, x′), temos G1(x) =A1x
−2
+B1x
−3
∴ G1(1) = 0 → A1+B1 = 0 ∴ B1 =−A1
ou seja
G1(x) =A1(x−2 −x−3
) =A1u(x)
De maneira análoga, para(x′
,2]teremos
G2(x) =A2x
−2
+B2x
−3
∴ G2(2) = 0 → A2/4 +B2/8 = 0 ∴ B2 =−2A2
ou seja
G2(x) =A2(x−2
−2x−3
) =A2v(x)
Usar as condições de continuidade para a função de Green em x = x′ e
descontinui-dade de suas derivadas i.e.
G1(x′
) =G2(x′
) e G′
2(x
′
)− G′
1(x
′
) = 1
x′2
que pode ser reescrito como um sistema de equações lineares para obter as constantes
A1e A2, i.e.
A1u(x′)−A2v(x′) = 0
A1u′(x′)−A2v′(x′) = − 1
x′2
→
A1 =
v(x′
)
x′2W(x′)
A2 =
u(x′
)
x′2W(x′)
ondeW(x′
)é Wronskiano, que é dado por
W(x′
) =u(x′
)v′
(x′
)−u′
(x′
)v(x′
) = = (x′−2
−x′−3
)(−2x′−3
+ 6x′−4
)−(−2x′−3
+ 3x′−4
)(x′−2
−2x′−3
) = 2x′−5
+ 6x′−6
+ 2x′−6
−6x′−7
+ 2x′−5
−4x′−6
−3x′−6
+ 6x′−7
Logo a função de Green ficará
G(x, x′
) =
A1u(x) =
v(x′
)u(x)
x′2W(x′) = v(x′
)u(x)
x′−4 , x < x ′
A2v(x) =
u(x′
)v(x)
x′2 W(x′
) =
u(x′
)v(x)
x′−4 , x ′
< x
ou G(x, x′
) =
(x′2 −2x′
)(x−1)
x3 , x < x
′
(x′2 −x′
)(x−2)
x3 , x
′ < x
que não é simétrica, como esperado, porque o operador não é S-L.
(b) A solução de EDO para o casof(x) =x−1 será dada por
y(x) =
Z 2
1 G (x, x′
)f(x′
)dx′
=
=
Z x
1 (x′2
−x′
)(x−2)
x3
1
x′dx ′
+
Z 2
x
(x′2 −2x′
)(x−1)
x3
1
x′dx ′
=
= (x−2)
x3
Z x
1 (x′
−1)dx′
+ (x−1)
x3
Z 2
x
(x′
−2)dx′
= (x−2)
x3
x′2
2 −x
′
x
1
+(x−1)
x3
x′2
2 −2x
′
2
x
= (x−2)
x3
x2
2 −x+ 1 2
− (x−1) x3
x2
2 −2x+ 2
=
= (x−2)
2x3 [(x−1) 2]
− (x−1)
2x3 [(x−2) 2]
∴ y(x) = (x−1)(x−2)
2x3
Questão 4: Função de Green para a equação de Helmholtz
(2,0 pontos) Use o método da transformada de Fourier para construir a função de Green para
a equação de Helmholtz modificada em uma dimensão
d2
dx2 −κ 2
considerando que as condições de contorno são tais que a função de Green deve se anular emx→ ∞e x→ −∞.
Solução:
Considerar as expressões das T.F. para a função de Green D(x, x′
)e para a função-delta de Diracδ(x−x′
)dadas por
D(x, x′
) = √1
2π
Z ∞
−∞ eikx
F(k, x′
)dk onde F(k, x′
) = √1
2π
Z ∞
−∞ e−ikx
D(x, x′
)dx
δ(x−x′
) = 1 2π
Z ∞
−∞
dkeik(x−x′)
dk
Substituir nas equação para a função de Green
d2
dx2 −κ 2
D(x, x′
) =δ(x−x′
)
1
√
2π
Z ∞
−∞
d2
dx2 −κ 2
eikx
F(k, x′
)dk = 1 2π
Z ∞
−∞
dkeik(x−x′)
dk
1
√
2π
Z ∞
−∞ −k2
−κ2eikx
F(k, x′
)dk = 1 2π
Z ∞
−∞
dkeik(x−x′)
dk
∴ −k2−κ2F(k, x′) = √1
2πe −ikx′
ou F(k, x′
) =− e −ikx′
√
2π(k2+κ2)
Substituindo-se na expressão da função de Green resulta
D(x, x′
) =− 1 2π
Z ∞
−∞
e−ik(x−x′) (k2+κ2)dk
Para resolver a integral em k, fazer a continuação analítica ao plano complexo Ck e usar o método dos resíduos.
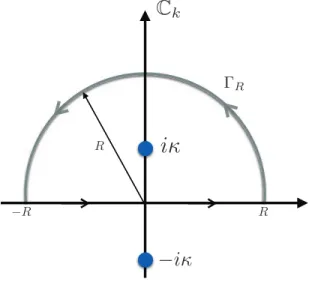
Usar como contorno de integração o semicírculo de raio R ancorado no eixo real e tomar o limiteR→ ∞, como mostra a figura (1).
Observar que o integrando tem dois polos simples em k = ±iκ, tomando κ > 0 sem perda de generalidade.
Quando x > x′ o contorno de integração
Γdeve ser fechado através do semiplano superior (vide figura). Nesse caso, apenas o polok =iκse encontra no interior deΓ.
Assim,
Z R
−R
eik(x−x′) (k2+κ2)dk+
Z
ΓR
eik(x−x′)
(k2+κ2)dk = 2πiRes
eik(x−x′) (k−iκ)(k+iκ)
k→iκ
= π
κe
Figura 1: Contorno de integração para o caso x > x′
.
No limite R → ∞ a integral sobre o contorno ΓR se anula (Lema de Jordan) e a integral
resulta
Z ∞
−∞
eik(x−x′) (k2+κ2)dk=
π κe
−κ(x−x′)
∴ D(x, x′) =− 1
2κe
−κ(x−x′)
x > x′
que se anula quandox→ ∞.
No caso em x < x′, o contorno de integração deverá ser realizado através do semiplano
inferior, nesse caso englobando o polok=−iκ. Assim, teremos
Z R
−R
eik(x−x′) (k2+κ2)dk+
Z
Γ′ R
e−ik(x′−x)
(k2+κ2)dk =−2πiRes
eik(x−x′) (k−iκ)(k+iκ)
k→−iκ
= π
κe
−κ(x′−x)
o sinal negativo indicando o sentido horário da trajetória de integração. No limiter → ∞a integral sobre o contornoΓ′
Rse anula (Lema de Jordan) e a integral resulta
na função de Green,
Z ∞
−∞
eik(x−x′) (k2+κ2)dk=
π κe
−κ(x′−x)
∴ D(x, x′) =− 1
2κe
−κ(x′−x) x < x′
Informações Gerais:
Funções Hipergeométricas generalizadas
mFn(α1, α2. . . αm;β1, β2, . . . βn;x) =
∞
X
j=0
(α1)j(α2)j. . .(αm)j
(β1)j(β2)j, . . .(βn)j
xj
j!
onde(x)j é o símbolo de Pochhammer definido por
(x)j =
(x+j −1)! (x−1)! =
Γ(x+j)
Γ(x) , Γ(x) = Função Gama
Função Gamma
Γ(t) =
Z ∞
0
xt−1
e−xdx. Γ(t+ 1) =tΓ(t), t
∈R
Γ(n+ 1) =n! n inteiro, positivo
Funções de Laguerre Associadas
Lkn= n
X
j=0
(−1)j (n+k)!
(n−j)!(k+j)!j! x
j
Transformada de Fourier
f(x) = √1
2π
Z ∞
−∞
eikxF(k)dk e F(k) = 1
√
2π
Z ∞
−∞ e−ikx
f(x)dx
Funçãoδ-Dirac
δ(x−x′
) = 1 2π
Z ∞
−∞
dkeik(x−x′)