Manual de Soluções - Métodos Matemáticos em Economia

Manual de Soluções - Métodos Matemáticos em

Economia

Gil Riella

Sumário

I

Análise Real

1

1 Espaços Métricos 3

2 Conjuntos Compactos 7

3 Continuidade 9

4 Correspondências 11

5 Conjuntos Convexos 15

6 Hiperplanos e Teoremas de Separação 17

II

Otimização

21

7 Otimização Estática 23

8 Teorema do Ponto Fixo de Banach 37

9 Programação Dinâmica 41

Prefácio

Parte I

Capítulo 1

Espaços Métricos

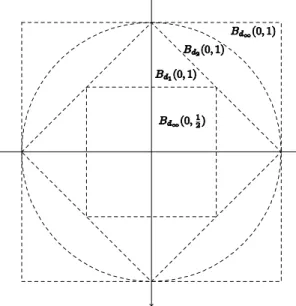
Exercício 1.1. Mostre que as três métricas que de…nimos acima são equivalentes no sentido de que, para qualquerA Rn_{,Aé aberto em(R}n_{; d}

1)se e somente seAé aberto em(Rn; d2)

se e somente se A é aberto em (Rn_{; d}

1).

Solução. O segredo para resolver a questão é notar que, para qualquer x 2 Rn _{e " > 0,} Bd1(x; "=n) Bd1(x; ") Bd2(x; ") Bd1(x; ") (ver …gura 1.1). Para ver isto, note que,

Figura 1.1: Relação entre bolas abertas emR2_.

para qualquery₂Rn_,

d1(x; y) =

n

X

i=1

jxi yi_j

nmax_fjxi yi_j:i= 1; : : : ; n_g

4 CAPÍTULO 1. ESPAÇOS MÉTRICOS

Logo, para todo y ₂ Bd1(x; "=n); nós temos d1(x; y) n

"

n = ". Ou seja, Bd1(x; "=n)

Bd1(x; "). Observe agora que

d2(x; y) =

v u u t n X i=1

(xi yi)2

v u u t n X i=1

jxi yij

!2

=

n

X

i=1

jxi yi_j

= d1(x; y):

Logo, para todo y ₂ Bd1(x; "), nós temos y 2 Bd2(x; "). Ou seja, Bd1(x; ") Bd2(x; ").

Finalmente, note que

d₁(x; y) = maxfjxi yij:i= 1; : : : ; ng

= q

(maxfjxi yij:i= 1; : : : ; ng)2 v u u t n X i=1

(xi yi)2

= d2(x; y):

Logo, para todoy ₂Bd2(x; "), nós temos y2Bd1(x; "). Ou seja, Bd2(x; ") Bd1(x; ").

Suponha agora queAseja um conjunto aberto em(Rn_{; di), em quei}

2 f1;2;_1g. Fixex₂ A e j 2 f1;2;1g. Por hipótese, existe " >0 tal que Bdi(x; ") A. Pela observação acima,

isto implica queBdj(x; "=n) A. Comoxfoi escolhido arbitrariamente, nós concluímos que

A é aberto em (Rn_{; dj).}

Exercício 1.2.Seja(xm_{)uma sequência qualquer emR. Mostre que(x}m_{)tem uma subsequência} monótona.1.1

Solução. Pra m₂ N, nós dizemos que xm _{é um ponto de pico se x}m _xk _{pra todo k m.} Suponha primeiro que a sequência (xm_{) tenha um número in…nito de pontos de pico. Neste} caso, é claro que a subsequência de(xmk)formada pelos pontos de pico é não crescente. Se o

número de pontos de pico for …nito, então escolham1 2N tal que, pra nenhumm m1,xm

seja um ponto de pico. Agora escolham2 > m1 tal quexm2 > xm1. Por construção,xm2 não

é um ponto de pico e, consequentemente, existe m3 > m2 tal que xm3 > xm2. Procedendo

indutivamente desta forma, nós obtemos uma subsequência(xmk)de(xm)que é estritamente

crescente.

Exercício 1.3. Seja (xm_{) uma sequência limitada em R.}1.2 _{Mostre que (x}m_{) tem uma} subsequência convergente.

1.1_{Isto é, existe uma subsequência(x}mk

)de (xm

)tal que xmk+1 _xmk pra todo _k2Nou_xmk+1 _xmk

pra todok2N.

1.2_{Isto é, existema; b2Rtais quea x}m

5

Solução. Usando o exercício anterior, pegue uma subsequência (xmk) de (xm) que seja

monótona. Digamos que (xmk) seja não decrescente. Como (xm) é limitada, obviamente

(xmk)também é limitada. Isto implica que x := supfxmkg está bem de…nido. Vamos agora

mostrar quexmk !x . Pela de…nição desupfxmkg, pra qualquer" >0, existexmk 2 fxmkg

tal quex " < xmk . Como(xmk)é não decrescente, isto implica que para todok k nós

temosxmk 2(x "; x ] (x "; x +"). Como"foi escolhido arbitrariamente, isto mostra

que xmk ! x . Um raciocínio análogo pode ser aplicado quando (xmk) for uma sequência

não crescente.

Exercício 1.4. Seja (xm_{)uma sequência emR}n_{. Então x}m _{!x se, e somente se, x}m i !xi,

8i= 1;2; :::; n.

Solução. Suponha primeiro que xm _!x2Rn_{. Então, pra todo " >0 existeM 2N tal que}

kxm _{xk< ", pra todom M. Isto é,}

p (xm

1 x1)2+ + (xmn xn)2 < ",

pra todo m M. Então, pra todom M e i2 f1; : : : ; ng,

jxmi xij

p (xm

1 x1)2+ + (xmn xn)2 < ".

Ou seja,xm

i !xi. Suponha agora que pra todo" >0existamM1; : : : Mntais quejxmi xij< "

p_n pra todom Mi. De…na M := maxfM₁; : : : Mng. Note que, pra todom M, kxm _x

k = p(xm

1 x1)2+ + (xmn xn)2

<

r

"2

n + + "2

n

= ":

Ou seja, xm _!x.

Exercício 1.5. Seja (M; d) um espaço métrico e …xe x₂ M. Nós dizemos que N(x) M é uma vizinhança de x se existe >0 tal que B(x; ) N(x). Mostre que O M é aberto se e somente se pra todo x2O existe uma vizinhança N(x) de x tal que N(x) O.

Solução. Primeiramente, note que, pra todo x 2 M e todo > 0, B(x; ) B(x; ). Isto

é, toda bola aberta de centro x é uma vizinhança de x. Logo, por de…nição, se O é aberto, então pra todo x2 O existe uma vizinhança N(x) de x tal que N(x) O. Suponha agora

que O seja um conjunto tal que pra todo x 2 O exista uma vizinhança N(x) de x tal que N(x) O. Fixe x ₂ O e pegue qualquer vizinhança N(x) de x tal que N(x) O. Pela de…nição de vizinhança, existe >0 tal queB(x; ) N(x) O. Como x foi escolhido de forma arbitrária, isto mostra que para todo x2 O existe >0tal que B(x; ) O. Isto é,

O é um conjunto aberto.

Exercício 1.6. Seja (M; d) um espaço métrico e suponha queO M é um conjunto aberto e F M é um conjunto fechado. Mostre que

6 CAPÍTULO 1. ESPAÇOS MÉTRICOS

(b) F _nO :=_fx₂F :x =₂O_g é um conjunto fechado.

Solução.

(a) Note que O n F = O \(M nF). Pela de…nição de conjunto fechado, M nF é um conjunto aberto. Portanto,O_nF pode ser escrito como a interseção de dois conjuntos abertos e, pelo teorema que vimos em sala, é um conjunto aberto.

(b) Similarmente ao que …zemos na parte (i), note queF nO =F \(MnO). Novamente,

pela de…nição de conjunto fechado, M _nO é um conjunto fechado. Logo, F _nO pode ser escrito como a interseção de dois conjuntos fechados e, pelo teorema que vimos em sala, é um conjunto fechado.

Exercício 1.7. Mostre que as suas conclusões mudariam no exercício acima se F fosse aberto ou se O fosse fechado. Isto é, dê um exemplo de dois conjuntos abertos O e F tais que O_nF não é aberto, e dê um exemplo de dois conjuntos fechados O e F tais que F _nO não é fechado.

Solução. SejamO := (0;2)e F := (1;2). Note queO e F são abertos em R.1.3 _{No entanto,} OnF = (0;1], que não é um conjunto aberto. Sejam agoraF := [0;2] e O := [1;2]. Note

que O e F são fechados em R_{, mas} F _nO = [0;1), que não é um conjunto fechado.

Exercício 1.8. Seja (M; d)um espaço métrico e sejaAum subconjunto deM. Nós dizemos que x ₂ A é um ponto interior se existe > 0 tal que B(x; ) A. Nós dizemos que x é um ponto de fecho de A se existe sequência (xm_{) tal que fx}m_{g A e x}m _{! x. Mostre que} int(A) =fx2A:x é ponto interior de Ag e cl(A) = fx2M :x é ponto de fecho deAg. Solução. Pegue x ₂ int(A). Como int(A) é um conjunto aberto, existe > 0 tal que

B(x; ) int(A) A. Isto é, x é um ponto interior de A. Isto mostra que int(A) fx 2

A : x é ponto interior de A_g. Agora suponha que x seja um ponto interior de A. Isto é, suponha que exista >0tal queB(x; ) A. ComoB(x; )é um conjunto aberto e oint(A)

é a união de todos os conjuntos abertos contidos em A, isto implica que B(x; ) int(A).

Logo, x₂int(A)e, consequentemente, fx₂A:xé ponto interior de A_g int(A).

Agora, pegue x ₂ cl(A). Se existisse " > 0 tal que B(x; ")_\A = _;, então A (M _n B(x; "))\cl(A) e (M nB(x; "))\cl(A) é um conjunto fechado, o que é uma contradição

à de…nição de cl(A), já que x =₂ (M _nB(x; "))_\cl(A). Nós concluímos que, para qualquer " > 0, B(x; ")_\A ₆= _;. Ou seja, para cada m ₂ N, é possível encontrar xm

2 A tal que d(xm_{; x)<} 1

m. Note que fx

m_{g A e x}m _{!x. Isto é, cl(A) fx2M :x é ponto de fecho} de A_g. Suponha agora que exista (xm_{) tal que fx}m_{g A e x}m _{! x. Como fx}m_{g cl(A)} e cl(A) é um conjunto fechado, isto implica que x ₂ cl(A). Isto mostra que _fx ₂ M : x é ponto de fecho deAg cl(A).

Capítulo 2

Conjuntos Compactos

Exercício 2.1. Seja(M; d) um espaço métrico. Mostre que se(xm_{)é uma sequência tal que} xm

!x₂M, entãoxmk !x pra toda subsequência (xmk) de (xm).

Solução. Suponha que(xm_{)seja uma sequência tal quex}m _{!x2M e …xe uma subsequência}

(xmk) de (xm). Fixe " > 0. Como xm ! x, existe N 2 N tal que d(xm; x) < " pra todo

m N. SejaK 2Ntal que mK N. Observe que, pra todok K, nós temos mk N e, consequentemente, d(xmk; x)< ". Concluímos que xmk !x.

Exercício 2.2. Seja(M; d)um espaço métrico. Nós dizemos que uma coleçãoAde conjuntos tem a propriedade das interseções …nitas se \B 6= _; pra qualquer subcoleção …nita de A. Mostre que A M é um conjunto compacto se e somente se pra toda coleçãoA de conjuntos tal que B A e B é fechado em (A; d) pra todo B 2 A, e além disto A tem a propriedade das interseções …nitas nós temos \A 6=_;.

Solução. Suponha primeiro que A seja um conjunto compacto e que A seja uma coleção de conjuntos tal que B A e B seja fechado em (A; d) pra todo B 2 A, e além disto

A tenha a propriedade das interseções …nitas. Por um resultado que mostramos em sala, nós sabemos que, para cada B 2 A, existe um conjunto FB fechado em (M; d) tal que

B = A\FB. Suponha que \A = ;. Isto implica que A\(\fFB : B 2 Ag) = \A = ;. Mas então, fM _nFB : B _{2 Ag} é uma cobertura aberta de A. Como A é compacto, existe uma subcoleção …nita B de A tal que A [fM nFB : B 2 Bg. Mas isto implica que

\B=A\(\fFB : B 2 Bg) = ;, o que contradiz o fato de que A tem a propriedade das interseções …nitas. Nós concluímos que\A 6=_;.

Suponha agora que pra toda coleção _A de conjuntos tal que B A e B é fechado em

(A; d) pra todo B 2 A e que além disto A tenha a propriedade das interseções …nitas nós tenhamos \A 6=_;. Considere agora uma cobertura aberta,O, de A. Suponha que pra toda subcoleção …nita _{V O} nós tenhamos A_n(_[V)₆=_;. De…na_A :=_fA_\(M _nO) :O _{2 Og}. Note que, por construção, todoB 2 A é fechado em(A; d). Além disto, pra toda subcoleção

…nita B deA nós temos uma subcoleção …nitaV de O tal que B =_fA_\(M _nO) :O _{2 Vg}. Por hipótese, pra toda coleção _B como acima nós temos _\B = _\fA _\(M _nO) : O ₂

Vg = An([V)6= ;. Isto é, A tem a propriedade das interseções …nitas, o que implica que A_n(_[O) = _\fA_\(M _nO) : O _{2 Og} = _{\A 6}= _;. Como isto contradiz o fato de que O

8 CAPÍTULO 2. CONJUNTOS COMPACTOS

Exercício 2.3. Seja (M; d) um espaço métrico e considere uma coleção A de conjuntos compactos em (M; d). Mostre que \A é um conjunto compacto.

Solução. Considere uma cobertura aberta qualquer O de \A e …xe um conjunto qualquer A_{2 A}. Como qualquer interseção de conjuntos fechados é um conjunto fechado e conjuntos compactos necessariamente são fechados, nós sabemos que \A é um conjunto fechado e, consequentemente, M _n(_\A) é um conjunto aberto. Mas então, O [ fM n(_\A)_g é uma cobertura aberta de A. Como A é um conjunto compacto, nós sabemos que existe uma subcoleção …nitaV deOtal queA (Mn(\A))[([V). Agora …ca claro que\A [V. Ou seja,Vé uma subcobertura …nita deOque cobre\A. ComoOfoi escolhida arbitrariamente, isto mostra que _\A é um conjunto compacto.

É possível também resolver o exercício usando compacticidade sequencial. Considere uma sequência qualquer (xm_{)tal que fx}m_{g \A e …xe qualquer A2 A. Como fx}m_{g A eA é} compacto, nós sabemos que(xm_{)tem uma subsequência convergente(x}mk). Como\A é um

conjunto fechado, nós sabemos que limxm _{2 \A. Como (x}m_{)foi escolhida arbitrariamente,} isto mostra que \A é sequencialmente compacto e, consequentemente, é compacto.

Exercício 2.4. Seja (M; d) um espaço métrico e seja (Am_{) uma sequência de conjuntos} compactos e não vazios em (M; d) tal que, pra todo m 2 N, Am+1 _Am_{. Mostre que}

\1

m=1Am 6=;.

Solução. Pra cada m ₂ N, pegue xm _{2 A}m_{. Por construção, fx}m_{g A}1_{. Como A}1 _é

compacto, existe uma subsequência (xmk) de (xm) tal que xmk ! x 2 A1. Agora, pra

cada m 2 N, …xe k 2 N tal que mk m . Note que fxmkg1

k=k Am . Como Am é um conjunto fechado, isto implica que x ₂ Am _{. Como isto vale para todo m 2 N, nós} concluímos quex_{2 \}1

Capítulo 3

Continuidade

Exercício 3.1. SejamX,Y eZ espaços métricos e suponha quef :X _!Y e g :f(X)_!Z sejam funções contínuas.3.1 _{Mostre que h :X !Z de…nida por h :=g f (isto é, pra todo} x2X, h(x) := g(f(x))) é uma função contínua.

Solução. Seja OZ Z um conjunto aberto. Como g é uma função contínua, o conjunto g 1_{(OZ) é aberto em f(X). Por um resultado anterior, nós sabemos que existe OY aberto}

emY tal queg 1_{(OZ) = OY \f(X). Observe ainda quef} 1_(g 1_{(OZ)) =f} 1_{(OY \f(X)) =}

f 1_{(OY), o que, comof é contínua, implica que f} 1_(g 1_{(OZ))é aberto emX. Finalmente,}

note que

h 1_{(OZ) = fx2X :h(x)2OZg}

= fx2X :f(x)2g 1(OZ)g

= f 1(g 1(OZ)):

Ou seja, h 1_{(OZ) é um conjunto aberto. Como OZ foi escolhido de forma arbitrária, nós}

concluímos queh é uma função contínua.

Exercício 3.2. Mostre que a função f :Rn_{!R de…nida por f(x) := kxk, pra todo x2R}n é contínua.3.2 _{Dica: na verdade é mais fácil demonstrar um resultado mais geral. Mostre} que, em qualquer espaço métrico X e para qualquer ponto x 2 X, a função de…nida por f(x) := dX(x; x ) é contínua.

Solução. Seguindo a dica, suponha que X é um espaço métrico e …xex 2 X. Precisamos mostrar que f : X _! R _{de…nida por} f(x) := dX(x; x ), pra todo x ₂ X, é uma função contínua. O exercício corresponde ao caso especial em que X = Rn _{e x = 0. Fixe x 2 X} e " > 0. Note que, pela desigualdade triangular, pra qualquer y 2 BX(x; ") nós temos

dX(x; x ) dX(y; x ) dX(x; y) < " e dX(y; x ) dX(x; x ) dX(x; y) < ". Ou seja,

jdX(x; x ) dX(y; x )j< ". Isto mostra quef é uma função contínua.

Exercício 3.3. Nós dizemos que um conjunto A em um espaço métrico X é totalmente limitado se pra todo " > 0 existe um subconjunto …nito B de A tal que A [fBX(x; ") :

3.1_{Aqui estamos pensando emf(X)como um subespaço métrico deY, é claro.} 3.2_{Aqui você pode escolher qualquer uma das normas emR}n_{. Por exemplo,}

10 CAPÍTULO 3. CONTINUIDADE

x ₂ B_g. Suponha agora que X e Y sejam dois espaços métricos e que f : X _! Y seja uma função uniformemente contínua tal que f(X) = Y. Mostre que se X é totalmente limitado, então Y também é totalmente limitado. Dê um exemplo mostrando que isto não é necessariamente verdade quando f é apenas contínua.

Solução. Fixe " > 0. Como f é uniformemente contínua, existe > 0 tal que, pra todo

x ₂ X, f(BX(x; )) BY(f(x); "). Como X é totalmente limitado, existe A X, A …nito, tal que X = _[fBX(x; ) : x ₂ A_g. Isto agora implica que f(X) = _[ff(BX(x; )) :

x 2 Ag. Como, pra todo x 2 A, f(BX(x; )) BY(f(x); "), nós vemos que Y = f(X) =

[fBY(f(x); ") : x ₂ A_g. Isto mostra que Y é totalmente limitado. Como exemplo, use a função f(x) := 1=x em (0;1). O intervalo (0;1) é um conjunto totalmente limitado

(Você consegue demonstrar isto?), mas f((0;1)) = [1;1) que não é totalmente limitado

Capítulo 4

Correspondências

Exercício 4.1. Mostre que B :Rn+1

++ Rn+ de…nida por

B(p; l) := _fx₂Rn

+ :p x lg

é HCI usando diretamente a de…nição original de hemicontinuidade inferior. Solução. Fixe (p; l) ₂ Rn+1

++ e seja I um subconjunto aberto de Rn tal que I\B(p; l) 6= ;.

Pegue x 2 I \B(p; l) e note que, como I é aberto, existe 2 (0;1) tal que x 2 I. Note ainda que, comol >0, necessariamente nós temos p ( x)< l. Isto agora implica que existe

> 0 tal que p:^( x) < ^l pra todo (^p;^l) ₂ B_Rn+1

++((p; l); ) (Demonstração?). Ou seja, pra

todo (^p;^l) 2 B_Rn+1

++ ((p; l); ) nós temos x 2 I \B(^p;

^

l) e, consequentemente, B é HCI em

(p; l).

Exercício 4.2. Sejam X e Y espaços métricos e :X Y uma correspondência. Mostre que se é hemicontínua superior em x₂X e (x)é um conjunto fechado, então é fechada emx. Dica: pegue sequências convergentes (xm_{) e (y}m_{) comx}m _{!x ey}m _{2 (x}m_{) pra todo} m 2 N. Repetindo o raciocínio usado na segunda parte da demonstração da caracterização de hemicontinuidade superior usando sequências é possível construir uma subsequência(ymk)

de (ym_{)e uma sequência (^y}mk) tal quefy^mkg (x) e, pra todok 2N,dY(ymk;y^mk)<1=k.

Complete a demonstração observando que limymk = lim ^ymk e usando o fato de que (x) é

um conjunto fechado.

Solução. Suponha que seja hemicontínua superior em x e que (x) seja um conjunto fechado. Considere sequências convergentes (xm_{) e (y}m_{) tais que y}m

2 (xm_{) pra todo} m 2N. De…nax:= limxm _{e y:= limy}m_{. Pra cada k 2N, Ok :=UfBY(^y;1=k) : ^y2 (x)g} é um conjunto aberto tal que (x) Ok. Isto implica que, pra cada k ₂ N, existe k > 0 tal que (BX(x; k)) Ok. Como ym ! y, nós podemos usar um argumento indutivo para construir uma subsequência (ymk₎ de _(ym₎ tal que _ymk 2 _Ok pra todo _k 2 N.4.1 Isto

implica que, pra todo k ₂ N, existe y^k _{2 (x) tal que y}mk 2 BY(^yk;1=k). Nós podemos

4.1_{Comece comk= 1. Como y}m

!y, eventualmente nós teremosym

2O1. Escolha, então, m1 2N tal

queym1 _2O

1. Novamente, comoym!x, eventualmente, nós teremosym2O2. Isto nos permite encontrar

m2> m1tal queym2 2O2. Procedendo indutivamente desta forma, nós obtemos uma subsequência de(ym)

12 CAPÍTULO 4. CORRESPONDÊNCIAS

agora mostrar que y^k _{! y. Para ver isto, …xe " > 0. Como y}mk ! y, existe K 2 N

tal que ymk 2 BY(y; "=2) e 1=k < "=2 pra todo k K. Isto implica que, pra k K,

dY(^yk_{; y) dY(^y}k_{; y}mk) +dY(ymk; y) < "=2 +"=2 = ". Ou seja, y^k ! y. Como (x) é um

conjunto fechado, isto implica que y₂ (x). Ou seja, é fechada emx.

Exercício 4.3. Sejam X e Y dois espaços métricos e suponha que : X Y seja uma correpondência hemicontínua superior e de valores compactos (isto é, pra todo x ₂X, (x)

é um conjunto compacto). Mostre que se A X é um conjunto compacto, então (A) :=

fy₂Y :y₂ (x) pra algum x₂A_g também é um conjunto compacto. Dica: em Ok (2007) tem uma demonstração, mas tem uma demonstração mais simples usando sequências. Solução. FixeA X compacto e pegue uma sequência qualquer(ym_{)tal quefy}m_{g (A).} Para cada m ₂N, sejaxm _{2A tal que y}m _{2 (x}m_{). Como A é compacto, nós sabemos que} existe uma subsequência (xmk) de (xm) tal que xmk ! x 2 A. Como, por hipótese, (x)

é um conjunto compacto, a caracterização de hemicontinuidade superior usando sequências implica que existe uma subsequência de (ymk), que nós vamos fazer um pequeno abuso de

notação e chamar novamente de (ymk), tal que ymk ! y 2 (x) (A). Ou seja (ym)

tem uma subsequência convergente em (A). Como (ym_{) foi escolhida arbitrariamente, nós} concluímos que (A) é compacto.

Exercício 4.4 (Caracterizações alternativas para hemicontinuidade superior e inferior). Sejam X e Y espaços métricos e : X Y uma correspondência. Para qualquer conjunto O Y, de…na 1_{(O) := fx 2 X : (x) Og e}

1(O) := fx 2 X : (x)\O 6= ;g.

Os conjuntos 1_{(O) e}

1(O) são chamados de imagem inversa superior e inferior de O,

respectivamente. Mostre que é hemicontínua superior se, e somente se, pra todo O aberto em Y, 1_{(O) é aberto em X, e é hemicontínua inferior se, e somente se, pra todo O}

aberto em Y, 1(O) é aberto em X.

Solução. Suponha primeiro que é hemicontínua superior e …xe um conjunto aberto qualquer O Y. Pra cadax 2 1_{(O), nós temos (x) O. Como é hemicontínua superior, isto}

implica que existe >0 tal que (BX(x; )) O. Isto é,BX(x; ) 1_{(O), o que mostra}

que 1_{(O)é um conjunto aberto. Suponha agora que} 1_{(O)seja um conjunto aberto para}

todoO aberto emY. Fixe x2X e considere um conjunto aberto O Y tal que (x) O.

Por hipótese, 1_{(O) é um conjunto aberto. Como x 2} 1_{(O), isto implica que existe}

> 0 tal que BX(x; ) 1_{(O). Mas então, (BX(x; )) O e nós concluímos que é}

hemicontínua superior.

Agora, suponha que é hemicontínua inferior e …xe um conjunto aberto qualquerO Y. Pra cadax₂ 1(O)nós temos (x)\O 6=;. Como é hemicontínua inferior, existe >0

tal que (y) \ O 6= ; pra todo y 2 BX(x; ). Isto mostra que 1(O) é um conjunto

aberto. Finalmente, suponha que 1(O) seja um conjunto aberto para todo O aberto em

Y. Fixe x₂X e considere um conjunto aberto O Y tal que (x)_\O ₆=_;. Por hipótese,

1(O) é um conjunto aberto. Como x 2 1(O), isto implica que existe > 0 tal que

BX(x; ) 1(O). Isto é, (y)\ O 6= ; pra todo y 2 BX(x; ). Isto mostra que é

hemicontínua inferior.

13

(a) :R R de…nida por (x) :=_fy₂R: x2 _{y x}2_g;

(b) :R R _{de…nida por} (x) :=_fy₂Z:y < x_g;4.2 (c) :R R de…nida por (x) :=fy2Z:y xg;

(d) : R R de…nida por (x) := Q se x ₂ R_nQ e (x) := R_nQ se x ₂ Q.4.3 _Dica: você precisará usar os fatos de que tanto o conjunto dos números racionais quanto o conjunto dos números irracionais são densos emR. Isto é, qualquer subconjunto aberto e não vazio de R inclui números racionais e números irracionais.

Solução.

(a) A correspondência é hemicontínua superior e inferior. Para ver que é hemicontínua superior, …xex₂Re suponha queO é um conjunto aberto emRtal que[ x2_{; x}2_{] O.}

Como O é um conjunto aberto, existe" > 0 tal que( x2 _{"; x}2 _{+") O. Se x= 0,}

então de…na := p". É claro que sempre que jy xj < nós temos ( y2_{; y}2₎

( x2 _{"; x}2 _{+") O. Se x 6= 0, então de…na := minf} "

j3xj;jxjg. Fixe y tal que jy xj < . Note que a de…nição de implica que xy > 0 e jyj <2jxj. Se jyj <jxj, então[ y2_{; y}2_{] [ x}2_{; x}2_{] O. Suponha, então, que jyj>jxj. Se y > x >0, então}

y2 x2 = (y x)(y+x)

< "

3x3x

= ";

o que implica que[ y2_{; y}2_{] [ x}2 _{"; x}2_{+"] O. Se y < x <0, então}

y2 x2 = (x y)( y x)

< "

3x( 3x)

= ";

o que novamente implica que [ y2_{; y}2_{] [ x}2 _{"; x}2_{+"] O. Isto mostra que é}

hemicontínua superior emx.

Agora …xe x ₂ R e suponha que O seja um conjunto aberto em R tal que [ x2_{; x}2_]\

O 6= ;. Se x = 0, então pra qualquer y 2 R nós temos [ x2_{; x}2_{] [ y}2_{; y}2_{] e,}

consequentemente, pra qualquer >0nós temos (y)_\O =_{6 ;}pra todo y₂BX(x; ). Suponha, então, quex₆= 0. Neste caso, sabemos que existe y₂( x2_{; x}2_{)\O. De…na}

:= jxj pjyj. Note que se z 2 Bx(x; ), então necessariamente jzj > pjyj, o que implica que y₂( z2_{; z}2_{)e, consequentemente, (z)\O 6=;. Nós concluímos que é}

hemicontínua inferior emx.

4.2_{Notação. O símbolo Zrepresenta o conjunto dos números inteiros.}

14 CAPÍTULO 4. CORRESPONDÊNCIAS

(b) A correspondência não é hemicontínua superior, mas é hemicontínua inferior. Para ver que não é hemicontínua superior em zero, por exemplo, note que (0) ( ₁;0), no entanto, qualquer que seja >0, =22BR(0; ) e 02 ( =2)n( 1;0).4.4

Para ver que é hemicontínua inferior, …xex₂R e suponha que O seja um conjunto aberto tal que (x)\O 6= ;. Seja z o maior número inteiro tal que z < x e de…na

:= x z. Note que, pra todo y ₂ B(x; ), (y) = (x) se x y e (x) (y) se y > x. Os dois casos imediatamente implicam que (y)_\O ₆=_;.

(c) Agora é hemicontínua superior, mas não é hemicontínua inferior. Para ver que é hemicontínua superior, …xe x ₂ R e suponha que O é um conjunto aberto tal que

(x) O. Sejaz o menor número inteiro tal quez > xe de…na :=z x. Note que, pra todo y 2 B(x; ), (y) = (x) se y x e (y) (x) se y < x. Os dois casos

imediatamente implicam que (y) O.

Vamos agora mostrar que não é hemicontínua inferior em zero, por exemplo. Note que (0)_\( 1=2;₁) =_f0_{g 6}= _;. No entanto, para qualquer >0, =2 ₂B(0; ) e ( =2)\( 1=2;1) = ;. Isto mostra que não é hemicontínua inferior em zero.4.5 (d) A correspondência não é hemicontínua superior em ponto algum e é hemicontínua

inferior em todos os pontos. Para ver que não é hemicontínua superior, …xe um ponto x 2 R. De…na O := R_{n f}xg. Note que O é um conjunto aberto tal que (x) O.

No entanto, pra todo >0, existey ₂BR(x; ) tal quex 2 (y), o que mostra que

não é hemicontínua superior em x. Para ver que é hemicontínua inferior em todos os pontos, …xe x 2 R e suponha que O é um conjunto aberto tal que (x)\O 6= ;. Como Qe R_nQ são densos emR, para qualquer y₂R nós temos (y)_\O ₆=_;. Isto mostra que é hemicontínua inferior emx.

4.4_{Na verdade, é fácil ver que não é hemicontínua superior em xpara todo x 2 Z. Para x =2 Z, é}

hemicontínua superior.

Capítulo 5

Conjuntos Convexos

Exercício 5.1. Mostre que se A é convexo e int(A) 6= ?, então cl(int(A)) = cl(A) e

int(cl(A)) =int(A).

Solução. É claro quecl(int(A)) cl(A). Fixey₂int(A)e peguex₂cl(A). Pela observação

no enunciado da questão, pra cada m 2 N, 1

my+ (1

1

m)x =: x

m _{2 int(A). Note agora} que xm _{! x, o que implica que x 2 cl(int(A)). Nós concluímos que cl(A) cl(int(A)) e,} consequentemente, cl(A) =cl(int(A)).

Similarmente, é claro que int(A) int(cl(A)). Fixe x 2int(cl(A)) e pegue y 2int(A).

Como x ₂ int(cl(A)), existe > 0 tal que BRn(x; ) cl(A). Isto implica que, pra > 0

pequeno o su…ciente,x (y x)₂cl(A). Note agora quex= ₁₊ y+(1 ₁₊ )(x (y x)). Agora a observação no enunciado da questão implica que x 2 int(A). Nós concluímos que

int(cl(A)) int(A) e, consequentemente,int(cl(A)) =int(A).

Exercício 5.2. Dizemos que um subconjunto C de Rn _{é um cone se, pra todo x 2 C e} todo 0, nós temos x ₂ C. Se C é também convexo, nós dizemos que C é um cone convexo. Seja agora C um subconjunto qualquer de Rn_{. Mostre que C é um cone convexo} se, e somente se, x1; x2 2C and 1; 2 0 implica que 1x1 + 2x2 2C.

Solução. Suponha primeiro que C seja um cone convexo. Peguex1 e x2 em C e 1; 2 0.

Se 1 = 0 = 2, então 1x1+ 2x2 = 0 2C, já queC é um cone. Suponha, então, que 1 >0

ou 2 >0. ComoC é convexo, ₁₊1 ₂x1+ ₁₊2 ₂x2 2C. ComoC é um cone, isto implica que 1x1+ 2x2 = ( 1+ 2)( ₁₊1 ₂x1+ ₁₊2 ₂x2)2C.

Suponha agora que, pra todo x1; x2 2 C e 1; 2 0 nós tenhamos 1x1+ 2x2 2 C.

Como isto também vale quando 1+ 2 = 1, é imediato queC é um conjunto convexo. Por

outro lado, pra qualquer 0ex2C nós temos x= ₂x+₂x, o que implica que x2C. Nós concluímos queC é um cone.

Exercício 5.3. Mostre que se C1 e C2 são cones convexos emRn, então C1+C2 também é

um cone convexo.5.1 _{Além disto, mostre que C}

1+C2 =co(C1[C2).

Solução. Fixex ey em C1+C2, e x; y 0. Queremos mostrar que xx+ yy 2C1+C2.

Como x; y 2C1+C2, existemx1; y1 2 C1 e x2; y2 2 C2 tais quex =x1+x2 e y= y1 +y2.

5.1_{Notação: EscrevemosC}

16 CAPÍTULO 5. CONJUNTOS CONVEXOS

Como C1 eC2 são cones convexos, do exercício anterior nós sabemos que xx1 + yy1 2C1

e xx2 + yy2 2 C2. Mas então, xx+ yy = ( xx1 + yy1) + ( xx2 + yy2) 2 C1 +C2.

Aplicando novamente o exercício anterior, nós concluímos queC1+C2 é um cone convexo.

Como !0 ₂C1 e !0 2C2, (C1 [C2) C1 +C2. Como C1+C2 é um conjunto convexo,

isto implica que co(C1[C2) C1+C2. Agora, …xe z 2C1+C2. Isto implica que existem

x1 2 C1 e x2 2 C2 tais que z = x1 + x2. Como C1 e C2 são cones, nós sabemos que

2x1 2C1 e2x2 2C2. Finalmente, como fx1; x2g co(C1[C2) eco(C1[C2)é um conjunto

convexo, nós temos que z =x1 +x2 = 1₂(2x1) + 1₂(2x2)2 co(C1[C2). Nós concluímos que

Capítulo 6

Hiperplanos e Teoremas de Separação

Exercício 6.1. Suponha que A Rn _{seja convexo e esteja contido em algum semiespaço} fechado de Rn_{. Isto é, suponha que exista hiperplano H}

a tal que A Ha+. Mostre que cl(A) = _\fH +

a :A Ha+g. Isto é, cl(A) é a interseção de todos os semiespaços fechados que contêm A.

Solução. Note primeiro que se o semiespaço fechado H +

a é tal que A Ha+, então, como H +

a é um conjunto fechado, nós necessariamente temos cl(A) Ha+. Isto implica que cl(A) _\fH +

a : A Ha+g. Pegue agora um ponto y em Rn ncl(A). Pelo teorema de separação entre ponto e um conjunto fechado e convexo, nós sabemos que existe hiperplano Ha tal que ha; xi > > ha; yi, pra todo x 2 cl(A). Isto mostra que cl(A) Ha+, mas não é verdade que y ₂ H +

a . Como y foi escolhido arbitrariamente, nós concluímos que cl(A) = _\fH +

a :A Ha+g.

Exercício 6.2 (Teorema do Hiperplano Suporte). Seja A um conjunto convexo e suponha quez seja um ponto de fronteira deA.6.1 Mostre que existe hiperplanoHa tal queha; xi pra todo x₂A e ha; z_i= . Além disto, pra todo x₂int(A) nós temos ha; x_i< .

Solução. A demonstração segue os mesmos passos do teorema de separação entre pontos e conjuntos convexos arbitrários. ComoA é um conjunto convexo, nós sabemos que int(A) =

int(cl(A)). Como z 2 cl(A)nint(A), isto implica que z 2 cl(A)nint(cl(A)). Isto agora

implica que, pra todo m ₂ N_{, existe} zm _{2 B}

Rn(z;1=m)ncl(A). Note que zm ! z. Além

disto, pelo teorema de separação entre ponto e conjunto convexo e fechado, pra cada m ₂

N, existe hiperplano Hamm tal que ham; xi m ham; zmi. Sem perda de generalidade,

nós podemos normalizar am _{de modo que ka}m_{k = 1. Dada esta normalização, nós temos} que _fam

g BRn(0;1). Como B_Rn(0;1) é um conjunto compacto, nós sabemos que existe

uma subsequência (amk₎ de _(am₎ tal que _amk ! _a 2 _B

Rn(0;1). Fixe x 2 cl(A). Como

amk ! a e zmk ! z, a continuidade do produto interno implica que ha; xi ha; zi. Para

completar a demonstração da primeira parte do enunciado, simplesmente de…na :=_ha; z_i. A demonstração de queha; xi< sempre quex2int(A)é exatamente a mesma da segunda

parte do teorema de separação entre ponto e conjunto convexo arbitrário.

18 CAPÍTULO 6. HIPERPLANOS E TEOREMAS DE SEPARAÇÃO

Exercício 6.3. Seja f :Rn _{! R uma função contínua, côncava (isto é, pra todo x e y em}

Rn_{, e todo 2[0;1],f( x+ (1 )y) f(x) + (1 )f(y)), homogênea de grau 1 (isto é,} pra todo x 2Rn _{e todo k >0, f(kx) =kf(x)). Os passos a seguir demonstram um famoso} resultado em análise convexa.

(a) Argumente que f(0) = 0.

(b) De…na o epigrafo da funçãof por epi(f) :=_f(x; l) :x₂Rn _{e l 2Rsatisfaz l f(x)g.} Use a continuidade def para mostrar que epi(f) é um subconjunto fechado de Rn+1 _e

use a concavidade de f para mostrar que epi(f) é um subconjunto convexo de Rn+1_.

(c) Fixe x 2 Rn_{. Argumente que (x ; f(x )) é um ponto de fronteira do conjunto epi(f)} (isto é, (x ; f(x ))₂cl(epi(f))_nint(epi(f))).

Aplicando o Teorema do Hiperplano Suporte ao que aprendemos no item (c), nós sabemos que existea₂Rn_{, 2R, com(a; )6= (}!_{0;0), e 2Rtal queh(a; );(x; l)i}

=_h(a; );(x ; f(x ))_i, pra todo (x; l)₂epi(f).

(d) Usando a homogeneidade de grau 1 da função f, argumente que = 0.

(e) Argumente que necessariamente >0. Dica: Use a estrutura do conjuntoepi(f) para

mostrar que 0. Depois disto argumente que não é possível que = 0.

(f) Use o que você aprendeu nos ítens anteriores para mostrar que, pra todo x 2 Rn_, f(x ) = min_fha; x _i:a₂Rn _{satisfaz ha; xi f(x)8x2R}n_g.

Solução.

(a) Fixe qualquer x 2 Rn_{. Como f é homogênea de grau 1, pra qualquer m 2 N nós} temos f(_m1x) = _m1f(x). Note que _m1x _! !0. Como f é contínua, isto implica que limm_!1f(_m1x) = f(limm_{!1 m}1x) = f(!0 ). Por outro lado, limm_!1f(_m1x) =

limm_!1m1f(x) = 0. Como em um espaço métrico o limite de uma sequência é único, nós concluímos que f(!0 ) = 0.

(b) Suponha que ((xm_{; l}m_{)) seja uma sequência tal que (x}m_{; l}m_{) ! (x; l) e, pra todo} m, (xm_{; l}m_{) 2 epi(f). Nós vimos em sala que que (x}m_{; l}m_{) ! (x; l) implica que} xm

! x e lm

! l. Note agora que (xm_{; l}m₎

2 epi(f) é o mesmo que lm _f(xm_). Novamente, comof é contínua, xm _{!x implica quef(x}m_{)!f(x). Mas então, segue} das propriedades da relação binária que f(x) = limf(xm_{) liml}m _{= l. Isto é,}

(x; l) ₂ epi(f). Como ((xm_{; l}m_{)) foi escolhida arbitrariamente, nós concluímos que} epi(f) é um conjunto fechado.

Agora, pegue (x1; l1) e (x2; l2) em epi(f) e 2 [0;1]. Isto implica que l1 f(x1) e

l2 f(x2), o que implica que l1+(1 )l2 f(x1)+(1 )f(x2). Finalmente, como

f é côncava, nós sabemos quef( x1+(1 )x2) f(x1)+(1 )f(x2) l1+(1 )l2.

19

(c) Fixe x ₂ Rn_{. Para ver que (x ; f(x )) é um ponto de fronteira de epi(f), note} primeiro que (x ; f(x )) ₂ epi(f) = cl(epi(f)). Além disto, qualquer que seja " > 0, existe l > f(x ) tal que(x ; l)2 BRn+1((x ; f(x )); "). Como para qualquerl > f(x )

nós temos que (x ; l) ₂= epi(f), isto mostra que (x ; f(x )) ₂= int(epi(f)). Ou seja,

(x ; f(x )) é um ponto de fronteira deepi(f).

(d) Suponha queh(a; );(x ; f(x ))i= >0 e note que

h(a; );(2x ; f(2x ))_i = _h(a; );(2x ;2f(x ))_i = h(a; );2(x ; f(x ))i

= 2h(a; );(x ; f(x ))i

= 2

> :

Como(2x ; f(2x ))2epi(f), isto é uma contradição. Suponha agora que nós tenhamos

h(a; );(x ; f(x ))_i= <0. Observe que neste caso, nós temos

(a; );(1 2x ; f(

1

2x )) = (a; );( 1 2x ;

1 2f(x ))

= (a; );1

2(x ; f(x ))

= 1

2h(a; );(x ; f(x ))i

= 1 2

> :

Uma vez mais, como (1 2x ; f(

1

2x ))2 epi(f), isto é uma contradição. Nós concluímos

que = 0.

(e) Seguindo a dica, suponha primeiro que <0 e …xe x ₂ Rn_{. Para qualquer l f(x),}

(x; l) ₂ epi(f), mas quando l < ha;xi, o que implica que l > _ha; x_i, nós temos

h(a; );(x; l)_i = _ha; x_i + l > _ha; x_{i h}a; x_i = 0 = , o que é uma contradição. Nós concluímos que 0. Suponha agora que = 0. Isto implica que a 6= !0 e,

consequentemente, h(a; );(a; f(a))_i=_ka_k2 >0. Como (a; f(a))₂epi(f), isto é uma contradição. Nós concluímos que >0.

(f) É claro que sefa ₂Rn _{:ha; xi f(x)8x2R}n_{g 6=;, entãof(x ) inffha; x i:a 2R}n satisfaz ha; x_i f(x)₈x ₂ Rn_{g. Note agora que os ítens anteriores mostram que, pra} todo x 2 Rn_{, existe a 2 fa 2 R}n _{: ha; xi f(x)8x 2 R}n_{g tal que f(x ) = ha ; x i.}

Parte II

Capítulo 7

Otimização Estática

Exercício 7.1. Considere o seguinte problema de otimização:

min

x;y x

2_+y2

s.a.

xy 1;

x 0; e

y 0:

(a) Argumente que tal problema tem solução. Dica: encontre uma forma de usar o teorema de Weierstrass.

(b) Encontre a solução do problema. Dica: será que todas as restrições podem ser satisfeitas com igualdade?

Solução.

(a) Note que(x; y) = (1;1)satisfaz todas as restrições do problema e faz com que a função objetivo assuma o valor2. Portanto, qualquer ponto em que a função objetivo assuma

um valor maior do que 2 certamente não será solução do problema. Em particular,

sempre que x > 2 ou y > 2 isto ocorre. Tal discussão mostra que as soluções do problema acima coincidem com a solução do seguinte problema:

min

x;y x

2_+y2

s.a.

xy 1; x 0; y 0;

x 2; y 2:

24 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

(b) Vamos primeiro escrever o problema no formato que estamos acostumados. Isto é, considere o seguinte problema:

max

x;y x

2 _y2

s.a.

xy 1;

x 0; e

y 0:

Claramente, a segunda e a terceira restrição não podem ser ativas, já que se x = 0

ou y = 0 nós temos xy = 0 < 1. Portanto, a segunda e terceira restrições não serão relevantes para o cálculo das condições de primeira ordem do problema.7.1 _O Lagrangeano do problema acima pode ser escrito como

L= 0( x2 y2) + 1(xy 1):

As condições de primeira ordem do problema são:

0 : 0 0;( 0; 1)6= (0;0)

1 : 1 0; xy 1; 1(xy 1) = 0

x: 2 0x+ 1y= 0

y: 2 0y+ 1x= 0

Como nós já argumentamos que x > 0 e y > 0, se 0 = 0 as condições de primeira

ordem em relação axeyimplicam que 1 = 0, o que não pode ocorrer. Nós concluimos

que 0 > 0 e, sem perda de generalidade nós podemos assumir que 0 = 1. Agora as

condições de primeira ordem em relação ax e yimplicam que x=y. Além disto, elas

implicam que 1 >0e, consequentemente, nós temos que terxy= 1. Nós aprendemos

que o único ponto crítico do problema éx=y= 1. Como nós já argumentamos que o

problema tem solução, esta é exatamente a solução. Exercício 7.2. Considere o seguinte problema de otimização:

min

x;y (x 2)

2_{+ (y 1)}2

s.a.

y x2 0;

x+y 4 0;

x 0; e

y 0:

7.1_{Alternativamente, nós podemos escrever o Lagrangeano do problema incorporando todas as restrições,}

25

(a) Argumente que tal problema tem solução. A dica para o exercício 7.1 continua válida. (b) Encontre a solução do problema. Dica: Uma das restrições é redundante.

Solução.

(a) Note que, como x 0 e y 0, a segunda restrição só pode ser satisfeita se x 4 e y 4. Portanto, o conjunto restrição do problema acima é compacto e o Teorema de

Weierstrass nos garante que ele tem solução.

(b) Vamos primeiro escrever o problema no formato que sabemos trabalhar. Isto é, considere o seguinte problema:

max

x;y (x 2)

2 _{(y 1)}2

s.a.

y x2 0;

4 x y 0;

x 0; e

y 0:

Note que a primeira restrição implica que y x2 _{0. Ou seja, a restrição y 0 é}

redundante e pode ser ignorada. O problema vira:

max

x;y (x 2)

2 _{(y 1)}2

s.a.

y x2 0;

4 x y 0;

x 0:

Antes de escrevermos o Lagrangeano do problema vamos simpli…cá-lo um pouco mais. Nós podemos argumentar que a terceira restrição não pode ser ativa. Para ver isto, note que se x = 0, então certamente a melhor escolha para o valor de y é y = 1. O valor da função objetivo em tal ponto é 4. No entanto, o ponto(x; y) = (1;1)satisfaz

todas as restrições e o valor da função objetivo nele é 1. Isto mostra que a solução do

problema necessariamente satisfaz x > 0. Portanto, nós podemos ignorar a terceira restrição na hora de escrever o Lagrangeano do problema. O Lagrangeano do problema pode ser escrito como:

L= 0( (x 2)2 (y 1)2) + 1(y x2) + 2(4 x y)

As condições de primeira ordem do problema são

0 : 0 0;( 0; 1; 2)6= (0;0;0);

26 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

2 : 2 0;4 x y 0; 2(4 x y) = 0;

x: 2 0(x 2) 2 1x 2 = 0;

y : 2 0(y 1) + 1 2 = 0:

Como x > 0, 1 0 e 2 0, se 0 = 0, então a condição de primeira ordem em

relação a x implica que 1 = 0 e 2 = 0, o que viola a condição de primeira ordem

em relação a 0. Nós concluimos que 0 > 0 e nós podemos assumir, sem perda de

generalidade, que 0 = 1. As condições de primeira ordem do problema viram:

1 : 1 0; y x2 0; 1(y x2) = 0;

2 : 2 0;4 x y 0; 2(4 x y) = 0;

x: 2(x 2) 2 1x 2 = 0;

y: 2(y 1) + 1 2 = 0:

Vamos dividir em casos:

Caso 1. As duas restrições são inativas. Neste caso, 1 = 2 = 0 e as condições de primeira

ordem em relação axeyimplicam quex= 2ey= 1. Como tais valores não satisfazem

a primeira restrição, nós concluimos que não existe ponto crítico neste caso.

Caso 2. Apenas a primeira restrição é ativa. Neste caso 2 = 0ey=x2. Agora as condições

de primeira ordem em relação a xe y nos dão

1 = 2(x2 1)

e

(x 2) + 2x(x2 1) = 0

()

x3 1

2x 1 = 0

A única raiz real para a equação acima é x = 1;1654, o que implica que y = 1;3582.

Note que tais valores fazem com que 1 > 0 e satisfazem todas as restrições do

problema. Ou seja, tais valores são um ponto crítico válido. O valor da função objetivo em tal ponto é aproximadamente 0;1274.

Caso 3. Apenas a segunda restrição é ativa. Neste caso 1 = 0 e x+y = 4. As condições

de primeira ordem em relação a xe y nos dão a equação x 2 = y 1. Resolvendo o

sistema acima nós obtemos x = 5=2 e y = 3=2. Substituindo tais valores na condição de primeira ordem em relação a x nós obtemos 2 = 1, o que não pode ocorrer. Nós

27

Caso 4. As duas restrições são ativas. Neste caso nós …camos com o sistema y = x2 _e

x+y = 4. A solução do sistema acima que satisfaz x > 0 é x = 1+p17

2 = 1;5616

e y = 4 1+₂p17 = 2;4384. Para saber se tais valores realmente con…guram pontos

críticos, ainda teríamos que veri…car se os valores 1 e 2 associados a eles realmente

são não negativos, mas é mais fácil checar que o valor da função objetivo em tais pontos é bem superior ao valor no caso em que apenas a primeira restrição era ativa.

A solução do problema éx = 1;1654 e y= 1;3582.

Exercício 7.3. Considere o seguinte problema de otimização:

max

x;y x

4_y3

s.a.

2x+y 8;

6x+ 7y 36;

x 0:

(a) Argumente que tal problema tem solução. A dica para o exercício 7.1 continua válida. (b) Encontre a solução do problema.

Solução.

(a) Note primeiro que o ponto (x; y) = (1;1) satisfaz todas as restrições do problema.

Se y < 0, então obviamente o valor da função objetivo é menor ou igual a zero e, consequentemente, menor do que 1, que é o valor da função objetivo no ponto (1;1).

Isto mostra que se adicionarmos a restriçãoy 0ao problema a solução não se altera.

Dadas as restriçõesx 0e y 0, é claro que a primeira restrição implica quex 4e y 8. Isto deixa claro que o conjunto restrição induzido pelas restrições originais mais

a restrição y 0 é compacto. Pelo Teorema de Weierstrass o problema tem solução.

(b) Note primeiro que se x = 0, então o valor da função objetivo é zero. Como o ponto

(1;1)satisfaz todas as restrições do problema e o valor da função objetivo em tal ponto

é 1, nós percebemos que a restrição x 0 não será ativa na solução do problema e,

portanto, nós podemos ignorá-la na hora de escrever as condições de primeira ordem do problema. O Lagrangeano do problema pode ser escrito como

L= 0x4y3+ 1(8 2x y) + 2(36 6x 7y)

As condições de primeira ordem do problema acima são

0 : 0 0, ( 0; 1; 2)6= (0;0;0);

1 : 1 0, 8 2x y 0, 1(8 2x y) = 0;

28 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

x: 4 0x3y3 2 1 6 2 = 0;

y: 3 0x4y2 1 7 2 = 0:

Como x > 0, y > 0, 1 0 e 2 0, tanto a condição de primeira ordem em relação

a x como a condição de primeira ordem em relação a y implicam que 1 = 2 = 0

se 0 = 0. Como isto contradiz a condição de primeira ordem em relação a 0, nós

concluimos que 0 >0e nós podemos assumir, sem perda de generalidade, que 0 = 1.

As condições de primeira ordem do problema viram

1 : 1 0, 8 2x y 0, 1(8 2x y) = 0; 2 : 2 0,36 6x 7y 0, 2(36 6x 7y) = 0;

x: 4x3_y3 ₂

1 6 2 = 0;

y: 3x4y2 1 7 2 = 0:

É claro que pelo menos uma das duas restrições tem que ser ativa, caso contrário poderíamos simplesmente aumentar x e y inde…nidamente. Isto nos deixa com três casos a considerar.

Caso 1. Apenas a primeira restrição é ativa. Neste caso, 2 = 0 e as condições de

primeira ordem em relação ax e y viram

x: 4x3y3 2 1 = 0;

y: 3x4y2 1 = 0:

Multiplicando a segunda condição por -2 e adicionando à primeira nós obtemos

4x3y3 6x4y2 = 0;

o que é equivalente a

2y 3x= 0:

Os valores dexeyque satisfazem o sistema formado pela condição acima e a primeira restrição em igualdade são x = 16₇ e y = 24₇ . No entanto, tais valores não satisfazem

a segunda restrição e, portanto, não são um ponto crítico válido. Concluimos que não existem pontos críticos neste caso.

Caso 2. Apenas a segunda restrição é ativa. Neste caso, 1 = 0 e as condições de

primeira ordem em relação ax e y viram

x: 4x3y3 6 2 = 0;

y: 3x4y2 7 2 = 0:

29

A condição acima é equivalente a

14y 9x= 0:

Resolvendo o sistema formado pela condição acima e a segunda restrição em igualdade nós obtemos x = 24₇ e y = 108₄₉. No entanto, tais valores não satisfazem a primeira

restrição. Novamente, nós concluimos que não existem pontos críticos neste caso. Caso 3. A primeira e a segunda restrições são ativas. Neste caso, o sistema formado pelas duas restrições nos dá x = 5₂ e y = 3. Como estes são os únicos candidatos a

pontos críticos restantes, esta tem que ser a solução do problema.7.2

Exercício 7.4. Uma …rma produz um produto y usando dois insumos x1 e x2. A função

de produção é y = px1x2. A …rma é obrigada a usar pelo menos uma unidade de x1 no

seu processo produtivo devido a um acordo com o sindicato. Os preços dos insumos x1 e x2

são w1 e w2, respectivamente. Suponha que a …rma queira minimizar o custo de produzir y

unidades do produto.

(a) Monte o problema de minimização de custos da …rma. O conjunto restrição (os pontos onde todas as restrições são satisfeitas) é fechado? Ele é compacto?

(b) Encontre a solução do problema quando w1 = 4, w2 = 1 e y= 2:

Solução.

(a) O problema da …rma é

min

x1;x2

w1x1+w2x2

s.a. _p

x1x2 =y;

x1 1;

x2 0:

Todas as restrições envolvem apenas funções contínuas e igualdades ou desigualdades fracas. Isto implica que o conjunto restrição é fechado. Note que, como x1 1,

a primeira restrição implica que x2 y2. No entanto, o conjunto restrição não é

limitado e, portanto, não é compacto. Para ver isto, note que (ty;y_t) satisfaz todas

as restrições do problema sempre que t 1_y. Apesar do conjunto restrição não ser compacto, nós podemos utilizar os nossos truques usuais para garantir que o problema tem solução. Por exemplo, note que x1 = 1 e x2 = y2 satisfaz todas as restrições do

problema. Isto implica que a solução do problema tem que satisfazer w1x1+w2x2 w1+w2y2;

o que implica quex1 tem que satisfazer

x1 1 +

w2

w1

30 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

Ou seja, nós podemos adicionar as restrições x2 y2 e x1 1 + w_w2₁y2 ao problema

que a sua solução não se altera. Como o conjunto restrição desse novo problema é compacto, nós concluimos que o problema original tem solução.

(b) O problema pode ser escrito como

max

x1;x2

4x1 x2

s.a.

x1x2 = 4;

x1 1;

x2 0:

É claro que se a segunda restrição for ativa a primeira restrição não é satisfeita, portanto, a terceira restrição não será importante para as condições de primeira ordem do problema. O Lagrangeano do problema é

L= 0( 4x1 x2) + 1(x1 1) + (x1x2 4):

As condições de primeira ordem do problema são

0 : 0 0;( 0; 1; )6= (0;0;0);

1 : 1 0; x1 1; 1(x1 1) = 0;

:x1x2 = 4

x1 : 4 0+ 1+ x2 = 0;

x2 : 0+ x1 = 0:

Como x1 1 > 0, se 0 = 0, então a condição de primeira ordem em relação a x2

implica que = 0. Agora a condição de primeira ordem em relação ax1 implica que 1

também é igual a zero quando 0 = 0. Como isto não pode ocorrer nós concluimos que 0 >0 e, sem perda de generalidade, nós podemos assumir que 0 = 1. As condições

de primeira ordem viram

1 : 1 0; x1 1; 1(x1 1) = 0;

:x1x2 = 4

x1 : 1+ x2 = 4;

x2 : x1 = 1:

Isolando na restrição em relação ax2 e substituindo na restrição em relação ax1 nós

…camos com

1 = 4

x2

x1

.

Note agora que, como x1 1, a primeira restrição implica quex2 4. Mas então, se

31

primeira ordem em relação a 1. Nós concluimos que necessariamente x1 = 1. Agora

a primeira restrição implica quex2 = 4. Note que com tais valores nós temos 1 = 0,

o que satisfaz a condição de primeira ordem em relação a 1. Isto é,(x1; x2) = (1;4)é

o único ponto crítico válido do problema. Como nós já argumentamos que o problema tem solução,(1;4)é exatamente a solução.

Exercício 7.5. Considere o seguinte problema de otimização:

min

x;y (3 x)(5 y) s.a.

2x+y 4;

x 0; e

y 0:

(a) Argumente que tal problema tem solução.

(b) Encontre a solução do problema. Dica: Uma das restriçõe com certeza tem que ser ativa. Que restrição é esta?

Solução.

(a) Note que, como x 0 e y 0, a primeira restrição implica que x 2 e y 4. Isto mostra que o conjunto restrição é um subconjunto fechado de um conjunto compacto e, portanto, é um conjunto compacto. Agora o Teorema de Wierstrass garante que o problema tem solução.

(b) Como as restrições implicam que x 2 < 3 e y 4 < 5, qualquer que seja o par x e y que satisfaz as restrições do problema, nós sempre podemos diminuir o valor da função objetivo aumentando um poucoxey. Logo, para que um parxey seja solução do problema não pode ser possível que aumentemos x e y e as restrições ainda sejam satisfeitas. Isto é, a primeira restrição tem que ser ativa. O problema vira

min

x;y (3 x)(5 y)

s.a.

2x+y= 4;

x 0; e

y 0:

32 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

de3. Isto mostra que a restriçãoy 0 não é ativa e, portanto, não é importante para as condições de primeira ordem do problema. O Lagrangeano do problema pode ser escrito como

L= 0( (3 x)(5 y)) + 1x+ (2x+y 4):

As condições de primeira ordem do problema são

0 : 0 0;( 0; 1; )6= (0;0;0);

1 : 1 0; x 0; 1x= 0;

: 2x+y= 4;

x: 0(5 y) + 1+ 2 = 0;

y : 0(3 x) + = 0:

Como x 2 < 3, a condição de primeira ordem em relação a y implica que = 0

sempre que 0 = 0. Agora, comoy 4<5, a condição de primeira ordem em relação

a x implica que também é verdade que 1 = 0 sempre que 0 = 0. Como isto viola a

condição de primeira ordem em relação a 0, nós concluimos que 0 >0e nós podemos

assumir, sem perda de generalidade, que 0 = 1. As condições de primeira ordem viram

1 : 1 0; x 0; 1x= 0;

: 2x+y= 4;

x: 5 y+ 1+ 2 = 0;

y: 3 x+ = 0:

Quando x = 0, nós já vimos que y = 4. Além disto, é fácil checar que 1 > 0 neste

caso. Portanto, (0;4) é um ponto crítico do problema. Suponha agora que x > 0. Neste caso 1 = 0 e as condições de primeira ordem em relação a x e y nos dão a

equação y

2 5

2 =x 3. Resolvendo o sistema formado por esta equação e a condição de

primeira ordem em relação a , nós obtemos x= 5

4 e y= 3

2. Como o valor da função

objetivo (do problema de minimização original) em tal ponto é maior do que 3, nós

concluímos que a solução do problema é (x; y) = (0;4).

Exercício 7.6. Resolva o problema

min

x;y;z(x 2)

2_{+ (y 2)}2_{+ (z 2)}2

s.a.

x+y+z = 2;

33

Solução. Note primeiro que, como x 0, y 0 e z 0, a primeira restrição implica que x 2, y 2 e z 2. Ou seja, o conjunto restrição é compacto e o Teorema de Wierstrass garante que ele tem solução. O Lagrangeano do problema é

L= 0( (x 2)2 (y 2)2 (z 2)2) + (x+y+x 2) + 1x+ 2y+ 3z:

As condições de primeira ordem do problema são

0 : 0 0;( 0; 1; 2; 3; )6= (0;0;0;0;0);

:x+y+z = 2;

1 : 1 0; x 0; 1x= 0;

2 : 2 0; y 0; 2y = 0;

3 : 3 0; z 0; 3z = 0;

x: 2 0(x 2) + + 1 = 0;

y: 2 0(y 2) + + 2 = 0;

z : 2 0(z 2) + + 3 = 0:

Claramente as três últimas restrições não podem ser ativas ao mesmo tempo, já que isto seria uma contradição à primeira restrição. Além disto, dada a simetria do problema, nós só precisamos nos preocupar com três casos:

Caso 1. Nenhuma das três últimas restrições é ativa. Neste caso, 1 = 2 = 3 = 0. Além

disto, se 0 = 0, então a condição de primeira ordem em relação a x, por exemplo, implica

que = 0. Como isto viola a condição de primeira ordem em relação a 0, nós concluimos

que 0 > 0 e nós podemos assumir, sem perda de generalidade, que 0 = 1. Agora as

condições de primeira ordem em relação a x; y e z implicam que x=y =z. Usando isto na

condição de primeira ordem em relação a nós obtemos x =y=z = 2₃. O valor da função

objetivo em tal ponto é 16 3.

Caso 2. Apenas a restrição x 0 é ativa.7.3 Neste caso, 2 = 3 = 0. Se 0 = 0,

então a condição de primeira ordem em relação a y, por exemplo, implica que = 0. Agora

a restrição de primeira ordem em relação a x também implica que 1 = 0, o que viola a

condição de primeira ordem em relação a 0. Nós concluimos que 0 > 0 e, sem perda de

generalidade, nós podemos assumir que 0 = 1. Agora, as condições de primeira ordem em

relação a y e z implicam que y = z. Substituindo isto na condição de primeira ordem em relação a nós obtemosy =z = 1. Juntamente comx= 0 tais valores implicam que = 2

e 1 = 2, o que viola a condição de primeira ordem em relação a 1. Nós concluimos que

não existem pontos críticos neste caso.

Caso 3. Apenas a primeira e a segunda restrições são ativas.7.4 _{Neste caso, a condição de} primeira ordem em relação implica que z = 2. Nós ainda teríamos que checar os valores

de 0, 1 e 2 para saber se(0;0;2)é um ponto crítico válido, mas é mais fácil veri…car qual

o valor da função objetivo em tal ponto. No ponto (0;0;2) a função objetivo (do problema

de minimização original) vale 8, que é maior do que 16₃ .

Nós concluimos que a solução do problema é x=y =z = 2 3.

34 CAPÍTULO 7. OTIMIZAÇÃO ESTÁTICA

Exercício 7.7. Considere o seguinte problema de minimização:

min

x;y;zx

2_{+xy+ 2y}2 _{6x 2y 12z}

sujeito a

x 2y z 3

2x2+y2 18

x; y; z 0

(a) Argumente que o problema tem solução. Dica: É possível mostrar que o conjunto restrição do problema já é compacto. Não é necessário adicionar restrições.

(b) Argumente que qualquer solução do problema necessariamente tem que satisfazer a primeira restrição com igualdade.

(c) Escreva o problema novamente, agora com a primeira restrição em formato de igualdade. Argumente que a solução desse novo problema necessariamente satisfaz y= 0.

(d) Use o que você aprendeu nas letras (b) e (c) para transformar o problema de modo que a única variável de escolha seja x. Encontre todos os pontos críticos de tal problema e, posteriormente, encontre a sua solução. Diga quais são os valores de x, y e z que são solução do problema original. Atenção! Mesmo que você saiba como resolver o problema de alguma outra forma, eu quero que você escreva o Lagrangeano e encontre todos os pontos críticos. Isto implica que você tem que se preocupar em testar os sinais dos multiplicadores de Lagrange, quando necessário.

Solução.

(a) Primeiramente, note que, como todas as restrições do problema são formadas por funções contínuas e desigualdades fracas, o conjunto restrição é fechado. Note agora que, como x 0 e y 0, a segunda restrição implica que y p18 e x 3. Agora a

primeira restrição implica que

z x 2y+ 3 3 0 + 3 = 6:

Ou seja, as restrições do problema implicam que 0 x 3, 0 y p18 e 0 z

6. Como estas condições formam um conjunto compacto, e o conjunto restrição do

35

(b) De…naf(x; y; z) :=x2 _{+xy+ 2y}2 _{6x 2y 12z. Ou seja, f é exatamente a função}

objetivo do problema. Suponha quex,yezsatisfaçam todas as restrições do problema e quex 2y z > 3. Isto é,z < x 2y+3. De…naz^:=x 2y+3> z. Note que(x; y;z^)

também satisfaz todas as restrições do problema. Além disto, f(x; y; z) f(x; y;z^) = 12(^z z) > 0. Isto mostra que (x; y; z) não pode ser solução do problema. Nós concluimos que qualquer solução do problema tem que satisfazer a primeira restrição com igualdade.

(c) O problema agora pode ser escrito como

min

x;y;zx

2_{+xy+ 2y}2 _{6x 2y 12z}

sujeito a

x 2y z = 3

2x2+y2 18

x; y; z 0

Suponha que x, y e z satisfaçam todas as restrições do problema acima e que y > 0.

De…nay^:= 0 ez^:=x+ 3. Note que (x;y;^ z^) satisfaz todas as restrições do problema

e que

f(x; y; z) f(x; y;z^) = xy+ 2y2 2y 12(x+ 3 2y) + 12(x+ 3) = xy+ 2y2+ 22y

> 0:

Novamente, isto mostra que(x; y; z)não pode ser solução do problema. Nós concluimos

que qualquer solução do problema tem que satisfazery= 0. (d) O problema agora pode ser escrito como

min

x;y;zx

2 _{6x 12z}

sujeito a

x z = 3

2x2 18

x; z 0

A primeira restrição pode ser escrita comoz=x+ 3. Isto mostra que a restriçãoz 0

é redundante e pode ser ignorada, já que x+ 3 3. Agora nós podemos substituir z =x+ 3 para obter o seguinte problema de uma única variável:

min

x;y;zx

2 _{18x 36}