Análise das Tensões, Cap. I - Mecânica dos Materiais e Estruturas Lineares. Teoria e Aplicações

(1)

CAPÍTULO I

ANÁLISE DAS TENSÕES

1.1. RESUMO DA TEORIA

1.1.1. Introdução. O Conceito de Tensão

Há, fundamentalmente, dois tipos distintos de forças exteriores que

podem actuar sobre um corpo material: (i)-forças de superfície e

(ii)-forças de volume. Considere-se o corpo (C) em equilíbrio sob a acção

destes dois tipos de forças, Fig. 1.1:

A Tensão Resultante

T

( n

P

,

r

)

r

, no ponto P, para uma superfície de corte

perpendicular a n

r

=(l, m, n), define-se pela expressão (Fig. 1.2):

A

F

lim

T

∆A

∆

=

→

r

0

(1.1)

Fig. 1.1 – Corpo em equilíbrio ) , , (lmn n =r 6 P r 1 Pr 2 P r 3 P r 5 P r z x y (I) O 7 P r 4 Pr (II) s P s

Fig. 1.2 – Tensão resultante no ponto P Fr ∆ ) , , (lmn n =r 4 P r 3 P r 2 Pr 1 P r A ∆ x y z O (I) s s P Tr

(2)

Em geral, o vector tensão resultante

)

,

P

( n

T

r

tem uma direcção distinta

da normal n

r

e poderá decompor-se

segundo duas direcções ortogonais,

conforme ilustrado na Fig.1.3:

Uma componente perpendicular ao

plano de corte, designada por

tensão normal e representada por

σ

;

e uma segunda componente no

plano de corte, designada por

tensão tangencial ou tensão de

corte, representada por

τ

.

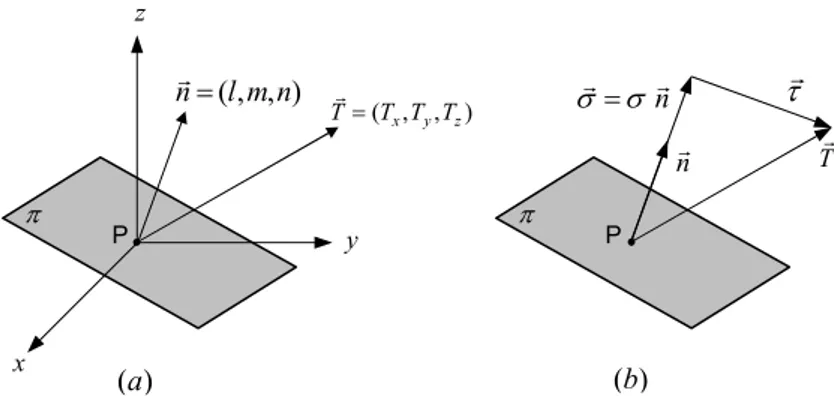
1.1.2. Componentes Cartesianas da Tensão

Em cada ponto P(x,y,z), é possível definir um conjunto de nove

componentes cartesianas do estado de tensão nesse ponto, Fig.1.4 e

Fig.1.5, que podem ser agrupadas numa matriz quadrada sob a forma

seguinte:

[ ]













=

zz zy zx yz yy yx xz xy xx

σ

τ

σ

τ

σ

τ

(1.2)

Fig. 1.5 - Representação gráfica das seis componentes cartesianas da tensão Fig. 1.4 - Componentes cartesianas

da tensão resultante T(P,k) r r zz σ k n r r ≡ T( ,k) r r P zy τ zx

τ

y z (I) x P zz σ yy σ σyy zz σ xx σ xx σ yx τ yx τ xz τ τxz yz τ yz τ zx τ zx τ xy τ xy τ zy τ zy τ x y z Fig. 1.3 - Decomposição do vector tensão resultante

T

r

σ

r

(I)

τ

r

s

P

n

r

(3)

A matriz das tensões [

τ

] é simétrica relativamente à diagonal principal,

isto é,

τ

yx =

τ

xy ,

τ

zy =

τ

yz e

τ

zx

=

τ

xz. Em alternativa, é possível representar

as seis componentes independentes da tensão pelo chamado vector das

tensões {σ

σ

σ}, definido pela seguinte expressão:

σ

σ = {σ

σ

σ}=

























xy xz yz zz yy xx

τ

σ

(1.3)

1.1.3. Tensão para uma Orientação Arbitrária

Em cada ponto P(x,y,z) dum corpo material, a intensidade e a direcção do

vector tensão resultante T

r

dependem da orientação do plano de corte (

π

)

que se considera, Fig. 1.6(a):

zz zy zx z yz yy yx y xz xy xx x

n

m

l

T

n

m

l

T

n

m

l

T

σ

τ

σ

τ

σ

+

=

+

=

+

=

(1.4a)

ou, sob a forma matricial:

Fig. 1.6 – Tensão resultante para um plano de orientação arbitrária ) , , (lmn n =r z x y P π ) , , (TxTyTz T =r P π nr Tr nr r σ σ=

τ

r

(a) (b)

(4)

































=





















n

m

l

T

zz zy zx yz yy yx xz xy xx z y x

σ

τ

σ

τ

σ

(1.4b)

As componentes normal (

σ

) e tangencial (

τ

) da tensão em P são dadas,

respectivamente, pelas expressões seguintes:

nl

mn

lm

n

m

l

_yy _zz _xy _yz _zx xx

σ

τ

σ

=

2

+

2

+

2

+

2 +

2 (1.5)

e

2 2 2 2 2

_σ

τ

=

T

_x

+

T

_y

+

T

_z

−

(1.6)

A direcção da tensão de corte

τ

no plano

π

,

n =r_c (l_c,m_c,n_c)

, fica definida

pelos respectivos co-senos directores:

τ

σ

τ

σ

τ

σ

/

)

(

/

)

(

/

)

(

n

T

n

m

T

m

l

T

l

z c y c x c

−

=

−

=

−

=

(1.7)

1.1.4. Equações de Equilíbrio

As seis funções que definem o campo das tensões estão ligadas entre si

por três equações diferenciais:













=

+

∂

+

∂

+

∂

=

+

∂

+

∂

+

∂

=

+

∂

+

∂

+

∂

0

z zz yz xz y zy yy xy x zx yx xx

F

z

y

x

F

z

y

x

F

z

y

x

σ

τ

σ

τ

σ

(1.8)

Estas são as chamadas equações de equilíbrio da teoria da elasticidade

ou equações de equilíbrio das tensões em coordenadas cartesianas.

Além das equações de equilíbrio, verifica-se também que as

componentes de corte em cada ponto são iguais duas a duas, isto é:

(5)

xz zx yz zy xy yx

τ

=

(1.9)

A simetria das tensões tangenciais expressa pelas equações (1.9) implica

uma lei de reciprocidade mais geral, que se pode exprimir através da

seguinte equação vectorial:

n

T

n

T

r

|

)

'

,

P

(

'

|

)

,

P

(

=

(1.10)

Este resultado traduz a denominada lei da reciprocidade das tensões ou

Teorema de Cauchy.

1.1.5. Leis de Transformação das Tensões

Por aplicação das equações (1.4),

podem calcular-se as componentes

cartesianas da tensão referidas a um

referencial particular Ox’y’z’, Fig.1.7,

em

função

das

componentes

cartesianas da tensão no referencial

global Oxyz e dos co-senos directores

que definem a posição relativa dos

dois referenciais:

)

(

)

(

)

(

)

(

)

(

)

(

(1.11)

)

(

)

(

)

(

2

' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 2 ' 2 ' 2 ' ' ' ' ' ' ' ' ' 2 ' 2 ' 2 ' ' ' ' ' ' ' ' ' 2 ' 2 ' 2 ' ' ' y x y x xy y x y x xz y x y x yz y x zz y x yy y x xx x z x z xy x z x z xz x z x z yz x z zz x z yy x z xx y x z x z y z y xy z y z y xz z y z y yz z y zz z y yy z y xx z y z z xy z z xz z z yz z zz z yy z xx z z y y xy y y xz y y yz y zz y yy y xx y y x x xy x x xz x x yz x zz x yy x xx x x

l

m

l

n

l

n

m

n

m

n

m

l

m

l

n

l

n

m

n

m

n

m

l

m

l

n

l

n

m

n

m

n

m

l

m

l

n

m

n

m

l

m

l

n

m

n

m

l

m

l

n

m

n

m

l

+

=

+

=

+

=

+

=

+

=

+

=

τ

σ

τ

σ

τ

σ

τ

σ

τ

σ

τ

σ

ou, inversamente:

Fig. 1.7– Referenciais Oxyz e Ox’y’z’ O=O' x x' y' y z' z

(6)

)

(

)

(

)

(

)

(

)

(

)

(

)

12 .

1 (

)

(

)

(

)

(

2

' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 2 ' ' ' 2 ' ' ' 2 ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 2 ' ' ' 2 ' ' ' 2 ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 2 ' ' ' 2 ' ' ' 2 ' ' ' x y y x y x z x x z y x y z z y z y z z z z y y y y x x x x x y y x y x z x x z z x y z z y z y z z z z y y y y x x x x xy xz x y y x y x z x x z z x y z z y z y z z z z y y y y x x x x yz y x y x x z z x z y z y z z z y y y x x x zz y x y x x z z x z y z y z z z y y y x x x yy y x y x x z z x z y z y z z z y y y x x x xx

m

l

m

l

m

l

m

l

m

l

m

l

m

l

m

l

m

l

n

l

n

l

n

l

n

l

n

l

n

l

n

l

n

l

n

m

n

m

n

m

n

m

n

m

n

m

n

l

n

m

n

m

n

m

l

+

=

+

=

+

=

+

=

+

=

+

=

τ

σ

τ

σ

τ

σ

τ

σ

τ

σ

τ

σ

Estas equações de transformação podem escrever-se de uma maneira

concentrada, sob a forma matricial seguinte:

[ ] [ ] [ ] [ ]

T

'

L

ττττ

L

ττττ =

(1.13)

onde [L] é a matriz de transformação de coordenadas e [L]

T

é a

respectiva matriz transposta.

Inversamente, pode escrever-se:

[ ] [ ] [ ] [ ]

ττττ =

L

T

ττττ

'

L

(1.14)

Em alternativa, quando se utiliza a notação vectorial da tensão, as

equações de transformação das tensões escrevem-se:

























xy xz yz zz yy xx

τ

σ

= [T]

























' ' ' ' ' ' ' ' ' ' ' ' y x z x z y z z y y x x

τ

σ

(1.15a)

ou, simplesmente :

{σ

σ

σ} = [T] {σ

σ

σ’}

(1.15b)

onde:

(7)

[T] =













66 65 64 63 62 61 56 55 54 53 52 51 46 45 44 43 42 41 36 35 34 33 32 31 26 25 24 23 22 21 16 15 14 13 12 11

T

(1.16)

com:

2 ' 11

l

x

T

=

;

T =

₁₂

l

_y2_'

;

T

₁₃

=

l

_z2_'

;

T

₁₄

=

2 l

_y_'

l

_z_'

;

T =15 2lz'lx'

;

T

16

=

2 l

x'

l

y'

;

2 ' 21

m

x

T

=

;

2 ' 22

m

y

T =

;

T

₂₃

=

m

2_z_'

;

T

₂₄

=

2 m

_y_'

m

_z_'

;

T₂₅=2mz_'mx_'

;

T

26

=

2 m

x'

m

y'

;

2 ' 31

n

x

T

=

;

2 ' 32

n

y

T =

;

T

₃₃

=

n

_z2_'

;

T

₃₄

=

2 n

_y_'

n

_z_'

;

T₃₅=2nz_'nx_'

;

T

36

=

2 n

x'

n

y'

;

T41=mx'nx'

;

' ' 42

m

y

n

y

T

=

;

T₄₃=l_z_'n_z_'

;

T

₄₄

=

m

_y_'

n

_z_'

+

m

_z_'

n

_y_'

;

T₄₅ =m_z_'n_x_'+m_x_'n_z_'

;

' ' ' ' 46

m

x

n

y

m

y

n

x

T

=

+

;

T =₅₁ l_x_'n_x_'

;

T

₅₂

=

l

_y_'

n

_y_'

;

T₅₃=l_z_'n_z_'

;

T

₅₄

=

n

_y_'

l

_z_'

+

n

_z_'

l

_y_'

;

' ' ' ' 55 nzlx nxlz T = +

;

T

₅₆

=

n

_x_'

l

_y_'

+

n

_y_'

l

_x_'

;

T =₆₁ l_x_'m_x_'

;

T

₆₂

=

l

_y_'

m

_y_'

;

T₆₃=l_z_'m_z_'

;

' ' ' ' 64

l

y

m

z

l

z

m

y

T

=

+

;

T₆₅ =l_z_'m_x_'+l_x_'m_z_'

;

T

₆₆

=

l

_x_'

m

_y_'

+

l

_y_'

m

_x_'

A matriz [T] definida pelos coeficientes (1.24d) é designada por matriz

de transformação das tensões.

Inversamente, pode escrever-se:

{σ

σ

σ'} = [T]

-1

{σ

σ

σ} = [R] {σ

σ

σ}

σ

(1.17)

onde:

[R] =













66 65 64 63 62 61 56 55 54 53 52 51 46 45 44 43 42 41 36 35 34 33 32 31 26 25 24 23 22 21 16 15 14 13 12 11

R

(1.18)

com:

(8)

2 ' 11

l

x

R

= ;

R

₁₂

=

m

_x2_'

;

R

₁₃

=

n

2_x_'

;

R14 =2mx'nx'

;

R15 =2nx'lx'

;

R16=2lx'mx'

;

2 ' 21

l

y

R =

;

R =

₂₂

m

2_y_'

;

R =

₂₃

n

2_y_'

R

₂₄

=

2 m

_y_'

n

_y_'

;

R

₂₅

=

2 n

_y_'

l

_y_'

;

R

₂₆

=

2 l

_y_'

m

_y_'

;

2 ' 31

l

z

R

= ;

R

₃₂

=

m

2_z_'

;

R

₃₃

=

n

_z2_'

;

R₃₄ =2mz_'nz_'

;

R35 =2nz'lz'

;

R36 =2lz'mz'

;

' ' 41

l

y

l

z

R

=

;

R

₄₂

=

m

_y_'

m

_z_'

;

R

₄₃

=

n

_y_'

n

_z_'

;

R

₄₄

=

m

_y_'

n

_z_'

+

n

_y_'

m

_z_'

;

' ' ' ' 45

n

y

l

z

ly

x

n

z

R

=

+

;

R

₄₆

=

l

_y_'

m

_z_'

+

m

_y_'

l

_z_'

;

R₅₁=l_x_'l_z_'

;

R₅₂ =m_x_'m_z_'

;

' ' 53 nxnz R =

;

R54=mz'nx'+nz'mx'

;

R55=nz'lx'+lz'nx'

;

R56 =lz'mx'+mz'lx' ' ' 61

l

x

l

y

R

=

;

R

₆₂

=

m

_x_'

m

_y_'

;

R

₆₃

=

n

_x_'

n

_y_'

;

R

₆₄

=

m

_x_'

n

_y_'

+

n

_x_'

m

_y_'

;

' ' ' ' 65

n

x

l

y

l

x

n

y

R

=

+

;

T

₆₆

=

l

_x_'

m

_y_'

+

m

_x_'

l

_y_'

Independentemente do referencial que se utilize, são sempre constantes

as seguintes grandezas:

1º Invariante das Tensões

1 ' ' ' ' ' yy zz xx yy zz

I

xx

+

σ

+

σ

=

σ

+

σ

+

σ

=

σ

(1.19)

2º Invariante das Tensões

2 ' ' 2 ' ' 2 ' ' ' ' ' ' ' ' ' ' ' ' ' 'x y y yy zz zz xx xy yz zx x

σ

τ

σ

+

−

=

2 2 2 2

_I

zx yz xy xx zz zz yy yy xx

+

−

=

σ

τ

(1.20)

3º Invariante das Tensões

' ' ' ' ' ' 2 ' ' ' ' 2 ' ' ' ' 2 ' ' ' ' ' ' ' ' ' 'x yy zz xx yz yy zx zz xy

2

xy yz zx x

σ

τ

σ

τ

σ

τ

σ

−

+

=

2 =

σ

_xx

σ

_yy

σ

_z

−

σ

_xx

τ

_yz2

−

σ

_yy

τ

_zx2

−

σ

_zz

τ

_xy2

+

τ

_xy

τ

_yz

τ

_zx

=

I

₃

(1.21)

1.1.6. Tensões Principais

Para determinadas orientações do plano de corte, o vector tensão

resultante T

r

é paralelo ao versor normal n

r

, Fig.1.8, sendo nula a

respectiva componente de corte (τ = 0). Tal plano diz-se um plano

principal de tensão e a direcção n

r

perpendicular a esse plano principal é

uma direcção principal de tensão. A tensão normal que lhe corresponde,

(9)

Em cada ponto P, existem pelo menos três planos principais mutuamente

ortogonais, aos quais estão associadas, no máximo, três tensões

principais distintas. As tensões principais

σ

1

≥

σ

2

≥

σ

3

são as três raízes

da seguinte equação algébrica do 3º grau em

σ

:

0 =

−

σ

τ

σ

τ

σ

zz yz xz yz yy xy xz xy xx

(1.22)

ou seja, desenvolvendo a expressão para o determinante acima:

) 23 . 1 ( 0 ) 2 ( ) ( ) ( 2 2 2 2 2 2 2 3 = + − − − − − − − + + + + + − xz yz xy xy zz xz yy yz xx zz yy xx xz yz xy xx zz zz yy yy xx zz yy xx

τ

σ

τ

σ

τ

σ

τ

σ

Para cada uma dessas tensões principais, a respectiva direcção é dada

pelo sistema de equações lineares seguinte:











=

−

+

=

+

−

+

=

+

−

0 )

(

0 )

(

0 )

(

n

m

l

n

m

l

n

m

l

zz yz xz yz yy xy xz xy xx

σ

τ

σ

τ

σ

(1.24)

onde

σ

assume os valores

σ

1

,

σ

2

ou

σ

3

, respectivamente.

Relativamente ao triedro principal {

n1,n2 ,n3

r r r

}, as expressões das

componentes da tensão normal e de corte para a um plano qualquer,

definido pelos respectivos co-senos directores (l, m, n), são as seguintes:

3 2 2 2 1 2

_σ

σ

=

l

+

m

+

n

(1.25)

e

Fig. 1.8 – Plano principal de tensão

z z T n T r r σ = y T nr x T x y (I) P

(10)

2 2 2 1 3 2 2 2 3 2 2 2 2 2 1 2 3 2 2 2 1 2 2 3 2 2 2 2 2 1 2 2

)

(

)

(

)

(

)

(

l

n

m

l

n

m

l

n

m

l

σ

τ

−

+

−

+

−

=

+

−

+

=

(1.26)

1.1.7. Valores Máximos das Tensões Normais e de Corte

Os valores estacionários das tensões normais num ponto ocorrem para

planos de corte coincidentes com os planos principais de tensão nesse

ponto. Considerando a convenção habitual em tomar

σ

₁≥

σ

₂ ≥

σ

₃

, o

valor máximo da tensão normal é igual à maior das tensões principais

σ

1

e o valor mínimo é igual a

σ

3

_.

Quanto à tensão de corte, o valor máximo em cada ponto é dado pela

expressão seguinte:

2

3 1

σ

τ

_max

=

−

(1.27)

e ocorre para um plano de corte definido por um versor normal

nr_c

, cujos

co-senos directores no triedro principal são os seguintes:

)

2 /

2 ,

0 ,

2 /

2 (

±

=

c

n

r

(1.28)

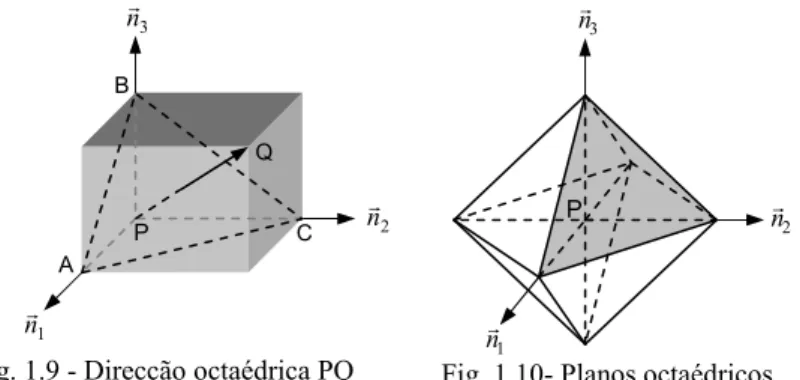
1.1.8. Tensões Octaédricas

As direcções e planos cujos co-senos directores, no referencial principal

no ponto P, satisfazem a condição:

3 1 2 2 2

=

_m

=

_n

=

l

(1.29)

são designadas direcções e planos octaédricos no ponto considerado,

respectivamente. Tais direcções estão orientadas segundo as diagonais de

um cubo de aresta unitária centrado no ponto considerado, Fig.1.9.

(11)

A área triangular ABC na Fig. 1.9 representa o plano octaédrico

correspondente ao primeiro quadrante, perpendicular à diagonal PQ.

Considerando todos os planos octaédricos à volta do ponto, obtém-se um

octaedro regular, conforme ilustrado na Fig.1.10.

A tensão normal em qualquer um dos planos octaédricos obtém-se

através da expressão habitual definida pela equação (1.25):

m zz yy xx oct

l

m

n

σ

=

+

=

+

=

+

=

)

(

)

(

3 1 3 2 1 3 1 3 2 2 2 1 2

(1.30)

A tensão de corte octaédrica τoct

é a tensão num plano octaédrico e

obtém-se a partir da equação (1.26), fazendo l

2

=m

2

=n

2

=1/3, isto é:

[

]

[

2 2 2 2 2 2

]

9 1 2 1 3 2 3 2 2 2 1 9 1 2 2 2 1 3 2 2 2 3 2 2 2 2 2 1 2

6

6 )

(

)

(

)

(

(1.31)

)

(

)

(

)

(

)

(

)

(

)

(

zx yz xy xx zz zz yy yy xx oct

l

m

n

l

τ

σ

τ

+

−

+

−

+

−

=

−

+

−

+

−

=

−

+

−

+

−

=

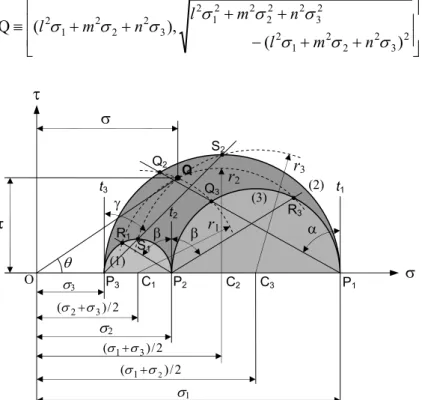
1.1.9. Construção de Mohr

(i)-Num diagrama rectangular plano, em que se toma a tensão normal (

σ

)

como abcissa e a tensão de corte (τ) como ordenada, Fig. 1.11,

marque-se sobre o eixo das abcissas os pontos P

1

, P

2

e P

3

de tal modo que:

3 3 2 2 1 1 , OP , OP OP =

σ

=

σ

=

σ

Fig. 1.10- Planos octaédricos P 1 nr 2 nr 3 nr

Fig. 1.9 - Direcção octaédrica PQ

1 nr 3 nr 2 nr Q P A B C

(12)

(ii)-Tomando os segmentos P

2

P

3

, P

1

P

3

e P

1

P

2 como diâmetros, desenhar

os três círculos de Mohr (1), (2) e (3) com centros nos pontos médios C

1

,

C

2

e C

3

, respectivamente.

(iii)-A partir da vertical t

1

em P

1

marcar o ângulo

α

=arcos(l) que define a

recta P

1

Q

3

Q

2

, que intersecta os círculos de Mohr (2) e (3) nos pontos Q

2

e Q

3

, os quais estão sobre uma mesma circunferência com centro em C

1

.

(iv)-Com centro nesse ponto C

1

, desenhar o arco de circunferência

Q

2

QQ

3

;

(v)-Seguindo um procedimento análogo a (iii), a partir da vertical t

3

em

P

3

, marcar o ângulo

γ

=arcos(n) e desenhar a recta P3

S

1

S

2 que intersecta

os círculos de Mohr (1) e (2) nos pontos S

1

e S

2

, respectivamente.

(vi)- Com centro no ponto C

3

, desenhar o arco de circunferência S

1

QS

2;

(vii)-A intersecção dos dois arcos de circunferência (iv) e (vi) define o

ponto Q, cujas coordenadas no plano (

σ

,

τ

) são:













+

−

+

≡

2 3 2 2 2 1 2 2 3 2 2 2 2 2 1 2 3 2 2 2 1 2

)

(

),

(

Q

σ

n

m

l

n

m

l

n

m

l

Fig. 1.11- Diagrama de Mohr para as tensões

τ

θ 2 / ) (σ +₂ σ₃ 2 / ) (σ₁+σ₃ 2 / ) (σ +1 σ2

σ

τ

t2 _α β β γ

r2

r3 (2) (3) (1) R₁ S1 Q3 Q2 Q R3 P1 C2 C3 σ3 σ2 σ1 P 3 O C1 P2 t₃ t₁

r1

S2

(13)

O ponto Q representativo da tensão para o plano considerado tem

coordenadas tais que a sua abcissa é igual à componente normal da

tensão e a ordenada é igual à respectiva componente tangencial.

O raio vector OQ materializa o vector tensão resultante

T

(

P

,

n

r

)

r

e ângulo

θ=arctg(τ/σ), que o raio vector OQ faz com o eixo das abcissas,

representa a inclinação da tensão resultante

T

(

P

,

n

r

)

r

em relação à

semi-normal positiva n

r

do plano sobre o qual actua.

A terceira circunferência a tracejado na Fig. 1.11, com centro no ponto

C

2

, pode também obter-se por um processo idêntico e permite confirmar

o rigor da construção anterior para a determinação do ponto Q:

(a)-Marcar o ângulo ß=arcos(m), para um e outro lado da vertical t

2

em

P

2

, e determinar os pontos de intersecção R

1

e R

3

com os círculos de

Mohr (1) e (3), respectivamente;

(b)-Com centro no ponto C

2

, desenhar o arco de circunferência R

1

QR

3

.

Se o diagrama anteriormente construído estiver correcto, a circunferência

agora desenhada intersecta as outras duas no mesmo ponto Q.

1.1.10. Estado Plano de Tensão

Um estado plano de tensão corresponde ao caso em que as forças de

volume e as forças de superfície definem um plano único - o plano (x,y),

por exemplo - que contém as tensões em cada ponto. É o caso de uma

placa de espessura reduzida solicitada por um sistema de forças paralelas

ao plano da própria placa, Fig.1.12(a).

(14)

Um estado plano de tensão fica caracterizado pelas três componentes

σ

xx,

σ

yy,

τ

xy, sendo nulas as restantes componentes, isto é,

σ

zz=τxz=τyz

= 0.

Qualquer plano de corte perpendicular ao plano da placa ficará

identificado pelo ângulo θ que a respectiva normal faz com a direcção do

eixo Ox. Considerando o equilíbrio do elemento triangular ABC, Fig.

1.12(b), obtém-se:

)

2 (

)

2 (

2

2 θ

τ

θ

σ

=

xx

+

yy

+

xx

−

yy

cos

+

_xy

sen

(1.32)

)

2 (

)

2 (

2 θ

τ

θ

σ

τ

=

−

xx

−

yy

sen

+

_xy

cos

(1.33)

A tensão de corte

τ

anula-se para um ângulo θ

p

tal que:

( )

yy xx xy

tg

σ

τ

θ

−

=

2

_p

(1.34)

Atendendo

a

que

tg(2θp

)

=

tg(2θp+π), existem duas direcções

mutuamente perpendiculares que

satisfazem a condição (1.34). Estas

Fig. 1.12 - Solicitação correspondente a um estado plano de tensão

(a) (b) nr yy σ yy σ xy τ z x x y y yy σ xx σ xy τ yx τ σ σ τ τ θ A B C 1 P r 2 P r 3 P r 4 P r 5 P r 6 P r 7 Pr 8 P r 9 Pr 10 P r θ xx σ σxx xy τ O x y θp 1 nr 2 nr

(15)

são as duas direcções principais de

tensão

n1 ne 2 r r

no plano (x,y),

Fig.1.13.

Ao utilizar a equação (1.34) é habitual recorrer-se à seguinte regra

prática para identificar os ângulos

θ

1

e

θ

2

:

(i) - Se

τ

_xy

>

0 , o ângulo

θ

1

está no intervalo

0<

θ

1<

π

/2

(ii) - Se

τ

_xy

<

0 , o ângulo

θ

1

está no intervalo

−

π

/2<

θ

1<0

As tensões principais correspondentes são:

2 2 2 2 2 1

)

2 (

2 )

2 (

2

xy yy xx yy xx xy yy xx yy xx

τ

σ

τ

σ

+

−

+

=

+

−

+

=

(1.35)

As tensões

σ

1

e

σ

2 dadas pelas expressões (1.35) correspondem ao valor

máximo e ao valor mínimo, respectivamente, da componente normal da

tensão no ponto considerado.

1.1.11. Tensões Principais Secundárias

Na situação mais geral duma solicitação tridimensional, as equações

(1.32)-(1.35) continuam válidas para as tensões no plano (x, y), embora

possam ser diferentes de zero as componentes

σ

zz, τxz e τyz

. Neste caso as

tensões dadas pelas equações (1.35) dizem-se as tensões principais

secundárias no plano (x, y) e representam-se pelos símbolos

σ

’

1

e

σ

’

2

,

respectivamente:

2 2 2 2 ' 1

)

2 (

2

2 )

2 (

2

xy yy xx yy xx xy yy xx yy xx

τ

σ

τ

σ

+

−

+

=

+

−

+

=

(1.36)

(16)

As direcções definidas pela equação (1.34) são as direcções principais

secundárias

n

r

₁'

n

e

r

₂'

da tensão em P, no plano (x, y).

1.1.12. Círculo de Mohr para as Tensões num Plano

Adoptando para referência as duas direcções principais de tensão

n1 ne 2

r r

,

no caso dum estado plano de tensão, ou

n

r

₁'

n

e

r

₂'

, no caso mais geral, de

acordo com as equações (1.32) e (1.33), a tensão normal

σ

e a tensão de

corte τ para um plano oblíquo qualquer definido pelo ângulo θ,

relativamente a

nr₁

, Fig. 1.14, são dadas pelas seguintes expressões:

)

2 (

2

2 1 2 1

σ

_θ

σ

=

+

−

cos

(1.37)

)

2 (

2

2 1

σ

_θ

σ

τ

=

−

sen

(1.38)

Aquelas duas componentes da tensão em P são as coordenadas do ponto

D sobre o círculo de Mohr desenhado num diagrama (

σ

, τ), conforme

ilustrado na Fig.1.15(a). O centro do círculo de Mohr é o ponto C sobre

o eixo das abcissas, à distância (

σ

1+

σ

2

)/2 da origem do diagrama, sendo

Fig. 1.14 - Plano oblíquo Fig. 1.15 - Círculo de Mohr no plano xy nr 1 nr 2 nr _σ(θ+π/2) σ(θ) θ O A B C τ τ σ τ max τ yx τ xy τ yy σ xx σ 2 σ 1 σ 2 / ) (σ +₁ σ₂ θ 2 θ E’ D D’ P1 P2 C xy τ xy τ yy σ xx σ xx σ yy σ θ 1 σ 1 σ 2 σ 2 σ a d c b (a) (b) O E

(17)

o respectivo raio igual à semi-diferença das duas tensões principais

σ

1

e

σ

2

no plano xy, isto é, igual a (

σ

1-

σ

2

)/2.

Na construção do círculo de Mohr, o eixo τ é orientado positivamente no

sentido ascendente e o eixo

σ

no sentido da esquerda para a direita. As

tensões normais positivas indicam tracção e as tensões de corte são

consideradas positivas quando definem um binário que tende a fazer

rodar o elemento sobre que actuam no sentido do movimento dos

ponteiros do relógio. É o caso das tensões de corte que actuam nas faces

bc e ad do elemento abcd representado na Fig.1.15(b). À medida que o

ângulo θ varia, desde o valor θ = 0 até θ = π/2, o ponto D sobre a

Fig.1.15(a), desloca-se de P

1

para P

2

, de tal forma que a parte superior do

círculo de Mohr representa as tensões para todos os valores de θ

compreendidos entre aqueles dois limites. A metade inferior do círculo

de Mohr representa as tensões para valores do ângulo θ compreendidos

entre θ =

−

π /2 e θ =0.

Prolongando o raio CD até ao ponto D’, Fig.1.15(a), isto é, se se

considerar o ângulo π+2θ em vez de 2θ, obtêm-se as tensões que actuam

no plano BC perpendicular a AB, conforme representado na Fig.1.14.

A construção representada na Fig.1.15(a) pode também ser utilizada para

determinar as direcções principais de tensão no ponto considerado. Com

efeito, se forem conhecidas as componentes

σ

xx,

σ

yy e τxy

da tensão

relativamente a um sistema de eixos arbitrário Oxy, ficam perfeitamente

identificados os pontos D e D’, que definem um diâmetro do círculo de

Mohr. Traçando depois a respectiva circunferência com centro no ponto

C, obtêm-se os pontos P

1

e P

2

sobre o eixo das abcissas, cujas distâncias

à origem definem as amplitudes das duas tensões principais. O ângulo

2θ, que define a orientação dos eixos principais de tensão, é dado pela

inclinação do diâmetro DD’ em relação ao eixo das abcissas.

1.2. PROBLEMAS RESOLVIDOS

(18)

Num determinado ponto P de um corpo material, a tensão resultante

T

r

para um plano de corte perpendicular ao eixo dos zz é

T

=

(

1 ,

0 ,

0 )

r

. Determine as componentes cartesianas σzz, τzx e τzy.

RESOLUÇÃO:

Geometricamente, tem-se uma situação conforme a representada na figura:

Aplicando, agora, a definição de cada uma das componentes cartesianas da tensão no ponto P, obtém-se:

0 ) 0 , 1 , 0 ( ) 0 , 0 , 1 ( 1 ) 0 , 0 , 1 ( ) 0 , 0 , 1 ( 0 ) 1 , 0 , 0 ( ) 0 , 0 , 1 ( = = = = = = = = = j T i T k T n zy n zx n zz r r r r r r τ τ σ PROBLEMA 1.2.2.

Para o caso considerado no problema anterior, determine a componente normal

σ e a componentede corte (τ) da tensão no ponto mesmo ponto P e para o plano de corte indicado. RESOLUÇÃO: z x y O ) 1 , 0 , 0 ( = nr ) 0 , 0 , 1 ( = n T r P

(19)

A componente normal (σσσσ ) é a projecção da tensão resultante (T_n r

) sobre a direcção (nr) da normal ao plano de corte, isto é:

0 ) 1 , 0 , 0 ( ) 0 , 0 , 1 ( = = =T_nnr r σ

A tensão de corte (ττττ ) é a projecção da tensão resultante (T_n r

) sobre o plano de corte. Neste caso particular, em que σ = 0, tem-se:

τ = |Tn| = 1

Ou, aplicando a expressão geral:

τ2

= T 2 - σ2 = 1 – 0 = 1

PROBLEMA 1.2.3.

No ponto P≡(1, 1, 1) de um corpo material, para um plano de corte (α) definido pela equação x+y-z-1=0, a tensão resultante correspondente é . Determine, no ponto P e para o plano de corte considerado:

a)-As componentes normal e tangencial da tensão. b)-A direcção da tensão de corte no plano α.

RESOLUÇÃO:

a) Componentes normal e tangencial da tensão em P

O versor (nr) da normal ao plano (α) é:

) ( ) , , ( 2 2 2 C B A C B A n + + = r

Onde A, B e C são os coeficientes de x, y e z, respectivamente, na equação do plano de corte (α). Isto é, para o caso em questão:

(

3/3, 3/3 , 3/3

)

3 ) 1 , 1 , 1 ( − = − = nr donde a tensão normal:

3 2 ) 3 / 3 3 / 3 2 3 ( ) 3 / 3 , 3 / 3 , 3 / 3 ( ) 1 , 2 , 3 ( = + + = − − = =T_nnr r σ e a tensão de corte: τ2 = T 2 − σ2 = (9 + 4 + 1) – 12 = 2

(20)

ou seja: τ= 2

b) Direcção da tensão de corte no plano αααα

Partindo da relação vectorial entre o vector tensão resultante e as suas componentes normal e de corte:

T r r r = τ + σ Pode escrever-se:      = + = + = + y c y c x c T n τ n σ T m τ m σ T l τ l σ Donde: 2 2 2 3 / 3 3 2 1 0 2 3 / 3 3 2 2 2 2 2 3 / 3 3 2 3 = × + − = − = = × − = − = = × − = − = τ n σ T n τ m σ T m τ l σ T l z c y c x c PROBLEMA 1.2.4.

O campo das tensões num corpo material é definido pelas seguintes componentes cartesianas:

σxx=0 ; σyy=2y−2; σzz=1−z;

τxy=τyx=2y−5x; τyz=τzy=2y+4z−1; τxz=τzx=2−2z

Desenhe um paralelepípedo rectangular elementar centrado na origem das coordenadas (O) e, sobre cada uma das faces, represente as componentes das tensões que sobre ela actuam.

RESOLUÇÃO:

Na origem das coordenadas O≡(0, 0, 0) tem-se:

σxx= 0 ; σyy= −2; σzz= 1; τxy=τyx= 0; τyz=τzy= −1; τxz= τzx= 2

(21)

PROBLEMA 1.2.5

O estado de tensão num ponto de um corpo material é definido pelas seguintes componentes: MPa MPa MPa MPa MPa MPa zx yz xy zz yy xx 60 75 50 100 160 80 = − = = = = = τ τ τ σ σ σ

a) - Determine a componente normal e a componente de corte para um plano cuja normal está inclinada de α = 68° e β= 35° em relação aos eixos x e y, respectivamente.

b) - Determine os cossenos directores da tensão de corte no plano considerado.

RESOLUÇÃO:

a)-Cálculo das componentes normal (σσσ σ) e de corte (ττττ ) da tensão

As componentes do versor (

n

r

) da normal ao plano de corte são:

(

)

0.43) , 82 . 0 , 37 . 0 ( 82 . 0 37 . 0 1 , 82 . 0 , 37 . 0 ) cos , º 35 cos , º 68 (cos ) cos , cos , (cos 2 2 =       ₋ ₊ = = = γ γ β α nr Isto é,

y

2 − = yy σ 2 + = xz τ 1 − = yz τ 1 − = zy τ

x

2 + = xz τ 2 + = zx τ 1 + = zz σ 2 − = yy σ 1 − = yz τ 1 − = zy τ º 45 2=− θ x

z

(22)

l = 0.3746 ; m = 0.8192 ; n = 0.4344 O vector tensão resultante (T_n

r

) obtém, então, a partir da equação geral:

=           z y x T T T           zz yz xz zy yy xy zx yx xx σ τ τ τ σ τ τ τ σ x           n m l

Donde, substituindo os valores para as componentes cartesianas da tensão e para os co-senos directores l, m e n, obtém-se, sucessivamente:

=           z y x T T T           − − 100 75 60 75 160 50 60 50 80 x 4344 , 0 8192 . 0 3746 . 0           =           z y x T T T =           × + × − × × − × + × × + × + × 43 . 0 100 82 . 0 75 37 . 0 60 43 . 0 75 82 . 0 160 37 . 0 50 43 . 0 60 82 . 0 50 37 . 0 80           5 . 4 2 . 117 0 . 97

Agora, as componentes normal (σσσσ ) e de corte (ττττ ) calculam-se da forma

habitual: = =T_nnr r σ           5 . 4 2 . 117 0 . 97 | 43 , 0 82 . 0 37 . 0           = 134.3 (MPa) τ2 = T 2 – σ2 =

T

_x2

+

T

_y2

+

T

_z2

−

σ

2 = 97.02 + 117.22 + 4.52 – 134.22 = 5131.5

5 .

5131

=

τ

= 71.6 (MPa)

b)-Direcção da Tensão de Corte

Partindo da relação vectorial

T r r r = +τ σ Pode escrever-se:

(23)

     = + = + = + z c y c x c T n n T m m T l l τ σ τ σ τ σ Donde: 65 . 0 7 . 71 37 . 0 2 . 134 0 . 97 − × ₌ = − = τ σl T l x c 10 . 0 7 . 71 82 . 0 2 . 134 2 . 117 = × − = − = τ σm T m_c y 75 . 0 7 . 71 43 . 0 2 . 134 5 . 4 − = × − = − = τ σn T n z c PROBLEMA 1.2.6.

Num ponto P de um corpo material considere um plano de corte π cuja normal tem cossenos directores l = 0.651, m = 0.520 e n = 0.553. A tensão resultante nesse ponto, para o plano considerado, é de 140 MPa e actua segundo uma direcção inclinada de 35° e 80° em relação aos eixos coordenados x e z, respectivamente.

a) -Determine a tensão normal e a tensão de corte no ponto P, para o plano considerado.

b) -Determine os cossenos directores da tensão de corte nesse plano.

c) - Se for τxy=20 MPa, τyz=-15 MPa e τzx=12 MPa, determine as componentes σxx, σyy e σzz.

RESOLUÇÃO:

a)-Cálculo da tensão normal e da tensão de corte

Sejam α, β e γ os ângulos de inclinação do vector tensão resultante relativamente aos eixos cartesianos x, y e z, respectivamente. Conhecidos os ângulos α=35º e γ=80º, o 3º ângulo β obtém-se a partir da equação seguinte:

cos2(α) + cos2(β) + cos2(γ) = 1 Donde: 55 . 0 ) ( cos ) ( cos 1 ) ( cosβ = − 2α − 2 γ =

(24)

Tx = T x cos(α) = 140 x cos(35º) = 114.68 (MPa)

Ty = T x cos(β) = 140 x 0.55 = 76.53 (MPa)

Tz = T x cos(γ) = 140 x cos(80º) = 24.31 (MPa)

Agora, as componentes normal (σ ) e de corte (τ ) calculam-se da forma habitual: = =T_nnr r σ           31 . 24 53 . 76 68 . 114 | 553 , 0 520 . 0 651 . 0           = 127.90 (MPa) τ2 = T 2 – σ2 =

T

_x2

+

T

_y2

+

T

_z2

−

σ

2 = 19600- 16358 = 3242 3242 = τ = 56.94 (MPa)

b)-Direcção da Tensão de Corte

Tal como no problema anterior, partindo da relação vectorial T r r r = +τ σ Pode escrever-se:      = + = + = + z c y c x c T n n T m m T l l τ σ τ σ τ σ

Donde, os cossenos directores da direcção segundo a qual actua a tensão de corte: 55 . 0 94 . 56 651 . 0 90 . 127 68 . 114 − × ₌ = − = τ σl T l_c x 18 . 0 94 . 56 52 . 0 90 . 127 53 . 76 − × ₌ = − = τ σm T m_c y 82 . 0 94 . 56 553 . 0 90 . 127 31 . 24 − × ₌₋ = − = τ σn T n_c z

c)- Cálculo das componentes σσσσxx, σσσσyy e σσσσzz

(25)

=           z y x T T T           zz yz xz zy yy xy zx yx xx σ τ τ τ σ τ τ τ σ x           n m l

obtém-se, por substituição dos valores conhecidos para as três componentes de corte da tensão, para os cossenos directores l, m e n, e para as componentes Tx,

Ty e Tz: =           31 . 24 53 . 76 68 . 114           − − zz yy xx σ σ σ 15 12 15 20 12 20 x 553 , 0 520 . 0 651 . 0          

Donde, desenvolvendo a multiplicação matricial:

σ σσ

σxx x 0.651 + 20 x 0.520 + 12 x 0.553 = 114.68

20 x 0.651 + σσσσyyx 0.520 -15 x 0.553 = 76.53

12 x 0.651 - 15 x 0.520 + σσσσzzx 0.553 = 24.31

Finalmente, resolvendo em ordem às componentes normais σxx, σyy e σzz: σxx = 150 (MPa)

σyy = 138 (MPa) σzz = 44 (MPa)

PROBLEMA 1.2.7.

Num determinado referencial global Oxyz, as componentes cartesianas da tensão num ponto P são as seguintes:

MPa MPa MPa MPa MPa MPa zx yz xy zz yy xx 3 1 2 1 2 1 − = = = − = = = τ τ τ σ σ σ

Determine as componentes da tensão num referencial Ox’y’z’, onde as orientações dos eixos x’, y’, z’ são definidas pelos seguintes ângulos:

a)- (x, x’) = π/4 ; (y, y’) = π/4; (z, z’) = 0. b)- (x, x’) = π/2 ; (y, y’) = π/2; (z, z’) = 0. c)- (x, x’) = 0 ; (y, y’) = π/2; (z, z’) = π/2. d)- (x, x’) = π/2 ; (y, y’) = 0; (z, z’) = π/2.

(26)

RESOLUÇÃO:

a)- (x, x’) = ππππ/4 ; (y, y’) = ππππ/4 ; (z, z’) = 0

Os eixos z e z’ são coincidentes, pelo que temos a situação representada geometricamente na figura seguinte:

Os co-senos directores dos eixos particulares x’, y’ e z’ no referencial global Oxyz são, respectivamente:

      = = = = = = 0 ) 2 / cos( 2 / 2 ) 4 / cos( 2 / 2 ) 4 / cos( ' ' ' π π π x x x n m l ,       = = = + = − = − = 0 ) 2 / cos( 2 / 2 ) 4 / cos( 2 / 2 ) 4 / cos( ' ' ' π π π y y y n m l e      = = = = = = 1 ) 0 cos( 0 ) 2 / cos( 0 ) 2 / cos( ' ' ' z z z n m l π π

Donde a matriz de transformação de coordenadas:

[ ]

          − =           = 1 0 0 0 2 / 2 2 / 2 0 2 / 2 2 / 2 ' ' ' ' ' ' ' ' ' z z z y y y x x x n m l n m l n m l l

As componentes cartesianas da tensão no referencial particular Ox’y’z’ calculam-se, agora, a partir das expressões habituais: