Simulações microcanônicas de proteínas

Fauldade de Filosoa, Ciênias e Letras de Ribeirão

Preto, Departamento de Físia e Matemátia

SIMULAÇÕES MICROCANÔNICAS DE

PROTEÍNAS

Rafael Bertolini Frigori

Teseapresentadaà Fauldade

deFilosoa, Ciêniase Letras

deRibeirão Pretoda USP,

omopartedasexigênias para

aobtenção dotítulo deDoutor

emCiênias: Físia Apliada à

Mediina eBiologia.

Orientador:

Prof. Dr. NelsonA. Alves

Wenn Sie mih nah meiner innersten Uberzeugung fragen ob

man unser (das 19.) Jahrhundert einmal das eiserne Jahrhundert

oder das Jahrhundert des Dampfes oder der Elektrizität nennen

wird, soantworte a ih ohne Bedenken, das Jahrhundert der

meha-nishen Naturauassung, das Jahrhundert Darwins wird es heiÿen

[L. Boltzmann, Populäre Shriften, 1886℄ 1

1

Sevoêperguntarsobreminhamaisprofundaonviçãosenossoséulo(XIX)seráhamado

deoséulo doferroouoséulodovaporouodaeletriidade, respondereisemhesitação: ele

Atodososolegas,amigosefamiliaresquede algummodoolaboraramparaosuesso

dessa minha nova empreitada. E empartiular:

A Deus pelagênesedeste pequeno Universo quetanto nos fasina investigar;

Ao Prof. Nelson, não só pelos bons exemplos, paiênia e dediação à orientação deste

doutorado mas tambémpelaamizadee ompreensãonos momentosmais difíeis;

Aoamigo LeandroG. Rizzipelo ompanherismo evalorosapareriaientía;

Aos funionáriose professores doDFM/FFCLRP/USP por ultivarem um ambiente

ao-lhedor epropíio àpesquisa ientía;

Aos velhos amigos Cesar A.V. Moura, Fábio V. Boas, Felipe L. Sanavini, Guilherme

C.P. Innoentini e TiagoM. Franoy; porvezes distantes, mas sempre presentes;

Aos olegas e amigos do departamento: André S.C. Peres, Aquino L. Espindola, Ariadne

de A. Costa, Brenno T. Cabella, César A.S. Terçariol, Denise de Arruda, Diogo Porfírio,

Ebenézer S.Cavalanti,FabianoL.Ribeiro,Fernanda M. Oliveira, Guidolins(LeilaB.M-.

& Luis C.B.M-.), Jayana S.M. Fonsea, Juliana M.S. Berbert, Lindomar S.Santos, Luis

A.Cabral,MareloA.Pereira,MatheusR.Mendonça,MatheusS.deMoura,Natália

Des-tefano, Olavo H. Menin, Raimundo N.A. Costa, Rodrigo S. Gonzalez, Tiago J. Arruda e

Wilnie T.R. Oliveirapelos bons momentosompartilhados;

À Ana Boneurpeloarinho eapoiodurantea onlusão desta tese;

Aopessoalda UTFPR-Toledo pela aolhidanaminha nova asa;

Aopovobrasileiro,que por meio daCAPES, naniou a exeução destetrabalho;

À Carla B.F.Junqueira e aoOlavoG. Junqueirapelaamizadee inentivo;

... I reognize that manyphysiists are smarter than I am most of them

theoretialphysiists. A lot of smart people have gone into theoretialphysis,

therefore the eldis extremelyompetitive. I onsole myself with the thought

that although they may be smarter and maybe deeper thinkers than I am, I

have broader interests than they have ...

[Linus Pauling,TheMeaning ofLife, 1990℄

À memóriade Maro Alberto Perez

†

Resumo

Transições de fase termodinâmias são usualmente estudadas por meio do ensemble

annio e estão assoiadas a sistemas marosópios. Entretanto, tem-se tornado ada

vez mais frequente e importante o estudo de sistemas físios pequenos, ujos alanes

araterístiosdasinteraçõesequivalemaos tamanhosdos sistemas. Nestesasos pode

ha-verinequivalêniaentre grandezasfísiasobtidasnos ensembles annio emiroannio.

Enontramos inúmeros exemplos destes sistemas em diversas áreas da Físia. Na área de

matériaondensadatemos,porexemplo,omodeloBlume-Capelominteraçõesde alane

innito. Neste modelo as soluções exatas annia e miroannia são inequivalentes.

Este modelo é investigado nesta tese por meio de um ensemble interpolante, onheido

omo gaussiano estendido, omo uma apliação teória preliminar. Adiionalmente,

em-pregamos o arabouço meânio-estatístio no estudo de ertas biomoléulas om ampla

importâniabiológia: proteínas. Atualmenteoestudodo omportamentotermodinâmio

destas moléulas tem ado restrito quase que exlusivamente a abordagem via ensemble

annio. Neste trabalho analisamosos resultados daetapa miroannia de simulações

multiannias prourando obter aspetos físios de biomoléulas omo os domínios Sr

SH3 (pdb: 1NLO) e as Príons humanas (pdb: 1HJM). Caraterizamos om esta

aborda-gem as transições de fase de enovelamento e de agregação destes sistemas. Os resultados

obtidos são interpretados à luz da termoestatístia miroannia, ofereendo um ponto

Abstrat

Thermodynami phase transitions are usualy studied by the anonial ensemble and

they are assoiated to marosopi systems. However, it is beoming more frequent and

important the study of small physial systems: whose harateristi interation-lengths

are equivalent to system sizes. In these ases there an happen inequivalenes among

quantitiesomputedimtheanonial andmiroanonialensembles. Thereare inumerous

examplesofthatsystemsinvariousareasofphysis. Intheeldofondensedmatterthere

isfor instane the Blume-Capelmodelwith innite-rangeinterations. Theanonial and

miroanonialexat solutionsofthis modelare inequivalents. Thatmodelisinvestigated

on this thesis through an interpolating ensemble, known as the extended gaussian, as a

preliminartheoretialappliation. Additionally,wehaveemployedthestatisti-mehanial

frameworktostudysome biomoleulesoflargebiologialinterest: proteins. Nowadaysthe

study of the thermodynami behavior of that moleules has been restrited almost only

tothe anonial approah. However, inthis workwehaveanalysed by the miroanonial

step of multianonialsimulationsthe physialaspets of biomoleules asthe domainSr

SH3 (pdb: 1NLO) and the human Prions (pdb: 1HJM). Thus, we haraterize with this

approah the phase transitions of folding and aggregation of that systems. The results

obtained are interpretatedunder the light of the miroanonialthermostatistis, oering

2.1 Esquerda: situaçãoque exemplia uma entropia nava, i.e., fase únia.

Di-reita: ilustração de um intruso onvexo na entropia, omo o que oorre nas

transiçõesannias de primeiraordem; aquios dois pontos-de-sela

orrespon-dem a duas fases distintas. Adaptado da referênia[2℄. . . 20

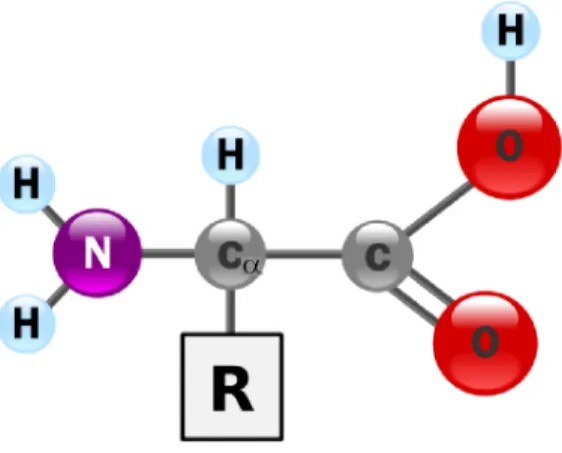
4.1 Estrutura geralde um aminoáido,omoarbono alfa

C

α

destaado aoentro, o grupo amina

(NH

2

)

à esquerda, o arboxila

(CO

2

H)

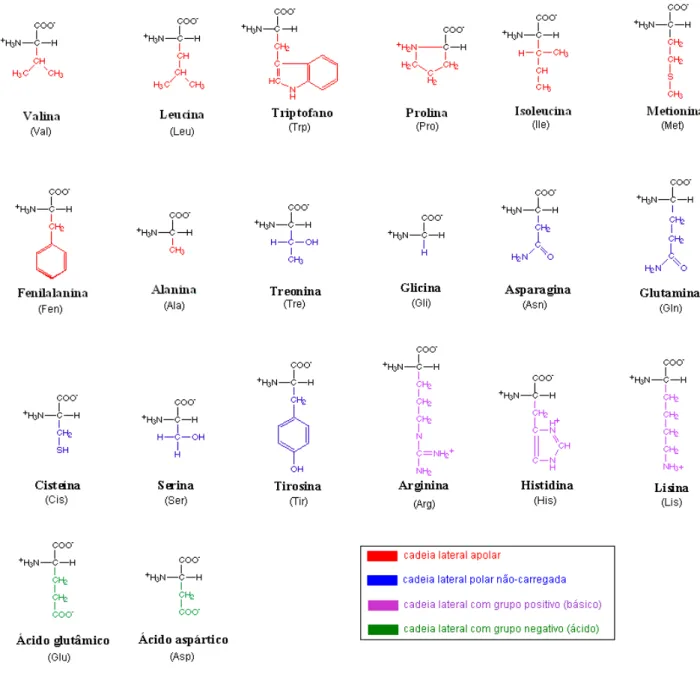
à direita e a adeia lateral R abaixo. . . 36

4.2 Estrutura químia, nomenlatura, abreviação om ódigo de 3 letras e

lassi-ação quanto ahidrofobiidade dos 20aminoáidos primários. . . 37

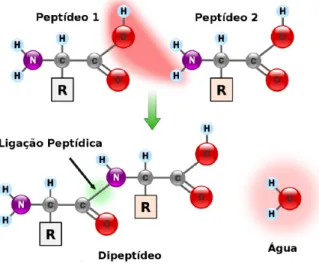
4.3 Formação de um dímero (dipeptídeo) pelaondensação de aminoáidos. . . 38

4.4 Hierarquia de estruturas em proteínas. (a) Primária: om abreviações de uma

letra. (b)Seundária: (1)héliealfae(2)tabeta. () Teriária: assoiaçãode

motivos enovelados, (d) Quaternária: união de adeiaspeptídiasmonomérias. 39

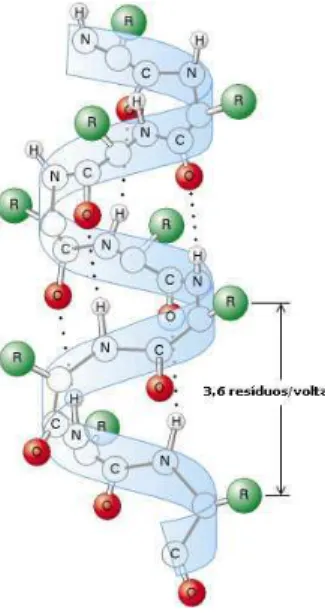
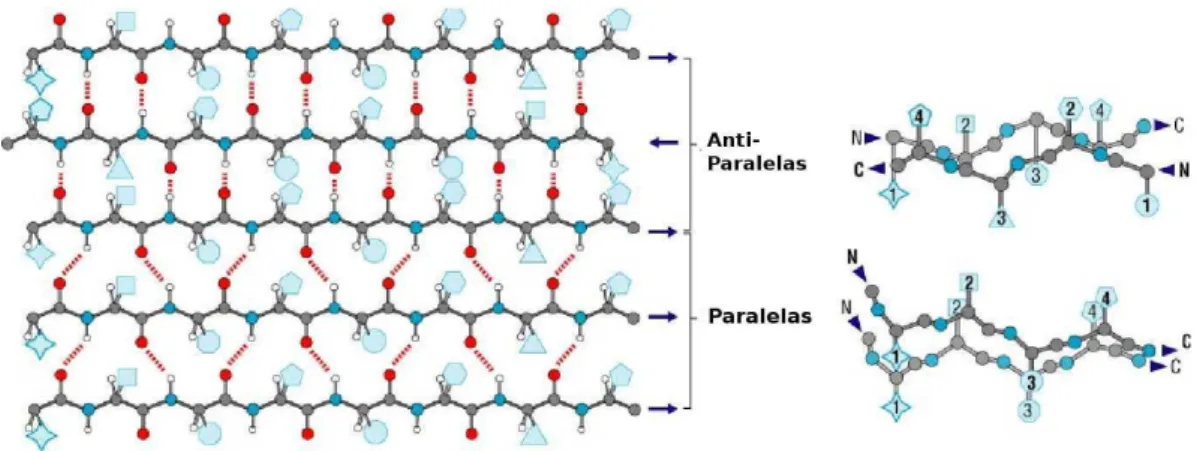
4.5 Estrutura seundária: arranjoespaialtípiodeumahéliealfa,noteasadeias

laterais externas aoeixode simetriaea frequênia espaialde 3,6resíduos por

volta[23℄. . . 40

4.6 Estrutura seundária: onformações usuais de folhas beta, notam-se as tas

orientadas antiparalelas (superior) e paralelas(inferior), além das terminações

amina (N) earboxila (C). . . 41

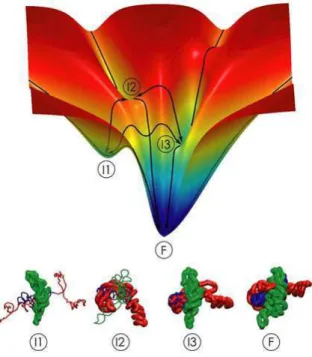
4.7 O perl da energia livre (energy landsape) em formato de funil é um modelo

aeito para a desrição do enovelamento protéio. Os estados 11, 12, 13 são

intermediáriosenquantoF éaestrutura protéianativa,oude menorenergia

livre. As rotas prefereniais são representadas por setas. . . 43

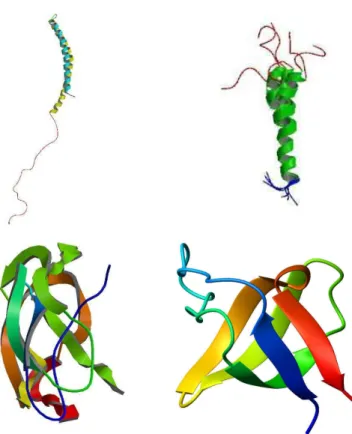
4.8 Proteínas envolvidas na formação de agregados. Superior à esquerda:

Alfa-Sinuleina, assoiada ao mal de Parkinson. Superior à direita: Amilina, uja

formação deagregados oorre naDiabetes doTipoII. Inferioràesquerda:

pro-teína preursora do Amiloide-Beta

(Aβ)

,

agregados de

Aβ

oasionam o mal de Alzheimer. Inferior à direita: domínio Sr SH3, assoiado à transdução de

sinais, não patológia. Adaptado doprotein data bank (PDB). . . 45

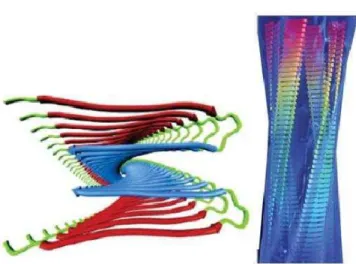
4.9 Modelo de brilas amilóides, rias em formações de tas beta omo as hélies

4.10 Representação esquemátia dos possíveis estados onformaionais assumidos

poradeias peptídiase suas interonversões usuais. Adaptado da Ref. [33℄. . 47

4.11 ConguraçõesassumidasporPríons: aformausual

P rP

C

representadapor(A);

eapatogênia

P rP

sc

assoiadaaosmalesdeCreutzfeld-JakobeàEnefalopaia

Espongiforme ilustradaem (B). . . 48

4.12 EsquemadeumúniopeptídionomodeloABom

N

resíduos[46,65,87℄. Note arepresentaçãodaadeiaprinipaldosarbonosalfa(esferas),assimomoseus

2N

graus de liberdadede rotação (i.e. ângulos

θ

e

ϕ

).. . . 51

5.1 Comportamentono limite miroannio da solução domodelo BC via

forma-lismo EGE, om aoplamento

∆/J

= 0.462407,

orrespondendo à região de

transição de fase de primeira ordem annia e de segunda ordem

miroan-nia.

(a)

Temperaturamiroannia omofunçãodaenergiamédia

ε

. A linha traejada horizontal orresponde à temperatura rítia annia.

(b)

A

entro-pia desloada

˜

s(ε) =

s

micro

(ε)

−

(A

+

Bε),

om

A

= 0.401447

e

B

= 1.398397.

A subtração é efetuada para uma melhor visualização da não onavidade da

entropia em relação a função linear ligando

s(ε

a

)

a

s(ε

b

),

om

ε

a

= 0.328959

e

ε

b

= 0.330646

.

(c)

Calor espeío

c(ε)

. Ele apresenta dois polos loalizados pelos zeros do determinante

d

S

micro

(ε, m)

, onde

m

denota os valores da mag-netização que maximizam a entropia em dado

ε

. Esses pólos também podem ser observados apartirdoomportamentode

T

(ε)

em

(a)

.

(d)

Suseptibilidade magnétia

χ(ε)

. Elaapresentadoispolos, novamenteposiionadosnos zerosdo determinante

d

S

micro

(ε, m)

e torna-se negativa entre eles.

(e)

Comportamento do determinante

d

S

micro

(ε, m)

omo função de

ε

. As linhas traejadas vertiais mostram oszeros de

d

S

micro

(ε, m)

. . . 58 5.2 Entropia

s(ε, m)

para alguns valores de

ε

e

m

om

∆/J

= 0.462407

. Para

val-ores inferioresdaenergia

ε

, algunsintervalosdamagnetização são inaessíveis; o que demonstra quebra de ergodiidade neste modelo. Domínios magnétios

desonexos pareem ser típios de sistemas om interações de longo alane,

exibindo transições de fase (annia) de primeiraordem. . . 59

5.3 Curva alória

T

(ε)

×

ε

omputadas para diversos valores de

γ

a partir da solução geral do modelo Blume-Capel no EGE. O aoplamento empregado é

∆/J

= 0.462407

e no limite de

γ

→ ∞

reobtemos a urva miroannia

(a)

da Figura(5.1). . . 60

5.4 Valores mínimos que o parâmetro

γ,

e

alulado segundo a Eq. (5.19), deve assumir para que a termodinâmia deduzida via EGE para o modelo

5.5 (A) Temperaturas EGEobtidas nolimiteannio (

γ

= 0

)para algunsvalores de

∆/J.

Para

∆/J

= 0.462098

temossimultaneamentetransiçõesde fase

an-niaemiroanniadesegundaordem. Quando

∆/J

= 0.4622

e

∆/J

= 0.4623

as transições de fase annias são de primeira ordem, mas as

miroanni-as são ainda de segunda ordem. (B) Temperaturas EGE no limite annio

(

γ

= 0

),todososvaloresde

∆/J

estãonaregiãodetransiçãodeprimeiraordem annia e miroannia. (C) Temperaturas omputadas via EGE no limite

miroannio

(γ

∼

= 10

12

₎

_,

para

∆/J

= 0.4622

e

∆/J

= 0.4623

emqueoorrem

transiçõesdefasemiroanniasdesegundaordemeanniasdeprimeira

or-dem. (D) Temperaturas EGE no limitemiroannio

(γ

∼

= 10

12

₎

naregião de

aoplamentos

∆/J

= 0.4625

e

∆/J

= 0.4627,

ujas transição de fase são de

primeira ordem. . . 61

5.6 Na gura a esquerda temos linhas de transição de fase annias. A linha

rítia (inza pontilhada) termina no ponto trirítio annio

•

, a partir do

qual a transição torna-se de primeira ordem (linha heia). A gura menor é

uma ampliação que mostra a linha (heia) da transição de fase de primeira

ordem annia e aslinhas (ponto-traejadas) datransição de fase de primeira

ordemmiroannia. Naguraadireitatemosumarepresentaçãoesquemátia

do diagrama de fase do modelo Blume-Capel, ampliado ao redor dos Pontos

TrirítioCannio(CTP)eMiroannio(MTP).Alinhadetransiçãodefase

de segunda ordem(omum a ambosensembles) é pontilhada; alinha annia

de primeiraordeméheia easlinhasmiroanniastraejadassão desegunda

ordem emnegrito ede primeiraordem eminza. Adaptado dareferênia [10℄. 63

5.7 Valormínimodoparâmetrointerpolante

γ

paraqueasoluçãoEGEseja termo-dinamiamenteequivalenteàmiroanniaentre ospontostrirítiosannio

(∆/J

∼

= 0.4621)

e miroannio

(∆/J

∼

= 0.4624)

. . . 63

6.1 Esquema da atualização de Monte Carlo empregada em nossos estudos. Uma

proteínaposiionadaadistânia

R

~

daorigemomângulopolar

”a”

e

equato-rial

”b”

é atualizada para outra posição

R

~

→

R

~

′

_:

_{|

_R

′

_|

_{, a}

′

_{, b}

′

_}

_.

Por outro lado,

simultaneamenteaposiçãorelativadeadaumdos

(N

+ 1)

-ésimosaminoáidos,

em relaçãoaos

N

-ésimos aminoáidos, éalteradade modoque

~r

→

~r

′

₌

_~r

₊

_dr.

~

65 6.2 Estrutura nativa de bakbone de sequênias Fibonai. (Painel esquerdo)

on-guração om energia mínima,

E

1

×

F ibo.

=

−

5,

75

e

△

E

= 0,

1

para a sequênia artiial om 13 resíduos

F ibonacci

13

:

"ABBABBABABBAB". (Painel direito) on-guração de energia mínima para a estrutura agregada

E

2

×

F ibo.

=

−

29,

15

e

△

E

= 0,

1

de duas sequênias idêntias de

F ibonacci

6.3 Termodinâmia miroannia para uma únia sequênia Fibonai. (Painel

superior): urva alória

β

×

E,

barras de erro orrespondem aodesvio padrão de 50 onjuntos de parâmetros MUCA. As linhas ontínuas são obtidas pela

apliação reursiva de

k

ltragens do tipo média móvel de 10 pontos. (Painel entral): álulodaderivadadaurvainterpolante(vermelha)de

β

×

E,

ouseja

dβ

dE

×

E.

(Painelinferior): alorespeíomiroanniodosistema,nota-seque oorre um pio positivo araterizando uma transição de fase ontínua, ou de

segunda ordem,assoiada aoenovelamento.. . . 68

6.4 Termodinâmia miroannia para duas sequênias Fibonai interagentes.

(Painel superior): urva alória

β

(E)

×

E,

barras de erro orrespondem ao desvio padrão de 50 onjuntos de parâmetros MUCA. As linhas ontínuas são

obtidas pelaapliaçãoreursiva de

k

ltragens dotipomédiamóvelde 10 pon-tos. (Painel entral): álulo daderivada da urva interpolante (vermelha) de

β

(E)

×

E,

ouseja

dβ(E)

dE

×

E.

(Painelinferior): alorespeíomiroanniodo sistema, nota-se uma transição de fase de primeira ordem(de agregação), om

alores espeíos negativos. Os pequenos pios positivos assinalamformação

de domínios ou enovelamento. . . 69

6.5 Estrutura nativa de bakbone para domínios Sr SH3 om 56 resíduos e

ó-digo 1NLOnoProteinDataBank(PDB). Foimapeadanomodelo ABsegundo

sua naturezahidrofóbia/polar,resultandonasequênia

SH

3

56/AB

:

"BAABABBB-BAABBBBAAABBABAABAABBBBABAAABBAABBABBABABABBABBA". (Painel esquerdo):

onguração nativa, ou om energia mínima

E

1

×

SH3

=

−

41,

48

e

△

E

= 1,

0

para a uma únia sequênia Sr SH3. (Painel direito): onguração de

ener-gia mínima om

E

2

×

SH3

=

−

29,

15

e

△

E

= 1,

0

da forma agregada de dois peptídeos

SH

3

56/AB

interagentes. . . 72 6.6 Termodinâmia miroannia para um únio domínio Sr SH3. (Painel

su-perior): urva alória

β

×

E,

barras de erro orrespondem ao desvio padrão de 54 onjuntos de parâmetros MUCA. As linhas ontínuas são obtidas por

apliações reursivas de ltros de média móvel de 5 pontos. (Painel entral):

áluloda derivada de

β

×

E,

ouseja

dβ

dE

×

E.

(Painel inferior): alor espeío miroannio do sistema, nota-se que oorrem dois pios positivos indiando

transições de fase ontínuas (ou de segunda ordem). Biologiamente

assinala-riam o enovelamento (pio menor) e formação de estruturas seundárias (pio

maior).. . . 73

6.7 Termodinâmiamiroannia para dois domíniosSr SH3 interagentes.

(Pai-nelSuperior): urvaalória

β

×

E,

barrasvemdodesviopadrãode26onjuntos de parâmetros MUCA. Linhas azul/vermelho emergem de 1 a 7 ltragens

re-ursivas de médias móveis (de 5 pontos). (Painel Central): é a derivada da

urvainterpolante(vermelha)de

β

×

E,

ouseja

dβ

dE

×

E.

(Painel Inferior): alor espeío miroannio do sistema (ltro 7x5). Há uma transição de

pri-meira ordem (annia, de agregação), om alores espeíos miroannios

6.8 Estrutura de bakbone de príons humanasom 104 resíduos eódigo 1HJM no

Protein Data Bank (PDB). Foi mapeada nomodelo AB segundo sua natureza

hidrofóbia/polar,resultandonasequênia

P rion

104/AB

:

AAABAAAABAAABAABAAA BBBBABBABBABABBBBABBABABBBABBBBAABBAABAB

ABBBBABBBBBABBABBBBABAABAAAB-BAAABBBBABAB.(Painelesquerdo): onguraçãonativa,ouomenergiamínima,

E

=

−

8,

35

e

△

E

= 1,

0

paraasequênia

P rion

104/AB

. (Paineldireito):

ongu-raçãodeenergiamínima,ditanaformaagregadaoudimerizada,om

E

= 12,

59

e

△

E

= 1,

0

para dois peptídeos

P rion

104/AB

interagentes. . . 76 6.9 Termodinâmia miroannia para uma proteína 1HJM, a Príon humana.

(Painelsuperior): urva alória

β

×

E,

barras de erro orrespondemaodesvio padrão de 22 onjuntos de parâmetros MUCA. As linhas ontínuas são

obti-das porltragensreursivasdotipomédiamóvel de 5pontos. (Painel entral):

álulodaderivadadeurvasinterpolantesde

β

×

E,

ouseja

dβ

dE

×

E.

(Painel in-ferior): alor espeíomiroannio dosistema,nota-seque oorre um únio

pio positivo (estável), araterizando uma transição de fase ontínua (ou de

segunda ordem),assoiada ao enovelamento sem formação de intermediários:

um fenmenojá observado in vitro [73, 74℄. . . 77

6.10 Termodinâmiamiroannia paraduas proteínas1HJM, ouPríonshumanas.

(Painel superior): urva alória

β

×

E,

barras de erro são o desvio padrão de 10 onjuntos de parâmetros MUCA. Linhas emverde/vermelho emergem de 1

a 10 ltragens reursivas de médias móveis (de 5 pontos). (Painel entral): é

a derivadada urva interpolante(vermelha) de

β

×

E,

ouseja

dβ

dE

×

E.

(Painel inferior): alor espeío miroannio do sistema (ltro 10x5). Há apenas

uma transição de primeiraordem(annia,de agregação), omalores

espeí-os negativos. Nenhuma outratransição de fase(e.g. ontínua) foiobservada,

apesar de grandes esforços omputaionais. . . 78

7.1 O gráo aima mostra um onjunto de dados (100 pontos, em preto) e suas

médiasmóveisomtamanhosdiferentes[5℄. Temosrespetivamenteasseguintes

urvas: 2-pontos (vermelha), 4-pontos (amarela), 6-pontos (verde) e 8-pontos

(azul). Noteo efeitode ltragemdoruído nestas urvas. . . 85

7.2 Esquematermodinâmioutilizadonadeduçãodoensembleannio. Osistema

1 está aoplado energetiamente a um reservatório térmio, dito sistema 2,

Lista de Figuras 7

Conteúdo 12

1 Introdução 14

2 Termoestatístia miroannia 17

2.1 Oensemble miroannio . . . 18

2.2 Transições de fase miroannias . . . 19

2.3 Inequivalêniade ensembles e transições de fase . . . 21

2.4 Ensembles generalizados . . . 23

2.4.1 Oensemblemultiannio . . . 23

2.4.2 Oensemblegaussiano estendido . . . 25

3 Simulações 28 3.1 Métodos de Monte Carlo markovianos. . . 29

3.1.1 Oalgoritmode Metropolis . . . 30

3.1.2 Erros numérios . . . 31

3.2 Simulações miroannias . . . 32

3.2.1 Relaçõesde reorrênia . . . 33

3.2.2 Implementação alternativa . . . 34

4 Proteínas e o modelo AB 35 4.1 Proteínasin vitro e in vivo: um panorama . . . 38

4.1.1 Estrutura . . . 39

4.1.2 Funionalidades . . . 42

4.1.3 Enovelamentoprotéio . . . 42

4.2 Agregaçãoprotéiae proteinopatias . . . 44

4.3 Proteínasin silio . . . 49

4.3.1 Omodelo AB oarse-grained . . . 50

5 Resultados exatos: modelo de spin 52 5.1 Omodelo Blume-Capelnoensemble gaussiano estendido . . . 52

5.2 Soluçãoexata no ensemble gaussiano estendido. . . 53

5.3 Limitestermodinâmios: inequivalênia de ensembles . . . 55

5.4 Pontos trirítios . . . 62

6 Resultados numérios: proteínas 64 6.1 Implementação omputaional . . . 65

6.2 Enovelamentoe agregação . . . 66

6.2.1 Sequênias Fibonai . . . 66

6.2.2 Domínios Sr SH3. . . 70

6.2.3 Príons humanas . . . 72

7 Considerações nais 79

Apêndies 82

Introdução

... What an organism feeds upon is negative entropy. Or to put it less

pa-radoxially, the essential thing in metabolism is that the organism sueeds in

freeing itself from all the entropy it annothelp produing while alive ...

[E. Shrödinger, Whatis life?,1944℄

A meânia estatístia miroannia, omo formulada por Ludwig Boltzmann [1, 2℄,

onstitui um dos prinipaispilares damoderna abordagem físiapara sistemas de muitos

orpos. Originalmenteonebida om o intuito de alançar uma expliação mirosópia,

ouinétia,datermodinâmiadosgases,elapermitiuinferiraexistêniadeátomosdéadas

antes dasua observação experimental. Aqui, a entropia aparee omo oneito have que

oneta, via teoria dos ensembles, as onguraões mirosópias de um sistema om seu

omportamentomarosópio. Porsuavez,olimitetermodinâmioqueasseguraa

existên-iadestaonexãomiro

↔

maro,assenta-se sobreooneitofundamentalde extensividade

daenergia eda entropia.

Contrárioaosenso omum,olimite termodinâmio[3℄nãoéimpresindívelàdenição

da meânia estatístia miroannia ou à desrição de transições de fase [4, 5℄. Este

preoneito onsolidou-se om o uso de ensembles derivados do miroannio, omo o

annio e o grandeannio, ujas formulaçõesneessitam taitamente do limite

termo-dinâmio[5℄. Comoaabordagemmiroanniabaseia-senaexataontagemde

miroesta-dos,elaéidealaoestudodesistemaspequenos [2,6,7℄. Otermopequenos designaaqui

sistemas que interagem via forças de longo alane e, ou tem pouos graus de liberdade.

Dentreosquaisenontram-seossistemasgravitaionais[8℄,despin[9,10,11,12,13,15,16℄,

plasmas [17, 18, 19, 20, 21,22℄e biomoleularesomo asproteínas.

Proteínas [23, 24℄são heteropolímerosde elevada massa moleular, ompostas porum

grande número de aminoáidos de até 20 diferentes tipos [24, 25℄. Dentre as prinipais

funções protéias, que apresentam alta espeiidade em sistemas biológios vivos, estão

a estrutural e a metabólia. Essas araterístias devem-se em grande parte à estrutura

geométria tridimensional,tambémhamadade teriária,que araterizaada proteína e

aminoáidosemsua estrutura nativadenomina-seenovelamento(no inglês, folding). Suas

origens físias estão nas omplexas interações atmias, que produzem pers de energias

livresrugososeafunilados[26℄. Atualmente,poteniaisinteratmios[27,28,29,30℄de

ori-gem elétromagnétia[31℄já onseguemreproduzirertasestruturas nativasviasimulações

ab initio.

Sabemos aindaque emdeterminadosmomentosda síntese protéia[23℄ podemoorrer

defeitosonformaionais(misfoldings)quedegradamfunionalmenteasproteínasafetadas.

Esses asos isoladospodem repetir-se originandoagregados protéios [32, 33, 34℄rios em

hélies beta-ruzadas. Este tipo de estrutura é onheida por sua tenaidade ehabilidade

em induzirdoenças degenerativas. Dentre essas doenças estão as neurodegenerativas, um

termo quedesigna perda progressivade estruturas e funçõesneuronais, levando à morte.

A neurodegeneração pode aonteer em diferentes níveis neurais, variando dos níveis

moleular ao sistêmio. Vários males, omo o de Parkinson [35℄, Alzheimer [36℄ e

Hun-tington [37℄, são proteinopatias relaionadas a agregação protéia em nível subelular.

Normalmente essas doenças não são transmissíveis por um vetor etiológio. Contudo, os

males da vaa loua e de Creutzfeldt-Jakob (DCJ) [38, 39℄ são ausados por proteínas

infeiosas e auto-repliantes hamadas Príons [40, 41℄, que violamo dogma entral da

biologia [42℄. Do ponto de vista físio, existem muitas similaridades no desenvolvimento

de diversas proteinopatias [32, 34℄. Uma melhor ompreensão destes aspetos pode ser

alançada por meio de simulações omputaionais, aliadas à modelagem físio-estatístia

[26, 43,44, 45℄, asquais poderãoauxiliarnodesenvolvimento de novas terapias.

A presente tese proura investigar o omportamento de algumas proteínas de grande

interessebiológio,omoéoasodos domíniosSr SH3[48℄ edas Príonshumanas[40,41℄.

Os métodos que utilizamos, omo os ensembles generalizados [49, 50, 51, 52, 53, 54, 55,

56, 57, 58, 59, 60, 61, 62℄ e as simulações de Monte Carlo [63, 64℄, permitem alular

diretamente a entropia miroannia. Deste modo, é possível onstatar profundas

se-melhanças físias no omportamento de proteínas e ertos modelos de spin, lassiados

omopequenos. Esteéoaso domodelodespin de Blume-Capelde alaneinnito,que

estudamos nesta tese omo laboratórioteório, por ausa doseu peuliar omportamento

termodinâmio. A abordagem miroannia mostra-se valiosa nestassituações, pois

per-mite formalizar e desrever uniadamente transiçõesde fase mesmo em sistemas nitos,

omo noaso biológiodo enovelamentoe daagregação protéios [43, 44, 45,46,47℄.

Visandominimizarasexigêniasdepoderomputaionaladotamospoteniais

interat-mios simpliados,dotipogrão grosso(oarse-grained)[46, 65,66,67,68,69,70,71℄,ao

invésdos poderosos eomplexos CHARM eAMBER [27℄. Pelasua simpliidade,

esolhe-mos o hamado modelo AB [68, 69℄, uja literatura reporta apenas apliações no estudo

de sequênias artiiais,asFibonai [43, 44,46℄.

NomodeloABasprinipaisinteraçõesonsideradassãode aráterefetivo,edesrevem

o omportamento hidrofóbio-hidrofílio dos aminoáidos [72℄ envolvidos. As interações

são modeladas por meio de pseudo-átomos, o que reduz notavelmente o número de graus

de liberdadedosistema, onferindoao modelo grandeleveza omputaional. Por sua vez,

a interação interprotéia, responsável pela biologia da agregação e dos diversos tipos de

aminoái-dos. Nossosresultadosmostraram-sepromissores,revelandosimilaridadesomobservações

experimentais [34, 73,74℄e estudos teóriosprévios [48℄.

O texto é organizado omo segue. No Capítulo 2 introduzimos a termoestatístia

mi-roannia segundo a formulação Boltzmanniana [1,3℄ eapresentamos o formalismo

ela-borado por Gross [2℄e generalizadoporKastner [75, 76℄para desrever transiçõesde fase

miroannias. Noteque o limitetermodinâmionão é exigido por este formalismo. Por

m,abordamosalgunsensemblesgeneralizadosomoomultiannio[61℄eogaussiano

es-tendido(EGE) [51,56℄,osquaisforneemrobustasregularizaçõesmiroanniaseformas

alternativaspara estimar aentropia [62, 77℄.

No Capítulo 3 abordamos as simulações de Monte Carlo que em meânia estatístia

são importantes ferramentas numérias. Revisamos os métodos de Monte Carlo estátios

e dinâmios, omo o algoritmo de Metropolis [64℄, além de desrevermos omo estimar

erros estoástios via rigorosas estimativas da autoorrelação [78℄. Introduzimos em

se-guidaoalgoritmomultiannio(MUCA)[61,62℄quedeterminaobserváveisannios via

repesagem [63℄ emiroannios via ospróprios parâmetrosmultiannios.

Sendo esta uma tese interdisiplinar apresentamos no Capítulo 4 uma revisão sobre

proteínasnoqueserefereàsua onstituiçãoquímia[23℄,funionalidadeetaxonomia[24℄.

Revisitamos o oneito de proteinopatias enquanto doenças degenerativas resultantes do

mal enovelamento e agregação protéios subelulares. Além disso, a modelagem teória

dessessistemas biomoleulareséenfoadapelaapresentaçãodomodelo AB, onsideradoo

mais propíioaos nossos propósitos.

No Capítulo 5 utilizamos o ensemble gaussiano estendido para proeder a uma nova

resolução analítia do modelo Blume-Capel de alane innito [13, 79, 80, 81, 82℄. Este

modelo de spin 1 é semelhante ao de Ising, possuindo ontudo interações ompetitivas

de alane innito. A literatura moderna reporta a inequivalênia entre suas onheidas

soluçõesnos ensembles annioemiroannio[9℄. Todavia,umasoluçãoemum

ensem-ble interpolante era até agora desonheida. Nossa nova solução [83℄ além de reuperar

os resultados anteriores omo asos limite, também evidenia as metaestabilidades

an-nias. Efetuamos por m um estudo dos pontos trirítios do modelo BC para ilustrar

propriedades daabordagemEGE.

O apítulo 6 dedia-se às simulações miroannias de proteínas propriamenteditas.

Os exemplares que investigamos são adeias de Fibonai, o domínio Sr SH3 (ódigo

PDB: 1NLO) e a Príon humana (ódigo PDB: 1HJM). As adeias Fibonai, que foram

artiialmente desenhadas [46℄, são simuladas para efeito de omparação om proteínas

reais. Os peptídeos 1NLO e 1HJM foram mapeados em sequênias do tipo AB, om as

quais efetuamos extensas simulações para obter a sua termodinâmia miroannia pela

análisedosparâmetrosmultiannios. Nossosresultadosnumériosmostram-seoerentes

eindiamaexistêniade umomportamentobiológiouniversal. Alémdisso, onstatamos

semelhanças meânio-estatístias típias de sistemas pequenos entre as transições de

enovelamento,de agregação eas exibidaspelomodelo BC resolvido noEGE.

O Capítulo 7 onlui esta tese om disussões nais e o delineamento de perspetivas

futuras. Apontamos aqui novas questões surgidas neste estudo e vias para investigá-las.

Termoestatístia miroannia

... By the study of Boltzmann I have been unable to understand him. He

ould not undestand meon aount of my shortness, and his length was and is

an equal stumbling-blok to me. Hene I am very inlined to join the glorious

ompany of supplanters and to put the whole business in about six lines ...

[J.C. Maxwella P.G.Tait, agosto de 1873℄

A meânia estatístia permitiuuma ompreensão da fenomenologia desritapela

ter-modinâmia a partir de abordagens mirosópias. Iniialmente onebida para expliar

fenmenos simples, omo o omportamento de gases monoatmios, interagindo via

po-teniais de urto alane, essa área da físia desenvolveu-se rápido e atualmente é ruial

paraoentendimentodesistemasomplexos. Entretanto, paraassegurarsua ampla

empre-gabilidade é preiso garantir a existênia dolimite termodinâmio,de modoque todas as

formulaçõesmeânio-estatístias, dadas pela teoriade ensembles, sejam equivalentes [3℄.

Por outro lado, nos asos em que o limite termodinâmio não se aplia, omo oorre

om sistemas ditos pequenos [2, 6℄, ujo alanedas interações equivale aotamanho do

sistema, surge o fenmeno da inequivalênia de ensembles. Nesta situação as previsões

físias efetuadas dependem do formalismo estatístio adotado. Dado tal grau de

arbitra-riedade, que é antes formal do que realmente físio, resta entender qual das abordagens

meânio-estatístiasé arelevante.

NesteapítulorevisamosaabordagemmiroanniausualàlaBoltzmann [2,3,6℄,pois

dela se deduzem, via teoria das transformações de Laplae e Legendre, todas as demais 1

.

Este formalismo fornee ainda uma presrição simples e direta para a araterização das

transições de fase, sendo apliável mesmo a sistemas pequenos. Por m, introduzimos

noçõessobreensemblesgeneralizados,omoogaussianoestendidoeomultiannio. Estes

ensemblessãouniversalmenteequivalentesaomiroannioeimportantesparasimulações

numérias.

1

Nosasosem quehá inequivalênia deensemblesas transformaçõesde Laplae não sãoinversíveis,

poisoorremregiõesnãonavasnaentropia. Ainda assimosensemblesannioegrandeanniosão

2.1 O ensemble miroannio

A formulação miroanniasurgiu das investigações dofísioaustríao Ludwig

Boltz-mann [1℄ visando desrever o omportamentoinétio dos gases a partir de um ponto de

vistamirosópio. Ooneitotermodinâmiode entropiaéfundamentalnessaabordagem

eaelefoiassoiado,emnívelmirosópio,aidéiadedesorganizaçãoestatístiadesistemas

físios isolados. O equilíbrio termodinâmionesse ontexto é realizadopelamaximização

daentropia do sistema.

Dene-seentropiamiroannia

S

(E, N, V

)

, queparaum sistemameânioextensivo dependeráda energia

E

, donúmerode partíulas

N

edovolume

V

, omo

S

(E, N, V

) =

k

B

ln

W

(E, N, V

)

,

(2.1)

emque

k

B

éaonstantedeBoltzmanne

W

éafunçãodepartiçãomiroannia 2

. Ouseja,

W

representaonúmerodemiroestadosaessíveiseompatíveisomumdadomaroestado

termodinâmio,uja oupação é equiprovávelmiroanoniamenteemsistemas ergódios.

Por ausa da propriedade de equiprobabilidade dos estados a abordagem miroannia

não exibe barreirasde probabilidadenas vizinhanças de transiçõesde fase.

O formalismomiroannioinorpora naturalmenteuma presrição para o álulode

W

(E, N, V

)

atravésde umproessode partiionamentodoespaçodefase. Comoexemplo,

onsideremos um sistema de

N

orpos uja energia total é xada em

E.

Se sua dinâmia for regida pelahamiltoniana

H

N

,

pode-se obter

W

alulando-sea integral vinulada,

W

=

ǫ

0

Z

1

N

!

d

3

_pd

³

q

h

3

N

δ

(E

₋

H

N

(p, q))

,

(2.2)

em que asonstantes

ǫ

0

e

h

(de Plank)tem dimensõesapropriadas.

De fato, omo a abordagemmiroannia é meaniamentebemdenida, mesmo em

um nível mirosópio, os vínulos do sistema são impostos a ada um dos membros do

ensemble, ou seja, a ada ponto noespaço de fase. Por isso, a formulação miroannia

tem sentido físio mesmo para sistemas pequenos, e independentemente da existênia

do limite termodinâmio. Este aspeto ontrasta, por exemplo, om a abordagem grande

annia. Esta abordagem sededuz damiroannia via transformadadupla de Laplae

[2, 3℄em que os meanismos de troa de energiae partíulas neessitam de aoplamentos

om banhos térmiosinnitos(i.e. reservatórios).

Fia laro que uma das prinipais virtudes da abordagem miroannia é sua

habili-dadeemdesrever diretamenteede modoestatístio, oomportamentoglobalde sistemas

demuitos-orposempregandoapenasalgunspouosparâmetrosmeâniosdeontrole(e.g.

E, N, V

). Ainda, a entropia denida porBoltzmann é,emnívellássio,uma função

on-tínua, multiplamentedifereniávelomrelaçãoàenergiaenava 3

globalmente 4

nolimite

termodinâmio.

2

DoalemãoWahrsheinlihkeit: probabilidade.

3

Formalmente,umafunçãoreal

f

denidaemumintervaloéditanava,separaquaisquerdoispontos

x

1

e

x

2

emseudomínio

C

,eparaqualquer

t

em

[0

,

1]

,umpre-se

f

(

tx

1

+ (1

−

t

)

x

2)

≥

tf

(

x

1) + (1

−

t

)

f

(

x

2)

. Emadição,

f

(

x

)

énavaem

[

a, b

]

seesomente seafunção

−

f

(

x

)

éonvexaem

[

a, b

]

.

4

Porsua vez, a onexão do formalismomiroannio om a termodinâmiase dá pela

entropia, ujas razões entre taxas de variação fornee observáveis termodinâmios omo

a temperatura ou o alor espeío. Como ilustração, onsideremos um sistema

magné-tio desrito pela hamiltoniana

H

N

(m)

, em que o número de partíulas

N

, a energia por partíula

e

=

H

N

/N

e a magnetização por partíula

m

=

M/N

[2℄ são utilizados para obter:

ˆ Temperatura

(T

)

1

T

(e)

.

=

β

(e) =

∂

∂e

s

(e, m)

,

(2.3)

ˆ Calor espeío

(c

V

)

c

V

(e)

=

.

de

dT

=

−

s

mm

T

2

_d

_{(e, m)}

,

(2.4)

ˆ Suseptibilidade magnétia espeía

(χ

T

)

χ

T

=

.

∂m

∂B

T

=

₋

s

ee

d

(e, m)

.

(2.5)

Fizemos usonaEq. (2.5)daurvaturagaussiana. Esta urvatura orrespondeao

determi-nanteda matrizhessiana daentropia

d

[s

(e, m)]

, denida omo

d

S

(e, m) = det

s

ee

s

em

s

me

s

mm

.

(2.6)

2.2 Transições de fase miroannias

Transições de fase são usualmente estudadas em meânia estatístia pela abordagem

de Lee e Yang [4℄, em que os hamados zeros omplexos da função de partição grande

annia são analisados. Uma revisão detalhada dessa abordagem foge ao esopo desta

tese, mas é importantenotar que nesse esquema inexistem transições de fase em sistemas

nitos 5

. Entretanto, é ruial aos nossos propósitos entender se na ausênia do limite

termodinâmioinexistem de fatotransiçõesde fase, ouseeste efeitoé apenas um artefato

de um partiular formalismo.

Consideramosquequando háequivalêniade ensembles adesrição físiade transições

de fase é naturalmente independente do formalismo adotado. Mas nos asos em que há

inequivalêniadeensemblesaformulaçãoestatístiaédeterminantequantoàfenomenologia

observável. No aso miroannio, uja onexão termodinâmia se dá via entropia de

Boltzmann, é o omportamento desta grandeza que disriminaa natureza das transições

de fase [2,6, 7℄.

5

Issoporqueforadolimitetermodinâmiotem-se

N

nito,eportantoafunçãodepartição

Z

podeser

esritaomo uma soma nita eanalítiade

(

z

=

e

µ/T

₎

N

termos. Paraompletar oraioínio, devemos

lembrarqueograndepotenialé

∝

1

Figura 2.1: Esquerda: situação que exemplia uma entropia nava, i.e., fase únia.

Direita: ilustração de um intruso onvexo na entropia, omo o que oorre nas transições

annias de primeira ordem; aqui os dois pontos-de-sela orrespondem a duas fases

dis-tintas. Adaptado dareferênia [2℄.

De formageral,transiçõesde fasemiroanniassão denidaspelos: pontose regiões

de urvatura não negativa da hipersuperfíie entrópia

S

N

(P

1

,

· · ·

, P

i

)

,

desrita noespaço de fase em função das quantidades meânias onservadas e extensivas

{

P

1

,

· · ·

, P

i}

das quais

S

N

depende,omoaenergia,massa,magnetização, momentumangular,et [2,6,7℄. Portanto, para uma rigorosa utilização destes oneitos dene-se a urvatura, ou matriz

hessiana(

H

S

), daentropia

S

N

(P

1

,

· · ·

, P

i

)

omo

H

S(P

1

,P

2

,...,P

i

)

=







∂

P

1

∂

P

1

S . . . ∂

P

1

∂

P

i

S

.

.

. .

.

. .

.

.

∂

P

i

∂

P

1

S

· · ·

∂

P

i

∂

P

i

S







.

(2.7)

Paraaraterizardevidamenteasregiõesde transiçãodefaseutilizam-seténias

apa-zes de extrair invariantes geométrios e algébrios da hipersuperfíie

S

N

. Por exemplo, a geometriadiferenial[5℄fornee-nosaurvaturagaussiana

(d

S

)

,

i.e. odeterminantede

H

S

,

queéum importanteinvariante[2℄. Podemosaindaexpressá-laemtermosdos autovalores

ordenados

{

λ

1

,

· · ·

, λ

N

}

daurvatura entrópia omo

d

S

=

det

H

S(P

1

,

···

,P

i

)

=

λ

1

λ

2

· · ·

λ

N

.

(2.8)

Assim, todos os possíveis omportamentos fenomenológios onheidos nas abordagens

annia ougrande annia enquadram-se nos seguintes asos:

ˆ Umaúniafase estável: éobservada quando

d

S

>

0

e

λ

1

<

0

. Nessasituação

S

N

é nava emtodas asdireçõesnolimitetermodinâmio. Temos aquium mapeamento

bi-unívooentre as grandezas termodinâmiasomputadasvia quaisquer ensembles.

ˆ Transição de fasede primeira ordem: nesse asoobserva-seseparação defasese

tensão interfaial eé araterizadapor

d

S

<

0

e

λ

1

>

0

. Aqui

S

N

possui um intruso onvexo (urvaturapara ima, Figura2.1) nadireção doautovetor

v

λ

1

assoiado à

omponentede maiorurvatura

λ

1

.

Existemaquidoispontos-de-sela: naquelemaisà esquerdaosistemaétotalmentelíquidoenooutroégasoso. Todaaregiãoonvexa

da entropia é mapeada em um únio pontono ensemble grande annio; portanto,

se a urvatura de

S

N

for, por exemplo, igual a

λ

1

≥

0

haverá inequivalênia de ensembles

6

. Surgemvaloresnegativosdas funçõesresposta,omonoalorespeío,

omo sepode onstatar através das deniçõesnas Eqs. (2.4) e (2.5), Figura(2.1).

ˆ Transiçãode fasede segunda ordemou ontínua: trata-sedotipodetransição

de fase em que desaparee a tensão interfaial, ambas as fases vizinhas tornam-se

indistinguíveis. Nesteasoaslinhasrítiassãoaquelasonde

d

S

= 0

e

~v

λ=0

·

∇

~

d

S

= 0,

em que

~v

λ=0

é o autovetor de

H

S

assoiado aoautovalor

λ

= 0

de maior urvatura. Nessassituaçõespodemoorrerasonheidasatástrofesdatransformadainversade

Laplae 7

E

_→

T

.

ˆ Pontos multirítios: oorrem em regiões em que mais de duas fases tornam-se

indistinguíveis; estão assoiados a loais em que oorrem divisões das linhas de um

diagramade fases. Matematiamentesão desritos por

d

S

= 0

e

∇

~

d

S

= 0.

2.3 Inequivalênia de ensembles e transições de fase

A grandeza termodinâmia que arateriza transições de fase no formalismo annio

dameâniaestatístiaéaenergialivrede Helmholtz

(F

)

. Elaéobtidadaenergiainterna

U

e da entropia

S

pela transformação de Legendre 8

F

=

U

₋

T S,

videapêndie C. Para

6

Soboutroaspeto,valenotarqueafunçãodepartiçãograndeanniaédenidaviadupla

transfor-madadeLaplaedadensidadedeestadosmiroannia[i.e.,de

Ω (

e, n, V

) =

e

s

(

e,n,V

)

℄omo

Ξ (

µ, T, V

)

=

.

e

−

βF

(

µ,T,V

)

=

V

2

ǫ

0

∞

Z

0

de

∞

Z

0

dne

−

V

[

e

−

µn

−

T s

(

e,n,V

)]

/T

,

deondepode-semostrar[2℄queassintotiamente

F

(

µ, T, V

)

V

→

e

−

µn

−

T s

+

T

ln

√

dS

V

+

O

ln

V

V

.

Portanto, para

dS

>

0

aenergia livre espeía tende ao limite termodinâmio aseu valor típio

f

→

e

₋

µn

₋

T s.

Entretanto,se

dS

= 0

oorremdivergêniasem

F,

mesmoparasistemasnitos,epara

dS

<

0

inexisteuma deniçãodaenergialivre!

7

Porexemplo,nessasituaçãoatransformadadeLaplaequeonverteadensidadedeestados

Ω = Ω (

e

)

nafunçãodepartiçãoannia:

Z

(

β

) =

R

∞

0

e

−

βe

Ω (

e

)

de

nãoéinversívelparatodo

β

poisaurva

e

×

β

(

e

)

tem loops em formato de S. Logo, falha adesrição fenomenológia detransiçõesde faseem termos de

variáveisintensivas,omo

T

(

e

)

queneessitadeonstruçõesauxiliaresomoadeMaxwellsobreosloops

deVanderWalls.

8

que esta transformação e sua inversa façam sentido,

S

preisa ser loalmente nava, o que termodinamiamenteesta assoiado aoritério de estabilidade deste ensemble

9

. Uma

vez onheida

F

a análise das suas divergênias e de suas funções resposta, omo função de um parâmetro intensivo(porexemplo, atemperatura), permite lassiar

fenomenolo-giamente[5℄astransiçõesde fase. Assim, nestaabordagemastransiçõesde fasesãoditas

de

n

−

esima

´

ordem se a derivada

n

−

´

esima

de

F

for desontínua 10

, ao passo que suas

funçõesresposta são positivasdenidas 11

.

Poroutrolado,segundooformalismomiroannio,transiçõesdefasesãolassiadas

[2, 75℄ pelo omportamento da entropia

S

e de suas funções resposta om relação a um parâmetro extensivo omo a energia

U.

Por exemplo, a Eq. (2.3) implia que transições de fase de primeira ordem neste formalismo exibem desontinuidades na temperatura.

Como é amaximizaçãode

S

quegarantea estabilidade termodinâmianesta abordagem, e não a onavidade loal de

S

omo no aso annio, ambos ensembles podem exibir (em prinípio)fenomenologias bastante distintas. Este é o aso quando

S

for loalmente onvexa, oqueimpliaemfunçõesrespostamiroanniasnegativassegundoasEq. (2.4)

e Eq. (2.5)[14℄.

Normalmente a esolha de determinado ensemble é uma questão de onveniênia

té-nia,poisnolimitetermodinâmioosresultadosfísiosindependemdoformalismoadotado.

Existem ontudosituaçõesem queresultados, omoa ordemdatransição de fase,diferem

e originam inequivalênia de ensembles. Isto pode oorrer apenas quando há transições

de fase annias de primeira ordem em sistemas que interagem via poteniais de longo

alane 12

,omonos gravitaionais[8,13℄. Nestessistemasaentropiamiroanniaapesar

de ser ontínua exibe regiões onvexas. Ao leitor interessado apontamos [2, 13, 14℄, que

9

Situaçõesemque

S

nãoénavaimpliammetaestabilidadestermodinâmiasnoensembleannio,

omooorreemtransiçõesdefasedeprimeiraordem. Nestesasoséusual apareeremloops deVander

Waalsnosdiagramasdefasedosistema,oqueexigeonstruçõesalàMaxwellparareproduziraurvados

aloreslatentes[3℄.

10

Nasvizinhançasdeumatransiçãodefaseontínua,oudesegundaordem,háumatemperaturarítia

Tc

emqueasfunçõesrespostade

F

omo

c

e

χ

apresentamdivergêniasdaforma

c

∝ |

T

−

Tc

|

−

α

χ

_{∝ |}

T

₋

Tc

_|

−

γ

.

(2.9)

Ograudedivergêniaditadopeloshamadosexpoentesrítios,omo

α

e

γ,

permitelassiaremlasses

deuniversalidadeoomportamentofísiodestes sistemasdurante transiçõesdefase. Poroutrolado,em

transiçãodefasedeprimeiraordemtais expoentesrítiosnão seassoiamaooneitodeuniversalidade

[5,3℄.

11

Considerepor exemplooasodoalorespeíoaluladoomoformalismoannio,

cV

=

.

dU

dT

=

−

β

2

∂

h

E

i

∂β

=

β

2

∂

ln (

Z

)

∂β

=

β

2

_E

2

− h

E

_i

2

_≥

0

,

onde

β

= 1

/T

éoinversodatemperaturafísia

T

deequilíbriodosistemaaopladoaoreservatóriotérmio.

Aquiaenergiamédiaannia

h

E

i

β

étermodinamiamenteidentiadaomaenergiainternadosistema

U.

12

Éusualdenirem-sepoteniaisdelongoalane[13℄omoaquelesquedependamdadistânia

r

omo

r

−

α

justiam eexempliam a fundamentalidademiroannia.

Para efeitode ilustração onsideremos duas situações de transições de fase em que as

desrições ofereidaspor ambos osensembles podem apresentar inequivalênias:

ˆ Sempre que as transições de fase miroannias forem de primeira ordem, ou seja,

desontínuas nas urvas alórias (i.e.,

β

×

E

tendo saltos), elas serão de primeira ordem também no ensemble annio. Apesar de neste aso haver onordânia na

ordem da transição de fase segundo ambos os ensembles, a termodinâmia obtida a

partir das duas abordagens será inequivalente. Isto porque transições de fase

miro-annias de primeira ordemapresentam normalmentefunções resposta negativas.

ˆ Quandoastransiçõesde faseforemdeprimeiraordemnaabordagemannia,oque

se reete na presença de uma urva alória (miroannia)

β

×

E

ontínua mas dotadadeloopsdeVanderWalls,haverápossíveisinequivalênias. Nestasituaçãohá

loops na referida urva alória, que são anniamente alterados (i.e., aplainados)

a là Maxwell, e são nestas regiões que surgem alores espeíos miroannios

negativose divergentes, o quesinaliza transiçõesde segunda ordem neste ensemble.

Devemosaindamenionarquenosasosemqueatransiçãode faseérítia,oudesegunda

ordem annia, háequivalênia total de ensembles.

2.4 Ensembles generalizados

Apresentaremosnassubsessõesseguintesdois ensemblesgeneralizados,quesão

extrema-menteúteis para a estimativa tanto analítiaquanto numériada entropia miroannia

omo denida na Eq. (2.2) [2, 6,7℄.

Noprimeiroasotemosoensemblemultiannio,quesurgiusobinspiraçãopuramente

algoritmiaparadriblaradegradaçãode desempenhoquesimulaçõesnumériasenfrentam

ao redor de transições de fase [61, 62℄. Nele, uma estimativa do tipo pieewise para a

entropia miroanniaé implementada através de parâmetros ditos multiannios.

O segundo ensemblepor sua vez éonheido omogaussiano estendido (EGE) [50,51,

52, 54, 55, 56, 58℄ e omporta-se omo um ensemble interpolante entre o miroannio

e o annio [56℄. Esta situação interpolante desreve sistemas aoplados a banhos

tér-mios nitos. Reentemente, foi mostrado ainda que o EGE é equivalente aos ensembles

miroannio eMUCA [17, 19, 20, 21, 22,49, 57,59,60℄.

2.4.1 O ensemble multiannio

Um onsiderável avanço nadeterminação miroannia das densidades de estadodata

a 1991 om a introdução do hamado ensemble multiannio [61, 62℄. Reordemos que

naabordagemannia tradiional o sistema permanee em ontato om um reservatório

om temperatura xa

T

= 1/k

B

β,

e tem as energias

E

k

da onguração

k

desritas pelo peso de Boltzmann-Gibbs

Enquantoos estadosom energia

E

são distribuídos om probabilidade

P

B

(E) =

c

β

w

B

(E) =

c

β

Ω (E)

e

−

βE

,

(2.11)

onde a onstante de normalização

c

β

éintroduzidapara garantir que

P

E

P

B

(E) = 1.

Como adensidade de estados

Ω (E)

é uma função querese rapidamente, enquanto o fator de Boltzmann deai exponenialmente om

E

, temos que

P

B

(E)

tem geralmente a forma de uma gaussiana ouapresenta pios duplos [3℄. No aso de uma transição de fase

de primeira ordem, o ponto rítio

β

c

(L)

em um sistema de volume nito

L

d

é denido

de forma que a distribuição de energia

P

B

(E, L)

apresente dois pios de alturas iguais nas energias

E

1

max

e

E

2

max

,

P

B

(E

1

max

, L) =

P

B

(E

max

2

, L)

.

Entre estes dois valores oorre a energia

E

min

,orrespondendo aomínimode

P

B

(E, L)

[63℄.

Sabemos que asonguraçõesem

E

min

são exponenialmente suprimidassegundo

P

min

=

P

(E

min

) =

c

f

L

p

exp (

−

f

s

A)

,

(2.12)

onde

f

s

é a tensãointerfaiale

A

= 2L

d

−

1

éa área entre asduas fases para uma rede

L

d

_.

Temos ainda as onstantes

c

f

e

p

(p

=

d

−

1)

.

Entretanto, ainda que lidando om a meânia estatístia annia, o peso de

Boltz-mann não éneessariamenteuma presrição omputaionalmenteadequada para todos os

asos. Numeriamente, este peso não seleiona ongurações representativas da interfae

emtransições de primeira ordem[63℄.

Umasoluçãoéousodoensemblemultiannio[61, 62℄,quefoi iniialmenteprojetado

para alular a tensão interfaial em simulações no ensemble annio de Gibbs. Ele foi

desenvolvidoempiriamenteomanalidadedeproduzironguraçõesrepresentativasdas

fases do sistema e om a exigênia de eientemente ultrapassar as barreiras de energia

livre. Prourou-se então amostrar, em um intervalo apropriado daenergia, ongurações

geradas om oseguintepeso

w

muca

=

e

−

b(E

k

)E

k

+a(E

k

)

,

(2.13) ao invés do tradiional peso de Boltzmann-Gibbs. O objetivo era obter uma nova

distri-buição de probabilidades, om densidade de estados

n

(E)

multiannia

P

muca

(E) =

c

muca

n

(E)

w

muca

(E)

≈

constante,

(2.14)

que não fossefortementeonentrada, omo noaso usual da Eq. (2.11).

Essa novadistribuiçãofazomquenaregiãoaoredorde

P

min

nãooorramaisa supres-são de ongurações, logo, o sistema passaria a visitar igualmente todas as ongurações

disponíveis nesse intervalode energias. A novafunção

b(E)

é interpretada nesse esquema omo uma temperatura miroannia na energia

E

e

a

(E)

passa a ser uma espéie de fugaidade. A distribuição annia original

P

(E)

pode ser obtida [63℄ pormeio de uma repesagem,istoé

P

(E) =

P

muca

(E)

c

muca

w

muca

(E)

c

β

e

−

βE

.

(2.15)

Perebeu-se posteriormente que os pesos prourados

w

muca

(E

k

)

orrespondem a uma boa aproximação para os pesos miroannios

w

1/Ω(E)

(E

k

)

,

istoé

w

muca

(E

k

)

≈

w

1/Ω(E)

(E

k

) =

1

Ω (E

k

)

(2.16)

omo onsequênia direta daEq. (2.14). Ou seja,aqui a entropia miroannia é

direta-menteestimadaomo uma função pieewise dotipo

S

(E

k

) =

b

k

(E

k

)

E

k

−

a

k

(E

k

)

.

Contudo,háuma diuldadeiniialemapliaroalgoritmomultiannioparaestimar

a densidade de estados miroannia visto que os pesos na Eq. (2.16) são a priori

des-onheidos. Portanto,para estimar adequadamente o onjunto de pesos

{

a

k

, b

k

}

é preiso utilizar relações de reorrênia em simulações preliminares suessivas

13

, que anteedem a

simulação produtiva propriamente dita. Uma vez xados os

w

muca

(E

k

)

, a simulação é efetuada segundo métodos usuais [64℄.

Porm, oálulode grandezastermodinâmiasdesritas peloensembleanniopode

ser obtido do ensemble multiannio via repesagem dos dados provindos de sua série

temporal. Por exemplo, a energia média annia a uma temperatura

1/β

é alulada a partir das medidasmultiannias

E

i

,

¯

E

(β) =

P

n

i=1

E

i

w

muca

−

1

(E

i

)

e

−

βE

i

P

n

i=1

w

muca

−

1

(E

i

)

e

−

βE

i

.

(2.17)

2.4.2 O ensemble gaussiano estendido

O ensemble gaussiano surgiu nos anos 80 om a nalidade de aelerar os métodos de

Monte Carlo usuais [50, 51, 52, 54, 58℄. Posteriormente, este ensemble foi reinterpretado

omo um esquema regularizador para o ensemble miroannio [55℄. Ele interpola por

meio de um parâmetro

γ

, relaionado àapaidade aloríade um banho térmio nito, afísiados ensemblesannio e miroannio [13,83℄. Umageneralizaçãoulteriordeste

esquemaproduziuoensemblegaussianoestendido(EGE)[47,56,77℄. Reentementefoi

de-monstrado[57℄haverequivalêniasentreosensemblesmiroannio,gaussianoestendido,

multiannio ede Tsallisem ertos regimes termodinâmios.

Deduzimos aqui as propriedades do EGE [56, 83℄ utilizando métodos omumente

en-ontrados naliteraturapara obter oensemble annio [3℄ apartir domiroannio, por

exemplo, omo éilustradono Apêndie E.

Iniialmente, onsideremos um sistema

a

om energia

E

e entropia

S

, aoplado a um banho térmio

b

om energia

E

b

e entropia

S

b

que troa energia om

a.

Logo, a energia total dosistemaisoladoserá

E

t

=

E

+

E

b

esua entropiatotal é

S

t

.

Neste asoo equilíbrio

13

Geralmenteutilizam-serelaçõesdereorrêniaentreosparâmetros

bn

e

an

an

(

E

−

ǫ

) =

an

(

E

) + [

bn

(

E

−

ǫ

)

−

bn

(

ǫ

)]

E,

bn

+1

(

E

) =

bn

(

E

) + [ln

H

n

muca

(

E

+

ǫ

)

−

ln

H

n

muca

(

E

)]

/ǫ

térmio é alançado quando

S

t

é máxima e a energia

E

do sistema

a

utuar ao redor de um valor médio

U

de equilíbrio. Então, a energia mais provável é tal que uma expansão daentropiadobanhotérmio

S

b

,

aoredordoequilíbrio

E

t

−

U,

resultaemsegunda ordem

S

b

(E

b

) =

S

b

(E

t

−

U) +

dS

b

dE

b

E

t

−

U

(U

₋

E) +

1

2

d

²

S

b

dE

b

²

E

t

−

U

(U

₋

E)

²

+

....

(2.18)

Seonsiderarmosqueestasderivadasdependemdaspropriedadesfísiasdobanhotérmio,

é onveniente denirmos

dS

b

dE

b

E

t

−

U

=

α,

(2.19)

e

1

2

d

²

S

b

dE

b

²

E

t

−

U

=

₋

γ.

(2.20)

Noaso de haver umbanho térmioinnito,representado porum reservatório,estaríamos

trabalhando no ensemble annio tradiional, ou seja

α

=

β

= 1/

(k

B

T

)

e

γ

= 0.

No limiteoposto, emqueháumbanhotérmioinnitesimal,temosoasomiroannioom

γ

_{→ ∞}

e

E

t

≡

U.

O métododos multipliadores de Lagrange[3, 56℄ nos dá opeso gaussiano estendido

w

EGE

=

e

−

αE

−

γ(E

−

U)

²

,

(2.21)

e adensidade de probabilidadepara o EGE

P

γ,α

(E) =

ρ

(E)

e

−

αE

−

γ(E

−

U)

²

Z

γ

(U, α)

,

(2.22)

om a qualdene-se a função de partiçãodeste ensemble,

Z

γ

(U, α) =

Z

ρ

(E)

e

−

αE

−

γ(E

−

U)

²

dE.

(2.23)

Daqui, dene-se o potenialtermodinâmiogeneralizado,

Φ

γ

(U, α) =

−

ln

Z

γ

(U, α)

.

(2.24)

Enquanto o parâmetro

U

pode ser determinado autoonsistentemente pela seguinte relação

U

=

.

∂Φ

γ

∂α

=

Z

EP

γ,α

(E)

dE.

(2.25)

Se apliarmos atransformaçãode Legendre-Fenhel(LF)[3℄ aopotenial

Φ

γ

(U, α)

enon-traremosa entropia generalizada

S

γ

doEGE,

S

γ

(U

) =

α

∂Φ

γ

∂α

γ

+

γ

∂Φ

γ

∂γ

α

Vale notar também que, omo oorre no aso da termodinâmia annia, pode-se

denir um alor espeío generalizado para o sistema [51, 52℄. Este alor espeío é

dependente de

γ,

C

γ

=

.

−

α

2

∂U

∂α

γ

=

h

(E

−

U

)

²

i

1

−

2γ

h

(E

−

U

)

²

i

.

(2.27)

Simulações

God does not are about our mathematial diulties. He integrates empirially

[A. Einsteina L.Ineld,1942℄.

Aobtençãodaentropiamiroanniapartindo-sediretamentedadeniçãonaEq. (2.2)

éumatarefa nemsemprepossívelanalitiamente. Oquereforçaa neessidadede métodos

numérios omo as simulaçõesde Monte Carlo (MC) [64℄ para esse tipo de álulo.

Nes-tas simulaçõesutilizam-sedinâmiasestoástiasparaevoluirtemporalmenteum sistema.

Neste aso produzimosuma adeia markovianade onguraçõesna variável temporalnão

físia

τ

dita de Monte Carlo. O algoritmoempregado deverá amostrarongurações esta-tistiamentedistribuídasde aordoomum dado ensembleaolongodaevolução temporal

da simulação. Assim, assumindo ergodiidade, substituem-se médias térmias

h

. . .

iT

de ensemble pormédias temporais

h

. . .

iτ

nas simulação de MC.

Na iminênia de uma transição de fase, a produção de ongurações independentes é

afetadafortementepeloefeitodofrenamentorítio(doinglês,ritialslowingdown: CSD)

[63℄. Este efeitoestá assoiadoà existêniade omprimentosde orrelação divergentes em

transiçõesde fasedesegunda ordem,eàpresençadeenormes barreirasinterfaiaisna

ener-gia livre annia em transições de primeiraordem. Isto produz divergênias nos tempos

de autoorrelação entre onguraçõessuessivas. Para ontornar o problema, sostiados

algoritmosde atualização globais devemser empregadossempre que possível.

Outraalternativaéautilizaçãodeensemblesgeneralizadosemqueopesoanniousual

de Boltzmann-Gibbs

e

−

βE

_,

típio do ensemble annio, é substituido por outros, om a

nalidade de diminuira inuênia numériadas barreirasde energia livre[61, 62, 77℄.

Iniiamos o apítulo revisando brevemente alguns tipos de simulações, o oneito de

adeias de Markov é então introduzido e utilizado na formulação do algoritmode

Metro-polis. Disutimos emseguida omo estimarerros numérios e omoo efeitodo CSDpode

afetá-los. Estas observações orientaram historiamente o desenvolvimento de algoritmos

mais eientes, hamados de miroannios, imunes ao efeito de CSD. Finalizamos este

apítulomostrando omo adaptarosmétodos de Monte Carlousuais, onjuntamenteom