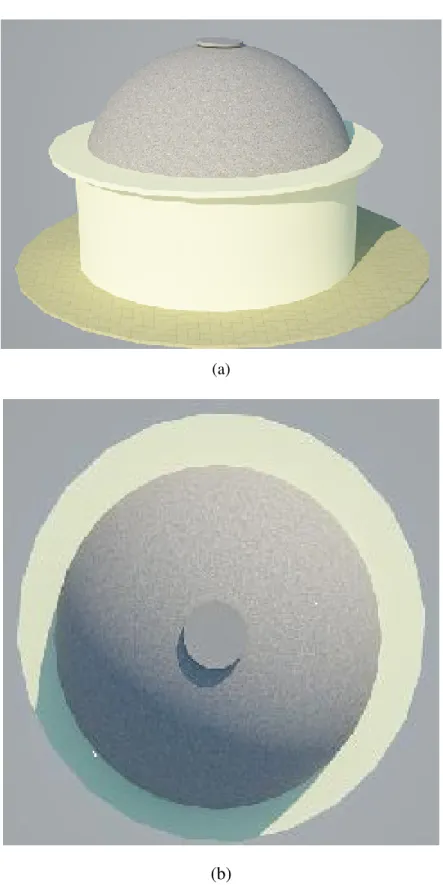
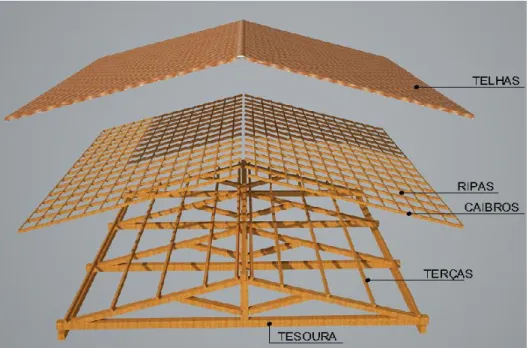
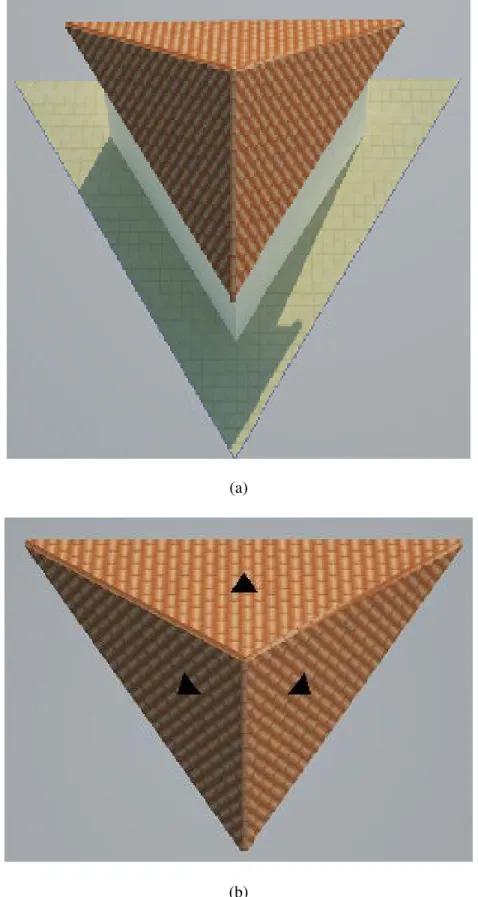
AVALIAÇÃO DO DESEMPENHO DE SOLUÇÕES ESTRUTURAIS EM AÇO PARA TELHADOS COLONIAIS
Texto
Imagem



Documentos relacionados
À vista de tudo quanto foi dito, a forma mais adequada para compreender a questão parece ser a seguinte: (i) os direitos fundamentais são, em princípio,
Os sais hidratados podem ser considerados ligas de um sal inorgânico e água, formando um sólido crsitalino de fórmula geral
Discussion The present results show that, like other conditions that change brain excitability, early environmental heat exposure also enhanced CSD propagation in adult rats.. The
novo medicamento, tendo como base para escolha as necessidades de cada segmento do mercado farmacêutico; e c) licenciamento do produto, o processo mais demorado
Dessa maneira, os resultados desta tese são uma síntese que propõe o uso de índices não convencionais de conforto térmico, utilizando o Índice de Temperatura de Globo Negro e
As sementes tem dormência imposta pelo tegumento e para a superação é necessário submetê-las à embebição em água (24 a 48 horas), escarificação mecânica ou
Mineração de conhecimento interativa em níveis diferentes de abstração: Como é difícil prever o que exatamente pode ser descoberto de um banco
Esse foi um dos fatores que le- vou à extinção das Rodas de Expostos, que acabaram por desaparecer definitivamente da paisagem europeia em fins do século XIX (MARCÍLIO, 1998, p..