Modelagem de volatilidade via modelos GARCH
com erros assimétricos: abordagem Bayesiana
Modelagem de volatilidade via modelos GARCH com
erros assimétricos: abordagem Bayesiana
José Augusto Fioruci
Orientador: Prof. Dr. Ricardo Sandes Ehlers
Dissertação apresentada ao Instituto de Ciências Matemáticas e de Computação - ICMC-USP, como parte dos requisitos para obtenção do título de Mestre em Ciências - Ciências de Computação e Matemática Computacional. VERSÃO REVISADA
USP – São Carlos
Agosto de 2012
SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP
Data de Depósito:
A minha família, em especial aos meus pais,
José Airton Fioruci e Luzia Neuza Dalaqua, pelo
incentivo e o esforço pela minha formação.
Aos meus amigos do laboratório da
Agradecimentos
Agradeço primeiramente a Deus por me permitir estudar os mistérios da sua criação
e por ter me concedido saúde e sabedoria para realizar este trabalho.
A minha família, em especial aos meus pais que sempre me ajudam, apoiam e me
incentivam e a quem sempre estarei em dívida.
Ao meu orientador, Ricardo Sandes Ehlers, pela orientação, sugestões e amizade
que contribuíram no meu crescimento e na minha formação acadêmica.
Aos professores Francisco Louzada Neto e Mauricio Enrique Zevallos Herencia,
membros da banca de defesa, pelas valiosas sugestões feitas.
Aos professores Francisco Antonio Rojas Rojas e Marinho Gomes de Andrade Filho,
membros da banda de qualificação, pelas valiosas sugestões feitas.
Aos diversos amigos e colegas do ICMC, em especial aos amigos do laboratório da
estatística.
Aos professores e aos demais funcionários do ICMC pelo excelente convívio.
Por fim, agradeço ao Conselho Nacional de Desenvolvimento Científico e
Resumo
A modelagem da volatilidade desempenha um papel fundamental em Econometria.
Nesta dissertação são estudados a generalização dos modelos autorregressivos
condi-cionalmente heterocedásticos conhecidos como GARCH e sua principal generalização
multivariada, os modelos DCC-GARCH (Dynamic Condicional Correlation GARCH).
Para os erros desses modelos são consideradas distribuições de probabilidade
possivel-mente assimétricas e leptocúrticas, sendo essas parametrizadas em função da assimetria
e do peso nas caudas, necessitando assim de estimar esses parâmetros adicionais aos
modelos. A estimação dos parâmetros dos modelos é feita sob a abordagem Bayesiana
e devido às complexidades destes modelos, métodos computacionais baseados em
si-mulações de Monte Carlo via Cadeias de Markov (MCMC) são utilizados. Para obter
maior eficiência computacional os algoritmos de simulação da distribuição a posteriori
dos parâmetros são implementados em linguagem de baixo nível. Por fim, a proposta
de modelagem e estimação é exemplificada com dois conjuntos de dados reais.
Palavras-chave: series temporais, modelagem de volatilidade, modelos GARCH,
Abstract
The modeling of volatility plays a fundamental role in Econometrics. In this
disser-tation are studied the generalization of known autoregressive conditionally
heterosce-dastic (GARCH) models and its main principal multivariate generalization, the
DCC-GARCH (Dynamic Conditional Correlation GARCH) models. For the errors of these
models are considered distribution of probability possibility asymmetric and
leptokur-tic, these being parameterized as a function of asymmetry and the weight on the tails,
thus requiring estimate the models additional parameters. The estimation of
parame-ters is made under the Bayesian approach and due to the complexities of these models,
methods computer-based simulations Monte Carlo Markov Chain (MCMC) are used.
For more computational efficiency of simulation algorithms of posterior distribution of
the parameters are implemented in low-level language. Finally, the proposed modeling
and estimation is illustrated with two real data sets.
Keywords: time series, volatility modeling, GARCH models, asymmetric
Sumário
1 Introdução 1
1.1 Motivação . . . 1
1.2 Conceitos Básicos . . . 3
1.2.1 Retornos e Volatilidade . . . 3
1.2.2 Métodos de Monte Carlo via Cadeias de Markov . . . 6
1.3 Revisão Bibliográfica . . . 10
1.4 Apresentação de Capítulos . . . 14
2 Distribuições Assimétricas 16 2.1 Método Univariado . . . 16
2.2 Método Multivariado . . . 20
2.2.1 Normal . . . 22
2.2.2 t-Student . . . 23
2.2.3 GED . . . 24
3 Modelos GARCH 27
SUMÁRIO vi
3.1 Modelos Univariados . . . 28
3.2 Modelos Multivariados . . . 32
3.3 Estimação dos Parâmetros . . . 36
4 Estudo de Simulação 40
5 Aplicação 47
5.1 Modelo Univariado . . . 49
5.2 Modelo Multivariado . . . 53
6 Considerações Finais e Conclusão 59
Bibliografia 61
A Estimativa Bayesiana dos parâmetros dos modelos 66
B Gráficos da simulação a posteriori dos parâmetros do modelo
Lista de Figuras
1.1 Petrobrás PN: (a) Gráfico da série, (b) Gráfico dos retornos. . . 4
1.2 Petrobrás PN: (a) Autocorrelação nos retornos, (b) Autocorrelação nos
quadrados dos retornos. . . 5
2.1 Versão padronizada da distribuição Normal Assimétrica . . . 19
4.1 Gráficos das densidades utilizadas para os erros do modelo GARCH(1,1)
para gerar os dados artificiais: (a) SSN, (b) SST e (c) SSGED . . . 41
5.1 Série do IBOVESPA de 02/01/2001 até 28/12/2007. (a) Gráfico da série;
(b) Gráfico dos retornos; (c) Gráficos das autocorrelações dos retornos
e (d) Gráfico das autocorrelações do quadrado dos retornos. . . 50
5.2 A esquerda o histograma dos resíduos com a distribuição de
probabili-dade dos erros sobreposta e a direita o gráfico qqplot dos resíduos do
modelo com erros SST. . . 51
5.3 (a) Densidade a posteriori do parâmetro de assimetria (γ) e (b)
den-sidade a posteriori da persistência (α1 +β1), para o modelo com erros
SST. . . 52
LISTA DE FIGURAS viii
5.4 Gráfico das volatilidades estimadas pelo modelo GARCH(1,1) com erros
SST e intervalo com 95% de credibilidade. . . 52
5.5 Gráficos da série e dos retornos dos índices DAX, CAC40 e NIKKEI. . 53
5.6 Autocorrelações dos retornos (primeira coluna) e dos retornos ao
qua-drado (segunda coluna) dos índices DAX, CAC40 e NIKKEI. . . 54
5.7 Histogramas dos resíduos com as respectivas distribuições marginais
so-brepostas na coluna esquerda e gráficos qqplots dos resíduos na coluna
da direita: modelo com erros SST. . . 56
5.8 Densidade a posteriori dos parâmetros de assimetrias (γ) e das
persis-tências (α1+β1) do modelo com erros SST. . . 57
5.9 Gráfico das volatilidades estimadas pelo modelo DCC-GARCH(1,1) com
erros SST e intervalo com 95% de credibilidade. . . 58
B.1 Na coluna da esquerda os traços, na centro os gráficos das densidades
aproximadas e na direita o gráfico das autocorrelações da simulação da
distribuição a posteriori dos parâmetros do modelo GARCH(1,1) com
erros SST aplicado ao conjunto de dados univariado do Capítulo 5. . . 72
B.2 Traços da simulação a posteriori, densidades aproximadas e
autocorrela-ções do parâmetro de assimetria e dos parâmetro da volatilidade para a
série DAX. Modelo ajustado: GARCH(1,1) com errosSST ao conjunto
da dados multivariados do Capítulo 5. . . 73
B.3 Traços da simulação a posteriori, densidades aproximadas e
autocorre-lações do parâmetro de assimetria e dos parâmetro da volatilidade para
a série CAC40. Modelo ajustado: GARCH(1,1) com erros SST ao
LISTA DE FIGURAS ix
B.4 Traços da simulação a posteriori, densidades aproximadas e
autocorre-lações do parâmetro de assimetria e dos parâmetro da volatilidade para
a série NIKKEI. Modelo ajustado: GARCH(1,1) com errosSST ao
con-junto da dados multivariados do Capítulo 5. . . 75
B.5 Traços da simulação a posteriori, densidades aproximadas e
autocorre-lações dos parâmetros de correlação e do parâmetro de peso nas caudas.
Modelo ajustado: GARCH(1,1) com erros SST ao conjunto da dados
Lista de Tabelas
2.1 Razões entre a massa de probabilidade presente a esquerda de −q com
a massa de probabilidade presente a direita de q P(X<−q) P(X>q)
. . . 20
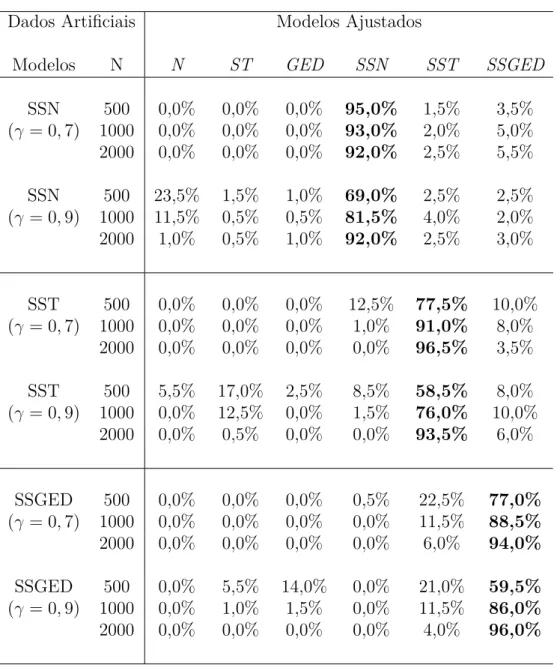
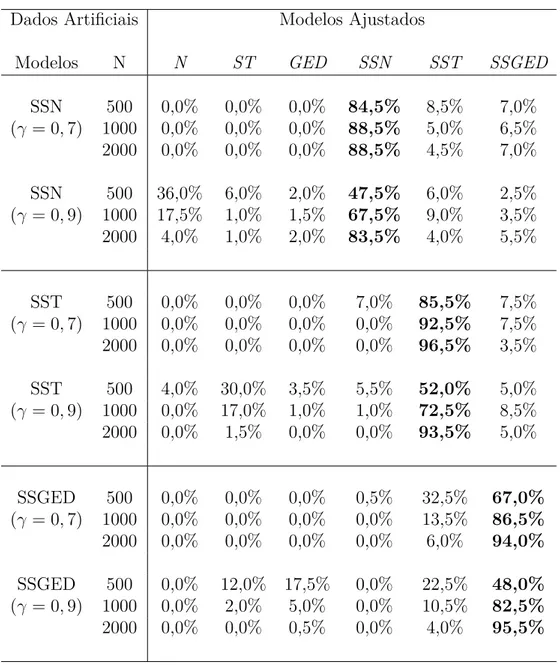
4.1 Porcentagem de vezes que cada modelo foi selecionado pelo critério EAIC no estudo de simulação. Em destaque a porcentagem de vezes que o modelo selecionado foi o mesmo utilizado na geração dos dados. . . 44
4.2 Porcentagem de vezes que cada modelo foi selecionado pelo critério EBIC no estudo de simulação. Em destaque a porcentagem de vezes que o modelo selecionado foi o mesmo utilizado na geração dos dados. . . 45
4.3 Porcentagem de vezes que cada modelo foi selecionado pelo critério DIC no estudo de simulação. Em destaque a porcentagem de vezes que o modelo selecionado foi o mesmo utilizado na geração dos dados. . . 46
5.1 Critérios para seleção dos modelos univariados. . . 49
5.2 Critérios para seleção dos modelos multivariados. . . 55
A.1 Estimativas do GARCH univariado com erros N. . . 66
A.2 Estimativas do GARCH univariado com erros SSN. . . 66
A.3 Estimativas do GARCH univariado com erros ST. . . 67
LISTA DE TABELAS xi
A.4 Estimativas do GARCH univariado com erros SST. . . 67
A.5 Estimativas do GARCH univariado com erros GED. . . 67
A.6 Estimativas do GARCH univariado com erros SSGED. . . 67
A.7 Estimativas do GARCH multivariado com erros N. . . 68
A.8 Estimativas do GARCH multivariado com erros SSN. . . 68
A.9 Estimativas do GARCH multivariado com erros ST. . . 69
A.10 Estimativas do GARCH multivariado com erros SST. . . 69
A.11 Estimativas do GARCH multivariado com erros GED. . . 70
Capítulo 1
Introdução
1.1
Motivação
Modelagem de volatilidade (variância condicional) é de grande interesse em Economia.
Gráficos de dados financeiros mostram que existem períodos mais voláteis do que
ou-tros, sendo que esses períodos geralmente estão distribuídos em grupos, sugerindo assim
um grau de dependência no tempo. Outra característica que geralmente esta presente
em séries financeiras, é que, em geral choques negativos tem mais influencia na
volati-lidade do que choques positivos, caracterizando assim, um certo grau de assimetria na
volatilidade.
Para levar em conta a presença de grupos de volatilidade é necessário a utilização de
modelos heterocedásticos condicionais, ou seja, modelos que consideram que a variância
condicional de uma série temporal não é constante. Diversos modelos para volatilidade
foram propostos na literatura, sendo que os modelos autorregressivos condicionalmente
heterocedásticos (ARCH) propostos por Engle (1982), e sua generalização os modelos
GARCH (Bollerslev 1986), bem como os modelos de volatilidade estocástica (Taylor
1.1 Motivação 2
Variações em diversas séries financeiras podem ser correlacionadas, de forma que a
volatilidade de uma série pode sofrer influencia das volatilidades de outras séries. Com
o intuito de considerar essas correlações na estimação dos modelos GARCH, diversas
extensões multivariadas surgiram na literatura, sendo que os modelos CCC-GARCH
(Constant Conditional Correlation GARCH) proposto em Bollerslev (1990) e
DCC-GARCH (Dynamic Conditional Correlation-GARCH) propostos simultaneamente em
Engle (2002) e Tse & Tsui (2002) estão entre os mais conhecidos.
Muitas vezes a utilização da distribuição de probabilidade Normal Padrão para os
erros dos modelos GARCH não é suficiente para adequar as características de caudas
pesadas e assimetria dos retornos financeiros. Assim, tanto para os erros dos modelos
GARCH como para os erros dos modelos DCC-GARCH, nesta dissertação é estudado
a utilização de distribuições de probabilidade com caudas mais pesadas do que a
dis-tribuição Normal Padrão e também consideramos uma forma de tornar possivelmente
assimétrica (skew) essas distribuições. A estimação é feita sob o enfoque Bayesiano o
que possibilita analisar essas características através da distribuição a posteriori dos
pa-râmetros, uma vez que as distribuições de probabilidade utilizadas são parametrizadas
em função de parâmetros de peso nas caudas e de assimetria.
Na literatura poucos trabalhos surgiram utilizando o enfoque Bayesiano, mesmo
para os modelos univariados. Isto ocorre devido a complexidade desses modelos e ao
custo computacional da utilização de métodos computacionais baseados em
simula-ção de Monte Carlos via Cadeias de Markov (MCMC). Nesta dissertasimula-ção, os métodos
MCMC são utilizados, mas para obter maior eficiência computacional os algoritmos de
simulação da distribuição a posteriori são implementados em linguagem de baixo nível.
As principais contribuições metodológicas deste trabalho são: o estudo de
distribui-ções possivelmente leptocúrticas e assimétricas para o termo do erro, tanto em modelos
Baye-1.2 Conceitos Básicos 3
siana para estimação desses modelos; avaliação da adequação de alguns critérios para
seleção entre os modelos aqui estudados através de um estudo de simulação.
1.2
Conceitos Básicos
Nesta seção apresentamos alguns conceitos que serão utilizados nesta dissertação. Os
conceitos relacionados a séries temporais podem ser vistos detalhadamente em
Moret-tin (2008). Um excelente texto introdutório sobre os conceitos relacionados a inferência
Bayesiana e métodos computacionais pode ser encontrado em Lynch (2007). Estudos
mais avançados sobre os algoritmos Amostrador de Gibbs e Metropolis-Hastings podem
ser encontrados em Casella & George (1992) e Chib & Greenberg (1995),
respectiva-mente.
1.2.1
Retornos e Volatilidade
ConsiderePtcomo sendo o preço de um ativo no instanteteptcomo sendo o logaritmo
na base e do preço deste ativo (pt = log(Pt)). Assim o log-retorno ou simplesmente,
retorno no instantet, é definido como sendo:
yt= log
Pt
Pt−1
!
=pt−pt−1.
Como exemplo, a Figura 1.1 (a) apresenta o gráfico da série diária dos fechamentos
da ação da Petrobrás PN, no período de 2 de janeiro de 1995 à 27 de dezembro de
2000, e a Figura 1.1 (b) apresenta o gráfico dos retornos da mesma série.
Pela Figura 1.1 podemos notar algumas das principais propriedades dos retornos,
como por exemplo estacionaridade. Isto faz com que em geral, seja preferível trabalhar
1.2 Conceitos Básicos 4
(a)
Tempo
Obser
vações
0 500 1000 1500
10000
50000
(b)
Tempo
Retor
nos
0 500 1000 1500
−0.2
0.1
Figura 1.1: Petrobrás PN: (a) Gráfico da série, (b) Gráfico dos retornos.
Outra características comum em séries de retornos financeiros consiste na existência
de autocorrelação nos quadrados dos retornos, enquanto que os retornos não possuem
autocorrelação ou em alguns casos possuem autocorrelação apenas nos primeiros lags.
Essa característica é exemplificada na Figura 1.2, onde para a mesma série da Petrobrás,
temos no gráfico (a) as autocorrelações dos retornos e no gráfico (b) as autocorrelações
dos quadrado dos retornos. Observe que no gráfico (a) existe autocorrelação apenas
para o lag 1, enquanto que no gráfico (b) existe autocorrelação para diversos lags.
Considerando uma série de retornos {yt, t = 1, . . . , T}, podemos escrever a
dis-tribuição conjunta dos retornos como o produto das distribuições de cada retorno,
condicionado os retornos anteriores:
1.2 Conceitos Básicos 5
0 5 10 15 20 25 30
0.0
0.6
Lag
A
CF
(a)
0 5 10 15 20 25 30
0.0
0.6
Lag
A
CF
(b)
Figura 1.2: Petrobrás PN: (a) Autocorrelação nos retornos, (b) Autocorrelação nos quadrados dos retornos.
sendoIt={yt−1, yt−2, . . .} a informação prévia até o instantet.
A variância das distribuições condicionais da equação (1.1) convencionou-se chamar
de Volatilidade e será o objetivo da modelagem. O formato de escrever distribuição
conjunta dos retornos apresentado em (1.1) é muito utilizada nos modelos para
volati-lidade, pois nessa modelagem sempre estaremos interessados na informação disponível
no instante t com relação ao que ocorreu nos instantes anteriores.
Algumas das características que geralmente são encontradas em séries de retornos
financeiros são:
• Retornos são em geral não autocorrelacionados;
• A distribuição incondicional dos retornos apresenta caudas mais pesadas do que
1.2 Conceitos Básicos 6
• Os quadrados dos retornos são em geral autocorrelacionados;
• A volatilidade aparece em grupos de maior, ou menor, volatilidade;
• A volatilidade reage de modo diferente a valores positivos e negativos da série;
Os modelos que serão vistos no Capítulo 3 assumirão que a esperança de cada
distribuição condicional da equação (1.1) é zero, enquanto que a variância
(vola-tilidade) é uma função da informação passada. Ou seja, estes modelos
assumi-rão heterocedasticidade. Para fixar a notação, considere a volatilidade como ht =
V ar(yt|It) = E(y2t|It), sendo It a informação prévia até o momento t, ou seja,
It = (yt−1, yt−2, . . . , ht−1, ht−2, . . .).
A seguir apresentaremos uma breve descrição de alguns dos principais métodos de
simulação computacional baseados em Monte Carlo via Cadeias de Markov.
1.2.2
Métodos de Monte Carlo via Cadeias de Markov
Suponha que temos interesse em obter características (por exemplo: média e a
variân-cia) de uma distribuição a posteriori π(θ|y), mas não podemos obter essa informação
diretamente. Entretanto, suponha que podemos construir uma Cadeia de Markov,
com espaço de estados no espaço paramétrico Θ (conjunto de todos valores possíveis
deθ), que é simples para simular e cuja distribuição de equilíbrio seja dada porπ(θ|y).
Por fim, sob algumas condições de regularidade, o Teorema 1.1 garante que podemos
utilizar os valores simulados da cadeia como base para sumarizar características da
posteriori π(θ|y). A demonstração do Teorema 1.1 pode ser encontrada em Tierney
(1994).
Teorema 1.1. Suponha que {Y(t)}M
t=1 é uma Cadeia de Markov irredutível, aperiódica
1.2 Conceitos Básicos 7
continua com respeito a π para todo y, então π é a única distribuição invariante de
P(.,.) e para toda função h que toma valores nos reais e integrável em relação a π,
temos
1
M
M
X
t=1
h(Y(t))−→
Z
h(y)π(y)dy,
quando M → ∞, q.c.
Recentemente, com a evolução computacional, os métodos de Monte Carlo via
Ca-deias de Markov (MCMC) vem sendo cada vez mais utilizados, por conta da facilidade
na utilização e pela possibilidade de trabalhar com modelos complexos.
A seguir serão apresentados os dois métodos MCMC mais empregados, o
Amostra-dor de Gibbs e o Metropolis-Hastings.
Amostrador de Gibbs
Considere θ = (θ1, . . . , θk) um vetor de variáveis aleatórias. O Amostrador de Gibbs
consiste em um algoritmo para gerar uma Cadeia de Markov da distribuição
con-junta π(θ) a partir das distribuições condicionais de θi|θ−i, i = 1, . . . , k, sendo
θ−i = (θ1, . . . , θi−1, θi+1, . . . , θk).
As distribuições condicionais são obtidas a partir de:
π(θi|θ−i) =
π(θ)
R
π(θ) dθi ∝
π(θ).
Assim, a menos de uma constante, para obter a distribuição condicionais de θi|θ(i),
basta considerar apenas os termos da distribuição conjuntaπ(θ) que dependem de θi.
A seguir é apresentado o esquema do algoritmo Amostrador de Gibbs:
1.2 Conceitos Básicos 8
2. Obtenha um novo valor de θ(j+1) a partir de θ(j), através da geração sucessiva
dos valores:
θ1(j+1) ∼ π(θ1|θ2(j), θ (j) 3 , . . . , θ
(j) k )
θ2(j+1) ∼ π(θ2|θ1(j+1), θ (j) 3 , . . . , θ
(j) k )
...
θk(j+1) ∼ π(θk|θ(1j+1), θ (j+1) 2 , . . . , θ
(j+1) k−1 )
3. Faça j =j+ 1 e volte ao Passo 2.
Os passo 2 e 3 devem ser repetidos até que a distribuição estacionária seja alcançada.
Em geral, as primeiras simulações são descartadas como uma amostra de aquecimento.
Pode-se considerar apenas os últimos valores gerados a cada bloco de k-simulações,
com k >1.
Observe que não é necessário conhecer a distribuição conjunta, mas é necessário
conhecer as distribuições condicionais completas. Se as distribuições condicionais
com-pletas coincidirem com alguma distribuição de probabilidade conhecida na literatura,
então deve-se gerar valores diretamente dessa distribuição. No caso, de uma ou mais
distribuições condicionais completas não coincidirem com alguma distribuição de
pro-babilidade conhecida, pode-se utilizar o algoritmo Metropolis-Hastings para simular da
distribuição conjunta. O algoritmo Metropolis-Hastings é apresentado a seguir.
Metropolis-Hastings
No algoritmo Metropolis-Hastings um valor é gerado de uma distribuição auxiliar (ou
distribuição proposta) e aceito com uma dada probabilidade. Este mecanismo de
1.2 Conceitos Básicos 9
Considerando θ = (θ1, . . . , θk), suponha que deseja-se gerar valores da distribuição
conjunta π(θ) e a cadeia esteja no estado θ, um valor θ′ é gerado de uma distribuição
proposta q(·|θ). Note que a distribuição proposta pode depender do estado atual da
cadeia, por exemplo q(·|θ) poderia ser uma distribuição multivariada centrada em θ.
O esquema geral do algoritmo Metropolis-Hastings é apresentado a seguir:
1. Inicialize o contadorj = 0 e determine um valor inicial θ(0).
2. Gere θ′ da distribuição proposta
q(·|θ(j)).
3. Gere u∼U(0,1).
4. Se u < p(θ′
,θ(j)) então faça θ(j+1) =θ′. Caso contrário, faça
θ(j+1) =θ(j).
5. Faça j =j+ 1 e volte para o Passo 2.
No passo 4 a probabilidade de aceitaçãop(θ′
,θ(j)) é dada por:
p(θ′
,θ(j)) = min
(
1, π(θ
′)
q(θ(j)|θ′)
π(θ(j)) q(θ′ |θ(j))
)
. (1.2)
Observe, que a probabilidade de aceitação não depende de constantes normalizadoras,
ou seja, π(θ) pode ser conhecido a menos de uma constante. Os passo 2−5 devem ser
repetidos até que seja obtida a distribuição estacionária π(θ).
Na inferência Bayesiana o algoritmo Metropolis-Hastings é bastante utilizado para
gerar amostras da distribuição a posteriori, neste caso, a distribuição pretendida é
a posteriori π(θ|y) ∝ L(θ)π(θ), sendo L(θ) e π(θ) a função de verossimilhança e a
distribuição a priori deθ, respectivamente. Assim, se considerarmos como distribuição
1.3 Revisão Bibliográfica 10
apresentada em (1.2) fica resumida na razão de verossimilhanças:
p(θ(j),θ′) = min
(
1, L(θ
′)
L(θ(j))
)
.
Um caso mais geral do Metropolis-Hastings e que em alguns casos pode ser mais
eficiente computacionalmente, consiste em dividir θ = (θ1, . . . , θk) em p blocos
{θ1, . . . ,θp}, sendo que cada bloco contém um ou mais elementos, assim dentro de
cada iteração teremos o algoritmo aplicado p vezes. Por exemplo, definindo o
ve-tor θ−i = (θ1, . . . ,θi−1,θi+1, . . . ,θp) que contém todos os elementos de θ exceto θi,
suponha que na iteração j + 1 os blocos 1,2, . . . , i −1 já foram atualizados, isto é
θ(−ji) = (θ (j+1) 1 , . . . ,θ
(j+1) i−1 ,θ
(j)
i+1, . . . ,θp(j)). Assim, para atualizar a i-ésima componente,
um valor θ′
i é gerado da distribuição proposta q(·|θ (j) i ,θ
(j)
−i) e este valor candidato é
aceito com probabilidade:
p(θ′ i,θ
(j)
i ) = min
1, π(θ
′ i|θ
(j)
−i)q(θ
(j) i |θ
′ i,θ
(j)
−i)
π(θi(j)|θ−(ji))q(θ ′ i|θ
(j) i ,θ
(j)
−i)
. (1.3)
Aqui, π(θi|θ−i) é a distribuição condicional completa do bloco θi.
Note que o Amostrador de Gibbs é um caso especial do algoritmo
Metropolis-Hastings, no qual os elementos de θ são atualizados um de cada vez (ou em blocos),
tomando a distribuição condicional completa como proposta e neste caso, a
probabili-dade de aceitação é igual a 1.
1.3
Revisão Bibliográfica
Os modelos ARCH (Autoregressive Conditional Heteroskedasticity) foram introduzidos
por Engle (1982) e têm como ideia básica que a volatilidade (variância condicional) em
1.3 Revisão Bibliográfica 11
uma classe de modelos que considera que a volatilidade depende, além dos valores
passados dos retornos, também dos valores passados da volatilidade, estes modelos são
os considerados GARCH (Generalized ARCH). Os modelos GARCH são considerados
mais parcimoniosos do que os ARCH, no sentido que, em geral descrevem a volatilidade
com menos parâmetros.
Desde a criação dos modelos GARCH diversas extensões multivariadas foram
pro-postas na literatura, uma revisão sobre vários desses modelos pode ser encontrada em
Bauwens et al. (2006). Os modelos multivariados mais utilizados foram propostos pelos
mesmos criadores dos modelos ARCH e GARCH, primeiramente foi proposto o modelo
CCC-GARCH (Constant Conditional Correlation GARCH) em Bollerslev (1990), esse
modelo considera correlação constante ao longo do tempo entre as séries de retornos.
Uma extensão do CCC-GARCH que hoje é mais utilizada é o modelo DCC-GARCH
(Dynamic Conditional Correlation GARCH) o qual foi proposto simultaneamente em
Engle (2002) e Tse & Tsui (2002), este modelo considera que a correlação entre as
volatilidades varia com o tempo através de um processo GARCH. Os modelos
CCC-GARCH e DCC-CCC-GARCH serão apresentados em detalhes na Seção 3.2.
Atualmente vem surgindo algumas abordagens Bayesianas para estimação dos
mo-delos GARCH. Ardia (2006) propõe um algoritmo para estimação Bayesiana do modelo
GARCH(1,1) com erros normais. O algoritmo consiste em amostrar valores da
distri-buição posteriori conjunta dos parâmetros, construindo assim, uma Cadeia de Markov
para ser utilizada na estimação dos parâmetros. Nos modelos GARCH as condicionais
completas da posteriori, em geral, não coincidem com funções de densidades de
proba-bilidade conhecidas na literatura, e assim, o algoritmo Metropolis-Hastings é utilizado.
Ainda no mesmo artigo, para melhorar o desempenho do algoritmo a amostragem é
feita por uma abordagem sugerida por Nakatsuma (1998), a qual utiliza uma
1.3 Revisão Bibliográfica 12
Devido a evidências na literatura de que muitas séries temporais financeiras tendem
a ter a curtose observada maior do que aquela considerada por um modelo GARCH
com erros normais, Ardia (2008) propõe a estimação Bayesiana do modelo GARCH(1,1)
com erros t-Student através de um algoritmo MCMC. A implementação em R de
am-bos algoritmos, pode ser encontrada no pacote bayesGARCH (Ardia 2011). Além da
distribuição t-Student, outra distribuição de probabilidade possivelmente leptocúrtica
que vem sendo usada para os erros do modelo GARCH é a GED (Generalized Error
Distribution), que pode ser encontrada na forma univariada e com uma das extensões
multivariada em Gómez et al. (1998).
Uma das preocupações atuais, tem sido com a evidência empírica de assimetria
nos retornos financeiros, não tratada pelos modelos GARCH, isto levou alguns
pes-quisadores a proporem extensões para o modelo. Nelson (1991) introduziu os modelos
EGARCH (Exponential GARCH), Glosten et al. (1993) introduziram os modelos GJR,
mas uma das extensões que mostrou-se mais promissora foi a APARCH (Asymmetric
Power ARCH) introduzidas por Ding et al. (1993). Os modelos APARCH generalizam
vários modelos GARCH assimétricos, entre eles, os EGARCH e os GJR (veja, Laurent
(2004)).
Outra forma de tratar a assimetria nos retornos através dos modelos GARCH
con-siste em assumir algum grau de assimetria na distribuição dos erros. Em Pipien (2006)
são revisados diversos métodos para inserir assimetria em qualquer distribuição de
pro-babilidade univariada, continua, unimodal e simétrica. Na literatura o método para
inserir assimetria que vem sendo mais explorado é o proposto em Fernandez & Steel
(1998) para distribuições de probabilidade univariadas e generalizado para as
distri-buições multivariadas em Bauwens & Laurent (2005). O método de Fernandez e Steel
transforma a distribuição de probabilidade simétrica em uma distribuição
possivel-mente assimétrica acrescentado apenas um parâmetro, o qual pode ser interpretado
1.3 Revisão Bibliográfica 13
se menor que 1, então a distribuição terá maior massa a esquerda da moda e se maior
que 1 terá maior massa a direita da moda. O método de Fernandez & Steel (1998) e
sua generalização multivarida de Bauwens & Laurent (2005) será explicada em detalhes
no Capítulo 2.
Outras propostas recentes para modelar características não captadas pelos modelos
GARCH usuais são: modelos com mudança de regime estocástica (Markov switching,
Bauwens et al. (2008), Ardia (2009)), e misturas de distribuições para os erros (ver
por exemplo Ausin & Galeano (2007)).
Outra classe de modelos para volatilidade são os modelos de Volatilidade Estocástica
(VE), propostos por Taylor (1982), os quais tem sido uma alternativa aos modelos da
família GARCH. Em alguns casos, estes modelos são conhecidos por modelarem melhor
a volatilidade do que os modelos GARCH (veja, Kim et al. (1998), Barossi-Filho
et al. (2010)), mas são considerados de difícil estimação, isso porque nesses modelos
não é possível obter a função verossimilhança de forma analítica, pois as volatilidades
aparecem como variáveis latentes. Iniciado, por Jacquier et al. (1994) os métodos
MCMC tem sido usados para estimar os parâmetros e as log-volatilidades do modelo
de VE do ponto de vista Bayesiano. Na classe de modelos VE também tem surgido
propostas na literatura para relaxar a hipótese de normalidade dos erros
introduzindo-se distribuições com caudas mais pesadas bem como distribuições assimétricas (ver
por exemplo, Liesenfeld & Jung (2000) e Cappuccio et al. (2004)). A utilização das
distribuições de probabilidade que serão obtidas no Capítulo 2 para os erros dos modelos
VE nos casos univariados e multivariados ficará como proposta futura de pesquisa nesta
1.4 Apresentação de Capítulos 14
1.4
Apresentação de Capítulos
No Capítulo 1 foi apresentada a motivação para o projeto e alguns conceitos básicos,
incluindo uma introdução aos conceitos de retornos e volatilidade em séries
tempo-rais e aos principais métodos computacionais baseados em Monte Carlo via Cadeias
de Markov (Amostrador de Gibbs e Metropolis-Hastings). Ainda neste capítulo,
tam-bém é feita uma revisão bibliográfica de alguns trabalhos referentes a distribuições
assimétricas e modelos GARCH.
O Capítulo 2 define o conceito de simetria em distribuições de probabilidade
uni-variadas e multiuni-variadas e apresenta um método para obter uma generalização
pos-sivelmente assimétrica (dependendo do valor do parâmetro de assimetria) dessas
dis-tribuições, desde que estas sejam, contínuas e unimodais. O método é então aplicado
a três distribuições de probabilidade comumente utilizadas para os erros dos modelos
GARCH.
Os modelos GARCH, foco do estudo dessa dissertação, são apresentados no
Ca-pítulo 3. Inicialmente, são introduzidos os modelos univariados conhecidos como
GARCH(p,q), em seguida são apresentadas duas de suas generalizações
multivaria-das, os modelos CCC-GARCH e DCC-GARCH. Ainda, neste capítulo, é apresentado
dois algoritmos para simulação da distribuição a posteriori dos parâmetros do modelo
DCC-GARCH. Lembrando que o modelo DCC-GARCH generaliza o modelo GARCH
univariado e portanto o mesmo algoritmo pode ser utilizado para o GARCH univariado.
No Capítulo 4 é apresentado um estudo de simulação para avaliar se alguns
crité-rios para seleção de modelos conhecidos na literatura são adequados para distinguir
entre os modelos aqui estudados. No Capítulo 5 os modelos estudados são aplicados a
dois conjuntos de dados reais, uma para os modelos univariados e outro para os
1.4 Apresentação de Capítulos 15
apresentados no Capítulo 3. Estes, então são comparados via critérios de seleção de
modelos e é feita a análise de resíduo para o modelo selecionado.
Por fim, no Capítulo 6 temos as considerações finais e a conclusão da dissertação.
Em seguida, são apresentadas as referências bibliográficas e o Apêndice A com as
Capítulo 2
Distribuições Assimétricas
Neste capítulo apresentaremos o método de Fernandez & Steel (1998) para inserir
assimetria em qualquer função de distribuição de probabilidade contínua, simétrica,
unimodal e definida nos reais. Em seguida apresentaremos o método de Bauwens
& Laurent (2005), o qual generaliza o método de Fernandez & Steel (1998) para as
distribuições multivariadas.
2.1
Método Univariado
Diversas propostas para introduzir assimetria em distribuições simétricas surgiram na
literatura, dentre elas podemos citar, Azzalini (1985), Fernandez & Steel (1998), Branco
& Dey (2001), Azzaline & Capitanio (2003), Jones & Faddy (2003). Mas devido a
sim-plicidade e generalidade neste capítulo nos concentraremos na proposta de Fernandez
& Steel (1998). Neste método os momentos são mais fáceis de serem calculados e não
é necessário obter a função de distribuição acumulada. Ainda, no contexto Bayesiano,
o método facilita a especificação das distribuições a priori separando os efeitos dos
parâmetros de assimetria e de cauda.
2.1 Método Univariado 17
Considerep(x) uma função de densidade unimodal, definida na reta e simétrica em
torno do zero. Neste caso, consideramos p(x) simétrica se p(x) = p(−x), para todo
x∈R. O método proposto em Fernandez & Steel (1998) é conhecido como método de
escala inversa de fatores. Este obtêm uma função de densidades(x|γ) a partir dep(x)
a qual é assimétrica e possui o grau de assimetria indexado pelo parâmetro adicional
γ >0. Quando o valor da variável aleatória é menor que zero entãos(x|γ)∝p(xγ), caso
contrário,s(x|γ)∝p(xγ). A função de densidade de probabilidades(x|γ) é apresentada
a seguir:
s(x|γ) = 2
γ+γ−1
n
p(xγ)I(−∞,0)(x) +p(x/γ)I[0,∞)(x)
o
= 2
γ+γ−1p(xγ
−sign(x)
),
sendoIA(x) a função indicadora no conjuntoAesign(x) é igual a−1, sex <0 e igual
a +1 , se x≥0.
Algumas das principais características de s(x|γ) são apresentadas a seguir:
1. Se γ = 1 então obtemos o caso simétrico, isto é, s(x|γ = 1) =p(x).
2. s(x|γ) mantém a mesma moda da p(x). Como p(x) é unimodal e simétrica em
torno do zero, a moda sempre é no zero.
3. A massa de probabilidade a esquerda e a direita de zero é independente dep(x):
P(X ≥0) = 2γ
1 +γ2
Z ∞
0 p(x/γ)dx=
γ2
1 +γ2,
P(X ≤0) = 1−P(X ≥0) = 1 1 +γ2,
P(X ≥0)
P(X ≤0) = γ
2.
2.1 Método Univariado 18
5. A existência dos momentos des(x|γ) depende unicamente dos momento absolutos
de p(x). O r-ésimo momento é dado por:
E(Xr|γi) =
γr+1+ (−1)r/γr+1
γ+ 1/γ Mr,
sendo
Mr = 2
Z ∞
0 x
r p(x)dx (2.1)
o r-ésimo momento absoluto de p(x).
6. A média e a variância são dados por:
µ = M1(γ−1/γ) (2.2)
σ2 = (M2−M12)(γ2+ 1/γ2) + 2M12−M2 (2.3)
7. A versão padronizada da função de densidade s(x|γ) é a distribuição de
proba-bilidade da variável aleatória Z = (X−µ)/σ, a qual é dada por:
p(z|γ) = s(zσ+µ|γ)dx
dz =s(zσ+µ|γ)σ
= 2σ
γ+γ−1p(z ∗
), (2.4)
sendo, z∗ =
(zσ+µ)γ, se z <−µ/σ
(zσ+µ)/γ, se z≥ −µ/σ
(2.5)
e p(z∗) a função de densidade simétrica calculada em
z∗.
Como exemplo, se aplicarmos o método apresentado em (2.4) na distribuição de
probabilidade Normal Padrão, obtemos:
p(x|γ) = (2/π)
1/2
γ+γ−1 exp
(
(x∗)2
2
)
2.1 Método Univariado 19
sendo, x∗ dado como em (2.5). No caso da função de distribuição simétrica
p(x) ser
padronizada temos o segundo momento absoluto será dado porM2 = 1. Neste exemplo
então, temos M2 = 1 e aplicando (2.1) obtemos M1 = (2/π)1/2. Desta forma, das
expressões (2.2) e (2.3) obtemos a média a variância da versão assimétrica da Normal
Padrão:
µ = (2/π)1/2(γ−1/γ)
σ2 = (γ2+γ−1
−1)−µ2.
A função de densidade (2.6) será referenciada no texto como SSN(0,1, γ) (Standard
Skew Normal). A Figura 2.1 apresenta o gráfico dessa distribuição nas versões com
parâmetro de assimetria igual a 1,0, 0,7 e 1,3, sendo respectivamente a versão
simé-trica, uma versão assimétrica a esquerda e uma versão assimétrica a direita. Observe
que no caso padronizado a função de densidade não possui moda igual a zero.
−4 −2 0 2 4
0.0
0.1
0.2
0.3
0.4
x
p(x|
γ
)
γ = 1.0
γ = 0.7
γ = 1.3
Figura 2.1: Versão padronizada da distribuição Normal Assimétrica.
pro-2.2 Método Multivariado 20
babilidade presente nas caudas da distribuição. Como exemplo, para a função de
densidade (2.6), a Tabela 2.1 apresenta os valores de P(X < −q)/P(X > q), isto é,
a razão entre a massa de probabilidade presente a esquerda de −q com a massa de
probabilidade presente a direita deq, sendo q ≥0. Observe que mesmo com γ = 0,9,
o que graficamente seria próximo de simetria, a massa de probabilidade presente na
cauda esquerda não é próxima da massa de probabilidade presente na cauda direita.
Note que o valor desta razão aumenta quando aumentamos o valor de q.
Tabela 2.1: Razões entre a massa de probabilidade presente a esquerda de −q com a
massa de probabilidade presente a direita de q P(X<−q) P(X>q)
.
q= 1 q= 2 q = 3
γ = 0,9 1,0192 1,5183 3,3238 γ = 0,7 1,0584 4,9009 119,7992
2.2
Método Multivariado
O conceito de distribuições simétricas em torno do zero apresentado na Seção 2.1 é
generalizado para distribuições multivariadas na definição a seguir (Bauwens & Laurent
(2005)):
Definição 2.1. Uma distribuição de probabilidade unimodal p(x) definida em Rm,
com E(X) = 0 e V ar(X) = Im é simétrica se, e somente se, para qualquer x,
p(x) =p(Qx)para qualquer matriz diagonalQ cujos elementos da diagonal são iguais
a 1 ou −1.
Considerando p(x) como na Definição 2.1 o método para inserir assimetria de
2.2 Método Multivariado 21
& Steel (1998) apresentado na Seção 2.1. Este método é dado por:
s(x|γ) = 2m
m
Y
i=1
γi
1 +γ2 i
!
p(x∗), (2.7)
sendo, x∗ = (x∗ 1, . . . , x
∗ m)
′,
x∗
i = xi/γi se xi ≥ 0 e x∗i =xiγi se xi <0. Os parâmetros
de assimetria são dados porγ = (γ1, . . . , γm)′, com γi >0. Seγi = 1 então a marginal
correspondente é simétrica.
Os momentos de p(x|γ) podem ser obtidos em função dos momentos absolutos das
distribuições marginais dep(x) como em Fernandez & Steel (1998). Isto é,
E(Xir|γi) =
γr+1
i + (−1)r/γr+1
γi+ 1/γi
Mr, (2.8)
sendo
Mr = 2
Z ∞
0 x r
i p(xi)dxi,
para qualquer r∈N.
Em geral, mesmop(x) sendo padronizada a distribuição resultantes(x|γ) não será
padronizada. Mas desde que o primeiro momento absoluto da distribuição marginal
p(xi) seja conhecido podemos utilizar a expressão (2.8) para obtermos o vetor de médias
µ = (µ1, . . . , µm)′ e o vetor de variâncias σ2 = (σ12, . . . , σm2)
′ de
s(x|γ). Como p(x)
é padronizada, é fácil ver que M2 = 1, logo da expressão (2.8) temos as médias e as
variâncias de p(x|γ):
µi = E(Xi|γi) = (γi−γ
−1
i )M1, (2.9)
σ2i = γ
3 i +γ
−3
i
γi+γ
−1
i
M2 −µ2i = (γi2+γ
−2
i −1)−µ2i, (2.10)
para i= 1, . . . , m.
pro-2.2 Método Multivariado 22
babilidade do vetor aleatório Z = (Z1, . . . , Zm)′, no qual Zi = (Xi −µi)/σi, a qual é
dada por:
p(z|γ) = 2m
"m Y
i=1
γi
1 +γ2 i
σi
#
p(z∗), (2.11)
sendo, z∗ i =
(ziσi+µi)/γi, se zi ≥ −µi/σi
(ziσi+µi)γi, se zi <−µi/σi.
(2.12)
A seguir aplicaremos o método para as distribuições de probabilidade Normal,
t-Student e GED multivariadas. Vale lembrar que para obter o caso univariado das
distribuições a seguir, basta utilizarm = 1.
2.2.1
Normal
A distribuição Normalm-Variada denotada por N(0,Im) é definida como produto de
m distribuições Normais Padrão N(0,1), logo possui distribuições marginais N(0,1).
A distribuiçãoN(0,Im) é dada por:
p(x) = 1
(2π)m/2 exp
(
−12
m
X
i=1
x2i
)
. (2.13)
Calculando o momento absoluto da N(0,1), temos:
M1 =
2 (2π)1/2
Z ∞
0 xiexp
( −x 2 i 2 ) dxi = 2
(2π)1/2. (2.14)
Logo, substituindo (2.14) em (2.9) obtemos as médias marginais da versão
assimé-trica da função de densidade (2.13):
µi = (2/π)1/2(γi−γ
−1
2.2 Método Multivariado 23
Para i = 1, . . . , m. As variâncias marginais são obtidas diretamente da expressão
(2.10). Por fim, da expressão (2.11) obtemos a distribuição de probabilidade Normal
Assimétrica e Padronizada (SSN(0,Im,γ),Standard Skew Normal).
p(z|γ) =
2
π
m/2 m Y
i=1
γiσi
1 +γ2 i
!
exp
(
−12
m X i=1 z∗ i 2 ) ,
sendo,z∗
i dado pelas expressões (2.12).
2.2.2
t-Student
Uma generalização multivariada da distribuição t-Student é definida como:
p(x|ν) = Γ((ν+m)/2)
Γ(ν/2)[π(ν−2)]m/2 1 +
x′x
ν−2
!−(m+ν)/2
. (2.15)
Essa distribuição de probabilidade será denotada por ST(0,Im, ν) (Standard
t-Student), sendo essa padronizada e com distribuições marginais ST(0,1, ν). A
dis-tribuição ST(0,Im, ν) satisfaz a Definição 2.1 e portanto, podemos aplicar o método
de Bauwens & Laurent (2005).
Calculemos inicialmente o primeiro momento absoluto da distribuição ST(0,1, ν):
M1 =
2Γ((ν+ 1)/2)
Γ(ν/2)(π(ν−2))1/2
Z ∞
0 xi 1 +
x2 i
ν−2
!−ν+1 2
dxi
= 2Γ((ν+ 1)/2) Γ(ν/2)(π(ν−2))1/2
(ν−2)
(ν−1)
= Γ((ν−1)/2)
√
ν−2
Γ(ν/2)√π . (2.16)
assi-2.2 Método Multivariado 24
métrica da função de densidade (2.15) são formados pelos elementos:
µi = (γi−γi−1)
Γ((ν−1)/2)√ν−2
Γ(ν/2)√π .
Por fim, da expressão (2.12) obtemos a distribuição de probabilidade t-Student
assimétrica e padronizada (SST(0,Im,γ, ν), Standard Skew t-Student).
p(z|γ, ν) = √2 π
!m m Y
i=1
γiσi
1 +γ2 i
!
Γ(ν+m 2 )
Γ(ν
2)(ν−2)m/2
1 + z∗
′
z∗
ν−2
!−
m+ν 2
, (2.17)
sendo,σi e zi∗ dado pelas expressões (2.10) e (2.12), respectivamente.
2.2.3
GED
A distribuição GED (Generalized Error Distribution) padronizada é escrita no caso
univariado como:
p(x|k) =
"
Γ(3/k)
Γ(1/k)
#1/2 exp
−hΓ(3Γ(1/k/k))x 2ik/2
2Γ((k+ 1)/k) . (2.18)
Essa distribuição generaliza a distribuição Normal podendo ter caudas mais leves
(k > 2) ou mais pesadas (k <2) do que a Normal Padrão (N(0,1)) e se k = 2 obtemos
a distribuição Normal.
Algumas generalizações multivariadas da distribuição GED foram propostas na
li-teratura, como por exemplo em Gómez et al. (1998) e Giller (2005), mas as marginais
dessas distribuições são difíceis de obter, assim como os momentos absolutos das
mar-ginais. Por este motivo, neste trabalho optou-se por utilizar a distribuição conjunta de
mvariáveis aleatórias independentes, garantindo assim, que as marginais serão a
2.2 Método Multivariado 25
do vetor aleatórioX = (X1, . . . , Xm)′ é dada por:
p(x|k) =
"
Γ(3/k)
Γ(1/k)
#m/2 exp
−hΓ(3Γ(1/k/k))
ik/2 Pm
i=1|xi|k
[2Γ((k+ 1)/k)]m . (2.19)
Como a distribuição (2.18) é padronizada, teremos E(X) = 0 e V ar(X) = Im
e assim podemos utilizar o método de Bauwens & Laurent (2005) para inserir
assi-metria. Para facilitar a notação referiremos a distribuição GED Multivariada como
GED(0,Im, k) e a distribuição resultante da aplicação do método e padronizada como
SSGED(0,Im,γ, k) (Standard Skew GED).
Calculemos inicialmente o primeiro momento absoluto da distribuiçãoGED(0,1, k):
M1 = 2
"
Γ(3/k)
Γ(1/k)
#1/2
1 2Γ((k+ 1)/k)
Z ∞
0 x exp
−
"
Γ(3/k)
Γ(1/k)x
2
#k/2
dx
=
"
Γ(3/k)
Γ(1/k)
#1/2
1 Γ((k+ 1)/k)
Γ((k+ 1)/k)Γ(2/k)
Γ(3/k)
= Γ(2/k)
[Γ(1/k)Γ(3/k)]1/2. (2.20)
Logo, substituindo (2.20) na expressão (2.8) temos que o vetor de médias da versão
assimétrica da função de densidade (2.19) é formado pelos elementos:
µi = (γi−γ
−1
i )
Γ(2/k)
[Γ(1/k)Γ(3/k)]1/2, (2.21)
para i= 1, . . . , m.
2.2 Método Multivariado 26
Assimétrica e Padronizada (SSGED(0,Im,γ, k), Standard Skew GED):
p(z|γ) = 2m
"m Y
i=1
γi
1 +γ2 i
σi
# "
Γ(3/k)
Γ(1/k)
#m/2 exp
−hΓ(3Γ(1/k/k))
ik/2 Pm
i=1|z ∗ i|k
(2/k)m[Γ(1/k)]m , (2.22)
sendoµi, σ2i e z ∗
i dados por (2.21), (2.10) e (2.12), respectivamente.
Assim, como a distribuição SSN consiste em caso particular da SST, também
consiste em um caso particular daSSGED, com k= 2.
As distribuições de probabilidade apresentadas neste capítulo serão aplicadas no
contexto de modelos GARCH univariados e multivariados, os quais serão apresentados
Capítulo 3
Modelos GARCH
Na modelagem estatística paramétrica de volatilidade, os modelos GARCH (
Genera-lized Autoregressive Conditional Heteroscedasticity) estão entre os principais modelos
empregados. O sucesso desses modelos deve-se principalmente à incorporação de
cer-tas características de dados financeiros em suas estruturas, tais como acomodação de
caudas pesadas e autocorrelação entre os quadrados de retornos financeiros.
É uma extensão natural considerar-se a modelagem simultânea de um conjunto de
séries de retornos definindo-se modelos GARCH multivariados. Podemos estar
inte-ressados por exemplo em estudar as relações entre as volatilidades e co-volatilidades
de vários mercados. Claramente, a construção de medidas de risco de um portfólio de
ativos financeiros será influenciada pela estrutura de dependência entre as séries que
compõem o portfólio.
Neste capítulo serão apresentados o modelo GARCH univariado de Bollerslev (1986)
e duas das principais extensões multivariadas, o CCC-GARCH de Bollerslev (1990) e
o DCC-GARCH de Engle (2002).
3.1 Modelos Univariados 28
3.1
Modelos Univariados
Considerey={yt, t= 1, . . . , T}como uma série de retornos. O modelo GARCH(p,q)
é definido como:
yt = ǫt
q
ht , ǫt ∼D(0,1) (3.1)
ht = ω+
p
X
i=1
αiy2t−i+ q
X
j=1
βjht−j, (3.2)
sendo os ǫt independentes e identicamente distribuídos e D(0,1) uma distribuição de
probabilidade com média zero e variância 1. Então ht é a variância condicional (não
observável) de yt dada a informação prévia It = {yt−1, yt−2, . . .}. As restrições
sufici-entes de positividade e estacionaridade deht são ω > 0, αi ≥ 0, i = 1, . . . , p, βj ≥ 0,
j = 1, . . . , q e Pp
i=1αi+Pqj=1βj <1.
Considerando a esperança e a variância de yt dadoIt, temos:
E[yt|It] =
q
htE[ǫt|It] =
q
ht E[ǫt] = 0 (3.3)
V ar[yt|It] = E[y2t|It] =ht V ar[ǫt] =ht. (3.4)
Logo, podemos utilizar a equação (3.3) para calcular a esperança incondicional:
E[yt] =E[E[yt|It]] = E[0] = 0.
Considerando agora a equação (3.4) para calcular variância incondicional, temos:
3.1 Modelos Univariados 29
Assumindo que a série y seja estacionária das equações (3.2) e (3.5) é fácil ver que
E[yt2] = ω
1− Pp
i=1αi+Pqj=1βj
. (3.6)
Da equação (3.6), temos que, para existir a variância incondicional deyté necessário
quePp
i=1αi+Pqj=1βj <1, justificando assim a restrição de estacionaridade do modelo.
Como da expressão (3.1) temos queǫt=yt/√ht, podemos escrever a fdp condicional
do retornoyt em função da fdp de ǫt. Obtemos assim,
p(yt|It) = (ht)−1/2pǫ(yt/
q
ht), (3.7)
sendopǫ a função de densidade de probabilidade deǫt. Agora, podemos obter a função
de verossimilhança do modelo substituindo (3.7) em (1.1). Logo, a função de
verossi-milhança do modelo será dada por:
L(θ) =
T
Y
t=1
(ht)
−1/2
pǫ(yt/
q
ht),
sendoθ = (ω, α1, . . . , αp, β1, . . . , βq)′ o conjunto de todos os parâmetros.
Vale notar que mesmo se ǫt ∼ N(0,1) a distribuição incondicional de yt não é
a Normal, em particular tendo caudas mais pesadas do que a Normal. No entanto,
existe evidência na literatura de que muitas séries temporais financeiras tendem a ter a
curtose observada ainda maior do que aquela implicada por um modelo GARCH com
erros normais. Sendo assim, alguns autores têm proposto distribuições com caudas
mais pesadas do que a Normal para os erros ǫt. Por exemplo, a distribuiçãot-Student
com ν graus de liberdade (Baillie & Bollerslev (1989), Ardia (2008)).
Identificar a ordem de um modelo GARCH a ser ajustado a uma série pode ser
3.1 Modelos Univariados 30
exemplo: (1,1), (1,2), (2,1) e (2,2)) e escolhe-se o modelo com base em critérios, como
o AIC (Akaike 1974) e o BIC (Schwarz 1978), entre outros. O autor também afirma,
que na maioria das series financeiras um modelo GARCH(1,1) é o mais parcimonioso
para descrever a volatilidade.
Nesta dissertação, o desenvolvimento do algoritmo de estimação será focado no
modelo GARCH(1,1), já que modelos GARCH de outras ordens podem ser estimados
de forma semelhante. A distribuição de probabilidade dos erros será considerada na
forma assimétrica apresentada no Capítulo 2, lembrando que para obter o caso simétrico
basta fixarγ = 1.
Sob o enfoque Bayesiano é necessário determinar a distribuição a priori dos
parâ-metros do modelo. Para os parâparâ-metros do GARCH(1,1) utilizaremos as distribuições
a priori propostas em Ardia (2006). Estás são normais truncadas no espaço
paramé-trico de cada um dos parâmetros, também assumiremos independência a priori entre
os parâmetros, desta forma obtemos: ω ∼ N(µω, σ2ω)I(ω>0), α1 ∼ N(µα, σα2)I(0<α<1)
e β1 ∼ N(µβ, σβ2)I(0<β<1), sendo µω, µα, µβ, σω2, σα2 e σβ2 hiperparâmetros. A notação
N(µ, σ2)I
(a<x<b), com b > a, representa a função densidade de probabilidade:
1
φ(b)−φ(a)×
1
√
2πσ2 exp −
(x−µ)2
2σ2
!
, x∈(a, b),
sendo φ(.) a função de densidade acumulada da distribuição normal com média µ e
variânciaσ2.
No caso, de utilizamos uma distribuição assimétrica, como as apresentadas no
Ca-pítulo 2, será necessário estimar o parâmetro assimetria, neste caso Fernandez & Steel
esco-3.1 Modelos Univariados 31
lher os valores de a e b de modo queE(γ) = 1.
1 =Eγ2(γ) =
ba
Γ(a)
Z ∞
0 γ (γ 2)a−1
e−bγ2
dγ2
= ba Γ(a)
Z ∞
0 (γ
2)(a+0,5)−1
e−bγ2
dγ2
= ba Γ(a)
Γ(a+ 0.5) ba+0.5 ,
o que implica,
b=
Γ
a+1 2
Γ(a)
2
. (3.8)
Considerando b como em (3.8) podemos fixar o valor de a controlando a variância
a priori e a probabilidade a priori de γ ∈ (0,1). Fixando a = 0,5 obtemos b ≈ 0,32,
o que nos leva a V ar(γ) = π/2−1 ≈ 0,57 e P(0 < γ < 1) ≈ 0,58 o que parece ser
uma escolha razoável. Além disso, esta particular escolha é equivalente a especificar
γ ∼N(0, 0,64−1)
I(γ>0), pois considerando Πγ e Πγ2 como as densidades a priori de γ
eγ2, respectivamente, temos:
Πγ(γ|a= 0,5, b= 0,32) = 2γ×Πγ2
γ2|a= 0,5, b = 0,32
∝ γ (γ2)1/2−1
exp(−0,32γ2)
∝ exp
−12 0,64γ2
∝ exp
(
− γ
2
2 (0,64)−1
)
, γ∈(0,∞).
Ainda, quando utilizarmos a distribuição SST(0,1, γ, ν) apresentada em (2.17)
ou SSGED(0,1, γ, k) apresentada em (2.22) devemos estimar o parâmetro de cauda
ν ou k, respectivamente. Neste caso, será utilizado ν ∼ N(µν, σν2)I(ν>2) e k ∼
N(µk, σk2)I(k>0), sendoµν, µk, σν2 e σ2k hiperparâmetros.
3.2 Modelos Multivariados 32
prioris, facilita a inserção de informação em uma determinada região de interesse
atra-vés dos parâmetros µ e σ2 da distribuição Normal (N(µ, σ2)), mesmo que no caso de
truncamento esses hiperparâmetros não representem a média e a variância, mas ainda
controlam a região de maior massa de probabilidade. A seguir apresentaremos os
mo-delos multivariados e logo, em seguida apresentaremos dois algoritmos de simulação
da distribuição a posteriori dos parâmetros que pode ser tanto usado para o modelo
multivariado quando para o modelo univariado.
3.2
Modelos Multivariados
Considere yt = (yt1, . . . , yt,m)′ como sendo um vetor de retornos no instantet para m
séries temporais. Assim, as extensões multivariadas dos modelos GARCH podem ser
escritas como:
yt =H
1/2
t ǫt, (3.9)
sendoHt a matriz de covariâncias condicionais eH
1/2
t a matrizm×mpositiva definida,
obtida pela decomposição de Cholesky da matrizHt. O vetor dos erros ǫt tem ordem
m×1 e tem média e variância dado por:
E(ǫt) = 0
V ar(ǫt) = Im,
sendo,Im a matriz identidade de ordem m.