4 Projeto de controladores por métodos clássicos

(1)

Capítulo 4

4 Projeto de controladores por métodos clássicos

4.1 Mapeamento entre plano Z e plano S

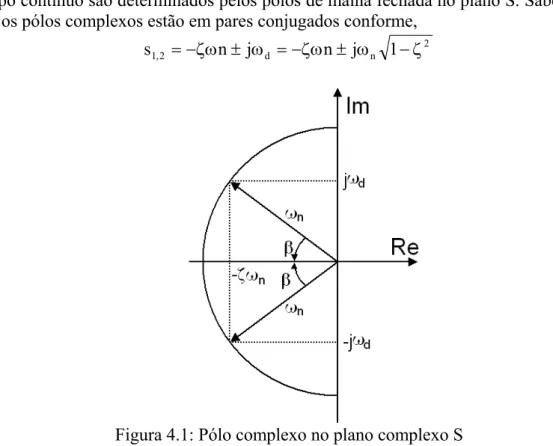
A estabilidade absoluta e relativa de sistemas lineares com parâmetros invariantes no tempo em se tratando de sistemas de controle em malha fechada em tempo contínuo são determinados pelos pólos de malha fechada no plano S. Sabendo-se que os pólos complexos estão em pares conjugados conforme,

2 n

d 2

,

1 n j n j 1

s =−ζω ± ω =−ζω ± ω −ζ

Figura 4.1: Pólo complexo no plano complexo S

Quando a amostragem é incorporada no processo, a relação que rege a transformação do plano complexo S para o plano discreto Z é dada por,

z ln T 1 s z

eTs = ⇒ =

onde T é o tempo de amostragem e s a raiz complexa.

Como a raiz s possui uma parte real e uma parte imaginária, ω

+ σ

= j

s Então,

( j ) T j T

T

Ts _e _e _e

e

z= = σ+ω = σ ω Como a exponencial complexa é dada por,

T sin j T cos

(2)

Significando que esta parte é repetida a cada 2πk, significando que freqüências que são múltiplas inteiras da freqüência de amostragem 2π/T são mapeadas na mesma região no plano Z, de acordo com a Figura 4.2, pois,

( j ) T j T T j( T2 k)

T Ts

e e e e e

e

z= = σ+ω = σ ω = σ ω π

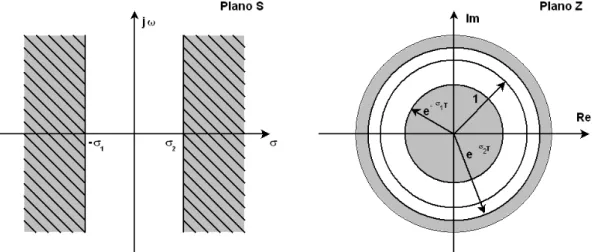
Figura 4.2: Faixas periódicas no plano complexo e a correspondente região no plano discreto, onde ωs corresponde à freqüência de amostragem.

Além disso, o lado esquerdo do plano S possui parte real negativa, significando que,

1 e z = σT <

Então todo o lado esquerdo do plano complexo é localizado no plano Z dentro de um círculo de raio unitário, o eixo jω é mapeado exatamente em cima do circulo e o lado direito do plano S é mapeado fora do circulo de raio unitário.

Além disso, quanto menor o tempo de discretização mais próximo do círculo de raio unitário encontra-se a raiz. Isto ocorre porque se T tende para zero então eσT tende para 1.

(3)

Figura 4.3: Localização das raízes complexas com a mesma parte real no plano discreto. No caso de raízes complexas com a mesma parte imaginária, elas encontram-se na forma de retas inclinadas de ω de acordo com a Figura 4.4.

Figura 4.4: Localização das raízes complexas com a mesma parte imaginária no plano discreto.

Para traçar as curvas de fator de amortecimento constante, basta lembrar que um pólo complexo pode ser dado por,

d n 2

n

n j 1 j

s=−ζω + ω −ζ =−ζω + ω Aplicando a transformação,

( ) ⎟

⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

ω ω π + ω ω ζ − πζ − ω + ζω

− ₌

=

= s

d s d 2 d

n

2 j 1 2

j Ts

e e

e z

Consequentemente,

⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

ω ω ζ −

πζ −

= s

d 2 1 2

e

z e

( )

s d

2 z angle

ω ω π =

(4)

Figura 4.5: Representação das curvas de fator de amortecimento constante.

Note que se a espiral de fator de amortecimento constante está no segundo ou terceiro quadrante do plano S, lado real negativo, então a espiral decai para dentro do circulo no plano Z. Se ela estiver no primeiro ou quarto quadrante, lado real positivo, que neste caso corresponderia a um caso com fator de amortecimento negativo, corresponderia a uma espiral crescendo para fora do circulo de raio unitário.

Além disso, deve- se notar que a medida que a freqüência aumenta, ela passa de uma banda para outra, sendo assim, só é necessário representar a primeira parte, que corresponde a 0 ≤ ω ≤ 1/2ωs, Figura 4.6, a parte correspondente de -1/2ωs ≤ ω ≤ 0 é uma imagem espelho para a parte de baixo.

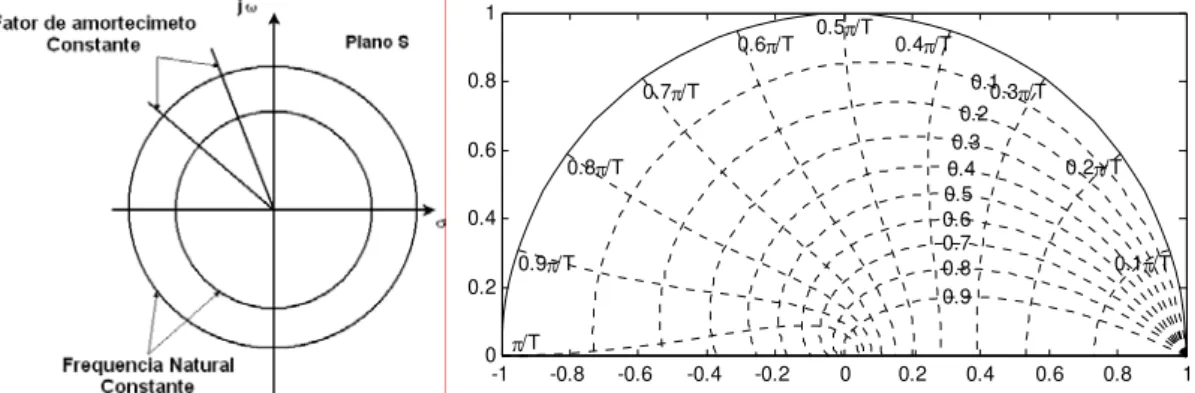
A curva para freqüência ωn constante, são círculos no plano S que são perpendiculares às curvas de fator de amortecimento constante, assim, a sua representação é dada na Figura 4.6, onde π/T é ωs/2.

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0

0.2 0.4 0.6 0.8 1

0.9 0.8 0.7 0.6 0.5 0.4 0.3

0.2 0.1

π/T 0.9π/T

0.8π/T 0.7π/T

0.6π/T 0.5π/T 0.4π/T 0.3π/T

0.2π/T 0.1π/T

Figura 4.6: Representação das curvas de freqüência natural constante e fator de amortecimento constante.

(5)

Figura 4.7: Localização das raízes complexas desejadas no plano discreto.

Aqui deve ser mencionado que se um sistema em tempo contínuo possui um par de pólos na forma s = - σ ± jω1 no plano s, e for feita uma amostragem tal que ω1 > 1/2ωs em que ωs = 2π/T, sendo T o tempo de amostragem, significando que este par de pólos complexo possui freqüência natural maior que a freqüência de Nyquist, ele cairá fora da primeira faixa de valores, mas como mencionado anteriormente, ele será transportado para dentro do circulo de raio unitário do plano Z como se estivesse posicionado no plano S em s = - σ ± j(ω1 - ωs).

4.2 Análise de Estabilidade de Sistemas no plano Z

Como mencionado anteriormente, para que um sistema seja assintoticamente estável no plano complexo S, os pólos deverão obrigatoriamente possuir a parte real negativa, que significa no plano Z estar localizado dentro do circulo de raio unitário, sendo assim,

• Assintoticamente estável, todos os pólos deverão apresentar z <1.

• Para que um sistema seja marginalmente estável no plano complexo S, o sistema deverá possuir pelo menos 1 pólo com a parte real nula e os demais possuírem parte real negativa, assim, marginalmente estável, pelo menos 1 pólo em z=1 e os demais com z <1;

• Para que o sistema seja instável no plano complexo S, ele deve possuir pelo menos 1 pólo com parte real positiva, que no plano Z corresponde à parte localizada fora do circulo de raio unitário, assim ,instável, pelo menos 1 pólo apresentando z >1.

Exemplo 4.1: Considerando o sistema em malha fechada apresentado abaixo,

(6)

Solução: Calculando a convolução do ZOH com a planta,

[

]

₍

₎

(

)

₍

₎

(

)

₍

₎

(

) (

[

₍

) (

_{) (}

₎

)

]

1 T 2 1 1 1 T T T 1 2 1 2 1 s p ZOH z e 1 z 1 z z Te e 1 e 1 T z 1 1 s s 1 Z z 1 1 s s 1 Z z 1 1 s s 1 s e 1 Z G G Z − − − − − − − − − − − − − − − − + + − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − =

Esta transformada foi obtida através de tabela de transformação. Item 13. fazendo a = 1. Agora substituindo os valores de T = 1 e simplificando, obtêm-se,

[

]

₍

₁

₎₍

1 ₁2

₎

p ZOH z 3679 . 0 1 z 1 z 2642 . 0 z 3679 . 0 ) z ( G G G

Z ₋ ₋

− − − − + = =

Como a função de transferência em malha fechada é dada por,

(

)(

)

(

)(

)

2 1 2 1 1 1 2 1 1 1 2 1 z 6321 . 0 z 1 z 2642 . 0 z 3679 . 0 z 3679 . 0 1 z 1 z 2642 . 0 z 3679 . 0 1 1 z 3679 . 0 1 z 1 z 2642 . 0 z 3679 . 0 1 ) z ( KG 1 ) z ( KG ) z ( R ) z ( C − − − − − − − − − − − − + − + = − − + + − − + = + =

Então, calculando as raízes do denominador, que são os pólos, encontra-se, 6181 . 0 j 5 . 0 z₁_,₂ = ± Pegando o valor absoluto,

( ) (

0.5 0.6181

)

0.7950 z₁_,₂ = 2 + 2 =

Como o valor é menor que 1, significa que o sistema é assintoticamente estável.

4.2.1 Teste de JURY

De modo análogo aos sistemas contínuos, podemos também estudar a estabiljdade BIBO dos sistemas discretos. Nos sistemas contínuos a condição de estabilidade é que os pólos da função de transferência estejam no semiplano esquerdo aberto do plano complexo. Para o caso dos sistemas discretos, como já vimos, o semiplano esquerdo aberto corresponde ao interior do circulo de raio unitário centrado na origem do plano Z. O teste de JURY serve para determinar se um dado polinômio tem ou não todas as suas raízes no interior do circulo de raio unitário.

(7)

-

'

-...

_

.

TESTE DE JURY- (E. L JURY)

O potinõmio

P(Z)

terá

todas as suas raizes no interior do árculo de raio unitário, se e

somentese:

1)

janj

<ao

2)P(z= 1)>0

>0 paranpar

3) P(

z

=

-1)

,

Condições necessálias

<

O para

n

unpar

onde: ( quadro de Jury ) :

zo

zl

z2

-·~

_L-

· zn-z

•

1 _an

_{0 n-l}

_{0 n- 2}

_{0 n-3}

_•

_a2

2 ao

_al

a2

.

aJ.

• ••

0 n-2

=>3

bn-1

bn-2

bn-3

bn-4

• •

• bl

=>4

bo

bt

b2

b3

_•

•

• bn-2

=>5

Cn-2

Cn-3

_Cn--4

Cn-s

_•••

Co

.

=>6

• Co

c1

c2

c3

Cn-2

.

'

~

•

• '

•

• _•

•

• 2n-5

P3

P2

Pl

_Po

2n-4

_Po

_Pt

_P2

P3

.

2n-3

_Q2

ql

qo

.

n-:-1

z

ai

0 n-l

.

bo

bn-1

•

• .

• ZR

ao

a,

.

,_

...

•

(8)

(9)

-zo

zl z2 z3

_z•

-

1 _a4

_~

_az

_llr

_~

2 _ao

_~

_a.

3 _b3

_b2

_~

_ho

.

4 ho

_~

_b2

_b3

5 _c2

c;

_Co

b3=

a4

Oo

_~b2

-

a4

~

_~bl

=

a4

~

_~bo

-

a4

~

a4

llo

_~

tlo

_~

ao

--

3 b(}

3 bl

b3.

b2

c2

=

bo

b3

;~

=

bo

b2

;co=

h

o

bl

Para P(Z) ser ESTÁVEL devemos

ter:

Condições necessárias:

1)

la

₄

1<a

₀

;2)

P(Z=l)>O

;3)

P(Z=-1)>0

-

_{TESTE DE JURY:}

--Observe que

Ct

não precisa ser calculado.

(10)

-excitação, mas ocorre uma subida rápida, o tr será pequeno ao passo que o td será grande.

3. Tempo de pico tp (Peak Time) é o tempo requerido para que a resposta do

sistema atinja o primeiro pico de sobresinal.

4. Máximo sobresinal Mp (Maximun Overshoot) é o pico máximo de sinal

acima da referência a ser atingida, isto é, se a referência for a resposta ao degrau, é o pico acima da amplitude 1. Por ser um fator que depende da excitação, costuma-se utilizar um percentual de sobresinal definido como,

% 100 )

( c

) ( c ) t ( c al sin sobre de m

porcentage ×

∞ ∞ − =

5. Tempo de estabilização ts (Settling Time) é o tempo necessário para a

resposta do sistema alcance e permaneça dentro de uma porcentagem da resposta em regime permanente, usualmente 2%.

Figura 4.8: Resposta ao degrau de um sistema com os parâmetros de projeto.

4.3 Resposta Transiente

Algumas aplicações de controle envolvem a melhora da resposta transitória do sistema segundo alguns critérios. A resposta transitória aparece na resposta do sistema quando ocorre alguma mudança de excitação, esta mudança pode ser do regime permanente para um outro regime permanente ou simplesmente quando o sistema sai do repouso.

As especificações para a resposta transiente envolvem normalmente os seguintes parâmetros apresentados na Figura 4.8,

1. Tempo de atraso td (Delay time) é o tempo requerido para que a resposta do

sistema alcance metade da resposta em regime permanente. Este parâmetro está relacionado com a velocidade de resposta do sistema.

2. Tempo de subida tr (Rise Time) é o tempo requerido para que a resposta do

sistema suba de 10% para 90% ou de 5% para 95% da resposta em regime permanente. Observe que se um sistema possui uma constante de tempo baixa, isto é, ele demore bastante para responder a uma mudança de

(11)

Figura 4.9: Sistema de malha fechada com controlador proporcional. O sistema em malha fechada possui a resposta dada por,

) z ( KG 1 ) z ( KG ) z ( R ) z ( C + =

onde K representa o ganho do controlador proporcional. O denominador ou equação característica é dado por,

0 ) z ( KG

1+ =

Que pode ser reescrita como,

(

)(

) (

)

(

)(

) (

)

0

p z p z p z z z z z z z K 1 n 2 1 m 2 1 = − − − − − − + L L

O método do lugar das raízes é baseado em dar valores para K na equação cima e encontrar os pólos correspondentes desejados. Interessante notar que,

(

)(

) (

)

(

)(

) (

)

K

1 p z p z p z z z z z z z n 2 1 m 2 1 = − − − − − − L L

Exemplo 4.2: Supondo que o sistema seja dado por,

[

]

T

T s p ZOH e z e 1 1 s 1 s e 1 Z G G Z ₋ − − − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − =

E o controlador seja na forma integral dada por, 1 z z K z 1 K ) z ( G 1

D ₋ = ₋

Observe que nem todas as especificações são aplicadas a todos os sistemas, isto é, se um sistema for superamortecido ou se for um sistema de primeira ordem ou se todas as raízes forem puramente reais negativas, não ocorrerá o sobre sinal e nem o tempo de pico.

4.4 Método de Projeto baseado no lugar das raízes

(12)

% Empacotando

sys=tf(num,den,T)

% aplicação do método do lugar das raízes

rlocus(sys);zgrid

Transfer function: 0.3935 z --- z^2 - 1.607 z + 0.6065

Sampling time: 0.5

Sampling time: 1

Sampling time: 2

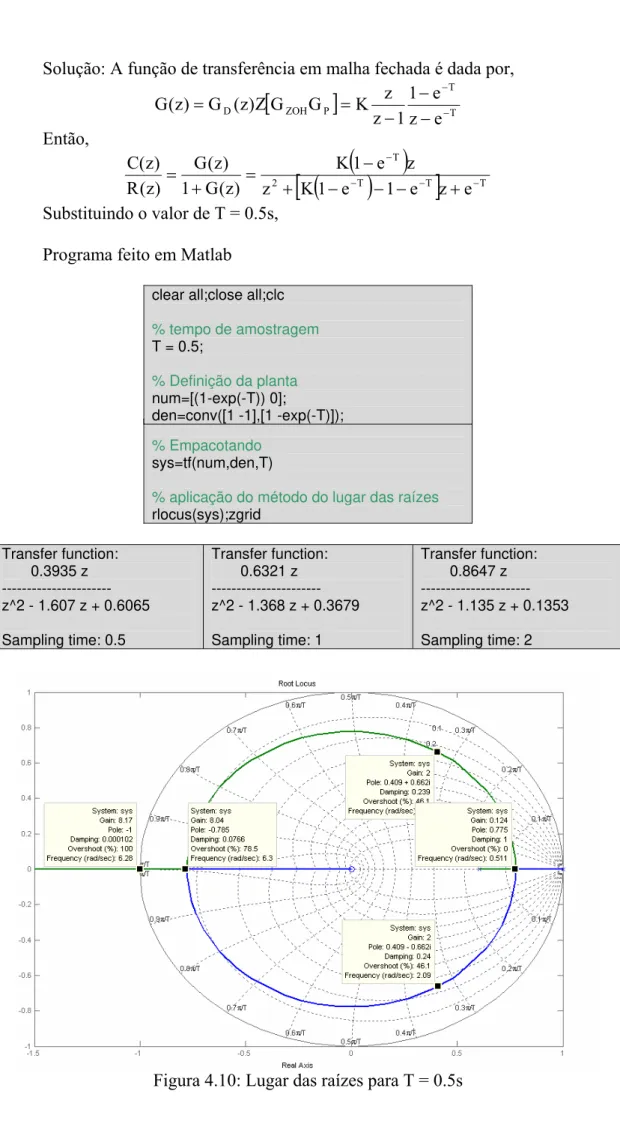
Figura 4.10: Lugar das raízes para T = 0.5s

= ₋

Solução: A função de transferência em malha fechada é dada por,

[

]

T_T

P ZOH D

e z

e 1 1 z

z K G G Z ) z ( G ) z (

G ₋

−

− − − = =

Então,

(

)

(

)

[

T T

]

T

2

T

e z e 1 e 1 K z

z e 1 K )

z ( G 1

) z ( G ) z ( R

) z ( C

− −

+ −

− − +

− =

+ =

Substituindo o valor de T = 0.5s, Programa feito em Matlab

clear all;close all;clc

% tempo de amostragem

T = 0.5;

% Definição da planta

num=[(1-exp(-T)) 0];

(13)

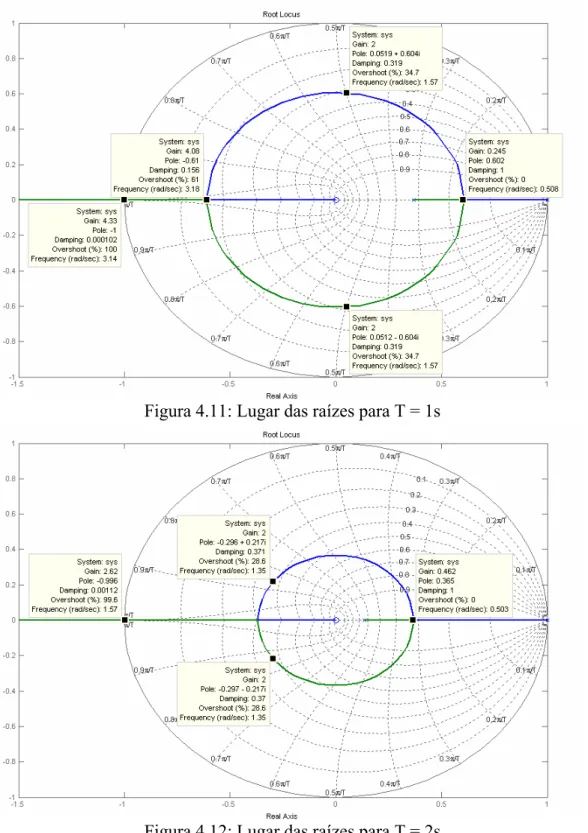
Figura 4.11: Lugar das raízes para T = 1s

Figura 4.12: Lugar das raízes para T = 2s

Exemplo 4.3: Observar a influência da variação dos parâmetros do controlador PID para o seguinte sistema,

(

s 1

)

(s 5) 1 )

s ( G_p

+ + =

(14)

[

]

₍

₎₍

₎

(

)

₍

₎₍

₎

(

)

₍

₎

₍

₎

(

_{) ( ) (}

₎

₍

₎

(

)(

) (

)(

) (

)(

)

(

)(

)

(

)

(

)

(

T 1

)(

5T 1

)

2 T T 5 T 6 1 T 5 T 1 T 5 1 T 1 T 1 1 T 5 1 1 T 1 T 5 1 T 5 1 T 1 1 1 1 s p ZOH z e 1 z e 1 20 z e e 5 e 4 z e e 5 4 z e 1 z e 1 20 z e 1 z 1 z e 1 z 1 5 z e 1 z e 1 4 z e 1 20 1 z e 1 4 1 z 1 5 1 z 1 5 s 20 1 1 s 4 1 s 5 1 Z z 1 5 s 1 s s 1 Z z 1 5 s 1 s s 1 s e 1 Z G G Z − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − + − + + − = − − − − + − − − − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − − − = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + − − = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + − =

O primeiro passo é calcular

clear all;close all;clc

% Planta contínua

num=1; % numerador

den=[conv([1 1],[1 5])]; % denominador

Gp=tf(num,den) % empacotando

% Planta discreta

T=0.1; % tempo de amostragem

b1=(4-5*exp(-T)+exp(-5*T));

b2=(4*exp(-6*T)-5*exp(-5*T)+exp(-T));

numd=[0 b1 b2]/20; % numerador

a1=-exp(-T)-exp(-5*T); a2=exp(-6*T);

dend=[1 a1 a2]; % denominador

Gz=tf(numd,dend,T) % empacotando

figure('Color',[1 1 1]) step(Gp,Gz)

legend('Contínuo','Discreto')

% diagrama de bode para escolher Kp

figure;rlocus(Gz);zgrid;set(gcf,'Color',[1 1 1])

0 1 2 3 4 5 6

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18

0.2 Step Response

Time (sec) A m pl it ude Contínuo Discreto Root Locus Real Axis Im agi n ar y A x is

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

0.1π/T 0.2π/T 0.3π/T 0.4π/T 0.5π/T 0.6π/T 0.7π/T 0.8π/T 0.9π/T

π/T

π/T 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 System: Gz Gain: 0 Pole: 0.607 Damping: 1 Overshoot (%): 0 Frequency (rad/sec): 5

System: Gz Gain: 10 Pole: 0.734 + 0.206i Damping: 0.705 Overshoot (%): 4.38 Frequency (rad/sec): 3.

(15)

Figura 4.13: Resposta do sistema considerando tempo contínuo e discreto e lugar das raízes

Calculando a resposta do sistema com o controlador proporcional,

% fechando a malha - Controle porporcional Kp

Sys1=feedback(2*Gz,1) % ganho Kp = 2

figure('Color',[1 1 1]);step(Sys1,Sys2,Sys3) legend('K_P = 2','K_P = 10','K_P = 50')

(16)

% Controle PD % Kp = 50 , Kd = 0

Kp=50;Kd=0;Ki=0;

num=[Kp+Kd+Ki -(Kp+2*Kd) +Kd];den=[1 -1 0]; GPIDz=tf(num,den,T)

sysMA=GPIDz*Gz

sysMF1=feedback(sysMA,1)

% Kp = 50 , Kd = 10

Kp=50;Kd=10;Ki=0;

sysMA=GPIDz*Gz

% Kp = 50 , Kd = 50

Kp=50;Kd=50;Ki=0;

num=[Kp+Kd+Ki -(Kp+2*Kd) +Kd]; den=[1 -1 0];

GPIDz=tf(num,den,T) sysMA=GPIDz*Gz

figure('Color',[1 1 1])

step(sysMF1, sysMF2, sysMF3,3) legend('K_D = 0','K_D = 10','K_D = 50')

% Controle PID

% Kp = 50 , Kd = 50 , Ki = 0

Kp=50;Kd=50;Ki=0;

sysMA=GPIDz*Gz

% Kp = 50 , Kd = 50 , Ki = 2

Kp=50;Kd=50;Ki=2;

sysMA= GPIDz*Gz

% Kp = 50 , Kd = 50 , Ki = 10

Kp=50;Kd=50;Ki=10;

sysMA=GPIDz*Gz

% Kp = 50 , Kd = 50 , Ki = 40

Kp=50;Kd=50;Ki=40;

num=[Kp+Kd+Ki -(Kp+2*Kd) +Kd]; den=[1 -1 0];

GPIDz=tf(num,den,T) sysMA=GPIDz*Gz

figure('Color',[1 1 1])

step(sysMF4,sysMF5,sysMF6,sysMF7,5) legend('K_I = 0','K_I = 2','K_I = 10','K_I = 40')

(17)

Figura 4.16: Respostadas do sistema controlado para vários valores de Ki, mantendo os valores de Kp = 50 e Kd = 50.

(18)

4.5 Projeto de Controladores PID

Os controladores PIDs são os controladores mais utilizados na prática devido a sua fácil implementação e ajuste. Aqui são apresentados os métodos Ziegler-Nichols de ajuste de controladores PID.

Deve ser lembrado que o PID Contínuo é dado por,

Tis K s T K s T T K s T 1 s T 1 K s K s K s K s K s K K ) s ( PID c i c 2 i d c i d c I p 2 d I d p + + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = + + = + + =

Enquanto que o PID discreto é dado por,

(

)

(

1

)

D 1 I P 1 d 1 1 i

c K 1 z

z 1 K K z 1 T T z 1 z 1 T 2 T 1 K ) z (

PID ₋ − ₋ −

− − + − + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − + + =

4.5.1 Ziegler-Nichols malha fechada

Supondo um controlador PID na forma,

Figura 4.18: Controlador PID

Para aplicar o método Ziegler-Nichols de malha fechada deve-se primeiro encontrar qual o ganho proporcional Kp, com o ganho integral Ki e o ganho Kd iguais a zero, que torna o sistema de malha fechada marginalmente estável, isto é, pelo menos um dos pólos do sistema de malha fechada deve ser puramente imaginário no plano complexo S, que no plano discreto Z significa tem módulo 1 ou estar em cima do círculo de raio unitário. Este ganho Kp passa a ser chamado de ganho crítico Kcr.

O sistema apresentado na Figura 4.18, fazendo o PID somente Kp, o sistema de malha fechada é dado por,

Kp ) z ( G 1 Kp ) z ( G ) z ( R ) z ( Y + =

(19)

Root Locus Real Axis Im ag in ar y A xi s

-3 -2 -1 0 1 2 3

-5 -4 -3 -2 -1 0 1 2 3 4 5 System: Gs Gain: 4.5 Pole: 0.00145 + 3.63i Damping: -0.0004 Overshoot (%): 100 Frequency (rad/sec): 3.63 System: Gs

Gain: 4.47 Pole: -0.00302 - 3.63i Damping: 0.000832 Overshoot (%): 99.7 Frequency (rad/sec): 3.63

Root Locus Real Axis Im agi nar y A xis

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

π/T

π/T 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 System: Gz Gain: 3.35 Pole: 0.807 + 0.59i Damping: 0.000454 Overshoot (%): 99.9 Frequency (rad/sec): 3.15

System: Gz Gain: 3.35 Pole: 0.807 - 0.59i Damping: 0.000454 Overshoot (%): 99.9 Frequency (rad/sec): 3.15

Figura 4.19: Lugar das Raízes no plano complexo S e no plano discreto Z

O segundo passo consiste em traçar a resposta ao degrau do sistema realimentado pelo ganho crítico Kcr. Desta resposta é retirado o tempo de oscilação Tu.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

0.5 1

Time (sec) Am pl itu de Tempo de Oscilação Tu

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

0.5 1

Time (sec) Am pl itu de Tempo de oscilação Tu

Figura 4.20: Resposta ao degrau do sistema realimentado com Kcr

Agora os parâmetros do controlador podem ser ajustados de acordo com a tabela abaixo.

Tabela 4-1: Ajustes do controlador PID para o método Ziegler-Nichols malha fechada.

Tipo do controlador Kc Ti Td

P 0,5 Kcr -- --

PI 0,45.Kcr Tu/1,2 ---

PID 0,6.Kcr 0,5Tu 0,125Tu

4.5.2 Ziegler-Nichols Malha Aberta

(20)

59 Figura 4.21: Resposta ao degrau unitário

A curva com o formato em S pode ser caracterizada por duas constantes, o atraso L e a constante de tempo T. O atraso e a constante de tempo são determinados desenhando-se uma linha tangente no ponto de inflexão da curva com o formato de S e determinando-se a interseção da linha tangente com o eixo do tempo. O ajuste do controlador PID, segundo este método, introduz no sistema dois zeros em -1/L se o projeto for feito em tempo contínuo.

Tabela 4-2: Ajustes do controlador PID para o método Ziegler-Nichols malha aberta.

Tipo de controlador Kc Ti Td

P T/L ∞ 0

PI 0,9T/L L/0,3 0

PID 1,2T/L 2L 0,5L

4.6 Exercícios Propostos

Exercício 4.1: Para o sistema abaixo, quais seriam os pólos em tempo discreto? 100

s 10 s

100 )

s (

G ₂

+ + =

Exercício 4.2: Para o Exemplo 4.1, encontrar quais os valores que K que tornam o sistema em malha fechada um sistema assintoticamente estável, marginalmente estável e instável.

(21)

(

s 1

)(

s 2

)(

s 3

)

2 )

s ( G

+ + +

= e

1 s 30

1 ) s ( H

+ =