Uma abordagem baseada em procura directa direccional a problemas com ruído

(1)

Samuel Pacheco Marques Vaz Marcos

Licenciado em Matemática

Uma abordagem baseada em procura directa

direccional a problemas com ruído

Dissertação para obtenção do Grau de Mestre em

Matemática e Aplicações – Actuariado, Estatística e Investigação Operacional

Orientadora: Ana Luísa Custódio, Professora auxiliar, Universidade NOVA de Lisboa

Júri

Presidente: Doutor Jorge Orestes Lasbarrères Cerdeira Arguente: Doutora Maria do Carmo Proença Caseiro Brás

(2)

(3)

Uma abordagem baseada em procura directa direccional a problemas com ruído

Por decisão pessoal, o autor do texto não escreve segundo o novo acordo ortográfico. A Faculdade de Ciências e Tecnologia e a Universidade NOVA de Lisboa têm o direito, perpétuo e sem limites geográficos, de arquivar e publicar esta dissertação através de exemplares impressos reproduzidos em papel ou de forma digital, ou por qualquer outro meio conhecido ou que venha a ser inventado, e de a divulgar através de repositórios científicos e de admitir a sua cópia e distribuição com objetivos educacionais ou de inves-tigação, não comerciais, desde que seja dado crédito ao autor e editor.

Este documento foi gerado utilizando o processador (pdf)LA_{TEX, com base no template “unlthesis” [1] desenvolvido no Dep.}

(4)

(5)

Agradecimentos

O mais sentido agradecimento à Professora Doutora Ana Luísa da Graça Batista Cus-tódio pela orientação, acompanhamento, paciência e disponibilidade neste percurso de aprendizagem. Não há palavras que quantifiquem a dedicação e disponibilidade demons-trada.

Agradeço a todos os meus Professores das várias unidades curriculares do Mestrado.

A todos os meus colegas, principalmente ao Rui Cândido, que me acompanharam neste percurso académico um grande agradecimento pela amizade, motivação e compa-nheirismo demonstrado.

(6)

(7)

Resumo

Em aplicações a nível industrial, principalmente em engenharia, é frequente ser-se confrontado com problemas de optimização desafiadores onde, em particular, a avaliação da função objectivo pode estar contaminada com ruído numérico. A presença deste ruído inviabiliza a utilização de métodos de optimização baseados em derivadas.

A procura directa direccional (PDD) é um dos métodos que não recorre a derivadas. Nesta dissertação procurou-se avaliar o seu desempenho numérico na optimização de funções sujeitas a ruído, propondo eventuais adaptações que a tornassem mais eficien-te/eficaz.

Foi feito um estudo numérico do seu desempenho considerando três tipos (baseado em polinómios de Chebyshev, Normal e Uniforme) e três níveis (5%, 10% e 20%) de ruído. Concluiu-se a necessidade da adaptação da PDD quando a inicialização considerada está longe do ponto óptimo, sobretudo na presença de níveis elevados de ruído, ou de ruído com oscilações mais irregulares (como é o caso do ruído Normal).

Adoptaram-se então abordagens não monótonas, onde se procura melhorar o valor da função objectivo não entre iterações consecutivas, mas ao longo de um histórico de itera-ções, permitindo escapar a mínimos locais espúrios, resultantes da presença do ruído.

Foram propostas duas variantes de PDD baseadas em abordagens não monótonas, analisadas as suas propriedades teóricas de convergência e o seu desempenho numérico. Estabeleceu-se a vantagem da utilização destes algoritmos, por comparação com algorit-mos monótonos de PDD, para orçamentos computacionais moderados.

Analisou-se ainda as eventuais mais valias da implementação de uma‘cache’. Em pro-blemas onde o ruído é estocástico, esta mostrou-se dispensável. No caso de ruído baseado em polinómios de Chebyshev, dada a natureza determinística do ruído, o uso de uma

‘cache’pode trazer algumas mais valias.

(8)

(9)

Abstract

Commonly, in industrial applications, mainly in engineering, we face challenging op-timization problems where, in particular, the evaluation of the objective function could be contaminated by numerical noise. The presence of this noise prevents the use of deriva-tive based optimization methods.

Directional direct search (DDS) is one of the methods that does not resort to deriva-tives. In this thesis we tried to evaluate its numerical performance on the optimization of noisy functions, proposing adaptations that would make it more robust/efficient, if

required.

A study on its numerical performance was conducted considering three types (based on Chebyshev polynomials, Normal, and Uniform) and three levels (5%, 10%, and 20%) of noise. We have concluded that DDS needs to be adapted when the initialization consid-ered is far from the optimal point, mainly if the level of noise is high, or when in presence of noise with quite irregular oscillations (as it is the case of Normal noise).

Nonmonotone approaches were adopted, where the value of the objective function is not required to improve between consecutive iterations, but along an historic of iterations. This would allow to escape from spurious minima, resulting from the presence of noise.

Two variants of DDS based on non monotonous approaches were proposed, the cor-responding theoretical properties related to convergence were analyzed, as well as their numerical performance. For moderate computational budgets, the advantage of using these algorithms was established, by comparison with monotonous variants of DDS.

The possible advantages of implementing a cache were also considered. In the pres-ence of stochastic noise, the use of a cache is not required. When the noise results from Chebyshev polynomials, given its deterministic nature, the use of a cache could bring some improvement.

(10)

(11)

Índice

Lista de Figuras xiii

Lista de Tabelas xv

1 Introdução - Optimização sem derivadas em problemas com ruído 1

1.1 Motivação . . . 1

1.2 Trabalhos anteriores . . . 2

1.3 Objectivos e organização da dissertação. . . 4

2 A classe da procura directa direccional 5 2.1 Breve enquadramento histórico . . . 5

2.2 Conjuntos geradores e bases positivas. . . 5

2.3 Descrição de um algoritmo básico . . . 6

2.4 Estratégias de globalização . . . 9

2.5 Eficiência computacional . . . 10

2.6 Análise de convergência . . . 11

2.7 Tendências recentes da procura directa direccional . . . 15

3 Análise de desempenho da procura directa direccional em optimização de problemas com ruído 17 3.1 Estudo exploratório do desempenho da procura directa direccional em quádricas . . . 17

3.2 Análise numérica do desempenho da procura directa direccional em pro-blemas com ruído . . . 23

3.2.1 A classe de problemas . . . 24

3.2.2 Perfis de dados. . . 26

3.2.3 Experiência numérica. . . 26

4 Estratégias não monótonas 29 5 Estratégias não monótonas em procura directa direccional na optimização de problemas com ruído 31 5.1 Descrição das variantes algorítmicas . . . 31

(12)

ÍNDICE

6 Análise de desempenho das estratégias não monótonas em PDD na

optimi-zação de problemas com ruído 37

6.1 Estratégias não monótonas . . . 38

6.1.1 Ruído baseado em polinómios de Chebyshev . . . 38

6.1.2 Ruído Normal . . . 39

6.1.3 Ruído Uniforme . . . 40

6.2 Impacto real do processo de optimização . . . 41

6.3 Utilização de uma‘cache’ . . . 42

7 Conclusões e questões em aberto 47 7.1 Conclusões . . . 47

7.2 Questões em aberto . . . 49

Bibliografia 51 A Tabelas 55 A.1 Estratégias não monótonas . . . 55

A.1.1 Ruído baseado em polinómios de Chebyshev . . . 56

A.1.2 Ruído Uniforme . . . 57

(13)

Lista de Figuras

2.1 Um algoritmo de procura directa direccional. . . 9

2.2 Minimização de uma função recorrendo a um método de procura directa direccional. . . 11

3.1 Gráfico da funçãof(x) =x2+ 2x−3. . . 18

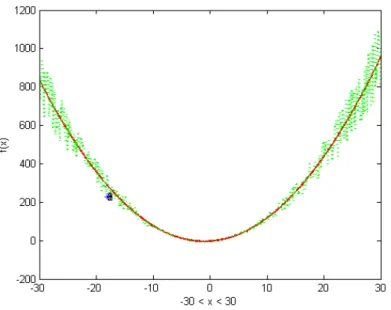
3.2 Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 5%, baseado em poli-nómios de Chebyshev (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas. . . 19

3.3 Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 10%, baseado em polinómios de Chebyshev (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas. . . 20

3.4 Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 20%, baseado em polinómios de Chebyshev (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas. . . 20

3.5 Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 20%, baseado em ruído Normal (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas. . . 21

3.6 Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 20%, baseado em ruído Uniforme (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspon-dentes a iterações bem sucedidas. . . 21

3.7 Perfis de dados para o conjunto de problemas perturbados com ruído baseado em polinómios de Chebyshev, para os níveis de ruído de 5%, 10% e 20%, respectivamente. . . 27

3.8 Perfis de dados para o conjunto de problemas perturbados com ruído Uniforme, para os níveis de ruído de 5%, 10% e 20%, respectivamente. . . 28

3.9 Perfis de dados para o conjunto de problemas perturbados com ruído Normal para os níveis de ruído de 5%, 10% e 20%, respectivamente. . . 28

5.1 Construção e actualização do histórico de pontos nas estratégias não monótonas. . . 32

5.2 Um algoritmo de procura directa direccional, considerando estratégias não monótonas. . . . 33

(14)

Lista de Figuras

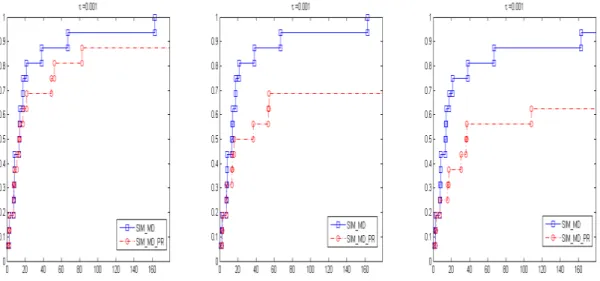
6.2 Perfis de dados para o conjunto de problemas perturbados com ruído Normal, para os níveis de ruído de 5%, 10% e 20%, respectivamente, em qualquer dos casos com o comprimento do histórico igual a 2. . . 39

6.3 Perfis de dados para o conjunto de problemas perturbados com ruído Uniforme, para os níveis de ruído de 5%, 10% e 20%, respectivamente, em qualquer dos casos com o comprimento do histórico igual a 2. . . 41

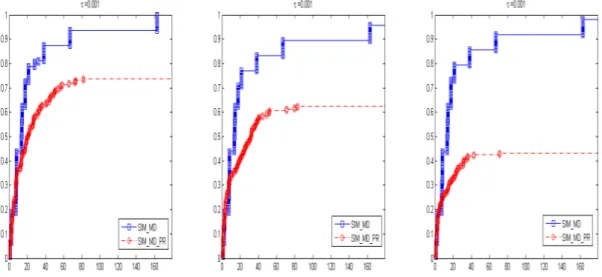
6.4 Perfis de dados para o conjunto de problemas sem contaminação com ruído, mas utilizando as sequências de iteradas geradas anteriormente pelos algoritmos, para ruído baseado em polinó-mios de Chebyshev, ruído Normal e ruído Uniforme, respectivamente, considerando um nível de ruído de 10%. . . 42

6.5 Comparação do desempenho entre a PDD utilizando uma‘cache’e a PDD sem‘cache’ conside-randoβ= 2 para os dois primeiros perfis de dados eβ= 1 para o terceiro.. . . 43

6.6 Perfis de dados para o conjunto de problemas perturbados com os três tipos de ruído

(baseado em polinómios de Chebyshev, Normal e Uniforme, respectivamente), considerando um nível de ruído de 10%, comβ= 2.. . . 44

(baseado em polinómios de Chebyshev, Normal e Uniforme, respectivamente), considerando um nível de ruído de 10%, comβ= 1.. . . 44

(15)

Lista de Tabelas

3.1 Resultados da aplicação da PDD a problemas contaminados com ruído Uniforme, considerando três níveis de ruído. . . 22

3.2 Resultados da aplicação da PDD a problemas contaminados com ruído Normal, considerando três níveis de ruído. . . 22

3.3 Resultados da aplicação da PDD a problemas contaminados com ruído baseado em polinómios de Chebyshev, considerando três níveis de ruído. . . 22

3.4 Resultados da aplicação da PDD considerando um nível de ruído de 5% e os diferentes tipos de ruído. . . 23

3.7 Número de problemas para cada uma das dimensões,np, consideradas no conjunto teste (2≤ np≤12). . . 24

3.8 Dimensões, valores óptimos encontrados na literatura e valores finais obtidos pela PDD consi-derando inicializações perto ou longe do óptimo. . . 25

A.1 Mínimo obtido para cada problema e para cada estratégia, considerando um nível de ruído de 5%. . . 56

A.4 Estatísticas descritivas da melhor estratégia (SUF_BWNMD), considerando um nível de ruído de 5%. . . 57

(16)

Lista de Tabelas

(17)

C

a

p

í

t

u

l

o

1

Introdução - Optimização sem derivadas em

problemas com ruído

1.1 Motivação

Em aplicações industriais, nomeadamente em engenharia, é frequente a necessidade de resolver problemas de optimização, desafiantes a vários níveis. O aumento da capa-cidade computacional faz com que cada vez mais se recorra a modelos complexos para representação de sistemas, que frequentemente necessitam de ser optimizados [21,26]. Neste contexto, não existe uma expressão analítica que represente a função objectivo e a sua avaliação numérica, com recurso ao modelo de simulação, é geralmente dispendi-osa. A dedução analítica de expressões para as derivadas, essenciais à generalidade dos algoritmos de optimização numérica, é inviável e aproximações numéricas ao seu valor, recorrendo a diferenças finitas, são impraticáveis devido ao custo computacional associ-ado à avaliação da função. Há casos ainda em que estas derivadas não existem nos pontos de interesse, devido ao carácter não suave da função.

Para além das dificuldades anteriormente descritas, a avaliação da função objectivo pode estar contaminada com ruído numérico, o que coloca desafios adicionais à optimi-zação, já que a avaliação de um mesmo ponto pode conduzir a valores distintos fruto da contaminação com ruído. Aplicações de optimização em que a função objectivo se encon-tra contaminada com ruído surgem nas mais diversas áreas. Exemplos podem ser dados em aerodinâmica [21,44], na área da medicina, mais concretamente no tratamento de tu-mores hepáticos e na simulação de modelos epidemiológicos para o cancro da mama [16], no transporte em gaseodutos [9] ou na definição de políticas económicas para recursos hídricos [31].

(18)

CAPÍTULO 1. INTRODUÇÃO - OPTIMIZAÇÃO SEM DERIVADAS EM PROBLEMAS COM RUÍDO

dificuldade inerente à classe de problemas a que se destinam e pelo elevado potencial de aplicação.

Estes algoritmos podem classificar-se em três grandes subclasses: os métodos de re-giões de confiança baseados em interpolação ou regressão polinomial, os métodos de procura directa e os métodos de procura unidireccional [13]. No primeiro caso, em cada iteração do algoritmo a função objectivo é aproximada por um modelo de interpolação ou de regressão polinomial, válido numa vizinhança da iterada corrente (a região de con-fiança). Este modelo é optimizado, sendo a função objectivo avaliada no ponto resultante do processo de optimização. A eventual concordância entre o decréscimo sentido no mo-delo e a correspondente variação sentida na função objectivo dita a forma como deve ser actualizado o raio da vizinhança de validade do modelo e a própria actualização do modelo.

No caso dos métodos de procura directa distinguem-se a procura directa direccional e a procura directa simplética. No primeiro caso, os algoritmos progridem por amostragem da função objectivo em conjuntos de pontos com uma geometria adequada. Esta classe de métodos será detalhada no Capítulo 2 do presente trabalho. Na procura directa simplé-tica, de que é exemplo o famoso algoritmo do simplex de Nelder-Mead [38], a amostragem é feita em vértices de conjuntos simpléticos (conjuntos não degenerados den+ 1 pontos, num espaço de dimensãon). Em cada iteração, o algoritmo pretende melhorar o pior vér-tice, efectuando operações de reflexão, expansão e contracção do simplex que pretendem adaptar a sua forma à curvatura da função objectivo.

Por último, como a própria terminologia indica, os métodos de procura unidireccio-nal consideram em cada iteração uma única direcção com boas propriedades de descida, que será explorada até que uma condição adequada de decréscimo do valor da função objectivo seja satisfeita.

Para uma abordagem mais detalhada de cada uma destas classes de métodos de opti-mização sem recurso a derivadas pode ser consultado o livro [13].

1.2 Trabalhos anteriores

No caso específico da optimização de funções sujeitas a ruído numérico, é comum considerar-se que os métodos de optimização sem recurso a derivadas permitem a obten-ção de bons óptimos locais, para níveis moderados de ruído (ver Secobten-ção 1.3 de [13]).

Exemplos pertencentes à classe de métodos de regiões de confiança encontram-se nos trabalhos [8,44]. Em [44], as considerações geométricas acerca da qualidade do conjunto de pontos usados na construção dos modelos são ignoradas na actualização do raio das regiões de confiança consideradas pelo algoritmo. O algoritmo é estendido à optimização sujeita a limites no valor das variáveis e aplicado num problema de optimização de forma em aerodinâmica.

(19)

pre-1.2. TRABALHOS ANTERIORES

proposta pelos mesmos autores, consiste no ajuste dinâmico do comprimento do passo, dando passos maiores quando o modelo e a função estão de acordo entre si e passos mais pequenos quando o modelo é menos preciso. Este método não requer que o utilizador especifique um padrão fixo de pontos para construção dos modelos locais e não utiliza a reamostragem de pontos. Esta pode ser uma boa estratégia para lidar com ruído determi-nístico, onde o processo de reamostragem é totalmente ineficiente.

Contudo, quando o ruído tem uma natureza estocástica, a reamostragem de pon-tos foi utilizada em diversos trabalhos para adaptar os algoritmos à presença de ruído. Em [17] é desenvolvida uma variante do algoritmo UOBYQA (Unconstrained Optimization BY Quadratic Approximation) [40] para problemas de optimização na presença de ruído estocástico. Esta variante aplica técnicas Bayesianas para decidir se um dado passo do UOBYQA deve ou não ser executado. Estas alterações têm o intuito de controlar o erro aleatório através de médias de múltiplas avaliações por ponto, de forma a que o algoritmo proceda apropriadamente.

Analogamente, os mesmos autores apresentaram uma extensão do algoritmo DIRECT (DIviding RECTangles) [18] para resolver problemas de optimização global de funções sujeitas a ruído. O método DIRECT [28,29] foi modificado, usando informação adquirida com amostras Bayesianas, para determinar um número apropriado de réplicas por ponto e através da sua média reduzir a incerteza presente na avaliação da função.

Métodos de procura unidireccional também foram sugeridos para optimizar proble-mas com ruído. Em [33] são utilizadas estratégias não monótonas, sendo escolhidas como direcções o gradiente espectral e as direcções de quasi-Newton, BFGS e SR1 [25]. Em qualquer dos casos, são feitas aproximações ao gradiente recorrendo a diferenças finitas centrais.

Num contexto em que a avaliação da função objectivo é dispendiosa, o uso de diferen-ças finitas pode ter um custo proibitivo. Uma solução de compromisso consiste na procura unidireccional usando gradientes simpléticos, também conhecida por filtro implícito [30]. De forma simplista, um gradiente simplético pode ser visto como o gradiente de um mo-delo linear de interpolação polinomial. A sua construção baseia-se então na amostragem da função objectivo em conjuntos simpléticos. Os conjuntos simpléticos estão também na base do famoso algoritmo de procura directa, o simplex de Nelder-Mead [38], para o qual existe uma variante adaptada a problemas sujeitos a ruído [2], novamente baseada em processos de reamostragem.

Refere-se ainda o uso de métodos de procura aleatória [10] que pretendem acelerar a optimização usando, para direcções de procura, vectores aleatórios. No caso do STARS (Stepsize Approximation in Random Search), o comprimento do passo é suavizado, de forma dinâmica e ajustada ao ruído presente na função objectivo, minimizando o erro dos mí-nimos quadrados entre a verdadeira derivada direccional da função com ruído e a sua aproximação com diferenças finitas.

(20)

CAPÍTULO 1. INTRODUÇÃO - OPTIMIZAÇÃO SEM DERIVADAS EM PROBLEMAS COM RUÍDO

robustas do algoritmo MADS (Mesh Adaptive Direct Search) [7]. Neste caso não é utilizada reamostragem de pontos, recorrendo-se a valores previamente avaliados para a função objectivo.

1.3 Objectivos e organização da dissertação

Da leitura da secção anterior conclui-se que são vários os trabalhos que analisam a utilização de métodos de optimização sem recurso a derivadas em problemas sujeitos a ruído. Contudo, pouco existe feito sobre procura directa direccional, uma classe de métodos que tem vindo a ser profundamente estudada, dadas as suas interessantes pro-priedades teóricas e os bons resultados em aplicações.

Neste trabalho pretende-se analisar o desempenho da procura directa direccional na optimização de funções sujeitas a ruído numérico, eventualmente equipando-a com uma abordagem não monótona que permita escapar aos óptimos locais espúrios resultantes da presença de ruído numérico.

No Capítulo 2 é feito um breve enquadramento histórico desta classe de métodos e a descrição de um algoritmo básico de procura directa direccional (PDD). É revista a aná-lise de convergência destes algoritmos, detalhando-se os requisitos básicos para assegurar essa convergência, nomeadamente o uso de conjuntos geradores positivos e de estratégias de globalização. São ainda feitas considerações sobre a eficiência computacional destes algoritmos e tendências recentes desta classe de métodos.

A análise do desempenho numérico da PDD em problemas com ruído é feita no Capí-tulo 3, onde numa primeira abordagem se faz um estudo exploratório em quádricas. Este estudo é posteriormente estendido a uma classe mais completa de problemas, que será utilizada nos restantes testes numéricos deste trabalho.

Uma resenha histórica do uso de estratégias não monótonas em optimização não li-near é feita no Capítulo 4. Neste capítulo são descritas várias variantes não monótonas, bem como a sua evolução ao longo do tempo e a sua introdução na classe de algoritmos de optimização sem recurso a derivadas.

As estratégias não monótonas em procura directa direccional para optimização de funções sujeitas a ruído são apresentadas no Capítulo 5. Descrevem-se duas variantes algorítmicas de PDD não monótona e é feita a respectiva análise de convergência.

Estes algoritmos são numericamente testados no Capítulo 6. Neste capítulo é ainda feita uma experiência numérica, tentando melhorar a eficiência computacional da PDD não monótona, com a introdução de uma‘cache’.

(21)

C

a

p

í

t

u

l

o

2

A classe da procura directa direccional

2.1 Breve enquadramento histórico

O primeiro algoritmo de procura directa direccional conhecido é referido num rela-tório técnico de Fermi e Metropolis [20], em 1952. Contudo, o termo procura directa só foi proposto em 1961 por Hooke e Jeeves [27], e é apenas na década de 90, com a tese de doutoramento de Torczon [41] e os consequentes trabalhos [42,43], que é feito um tratamento matemático para alguns algoritmos pertencentes a esta classe, nomeadamente para a procura em padrão. Esta classe de algoritmos é generalizada em 2002, por Audet e Dennis [4], surgindo pela primeira vez a organização de cada iteração num passo de procura e num passo de sondagem.

Os métodos de procura directa direccional caracterizam-se por em cada iteração não considerarem qualquer modelo explícito ou implícito da função objectivo, avaliando sim-plesmente o seu valor num conjunto de pontos com boas propriedades geométricas. Isto significa que, em cada iteração, o conjunto de pontos considerado deverá corresponder a pelo menos uma direcção de descida, independentemente da existência e/ou localização do vector gradiente. Os conjuntos geradores positivos ou as bases positivas são uma forma de definir estes conjuntos de pontos.

2.2 Conjuntos geradores e bases positivas

Definição 2.2.1. Um conjunto de vectores D ={di, i = 1,· · ·, r} ⊆ Rn diz-se um conjunto

gerador positivo do conjuntoA⊆Rn_{se qualquer vector de}_A_{pode ser escrito como combinação}

linear não negativa dos vectoresd_i(i= 1,· · ·, r), ou seja:

A={d∈Rn:_d=_α₁_d₁+_α₂_d₂+_{· · ·}+_α

(22)

CAPÍTULO 2. A CLASSE DA PROCURA DIRECTA DIRECCIONAL

Uma base positiva emRné um conjunto gerador positivo positivamente independente,

ou seja, é um conjunto de vectores que gera Rn através de combinações lineares não

negativas e tal que nenhum dos seus vectores pode ser obtido como combinação linear não negativa dos restantes. A cardinalidade de uma base positiva deRnestá compreendida

entren+ 1 e 2nelementos [15]. Uma base positiva com cardinalidaden+ 1 designa-se por base positiva minimal, enquanto que uma base positiva que possua cardinalidade 2n diz-se uma base positiva maximal.

Exemplos de bases positivas minimais e maximais deRn, são respectivamente:

                 

1 0 . . . 0 −1 0 1 . . . 0 −1

..

. ... . .. ... −1 0 0 . . . 1 −1

                                   

1 0 . . . 0 −1 0 . . . 0 0 1 . . . 0 0 −1 . . . 0

..

. ... . .. ... ... ... . .. ... 0 0 . . . 1 0 0 . . . −1

                 

Num contexto de optimização onde não é possível utilizar derivadas, mesmo que elas existam, qualquer conjunto gerador positivo contém pelo menos uma direcção com boas propriedades de descida. De facto, assumindo que ∇f existe, mas não está disponível para uso, prova-se que pelo menos uma das direcções de um conjunto gerador positivo faz um ângulo inferior a 90º com−∇f, ou seja, é uma direcção de descida [15].

Proposição 2.2.1. O conjunto {d1,· · ·, dr} gera positivamente Rn se e só se para qualquer

vectorv,0emRné possível encontrari∈ {1,· · ·, r}tal quev⊤di>0.

Esta proposição garante que, se se tiver uma função diferenciável numa vizinhança de um pontoxpara o qual∇f(x),0, ao explorar os vectores pertencentes a um conjunto

gerador positivo deRn, um desses vectores_d_i satisfaz_−∇_f(_x)⊤_d_i _>0. Isto significa que,

quando∇f(x) ,0, todo o conjunto gerador positivo deRn apresenta pelo menos uma

direcção de descida.

2.3 Descrição de um algoritmo básico

(23)

2.3. DESCRIÇÃO DE UM ALGORITMO BÁSICO

Considere-se um problema de optimização sem restrições:

minf(x), comf :Rn_→R_{∪ {}+_∞}_,

onde se assume que as derivadas def ou não existem, ou não estão disponíveis para uso, não podendo ser aproximadas numericamente. Um algoritmo de procura directa direcci-onal gera uma sucessão de iteradas{xk}k∈K ⊆Rn, cuja correspondente sucessão de valores

para a função objectivo{f(xk)}k∈K é decrescente em sentido lato. Cada iteração divide-se

em dois passos: o passo de procura e o passo de sondagem.

Passo de procura

O passo de procura é opcional e desnecessário para as propriedades de convergência do método. Este passo é normalmente definido pelo utilizador, frequentemente corres-pondendo a uma heurística que já era usada. Como requisito geral, em cada iteração terá que avaliar a função objectivo num número finito de pontos. Contudo, dependendo da estratégia de globalização utilizada, que será detalhada na Secção 2.4, os pontos avaliados poderão ter de pertencer a uma grelha implícita considerada pelo algoritmo. O passo de procura pode ainda ser usado para a implementação de heurísticas que permitem melho-rar a eficiência algorítmica. Este passo diz-se bem sucedido quando se encontra um ponto que corresponde a um melhor valor da função objectivo. Se tal não ocorrer, o algoritmo obrigatoriamente executa o passo de sondagem.

Passo de sondagem

Neste segundo passo, a função objectivo é avaliada numa vizinhança discreta da ite-rada corrente (x_k), definida à custa de uma base positiva ou de um conjunto gerador positivo – o chamadoconjunto de sondagem.

Definição 2.3.1. Seja D um conjunto finito de bases positivas ou de conjuntos geradores positivos deRn_{. O conjunto de sondagem}_P_k_{, associado à iterada}_x_k _{de um método de procura}

directa direccional é definido por:

P_k={x_k+∆

kd:d∈Dk},

onde∆

krepresenta um comprimento do passo eDk∈D. O vectord∈Dk diz-se uma direcção

de sondagem exk+∆kd∈Pk um ponto de sondagem.

(24)

Caso contrário, estar-se-á na presença de um insucesso.

No teste do conjunto de sondagem pode-se seguir uma estratégia oportunista ou completa. No primeiro caso aceita-se um ponto de sondagem logo que se encontre um ponto que reduz o valor da função objectivo, não avaliando os pontos correspondentes às restantes direcções de sondagem. No caso da estratégia completa, todas as direcções de sondagem são testadas, escolhendo-se como nova iterada o ponto correspondente ao valor mais baixo que melhore a função objectivo (caso exista). Note-se que no caso de um passo de sondagem mal sucedido, as duas estratégias são indistintas. Uma iteração dir-se-à bem sucedida se o passo de procura ou o passo de sondagem forem bem sucedidos. Caso contrário, dir-se-à um insucesso.

Actualização do comprimento do passo

Dependendo da existência de sucesso ou insucesso, o comprimento de passo,∆ k,

de-verá ser actualizado no final de cada iteração.

Para tal, fixe-se inicialmenteβ≥1 e 0< µ <1. Quando a iteração é bem sucedida, o com-primento do passo é mantido ou aumentado (∆

k+1=β∆k). Na presença de um insucesso,

(25)

2.4. ESTRATÉGIAS DE GLOBALIZAÇÃO

Uma descrição algorítmica da procura directa direccional encontra-se na Figura2.1.

Inicialização

Considerarx0∈Rncomf(x0)<+∞, um conjunto de conjuntos geradores positivos ou

de bases positivasDdeRne um comprimento inicial de passo∆₀_>0. Considerar ainda

β≥1 e 0< µ <1, utilizados na actualização do comprimento do passo. Sejak= 0.

Passo de Procura

Avaliar a função objectivo num número finito de pontos, tentando encontrar um ponto x ∈ Rn que satisfaça _f(_x) _{< f}(_x

k). Se tal for possível, definir a iteração como bem

sucedida, considerarxk+1=xe omitir o passo de sondagem. Caso contrário, realizar o

passo de sondagem.

Passo de Sondagem

EscolherDk∈De considerar o conjunto de sondagemPk={xk+∆kd:d∈Dk}. Avaliarf

emP_k.

Se existirxk+∆kd∈Pk tal quef(xk+∆kd)< f(xk), considerarxk+1=xk+∆kd e definir a

iteração como bem sucedida. Caso contrário, considerarxk+1=xk e definir a iteração

como um insucesso.

Actualização do Comprimento do Passo

Se a iteração foi bem sucedida, fazer∆_k₊₁=_β∆_k. Caso contrário, considerar∆_k₊₁=_µ∆_k.

Incrementar o contador de iterações, fazendok=k+ 1 e voltar ao passo de procura.

Figura 2.1:Um algoritmo de procura directa direccional.

2.4 Estratégias de globalização

Para garantir algum tipo de convergência para a sucessão de iteradas gerada por um algoritmo de procura directa direccional é necessário mostrar que existe pelo menos uma subsucessão de iteradas convergente. Para tal, um primeiro passo consiste em garantir que uma subsucessão de comprimentos de passo converge para zero. Este propriedade é obtida com as chamadas estratégias de globalização, que podem ser de dois tipos: uso de grelhas racionais ou imposição de decréscimo suficiente.

No primeiro caso, quando a estratégia de globalização é baseada na utilização de grelhas racionais, todos os pontos gerados pelo algoritmo devem pertencer a uma grelha implícita

Mk={xk+∆kDz:z∈N

(26)

em queDé uma matriz cujas colunas correspondem aos vectores de um número finito de conjuntos geradores positivos,|D|representa a sua cardinalidade eN₀é o conjunto de

inteiros maiores ou iguais a zero. Para garantir esta propriedade, há que impor algumas condições na forma como são construídas as bases positivas ou os conjuntos geradores positivos usados nas várias iterações do algoritmo e também na forma como são feitas as actualizações do comprimento do passo [4]. Esta estratégia permite a aceitação de novos pontos desde que haja um decréscimo simples no valor da função objectivo.

Alternativamente, a estratégia de globalização pode ser baseada na imposição de uma condição de decréscimo suficiente. Neste caso, a flexibilidade presente nas regras de actualização do comprimento de passo e na construção das direcções de sondagem tem como contrapartida uma maior exigência no critério de aceitação de novos pontos. Nesta variante, uma iterada é bem sucedida se a condição

f(xk+1)< f(xk)−ρ(∆k) (2.1)

for satisfeita, onde ρ representa uma função definida em ]0,+∞[, contínua, positiva e crescente, satisfazendo

lim

t→0+

ρ(t) t = 0.

Um exemplo de uma família de funções com estas características é a definida por ρ(α) =cαj, comc >0, j >1 constantes reais [32].

2.5 Eficiência computacional

(27)

2.6. ANÁLISE DE CONVERGÊNCIA

Figura 2.2:Minimização de uma função recorrendo a um método de procura directa direccional.

Para aumentar esta eficiência, uma estratégia simples consiste na implementação de uma ‘cache’, ou seja, de um histórico de pontos avaliados, por forma a impedir que o algoritmo volte a testar pontos cujo valor da função objectivo já tenha sido calculado. Antes da nova avaliação, o algoritmo verifica se o ponto em causa não consta já da‘cache’, evitando qualquer avaliação desnecessária da função objectivo.

Outras estratégias contemplam a ordenação das direcções de sondagem, testando, por exemplo, em primeiro lugar a última direcção bem sucedida. Versões mais elaboradas consistem na definição de indicadores de descida, sendo as direcções de sondagem orde-nadas de acordo com o menor ângulo que fazem com estes indicadores [14].

A utilização de vectores de comprimento de passo em vez de um parâmetro escalar [6] pode também ajudar a reduzir a sensibilidade da procura directa direccional ao escalona-mento das variáveis, contribuindo para o auescalona-mento da eficiência computacional.

2.6 Análise de convergência

Para esta classe de métodos de optimização sem recurso a derivadas pode ser deduzida uma hierarquia de resultados de convergência, que dependem da suavidade da função objectivo [4]. Mesmo no caso de funções descontínuas, pode-se estabelecer garantias de alguma forma de estacionaridade [45].

A análise de convergência apresentada baseia-se no trabalho de Audet e Dennis [4] e de Kolda, Lewis e Torczon [32]. A primeira hipótese considerada por estes autores pres-supõe que todas as iteradas produzidas por um algoritmo de procura directa direccional pertencem a um conjunto compacto. Para tal, uma condição suficiente seria supor que o conjunto

(28)

é compacto. No entanto, em alguns resultados basta assumir queL(x0) é limitado.

Hipótese 2.6.1. O conjuntoL(x0) ={x∈Rn:f(x)≤f(x0)}é limitado.

Em primeiro lugar, terá que se provar a existência de uma subsucessão de comprimen-tos de passo que converge para zero, garantindo assim, a convergência de subsucessões de pontos gerados pelo algoritmo.

Teorema 2.6.1. Sob a Hipótese2.6.1, um método de procura directa direccional, considerando uma estratégia de globalização baseada em grelhas racionais, gera uma sucessão de comprimen-tos de passo tal que,

liminf

k→+∞ ∆

k= 0.

Demonstração. Suponha-se que

liminf

k→+∞

∆_k_,0_.

Então existe um ∆∗ _> 0, tal que∆_k _> ∆∗,_∀_k _∈ N. Todos os pontos gerados pelo

al-goritmo pertencem a uma grelha racional implícita que constitui um reticulado [4]. A intersecção de um conjunto limitado com um reticulado é finita. Assim, há um número finito de pontos distintos que se podem aceitar como novas iteradas em iterações bem sucedidas, o que significa que há um número finito de sucessos e infinitos insucessos. Em cada iteração mal sucedida o comprimento de passo é reduzido emµ >0, o que conduz a um absurdo.

No caso da estratégia de globalização do algoritmo ser baseada numa condição de decréscimo suficiente, o conjunto das imagens é que terá que ser limitado.

Hipótese 2.6.2. O conjunto{f(x) :f(x)≤f(x0)}é limitado inferiormente.

Teorema 2.6.2. Sob a Hipótese2.6.2, um método de procura directa direccional, que usa a condição (2.1) para exigir decréscimo suficiente nas iterações com sucesso, gera uma sucessão de comprimentos de passo tal que,

liminf

k→+∞ ∆

(29)

2.6. ANÁLISE DE CONVERGÊNCIA

Demonstração. Suponha-se que

liminf

k→+∞

∆_k_,0_.

Então existe um ∆∗ _>0, tal que ∆

k >∆∗, ∀k ∈ N. Dado que em cada iteração sem

sucesso o factor utilizado para a actualização comprimento de passo é 0< µ <1, o número de iterações com sucesso é infinito. Atendendo às propriedades da função ρ(.), tem-se ρ(∆

k)≥ρ(∆∗)>0. Pode-se assim afirmar quef(xk+1)−f(xk)<−ρ(∆k)≤ −ρ(∆∗)<0 para

iterações bem sucedidas. Para iterações sem sucesso, f(x_k+1)−f(xk) = 0, o que leva a

concluir quef(xk)→ −∞contradizendo a Hipótese2.6.2.

Dado que

liminf

k→+∞ ∆

k= 0

e que o comprimento de passo só é reduzido em insucessos tem que existir uma subsuces-são{x_k}_k∈K′, correspondente a iterações sem sucesso, tal que

lim

k∈K′

∆ k= 0.

Uma subsucessão com estas características designa-se porsubsucessão refinada. Como

L(x0) pela Hipótese2.6.1é limitado, existe uma subsucessão de{xk}k∈K′ que

adicional-mente converge. Ou seja, existe uma subsucessão de iteradas sem sucesso {x_k}_k_∈_K′′ e K′′ ⊆K′ tal que

lim

k∈K′′ ∆

k= 0 e lim k∈K′′xk=x

∗

.

A convergência da procura directa direccional num contexto não suave é estabelecida ao analisar o comportamento do algoritmo em pontos limite de subsucessões refinadas. Para tal, começa-se por introduzir o conceito de derivada direccional generalizada de Clarke [12], definida para funções localmente contínuas à Lipschitz, ou seja, que local-mente satisfazem uma condição do tipo|f(x)−f(y)| ≤L||x−y||, comL≥0.

Definição 2.6.1. Sejaf uma função continua à Lipschitz perto dex∗. A derivada direccional generalizada de Clarke da funçãof, calculada emx∗, na direcçãod é dada por

fo(x∗;d) = limsup

x→x∗

t↓0

f(x+td)−f(x)

t .

(30)

Teorema 2.6.3. Sejax∗o ponto limite de uma subsucessão refinada convergente gerada com um método de procura directa direccional e f continua à Lipschitz numa vizinhança de x∗. Suponha-se ainda que f é avaliada num número infinito de vezes na direcção d usada na definição dos conjuntos de sondagem da subsucessão refinada. Então a derivada direccional generalizada de Clarke da funçãof definida emx∗, na direcção d, é não negativa, ou seja,

fo(x∗;d)≥0.

Demonstração. Seja{xk}k∈K uma subsucessão refinada convergente parax∗. Dado quef

é contínua à Lipschitz numa vizinhança dex∗, quando se considera uma estratégia de globalização baseada em grelhas racionais, pela definição de Clarke tem-se,

fo(x∗;d) = limsup

x→x∗ t↓0

f(x+td)−f(x) t ≥limk∈K

f(xk+∆kd)−f(xk) ∆

k

.

Este último quociente é não negativo, dado que xk é um elemento da subsucessão

refinada convergente para x∗, logo correspondente a uma iteração sem sucesso. Assim sendo, o limite superior inicial é também não negativo.

Se a estratégia de globalização for baseada numa condição de decréscimo suficiente, dado que ρ(∆k)

∆_k →0, quando∆k→0, tem-se

fo(x∗;d) = limsup

x→x∗

t↓0

f(x+td)−f(x)

t ≥

lim

k∈K

f(xk+∆kd)−f(xk) ∆

k

= lim

k∈K

f(xk+∆kd)−f(xk) +ρ(∆k) ∆

k

−ρ(∆k) ∆

k ≥0.

Uma versão mais robusta do resultado anterior pode ser obtida se se assumir mais suavidade acerca da função objectivo. Note-se que, como D tem cardinalidade finita, haverá sempre um conjunto gerador positivo que será utilizado um número infinito de vezes em cada subsucessão refinada.

Teorema 2.6.4. Sejax∗o ponto limite de uma subsucessão refinada convergente gerada com um método de procura directa direccional. Sef for estritamente diferenciável emx∗, então

∇f(x∗) = 0.

Demonstração. Sef é diferenciável emx∗, entãofo(x∗;v) =∇f(x∗)⊤v [12]. SejaD′ o con-junto gerador positivo que é usado um número infinito de vezes pela subsucessão refinada. Pelo Teorema 2.6.3, para cadad∈D′,∇f(x∗)⊤d≥0. Considere-sev∈Rn, não nulo e não

or-togonal a∇f(x∗). O vectorvpode ser escrito como combinação linear não negativa dos ele-mentos deD′, ou seja,v=P|_iD₌₁′|α_id_i comα_i ≥0. Assim∇f(x∗)⊤_v₌P|D′|

i=1αi∇f(x∗)⊤di≥0.

(31)

2.7. TENDÊNCIAS RECENTES DA PROCURA DIRECTA DIRECCIONAL

2.7 Tendências recentes da procura directa direccional

Quando se pretende a minimização de uma função não suave recorrendo a um método de procura directa direccional, o uso de um número finito de conjuntos geradores ou de bases positivas pode conduzir a situações de convergência para pontos que não corres-pondem ao mínimo da função. Alguns exemplos foram apresentados em [32], motivando o desenvolvimento de uma nova classe de algoritmos de procura directa direccional –

MADS (Mesh Adaptive Direct Search)[5].

Continuando a usar uma estratégia de globalização baseada em grelhas racionais, a característica distintiva desta nova classe de algoritmos resulta da reunião dos conjuntos geradores ou das bases positivas usadas ao longo das várias iterações ser assimptotica-mente densa na esfera unitária. A implementação original [5] de um conjunto de direcções de sondagem com as características mencionadas baseava-se em matrizes triangulares inferiores (LTMADS) e envolvia alguma aleatoriedade. Posteriormente, por forma a evitar esta aleatoriedade e a obter uma melhor distribuição espacial das direcções que consti-tuem cada conjunto gerador positivo, foi proposta a implementaçãoOrthoMADS[1], onde as direcções que constituem cada conjunto de sondagem são ortogonais entre si e geradas de forma determinística.

(32)

(33)

C

a

p

í

t

u

l

o

3

Análise de desempenho da procura directa

direccional em optimização de problemas

com ruído

Neste capítulo pretende-se estabelecer a eventual necessidade da definição de estra-tégias de adaptação da procura directa direccional (PDD) à optimização de problemas com ruído. Para tal, começou-se por analisar o seu desempenho numérico na presença de diferentes tipos e níveis de ruído, procurando-se ainda estudar a dependência da inicia-lização considerada. Em qualquer dos testes numéricos realizados o algoritmo de PDD descrito na Figura 2.1foi implementado em Matlab, considerando-se o conjunto gera-dor positivo [en,−en, In,−In], em queen é um vector coluna de uns de dimensão n eIn

representa a matriz identidade. Considerou-se uma estratégia de globalização baseada em grelhas racionais, um comprimento de passo inicial∆₀= 1 e os parâmetros_β= 2 e

µ=1₂ na actualização do comprimento de passo. O passo de sondagem foi efectuado de forma oportunista, tal como descrito na Secção 2.3. Como critério de paragem permitiu-se um máximo de 1500 avaliações da função.

3.1 Estudo exploratório do desempenho da procura directa

direccional em quádricas

(34)

CAPÍTULO 3. ANÁLISE DE DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM OPTIMIZAÇÃO DE PROBLEMAS COM RUÍDO

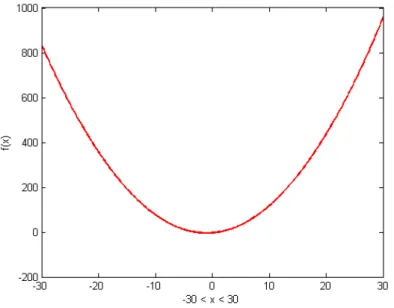
Figura3.1), sendo uma função simples, cujo mínimo global é conhecido (neste caso cor-responde ao par (−1,−4)).

Figura 3.1:Gráfico da funçãof(x) =x2+ 2x−3.

A quádrica anterior foi contaminada com três tipos distintos de ruído: baseado em po-linómios de Chebychev [36], Uniforme [36] ou Normal [33]. Para cada tipo de problemas, definido pelo ruído considerado, analisaram-se ainda três níveis de ruído distintos: 5%, 10% e 20%.

A classe de problemas com ruído Uniforme [36] é dada por:

¯

f(x) = (1 +U)f(x), (3.1)

em que U é uma variável com distribuição uniforme no intervalo [−ε, ε], sendoεo nível de ruído considerado.

A classe de problemas com ruído baseado em polinómios de Chebyshev [36] é definida por:

¯

f(x) = (1 +εα(x))f(x), (3.2)

em que novamenteεrepresenta a percentagem de ruído considerada,

α(x) =α0(x)(4α0(x)2−3) (3.3)

(35)

3.1. ESTUDO EXPLORATÓRIO DO DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM QUÁDRICAS

Finalmente, a classe de problemas com ruído Normal [33] é definida por:

¯

f(x) = (1 +N)f(x), (3.5)

comN uma variável com distribuição Normal de médiaµ= 0 e variânciaσ2=ε2, sendo εa percentagem de ruído considerada.

Adicionalmente ao máximo de 1500 cálculos para a função objectivo, considerou-se um comprimento mínimo de passo igual a 2.220E−16 (correspondente à precisão de

máquina utilizada pelo Matlab).

Os gráficos das Figuras3.2e3.3ilustram o impacto do aumento de 5% na percenta-gem de ruído considerado, quando este é baseado em polinómios de Chebyshev.

A análise dos dois gráficos seguintes torna claro o efeito da estrutura do ruído consi-derada. À medida que há um distanciamento do ponto óptimo, verifica-se que existe uma maior oscilação na avaliação da função objectivo. Observa-se também que um aumento de apenas 5% no nível de ruído (em relação à Figura3.2) tem um impacto significativo no nível de oscilação da função. Ainda assim, a PDD é bem sucedida na determinação do ponto óptimo.

(36)

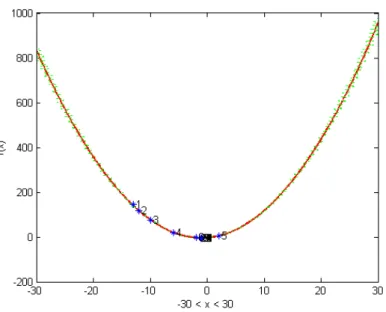
Figura 3.3:Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 10%, baseado em polinó-mios de Chebyshev (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas.

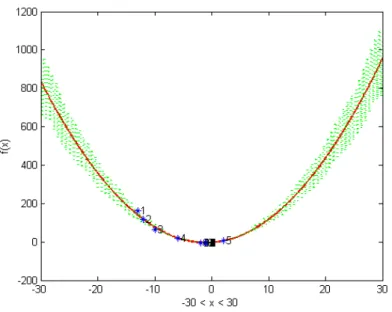
Considerando agora o nível de ruído mais elevado (20%), as Figuras3.4–3.6procuram ilustrar cada um dos três tipos de ruído adoptados (baseado em polinómios de Chebyshev, ruído Uniforme e ruído Normal, respectivamente).

(37)

3.1. ESTUDO EXPLORATÓRIO DO DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM QUÁDRICAS

Figura 3.5:Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 20%, baseado em ruído Normal (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas.

Figura 3.6:Gráfico da funçãof (a vermelho) perturbada com um nível de ruído de 20%, baseado em ruído

Uniforme (a verde). Os asteriscos azuis representam os pontos obtidos pela PDD, correspondentes a iterações bem sucedidas.

(38)

do problema.

Realizou-se então um estudo numérico que procura avaliar a capacidade da PDD em ser bem sucedida, considerando os três tipos de ruído numérico (baseado em polinómios de Chebyshev, ruído Uniforme e ruído Normal) e as três percentagens de ruído (5%, 10% e 20%). As Tabelas 3.1–3.3respeitam à variação da percentagem de ruído presente na função objectivo. As Tabelas3.4–3.6consideram uma percentagem de ruído fixa e fazem variar o tipo de ruído a que a função está sujeita.

Considerando inicializações inteiras, em qualquer uma das seis tabelas as colunas 2 e 6 registam as inicializações mais distantes do ponto óptimo que permitem a convergência da PDD para o óptimo (o correspondente valor da função objectivo encontra-se nas colu-nas 3 e 7). As colucolu-nas 4 e 8 representam as inicializações mais perto do ponto óptimo para as quais a PDD falha a sua determinação, sendo o correspondente valor final da função objectivo registado nas colunas 5 e 9.

Tabela 3.1:Resultados da aplicação da PDD a problemas contaminados com ruído Uniforme, considerando três níveis de ruído.

Ruído Uniforme x_ini f_final x_ini f_final x_ini f_final x_ini f_final

5% 61 -4,200 62 3.708E+03 -70 -4,200 -71 4.595E+03

10% 32 -4,200 33 1.053E+03 -54 -4,300 -55 2.693E+03

20% 20 -4,776 21 394.268 -22 -4,761 -23 427.030

Tabela 3.2:Resultados da aplicação da PDD a problemas contaminados com ruído Normal, considerando três níveis de ruído.

Ruído Normal x_ini f_final x_ini f_final x_ini f_final x_ini f_final

5% 52 -4,600 53 2.498E+03 -44 -4,500 -45 1.603E+03

10% 19 -4,794 20 361.673 -27 -4,858 -28 553.294

20% 12 -5,222 13 115.532 -17 -5,635 -18 155.774

Tabela 3.3:Resultados da aplicação da PDD a problemas contaminados com ruído baseado em polinómios de Chebyshev, considerando três níveis de ruído.

Ruído bas. pol. Chebyshev x_ini f_final x_ini f_final x_ini f_final x_ini f_final

5% 49 -4,200 50 2.540E+03 -67 -4,200 -68 4.348E+03

10% 31 -4,400 32 1.054E+03 -32 -4,400 -33 931.426

20% 25 -4,743 26 669.072 -26 -4,743 -27 576.761

(39)

3.2. ANÁLISE NUMÉRICA DO DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM PROBLEMAS COM RUÍDO

óptimos locais espúrios resultantes da presença desse ruído.

Tabela 3.4:Resultados da aplicação da PDD considerando um nível de ruído de 5% e os diferentes tipos de ruído.

5% x_ini f_final x_ini f_final x_ini f_final x_ini f_final Ruído Uniforme 61 -4,200 62 3.708E+03 -70 -4,200 -71 4.595E+03

Ruído Normal 52 -4,600 53 2.498E+03 -44 -4,500 -45 1.603E+03

Ruído bas. pol. Chebyshev 49 -4,200 50 2.540E+03 -67 -4,200 -68 4.348E+03

10% x_ini f_final x_ini f_final x_ini f_final x_ini f_final Ruído Uniforme 32 -4,200 33 1.053E+03 -54 -4,300 -55 2.693E+03

Ruído Normal 19 -4,794 20 361.673 -27 -4,858 -28 553.294

Ruído bas. pol. Chebyshev 31 -4,400 32 1.054E+03 -32 -4,400 -33 931.426

20% x_ini f_final x_ini f_final x_ini f_final x_ini f_final Ruído Uniforme 20 -4,776 21 394.268 -22 -4,761 -23 427.030

Ruído Normal 12 -5,222 13 115.532 -17 -5,635 -18 155.774

Ruído bas. pol. Chebyshev 25 -4,743 26 669.072 -26 -4,743 -27 576.761

Por outro lado, a análise das Tabelas3.4–3.6permite concluir que, em cada nível de ruído, o tipo de ruído afecta a distância do ponto óptimo a que se pode considerar a inicialização do método, por forma a que a PDD seja bem sucedida. As classes de ruído baseado em polinómios de Chebyshev e de ruído Uniforme permitem em geral maiores distâncias entre o ponto inicial e o ponto óptimo do que a baseada em ruído Normal.

3.2 Análise numérica do desempenho da procura directa

direccional em problemas com ruído

Esta segunda abordagem numérica tem objectivos semelhantes aos da abordagem anterior mas foi considerado um conjunto de 53 problemas recolhidos da literatura, cada um permitindo dois tipos de inicializações distintas (longe e perto do ponto óptimo, res-pectivamente). O código que define cada uma das funções objectivo pode obter-se em

http://www.mcs.anl.gov/~more/dfo.

(40)

a solução dos problemas perturbados com diferentes tipos/níveis de ruído, o que motivará eventualmente a sua adaptação a este tipo de optimização.

3.2.1 A classe de problemas

Na Tabela3.7regista-se o número de problemas para cada uma das dimensões,n_p, consideradas no conjunto teste (2≤np≤12).

Tabela 3.7: Número de problemas para cada uma das dimensões,np, consideradas no conjunto teste

(2≤np≤12).

Dimensão do problema(np) 2 3 4 5 6 7 8 9 10 11 12 Número de problemas 5 6 5 4 4 5 6 5 4 4 5

Cada um destes problemas pode ser combinado com os três tipos de ruído consi-derados na Secção 3.1: baseado em polinómios de Chebyshev [36], Uniforme [36] ou Normal [33]. Para cada classe de problemas, à semelhança do que foi feito na Secção 3.1, analisaram-se três níveis de ruído distintos: 5%, 10% e 20%.

Partindo de uma classe de problemas suaves, definida por:

f(x) =

m

X

k=1

f_k2(x), (3.6)

a classe de problemas com ruído Uniforme [36] é dada por

¯

f(x) = (1 +U)

m

X

k=1

f_k2(x), (3.7)

em queUé uma variável com distribuição uniforme no intervalo [−ε, ε], sendoεo nível de ruído considerado.

A classe de problemas com ruído baseado em polinómios de Chebyshev [36] é definida por:

¯

f(x) = (1 +εα(x))

m

X

k=1

f_k2(x), (3.8)

em que novamente εrepresenta a percentagem de ruído considerada, sendo α(x) eα0

definidos de acordo com as equações 3.3 e 3.4.

Finalmente, a classe de problemas com ruído Normal [33] é definida por:

(41)

3.2. ANÁLISE NUMÉRICA DO DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM PROBLEMAS COM RUÍDO

comN uma variável com distribuição Normal de médiaµ= 0 e variânciaσ2=ε2, sendo εa percentagem de ruído considerada.

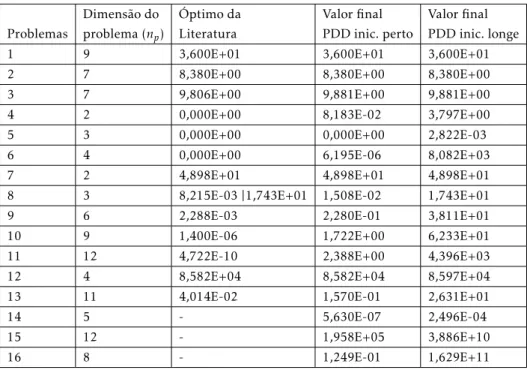
Dos 53 problemas descritos, apenas em 16 é sugerido utilizar inicializações longe do ponto óptimo, considerando um factor multiplicativo que afecte a inicialização proposta na literatura [36]. Na Tabela3.8representam-se as dimensões destes 16 problemas (se-gunda coluna) e os valores óptimos reportados na literatura [37], sem contaminação de ruído (terceira coluna). Pode-se observar que o problema 8 apresenta dois óptimos locais enquanto que para os problemas 14, 15 e 16 não foi encontrado registo dos respectivos valores óptimos. A quarta coluna apresenta o melhor ponto obtido pela procura directa direccional considerando os valores iniciais propostos na literatura. A quinta coluna apre-senta os melhores valores obtidos pela PDD considerando os valores iniciais propostos pela literatura multiplicados por 50, por forma a considerar inicializações longe do ponto óptimo.

Os resultados numéricos obtidos permitem concluir que, considerando um orçamento computacional de 1500 cálculos (razoável para problemas desta classe, com este tipo de dimensões), a PDD é, em geral, bem sucedida quando a inicialização considerada é a sugerida na literatura. Considerando o factor de 50 na inicialização, a PDD apresenta alguns casos de terminação prematura, resultante do critério de paragem considerado. Ainda assim, tendo em conta os resultados obtidos na Secção 3.1, onde a inicialização perto do óptimo permitia o sucesso da PDD, optou-se por considerar nos restantes testes computacionais o factor de 50 na inicialização.

Tabela 3.8:Dimensões, valores óptimos encontrados na literatura e valores finais obtidos pela PDD consi-derando inicializações perto ou longe do óptimo.

Dimensão do Óptimo da Valor final Valor final

Problemas problema (np) Literatura PDD inic. perto PDD inic. longe

1 9 3,600E+01 3,600E+01 3,600E+01

2 7 8,380E+00 8,380E+00 8,380E+00

3 7 9,806E+00 9,881E+00 9,881E+00

4 2 0,000E+00 8,183E-02 3,797E+00

5 3 0,000E+00 0,000E+00 2,822E-03

6 4 0,000E+00 6,195E-06 8,082E+03

7 2 4,898E+01 4,898E+01 4,898E+01

8 3 8,215E-03 |1,743E+01 1,508E-02 1,743E+01

9 6 2,288E-03 2,280E-01 3,811E+01

10 9 1,400E-06 1,722E+00 6,233E+01

11 12 4,722E-10 2,388E+00 4,396E+03

12 4 8,582E+04 8,582E+04 8,597E+04

13 11 4,014E-02 1,570E-01 2,631E+01

14 5 - 5,630E-07 2,496E-04

15 12 - 1,958E+05 3,886E+10

(42)

3.2.2 Perfis de dados

A comparação do desempenho numérico de algoritmos pode ser difícil quando estes são em grande número ou quando o conjunto teste apresenta um número elevado de problemas. Em optimização sem recurso a derivadas é frequente a utilização de perfis de dados [36] nesta comparação.

Estes perfis procuram medir a percentagem de problemas resolvidos por cada algo-ritmo, dentro de um certo orçamento computacional (medido em número de cálculos da função objectivo). Um problema é considerado resolvido quando satisfaz a seguinte condição:

f(x0)−f(x)≥(1−τ)(f(x0)−fL),

em queτ >0 representa o nível de tolerância considerado para a elaboração do perfil de dados,x0a inicialização considerada para o problema efLo menor valor obtido para a

função objectivo por qualquer um dos algoritmos considerados (idealmente o óptimo do problema).

Este teste de convergência significa que um problema é considerado como solucionado por um dado algoritmo se a reduçãof(x0)−f(x) obtida por esse algoritmo for igual a pelo

menos (1−τ) vezes a melhor reduçãof(x0)−fLobtida por qualquer um dos algoritmos

considerados na resolução do problema em causa.

Seja S o conjunto de todos os algoritmos considerados e P o conjunto de todos os problemas testados. A definição de um perfil de dados para o algoritmos ∈S consiste na representação gráfica da curva d_s(α) = _|1_P_|

p∈P: _nptp,s₊₁≤α

, onde n_p é a dimensão do problema p∈P etp,s>0 uma medida de desempenho para cadap∈P e s∈S (por

exemplo, o número de cálculos necessários para o algoritmosresolver o problemap). Esta medida é dividida pornp+ 1 normalizandotp,s, por forma a que a dimensão do problema

não influencie o desempenho do algoritmo.

Assim, pela definição anterior,ds(α) pode ser interpretado como a percentagem de

problemas resolvidos pelo algoritmos, para um máximo deα(n_p+ 1) cálculos da função objectivo [36].

3.2.3 Experiência numérica

(43)

elabo-3.2. ANÁLISE NUMÉRICA DO DESEMPENHO DA PROCURA DIRECTA DIRECCIONAL EM PROBLEMAS COM RUÍDO

Dado que os ruídos Normal e Uniforme são gerados aleatoriamente, por forma a dimi-nuir a dependência das sementes consideradas na sua geração, fixou-se um conjunto de várias sementes, também elas geradas de forma aleatória. Para tal, na função do Matlab

rngoptou-se pelo gerador‘twister’. No total utilizaram-se 10 sementes, fazendo com que, para estes dois tipos de ruído, o número de problemas a testar seja 160, ao contrário do ruído baseado em polinómios de Chebyshev que mantém os 16 problemas descritos, uma vez que se trata de ruído determinístico. Nas Figuras 3.7–3.9 encontram-se os resultados obtidos com a PDD para cada uma das classes de problemas.

Figura 3.7:Perfis de dados para o conjunto de problemas perturbados com ruído baseado em polinómios de Chebyshev, para os níveis de ruído de 5%, 10% e 20%, respectivamente.

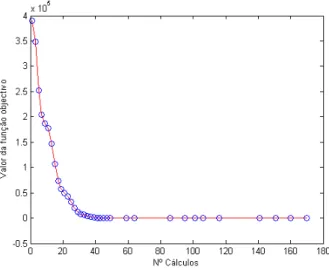
Ao analisar os três perfis de dados referentes ao ruído baseado em polinómios de Chebyshev (ver a Figura3.7) pode-se constatar que o nível de ruído presente na função objectivo afecta o desempenho da PDD. À medida que se aumenta este nível de ruído, o desempenho da PDD piora, sendo que para 20% de ruído apenas cerca de 61% dos pro-blemas são resolvidos. Nota-se ainda que, quando são permitidos até 20(n_p+ 1) cálculos para a função objectivo, a PDD parece competitiva, mesmo na presença de ruído.

Quando o ruído é baseado na distribuição Uniforme (ver a Figura3.8), tal como no caso da Secção 3.1, são extraídas conclusões idênticas às obtidas para o tipo de ruído anterior. Considerando um nível de ruído de 20% constata-se que a PDD apenas resolve cerca de 64% dos problemas, sendo competitiva para orçamentos de 20(np+ 1) cálculos,

independentemente do nível de ruído considerado.

(44)

Figura 3.8:Perfis de dados para o conjunto de problemas perturbados com ruído Uniforme, para os níveis de ruído de 5%, 10% e 20%, respectivamente.

no caso da presença de 20% de ruído gerado segundo a distribuição Normal. O limite ao número máximo de cálculos permitido para a função objectivo, dentro do qual a PDD é competitiva na presença de ruído é claramente mais baixo, por comparação com os dois tipos de ruído anteriormente considerados.

Figura 3.9:Perfis de dados para o conjunto de problemas perturbados com ruído Normal para os níveis de ruído de 5%, 10% e 20%, respectivamente.

(45)

C

a

p

í

t

u

l

o

4 Estratégias não monótonas

As estratégias não monótonas foram primeiramente propostas em métodos de procura unidireccional na presença de derivadas [24]. No trabalho mencionado, com o objectivo de acelerar a convergência em estádios intermédios do processo de optimização, facilitando a aceitação de comprimentos de passos unitários, os autores propuseram uma modificação do método de Newton em que a aceitação de um ponto como uma nova iterada implica que o correspondente valor da função objectivo satisfaça a condição de Armijo [3], não em relação ao valor da função objectivo da iterada corrente mas em relação ao valor máximo da função objectivo, considerando um número previamente fixo de iteradas anteriores.

Esta técnica de procura unidireccional pode ser vista como uma generalização da re-gra de Armijo, permitindo a convergência do método, mas relaxando o comportamento monótono. Por outras palavras, neste tipo de abordagem procura-se melhorar o valor da função objectivo considerando um histórico de iterações, o que pode conduzir a acrés-cimos no valor da função objectivo entre iterações consecutivas (daí a terminologia não monótona).

Para estes autores, um novo pontox_k+1=xk+αkdké bem sucedido se

f(x_k+1)≤ max

0≤j≤m(k){f(xk−j)}+γαkg ⊤

kdk,

ondeαk=σha, coma >0, σ∈(0,1),γ∈(0,1),dk,0 representa uma direcção,gko

gradi-ente def emxkeho primeiro inteiro não negativo que satisfaz a condição anterior, com

m(0) = 0, 0≤m(k)≤min{m(k−1) + 1, M}parak≥1. O histórico de iterações considerado é definido por{f(xl(k))}, em quek−m(k)≤l(k)≤k, comM um inteiro não negativo.