Dinâmica de homeomorfismos homotópicos à Dehn twists

(1)

Dinˆamica de homeomorfismos

homot ´opicos `a Dehn twists

Br´aulio Augusto Garcia

T

ese apresentada

ao

I

nstituto de

M

atem

atica e

´

E

stat

´

ıstica

da

U

niversidade de

S ˜

ao

P

aulo

para

obtenc

¸ ˜

ao do t

´

ıtulo

de

D

outor em

C

i

encias

ˆ

Programa: Matem´atica Aplicada

Orientador: Prof. Dr. Salvador Addas Zanata

Durante o desenvolvimento deste trabalho o autor recebeu aux´ılio financeiro da

FAPESP

(2)

Dinˆamica de homeomorfismos

homot ´opicos `a Dehn twists

Esta tese contém as correç ões e alteraç ões sugeridas pela Comissão Julgadora durante a defesa realizada por Bráulio Augusto Garcia em 02/02/2012. O original encontra-se dispon´ıvel no Instituto de Matemática e Estat´ıstica da Universidade de São Paulo.

Banca Examinadora:

• Prof. Dr. Salvador Addas Zanata (orientador) - IME-USP.

• Prof. Dr. Fabio Armando Tal - IME-USP.

• Prof. Dr. Pedro Antonio Santoro Salom˜ao - IME-USP.

• Prof. Dr. Andr´es Koropecki- UFF.

(3)

DEDICAT ´

ORIA

Dedico essa tese aos meus

pais.

(4)

AGRADECIMENTOS

Agradec¸o...

A minha fam´ılia por compreender e perdoar minha ausˆencia.

Ao meu amor Ira por estar sempre ao meu lado, por contribuir muito em minha vida (desde o in´ıcio da graduac¸˜ao) e por me deixar cada dia mais feliz. Te amo.

Ao meu amigo-irmão Felipe Chaves, pelas conversas sobre o universo, Raul Seixas, etc., nas montanhas de Minas, onde iniciamos nossos estudos sérios em f´ısica e depois em matemática.

Ao meu orientador Dr. Salvador, a quem posso chamar de amigo e a quem tenho uma d´ıvida impagável, por me introduzir na dinâmica topol ógica, por ser um ótimo professor, pesquisador, etc., e, principalmente, por ser uma pessoa de grande humildade e honestidade, tanto academicamente quanto pessoalmente. Gostaria de dizer que me sinto uma pessoa privilegiada de ter te conhecido e de ter trabalhado em minha tese sob sua orientação. Obrigado pelas caminhadas no campus da USP, onde realizávamos a pesquisa sobre Dehn twists.

Ao professor Dr. Fábio Tal, por participar dessas caminhadas pela USP, por sempre estar dispon´ıvel para conversar sobre matemática e por ter dado grandes ideias na elaboração da tese.

Aos professores Dr. Andre de Carvalho e Dr. Philip Boyland pelo excelente curso sobre teoria de Nielsen-Thurston.

Ao meu amigo e também companheiro de sala Valentim, pelas discuss ões sobre matemática, sistemas dinâmicos, f´ısica, literatura (brasileira, espanhola, ...) e a vida. Também a Sebastiam por estar muitas vezes nessas discuss ões.

`

A minha amiga Tatiane, por ser companheira de caf´e (mesmo ela sempre tomando

(5)

ch´a) e aos meus outros amigos do IME e CBPF, Lucas, Ant ˆonio, Anderson, Pricila, Gustavo, Humberto, Grasi, Bittencourt...

Aos funcionários e professores do IME, pelo ambiente acolhedor proporcionado. Aos professores que me deram aula (da UNIFEI e do IME), pela dedicação e profis-sionalismo.

`

A Universidade de S˜ao Paulo, pela oportunidade de estudo e por toda a in-fraestrutura oferecida.

`

A UNIFEI, por ter sido meu berço acadêmico. Bem como aos meus primeiros mestres de graduação, Baêta Segundo, Luis Fernando e Vit ório De Lorenci.

Aos professores (Clodoaldo, Saulo, ...) e colegas (Jaime, Borba, ...) do futebol. Sou grato por ter vivido com esses profissionais que levam o ensino p úblico a sério, o que s ó reforça minhas convicç ões.

Ao pessoal da rep ´ublica, que foram minha fam´ılia aqui em S˜ao Paulo, Danilo, Maguinho e Fabr´ıcio, companheiros de todas as horas!

`

A FAPESP, pelo apoio financeiro, que ´e fundamental numa cidade como S˜ao Paulo.

A todos aqueles que contribu´ıram, mesmo que indiretamente, na realizac¸˜ao desse trabalho. Muito obrigado!

(6)

Amanhece, amanhece, amanhece, amanhece, amanhece o dia Um leve toque de poesia Com a certeza que a luz que se derrama nos traga um pouco, um pouco, um pouco de alegria! A frieza do rel ógio n ão compete com a quentura do meu coraç ão Coraç ão que bate 4 por 4 sem l ógica e sem e sem nenhuma raz ão Bom dia sol !!! Bom dia, dia !

Corac¸ ˜aoNoturno: RaulSeixas.

(7)

RESUMO

Dinâmica de homeomorfismos homot ópicos à Dehn twists.

No presente trabalho apresentamos um estudo sobre a dinâmica de homeomor-fismos do toro homot ópicos à Dehn twists. No caso conservativo, provamos que se f preserva área e tem um levantamento ˆf para o cilindro com fluxo zero, então, precisamente, ou f é um homeomorfismo do anel, ou possui pontos no cilindro com velocidades verticais positiva e negativa, por iteradas de ˆf. Isso resolve a conjectura de Boyland para essa classe de homotopia. Já no caso geral, mostramos um resul-tado análogo. Além disso, fornecemos uma condição extremamente simples que, quando satisfeita, implica que o conjunto de rotação vertical contém um intervalo e, portanto, que f tem entropia topol ógica positiva.

Palavras-chave:conjunto de rotação vertical, Dehn twists, omega limites, decomposição por tijolos.

(8)

ABSTRACT

Dynamics of homeomorphisms homotopic to Dehn twists.

The present thesis is concerned with the dynamics of homeomorphisms of the torus homotopic to Dehn twists. We prove that if f is area preserving and it has a lift

ˆ

fto the cylinder with zero flux, then either f is an annulus homeomorphism, or there are points in the cylinder with positive vertical velocity and others with negative vertical velocity, for iterates of ˆf. This solves a version of Boyland’s conjecture to this setting. We extend some theorems we already obtained for Dehn twists with the area preservation hypothesis to a more general class. Finally, we also give a simple explicit condition which, when satisfied, implies that the vertical rotation set contains an interval and thus also implies positive topological entropy.

Keywords: vertical rotation set, Dehn twists, omega limits, brick decompositions.

(9)

SUM ´

ARIO

1 Introduc¸˜ao 1

1.1 Consideraç ões Preliminares . . . 2 1.2 Objetivos . . . 9 1.3 Contribuiç ões . . . 10

2 Fundamentos 12

2.1 O Conjunto de Rotação . . . 12 2.2 O Conjunto de Rotação Vertical . . . 14 2.3 Implicaç ões Dinâmicas deρv(•) . . . 19

3 Ferramentas B´asicas 22

3.1 Os conjuntosB−

S eB

+

N . . . 22

3.2 Os conjuntosω-limite deB−

S eB

+

N. . . 31

3.3 Homeomorfismos de Brouwer . . . 39 3.4 Decomposic¸˜ao do plano por tijolos . . . 40

4 Provas dos principais resultados 42

4.1 Demonstração do teorema 1.3.1 . . . 42 4.2 Demonstração do teorema 1.3.3 . . . 55

(10)

LISTA DE FIGURAS

1.1 Ac¸˜ao de um Dehn twist . . . 7

1.2 Dinˆamica de um Dehn twist emR2_/Z2 . . . 7

1.3 Dinˆamica reduzida de ˆf ao anel . . . 10

2.1 Levantamento ˆf com fluxo zero . . . 18

2.2 Aplicac¸ ˜oes de recobrimento. . . 21

3.1 Dinâmica na compactificação . . . 23

3.2 Arcos cont´ınuos simplesΓ_N e ¯Γ_N . . . 26

3.3 B− S e ¯B − S n˜ao vazios. . . 27

3.4 Os conjuntosB− S e ¯B − S . . . 28

3.5 Orbitas uniformemente limitadas no cilindro . . . .´ 29

3.6 Orbitas ilimitadas em apenas uma direc¸˜ao do cilindro . . . .´ 30

3.7 Levantamento deω(B− S) (vertical). . . 35

3.8 Levantamento deω(B− S) (horizontal). . . 36

3.9 Levantamento dos arcos cont´ınuos simples. . . 37

4.1 Transladado vertical deπ−1_(ω(_B− S)). . . 47

4.2 Decomposic¸˜ao do Plano por Tijolos Livres para ˜g. . . 53

4.3 Violac¸˜ao do fluxo zero. . . 56

(11)

CAP´ITULO

1

INTRODUC

¸ ˜

AO

Um par ordenado da forma (X, f) é dito ser umsistema din âmicose f é uma aplicação deXemX, isto é, f : X−→X. O conjuntoX é denominadoespaçoe f din âmica. A órbita (futura) de um ponto de X é dada por iteraç ões da dinâmica, ou seja, se x ∈ X, então orb(x) = {x, f(x), f(f(x)), ..., fn₍_x_{), ...}_}_{, em palavras, uma espécie de}

movimento que evolui com o tempo (no caso, os n úmeros naturais) sob aplicação de uma lei repetidamente.

Nesse contexto, a pergunta chave é a existência de pontos peri ódicos para a dinâmica f, isto é, existência dexf tal queorb(xf)={xf, f(xf), ..., fn−1(xf)}, para algum n∈N∗_{. Um sistema dinâmico é uma abstração matemática que serve para modelar e}

fornecer previs ões sobre in úmeros fen ômenos naturais, sociais, econ ômicos e outros. QuandoX é uma superf´ıcie topol ógica e a aplicação f um homeomorfismo sobre

X, temos um sistema dinâmico topol ógico (invers´ıvel). Nesse caso, a questão mais geral que órbitas peri ódicas é a existência de conjuntos minimais, onde K ⊂ X é minimal se, para todo x ∈ K, ω(x) = ∩∞

i=1∪

∞

j=ifj(x) = K, ou seja, o omega limite de

qualquer ponto deKé todoK(veja [24]). O estudo da dinâmica de homeomorfismos em superf´ıcies por métodos topol ógicos provavelmente se iniciou com H. Poincaré, com seu “ último teorema geométrico”, hoje em dia mais conhecido como teorema de Poincaré-Birkhoff.

Um conceito que tem-se mostrado muito útil em sistemas dinâmicos é a noção de

n úmero de rotaç ão, que foi introduzido por Poincaré no caso de um homeomorfismo do c´ırculo que preserva orientação, bem como as definiç ões e generalizaç ões a partir

(12)

1.1 Considerac¸ ˜oes Preliminares 2

desse. Para homeomorfismos do c´ırculo, ele mostrou que todas as órbitas possuem o mesmo n úmero de rotação e, juntamente com os trabalhos de Denjoy, esse n úmero (o n úmero de rotação do homeomorfismo) essencialmente classifica a dinâmica, sendo assim, um poderoso invariante topol ógico. De fato, quando este n úmero é racional, sempre existem órbitas peri ódicas, todas com o mesmo per´ıodo, e todas as órbitas são homocl´ınicas ou heterocl´ınicas às órbitas peri ódicas. Já no caso em que o n úmero de rotação é irracional, não existem órbitas peri ódicas e todas as órbitas se ”ordenam”como as órbitas de uma rotação irracional de mesmo n úmero. Além disso, ou todas são densas, ou existem intervalos errantes e um conjunto minimal, onde todas as outras órbitas nascem e morrem, veja [27] e [26].

Esse conceito foi estendido para endomorfismos do c´ırculo de grau um, por Newhouse, Palis e Takens, e para homeomorfismos de superf´ıcie como o anel e o toro, por M. Misiurewicz, K. Ziemian, J. Franks, e outros com a definição de intervalo e conjunto de rotação. Em termos grosseiros essa técnica permite medir, quando existir, a velocidade média da órbita de um ponto em rotação ao redor de buracos no espaço sob iteração da dinâmica. E, se o “ conjunto de rotação tiver interior ” então, temos que a dinâmica possuientropia topol ógica positiva, veja [24] e [29].

1.1 Considerac¸ ˜oes Preliminares

O objetivo da presente seção é motivar o estudo dos homeomorfismos homot ópicos àDehn twist no toro. Para isso, iniciemos com a classificação de homeomorfismos do toro. Primeiramente, considere o toro (plano) como sendoR2_/Z2e o denotemos porT2. O conjunto dos homeomorfismos deT2, Homeo(T2), pode ser particionado em, essencialmente, três classes de equivalência através da relação de homotopia entre aplicaç ões do toro, a saber:

Homeo(T2_)/_H_:_•• ={[Anosov linear ]; [ordem finita ]; [redut´ıvel]},

onde H : • • _{é a relação de homotopia, ou seja,} f,g ∈ Homeo(T2) são tais que

H : f gse, e somente se, existe uma aplicac¸˜ao (homotopia)H : T2×_[0,1] −→T2

cont´ınua e tal que H0(•) = H(•,0) = f(•) e H1(•) = H(•,1) = g(•). Se para todo

(13)

Observação 1.1.1. Em superf´ıcies fechadas o conceito de homotopia e isotopia entre aplicaç ões coincidem, veja [21].

Essa classificação será discutida nos pr óximos parágrafos. Seja f : T2_−→_T2_um

homeomorfismo do toro, então, temos uma aplicação induzida no grupo fundamen-tal do toro, da seguinte forma

[γ]∈_π₁(T2)7−→[f ◦_γ]∈_π₁(T2_),

isto é, pela ação de f nos laços deT2. Denotemos essa aplicação induzida por

f∗: π1(T2)−→π1(T2).

Utilizando a estrutura aditiva deπ1(T2), com sua base usual dado pelo isomorfismo

natural π1(T2) Z2, podemos ver que f∗ é um isomorfismo e, portanto, pode ser representado como um elemento de GL(2,Z₎ = {_A ∈ _M₂_x₂₍Z_{) :} _detA , ₀}_. Reci-procamente, se A ∈ _GL_(2,Z_{), a transformação linear invert´ıvel} _A _: R2 −→ R2 _se

projeta a um homeomorfismo de T2_{, denotado por} _φ_A_{. Pois,} A(( ˜x,y˜)+(n1,n2)) =

A( ˜x,y˜) +(m1,m2) onde ( ˜x,y˜) ∈ R2 e (n1,n2),(m1,m2) ∈ Z2. Portanto, a aplicac¸˜ao

( ˜x,y˜) 7→ A( ˜x,y˜) passa ao quociente deR2 porZ2, produzindo um homeomorfismo φAdo toro denominado automorfismo linear.

Não é dif´ıcil ver que todo f ∈ Homeo(T2) é homot ópico a um automorfismo linear φA, para algum A ∈ GL(2,Z). Desse modo, a caracterização dos automorfismos

lineares, φA, fornece a classificação dos elementos de Homeo(T2). Mas esses são o

conjunto GL(2,Z_{), que é caracterizado pela função} _traço _{(ou pelos autovetores de} A). Com efeito, seja A ∈ _GL_(2,Z_{), então,} _detA = ∓_{1. Estamos interessados nos} casos que preservam orientação, portanto, considereA∈_det−1₍₁₎_⊂_GL_(2,_Z_{), ou seja,}

A∈SL(2,Z_{) e tem autovalores dado por}

λ± = trac¸o(A)±

p

trac¸o(A)2₋₄

2 .

Nessas condiç ões, o traço deAdetermina univocamenteλ±no plano complexo e, consequentemente, fornece a partição de Homeo(T2_{) nas ditas classes Anosov linear,}

ordem finita e redut´ıvel. Pois:

1. |trac¸o(A)| _> 2, A tem autovalores λ e λ−1 _com _|_λ_| _> _{1. Nesse caso,} _A _{´e dita}

(14)

2. trac¸o(A)∈ {−_1,_0,1},Atem autovaloresλe ¯λcomλn₌_{1, para algum}_n_{∈ {}_3,_4,₆_}

e portantoAn₌_Id_{. Nesse caso}_φ

Aé de ordem finita. Também, setraço(A)=±2, A é de ordem finita (comn=1 ou 2) se seu autovalor não tiver multiplicidade 2, ou seja,Apossui dois autovetores associado ao autovalor.

3. Caso contr´arioA ´e dita redut´ıvel.

Pode-se mostrar que no ´ultimo caso, a menos de mudanc¸as de coordenadas,Atem a forma

A=

       

±1 m

0 ±1

       

2×2

ondem∈Z∗. Nesse caso, a aplicac¸˜ao induzidaφArecebe o nome de Dehn twist (ou

twist de Dehn, ou Shear), veja [16] e [7]. Em suma, temos o seguinte teorema de caracterizac¸˜ao:

Teorema 1.1.2. Seja f : T2 −→ T2 _{um homeomorfismo. Então,} f é homot ópico a, exatamente, um dos homeomorfismos abaixo:

1. Anosov linear;

2. Ordem finita;

3. Dehn twist.

A pr óxima proposição fornece algumas simples equivalências em termos da dinâmica no toro, grupo fundamental e no recobrimento.

Proposição 1.1.3. Seja f : T2 −→T2 _{um homeomorfismo. Então, são equivalentes:}

1. f ´e isot ´opico aφA.

2. f∗age sobreH1(T2)Z2na base can ˆonica pela matrizA.

3. Qualquer levantamento de f, ˜f para R2 (recobrimento universal) pode ser escrito como

˜

f( ˜x,y˜)=A( ˜x,y˜)+γ( ˜x,y˜),

(15)

4. Se ˜f ´e levantamento de f paraR2, ˜

f(( ˜x,y˜)+(n1,n2))= f˜( ˜x,y˜)+A(n1,n2),

para todo ( ˜x,y˜)∈R2 _{e para todo (}_n

1,n2)∈Z2.

No que segue, analisaremos as trˆes classes de homeomorfismos do ponto de vista dinˆamico.

Quando a matrizAéhiperb ólica, o seguinte teorema garante que homeomorfismos isot ópicos àφA possuem “mais dinâmica” queφA, em outras palavras, um Anosov

linear tem a menor complexidade dinˆamica em toda sua classe de isotopia. Esse teorema ´e frequentemente conhecido como teorema de (Franks [24]) estabilidade por isotopia sobre o toro.

Teorema 1.1.4. Se f :T2 −→T2 _{´e um homeomorfismo isot ´opico a um Anosov linear,}

φA, então existe uma aplicação cont´ınua e sobrejetora α : T2 −→ T2 homot ópica à

identidade tal queα◦ f =_φ_A◦_{α, ou como no diagrama comutativo:}

T2 T2

/

f

α

/

α

/

φA

Sendo assim, φA é um fator de f e, como é bem sabido, possui dinâmica bem

interessante. Em outras palavras,

• possui entropia topol ógica positiva, isto é,htop(φA) = log|λ|, ondeλ é o maior

autovalor deA;

• possui órbitas densas, isto é,φA é transitiva;

• _{o conjunto dos pontos peri ´odicos de}_φ_A _{´e denso em}T2_{; e}

• possui folheac¸ ˜oes invariantes transversais densas sobre T2_{, sendo que uma}

delas expande e a outra contrai a dinˆamica.

Já as aplicaç ões induzidas por A não hiperb ólicas, ou seja, o raio espectral de

(16)

Assim, uma questão natural é sob que condiç ões (dinâmicas, topol ógicas, etc) podemos garantir uma dinâmica não trivial?

Homeomorfismos homot ´opicos `a Dehn twists.

A questão colocada anteriormente será explorada para a classe dos homeomorfis-mos homot ópicos à Dehn twists, ou seja, querehomeomorfis-mos encontrar hip óteses topol ógicas e dinâmicas simples que produzam uma dinâmica complicada (rica) nessa classe.

O conjunto dos difeomorfismos twists (e tilts) do toro são exemplos particulares da classe Dehn twist e esses, como é bem sabido, possuem uma teoria muito impor-tante na área de sistemas dinâmicos, bem como diversas aplicaç ões em áreas afins. Essa condição de torção aparece com frequência em várias situaç ões aparentemente não relacionadas. Por exemplo, o modelo de Frenkel-Kontorova, as geodésicas no toro, as pertubaç ões peri ódicas de Hamiltonianos em dimensão dois, as aplicaç ões do tipo bilhar em curvas convexas, os Hamiltonianos com dois graus de liberdade, em particular no problema restrito de três corpos, a dinâmica numa vizinhança de um ponto el´ıptico. Portanto, a teoria dos difeomorfismos do tipo twist pode ser considerada como um modelo te órico unificador para vários fen ômenos. Veja [25], [23] e [24].

Sendo assim, estamos interessados e guiados por essa propriedade topol ógica de “entortar verticais ” de um Dehn twist. No caso, de aplicaç ões twists (ou tilts) uma restrição muito forte é imposta. E essa acarreta fortes restriç ões na dinâmica [14] e [2]. Desse modo, nosso interesse é o caso geral, ou seja, estudaremos somente os aspectos topol ógicos dessa propriedade, assim como suas imposiç ões dinâmicas.

(17)

Dehn

Twist

corta cola

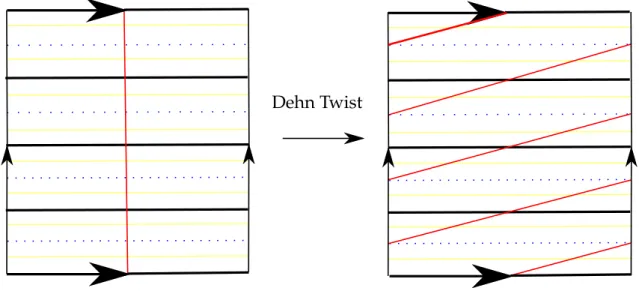
Figura 1.1: Ac¸˜ao de um Dehn twist

No caso do toro plano a dinˆamica de um Dehn twist ´e exemplificado na figura abaixo.

Dehn Twist

(18)

Este trabalho est´a organizado do seguinte modo:

Nas duas pr óximas seç ões, apresenta-se os objetivos e as contribuiç ões desse estudo.

No cap´ıtulo 2, introduz-se a noção de conjunto de rotação para dinâmicas de homeomorfismos homot ópicos à identidade e à Dehn twist. Apresenta-se algumas implicaç ões dinâmicas fornecidas por essa teoria de rotação, e mostra-se que essas classes (identidadeversusDehn twist) possuem comportamentos diferentes.

No cap´ıtulo 3 (e em diante), estuda-se os homeomorfismos Dehn twists através de uma técnica de compactificação da dinâmica, adicionamos dois pontos fixos no infinito do recobrimento e analisamos o comportamento assint ótico (o omega limite) de certos conjuntos a esses pontos. Demonstra-se que o omega limite de um conjunto espec´ıfico fornece informaç ões sobre o conjunto de rotação (vertical) e, consequente-mente, restriç ões na dinâmica. Enuncia-se alguns importantes resultados da teoria de Brouwer para homeomorfismos do plano.

(19)

1.2 Objetivos 9

1.2 Objetivos

O objetivo desse trabalho é estudar no contexto das aplicaç ões homot ópicas à Dehn twists algumas das muitas importantes conjecturas feitas para aplicaç ões ho-mot ópicas à identidade. Como por exemplo, a conjectura de Boyland :

Suponha que f tenha fluxo zero (2.2.5) e que exista uma medida Boreleana de probabilidade f-invariante com n úmero de rotação vertical positivo, então é verdade que existe um ponto com n úmero de rotação vertical negativo?

Outras quest ˜oes s˜ao: O conjunto dos Cr_{-difeomorfismos Dehn twists minimais}

possui interior vazio parar≥2?

Se f é um homeomorfismo Dehn twist que preserva área e tem n úmero de rotação vertical da medida de Lebesgue zero, então é verdade que ou f é um homeomorfismo do anel, ou seu intervalo de rotação vertical possui interior não vazio?

Ou mais geral, se f é um homeomorfismo Dehn twist cujo conjunto de rotação vertical contém o zero, então é verdade que ou f possui um anel invariante, ou seu intervalo de rotação vertical não se reduz s ó ao zero?

(20)

1.3 Contribuic¸ ˜oes 10

1.3 Contribuic¸ ˜oes

Sejam f :T2−→T2um homeomorfismo homot ´opico a um Dehn twist e ˆf : S1_×_R _−→

S1 _×_R _{um levantamento de} _f _{para o cilindro vertical. Nessas condic¸ ˜oes, pode-se}

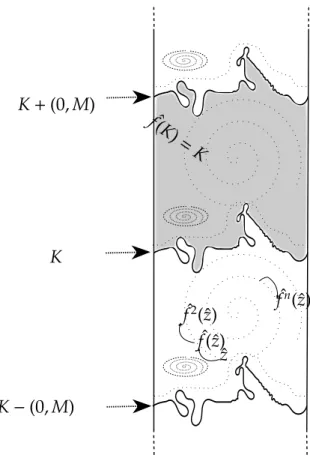
provar que o conjunto de rotaç ão vertical de fˆé degenerado azerose , e somente se, ˆf é um homeomorfismo doanel (ou seja, existem anéis invariantes emS1_×_R_),

veja a figura 1.3 abaixo. Reciprocamente, se zero pertence ao conjunto de rotação vertical de ˆf e as órbitas n ão s ão uniformemente limitadas na direç ão vertical, então ˆf tem conjunto de rotação vertical cominterior n ão vazio. E, nesse caso, veja 2.3, f tem entropia topol ógica positiva e infinitos pontos peri ódicos com per´ıodos arbitrariamente grandes.

K K+_(0,M)

K−(0,M)

ˆ

f₍_K

)₌

K

ˆ

z

ˆ

f(ˆz)

ˆ

fn_(ˆ_z₎

ˆ

f2_(ˆ_z₎

Figura 1.3: Dinˆamica reduzida de ˆf ao anel

(21)

1.3 Contribuic¸ ˜oes 11

• Caso Conservativo

Este resultado responde positivamente a conjectura de Boyland (observe 1.2) para essa classe de homotopia.

Teorema 1.3.1. Sejam f ∈DT(T2) preservando ´area e um levantamento ˆf ∈DT(S1_×

R) com fluxo zero. Se ρv( ˆf) não é degenerado a zero, zero é um ponto interior de

ρv( ˆf).

• Caso Geral

Teorema 1.3.2. Sejam f ∈ DT(T2_{) e um levantamento ˆ}f ∈ DT(S1 _× _R_{). Ent˜ao,}

ρv( ˆf)={0}se, e somente se, existeKum continuum essencial invariante por ˆf.

Um conjunto K ⊂ S1 _×_R _{´e dito ser} _continuum _{se for compacto e conexo. E, ´e}

essencialse separa os fins do cilindro.

O seguinte corol´ario ´e quase imediato do teorema anterior.

Corol´ario 1.3.3. Sejam f ∈ DT(T2_{) e um levantamento ˆ}_f _∈ _DT₍_S1 _× _R_{) tal que}

ρv( ˆf) = [a,p/q] para algum racionalp/q e algum n ´umero reala ≤ p/q. Ent˜ao, existe M>0 tal que para todo ponto ˆz∈S1_×_R_,

p2◦ fˆn(ˆz)−p2(ˆz)−np/q<M,

para todo inteiron>0.

O pr óximo importante corolário afirma, sob certas hip óteses extremamente simples, que deslocamento sublinear verticalimplica velocidade vertical. Isso é, de certo modo, uma versão mais fraca daconjectura de Boyland.

Corol´ario 1.3.4. Sejam f ∈ DT(T2_{) e um levantamento ˆ}_f _∈ _DT₍_S1 _× _R_{). Existe}

Mf =M(f)>0 tal que se para ˆz1,zˆ2 ∈S1×Rocorrer

p2◦ fˆn1(ˆz1)−p2(ˆz1)>Mf

e

p2◦ fˆn2(ˆz2)−p2(ˆz2)<−Mf,

comn1,n2 ∈N∗, ent˜ao 0 ´e um ponto interior deρv( ˆf).

De fato, ´e poss´ıvel mostrar que, sob as hip ´oteses anteriores, se 0 ∈ _ρ_v_{( ˆ}_f_{) e, para} algum ponto ˆz1 ∈S1×R,

p2◦ fˆn1(ˆz1)−p2(ˆz1)>Mf,

(22)

CAP´ITULO

2

FUNDAMENTOS

Neste cap´ıtulo definiremos um importante invariante topol ógico, o conjunto de rotaç ão, que serve para medir o deslocamento médio de um ponto no recobrimento.

2.1 O Conjunto de Rotac¸˜ao

Sejamp: R2 −→T2 a aplicação de recobrimento can ônica do toro, definida por,

p( ˜x,y˜)=( ˜xmod 1,y˜ mod 1 )

e ˜f : R2 _−→ _R2 _{um levantamento de um homeomorfismo do toro homot ´opico `a}

identidade f : T2 −→T2_{, isto ´e, ˜}_f _{´e um homeomorfismo tal que o diagrama abaixo}

´e comutativo

R2 R2

T2 T2

/

˜

f

p

/

p

/

f

Para todo (n1,n2)∈Z2,

˜

f(( ˜x,y˜)+(n1,n2))= f˜( ˜x,y˜)+(n1,n2).

Definição 2.1.1. Sejam f :T2−→T2um homeomorfismo homot ópico à identidade e ˜f um levantamento de f para o recobrimento universal.

(23)

2.1 O Conjunto de Rotac¸˜ao 13

1. Para cada ( ˜x,y˜)∈R2definimos o vetor de rotac¸˜ao de ( ˜x,y˜) com respeito a ˜f por

lim

n→∞ ˜

fn_{( ˜}_x_,_y_˜₎₋_{( ˜}_x_,_y_˜₎

n (2.1)

quando o limite existir.

2. Definimos o conjunto de rotação de ˜f,ρ( ˜f), como sendo o conjunto dos pontos de acumulação do conjunto

( ˜

fk_{( ˜}_x_,_y_˜₎₋_{( ˜}_x_,_y_˜₎

k : ( ˜x,y˜)∈R

2_,_k_∈_N∗

)

.

Equivalentemente,

ρ( ˜f)= \

n≥1

f echo              [

k≥n

( ˜

fk_{( ˜}_x_,_y_˜₎₋_{( ˜}_x_,_y_˜₎

k : ( ˜x,y˜)∈R

2 )              . (2.2)

Assim,v∈_{ρ( ˜}f) se, e somente se, existem subsequˆencias{ni} ⊂Ne{zi˜} ⊂R2tais que

v=lim

i→∞ ˜

fni_(˜_zi₎₋_(˜_zi₎

ni .

Essa definição se deve a Misiurewicz e Ziemian [18], e definido desse modo,ρ( ˜f) é sempre compacto e convexo (como no caso de endomorfismos do c´ırculo [26]).

O vetor de rotação é invariante por translaç ões de vetores de coordenadas inteiras, logo faz sentido falar no n úmero de rotação de (x,y) ∈ T2_{. Pelo mesmo motivo,}

o conjunto de rotac¸˜ao pode ser definido usando somente pontos de um dom´ınio fundamental, que pode ser pensado como correspondendo ao toro original.

O objetivo é usar informaç ões sobre os vetores de rotação e o conjunto de rotação para entender a dinâmica de f (deduzir a existência de pontos fixos, pontos peri ódicos, etc.), ver [18] e [9]. Por exemplo, foi obtido por John Franks que, se o conjunto de rotação tiver interior, então os pontos com coordenadas racionais são realizados por órbitas peri ódicas, isto é, para todo (p0,q0) ∈ Z2 ×N∗ (primos entre

si) tal que p0/q0 ∈ int (ρ( ˜f)), existe um ponto peri ´odicoz ∈ T2 (de per´ıodo q0) que

quando levantado para o plano satisfaz, para todo ˜z∈p−1₍_z_),

˜

fq0_(˜_z₎₌_z_˜₊_p

(24)

2.2 O Conjunto de Rotac¸˜ao Vertical 14

2.2 O Conjunto de Rotac¸˜ao Vertical

Consideremos agora a classe dos homeomorfismos homot ´opicos `a Dehn twists,

f : T2 −→ T2, isto ´e, tais que um levantamento de f para o plano, recobrimento universal do toro, ˜f :R2_−→_R2 _{´e um homeomorfismo que, para todo (}_n

1,n2)∈Z2,

˜

f(( ˜x,y˜)+(n1,n2))= f˜( ˜x,y˜)+Lm(n1,n2),

onde,

Lm( ˜x,y˜)=( ˜x+my˜,y˜),

é, para cadam∈ Z∗, uma transformação linear deR2.

A aplicação induzida no toro por Lm, φLm, é conhecida como Dehn twist. Vale observar que para cadam∈Z∗_{temos uma classe diferente de homotopia.}

Denotemos por DT(T2_{) o conjunto de homeomorfismos do toro homot ´opico a}

um Dehn twist

(x,y)7→_φ_L_m(x,y)=(x+mymod 1,ymod 1),

para algum m ∈ Z∗, e seja DT(R2) o conjunto dos levantamentos de elementos de

DT(T2) para o recobrimento universalR2.

Note que toda Lm deixa invariante a direção horizontal do plano, permitindo definir um n úmero de rotação (vertical) que mede a velocidade média (vertical) de um ponto ( ˜x,y˜) sobre a ação de um levantamento ˜f. Esse fato faz com que essa classe de homotopia seja mais simples, em um certo sentido, que a da identidade. Um modo de ver isso é supor que ˜f tem um ponto fixo, pois nesse caso, para algum ˜

z∈R2_,

˜

f(˜z)=z˜

e, da definic¸˜ao de Dehn twist,

˜

f(˜z+_(0,k))=z˜+_(0,k)+(mk,0), ondek∈Z∗_.

Sendo assim, não fica bem definido um vetor de rotação independente dep−1₍_p_(˜_z_)).

Para precisar melhor considere a proposic¸˜ao (veja [1] e suponham>0):

Proposição 2.2.1. Sejamp1,2 :R2 −→Ras projeç ões can ônicas na primeira e segunda

coordenadas de R2_{. Sejam} _f _∈ _DT₍_T2_{) e ˜}_f _∈ _DT₍_R2_{) tal que, para algum ˜}_z _∈ _R2_,

existeC>0 com|p2◦f˜n(˜z)|<C, para todon>0. Suponha ainda que existam ˜w+e ˜w− tais quep2◦ f˜n( ˜w±)−→ ±∞quandon−→ ∞.

(25)

p1◦ f˜n(˜z)−p1(˜z)

n

<K, para todon>0

e

p1◦ f˜n( ˜w±)−p1( ˜w±)

n −→ ±∞quandon−→ ∞.

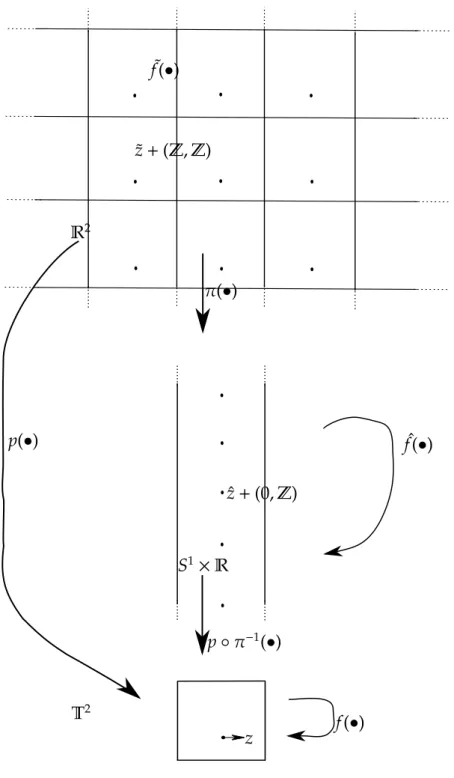
Assim, não faz sentido em definir um conjunto de rotação bidimensional para homeomorfismos do toro homot ópico a um Dehn twist. Ao invés disso, definimos o conjunto de rotação vertical em outro recobrimento do toro, veja [3].

Sejaπ:R2 −→S1_×_R_{a aplicac¸˜ao de recobrimento do cilindro,}

π( ˜x,y˜)=( ˜xmod 1,y˜).

Denotemos porDT(S1_×_R_{) o conjunto dos levantamentos de elementos de}_DT₍_T2₎

para o recobrimento S1 × R_{. Como usado na proposic¸˜ao anterior, denotemos as}

projeç ões can ônicas do cilindro também porp1 ep2e os homeomorfismos deDT(T2)

por f e seus levantamentos para o cilindro vertical e para o plano como ˆf e ˜f, respectivamente. A seguinte definição é dada em [2] e [7].

Definic¸˜ao 2.2.2. Sejam f ∈DT(T2) e um levantamento ˆf ∈DT(S1_×_R_{) fixado. Para}

cada ˆz ∈ S1 _× _R _{definimos o} _{n úmero de rotaç ão vertical} _{de ˆ}_z _{com respeito a ˆ}_f_,

denotado porρv(ˆz),

lim

n→∞

p2◦ fˆn(ˆz)−p2(ˆz)

n , (2.3)

quando o limite existir, ondep2 :S1×R−→R é a projeção na coordenada vertical.

Com essa definição, podemos definir oconjunto de rotaç ão vertical, análogo ao que foi feito para a classe de homeomorfismo homot ópico à identidade, digamos como o conjunto de pontos de acumulação de

    

n : ˆz∈S

1_×_R_,_n_∈_N∗

    .

Denotemos porρv( ˆf) o conjunto de rotac¸˜ao vertical de ˆf.

Observe que a restric¸˜ao para a segunda coordenada implica a importante pro-priedade, para todok∈Z,

(26)

onde ˆz∈S1_×_R_{. Portanto, a func¸˜ao}_ρ

v(•) est´a tamb´em bem definida quando restrita

ao toro, ou seja, depende somente de z = p(π−1_(ˆ_z_{)). Desse modo, podemos usar a}

notac¸˜aoρv(z) para isso.

Em ambos os casos, o conjunto de rotação possui as mesmas propriedades do caso unidimensional no que diz respeito a dependência do homeomorfismo no levantamento, em outras palavras:

Proposic¸˜ao 2.2.3. Sejam f ∈ DT(T2) e um levantamento ˆf ∈ DT(S1 _×_R_{) fixado.}

Ent˜ao, para todop∈Z∗eq∈N∗,

1. ρv( ˆfq−(0,p))=q.ρv( ˆf)−p;

2. ρv( ˆf−1)=−ρv( ˆf).

Para outras propriedades importantes veja [1],[7] e [8].

Vale notar que, fixado f e ˆf, podemos definir afunc¸ ˜ao deslocamentopor

△: T2 −→ R

z 7−→ △(z)_p₂◦ fˆ(ˆz)−p2(ˆz),

para qualquer ˆz∈π(p−1₍_z_)).

Isso motiva a seguinte definic¸˜ao:

Definic¸˜ao 2.2.4. Sejaµuma medida Boreleana de probabilidade emT2_, _f_-invariante,

ou seja, µ ∈ M_T2(f). Definimos o n úmero de rotaç ão verticalde µ, denotada por

ρv(µ), da seguinte forma

ρv(µ)=

Z

T2

△(z)dµ. (2.4)

A importância dessa definição é claramente ilustrada pelo teorema erg ódico de Birkhoff, que diz que, paraµ-quase todo pontoz∈T2e para qualquer ˆz∈_π(p−1₍_z_)),

ρv(z)= lim n→∞

1

n n−1

X

i=0

△ ◦ fi(z)= lim

n→∞

n , (2.5)

existe e

Z

T2

(27)

Além disso, se f for erg ódica com respeito aµ, temos queρv(z) é constanteµ-quase

sempre. Nesse caso, paraµ-quase todo pontoz∈T2e para qualquer ˆz∈π(p−1₍_z_)),

lim

n→∞

n =ρv(µ).

Comoρv(•), definido em 2.4, ´e um funcional linear cont´ınuo eMT2(f) um conjunto

convexo e compacto (na topologia fraca⋆, ver [30]) temos que

ρv(MT2(f))=[a,b]⊂R

onde

a= min µ∈MT2(f)

ρv(µ) eb= max

µ∈MT2(f)

ρv(µ),

ou seja, o m´ınimo e o m´aximo de ρv(•) quando µ varia sobre todas as medidas

Boreleanas de probabilidade em T2, f-invariantes. Al´em disso, veja [3] e [8], para toda sequˆencia de pontos ˆzi ∈S1_×_R_e_ni _−→₊_∞_(quando_i_→₊_∞_{) tal que}

lim

i→∞

p2◦ fˆni(ˆzi)−p2(ˆzi)

ni =v,

então,v∈[a,b]. A rec´ıproca também é verdadeira, ou seja, [a,b]⊂_ρ_v( ˆf). Portanto, ρv( ˆf)=ρv(MT2(f))=[a,b].

Definic¸˜ao 2.2.5. Diremos que um homeomorfismo f do toro tem fluxo zero se f

preserva ´area e satisfazρv(Leb)=0 para algum levantamento fixado ˆf.

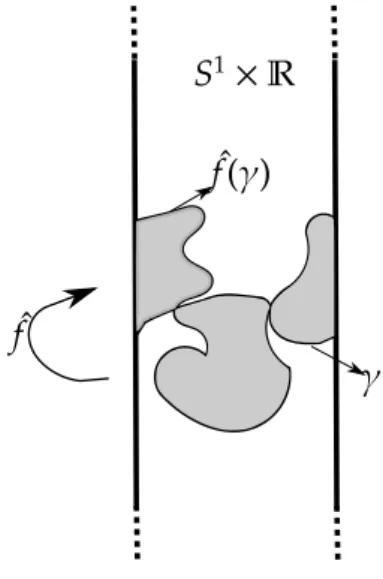
Veja a figura abaixo.

Nesse caso, se ˆf tem fluxo zero, temos o seguinte conceito geom´etrico, para todo

curva fechada simples homotopicamente n ˜ao trivial, γ : S1 _−→ _S1 _×_R_{, a ´area da}

região acima deγ(S1_{) e abaixo de ˆ}_f _◦_γ(_S1_{) é igual a área da região acima de ˆ}_f_◦_γ(_S1₎

e abaixo deγ(S1_{). Um resultado interessante que envolve essa definic¸˜ao aparece em}

[3] e diz o seguinte, se ˆf tem fluxo zero, então f tem ponto fixo (veja também [7]). De fato, o resultado de [3] é bem mais geral:

Teorema 2.2.6. Sejam f ∈ DT(T2_{) um levantamento ˆ}_f _∈ _DT₍_S1_×_R_{). Se} _f _{n˜ao tem}

(28)

ˆ

f

S1_×_R

γ ˆ

f(γ)

Figura 2.1: Levantamento ˆf com fluxo zero

Homot ´opicos `a identidade Vs Dehn twists

O estudo da geometria desses conjuntos de rotação e suas implicaç ões dinâmicas formam uma área de pesquisa extremamente rica, atual e de grande interesse.

Um caso particularmente interessante ocorre quando estes conjuntos possuem interior vazio (no plano para homot ópico à identidade e na reta para Dehn twists). Já uma das maiores dificuldades nessa teoria de rotação é saber se a existência de deslocamento sub-linear implica deslocamento linear. Isso significa, por exemplo no caso Dehn twist, que se

sup

n∈N∗_z_∈T2

||

n−1

X

i=0

△₍_fi₍_z₎₎ ||= sup

n∈N∗_z_ˆ_∈_S1_×R

|_p₂◦ _fˆn_(ˆ_z₎−_p₂_(ˆ_z₎|= +∞_,

ent˜ao,

ρv( ˆf),{0}.

Isso na classe da identidade n˜ao ocorre. Em um trabalho recente de F. Tal e A. Koropecki eles apresentam o seguinte teorema.

(29)

2.3 Implicaç ões Dinâmicas deρv(•) 19

Portanto, esse exemplo mostra que a existência de deslocamento sub-linear não implica deslocamento linear, pelo menos no caso de homeomorfismos do toro ho-mot ópico à identidade. Desse modo, aplicaç ões hoho-mot ópicas a Dehn twists possuem comportamento bem diferente.

2.3 Implicaç ões Dinâmicas de

ρ

v

(

• )

Apresentaremos algumas das implicaç ões do conjunto de rotação na classe de ho-meomorfismos Dehn twists. Para enunciados mais precisos e demonstraç ões veja [7] e [2]. Na classe de homeomorfismos homot ópicos à identidade veja [12].

O conjunto de rotação vertical de um homeomorfismo Dehn twist é um intervalo fechado (possivelmente um ponto, mas nunca vazio).

O pr óximo resultado afirma que se um homeomorfismo Dehn twist tem con-junto de rotação vertical com interior não vazio, então esse possui complexidade dinâmica “maior que” a de um pseudo-Anosov (veja [11] para algumas importantes propriedades dinâmicas de um pseudo-Anosov).

Teorema 2.3.1. Sejam f ∈ DT(T2_{) e um levantamento ˆ}_f _∈ _DT₍_S1 _×_R_{) tal que} _ρ

v( ˆf)

tenha interior não vazio. Então, f é isot ópico a uma aplicação pseudo-Anosov rela-tivo a um conjunto finito invariante. Consequentemente, f tem entropia topol ógica positiva.

Muito mais pode ser dito seρv( ˆf)=[a,b] coma<b. De fato,

• para todow∈]a,b[ existe um compacto, f-invarianteQwcom

ρv(z)= lim n−→+∞

1

n

X

0≤i≤n−1

△(fi(z))=w

para todoz∈Qw. Sew=p/q´e um n ´umero racional,Qp

q é uma órbita peri ódica. • os extremos deρv( ˆf) são realizados por medidas de probabilidade erg ódicas,

isto ´e, existem medidasµa eµberg ´odicas tais queρv(µa)=aeρv(µb)=b. Assim,

pelo teorema erg ´odico de Birkhoff, existem pontos za ezb tais que ρv(za) = aeρv(zb)=b.

(30)

• em geral, não é verdade que os pontos extremais racionais do conjunto de rotação vertical são realizados por órbitas peri ódicas (isso no caso homot ópico à identidade é falso).

(31)

˜

z+(Z_,Z₎

π(•)

p(•) _fˆ₍_•₎

T2

z f(•)

˜

f(•)

R2

ˆ

z+_(0,Z)

S1_×_R

p◦π−1₍_•₎

(32)

CAP´ITULO

3

FERRAMENTAS B ´

ASICAS

Nessa seção apresentaremos a teoria desenvolvida em [5] e [4]. Basicamente, a técnica é compactificar a dinâmica no recobrimento e estudar adin âmica induzida nas vizinhanças dos pontos no infinito.

3.1 Os conjuntos

B

−_S

e

B

+_N

Para estendermos as construc¸ ˜oes feita em [5] e [4] para nosso contexto, consideremos

f ∈DT(T2), um levantamento ˆf ∈DT(S1_×_R_{) e um levantamento de ˆ}_f _{para o plano,}

denotado por ˜f.

Definição 3.1.1. Para cada n úmero reala, definamos os conjuntos

Ha =S1× {a}_, H−_a =S1×]−∞_,a] eH_a+=S1×[a,+∞_[. Quandoa=0 escreveremos simplesmenteH,H−_e_H+_.

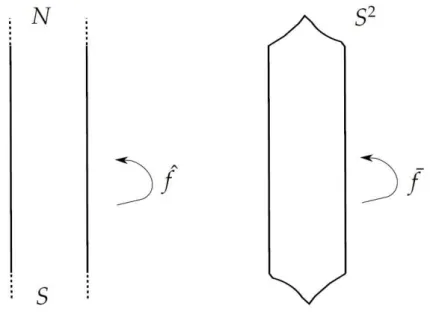
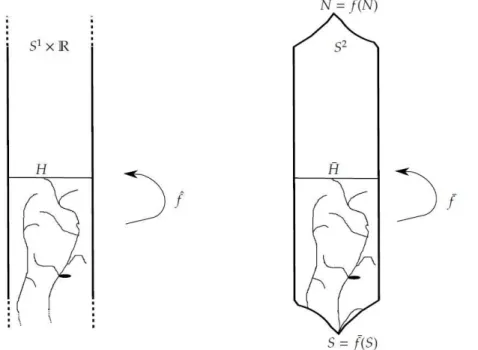
Consideremos a compactificac¸˜ao do cilindro vertical, S1 _×_R_{, denotada por} _N_,

S-compactificação, isto é, adicionamos dois pontosN(fim superior) eS(fim inferior) ao cilindro, obtendo a esfera topol ógica S2_{. Seja ¯}_f _: _S2 _−→ _S2 _{o homeomorfismo}

induzido por ˆf : S1 _×_R _−→ _S1_×_R_{. Ent˜ao, ¯}_f₍_N₎ ₌ _N _{e ¯}_f₍_S₎ ₌ _S _{(veja a figura 3.1}

abaixo).

(33)

3.1 Os conjuntosB−_S eB+

N 23

Figura 3.1: Dinâmica na compactificação

Denotemos por ¯A, um conjunto deS2_{, se esse for correspondente do conjunto}_A

no cilindro. Nessas condic¸ ˜oes, temos que os conjuntos fechados

¯

B− = \

n≤0 ¯

fn( ¯H−) (3.1)

e

¯

B+ = \

n≤0 ¯

fn( ¯H+), (3.2)

s˜ao ¯f-positivamente invariantes comS∈B¯−_e_N _∈_B_¯+_{. De fato, s˜ao fechados (e nunca}

vazios) pois são interseç ões de conjuntos fechados da forma ¯f−n_{( ¯}_H±_{), com}_n_≥_{0, que} contém um dos pontos fixosN,S. Pelo cálculo direto de ¯f( ¯B±),

¯

f( ¯H±∩_f¯−1_{( ¯}_H±

)∩_f¯−2_{( ¯}_H±

)∩_...)= f¯( ¯H±)∩_H¯±∩_f¯−1_{( ¯}_H±

)∩_f¯−2_{( ¯}_H±

)∩_...= f¯( ¯H±)\B¯±⊂_B¯±

temos que s˜ao positivamente invariantes.

Os conjuntos ¯B−

S e ¯B

+

N s˜ao, respectivamente, as componentes conexas de ¯B

− _e

¯

B+ _{que cont´em} _S _e_N_{. Desse modo,} _B−

S e B

+

(34)

N 24

cilindro. Em outras palavras,

B−_S = Uni˜ao das componentes conexas ilimitadas deB− = \

n≤0 ˆ

fn(H−)

e

B+_N = Uni˜ao das componentes conexas ilimitadas deB+ = \

n≤0 ˆ

fn(H+).

Assim, esses conjuntos s˜ao sempre fechados e ˆf(B−

S) ⊂ B

−

S, ˆf(B

+

N) ⊂ B

+

N, mas

eventualmente vazios. Provaremos que, se o zero pertence ao conjunto de rotação vertical de ˆf, entãoB−

S eB

+

N s˜ao n˜ao vazios.

Antes de enunciarmos precisamente esse teorema, consideremos os seguintes lemas intermedi´arios:

Lema 3.1.1. Suponha que 0 ∈ ρv( ˆf) e que para um dadoM > 0 existem um inteiro

positivo n e um ponto ˆz ∈ _S1 _×_[0,_{1] tal que} _p

2 ◦ fˆn(ˆz) > M. Ent˜ao B+_N ∩ H , ∅

(equivalentemente paraS2, ¯B+_N∩_H¯ ,∅_). Analogamente temos:

Lema 3.1.2. Suponha que 0 ∈ _ρ_v( ˆf) e que para um dadoM > 0 existem um inteiro positivo n e um ponto ˆz ∈ S1 _×_[0,_{1] tal que} _p

2◦ fˆn(ˆz) < −M. Ent˜ao B−_S ∩H , ∅

(equivalentemente paraS2_{, ¯}_B−

S ∩H¯ ,∅).

A prova desses dois lemas é análoga e aparece em um contexto diferente em Le Calvez [13] e em Birkhoff[22]. Portanto, demonstraremos somente o último.

Demonstração. Primeiramente, observe que se para algum inteiroM >0, existir um inteiro positivon0tal que ˆfn0(H−) está contido emH−−M =H

−₋_(0,_M_{), ou seja,}

ˆ

fn0₍_H−₎_⊂_H−

−M. (3.3)

Aplicando ˆfn0 _{em 3.3,}

ˆ

f2n0₍_H−₎_⊂ _fˆn0₍_H−₋_(0,_M₎₎₌ _fˆn0₍_H−₎₋_(0,_M_),

logo ˆf2n0₍_H−₎_⊂_H−₋_(0,₂_M_{). Indutivamente,}_k_∈_N∗_,

ˆ

(35)

N 25

Assim, para todo ponto ˆz ∈ H−_, _p

2 ◦ fˆkn0(ˆz) ≤ −kM. Mas, como H− cont´em um

dom´ınio fundamental, obtemos que para todo ponto ˆz∈S1_×_R_,

p2◦ fˆkn0(ˆz)−p2(ˆz)≤ −kM.

Nessas condic¸ ˜oes,

p2◦ fˆkn0(ˆz)−p2(ˆz)≤ −kM

para todo ponto do cilindro e para todokinteiro positivo. Portanto,

lim sup

i→∞

p2◦ fˆi(ˆz)−p2(ˆz)

i ≤

−M n0

<0

para todo ˆz∈S1_×_R_{. O que ´e um absurdo, pois estamos supondo que 0}_∈_ρ

v( ˆf).

Sendo assim, as hip ´oteses do lema implicam que para todo M > 0 existe um inteiro positivon=n(M), tal que

ˆ

fn(H)\H−M ,∅.

Claramente,Mentem a seguinte relação: tomandoMcada vez maior, necessitamos den(M) também maior para que ˆfn(M)₍_H₎T

H− −M ,∅.

Desse modo, dadoN>0 existea≤ −2 tal que

n=inf{_i_>_{0 : ˆ}_fi₍_H₎_∩_Ha _,_∅}_>_N_.

Além disso, por definição de n, ˆfi₍_H₎ _⊂ _H+

a para todo i ∈ {0,1, ...,n − 2,n − 1}.

Equivalentemente,

ˆ

f−i(Ha)⊂H− ∀i∈ {_0,_{1, ...,}n−_2,n−1} e

ˆ

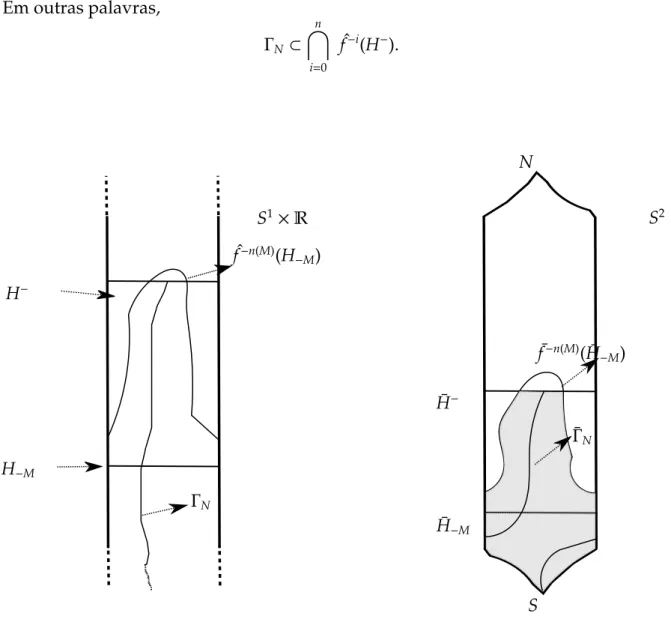
f−n(Ha)∩H,∅_. Assim, existe um arco cont´ınuo simples

Γ_N ⊂ fˆ−n(H_a−)∩H−

tal que ¯Γ_N conectaS a ¯H (um fim de ¯Γ_N ´e Se o outro est´a em ¯H). Veja a figura 3.2 abaixo.

Portanto, comoΓ_N ⊂ _fˆ−n₍_H−

a)∩H−,

ˆ

(36)

N 26

Em outras palavras,

Γ_N ⊂

n

\

i=0

ˆ

f−i(H−).

H−

H−M

¯

f−n(M)_{( ¯}_H

−M)

¯

Γ_N

N

S

S2

¯

H− S1_×_R

¯

H−M

Γ_N

ˆ

f−n(M)₍_H

−M)

Figura 3.2: Arcos cont´ınuos simplesΓ_N e ¯Γ_N

Na compactificaçãoS2_{, temos uma sequência}_{_Γ_¯

N}N>0de conjuntos compactos conexos,

logo existe um conjunto ¯Γcompacto, conexo e que conectaSaH, onde ¯Γé o limite de uma subsequência convergente na topologia de Hausdorffde{Γ¯_N}_N_>₀, isto é, ¯Γ_N_i →Γ¯

quandoi→ ∞. Assim, dadoǫ >0, seVǫ( ¯Γ) eVǫ( ¯Γ_N_i) s˜aoǫ-vizinhanc¸as de ¯Γe de ¯Γ_N_i, existek>0 tal que

(37)

N 27

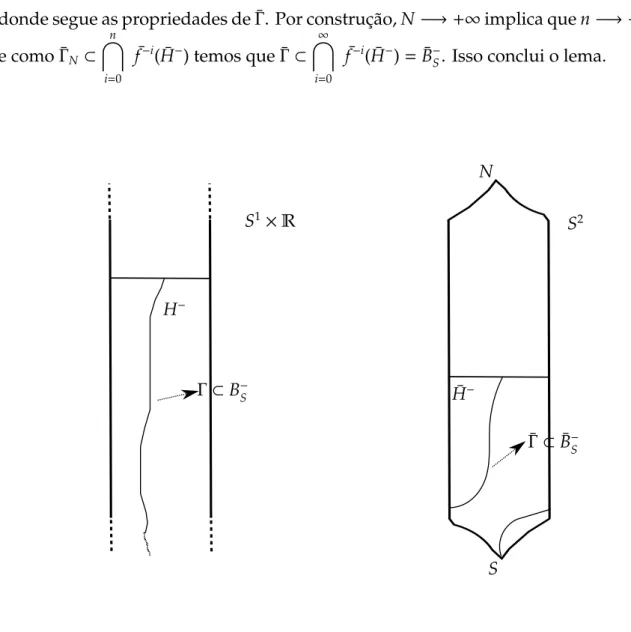
donde segue as propriedades de ¯Γ. Por construc¸˜ao,N−→+∞implica quen−→+∞

e como ¯Γ_N ⊂

n

\

i=0

¯

f−i( ¯H−) temos que ¯Γ⊂ ∞

\

i=0

¯

f−i( ¯H−)=B¯−_S. Isso conclui o lema.

N

S

S2

¯

H− S1_×_R

¯

Γ⊂B¯−

S

Γ⊂B−

S H−

Figura 3.3: B−

S e ¯B

−

S n˜ao vazios.

Esses lemas garantem que sob a hip ótese extra de pontos com deslocamentos ilimitados em ambas as direç ões, isto é, f echo(S

n≥1 f¯n( ¯H)) ⊃ {S,N}implica queB−S e B+

N são não vazios. Mas, como dito anteriormente, a existência desses conjuntos é

mais geral.

Teorema 3.1.2. Se 0 ∈_ρ_v_{( ˆ}f), ent˜aoB−

S ,∅eB

+

(38)

N 28

Figura 3.4: Os conjuntosB−_S e ¯B−_S

Demonstrac¸˜ao. Suponha que para cada M > 1, existem inteiros positivos n− _e _n+ _e

existem pontos ˆz−,zˆ+ _∈_S1_×_[0,_{1] tais que}

p2◦ fˆn

−

(ˆz−)−p2(ˆz−)<−Mep2◦ fˆn +

(ˆz+)−p2(ˆz+)>M.

Nesse caso, o lema 3.1.1 e o lema 3.1.2 implicam queB−

S eB

+

N s˜ao n˜ao vazios.

Suponha que a ´orbita de todo ponto seja uniformemente limitada no cilindro, isto ´e, existe um inteiroM0 >0 tal que

[

n∈Z ˆ

fn(S1×_[0,1])⊂S1×[−M0,M0]. (3.4)

Considere o conjunto

O=[

n∈Z ˆ

fnS1×]− ∞_,0[. Assim,O ´e aberto e invariante,

ˆ

f(O)= fˆ

      [ n∈Z ˆ

fn(S1×]− ∞,0[

      =[ n∈Z ˆ

fn(S1×]− ∞,0[=O.

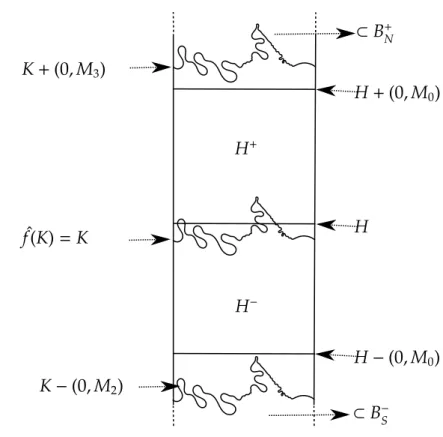
Por 3.4, temos que o bordo deO´e um subconjunto deS1×_]−∞_,_M₀_{] e existe}_K_{, a ´unica} componente de∂Oconexa, que separa os fins do cilindro e tal queK⊂S1_×_[₋_M

(39)

N 29

SendoOinvariante por ˆf, ˆf(K)=K.

Portanto,K´e um compacto, conexo que separa os fins do cilindro ˆf-invariante. Desse modo, existe um transladado inteiro de K que est´a abaixo de H, ou seja, existe (o primeiro)M1≥0 tal que

K−_(0,_M₁₎⊂_H−_.

SendoK−_(0,M1) ˆf-invariante, temos que a componente conexa do complementar de

K−_(0,M1) que contém o fim inferior do cilindro também é ˆf-invariante e, portanto,

est´a contida emB−

S.

De um modo an´alogo, obtemos queB+

N ´e n˜ao vazio.

ˆ

f(K)=K K+_(0,M3)

K−(0,M2)

H

H−_(0,M0)

H+_(0,M0)

⊂B−_S

⊂B+

N

H−

H+

(40)

N 30

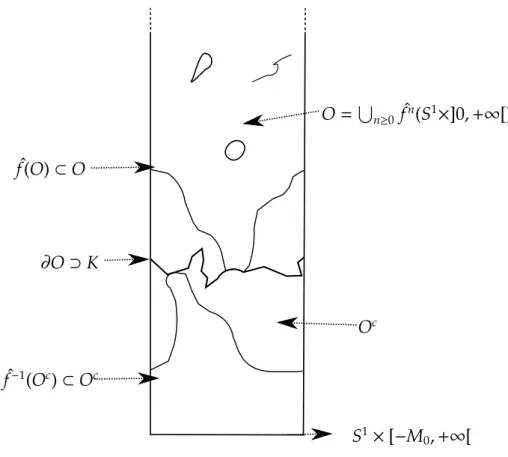
No pr óximo caso, vamos supor que existem órbitas ilimitadas em apenas uma direção. Em outras palavras, existeM0 >0 tal que

[

n>0

ˆ

fn(S1×[0,1])⊂S1×[−M0,+∞[,

ent˜ao existe um conjunto compacto conexoK ⊂ _S1_×_R_{, tal que}_K_{separa os fins do}

cilindro eK ´e o bordo do conjunto aberto e conexo O = S

n≥0 fˆn(S1×]0,+∞[). Note

queOcont´em o fim superior do cilindro e ˆf(O)⊂O.

Oc O=S

n≥0 fˆn(S1×]0,+∞[)

ˆ

f(O)⊂O

ˆ

f−1₍_Oc₎_⊂_Oc

S1_×_[₋_M 0,+∞[

∂O⊃_K

Figura 3.6: Órbitas ilimitadas em apenas uma direção do cilindro

Se

\

n≥0

ˆ

(41)

3.2 Os conjuntosω-limite deB−_S eB+

N. 31

ent˜ao 0<_ρ_v_{( ˆ}_f_{), pois, neste caso existiria um inteiro}_N₁ _>_{1 tal que ˆ}_fN1₍_H₎_⊂_H+₊_(0,_1).

Assim,

\

n≥0

ˆ

fn(f echo(O))

´e um subconjunto deOfechado, conexo, ilimitado e ˆf-invariante. Portanto,B+

N ´e n˜ao

vazio.

Como ˆf(O)⊂O, ˆf(Oc₎_⊃_Oc_{, ou seja, ˆ}_f−1₍_Oc₎_⊂_Oc_{, desse modo, fazendo a mesma}

construc¸˜ao paraOc_{, obtemos que}

\

n≤0

ˆ

fn(Oc)

é um subconjunto deOc _{fechado, conexo, ilimitado e ˆ}_f_{-invariante. Donde vem que} B−_S é não vazio.

A ´ultima possibilidade pode ser tratada de um modo an´alogo.

3.2 Os conjuntos

ω-limite de

B

−_S

e

B

+_N

.

Nessa subsec¸˜ao examinaremos algumas propriedades do conjunto ω-limite de ¯B−

S,

denotado porω( ¯B−

S), e definido como segue:

ω( ¯B−_S)= \

n≥0

f echo              [

i≥n

¯

fi( ¯B−_S)

             . (3.5)

Como ¯f( ¯B−

S)⊂B¯

−

S e ¯B

−

S ´e fechado, temos

ω( ¯B−_S)=

∞

\

n=0

¯

fn( ¯B−_S).

Nessas condic¸ ˜oes,ω( ¯B−

S) é a intersecção de uma sequência encaixante de compactos

conexos e, portanto, é um conjunto compacto conexo (possivelmente um único ponto, mas nunca vazio). Veremos que, se o omega limite de ¯B−_S é, somente, o ponto

S, ¯B−

S pode ser pensado como sendo o conjunto estável de S. Decorre da definição

3.5 acima o seguinte lema:

Lema 3.2.1. ω(B−_S) ´e um conjunto fechado, ˆf-invariante, limitado superiormente (de fatoω(B−

S)⊂B

− _⊂_H−

(42)

N. 32

Demonstração. As propriedades fechado, ˆf-invariante e limitado superiormente são consequências imediatas da definição do conjunto. Com efeito, como ˆfn₍_B−

S) ´e

fechado para todo n ∈ N e ˆf(B−

S) ⊂ B

−

S ⊂ H

− _{temos que} _ω(_B−

S) =

∞

\

n=0

ˆ

fn(B−_S) é um subconjunto fechado deH−_{. O seguinte cálculo fornece a prova da invariância} por ˆf. Sendo que ˆf(B−

S)⊂B

−

S,

ˆ

f(ω(B−_S))= fˆ(∩∞_n₌₀ fˆn(B−_S))=∩∞_n₌₁ fˆn(B−_S)=∩∞_n₌₁ fˆn(B−_S)\B−_S =_ω(B−_S). Como S ∈ B¯−

S e ¯f(S) = S, obtemos que S ∈ ω( ¯B

−

S). Assim, tendo que ω( ¯B

−

S) ´e

conexo, cada componente conexa deω(B−_S) ´e ilimitada. Note que, comoB−

S ´e fechado e positivamente invariante por ˆf,ω(B

−

S)⊂B

−

S. Mas

ainda ´e poss´ıvel queω(B−

S) seja vazio. O pr ´oximo lema assegura que se esse ´e o caso

então o conjunto de rotação vertical de ˆf não será degenerado, ou seja,ρv( ˆf)=[a,b]

coma<b.

Lema 3.2.2. Suponha que 0 ∈ _ρ_v_{( ˆ}_f_{) (ent˜ao,} _B−

S ´e n˜ao vazio) e queω(B

−

S) = ∅. Ent˜ao,

ρv( ˆf)⊃[−ǫ,0], para algumǫ >0.

Demonstrac¸˜ao. Como 0 ∈ _ρ_v( ˆf), temos, pelo teorema 3.1.2, que B−

S ´e n˜ao vazio. Por

definic¸˜ao, ˆf(B−

S)⊂B

−

S eω(B

−

S)=∩

∞

n=0 fˆ

n₍_B−

S). Por hip ´oteseω(B

−

S) ´e vazio.

Desse modo, se para todo inteiroN ≥0 existir um inteiron≥Ntal que

ˆ

fn(B−_S)\H−_(0,1),∅_, ter´ıamos que

∀k∈ {0,1, ...,n}, fˆk(B−_S)\H−(0,1),∅, pois, ˆfn₍_B−

S)⊂ fˆ k₍_B−

S), ∀k∈ {0,1, ...,n}.

Mas isso implica o absurdo, ∞

\

n=0

ˆ

fn(B−_S)\H−_(0,1),∅_. Portanto, existe um inteiroN1>0 tal que para todon≥N1,

ˆ

fn(B−_S)⊂H−−_(0,_1). _(3.6) De fato, podemos provar que

ˆ

fN1₍_B−

S)⊂B

−

(43)

N. 33

Suponha, por contradic¸˜ao, que

ˆ

fN1₍_B−

S)1B

−

S −(0,1).

Assim, existe um ponto ˆz∈B−

S tal que

ˆ

fN1_(ˆ_z₎_<_B−

S −(0,1).

Sejaγa componente conexa deB−

S que cont´em o ponto ˆz. Ent˜ao, por 3.6, ˆf

N1(γ)⊂H−

−1

e ˆfN1_(γ)₁_B−

S−(0,1), ou seja,

ˆ

fN1_(γ)₊_(0,₁₎₁_B−

S. (3.7)

Como ˆfN1_(γ)₊_(0,_{1) ´e um subconjunto de}_H−_{conexo e ilimitado, deve existir um}

inteiroN2 >0 tal que

ˆ

fN2_{( ˆ}_fN1_(γ)₊_(0,₁₎₎₁_H−_,

pois vale 3.7. Equivalentemente,

ˆ

fN1+N2_(γ)₊_(0,₁₎₁_H−_,

isto é, ˆfN1+N2_(γ)₁_H−₋_(0,_1)._{O que é um absurdo, já que vale 3.6. Nessas condiç ões,}

ˆ

fN1(B−

S)⊂B

−

S −(0,1), para algumN1 >0.

Sendo assim, indutivamente em k ∈ N∗, ˆfkN1₍_B−

S) ⊂ B

−

S −(0,k) ⊂ H

−₋_(0,_k_{), donde} segue, para todo ˆz∈B−

S,

lim sup

n−→+∞

p2( ˆfn(ˆz))−p2(ˆz)

n ≤ −

1

N1

.

Note que, △(z) p2 ◦ fˆ(ˆz)−p2(ˆz) para qualquer ˆz ∈ π(p−1(z)) é uma função (bem

definida) cont´ınua deT2. SejaM> 0 um inteiro tal que| △(z)|_<Mpara todo ponto

zdo toro. Definindo

△n(z)=

n−1

X

i=0

△(fi(z)),

temos que|△n₍_z₎_|_<_nM_{. Desse modo, uma vez que}

△n₍_z₎₌_△₍_z₎₊_△₍_f₍_z₎₎₊_...₊_△₍_fn−1₍_z₎₎₌_p

2◦ fˆn(ˆz)−p2(ˆz),

n

(44)

N. 34

Assim,

n

n∈N∗

⊂ [−M,M] ⊂ R tem uma subsequˆencia convergente. Por-tanto, se ˆz∈ B−

S, existeN1 ⊂Ntal que

ρv( ˆf)∋ lim

N₁∋n−→+∞

n ≤ −

1

N1

.

Dessa feita, existeǫ > 0 tal queρv( ˆf)⊃[−ǫ,0].

Como foi dito antes, seω(B−

S)=∅ent˜aoB

−

S se comporta como se fosse o conjunto

est´avel do pontoS, pois para todo ponto ˆzdeB−

S,

lim

n−→+∞p2( ˆf

n_(ˆ_z₎₎₋_p

2(ˆz)=−∞.

O conjuntoBS foi definido como sendo o conjunto dos pontos que est˜ao abaixo da horizontal pelo zero,H, e que permanecem emH− _{por iteradas futuras de ˆ}_f_{. J´a}

B−

S ´e a uni˜ao de todas componentes conexas ilimitadas deBS. Denotemos porB

−

S(inv)

o an´alogo deB−

S para ˆf

−1_.

O pr óximo lema estabelece uma relação entre esses conjuntos.

Lema 3.2.3. Os conjuntosω(B−_S) eω(B−_S(inv)) s˜ao iguais.

Demonstrac¸˜ao. Do lema 3.2.1,ω(B−

S) ´e invariante por ˆf. Assim,ω(B

−

S(inv)) ´e invariante

por ˆf−1_(portanto, _f_{-invariante). De fato, sendo}

ω(B−_S(inv))=

∞

\

n=0

ˆ

f−1n(B−_S(inv))=B−_S(inv)∩ fˆ−1(B−_S(inv))∩ fˆ−2(B−_S(inv))∩_... e

B−_S(inv) a uni˜ao das componentes conexas ilimitadas de

\

n≤0

ˆ

f−1n(H−)=H−∩ fˆ(H−)∩ fˆ2(H−)∩_..., decorre que

ˆ

f−1(ω(B−_S(inv)))=ω(B−_S(inv)), pois ˆf−1₍_B−

S(inv))⊂B

−

S(inv). Mostremos que esses conjuntos ˆf-invariantes s˜ao iguais.

Considere uma componente conexa de ω(B−_S), digamos Γ. Como ω(B−_S) ´e um subconjunto deH−

e ´e (totalmente) invariante por ˆf, temos ˆf−i₍_Γ₎ _⊂ _H−

(45)

N. 35

i∈Z. Assim,Γ⊂T

i≥0 fˆi(H−) e ´e um conexo ilimitado, logoΓ⊂B−S(inv). Mas, (como

feito paraΓ) para todo inteiron ≥ 0, ˆfn₍_Γ_{) ´e uma componente conexa ilimitada de}

T

i≥0 fˆi(H−), ent˜ao ˆfn(Γ)⊂B−S(inv), para todoninteiro positivo. Desse modo,

Γ⊂\

n≤0

ˆ

fn(B−_S(inv))=_ω(B−_S(inv)).

Portanto,ω(B−

S)⊂ω(B

−

S(inv)). O mesmo racioc´ınio prova queω(B

−

S)⊃ω(B

−

S(inv)).

Tendo em mente esses resultados, podemos fornecer uma condição topol ógica para que um homeomorfismo Dehn twist tenha o zero como ponto interior do conjunto de rotação vertical de um levantamento fixado.

Teorema 3.2.1. Sejam f ∈_DT₍T2_{) e um levantamento ˆ}_f _∈_DT₍_S1_×_R_{) tal que 0}_∈_ρ

v( ˆf)

e que o conjuntoω(B−_S) seja vazio. Ent˜ao, zero ´e um ponto interior deρv( ˆf).

π

R× {0}

S1_{× {}₀_}

ω(B−

S)

S1_×_R _R2

π−1_(ω(_B−

S))=π

−1_(ω(_B−

S))+(0,1)

Figura 3.7: Levantamento deω(B−

(46)

N. 36

Demonstrac¸˜ao. Do teorema 3.1.2 temos queB−

S eB

−

S(inv) s˜ao n˜ao vazios. Comoω(B

−

S)

´e vazio, o lema 3.2.3 implica que, ω(B−

S)(inv) = ∅. Nessas condic¸ ˜oes, aplicando o

lema 3.2.2 duas vezes, obtemos que existe umǫ >0 tal queρv( ˆf)⊃[−ǫ, ǫ].

Resultados an´alogos valem para

B+_N, B+_N(inv), ω(B+_N) e ω(B+_N(inv)).

Os seguintes lemas esclarecem um pouco sobre a estrutura topol ógica desses con-juntos quando levantados para o plano pela aplicação de recobrimento do cilindro π:R2 −→S1_×_R_{, veja a figura anterior.}

Lema 3.2.4. Toda componente conexa ˜Γdeπ−1_(ω(_B−

S)) é ilimitada. Demonstração. Seja ˜Γuma componente conexa deπ−1_(ω(_B−

S)). Suponha, por contradic¸˜ao,

que ˜Γ⊂interior(Q), ondeQ ´e uma bola compacta. Veja a seguinte figura.

S1_×_R _R2

Γ

π

˜

Γ

Q

˜

p