Identificação de sistemas métodos para identificação de modelos de estado

(1)

Identifica¸

c˜

ao de sistemas

M´

etodos para identifica¸

c˜

ao de modelos de estado

Por

Marta Soﬁa Alves Esteves

Orientador: Doutora Teresa Paula Coelho Azevedo Perdico´

ulis

Co-orientador: Doutor Paulo Jorge de Azevedo Lopes dos Santos

Disserta¸c˜ao submetida `a

UNIVERSIDADE DE TR ´AS-OS-MONTES E ALTO DOURO para obten¸c˜ao do grau de

MESTRE

em Engenharia Electrot´ecnica e de Computadores, de acordo com o disposto no DR – I s´erie–A, Decreto-Lei n.o _{74/2006 de 24 de Mar¸co e no}

Regulamento de Estudos Pós-Graduados da UTAD DR, 2.a série – Delibera¸cão n.o 2391/2007

(2)

(3)

Identifica¸

c˜

ao de sistemas

M´

etodos para identifica¸

c˜

ao de modelos de estado

Por

Marta Soﬁa Alves Esteves

Orientador: Doutora Teresa Paula Coelho Azevedo Perdico´

ulis

Co-orientador: Doutor Paulo Jorge de Azevedo Lopes dos Santos

Disserta¸c˜ao submetida `a

UNIVERSIDADE DE TR ´AS-OS-MONTES E ALTO DOURO para obten¸c˜ao do grau de

MESTRE

em Engenharia Electrot´ecnica e de Computadores, de acordo com o disposto no DR – I s´erie–A, Decreto-Lei n.o _{74/2006 de 24 de Mar¸co e no}

Regulamento de Estudos Pós-Graduados da UTAD DR, 2.a série – Delibera¸cão n.o 2391/2007

(4)

(5)

Orienta¸c˜ao Cient´ıfica :

Doutora Teresa Paula Coelho Azevedo Perdico´ulis

Professora Auxiliar com Agrega¸c˜ao do Departamento de Engenharias

Universidade de Tr´as-os-Montes e Alto Douro

Doutor Paulo Jorge de Azevedo Lopes dos Santos

Professor Auxiliar do

Departamento de Engenharia Electrot´ecnica e de Computadores Faculdade de Engenharia da Universidade do Porto

(6)

(7)

”Da determina¸cão, que tens tomada, Não tornes por detrás, pois é fraqueza Desistir-se da cousa come¸cada.”

Lus´ıadas, Canto I

”Nós somos o que fazemos. O que não se faz não existe. Portanto, só existimos nos dias em fazemos. Nos dias em que não fazemos, apenas duramos”

Padre Ant´onio Vieira

”Al andar se hace el camino. | O caminho faz-se caminhando.”

Antonio Machado(1875 – 1939)

Para os meus pais e irm˜ao

(8)

(9)

UNIVERSIDADE DE TR ´AS-OS-MONTES E ALTO DOURO Mestrado em Engenharia Electrot´ecnica e de Computadores

Os membros do Júri recomendam à Universidade de Trás-os-Montes e Alto Douro a aceita¸cão da disserta¸c˜ao intitulada “ Identifica¸cão de sistemas Métodos para identifica¸cão de modelos de estado” realizada por

Marta Sofia Alves Esteves para satisfa¸c˜ao parcial dos requisitos do grau de

Mestre.

Dezembro 2013

Presidente: Doutor Jos´e Paulo Barroso Moura Oliveira,

Professor Associado com Agrega¸c˜ao da Universidade de Tr´as-os-Montes e Alto Douro

Vogais do J´uri: Doutora Maria do Ros´ario Marques Fernandes Teixeira de Pinho,

Professora Associada da Faculdade de Engenharia da Universidade do Porto

Doutora Teresa Paula Coelho Azevedo Perdico´ulis,

Professora Auxiliar com Agrega¸c˜aoda Universidade de Tr´as-os-Montes e Alto Douro

Doutor Paulo Jorge de Azevedo Lopes dos Santos,

Professor Auxiliarda Faculdade de Engenharia da Universidade do Porto

(10)

(11)

Identiﬁca¸c˜

ao de Sistemas

M´

etodos para Identiﬁca¸c˜

ao de modelos de estado

Marta Sofia Alves Esteves

Submetido na Universidade de Tr´as-os-Montes e Alto Douro para o preenchimento dos requisitos parciais para obten¸c˜ao do grau de

Mestre em Engenharia Electrot´ecnica e de Computadores

Resumo — Nesta disserta¸c˜ao, são estudados alguns conceitos geométricos com vista à identifica¸cão em subespa¸cos de parâmetros de sistemas variáveis, lineares e invariantes no tempo. Os métodos de identifica¸cão em subespa¸cos de estados constituem um novo campo da identifica¸cão de sistemas, combinando desde conceitos geométricos de álgebra linear e ferramentas numéricas até à introdu¸cão de ideias inovadoras, nunca antes utilizadas nos métodos clássicos, tais como a inser¸cão do conceito da estima¸cão do estado inicial de um sistema dinâmico.

No caso de sistemas multivariáveis, a identifica¸cão de sistemas surge sempre associada `

a identifica¸cão no espa¸co de estados, dadas as vantagens deste tipo de representa¸cão. A aprendizagem em identifica¸cão de sistemas pode ser coadjuvada através de ferramen-tas de software espec´ıficas. O presente trabalho consiste na implementa¸cão de uma

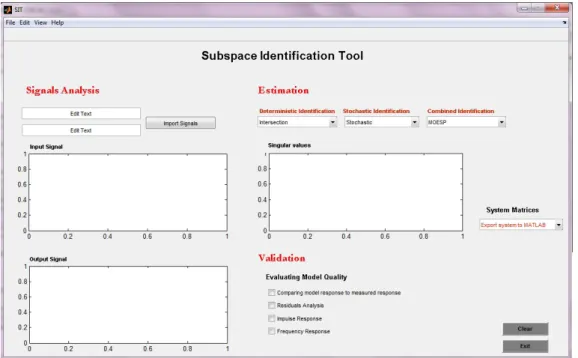
toolbox de identiﬁca¸c˜ao em subespa¸cos de sistemas determin´ısticos, estoc´asticos e determin´ıstico-estoc´asticos, designada Subspace Identification Tool, que permite estimar as matrizes para cada um destes tipos de sistemas, de forma interativa e onde se pode acompanhar passo a passo um determinado caso de estudo na mesma janela.

Palavras Chave: Identifica¸c˜ao em subespa¸co de estados, identifica¸cão de sistemas, sistemas multivari´aveis, Subspace Identification Tool.

(12)

(13)

System Identiﬁcation

Methods for Identiﬁcation of state models

Marta Sofia Alves Esteves

Submitted to the University of Tr´as-os-Montes and Alto Douro in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering and Computers

Abstract — In this dissertation, we study some geometrical concepts in view to

subspace identification of linear time invariant systems. This type of identification methods is a new field of system identification that combines geometrical notions from linear algebra, numerical tools as well as innovative ideas as the concept of the estimation of initial states of a dynamic system.

For multivariable systems, the identiﬁcation will be always done through a subspace model for being more adequate to the system structure.

Learning subspace system identification could benefit substantially from the use of software tools to assist the user to discover the many features of this type of parameters estimation. The present work is an implementation of such a toolbox, named Subspace Identification Tool, where in a single interactive window all the features of the subspace identification are come together and the user is guided through a pre-defined path to identify deterministic, stochastic and deterministic-stochastic systems.

Key Words: Subspace system identiﬁcation, system identiﬁcation, multivariable

systems, Subspace Identiﬁcation Tool.

(14)

(15)

Agradecimentos

Os meus agradecimentos ao Magn´ıfico Reitor da Universidade de Trás-os-Montes e Alto Douro, Professor Doutor António Augusto Fontainhas, ao diretor de Mestrado em Engenharia Electrotécnica e de Computadores, Professor Paulo Moura Oliveira e aos restantes professores que me acompanharam ao longo deste percurso.

`

A Professora Doutora Teresa Paula Coelho Azevedo Perdicoúlis, Professora Auxiliar com Agrega¸cão do Departamento de Engenharias da Universidade de Trás-os-Montes e Alto Douro, orientadora deste trabalho, pela sua motiva¸cão, pelas suas sugestões, ideias inovadoras, orienta¸cões, disponibilidade e sobretudo por todo o apoio prestado ao longo destes anos.

Ao Professor Doutor Paulo Jorge de Azevedo Lopes dos Santos, Professor Auxiliar do Departamento de Engenharia Electrotécnica e de Computadores da Faculdade de Engenharia da Universidade do Porto, na qualidade de co-orientador, pelas suas observa¸cões, orienta¸cões, motiva¸cão e pelo apoio igualmente prestado.

A todos os meus colegas do curso Engenharia Electrotécnica e de Computadores da Universidade de Trás-os-Montes e Alto Douro pela amizade, simpatia e apoio ao longo deste percurso académico. Aos meus amigos de sempre e que cresceram comigo nesta viagem, àqueles que chegaram um pouco depois e àqueles que nunca deixaram de caminhar ao meu lado e que são um bocadinho de mim.

(16)

que conseguisse terminar a ´ultima fase deste longo percurso. `

A minha fam´ılia com especial enfoque, aos meus tios Manuel Machado e Maria da Luz Machado e prima Joana, por todo o tempo, aten¸c˜ao e apoio prestado ao longo destes anos.

Aos meus pais e irmão por me terem acompanhado e incentivado ao longo deste trabalho, que não se esquecem nunca de me ensinar que a vida sem um sorriso não é viver e sobretudo por me terem incutido sempre o espirito de ambi¸cão, luta, sacrif´ıcio, lealdade para comigo própria.

A todos, um sincero obrigado!

UTAD, Marta Soﬁa Alves Esteves

Vila Real, 2013

(17)

´Indice geral

Resumo xi

Abstract xiii

Agradecimentos xv

´_{Indice de figuras} _xxi

Gloss´ario, acr´onimos e abreviaturas xxiii

1 Introdu¸c˜ao 1

1.1 M´etodos Cl´assicos. . . 2

1.2 M´etodos de subespa¸co de estados . . . 3

1.2.1 Porquˆe usar m´etodos de subespa¸co? . . . 4

1.2.2 Identiﬁca¸c˜ao em subespa¸cos de estados . . . 5

1.3 Metodologia adotada nesta disserta¸c˜ao . . . 6

1.4 Motiva¸cão e contribui¸cões da disserta¸cão . . . 6

1.5 Principais objetivos do trabalho . . . 7

1.6 Estrutura da disserta¸c˜ao . . . 7

2 Fundamentos de ´Algebra Linear Num´erica 9 2.1 Espa¸cos e subespa¸cos vetoriais . . . 9

2.1.1 Independˆencia linear . . . 11

2.1.2 Base de um espa¸co linear . . . 12

(18)

2.4 Matrizes . . . 19

2.4.1 Caracter´ıstica de uma matriz . . . 19

2.4.2 Equivalˆencia e semelhan¸ca de matrizes . . . 20

2.4.3 Valores e vetores pr´oprios . . . 24

2.4.4 Polin´omio caracter´ıstico . . . 25

2.4.5 Quatro subespa¸cos fundamentais associados a uma matriz . . 29

2.5 Sistemas de equa¸c˜oes lineares . . . 33

2.5.1 Ferramentas num´ericas . . . 34

2.5.2 M´etodos computacionais . . . 34

2.6 Valores Singulares e Decomposi¸c˜ao de Valores Singulares . . . 36

2.6.1 SVD . . . 38

2.6.2 Problema dos MQ . . . 40

2.7 Considera¸c˜oes ﬁnais . . . 41

3 Eqs. de E/S de sistemas LTI descritos por modelos de estado 43 3.1 Sistemas determin´ısticos . . . 43

3.1.1 As matrizes de dados . . . 44

3.1.2 Matrizes associadas . . . 46

3.1.3 As equa¸c˜oes matriciais de E/S . . . 47

3.2 Sistemas Estoc´asticos . . . 48

3.2.1 Propriedades dos sistemas estoc´asticos . . . 50

3.2.2 Subsistemas Estoc´asticos . . . 50

3.2.3 Matrizes de Hankel . . . 53

3.2.4 Estados do ﬁltro de Kalman . . . 55

3.2.5 Sequˆencias reais deﬁnidas positivas . . . 57

3.3 Sistemas determin´ıstico-estoc´asticos . . . 58

3.3.1 Nota¸c˜ao . . . 58

3.3.2 Matrizes de Hankel . . . 60

3.3.3 Estados de ﬁltro de Kalman . . . 61

3.3.4 As equa¸c˜oes matriciais de E/S . . . 62

4 Identifica¸cão de sistemas em subespa¸cos de estados 65 4.1 Identifica¸cão de sistemas determin´ısticos . . . 65

4.1.1 Algoritmos de identiﬁca¸c˜ao determin´ıstica . . . 68

4.2 Identifica¸cão de sistemas estocásticos . . . 73

4.2.1 Algoritmos de identifica¸cão estocástica . . . 75

4.3 Identifica¸cão de sistemas determin´ıstico-estocásticos . . . 78

(19)

4.3.1 Algoritmos de identifica¸cão determin´ıstico-estocástica . . . 82

5 Usar SIT 91 5.1 Funcionalidades do SIT . . . 92

5.1.1 Como usar o SIT . . . 93

5.2 Caso de estudo - Sistema SISO . . . 95

5.2.1 Passo 1 - Importa¸c˜ao dos sinais . . . 96

5.2.2 Passo 2 - Estima¸c˜ao dos parˆametros do sistema . . . 97

5.2.3 Passo 3 - Valida¸c˜ao do modelo . . . 98

6 Conclus˜ao 107 6.1 S´ıntese das Conclus˜oes . . . 107

6.2 Avalia¸c˜ao e principais conclus˜oes . . . 108

6.3 Trabalho futuro . . . 109

Referˆencias bibliogr´aficas 111

(20)

(21)

´Indice de figuras

1.1 Rela¸c˜ao entre os sinais de E/S de um sistema . . . 2

1.2 M´etodos de subespa¸cos e cl´assicos de IS. . . 5

2.1 Interpreta¸cão da proje¸cão ortogonal num espa¸co de dimens˜ao j (neste caso j = 2). A/B ´e formado pela proje¸c˜ao do espa¸co linha de A no espa¸co linha de B. Por outro lado, A/B⊥é formado pela proje¸cão do espa¸co linha de A no complemento ortogonal do espa¸co linha de B . . 15

2.2 Interpreta¸cão da proje¸cão obl´ıqua num espa¸co de dimens˜ao j (neste caso j = 2). A proje¸c˜ao obl´ıqua é formada pela proje¸cão do espa¸co linha de A ao longo do espa¸co linha de B, no espa¸co linha de C . . . 16

4.1 Ilustra¸cão gráfica do Teorema 7 . . . 68

5.1 Disposi¸cão gráfica das várias etapas da ISE . . . 95

5.2 Representa¸c˜ao do sinal de entrada, u(t) e de sa´ıda, y(t) . . . 95

5.3 Menu interativo . . . 97

5.4 Representa¸c˜ao do sinal de entrada e sa´ıda . . . 97

5.5 Representa¸c˜ao dos valores singulares . . . 98

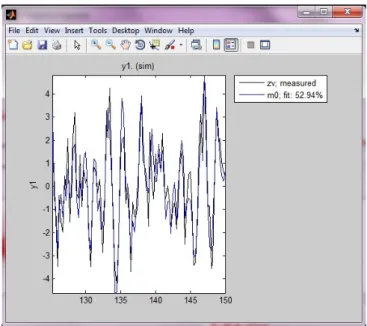
5.6 Compara¸c˜ao entre as sa´ıdas simuladas com as sa´ıdas medidas. . . 99

(22)

5.9 Representa¸cão da resposta em frequência . . . 102 5.10 Representa¸cão dos sinais de E/S . . . 103 5.11 Representa¸cão do sinal de entrada . . . 104 5.12 Representa¸cão do sinal de sa´ıda . . . 104 5.13 Compara¸cão entre as sa´ıdas simuladas com as sa´ıdas medidas. . . 105 5.14 Representa¸cão da resposta impulsional . . . 105

(23)

Gloss´

ario, acr´

onimos e

abreviaturas

Lista de acr´

onimos

Sigla Expans˜ao

A, B, C, D Matrizes do sistema dinˆamico AR Autoregressive

ARMA Autoregressive moving average

ARX Autoregressive exogenous

ARMAX Exogenous ARMA

BJ Box-Jenkins

E/S Entrada e sa´ıdas

IS Identiﬁca¸c˜ao de sistemas

ISE Identiﬁca¸c˜ao em subespa¸cos de estados LTI Linear Time invariant system

(24)

MQ M´ınimos quadrados

MOESP Multi-Input Multi-Output Error State-Space Model

Realization, classe de m´etodos introduzida por Verhaegen N4SID Numerical State-Space Subspace System Identification,

classe de m´etodos proposta por Van Overschee e Bart De Moor (1996)

OE Output-error

PEM Prediction error method

SISO Single input and single output

SIMO Single input and multiple output

MIMO Multiple input and multiple output

MISO Single input and single output

SVD Decomposi¸c˜ao em valores singulares

Lista de nota¸

c˜

ao

Nota¸c˜ao Significado(s)

R(A) Espa¸co coluna de A (Tamb´em designado por

columnspace(A))

i N´umero de blocos-linha da matriz de Hankel

j N´umero de blocos-coluna da matriz de Hankel

l N´umero de sa´ıdas

m N´umero de entradas do sistema

(continua na p´agina seguinte)

(25)

(continua¸c˜ao)

Nota¸c˜ao Significado(s)

n N´umero de estadas do sistema

A† Pseudo-inversa da matriz A

A∗ Matriz conjugada de A

Γi Matriz de observabilidade estendida

Hi Matriz de Toeplitz que cont´em os parˆametros de Markov

Ci Matriz de controlabilidade estendida do par{A, C}

Oi Matriz de observabilidade estendida

N N´umero de amostras recolhidas

N (A) Espa¸co n´ucleo de A

R(AT₎ _{Espa¸co linha de A (Tamb´}_{em designado por rowspace(A))}

RU U Covariˆancia da matriz de entrada

u(t)∈ Rm _{Entrada do sistema}

y(t) ∈ Rl Sa´ıda do sistema

U = U0 Matriz de Hankel de todos os dados de entrada

Y = Y0 Matriz de Hankel de todos os dados de sa´ıda

Up Matriz de Hankel dos dados de entrada passados

Yp Matriz de Hankel dos dados de sa´ıda passados

Uf Matriz de Hankel dos dados de entrada futuros

Yf Matriz de Hankel dos dados de sa´ıda futuros

x(t)∈ Rn _{Estado do sistema}

Xf Vetor de estados futuros

Xp Vetor de estados passados

w(k), v(k) Sequˆencia de ru´ıdo branco (ru´ıdos do processo e de medida, respetivamente)

0V Vetor zero do conjunto V

S(W ) Subespa¸co gerado pelo conjunto W

(continua na p´agina seguinte)

(26)

WT Complemento ortogonal do subespa¸co linear W

r(A) Caracter´ıstica da matriz A (tamb´em pode ser denominada de

rank(A))

rl(A) Caracter´ıstica de linha da matriz A

rc(A) Caracter´ıstica de coluna da matriz A

δpq Delta de kronecker

Este glossário está escrito pela ordem alfabética das siglas e nota¸cão.

(27)

1

Introdu¸c˜

ao

A identifica¸cão de sistemas (IS) utiliza sinais de entrada e sa´ıda (E/S) de um sistema, a fim de estimar os valores dos parâmetros de um modelo com uma dada estrutura.

Um modelo descreve o comportamento dinâmico de um sistema como uma fun¸cão de tempo. Os modelos matemáticos são usados para simula¸cão, análise, monitoriza¸cão, dete¸cão de falhas, previsão, otimiza¸cão, projeto dos sistemas de controlo, controlo de qualidade, entre outros.

A obten¸cão de um bom modelo para o sistema, depende de quão bem os dados medidos refletem o seu comportamento. Assim, é conveniente distinguir sinais de E/S. As sa´ıdas são, em parte, determinadas pelas entradas. Na maioria dos casos, as sa´ıdas também são afetadas por outros sinais, denominados de perturba¸cões ou ru´ıdo (Lennart, 1999). A rela¸cão entre estas variáveis pode ser ilustrada pelo diagrama da Figura1.1, em que u representa o sinal de entrada, y o sinal de sa´ıda e d o sinal de perturba¸cão.

(28)

u

−→

↓d

sistema −→y

Figura 1.1 – Rela¸c˜ao entre os sinais de E/S de um sistema.

Neste caso, os modelos são basicamente equa¸cões diferenciais (no caso cont´ınuo) ou equa¸cões às diferen¸cas (no caso discreto) que descrevem o comportamento do sistema, podendo ser utilizados na sua simula¸cão ou no dimensionamento de con-troladores. A IS consiste, fundamentalmente, nos seguintes passos (Lennart, 1999), (Pintelon and Schoukens,2012) :

• Recolha dos dados de E/S.

• Sele¸c˜ao da estrutura de modelo entre v´arios candidatos.

• Aplica¸cão de um método para estimar os valores dos parâmetros do modelo. • Valida¸cão do modelo estimado.

Este trabalho tem especial enfoque na IS lineares, em particular, nos sistemas li-neares e invariantes no tempo (LTI). Utilizar este tipo de sistemas, significa que a rela¸cão entre os sinais de E/S é linear e os seus parâmetros não mudam ao longo do tempo e, por isso, para a mesma entrada, a sa´ıda será a mesma para qualquer instante do tempo.

1.1 M´

etodos Cl´

assicos

Os diferentes algoritmos de IS pressup˜oem um certo tipo de modelo com uma de-terminada parametriza¸c˜ao. Existem diferentes tipos de modelos, sendo contudo os modelos polinomiais — Moving average (MA), Autoregressive (AR), Autoregressive

moving average (ARMA), Autoregressive exogenous (ARX), Exogenous ARMA

(AR-MAX), Output-Error (OE) e Box-Jenkins (BJ) — os mais utilizados pelos m´etodos clássicos, tais como os M´ınimos Quadrados (MQ), Variáveis Instrumentais e Métodos do erro de prognóstico (conhecidos na literatura anglo-sax´onica com Prediction

(29)

1.2. M´ETODOS DE SUBESPAC¸ O DE ESTADOS 3

Os métodos que determinam os parâmetros de estruturas de modelos parametrizados são conhecidos como métodos paramétricos1. Os métodos paramétricos são técnicas para estimar os parâmetros de determinadas estruturas de modelos. Basicamente, são formas de encontrar os valores numéricos dos parâmetros de uma dada estrutura que indiquem a melhor rela¸cão entre a sa´ıda (simulada e prevista) e a sa´ıda medida.

Os métodos PEM são mais precisos para estimar os parâmetros do modelo. Estes métodos minimizam um critério quadrático do erro de previsão e, por isso, podem ser utilizados para qualquer tipo de estrutura desde que o erro de previsão esteja devidamente parametrizado. No entanto, como no caso geral, o erro de previsão não é uma fun¸cão linear dos parâmetros. O critério quadrático poderá conter vários m´ınimos locais para onde o processo de minimiza¸cão poderá convergir se não for convenientemente inicializado.

1.2 M´

etodos de subespa¸

co de estados

A escolha de um modelo é um processo complicado em IS. No entanto os modelos LTI são frequentemente usados porque são simples e podem descrever com precisão adequada a dinâmica de um grande número de sistemas. Estes modelos do sistema podem ser representados por métodos de estado, como é o caso do apresentado de seguida:

x(k + 1) = Ax(k) + Bu(k) + w(k),

y(k) = Cx(k) + Du(k) + v(k), (1.1) onde x(k) ∈ Rn ´e o estado, u(k) ∈ Rm ´e a entrada, y(k) ∈ Rl a sa´ıda, com k = 1, . . . , N . A ∈ Rm×n, B ∈ Rn×m, C ∈ Rl×n e D ∈ Rl×m s˜ao os parˆametros e

w(k)∈ Rn e v(k)∈ Rl são ru´ıdo branco de média nula com covariância conjunta,

E     w(k) v(k)  ( w(k)T _v(k)T )  =   Q S ST _R   . (1.2)

1_{Os sistemas LTI tamb´}_{em podem ser descritos por modelos n˜}_{ao param´}_{etricos tais como a} resposta impulsional e a resposta em frequência. Os métodos que estimam estes modelos são classificados na literatura como métodos não paramétricos (Katayama,2005).

(30)

O problema geral da identiﬁca¸c˜ao em subespa¸cos de estados (ISE) consiste em de-terminar, a partir de um conjunto dispon´ıvel de amostras dos sinais de E/S, a ordem

n do sistema e o valor das matrizes [A, B, C, D] do modelo de espa¸co de estados.

Os parˆametros A, B, C e D s˜ao desconhecidos e têm de ser identificados fazendo uso apenas dos dados de E/S, que são sequências do tipo:

{u(k), u(k + 1), . . . , n}

e

{y(k), y(k + 1), . . . , n} .

1.2.1 Porquˆ

e usar m´

etodos de subespa¸

co?

Apesar das técnicas de controlo baseados em modelos de estado terem evolu´ıdo, os métodos clássicos de IS que identificam modelos de E/S foram desenvolvidos até meados do ano de 1980 (Katayama,2005). Mais ou menos nessa altura, descobriu-se que se poderia estimar o estado de um sistema com base em opera¸cões geométricas tais como proje¸cões ortogonais e obl´ıquas, sem necessidade do conhecimento do modelo o que levou ao aparecimento das técnicas de ISE.

Na Figura 5.1, vemos no lado esquerdo as caracter´ısticas dos métodos de ISE e no lado direito as dos métodos clássicos.

´

E interessante observar a diferen¸ca entre as duas abordagens: no método clássico, a fun¸cão de transferência é primeiro identificada, e só depois o modelo de espa¸co de estados é obtido por meio de uma realiza¸cão conveniente; através do modelo de espa¸co de estados, podemos determinar o filtro de Kalman. Nos métodos ISE, come¸camos por construir estimativas dos estados através dos dados de E/S usando ferramentas de álgebra linear numérica, onde um modelo de espa¸co de estado é então obtido através da solu¸cão de um problema dos MQ. Um elemento chave dos métodos de subespa¸co é compreender como é que os vetores de estado do filtro de Kalman e a matriz de observabilidade estendida são obtidos pelo uso de ferramentas da álgebra linear numérica.

(31)

1.2. M´ETODOS DE SUBESPAC¸ O DE ESTADOS 5

baseados na decomposi¸cão em valores singulares (SVD) e na decomposi¸cão QR, não sendo necessárias quaisquer técnicas de otimiza¸cão, nem de impor que o sistema se encontre numa dada realiza¸cão. Isto implica que os algoritmos de subespa¸co possam ser igualmente aplicados a todos os sistemas.

Figura 1.2 – M´etodos de subespa¸cos e cl´assicos de IS (Katayama,2005).

1.2.2 Identifica¸

c˜

ao em subespa¸

cos de estados

Na seçcão anterior foi definido que uma das ideias chave da identifica¸cão em su-bespa¸cos é a da importância do estado para o processo de identifica¸cão, pois de facto, enquanto que na identifica¸cão clássica as estimativas do filtro de Kalman são obtidas apenas depois da estima¸cão das matrizes do sistema, na identifica¸cão em subespa¸cos tem-se a ordem inversa: a sequência de estados do filtro de Kalman é determinada primeiro a partir dos dados de E/S, sem qualquer conhecimento prévio do modelo. Uma vez conhecida a sequência de estados, o problema de identifica¸cão passa a ser um problema linear de MQ em termos das matrizes desconhecidas do espa¸co de estados. Uma vez que a sequência de estados pode ser calculada usando as ferramentas de álgebra linear numérica, as implementa¸cões destes algoritmos são numericamente eficientes e robustas, sendo, por isso, adequadas a sistemas e conjun-tos de dados de elevada dimensão. A ISE pode ser usada na IS de sistemas MIMO,

(32)

evitando-se, desta forma, o problema de longos tempos de execu¸cão à medida que o número de parâmetros aumenta.

´

E importante salientar que os algoritmos de ISE possuem dois passos principais. No primeiro passo é determinada uma base, a partir dos dados de E/S, para o subespa¸co gerado pelas colunas de uma certa matriz, denominada de ”matriz de observabilidade estendida”. A base, tal como aquele subespa¸co, tem dimens˜ao n, que por conseguinte é a ordem do sistema a ser identificado.

No segundo passo, são estimadas as matrizes do sistema, em que para tal existem varia¸cões de métodos, nomeadamente usa-se a matriz de observabilidade estendida e a proje¸cão das matrizes de dados.

1.3 Metodologia adotada nesta disserta¸

c˜

ao

Este trabalho tem um caracter pedag´ogico com vista ao desenvolvimento de uma

toolbox com um painel ´unico que contenha os diferentes conceitos de ISE de uma forma integrada.

Para tal será necessário introduzir alguns conceitos de álgebra linear, imprescind´ıveis `

a compreens˜ao dos m´etodos de subespa¸co estudados.

1.4 Motiva¸

c˜

ao e contribui¸

c˜

oes da disserta¸

c˜

ao

A atual crescente competitividade do mercado gera a necessidade do desenvolvi-mento de produtos cada vez mais elaborados, com maiores capacidades de produ¸cão, desempenho e fiabilidade e mais imunes a perturba¸cões que interfiram na qualidade do produto final.

Deste modo a ISE assume especial importância pois tem como principal objetivo es-timar modelos precisos e flex´ıveis capazes de servirem de suporte ao desenvolvimento de sistemas de controlo de alto desempenho. A ISE de sistemas lineares possui um vasto leque de métodos que se poderão compilar em algoritmos que se baseiam no estado como chave da identifica¸cão.

(33)

1.5. PRINCIPAIS OBJETIVOS DO TRABALHO 7

Esta disserta¸cão, focada na ISE, tem como objetivo construir um suporte lógico para IS que vise implementar algoritmos de constru¸cão de modelos de estados, lineares e não lineares, em malha aberta. Estes algoritmos têm grande aplicabilidade, pois existem muitos problemas do mundo real cuja solu¸cão poderá ser obtida através destes modelos, como é, por exemplo, a dete¸cão de fugas e o controlo de redes de gás.

Para testar os algoritmos utilizar-se-˜ao dados simulados e dados reais, para todos os sistemas.

1.5 Principais objetivos do trabalho

Esta disserta¸c˜ao, visa a viabilidade da toolbox desenvolvida, Subspace

Identifica-tion Tool (SIT), com vista `a sua utiliza¸cão em identifica¸cão de subespa¸cos, com o desenvolvimento necessário das seguintes tarefas:

• Familiariza¸c˜ao inicial com o tema e recolha de bibliograﬁa.

• Familiariza¸cão com os métodos de subespa¸co de estados e clássicos de IS. • Estudo da toolbox de IS do Matlab através de exemplos, tendo em vista o

projeto de controladores.

• Implementa¸cão, em Matlab, de métodos de identifica¸cão de modelos de estado

lineares discretos com vista `a implementa¸c˜ao de uma toolbox.

• Implementa¸cão de métodos para o caso determin´ıstico, estocástico e

deter-min´ıstico-estoc´astico na mesma toolbox.

• Identifica¸cão de alguns sistemas utilizando o(s) método(s) implementado(s),

com vista ao seu estudo e posterior discuss˜ao de resultados.

1.6 Estrutura da disserta¸

c˜

ao

Nesta seçcão explicamos como esta disserta¸cão se encontra estruturada e como os diferentes cap´ıtulos se relacionam entre si. Desta forma, esta disserta¸cão encontra-se

(34)

organizada em seis cap´ıtulos.

No presente cap´ıtulo fez-se uma introdu¸c˜ao de enquadramento do tema e apresentou-se a motiva¸c˜ao e os objetivos do trabalho.

A primeira parte compreende o Cap´ıtulo 2, o qual contém todos os conceitos fun-damentais, nomeadamente, todos os conceitos fundamentais da Álgebra Linear ne-cessários à compreensão dos métodos de ISE, constituindo assim uma base para os próximos cap´ıtulos.

O Cap´ıtulo3, retrata toda a descri¸cão dos métodos de subespa¸cos de estados, para o caso determin´ıstico, estocástico e o combinado determin´ıstico-estocástico, onde são apresentados as propriedades fundamentais de cada sistema.

O Cap´ıtulo 4, trata dos teoremas respetivos a cada método apresentado no cap´ıtulo anterior, onde estão presentes todas as propriedades que são importantes para a constru¸cão de algoritmos e, consequentemente, sobre os algoritmos sobre os quais esta disserta¸cão se debru¸cou.

Por sua vez no Cap´ıtulo 5, tratamos da implementa¸cão numérica dos algoritmos de identifica¸cão em subespa¸cos. Esta implementa¸cão será levada a cabo num ambiente de interface gráfica de utilizador que fora desenvolvida — SIT. Os conceitos e novas ideias por trás dessa implementa¸cão serão nesse cap´ıtulo esbo¸cados. O SIT, para além dos algoritmos de identifica¸cão em subespa¸cos, contém uma escala inteira de processamento, e todos os métodos necessários de valida¸cão.

Finalmente, no Cap´ıtulo6 são apresentadas as conclusões desta disserta¸cão e ideias de trabalho futuro, uma vez que a pesquisa nos algoritmos de ISE está longe de ser uma área fechada, e os principais problemas, que foram vistos durante a nossa pesquisa, continuam em aberto.

(35)

2

Fundamentos de ´

Algebra

Linear Num´erica

Os métodos de ISE são uma área de IS onde se combinam conceitos geométricos de Álgebra Linear com ferramentas numéricas robustas, introduzindo desta forma ideias inovadoras nunca antes usadas nos métodos ”clássicos” de IS.

Este cap´ıtulo contém uma revisão de tópicos de Álgebra Linear e de Teoria de Matrizes em particular, necessários à compreensão de todos os fundamentos teóricos a apresentar ao longo desta disserta¸cão.

Este cap´ıtulo foi escrito com base no livro (Antsaklis and Michel, 2007).

2.1 Espa¸

cos e subespa¸

cos vetoriais

Iniciamos esta seçcão com a no¸c˜ao de espa¸co linear sobre um corpo F , seguindo-se a no¸cão de subespa¸co linear.

Defini¸c˜ao 1 (Corpo). Seja F um conjunto n˜ao singular sobre o qual estão definidas duas opera¸cões, que representamos por ”+” e ”·” e designamos por soma e produto, respetivamente (isto significa que estas opera¸cões são aplica¸cões de F × F → F ). Então, a cada dois elementos α, β ∈ F corresponde um único elemento α + β ∈ F , designado por soma de α com β, e um único elemento α· β ∈ F, designado por

(36)

produto de α por β. O termo ordenado (F, +,·) designa-se por corpo (Antsaklis and Michel, 2007, p´ag. 37).

Defini¸c˜ao 2 (Espa¸co linear). Seja V um conjunto n˜ao vazio, definido sobre um corpo (F, +,·), + uma aplica¸cão de V × V → V e · uma aplica¸cão de F × V → V . Os elementos x∈ V são designados vetores e os elementos de α ∈ F são designados escalares. Então a opera¸cão ”+” é designada adi¸cão de vetores e ”·” é designada por multiplica¸cão escalar. Então para cada x, y∈ V existe um único elemento x+y ∈ V, designado soma de x com y, e para cada x ∈ V e α ∈ F existe um único elemento αx∈ V, designado múltiplo de x por α. O termo (V, +, ·) sendo V definido sobre o corpo F designa-se como espa¸co linear se os axiomas seguintes são satisfeitos:

(i) x + y = y + x para cada x, y ∈ V

(ii) x + (y + z) = (x + y) + z para cada x, y, z ∈ V

(iii) existe um ´unico x∈ V, designado vetor zero e representado por 0V, que verifica

a propriedade 0V + x = x + 0V = x para todo o x∈ V.

(iv) α (x + y) = αx + αy para todo o α∈ F e x, y ∈ V. (v) (α + β) x = αx + βx para todo o α, β ∈ F e x ∈ V. (vi) (αβ) x = α (βx) para todo o α, β ∈ F e x ∈ V. (vii) 0Fx = 0V para todo o x∈ V.

(viii) 1Fx = x para todo o x∈ V.

Quando, a partir do contexto, se torna claro qual o corpo F sobre o qual V est´a deﬁnido, falamos simplesmente em espa¸co linear V .

Exemplo 1 (Espa¸co linear). O conjunto dos n´umeros complexos,C, com as opera¸c˜oes usuais, ´e um espa¸co vetorial sobre ele mesmo.

Defini¸c˜ao 3 (Subespa¸co linear). Seja W um subconjunto n˜ao vazio de V se (i) w1+ w2 ∈ W sempre que w1, w2 ∈ W e (ii) αw ∈ W sempre que α ∈ F e w ∈ W.

Exemplo 2 (Subespa¸co linear). Um exemplo simples de um subespa¸co linear deR2_,

´

(37)

2.1. ESPAC¸ OS E SUBESPAC¸ OS VETORIAIS 11

Observa¸c˜ao 1. Sejam W1, W2 dois subespa¸cos lineares de um espa¸co linear V, ent˜ao

o subespa¸co interse¸cão, W1∩ W2 é também um subespa¸co de V.

Observa-se que o mesmo n˜ao acontece com a uni˜ao de subespa¸cos.

No que se segue, considere-se o conjunto indexado de escalares {α1, . . . , αn} , αi ∈

F, i = 1, . . . , n, e o conjunto indexado de vetores {v1, . . . , vn} , vi ∈ V, i = 1, . . . , n.

2.1.1 Independˆ

encia linear

Nesta seçcão revêem-se os conceitos de combina¸cão linear, espa¸co gerado e indepen-dência e dependência de vetores.

Defini¸cão 4 (Combina¸c˜ao linear finita). Seja W um conjunto do espa¸co vectorial V (podendo ser finito ou infinito), v diz-se uma combina¸cão linear finita dos vetores de W se, considerando um conjunto finito de elementos de W, {w1, . . . , wn} , e um

conjunto finito de escalares de F, {α1, . . . , αn} , se tem:

v = α1w1+· · · + αnwn.

Defini¸c˜ao 5 (Subespa¸co gerado). Seja W ̸= ∅ um subconjunto de V e S(W ) o

conjunto de todas as combina¸c˜oes lineares finitas dos vetores de W, i.e., w∈ S(W ) se e s´o se existir um conjunto finito de escalares de F ,{α1, . . . , αm} , e um conjunto

finito de vetores de W, {w1, . . . , wm} , tais que w = α1w1 +· · · + αmwm, sendo m

um inteiro positivo. Ent˜ao S(W ) ´e subespa¸co de V, designado subespa¸co gerado pelo conjunto W.

Observa¸c˜ao 2. 1. Seja U um subespa¸co linear de um espa¸co vetorial V, se existir um conjunto W ⊂ V tal que o subespa¸co linear S(W ) coincide com U ent˜ao diz-se que W gera U.

2. S(W ) ´e o mais pequeno dos subespa¸cos de V que cont´em o subconjunto W de V.

3. Sendo U um subespa¸co de V e W ⊂ U, ent˜ao tamb´em S(W ) ⊂ U.

Defini¸c˜ao 6 (Dependˆencia linear). Seja S ={v1, . . . , vm} um conjunto n˜ao vazio do

espa¸co vectorial V. Se existem escalares {α1, . . . , αm} com αi ̸= 0, para pelo menos

(38)

Por outro lado, se tivermos∑m_j=1ajxj = 0 =⇒ αi = . . . = αm = 0 ent˜ao{v1, . . . , vm}

dizem-se linearmente independentes.

Exemplo 3 (Independˆencia linear). 1. Considere o espa¸co linear (Rn_,_{R) e e}1 ₌ [1, 0, . . . , 0]T_{, e}2 _{= [0, 1, . . . , 0]}T_{, . . . , e}n _{= [0, 0, . . . , 1]}T_{. Claramente,}∑n

i=1αie i ₌ 0 implica que αi = 0, i = 1, . . . , n. Por isso, o conjunto S = e1, . . . , en ´e

um conjunto de vetores linearmente independentes em Rn _{sobre o corpo dos}

n´umeros reais de R.

2.1.2 Base de um espa¸

co linear

Estamos agora em posi¸cão de definir base de um espa¸co vetorial, bem como de dimensão de um espa¸co vetorial.

Defini¸c˜ao 7 (Base). Um conjunto W dum espa¸co vetorial V ´e uma base de V se:

1. W ´e linearmente independente.

2. O espa¸co gerado por W ´e o pr´oprio espa¸co linear V , i.e., S(W ) = V .

Uma consequência imediata desta defini¸cão é o facto de qualquer conjunto linearmen-te independenlinearmen-te, W ⊂ V, ser uma base de S(W ).

Para definir a dimens˜ao de um espa¸co vetorial, V, mostra-se que se V for gerado por um número finito de elementos, então existindo outro conjunto de elementos que gere o mesmo espa¸co V , o n´umero de elementos deste conjunto será igual ao do primeiro. Vejamos então que se {v1, . . . , vn} for uma base dum espa¸co vetorial, ent˜ao cada v ∈ V se escreve de forma única como combina¸cão linear deste conjunto de vetores, i.e. v = α1v1+· · · + αnvn. Além disso, se u1, . . . , um é um conjunto de vetores de V linearmente independentes então m ≤ n e qualquer base de V possui exatamente n elementos.

Defini¸cão 8 (Dimens˜ao). Seja V um espa¸co vetorial com uma base cujo número de elementos é finito então V diz-se um espa¸co vetorial de dimensão finita e igual ao número de elementos da base. Não sendo V um espa¸co vetorial de dimensão finita, diz-se um espa¸co vetorial de dimensão infinita.

(39)

2.2. SOMA DIRETA DE SUBESPAC¸ OS LINEARES 13

Este resultado permite introduzir o conceito das coordenadas de um vetor. Seja

{v1, . . . , vn} uma base de um espa¸co vetorial V. Ent˜ao v ∈ V ´e representado nessa base por

v = ξ1v1+ . . . + ξnvn, (2.1) tendo-se que os escalares únicos {ξ1, . . . , ξn} são denominadas de coordenadas de v no que diz respeito à base {v1, . . . , vn}.

Exemplo 4 (Base can´onica). Para um espa¸co linear (Rn_,_{R), com S = {e1}_{, . . . , e} n},

onde ei ∈ Rn, i = 1, . . . , n, S ´e uma base para (Rn,R). Tem-se ainda que todo o

vetor v ∈ Rn pode ser associado a um ´unico n– uplo de escalares

    αi .. . αn     , relativo `a

base {e1, . . . , en} , a que se chama coordenadas de representa¸c˜ao do vetor v na base

S. Doravante, a base S ser´a designada de base natural ou can´onica de Rn.

A base natural do Exemplo 4 tem como propriedade o facto de todos os vetores terem norma unit´aria e serem ortogonais entre si 1. Uma base deste tipo designa-se de base ortonormada.

2.2 Soma direta de subespa¸

cos lineares

Seja V um espa¸co vectorial e W e U dois quaisquer subconjuntos de V. A soma dos conjuntos, denotada por W + U , ´e o conjunto de todos os vetores de V tal que

v = w + u, w∈ W, u ∈ U. Em particular, se W e U forem subespa¸cos lineares de V ,

ent˜ao W + U ´e tamb´em um subespa¸co linear de V.

Mais, ainda se W e U forem subespa¸cos lineares de V e W ∩ V = {0} ent˜ao W e U dizem-se conjuntos disjuntos.

Se W e U são subespa¸cos lineares de V então para cada v ∈ W + U existe um único

w∈ W e um ´unico u ∈ U tal que v = w + u se e s´o se W ∩ V = {0}.

Estendendo estas ideias a um n´umero ﬁnito de subespa¸cos de V tem-se que:

1_{Dois vetores dizem-se ortogonais quando o seu produto interno ´}_{e igual a zero (ver em pormenor} na Sec¸c˜ao2.3)

(40)

Defini¸c˜ao 9 (Soma direta de subespa¸cos). Sendo V1, . . . , Vr subespa¸cos lineares de

V, sempre que para cada v ∈ V1+· · · + Vr existir um conjunto ´unico de vi ∈ Vi, i =

{1, . . . , r} tal que v = v1+· · · + vr, chama-se soma direta a V1+· · · + Vr e denota-se

por V1⊕ · · · ⊕ Vr.

Defini¸c˜ao 10 (Proje¸c˜ao). Considere-se a soma direta de dois subespa¸cos, i.e., V1⊕

V2, e seja v = v1+ v2, v1 ∈ V1, v2 ∈ V2 a representa¸c˜ao ´unica de v ∈ V. Chama-se

proje¸cão de v em V1 ao longo de V2 à transforma¸cão linear definida por:

P(v) = v1.

Observa¸c˜ao 3. Tem-se ent˜ao que:

(i) P ∈ L(V, V ) (em que L(V, V ) ´e o espa¸co das transforma¸c˜oes lineares de um espa¸co vectorial nele mesmo (Halmos, 1958) e (Strang, 1988).)

(ii) R(P) = V1.

(iii) N (P) = V2.

No caso geral, tem-se que seP ∈ L(V, V ) então P é uma proje¸cão em R(P) ao longo deN (P) (ver defini¸cão de R(P) e N (P) na Seçcão 2.4.5) se e só se PP = P2 ₌P. Tem-se então que:

Defini¸c˜ao 11 (Idempotˆancia). P ∈ L(V, V ) diz-se idempotente se P2 ₌_P.

Outras propriedades:

1. P é uma proje¸cão sobre um subespa¸co se e só se (I − P) é uma proje¸cão. 2. SeP é uma proje¸cão sobre em V1 ao longo de V2 então (I − P) é uma proje¸cão

sobre em V2 ao longo de V1.

3. SeP é uma proje¸cão sobre um subespa¸co de V então

(41)

Defini¸c˜ao 12 (Proje¸c˜ao Ortogonal). ΠB define o operador que projeta o espa¸co

linha (ver defini¸cão de espa¸co linha na Seçcão 2.4.5) de uma matriz B ∈ Rn×m:

ΠB = BT(BBT)†B, (2.2)

onde† define a pseudo-inversa de Moore-Penrose. A/B ´e abreviatura para a proje¸c˜ao do espa¸co linha da matriz A∈ Rn×n _{no espa¸}_{co linha da matriz B:}

A/B = AΠB

= ABT(BBT)†B. (2.3)

O operador de proje¸cão pode ser interpretado num espa¸co de dimensão j, como é indicado na figura seguinte:

Figura 2.1 – Interpreta¸c˜ao da proje¸c˜ao ortogonal num espa¸co de dimens˜ao j (neste caso

j = 2). A/B ´e formado pela proje¸c˜ao do espa¸co linha de A no espa¸co linha de B. Por outro lado, A/B⊥ ´e formado pela proje¸c˜ao do espa¸co linha de A no complemento ortogonal do espa¸co linha de B (Overschee and Moor,1996).

Defini¸cão 13 (Proje¸c˜ao Obl´ıqua). Em vez de decompormos A como combina¸cão linear de duas matrizes ortogonais (B e B⊥), podemos decompor como combina¸cão linear de duas matrizes não ortogonais B e C e dos complementos ortogonais de B e C. As linhas de uma matriz A são decompostas como combina¸cão linear das linhas de B e C. Isto pode ser escrito como:

(42)

A = LBB + LCC + LB⊥,C⊥ [ C D ]⊥ . (2.4)

A matriz LCC ´e definida como a proje¸c˜ao obl´ıqua do espa¸co linha de A ao longo do

espa¸co linha de B no espa¸co linha de C:

A/BC = LCC. (2.5)

A seguinte figura ilustra a proje¸cão obl´ıqua no espa¸co dimensional j. O nome obl´ıqua refere-se à dire¸cão da proje¸cão não ortogonal. A proje¸cão obl´ıqua poderá ser inter-pretada através do seguinte enunciado: projetar o espa¸co linha de A ortogonalmente sobre o espa¸co linha de B e C; e decompor o resultado ao longo do espa¸co linha de C. Matematicamente, a proje¸cão obl´ıqua do espa¸co linha de A no espa¸co linha de B e C pode ser estabelecida como:

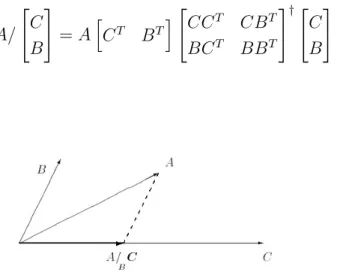
A/ [ C B ] = A [ CT _BT] [CC T _CBT BCT _BBT ]_†[ C B ] (2.6)

Figura 2.2 – Interpreta¸c˜ao da proje¸c˜ao obl´ıqua num espa¸co de dimens˜ao j (neste caso

j = 2). A proje¸c˜ao obl´ıqua ´e formada pela proje¸c˜ao do espa¸co linha de A ao longo do espa¸co linha de B, no espa¸co linha de C (Overschee and Moor,1996).

Defini¸c˜ao 14 (Subespa¸co invariante). Seja T ∈ L(V, V ). Um subespa¸co W ⊂ V

diz-se T –invariante se w ∈ W =⇒ T w ∈ W.

(43)

(i) V ´e T –invariante. (ii) {0} é T –invariante. (iii) R(P) é T –invariante. (iv) N (P) é T –invariante.

Seja V um espa¸co linear tal que V = W ⊕ V. Se W e U forem ambos subespa¸cos

T – invariantes então diz-se que T é reduzida por W e U. Usando as defini¸cões

anteriores, verifica-se que T ∈ L(V, V ) é reduzida por W e U se e só se PT = T P , sendo P uma proje¸cão sobre W ao longo de U.

Exemplo 5. Seja V um espa¸co vetorial de dimensão n e P ∈ L(V, V ). Se P é uma proje¸cão então existe uma base {v1, . . . , vn} de V cuja matriz P de P relativa a esta

base ´e da forma: P =                   1 0 . . . 0 ... 0 1 . . . 0 ... .. . ... ... ... 0 0 0 . . . 1 ... . . . . .. . 0 . . . 0 0 ... ... ... .. . 0 . . . 0                                    r sendo r = dimR(P).

Seja V um espa¸co vetorial de dimensão n e A ∈ L(V, V ). Seja W um subespa¸co invariante de V e dimensão p tal que V = W ⊕ U. Então existe uma base de V à

(44)

qual corresponde a matriz A deA tal que A =     A11 ... A12 . . . . . . . . . A21 ... A22     sendo A11 uma matriz quadrada de dimens˜ao p.

2.3 Complemento ortogonal de um conjunto

Seja W um subespa¸co linear do espa¸co vetorial V e considere-se tamb´em

W⊥ ={v ∈ V : (v, w) = 0 para todo o elemento w ∈ W } sendo (v, w) o produto interno 2 _{de v por w.}

Tem-se ent˜ao as seguintes propriedades:

(i) Suponhamos que {w1, . . . , wk} gera W. Ent˜ao v ∈ W⊥ se e s´o se v ⊥ wj, j = 1, . . . , k.

(ii) W⊥ ´e um subespa¸co linear de V.

(iii) n = dimV = dimW + dimW⊥., em que dim se refere `a dimens˜ao.

(iv) (W⊥)⊥ = W. (v) V = W ⊕ W⊥.

(vi) Sejam u, v ∈ V , se u = u1+ u2 e v = v1 + v2 com u1, v1 ∈ W e u2, v2 ∈ W⊥ ent˜ao3 (u, v) = (u1, v1) + (u2, v2) ∥u∥2 = √ ∥u1∥ 2 2 +∥u2∥ 2 2.

2_{Seja u e v dois vetores de W , define-se como produto interno de u por v e designa-se por} (u, v), qualquer aplica¸c˜ao W × W → R com as propriedades que obedecem aos seguintes axiomas (Antsaklis and Michel, 2007, p´ag. 438)

3_{A norma quadr´}_{atica ´}_{e definida `}_{a custa do produto interno como}_∥v∥2

2= (v, v) = √

(45)

2.4. MATRIZES 19

O subespa¸co WT assim deﬁnido designa-se complemento ortogonal do subespa¸co linear W.

Diz-se que dois vetores u e w s˜ao ortogonais segundo um determinado produto interno (u, v) se e s´o se (u, v) = 0.

Exemplo 6 (Complemento ortogonal). Se W = 0V ⊂ V , ent˜ao W⊥ = V . Se

W = V , ent˜ao S⊥ = 0V.

2.4 Matrizes

Na próxima seçcão vamos enunciar como é que se define a caracter´ıstica de uma matriz e quais os outros aspetos teóricos que são importantes nesta disserta¸cão.

2.4.1 Caracter´ıstica de uma matriz

Considere-se uma matriz A = [aij], em que A∈ Rm×n. As linhas desta matriz podem ser encaradas como vetores de Rn: Li = (ai1, ai2, . . . , ain), com i ∈ {1, . . . , m}. Do mesmo modo as colunas da matriz A podem ser encaradas como vetores de Rm _{: C}

j = (aij, a2j, . . . , amj), com j ∈ {1, . . . , n}. Assim consideradas, as linhas e as colunas de A geram subespa¸cos vetoriais de Rn eRm, respetivamente. Chama-se caracter´ıstica de linha (ou caracter´ıstica de coluna) de uma matriz A ∈ Rm×n, e representa-se por rl(A) ou rc(A), respetivamente, a dimens˜ao do subespa¸co vetorial deRm (respetivamente de Rn) gerado pelas m linhas (n colunas) da matriz A. Assim, rl(A) ´e o n´umero m´aximo de linhas linearmente independentes de A, en-quanto que rc(A) ´e o n´umero m´aximo de colunas linearmente independentes de A.

Exemplo 7 (Caracter´ıstica de uma matriz). 1. rc(In) = rl(In) = n, para

qual-quer n∈ N sendo In a matriz identidade de ordem n.

2. A caracter´ıstica de linha e a caracter´ıstica de coluna de uma matriz nula s˜ao claramente iguais a zero.

(46)

3. Consideremos a seguinte matriz: A = [ Ir 0 0 0 ] =                1 0 . . . 0 0 . . . 0 0 1 . . . 0 0 . . . 0 . . . 0 . . . . 0 1 . . . 1 0 . . . 0 0 0 . . . 0 0 . . . 0 . . . 0 . . . . 0 0 . . . 0 0 . . . 0               

i.e., a matriz do tipo m× n com elementos sobre o corpo R cujas r primeiras colunas (1 ≤ r < n) s˜ao os primeiros r vetores da base can´onica de Rm _{e as}

restantes colunas s˜ao nulas. Tem-se que rc(A) = r = rl(A).

A caracter´ıstica de linha (o mesmo para a de coluna) de uma matriz não se altera quando nela se efetua qualquer opera¸cão elementar de matrizes, como a troca de linhas (ou colunas), multiplica¸cão de uma linha (ou coluna) por um escalar não nulo e a adi¸cão a uma linha (ou coluna) de uma outra linha (ou coluna) previamente multiplicada por um qualquer escalar.

Seja, agora, f : E → E′ uma aplica¸cão linear entre espa¸cos vetoriais de dimensão fi-nita, representada em rela¸c˜ao a bases previamente fixadas pela matriz A∈ Mm×n(K). Ent˜ao a caracter´ıstica da matriz A, designada por r(A), ´e igual à dimensão do espa¸co imagem de f.

2.4.2 Equivalˆ

encia e semelhan¸

ca de matrizes

Uma transforma¸cão linearA de um espa¸co vetorial V de dimensão finita num espa¸co vectorial W, tamb´em de dimensão finita, pode ser representada através de diferentes matrizes, dependendo da escolha de bases particulares em V e W . A escolha da base, em diferentes casos, resulta em diferentes matrizes, as quais são fáceis ou dif´ıceis de utilizar. Muitas das resultantes formas das matrizes standard, que surgem, s˜ao denominadas de formas canónicas.

SejaA ∈ L(V, W ) e {v1, . . . , vn} e {w1, . . . , wm} bases de V e W , respetivamente. A ´

(47)

base de V e a matriz de representa¸c˜ao de{¯v1, . . . , ¯vn} em rela¸cão a {v1, . . . , vn} é P . Outra base para W ´e{ ¯w1, . . . , ¯wm} e Q é a matriz de representa¸cão de { ¯w1, . . . , ¯wm} em rela¸cão a{w1, . . . , wm} . A é a matriz de A relativamente às bases {¯v1, . . . , ¯vn} e

{ ¯w1, . . . , ¯wm}. Tem-se ent˜ao que:

A = Q−1_AP. _(2.7)

Defini¸cão 15 (Equivalˆencia de matrizes). Uma matriz A, de dimens˜ao m×n, diz-se ser equivalente a uma matriz A, de igual dimensão, se existir uma matriz Q n˜ ao-singular e de dimensão m× m e uma matriz P , de dimensão m × m, tal que (2.7)

se verifica. Se A ´e equivalente a A, tem-se que A∼ A.

Exemplo 8 (Como obter a matriz P ). Seja V =R3, F = R e a = [1, 2, 3]T ∈ R3. {v1, v2, v3} = {e1, e2, e3} define a base natural ou can´onica para R3. Claramente, as

coordenadas de α em rela¸cão à base natural são α1 = 1, α2 = 2 e α3 = 3, α = [α1, α2, α3]

T

. {¯v1, ¯v2, ¯v3} é outra base para R3, tal que por ¯v1 = [1, 0, 1]T, ¯v2 = [0, 1, 0]T e ¯v3 = [0, 1, 1]T. Através das rela¸cões:

¯ v1 = [1, 0, 1]T = p11v1+ p21v2+ p31v3 = p11     1 0 0     + p21     0 1 0     + p31     0 0 1     ,

o que implica que p11= 1, p21 = 0, p31= 1. ¯ v2 = (0, 1, 0)T = p12v1+ p22v2+ p32v3 = p12     1 0 0     + p22     0 1 0     + p32     0 0 1     ,

o que implica que p12= 0, p21 = 1, p31= 0. ¯ v3 = (0, 1, 1)T = p13v1+ p23v2+ p33v3 (2.8) = p13     1 0 0     + p23     0 1 0     + p33     0 0 1     , (2.9)

(48)

o que implica que p13 = 0, p23 = 1, p33 = 1. A matriz P = [pij], de base ¯v1, ¯v2, ¯v3 ´e,

por isso, determinada por _

  1 0 0 0 1 1 1 0 1   

e as coordenadas ¯α de a na base {¯v1, ¯v2, ¯v3}, s˜ao dadas por

¯ α = P−1α =    1 0 0 0 1 1 1 0 1    −1   1 2 3    =    1 0 0 1 1 −1 −1 0 0       1 2 3    =    1 0 2    .

Seja V = W e A ∈ L(V, V ). Seja {v1, . . . , vn} uma base de V e A a matriz de

A correspondente à base {v1, . . . , vn}. Seja {¯v1, . . . , ¯vn} uma outra base de V cuja matriz correspondente à base{v1, . . . , vn} é P. Seja eA a matriz deA correspondente `

a base {¯v1, . . . , ¯vn}. Ent˜ao

e

A = P−1AP.

Defini¸c˜ao 16 (Matrizes semelhantes). Uma matriz eA de dimensão n× n diz-se semelhante a uma outra matriz A de igual dimensão se existir uma matriz não singular P, também com a mesma dimensão, que verifique eA = P−1AP.

Se eA ´e similar a A ent˜ao tamb´em A ´e similar a eA e tem-se A = P−1AP.e

A rela¸cão de semelhan¸ca entre matrizes é uma rela¸cão de equivalência.

Seguidamente tem-se que se A ´e uma matriz de dimens˜ao n× n e semelhante a B, ent˜ao demonstra-se que Ak ´e semelhante a Bk, onde k ´e um inteiro positivo, i.e.,

Bk = P−1AkP .

Este resultado pode ser estendido considerando

f (λ) = m ∑ i=0 αiλi = α0+ α1λ + . . . + αmλm (2.10) o que veriﬁca f (P−1AP ) = P−1f (A)P, (2.11) onde α0, . . . , αm ∈ F.

(49)

Isto mostra que se B é semelhante a A, então f (B) é semelhante a f (A), sendo a transforma¸c˜ao de semelhan¸ca P igual em ambos os casos. Além disso, se A ´e semelhante a A, sendo f (λ) dado em (2.10) ent˜ao f (A) = 0 se e só se f (A) = 0.

SejaA ∈ L(V, V ) e A é uma matriz de A em rela¸cão a uma base {v1, . . . , vn} em V. Seja f (λ) o polin´omio dado em (2.10) f (λ) e A como sendo qualquer matriz de A, então é imediatamente verific´avel que f (A) = O se e só se f(A) = 0.

Podemos tirar vantagem destes resultados. Por exemplo, se A deﬁnir uma matriz

di-agonal, A =          λ1 0 0 . . . 0 0 0 λ2 0 . . . 0 0 . . . . . . . . . . 0 0 0 . . . λ_n−1 0 0 0 0 . . . 0 λn          , tem-se que Ak=          λk 1 0 0 . . . 0 0 0 λk 2 0 . . . 0 0 . . . . . . . . . . 0 0 0 . . . λk_n₋₁ 0 0 0 0 . . . 0 λk n          Substituindo A na express˜ao (2.10) tem-se:

f (A) = α0          1 0 . . . . 0 0 1 . . . . 0 . . . . 0 0 . . . 1 0 0 0 . . . 0 1          + α1          λ1 0 . . . . . . 0 0 λ2 . . . . . . 0 . . . . . . . . . . 0 0 . . . λn−1 0 0 0 . . . 0 λn          +· · · +αm          λm₁ 0 . . . . . . 0 0 λm 2 . . . . . . 0 . . . . . . . . . . . . . 0 0 . . . λm_n₋₁ 0 0 0 . . . 0 λm_n          =          f (λ1) 0 . . . . . . 0 0 f (λ2) . . . . . . 0 . . . . . . . . . . . . . . . 0 0 . . . f (λn−1) 0 0 0 . . . 0 f (λn)         

Como A ∈ L(V, V ), A é a matriz A em rela¸cão à base {v1, . . . , vn} em V , A é a matriz de A relativamente à base {¯v1, . . . , ¯vn} também em V . Então é facilmente verificado que det(A) = det(A). Deste segue-se que para qualquer duas matrizes semelhantes A e B, se tem que det(A) = det(B).

Tendo em conta estes resultados, não há ambiguidade na defini¸cão de determinante de uma transforma¸cão linear A de um espa¸co vetorial V em torno de V como determinante de qualquer matriz A, i.e, det(A) = det(A).

(50)

2.4.3 Valores e vetores pr´

oprios

Nesta subseçc˜ao, V ´e definido como um espa¸co vectorial de dimens˜ao n sobre um corpo F. Assumindo novamenteA ∈ L(V, V ) e a existência dos conjuntos de vetores

{v1, . . . , vn} e {¯v1, . . . , ¯vn}, os quais s˜ao bases de V , ent˜ao tem-se que

¯ v1 = Av1 = λ1v1 ¯ v2 = Av2 = λ2v2 .. . ¯ vn = Avn = λnvn,

onde λi ∈ F, i = 1, . . . , n. Se este é o caso, então a matriz A de A em rela¸cão às

bases dadas ´e A =          λ1 0 λ2 . . . . 0 λn          .

O que motiva o seguinte resultado: para A ∈ L(V, V ) e λ ∈ F , o conjunto de todos os vetores v∈ V , tal que

Av = λv, (2.12)

´

e um espa¸co linear de V. De facto, este ´e o espa¸co nulo da transforma¸cão linear (A − λI), onde I é o elemento identidade de L(V, V ). Tem-se então

Nλ = v∈ V : (A − λI)v = 0. (2.13)

Estamos agora em condi¸c˜oes de deﬁnir importantes conceitos.

Defini¸c˜ao 17 (Valor pr´oprio e vetor pr´oprio). Todo o escalar λ para o qual Nλ

contenha mais do que o vetor nulo é designado valor próprio de A (i.e., se existir um v̸= 0 tal que Av = λv). Sendo λ um valor próprio de A, então cada v ̸= 0 em Nλ é designado vetor próprio de A correspondente ao valor próprio λ. À dimensão

do subespa¸co linear Nλ chama-se multiplicidade (geom´etrica) do valor pr´oprio λ. Se

a dimensão do subespa¸co linear Nλ é 1, então λ diz-se um valor próprio simples.

(51)

Seja A uma matriz de dimens˜ao n× n, cujos elementos pertencem ao corpo F , se existir λ ∈ F e um vector n˜ao nulo α ∈ F tal que

Aα = λα, (2.14)

ent˜ao λ diz-se valor pr´oprio de A e α ´e designado vetor pr´oprio de A em rela¸c˜ao ao valor pr´oprio λ.

Tem-se que se A ∈ L(V, V ) e A é a matriz de A em rela¸cão à base {v1, . . . , vn} , ent˜ao λ ´e um valor próprio deA se e só se λ é um valor próprio de A. Mais ainda, se

v ∈ V é um vector próprio de A, cujas coordenadas em rela¸cão à base {v1, . . . , vn} s˜ao o vetor α, ´e um vetor pr´oprio de A em rela¸cão a λ.

Observe-se que se v (ou α) ´e um vetor próprio deA ou (A), então qualquer múltiplo n˜ao nulo de v (ou α) ´e também um vetor próprio de A (ou A).

No caso das matrizes, no lugar de (2.14), pode tamb´em considerar-se a rela¸c˜ao

αA = λα, (2.15)

onde α deﬁne um vetor linha 1× n.

Neste contexto, α em (2.14) e α em (2.15) dizem-se um vetor próprio à direita e um vetor próprio à esquerda, respetivamente.

Tendo-seA ∈ L(V, V ) e A define a matriz de A em rela¸cão à base {v1, . . . , vn} em V , ent˜ao λ∈ F é um valor próprio de A (e, portanto de A) se e só se (det(A−λI) = 0), ou equivalente se e s´o se (det(A − λI) = 0).

2.4.4 Polin´

omio caracter´ıstico

O seguinte resultado permite determinar os valores próprios de A (ou A) numa maneira sistemática. Com efeito, examina-se a equa¸cão

(52)

ou equivalentemente a seguinte equa¸c˜ao det(A− λI) =        a11− λ a12 . . . a1n a21 a22− λ . . . a2n . . . . . . . . . . . . an1 an2 . . . ann− λ        (2.17)

A expansão do determinante (2.17) origina um polin´omio em λ de grau n. Para λ ser um valor próprio de A (ou A) deve satisfazer (2.16) ou (2.17) e pertencer a F. De salientar que no geral não se tem garantia que um polin´omio de grau n, dado por (2.16), n˜ao tenha quaisquer ra´ızes em F. Um corpo F ´e dito ser algebricamente fechado se para todo o polin´omio p(λ) existe pelo menos um λ∈ F , tal que

p(λ) = 0. (2.18)

Qualquer λ que satisfa¸ca (2.18) é designado solu¸cão do polinómio (2.18).

Tendo A ∈ L(V, V ) e A é a matriz de A em rela¸cão às bases {v1, . . . , vn} de V . Então:

1. det(A − λI) = det(A − λI) é um polinómio de grau n no parâmetro λ, i.e., existem os escalares α0, α1, . . . , αn que dependem de A, e também de A, tal que:

det(A− λI) = α0+ α1λ + α2λ2+ . . . + αnλn, (2.19) deﬁnindo-se α0 = det(A) e αn= (−1)n.

2. Os valores próprios de A são precisamente as ra´ızes da equa¸cão

det(A− λυ) = det(A − λυ) = α0+ α1λ + α2λ2+ . . . + αnλn= 0. (2.20)

3. A tem no m´aximo n valores pr´oprios distintos.

A (2.19) chama-se polin´omio caracter´ıstico de A (ou de A) e chama-se a (2.20) a equa¸c˜ao caracter´ıstica de A (ou de A).