Notas para o acompanhamento das aulas de

Notas para o acompanhamento das aulas de

Integrais de Fun¸c˜

oes de Uma Vari´

avel

Sum´

ario

1 Integrais Indefinidas 3

1.1 Primitivas . . . 3

1.2 Algumas Primitivas Imediatas . . . 4

1.3 T´ecnicas de Integra¸c˜ao . . . 6

1.3.1 M´etodo da Substitui¸c˜ao (ou M´etodo da Mudan¸ca de Vari´aveis) . . . 6

1.3.2 M´etodo da Integra¸c˜ao por Partes . . . 11

1.3.3 M´etodo da Integra¸c˜ao de Fun¸c˜oes Racionais por soma de Fra¸c˜oes Parciais . . . 14

2 Integrais Definidas 19 2.1 Integrais e ´Areas . . . 19

2.2 O Teorema Fundamental do C´alculo . . . 23

2.3 T´ecnicas de Integra¸c˜ao na Integral Definida . . . 29

2.3.1 O M´etodo da Substitui¸c˜ao (ou M´etodo da Mudan¸ca de Vari´aveis) na Integral Definida . . . 29

2.3.2 O M´etodo da Integra¸c˜ao por Partes na Integral Definida . . . 31

2.4 Integrais Definidas em Coordenadas Polares . . . 32

2.4.1 O Sistema de Coordenadas Polares . . . 32

2.4.2 Curvas e Fun¸c˜oes em Coordenadas Polares . . . 34

2.4.3 Areas e Integrais Definidas no Plano Polar . . . .´ 36

3 Integrais Impr´oprias 39 4 Volumes, ´Areas e Comprimentos com Integrais Definidas 45 4.1 Volume de S´olidos - M´etodo das Sec¸c˜oes Planas Paralelas . . . 45

4.1.1 Caso Particular: Volume de S´olidos de Revolu¸c˜ao - M´etodo dos Discos . . . 47

4.1.2 Caso Particular: Volume de S´olidos de Revolu¸c˜ao - M´etodo dos An´eis Circulares . . . 49

4.2 Volume de S´olidos de Revolu¸c˜ao - M´etodo das Cascas Cil´ındricas . . . 51

4.3 Comprimento de Curvas no Plano . . . 54

Cap´ıtulo 1

Integrais Indefinidas

1.1

Primitivas

Recordemos que umafun¸c˜aofcom dom´ınioX_⊂R_{e contradom´ınio}R_{, que associa cada elementox∈Xa um´unico}

elementoy_∈R_{, ´e denotada porf}:X_⊂R_→R_,y=f(x).

Geralmente, quando n˜ao h´a d´uvidas sobre o dom´ınio e contradom´ınio def, ´e comum indicar a fun¸c˜ao apenas pela express˜ao anal´ıtica def. Por exemplo,f(x) =x2 _{indica a fun¸c˜aof com dom´ınio Re contradom´ınio Rque associax} em R_{a y}=x2tamb´em emR_.

`

As vezes utilizamos a nota¸c˜ao mais completa para indicar uma fun¸c˜ao:

f: X_⊂R _−→ R x _7−→ y=f(x)

.

Dada uma fun¸c˜aof:X_⊂R_→R_, y=f(x), umaprimitiva (ouantiderivada) defem X´e uma fun¸c˜ao deriv´avel

F:X_⊂R_→R_{,y=F(x), tal que F}′_{(x) =f(x)para qualquerx∈X.}

Por exemplo,F(x) =cos(x) +1´e uma primitiva def(x) = −sen(x), poisF′_{(x) =f(x)para qualquerx∈}R_.

Observemos que a defini¸c˜ao acima n˜ao estabelece unicidade de primitiva para f. De fato, podem existir infinitas fun¸c˜oes F tais que F′ _{=f. Por exemplo, F}

1(x) = x2+1, F2(x) = x2+2 s˜ao primitivas de f(x) = 2x, pois F′1(x) =

F′

2(x) =f(x).

Neste ponto ´e natural questionar a respeito da rela¸c˜ao entre as primitivas de uma dada fun¸c˜ao. A proposi¸c˜ao abaixo esclarece a esse respeito.

Proposi¸c˜ao 1. Se F1, F2:X⊂R→Rs˜ao primitivas de f:X⊂R→R, ent˜ao existe k∈Rtal que F1(x) =F2(x) +k para qualquer x_∈X, ou seja, as primitivas de uma fun¸c˜ao diferem apenas por uma constante.

O conjunto de todas as primitivas de f : X ⊂ R _→ R_{´e chamado de integral indefinida de f e indicado por} R

f(x)dx. Al´em disso, dizemos quef´eintegr´avele, tamb´em, quef´e ointegrandoda integral indefinida.

Inspirados pela proposi¸c˜ao acima, ´e comum escreverRf(x)dx=F(x) +k, sendoFuma primitiva defekconstante real gen´erica, chamada deconstante de integra¸c˜ao.

A justificativa para a nota¸c˜ao Rf(x)dx de integral indefinida vem das chamadas integrais definidas, que ser˜ao estudadas adiante.

Exemplos.

Exemplo (1)Rx3_dx= x4 4 +k;

Exemplo (2)Rcos(x)dx=sen(x) +k;

Exemplo (3)R 1

√

xdx=

R

x−12dx=2x12 +k=2√x+k;

Exemplo (4)Rsec2_{(x)dx=tg(x) +k.}

Proposi¸c˜ao 2. (Propriedades da integral indefinida) Sejam f, g:X_⊂R_→R_{integr´aveis e} αconstante real.

(1)R(f(x)_±g(x))dx=Rf(x)dx_±Rg(x)dx;

Demonstra¸c˜ao da Proposi¸c˜ao 2.

Sejam F : X _⊂ R _→ R _{e G : X ⊂} R _→ R _{primitivas de f e g respectivamente. Logo,} R_{f(x)dx = F(x) e} R

g(x) =G(x).

(1)Como (F(x)_±G(x))′ =F′_(x)±G′_{(x) =f(x)±g(x), temos} R_{(f(x)±g(x))dx=F(x)±G(x).}

Conclus˜ao: R(f(x)_±g(x))dx=Rf(x)dx_±Rg(x)dx.

(2)Como (αF(x))′ _=αF′_{(x) =αf(x)temos} R_{αf(x)dx=αF(x).}

Conclus˜ao: R(αf(x))dx=αRf(x)dx.

1.2

Algumas Primitivas Imediatas

R

cdx=cx+k, x_∈R_{, sendoc∈}R_constante.

R

xc_dx= xc+1

c+1 +k,x∈R, sendoc∈R,c6= −1, constante.

R₁

xdx=ln(|x|) +k,x∈R∗.

R

cx_dx= cx

ln(c)+k,x∈R, sendoc∈R+,c6=1, constante.

R

ex_dx=ex_+k,x∈R.

R

sen(x)dx= −cos(x) +k,x_∈R_. R

cos(x)dx=sen(x) +k,x_∈R_. R

tg(x)dx=ln(|sec(x)|) +k,x_∈R_,x6= π

2+nπ, comn∈Z.

R

cotg(x)dx=ln(|sen(x)|) +k,x∈R_,x6=nπ, comn∈Z_. R

sec(x)dx=ln(|sec(x) +tg(x)|) +k,x_∈R_,x₆= π

2 +nπ, comn∈Z.

R

cosec(x)dx=ln(|cosec(x) −cotg(x)|),x_∈R_{,x6=nπ, comn∈}Z_.

R

sec(x)tg(x)dx=sec(x) +k,x_∈R_,x6= π

2+nπ, comn∈Z.

R

cosec(x)cotg(x)dx= −cosec(x) +k,x_∈R_,x6=nπ, comn_∈Z_. R

sec2_{(x)dx=tg(x) +k, x∈R, x6=} π

2 +nπ, comn∈Z.

R

cosec2_{(x)dx= −cotg(x) +k, x∈R, x6=nπ, comn∈Z.}

R 1

1+x2dx=arctg(x) +k,x∈R. R ₋₁

1+x2dx=arccotg(x),x∈R. R ₁

√

1−x2dx=arcsen(x) +k, −1 < x < 1. R −1

√

1−x2dx=arccos(x) +k,−1 < x < 1.

Exemplos.

Exemplo (1)CalcularR 3x2₊₅₊√3_xdx.

Temos:

Z

3x2+5+ √3 x

dx= Z

3x2dx+ Z

5dx+ Z

x13dx

=x3+k1+5x+k2+

3 4x

4 3 +k

3

=x3+5x+3 4x

3 √

x+k.

Exemplo (2)CalcularRx4+3√3_x√xdx.

Resolu¸c˜ao.

Temos:

Z _x4₊₃√_x

3 √

x dx= Z

x4−13 +3x12−13

dx

= Z

x113 +_3x16

dx

= Z

x113 dx+ Z

3x16dx

=

11 3 +1

−1

x113+1+k₁+3 Z

x16dx

= 3 14x

14 3 +k

1+3

1 6 +1

−1

x16+1+k

2

!

= 3 14x

14 3 +_k

1+3

6 7x

7 6+_k

2

= 3 14x

4√3

x2₊ 18

7 x 6 √

x+k.

Exemplo (3)CalcularR sec2_{(x) +} 2 x2

dx.

Resolu¸c˜ao.

Temos:

Z

sec2_{(x) +} 2

x2

dx=

Z

sec2_(x)dx+

Z

2x−2dx

=tg(x) +k1+2

Z x−2dx

=tg(x) +k1+2

x−1 −1 +k2

=tg(x) − 2 x+k.

Exemplo (4)CalcularR x2

x2₊₁dx.

Resolu¸c˜ao.

Temos:

Z x2 x2₊₁dx=

Z

x2+1−1 x2₊₁ dx

= Z

1− 1 x2₊₁

dx

= Z

1dx− Z

1 1+x2dx

=x+k1−arctg(x) +k2

=x−arctg(x) +k.

Resolu¸c˜ao.

Temos:

Z

x+√1−x2

x√1−x2 dx=

Z 1 √

1−x2+

1 x

dx

=

Z ₁

√

1−x2dx+

Z ₁

xdx =arcsen(x) +k1+ln(|x|) +k2

=arcsen(x) +ln(|x|) +k.

Exemplo (6)CalcularR2sen x 2

cos x 2

dx.

Resolu¸c˜ao.

Temos:

Z

2senx

2

cosx

2

dx= Z

sen(x)dx

= −cos(x) +k.

Exemplo (7)CalcularRcos2 x 2

dx.

Resolu¸c˜ao.

Lembrando que cos(x) =cos2 x 2

−sen2 x 2

e que sen2 x 2

=1−cos2 x 2

temos cos2 x 2

= 1+cos₂(x). Assim,

Z

cos2x

2

dx= Z

1+cos(x)

2 dx

= Z

1 2dx+

Z _cos (x) 2 dx

= 1

2x+k1+ 1 2 Z

cos(x)dx

= 1

2x+k1+ 1

2sen(x) +k2

= 1

2(x+sen(x)) +k.

Exemplo (8)CalcularRsen2 x 2

dx.

Resolu¸c˜ao.

Lembrando que cos(x) =cos2 x 2

−sen2 x 2

e que cos2 x 2

=1−sen2 x 2

temos sen2 x 2

= 1−cos₂(x). Assim,

Z

sen2x

2

dx= Z

1−cos(x)

2 dx

= Z

1 2dx−

Z_cos (x) 2 dx

= 1

2x+k1− 1 2 Z

cos(x)dx

= 1

2x+k1− 1

2sen(x) +k2

= 1

2(x−sen(x)) +k.

1.3

T´

ecnicas de Integra¸c˜

ao

A seguir introduziremos algumas t´ecnicas para encontrar primitivas de fun¸c˜oes.

1.3.1

M´

etodo da Substitui¸c˜

ao (ou M´

etodo da Mudan¸ca de Vari´

aveis)

(1)Integrais indefinidas da formaRf(g(x))g′_(x)dx.

Proposi¸c˜ao 3. Sejam f:I_⊂R_→R_{cont´ınua e g:J⊂}R_→R_{deriv´avel com g(J)⊂Ieg}′_:J⊂R_→R_{. Suponhamos}

que F:I_⊂R_→R_{seja uma primitiva de f. Ent˜ao,}

Z

f(g(x))g′_{(x)dx=F(g(x)) +k}

sendo k constante de integra¸c˜ao.

Observa¸c˜oes.

(i)A demonstra¸c˜ao do teorema acima ´e uma aplica¸c˜ao imediata daRegra da Cadeia, poisF_◦g:J_⊂R_→R_{´e primitiva}

de(f_◦g)_·g′ _:J⊂R_→R_{. De fato:}

((F_◦g) (x) +k)′_=F′_(g(x))g′_{(x) =f(g(x))g}′_{(x) = (f◦g) (x)g}′_(x).

(ii)Um procedimento pr´atico: chamandou=g(x)temosu′_=g′_{(x)que na nota¸c˜ao de Leibniz ´e}du

dx =g′(x), ou seja,du=g′_{(x)dx. Fazendo essa substitui¸c˜ao na integral temos}

Z

f(g(x))g′_(x)dx= Z

f(u)du=F(u) +k=F(g(x)) +k,

ou seja, podemos fazer uma mudan¸ca de vari´aveis (dexpara u) com o objetivo de tornar a integral mais simples de ser calculada.

Exemplos.

Exemplo (1)Calcular a integralRxcos x2dx.

Resolu¸c˜ao.

Fazendou=x2 _temos du

dx =2x, ou seja,xdx= du

2 . Logo,

Z

xcos x2 dx=

Z

cos(u)du 2 =

1 2 Z

cos(u)du= 1

2sen(u) +k= 1 2sen x

2 +k.

Fazendo a correla¸c˜ao com o teorema acima: Rxcos x2 dx= 1

2

R

cos x2

2xdxe, portanto,f(x) =cos(x),g(x) = x2_,g′_{(x) =2xeF(x) =sen(x).}

Exemplo (2)Calcular a integralRe3xdx.

Resolu¸c˜ao.

Fazendou=3x temos du

dx =3, ou seja,dx= du

3 . Logo,

Z

e3xdx= Z

eudu 3 =

1 3 Z

eudu= 1 3e

u_+k= 1

3e

3x_+k.

Exemplo (3)Calcular a integralR(2x+1)3dx.

Resolu¸c˜ao.

Fazendou=2x+1temos du

dx =2, ou seja,dx= du

2 . Logo,

Z

(2x+1)3dx= Z

u3du 2 =

1 2 Z

u3du= 1 2 1 4u

4_+k= 1

8(2x+1)

4

+k.

Exemplo (4)Calcular a integralR x 1+x2dx.

Resolu¸c˜ao.

Fazendou=1+x2temos du

dx =2x, ou seja,xdx= du

2 . Logo,

Z x 1+x2dx=

Z 1 u

du 2 =

1 2 Z

1 udu=

1

2ln(|u|) +k= 1

2ln 1+x

2 +k.

Exemplo (5)Calcular a integralR_3x+21 dx,x₆= −2₃.

Fazendou=3x+2temos du

dx =3, ou seja,dx= du

3 . Logo,

Z 1

3x+2dx= Z

1 u

du 3 =

1 3 Z

1 udu=

1

3ln(|u|) +k= 1

3ln(|3x+2|) +k.

Exemplo (6)Calcular a integralR x 1+x4dx.

Resolu¸c˜ao.

Neste caso, n˜ao adiante fazeru=1+x4, pois nesse caso, du dx =4x

3_{e, portanto,xdx=} du

4x2 n˜ao ficaria em fun¸c˜ao

deuapenas.

Entretanto, se fizermosu=x2temos du

dx =2x, ou seja,xdx= du

2 . Logo,

Z x 1+x4dx=

Z 1 1+u2

du 2 =

1 2 Z

1

1+u2du=

1

2arctg(u) +k= 1

2arctg x

2 +k.

Exemplo (7)Calcular a integralRx√1+x2_dx.

Resolu¸c˜ao.

Fazendou=1+x2_temos du

dx =2x, ou seja,xdx= du

2 . Logo,

Z

xp1+x2_dx=

Z_√ udu

2 = 1 2

Z_√

udu= 1 2 Z

u12du= 1 2

u32

3 2

+k= 1 3

√

u3_+k= 1

3 q

(1+x2₎3_+k.

Exemplo (8)Calcular a integralRtg(x)dx,x=₆ π₂ +kπ,k_∈Z_.

Resolu¸c˜ao.

Aqui temos um “truque”: multiplicar e dividir tg(x)por sec(x). Logo,

Z

tg(x)dx=

Z_sec(x)tg(x)

sec(x) dx.

Fazendou=sec(x)temos du

dx =sec(x)tg(x), ou seja, sec(x)tg(x)dx=du. Logo,

Z

tg(x)dx=

Z _sec(x)tg(x)

sec(x) dx= Z ₁

udu=ln(|u|) +k=ln(|sec(x)|) +k.

Exemplo (9)Calcular a integralRsec(x)dx,x₆= π

2+kπ,k∈Z.

Resolu¸c˜ao.

Aqui tamb´em temos um “truque”: multiplicar e dividir sec(x)por tg(x) +sec(x). Logo,

Z

sec(x)dx=

Z _sec2_{(x) +sec(x)tg(x)}

tg(x) +sec(x) dx.

Fazendou=tg(x) +sec(x)temos du

dx =sec2(x) +sec(x)tg(x), ou seja, sec2(x) +sec(x)tg(x)

dx=du. Logo,

Z

sec(x)dx=

Z _sec2_{(x) +sec(x)tg(x)}

tg(x) +sec(x) dx= Z

1

udu=ln(|u|) +k=ln(|tg(x) +sec(x)|) +k.

Exerc´ıcios. Resolva:

Exerc´ıcio (1)Rsen2_(x)cos(x)dx;

Exerc´ıcio (2)Rsen(2x+7)dx; Exerc´ıcio (3)R 1

(3x−5)8dx;

Exerc´ıcio (4)Rsec2_(5x)dx.

Consideremos integrais indefinidasRf(x)dxtais que a express˜ao anal´ıtica defpossui alguma das seguintes ra´ızes quadradas:

p

a2_+x2_, p_a2_−x2 _ou p_x2_−a2_,

sendoaconstante positiva.

Neste caso fazemos a mudan¸ca de vari´aveisx=g(u)sendo:

g(u) =atg(u) para a primeira das ra´ızes acima;

g(u) =asen(u) oug(u) =acos(u) para a segunda das ra´ızes acima e;

g(u) =asec(u) para a terceira das ra´ızes acima.

Com essas substitui¸c˜oes nas ra´ızes temos

q

a2_+a2_tg2_{(u) =a}q_1+tg2_{(u) =a}q_sec2_(u)

q

a2_−a2_sen2_{(u) =a}q_1−sen2_{(u) =a}q_cos2_(u)ouq_a2_−a2_cos2_{(u) =a}q_1−cos2_{(u) =a}q_sen2_(u)

q

a2_sec2_{(u) −a}2_=aq_sec2_{(u) −1=a}

q

tg2_(u)

o que as tornam consideravelmente mais simples.

Geralmente, com essas substitui¸c˜oes a integralRf(x)dxpode ser calculada:

Z

f(x)dx= Z

f(g(u))g′_(u)du

pois dex=g(u)temos dx

du =g′(u), ou seja,dx=g′(u)du. Neste caso, a segunda integral acima pode ser simplificada ou transformada em soma de integrais mais simples, conforme veremos nos exemplos a seguir.

Ap´os o c´alculo da integral devemos retornar `a vari´avelxfazendou=arctg x a

,u=arcsen x a

(ouu=arccos x a

) eu=arcsec x

a

. Isso significa que o dom´ınio defe, portanto, o dom´ınio degdeve estar restrito de tal modo que as fun¸c˜oes trigonom´etricas envolvidas possam ser invertidas.

Exemplos.

Exemplo (1)Calcule a integralR√1−x2_{dx,−1≤x≤1.}

Resolu¸c˜ao.

Fazendo x = sen(u) temos dx

du = cos(u), ou seja, dx = cos(u)du. Para que possamos inverter a fun¸c˜ao seno tomemos −π

2 ≤u≤ π 2. Logo,

Z p

1−x2_dx=

Z_q

1−sen2_(u)cos(u)du

= Z_q

cos2_(u)cos(u)du

= Z

cos2(u)du

=

Z _1+cos(2u)

2 du

= u 2 +

sen(2u)

4 +k

= arcsen(x)

2 +

sen(2arcsen(x))

4 +k

= arcsen(x)

2 +

2sen(arcsen(x))cos(arcsen(x))

4 +k

= arcsen(x)

2 +

2xp1−sen2_(arcsen(x))

4 +k

= arcsen(x) +x √

1−x2

2 +k

Exemplo (2)Calcule a integralR√1−4x2_dx,−1 2 ≤x≤

1 2.

TemosR√1−4x2_dx=R₂

q

1 2

2

−x2_dx. Fazendo x = sen₂(u) temos dx

du = cos_(u)

2 , ou seja, dx = cos_(u)

2 du. Para que possamos inverter a fun¸c˜ao seno em

x= sen₂(u) tomemos −π 2 ≤u≤

π 2. Logo,

Z p

1−4x2_dx=

Z 2

s

1 2

2 −x2_dx

= Z

2 s

1 2

2 −

_sen(u) 2

2_cos(u)

2 du

= Zq

1−sen2_(u)cos(u)

2 du

= 1 2 Z

cos2_(u)du

= 1 2 Z

1+cos(2u)

2 du

= 1 2

u 2 +

sen(2u) 4

+k

= arcsen(2x)

4 +

sen(2arcsen(2x))

8 +k

= arcsen(2x)

4 +

2sen(arcsen(2x))cos(arcsen(2x))

8 +k

= arcsen(2x)

4 +

2(2x)p

1−sen2_(arcsen(2x))

8 +k

= arcsen(2x) +2x √

1−4x2

4 +k

Exemplo (3)Calcule a integralR 1

√

4−x2dx,−2 < x < 2.

Resolu¸c˜ao.

Fazendox=2sen(u)temos dx

du =2cos(u), ou seja,dx=2cos(u)du. Para que possamos inverter a fun¸c˜ao seno em x=2sen(u)tomemos−π

2 < u < π

2 (observe queun˜ao pode ser± π

2, sen˜aox=±2. Desta forma,

Z 1 √

4−x2dx=

Z

1 p

4−4sen2_(u)2cos(u)du

=

Z ₁

p

1−sen2_(u)cos(u)du

=

Z ₁

p

cos2_(x)cos(u)du

= Z

1du

=u+k

=arcsenx

2

+k

Exemplo (4)Calcule a integralR√1+x2_dx.

Resolu¸c˜ao.

Fazendox=tg(u)temos dx

du =sec2(u), ou seja, dx=sec2(u)du. Para que possamos inverter a fun¸c˜ao tangente tomemos −π

2 < u < π

2. Desta forma,

Z p

1+x2_dx=

Zq

1+tg2_(u)sec2_(u)du

= Z_q

sec2_(u)sec2_(u)du

= Z

O M´etodo de Integra¸c˜ao por Partes que veremos adiante permite calcular essa ´ultima integral:

Z

sec3_(u)du= sec(u)tg(u) +ln(|sec(u) +tg(u)|)

2 +k

(veremos detalhadamente esse c´alculo posteriormente). Logo,

Z p

1+x2_dx= sec(arctg(x))tg(arctg(x)) +ln(|sec(arctg(x)) +tg(arctg(x))|)

2 +k

= p

1+tg2_{(arctg(x))x+ln}

p

1+tg2_{(arctg(x)) +x}

2 +k

=

x√1+x2_+ln √

1+x2_+x

2 +k

(3)Substitui¸c˜ao “Gen´erica”.

OM´etodo da Substitui¸c˜ao Trigonom´etrica pode ser generalizado para fun¸c˜oes n˜ao necessariamente trigonom´etricas. Em Rf(x)dx, desde que x = g(u) seja deriv´avel e invert´ıvel, e Rf(g(u))g′_{(u)du seja simplific´avel, o m´etodo de}

substitui¸c˜ao tamb´em funciona. Naturalmente, n˜ao h´a uma “receita geral” sobre qual fun¸c˜aog´e conveniente para a mudan¸ca de vari´aveis. A escolha degdepende da integral a ser calculada. A procura deve sempre ser feita de modo que Rf(g(u))g′_{(u)du seja mais f´acil de ser calculada do que a integral} R_{f(x)dx original. Os exemplos a seguir}

ilustram o m´etodo.

Exemplo. Calcular a integralRx2√_1+xdx.

Resolu¸c˜ao.

Fazendox=u−1 temos dx

du =1, ou seja,dx=du. Logo,

Z

x2√1+xdx= Z

(u−1)2√1+u−1du

= Z

u2−2u+1√udu

= Z

u2−2u+1 u12_du

= Z

u52 −2u 3 2 +u

1 2

du

= u 7 2

7 2

−2u 5 2

5 2

+u 3 2

3 2

+k

= 2 7

q

(1+x)7− 4 5

q

(1+x)5+2 3

q

(1+x)3+k

1.3.2

M´

etodo da Integra¸c˜

ao por Partes

Este m´etodo ´e ´util para o c´alculo de integrais do tipoRf(x)g′_(x)dx.

Proposi¸c˜ao 4. Sejam f, g:I_⊂R_→R _{deriv´aveis. Suponhamos que} (gf)′ : I_⊂R_→R _e gf′ _:I⊂R_→R_possuam

primitivas. Ent˜ao, uma primitiva para fg′_:I⊂R_→R_{´e dada por f(x)g(x) −}R_g(x)f′_{(x)dx, ou seja,} Z

f(x)g′_{(x)dx=f(x)g(x) −} Z

g(x)f′_(x)dx.

Observa¸c˜oes.

(i)O teorema acima ´e justificado pelaRegra do Produto para deriva¸c˜ao, pois:

(f(x)g(x))′ _=f′_{(x)g(x) +f(x)g}′_(x)⇒f(x)g′_{(x) = (f(x)g(x))}′_−f′_(x)g(x)⇒ Z

f(x)g′_(x)dx= Z

(f(x)g(x))′dx−f′_(x)g(x) dx=

Z

(f(x)g(x))′dx− Z

g(x)f′_(x)dx⇒ Z

f(x)g′_{(x)dx=f(x)g(x) −} Z

sendo que no c´alculo deR(f(x)g(x))′_{dxa constante de integra¸c˜ao foi tomada nula.}

(ii)A nota¸c˜ao de Leibniz para derivada fornece um procedimento pr´atico para o c´alculo de integrais por partes. Em

R

f(x)g′_{(x)dxfa¸camos:}

 



u=f(x)_⇒ du

dx =f′(x)⇒du=f′(x)dx

dv=g′_(x)dx⇒ dv

dx=g′(x)⇒v=g(x) Logo,

Z

f(x)g′_{(x)dx=f(x)g(x) −} Z

g(x)f′_(x)dx⇒

Z

udv=uv− Z

vdu

Exemplos.

Exemplo (1)Calcule a integralRxcos(x)dx.

Resolu¸c˜ao.

Fazendo: _





u=x⇒ dudx =1⇒du=dx

dv=cos(x)dx_⇒ dv_dx=cos(x)_⇒v=sen(x)

temos: _Z

xcos(x)dx= Z

udv=uv− Z

vdu=xsen(x) − Z

sen(x)dx=xsen(x) +cos(x) +k.

Exemplo (2)Calcule a integralRarctg(x)dx.

Resolu¸c˜ao.

Fazendo: _





u=arctg(x)_⇒du dx =

1

1+x2 ⇒du=

dx 1+x2

dv=1dx_⇒ dv

dx =1⇒v=x

temos: _Z

arctg(x)dx= Z

udv=uv− Z

vdu=arctg(x)x− Z

x dx

1+x2 =xarctg(x) −

Z _x

1+x2dx.

Para resolver a integralR x

1+x2dxfazemos a substitui¸c˜aow=1+x2, portanto, dw₂ =xdx. Logo, Z

x 1+x2dx=

1 2 Z

1 wdw=

1

2ln(|w|) +k= 1

2ln 1+x

2 +k0.

Assim, _Z

arctg(x)dx=xarctg(x) − 1

2ln 1+x

2 +k.

Exemplo (3)Calcule a integralRx2_sen(x)dx.

Resolu¸c˜ao.

Fazendo: _





u=x2⇒ dudx =2x⇒du=2xdx

dv=sen(x)dx_⇒ dv_dx =sen(x)_⇒v= −cos(x)

temos:

Z

x2sen(x)dx= Z

udv=uv− Z

vdu= −x2_{cos(x) −}

Z

−cos(x)2xdx= −x2_{cos(x) +2}

Z

xcos(x).

Do Exemplo(1)logo acima temos:

Z

Assim,

Z

x2sen(x)dx= −x2cos(x) +2xsen(x) +2cos(x) +k

= 2−x2

cos(x) +2xsen(x) +k.

Exemplo (4)Calcule a integralRex_cos(x)dx.

Resolu¸c˜ao.

Fazendo: _





u=ex⇒dudx =e x

⇒du=exdx

dv=cos(x)dx_⇒ dv_dx=cos(x)_⇒v=sen(x)

temos: _Z

excos(x)dx= Z

udv=uv− Z

vdu=exsen(x) − Z

sen(x)exdx. (_∗)

Quanto aRex_{sen(x)dxprocedemos por integra¸c˜ao por partes de novo:}

 



u=ex⇒ dudx =e x

⇒du=exdx

dv=sen(x)dx_⇒ dv_dx =sen(x)_⇒v= −cos(x)

Logo, _Z

exsen(x)dx= Z

udv=uv− Z

vdu= −excos(x) − Z

−cos(x)exdx.

Substituindo em(_∗)temos:

Z

excos(x)dx=exsen(x) −

−excos(x) − Z

−cos(x)exdx

⇒ Z

excos(x)dx=exsen(x) +excos(x) − Z

cos(x)exdx⇒

2 Z

excos(x)dx=exsen(x) +excos(x)_⇒ Z

excos(x)dx= e

x

2 (sen(x) +cos(x)),

Acrescentando a constante de integra¸c˜ao:

Z

excos(x)dx= e

x

2 (sen(x) +cos(x)) +k.

Exemplo (5)Calcule a integralRcos2_(x)dx.

Resolu¸c˜ao.

Fazendo: _





u=cos(x)_⇒ du_dx = −sen(x)_⇒du= −sen(x)dx

dv=cos(x)dx_⇒ dv

dx =cos(x)⇒v=sen(x) temos:

Z

cos(x)2dx= Z

udv=uv− Z

vdu=cos(x)sen(x) − Z

−sen2_(x)dx

⇒ Z

cos(x)2dx=cos(x)sen(x) + Z

1−cos2_(x) dx⇒ Z

cos(x)2dx= sen(2x)

2 +

Z 1dx−

Z

cos2_(x)dx

⇒

2 Z

cos(x)2dx= sen(2x)

2 +x+k0⇒ Z

cos(x)2dx= sen(2x)

4 +

Exemplo (6)Calcule a integralRxln(x)dx,x > 0.

Resolu¸c˜ao.

Fazendo: _





u=ln(x)_⇒du dx =

1

x⇒du= dx

x

dv=xdx_⇒ dv_dx=x_⇒v= x₂2

temos:

Z

xln(x)dx= Z

udv=uv− Z

vdu= x

2

2 ln(x) − Z

x2

2 dx

x ⇒ Z

xln(x)dx= x

2

2 ln(x) − 1 2 Z

xdx⇒ Z

xln(x)dx= x

2

2 ln(x) − x2

4 +k⇒ Z

xln(x)dx=x2

ln(x)

2 −

1 4

+k.

Exemplo (7) Calcule a integral Rsec3_{(x)dx, x 6=} π

2 +kπ, k ∈ Z. (usamos essa integral em um dos exerc´ıcios de substitui¸c˜ao trigonom´etrica acima)

Resolu¸c˜ao.

Fazendo: _





u=sec(x)_⇒ du

dx =sec(x)tg(x)⇒du=sec(x)tg(x)dx

dv=sec2_(x)dx

⇒ dvdx=sec 2_(x)

⇒v=tg(x)

temos:

Z

sec3_(x)dx=

Z

udv=uv− Z

vdu=sec(x)tg(x) − Z

tg2_(x)sec(x)dx

⇒ Z

sec3_{(x)dx=sec(x)tg(x) −}

Z

sec2_{(x) −1}

sec(x)dx_⇒ Z

sec3_{(x)dx=sec(x)tg(x) −}

Z

sec3_{(x) −sec(x)} dx_⇒ Z

sec3(x)dx=sec(x)tg(x) − Z

sec3(x)dx+ Z

sec(x)dx_⇒

2 Z

sec3(x)dx=sec(x)tg(x) +ln(|sec(x) +tg(x)|) +k0⇒

Z

sec3_(x)dx= sec(x)tg(x) +ln(|sec(x) +tg(x)|)

2 +k.

Exerc´ıcios.

Exerc´ıcio (1)ResolvaRcos3_{(x)dxpor dois m´etodos: integra¸c˜ao por partes e substitui¸c˜ao.} Dicas:

- por partes: escreva cos3_{(x) =cos}2_{(x)cos(x)e fa¸cau=cos}2_{(x)edv=cos(x)dx;} - por substitui¸c˜ao: escreva cos3_{(x) = 1−sen}2_(x)

cos(x)e fa¸cau=sen(x). A resposta ´eRcos3_{(x)dx=sen(x) −} 1

3sen3(x) +k.

Exerc´ıcio (2)ResolvaRarcsen(x)dx. Dica: fa¸cau=arcsen(x)edv=1dx.

A resposta ´eRarcsen(x)dx=xarcsen(x) +√1−x2_+k.

1.3.3

M´

etodo da Integra¸c˜

ao de Fun¸c˜

oes Racionais por soma de Fra¸c˜

oes Parciais

Neste m´etodo estamos interessados em integrar fun¸c˜oes do tipof(x) = p(x)_q(x) sendopeqpolinˆomios com o grau dep

(indicado por∂p) menor do que o grau deq(indicado por∂q).

Proposi¸c˜ao 5. Sejam f:I_⊂R_→R_{dada por f}(x) = p_q(₍x_x)₎ fun¸c˜ao racional com coeficientes reais de tal modo que as ra´ızes de qsejam todas reais e ∂p < ∂q. Ent˜ao, para ∂q=2existem A, Bconstantes reais tais que:

(1)f(x) = _qp₍(x_x)₎ = _a(x−xp₁₎₍(x)_x−x2) = 1_ax−A_x 1 +

B x−x2

sendo x16=x2ra´ızes de q.

(2)f(x) = p_q(_(xx)₎ = p(x)

a(x−x1)2 = 1_a

A x−x1+

B

(x−x1)2

sendo x1raiz de multiplicidade 2 de q.

Proposi¸c˜ao 6. Sejam f:I_⊂R_→R_{dada por f}(x) = p_q(₍x_x)₎ fun¸c˜ao racional com coeficientes reais de tal modo que as ra´ızes de qsejam todas reais e ∂p < ∂q. Ent˜ao, para ∂q=3existem A, B, Cconstantes reais tais que:

(1)f(x) = p_q((x_x)₎ = _a(x−x1)(p_x(₋x_x)_2)(x−x3) = _a1_x−A_x 1 +

B x−x2 +

C x−x3

sendo x1, x2, x3 ra´ızes distintas de q.

(2)f(x) = p_q(_(xx)₎ = p(x)

a(x−x1)(x−x2)2 = _a1

A x−x1 +

B x−x2 +

C

(x−x2)2

sendo x16=x2 e x2 raiz de multiplicidade 2 de q.

(3)f(x) = p_q(_(xx)₎ = p(x)

a(x−x1)3 =

1 a

A x−x1+

B

(x−x1)2 +

C

(x−x1)3

sendo x1raiz de multiplicidade 3de q.

Observa¸c˜oes.

(i)Naturalmente, R_q(x)p(x)dx´e facilmente calculada depois da substitui¸c˜ao de _q(x)p(x) por uma das express˜oes fornecidas pelos teoremas acima. As constantes A, B, Cque os teoremas garantem existir s˜ao facilmante encontradas, conforme podemos constatar nos exemplos a seguir.

(ii)Percebemos facilmente que os teoremas acima podem ser generalizados paraqcom qualquer grau. Por exemplo, se∂q=ne todas as suas ra´ızes forem reais e distintas, podemos escrever

p(x) q(x) =

1 a

A1

x−x1

+_{· · ·}+ An x−xn

e se h´a apenas uma raiz real de multiplicidaden, podemos escrever

p(x) q(x) =

1 a

A1

x−x1

+ A1

(x−x1)2

+_{· · ·}+ An (x−x1)n

!

Exemplos.

Exemplo (1)Calcule a integralR x+3

x2_−3x+2dx,x6=1ex6=2.

Resolu¸c˜ao.

Temosx2_{−3x+2= (x−1) (x−2).} Assim,

x+3 x2_−3x+2 =

A x−1+

B x−2 ⇒ x+3

x2_−3x+2 =

A(x−2) +B(x−1) (x−1) (x−2) ⇒ x+3= (A+B)x−2A−B⇒

A+B=1

−2A−B=3 ⇒A= −4eB=5.

Logo,

Z

x+3

x2_−3x+2dx=

Z A x−1+

B x−2

dx

= Z

− 4

x−1 + 5 x−2

dx

= −4ln(|x−1|) +5ln(|x−2|) +k.

Exemplo (2)Calcule a integralR x2₊₂

x2_−3x+2dx,x6=1ex6=2.

Resolu¸c˜ao.

Observemos que o grau do polinˆomio do numerador ´e igual ao grau do polinˆomio do denominador. Logo, podemos dividir um polinˆomio pelo outro:

x2_{+2 x}2_−3x+2

−x2_{+3x−2 1}

3x

Logo,

x2₊₂

x2_−3x+2 =

1 x2_−3x+2 +3x x2_−3x+2 =1+

3x

x2_−3x+2 ⇒

Z _x2₊₂

x2_−3x+2dx=

Z 1dx+

Z _3x

x2_−3x+2dx=x+

Z _3x

x2_−3x+2dx.

Quanto ao c´alculo deR 3x

x2_−3x+2dxtemosx2−3x+2= (x−1) (x−2). Assim,

3x x2_−3x+2 =

A x−1+

B x−2 ⇒ 3x

x2_−3x+2 =

A(x−2) +B(x−1) (x−1) (x−2) ⇒ 3x= (A+B)x−2A−B_⇒

A+B=3

−2A−B=0 ⇒A= −3eB=6.

Logo,

Z 3x

x2_−3x+2dx=

Z A x−1+

B x−2

dx

= Z

− 3

x−1 + 6 x−2

dx

= −3ln(|x−1|) +6ln(|x−2|) +k.

Conclus˜ao: _Z

x2₊₂

x2_−3x+2dx=x−3ln(|x−1|) +6ln(|x−2|) +k

Exemplo (3)Calcule a integralR x4_+2x+1

x3_−x2_−2xdx,x6= −1,x6=0ex6=2.

Resolu¸c˜ao.

Observemos que o grau do polinˆomio do numerador ´e maior do que o grau do polinˆomio do denominador. Logo, podemos dividir um polinˆomio pelo outro:

x4_{+2x+1 x}3_−x2_−2x

−x4_+x3_+2x2 _x+1

x3_+2x2_+2x+1

−x3_+x2_+2x

3x2_+4x+1

=_⇒x4+2x+1= x3−x2−2x

(x+1) + 3x2+4x+1

.

Logo,

x4_+2x+1

x3_−x2_−2x =

x3_−x2_−2x

(x+1) + 3x2_+4x+1

x3_−x2_−2x =x+1+

3x2_+4x+1

x3_−x2_−2x ⇒

Z

x4_+2x+1

x3_−x2_−2xdx=

Z

(x+1)dx+ Z

3x2_+4x+1

x3_−x2_−2xdx=

x2

2 +x+ Z

3x2_+4x+1

x3_−x2_−2xdx.

Quanto ao c´alculo deR3x2_+4x+1

x3_−x2_−2xdxtemosx3−x2−2x= (x+1)x(x−2). Assim,

3x2_+4x+1

x3_−x2_−2x =

A x+1 +

B x +

C x−2 ⇒ 3x2_+4x+1

x3_−x2_−2x =

A x2−2x+B x2−x−2+C x2+x

(x+1)x(x−2) ⇒

3x2+4x+1= (A+B+C)x2+ (−2A−B+C)x−2B_⇒ 





A+B+C=3 −2A−B+C=4 −2B=1

⇒A=0, B= −1 2 eC=

Logo,

Z

3x2+4x+1 x3_−x2_−2xdx=

Z A x+1+

B x +

C x−2

dx

= Z ₋1

2

x +

7 2

x−2 !

dx

= −1

2ln(|x|) + 7

2ln(|x−2|) +k.

Conclus˜ao:

Z

x4_+2x+1

x3_−x2_−2xdx=

x2

2 +x− 1

2ln(|x|) + 7

2ln(|x−2|) +k

Exemplo (4)Calcule a integralR 2x+1

x3_−x2_−x+1dx,x6= −1ex6=1.

Resolu¸c˜ao.

Temosx3−x2−x+1= (x+1) (x−1)2. Assim,

2x+1 x3_−x2_−x+1 =

A x+1+

B x−1+

C (x−1)2 ⇒

2x+1 x3_−x2_−x+1 =

A(x−1)2+B x2₋₁

+C(x+1)

(x+1) (x−1)2 ⇒

2x+1= (A+B)x2+ (−2A+C)x+A−B+C⇒ 





A+B=0 −2A+C=2 A−B+C=1

⇒A= −1 4 eB=

1 4 eC=

3 2

Logo,

Z _2x+1

x3_−x2_−x+1dx=

Z _A

x+1 + B x−1+

C (x−1)2

! dx

= Z

−

1 4

x+1 +

1 4

x−1 +

3 2

(x−1)2 !

dx

= −1

4ln(|x+1|) + 1

4ln(|x−1|) + 3 2

(x−1)−1

−1 +k

= −1

4ln(|x+1|) + 1

4ln(|x−1|) − 3

2(x−1)+k

Uma Observa¸c˜ao Importante.

Notemos que o m´etodo da fra¸c˜oes parciais exposto acima pressup˜oe que as ra´ızes do polinˆomio do denominador sejam todas reais. Mas, e quando isso n˜ao acontece? Os dois pr´oximos exerc´ıcios ilustram essa situa¸c˜ao.

Exemplo (5)Calcule a integralR 2x+1 x2_+2x+2dx.

Resolu¸c˜ao.

As ra´ızes do polinˆomio do denominador s˜ao−1+ie−1−i(complexas!). Logo, o m´etodo estudado acima n˜ao se aplica. Entretanto,

Z

2x+1

x2_+2x+2dx=

Z

Fazendo u=x+1temos du

dx =1, ou seja,dx=du. Logo,

Z

2x+1

1+ (x+1)2dx= Z

2(u−1) +1 1+u2 du

= Z

2u−1 1+u2du

= Z _2u

1+u2du−

Z ₁

1+u2du

=ln 1+u2

−arctg(u) +k

=ln1+ (x+1)2−arctg(x+1) +k

=ln x2+2x+2

−arctg(x+1) +k

(6)Calcule a integralR 2x+3 x2_+x+1dx.

Resolu¸c˜ao.

As ra´ızes do polinˆomio do denominador s˜ao−1 2+

√

3 2 i e−

1 2−

√

3

2 i(complexas!). Logo, o m´etodo estudado acima n˜ao se aplica. Entretanto,

Z _2x+3

x2_+x+1dx=

Z _2x+1

x2_+x+1dx+

Z ₂

x2_+x+1dx

= Z

2x+1

x2_+x+1dx+2

Z

1

x+ 1 2

2 +3

4

dx

=

Z _2x+1

x2_+x+1dx+2

Z ₁

3 4 1+

x+1 2 √

3 2

2!dx

= Z

2x+1 x2_+x+1dx+

8 3 Z

1

1+2x+1√

3

2dx.

Fazendou=x2_{+x+1 na primeira integral temos} du

dx =2x+1, ou seja,(2x+1)dx=du. Fazendov= 2x+1

√

3 na segunda integral temos dv dx=

2

√

3, ou seja,dx=

√

3 2 dv. Logo,

Z

2x+3 x2_+x+1dx=

Z 1 udu+

8 3

Z √

3 2

1+v2dv

=ln(|u|) + 4 √

3

3 arctg(v) +k

=ln x2+x+1 +4

√ 3 3 arctg

2x+1

√ 3

Cap´ıtulo 2

Integrais Definidas

2.1

Integrais e ´

Areas

Para esse cap´ıtulo ´e importante recordarmos a nota¸c˜ao sigma para soma. (Σ_→sigma mai´usculo,σ_→sigma min´usculo)

Escrevemos n

P

i=m

xi= n

P

j=m

xj= n

P

k=m

xk=xm+xm+1+· · ·+xne notamos que h´a liberdade para escolha do ´ındice (i,

j, ou k) utilizado para representar a soma na nota¸c˜ao sigma. Naturalmente m_≤ns˜ao n´umeros inteiros, geralmente positivos.

Alguns exemplos:

5

P

i=1

2i=2+4+6+8+10

6

P

j=3

j 2j+1 =

3 7+

4 9+

5 11+

6 13

n

P

k=1

k=1+2+3+_{· · ·}+n

A chamadaintegral definida, que definiremos abaixo, est´a relacionada com o chamado “Problema das ´Areas”: como calcular a ´area de figuras planas mais gerais que as elementares?

ÁreaA= ?

A _A

A

Por volta do s´eculoIII a.C., Arquimedes estudou esse problema por meio do chamado “M´etodo da Exaust˜ao” que consiste em aproximar a ´area da figura em quest˜ao pela soma das ´areas de figuras elementares (geralmente triˆangulos).

A

B

C D

E A1

A2

A3

A

r1 r₂

r3

S

i 1=

3

r r

r 1

2

3 //AB // //

AC

BC

Vamos considerar a situa¸c˜ao no qual desejamos calcular ´areaAda regi˜ao sob o gr´afico de uma fun¸c˜ao limitada n˜ao negativa f: [a, b]_⊂R_→R_{,y=f(x)≥0, sendoa < b.}

y

x b a

gráfico def

A

Seja P = {x0, x1, . . . , xn} ⊂ Rtal que a = x0 < x1 < · · · < xn = b. O conjunto P ´e chamado de parti¸c˜ao de

[a, b]e divide esse intervalo em nsubintervalos. Tamb´em chamamos denorma da parti¸c˜ao, e indicamos por |P|, o comprimento do maior desses subintervalos.

Tomemosxi∈[xi−1, xi]comi=1, . . . , ne consideremos os retˆangulosRi de base em[xi−1, xi]e alturaf(xi).

y

x a=x0

gráfico def

x1 x2 x3x4 x5 x6 b=x7 0 < f x( 1)

x2 x3 x4 x5 x6 x7 x1

n=7

SejaAi a ´area do retˆanguloRi. Logo,

A=∼

n

P

i=1

Ai= n

P

i=1

f(xi)

| {z } altura

(xi−xi−1)

| {z } base

.

Seja ∆xi = xi−xi−1. Assim, A=∼ n

P

i=1

f(xi)∆xi e esta soma ´e chamada de Soma de Riemannde f relativa `a parti¸c˜ao Pe aos n´umerosxi.

´

E claro que se fizermos a norma de P diminuir e, consequentemente, aumentarmos o n´umero de elementos na parti¸c˜ao P, a ´area A ser´a melhor aproximada por uma Soma de Riemann, conforme podemos observar na figura abaixo.

y

x y

y y

y y

Desta forma, podemos definir a ´areaAcomo sendolimite de Somas de Riemann quando|P|tende a zero, ou seja,

A= lim

|P|→₀

n

P

i=1

f(xi)∆xi.

Quando o limite acima existe, ele ´e chamado deIntegral de Riemann, ouIntegral Definida, defno intervalo

[a, b], denotado por

A= Zb

a

f(x)dx

e dizemos quef´eintegr´avelem[a, b].

Notemos que h´a uma similaridade muito grande entre as nota¸c˜oes da integral indefinida e da integral definida. A justificativa para tal similaridade ser´a dada adiante, no chamadoTeorema Fundamental do C´alculo.

A fun¸c˜ao f ´e chamada de integrando de

Zb

a

Notemos tamb´em que, ao contr´ario da integral indefinida, que ´e um conjunto de fun¸c˜oes, a integral definida ´e um n´umero.

Por fim, devemos notar que a s´ımbolo

Z

da integral lembra um “s” e ´e inspirado no sigma mai´usculoPda soma

que aparece no limite da defini¸c˜ao da integral definida. Al´em disso o elemento de comprimentodxest´a correlacionado com o∆x.

Observa¸c˜oes importantes:

(i)Sey=f(x)_≤0for limitada n˜ao positiva, o racioc´ınio acima nos conduz a

Zb

a

f(x)dx= −A, sendoAa ´area acima

do gr´afico def, abaixo do eixox, entrex=aex=b.

y

x b a

gráfico def

xi

0 > f x( i)

(ii)Sejaf: [a, b]_→R_{limitada. Se}f(x)_≥0para a_≤x_≤cef(x)_≤0parac < x_≤btemos

Zb

a

f(x)dx=A1−A2,

sendo:

A1 a ´area abaixo do gr´afico def, acima do eixo x, entrex=aex=c.

A2 a ´area acima do gr´afico def, abaixo do eixox, entrex=cex=b.

y

x b a

gráfico def

A1 _c

A2

(iii)Sea=b, n˜ao ´e poss´ıvel tomar parti¸c˜oes de[a, b]conforme fizemos acima, mas ´e natural considerar

geometrica-mente que, neste caso,

Zb

a

f(x)dx=0.

Sendo assim,definimosque

Zk

k

f(x)dx=0 sendokn´umero real fixo.

(iv)O desenvolvimento que fizemos acima s´o faz sentido para a < b. Entretanto, h´a situa¸c˜oes em que ´e interessante

considerar

Zb

a

f(x)dxcoma > b. Neste caso,definimosque

Zb

a

f(x)dx= − Za

b

f(x)dx.

(v)Toda fun¸c˜aofcont´ınua em[a, b]´e, naturalmente, integr´avel. Entretanto, h´a fun¸c˜oes limitadas n˜ao cont´ınuas que tamb´em s˜ao integr´aveis.

y

x b a

gráfico def

A

c

Proposi¸c˜ao 7. (Propriedades) Sejamf, g: [a, b]_⊂R_→R_{fun¸c˜oes integr´aveis em}[a, b].

(1)

Zb

(f(x)_±g(x))dx=

Zb

f(x)dx_±

Zb

(2)

Zb a

kf(x)dx=k

Zb a

f(x)dxpara qualquerkconstante real.

(3)Sea < c < b, ent˜ao

Zb a

f(x)dx=

Zc a

f(x)dx+

Zb c

f(x)dx.

(4) Se f(x) _≤ g(x) para qualquer x ∈ [a, b], ent˜ao

Zb a

f(x)dx ≤

Zb a

g(x)dx. Como caso particular, se 0 ≤ g(x),

ent˜ao 0 ≤

Zb a

g(x)dx. Al´em disso, a ´area A da regi˜ao entre os gr´aficos das fun¸c˜oes f e g entre a e b´e dada por

A=

Zb a

g(x)dx−

Zb a

f(x)dx=

Zb a

(g(x) −f(x))dx≥0.

y

x gráfico def

b A

a

gráfico deg

(5) Zb a

f(x)dx

≤ Zb a

|f(x)|dx.

Demonstra¸c˜ao da Proposi¸c˜ao 7.

(1) Zb

a

(f(x)_±g(x))dx= lim

|P|→0 n

P

i=1

(f(xi)±g(xi))∆xi= lim

|P|→0

_n P

i=1

f(xi)∆xi± n

P

i=1

g(xi)∆xi

= lim

|P|→0 n

P

i=1

f(xi)∆xi±

lim

|P|→0 n

P

i=1

g(xi)∆xi=

Zb

a

f(x)dx_± Zb

a

g(x)dx.

(2) Zb

a

kf(x)dx= lim

|P|→₀

n

P

i=1

kf(xi)∆xi= lim

|P|→₀ k

n

P

i=1

f(xi)∆xi=k lim

|P|→₀

n

P

i=1

f(xi)∆xi=k

Zb

a

f(x)dx.

(3) Sejam P1 = {y0, y1, . . . , yn1} e P2 = {z0, z1, . . . , zn2} parti¸c˜oes de [a, c] e [c, b], respectivamente. Logo, yn1 = z0=c. Definamos P=P1∪P2como parti¸c˜ao de [a, b]. Adotemos a nota¸c˜ao P={x0, x1, . . . , xn}sendo n=n1+n2

(isto significa que x0 = y0, . . . , xn1 = yn1, xn1+1 = z1, . . . , xn1+n2 = zn2 e que x1 = y1, . . . , xn1 = yn1, xn1+1 = z1, . . . , xn1+n2=zn2).

Definamos

f(x) =

f(x), sex_∈[a, c] 0, sex_∈(c, b]

f(x) =

0, sex_∈[a, c) f(x), sex_∈[c, b]

Logo,

Zc

a

f(x)dx+ Zb

c

f(x)dx= lim

|P1|→0

n1 P

i=1

f(y_i)∆yi+ lim

|P2|→0

n2 P

i=1

f(zi)∆zi= lim

|P|→0 n

P

i=1

f(xi)∆xi+ lim

|P|→0 n

P

i=1

f(xi)∆xi

= lim

|P|→0

_n P

i=1

f(xi)∆xi+ n

P

i=1

f(xi)∆xi

= lim

|P|→0 n

P

i=1

f(xi) +f(xi)

∆xi

= lim

|P|→₀

n

P

i=1

f(xi)∆xi=

Zb

a

(4) Zb

a

f(x)dx= lim

|P|→₀

n

P

i=1

f(xi)∆xi≤ lim

|P|→₀

n

P

i=1

g(xi)∆xi=

Zb

a

g(x)dx.

(5)Lembremos que se|r|_≤s, ent˜ao −s_≤r_≤s. Particularmente, como|f(x)|_≤|f(x)|, ent˜ao−|f(x)|_≤f(x)_≤|f(x)|. Destas ´ultimas desigualdades, e das propriedades (2)e (4)acima, temos

Zb

a

−|f(x)|dx_≤ Zb

a

f(x)dx_≤ Zb

a

|f(x)|dx_⇒

− Zb

a

|f(x)|dx_≤ Zb

a

f(x)dx_≤ Zb

a

|f(x)|dx_⇒

Zb

a

f(x)dx

≤ Zb

a

|f(x)|dx,

como quer´ıamos.

2.2

O Teorema Fundamental do C´

alculo

A seguir apresentamos o teorema mais importante do C´alculo Diferencial e Integral de fun¸c˜oes de uma vari´avel. Este teorema tamb´em estabelece a rela¸c˜ao entre as integrais definidas e as integrais indefinidas (primitivas).

Teorema Fundamental do C´alculo (TFC).Seja f: [a, b]_⊂R_→R_{integr´avel e F: [a, b]⊂}R_→R_{uma primitiva}

de f. Ent˜ao,

Zb a

f(x)dx=F(b) −F(a).

´

E comum escreverF(b) −F(a) = F(x)|x=b_x=aou, simplificadamente,F(b) −F(a) = F(x)|b_a. Desta forma,

Zb

a

f(x)dx=

F(x)|b_a.

Demonstra¸c˜ao do TFC.

Seja P={a=x0, x1, . . . , xn−1, xn =b}uma parti¸c˜ao de [a, b].

Podemos escrever

F(b) −F(a) =F(xn) −F(xn−1) +F(xn−1) −F(xn−2) +F(xn−2) −F(xn−3) +· · ·+F(x2) −F(x1) +F(x1) −F(x0)

= Pn

i=1

(F(xi) −F(xi−1)).

Mas F´e uma primitiva, portanto, deriv´avel e, consequentemente, cont´ınua em]a, b[. Assim, peloTeorema do Valor M´edio, para cada i, existe xi ∈]xi−1, xi[ tal que F(xi) −F(xi−1) =F′(xi) (xi−xi−1), ou seja, F(xi) −F(xi−1) =

f(xi)∆xi. Logo,

F(b) −F(a) =

n

P

i=1

(F(xi) −F(xi−1)) = n

P

i=1

f(xi)∆xi⇒

lim

|P|→₀

(F(b) −F(a)) = lim

|P|→₀

n

P

i=1

f(xi)∆xi⇒

F(b) −F(a) = Zb

a

f(x)dx,

como quer´ıamos.

Notemos que a demonstra¸c˜ao acima fez uso do importanteTeorema do Valor M´edio (TVM), que vimos no cap´ıtulo de derivadas. Entretanto, h´a uma outra demonstra¸c˜ao do TFC, para o caso em quef´e cont´ınua, que faz uso de um teorema muito interessante, similar ao TVM, s´o que para integrais.

Teorema do Valor M´edio para Integrais. Seja f : [a, b] _⊂ R_→ R _{cont´ınua. Ent˜ao, existe θ ∈} ]a, b[ tal que

Zb

y

x gráfico def

b f(q)

A

a q

Na figura acima, sendo f positiva, A ´e a ´area abaixo do gr´afico de f entre a e b, e as duas regi˜oes hachuradas

possuem a mesma ´area. Claramente temosA= Zb

a

f(x)dx=f(θ) (b−a).

Vamos fazer novamente a demonstra¸c˜ao do TFC, para o caso em quef´e cont´ınua, usando o TVM para integrais.

Demonstra¸c˜ao do TFC para o caso em que f´e cont´ınua.

Definamos a fun¸c˜ao A: [a, b]_⊂R_→R_{tal que} A(x) = Zx

a

f(u)du(estamos utilizando a vari´avel uno integrando

para n˜ao confundir com a vari´avel x do extremo).

Notemos que A est´a bem definida, pois quando se f ´e cont´ınua em [a, b], ent˜ao f ´e integr´avel em [a, b], o que

significa que

Zx

a

f(u)du´e um n´umero para qualquer x_∈[a, b].

Quando f´e n˜ao negativa,A(x)representa a ´area abaixo do gr´afico de f, acima do eixo das abscissas no intervalo

[a, x].

y

x b a

gráfico def

A x( )

x

Duas perguntas: A´e deriv´avel em ]a, b[? Se Afor deriv´avel, como calcular sua derivada? Vamos respondˆe-las.

Consideremos h > 0“pequeno” de tal modo que x+h_∈]a, b[. Temos

A(x+h) −A(x) = Zx+h

a

f(u)du− Zh

a

f(u)du= Zx

a

f(u)du+ Zx+h

x

f(u)du− Zx

a

f(u)du

= Zx+h

x

f(u)du.

Sendo f cont´ınua, podemos aplicar o Teorema do Valor M´edio para Integrais, ou seja, existe θ_∈]x, x+h[

tal que

Zx+h

x

f(u)du=f(θ) (x+h−x) =f(θ)h.

Assim,

A(x+h) −A(x) =f(θ)h⇒ A(x+h) −A(x)

h =f(θ).

Tomando limites com h_→0 temos

lim h→₀

A(x+h) −A(x) h =hlim→₀

f(θ).

Quanto ao primeiro limite, ´e precisamente o limite da defini¸c˜ao de derivada de Aem x, ou seja, A′_{(x). Quanto}

ao segundo limite, notemos que quando h→0 temos θ→x, ou seja, lim h→0

f(θ) = lim θ→x

f(θ). Mas f´e cont´ınua. Logo, recordando a defini¸c˜ao de continuidade de fun¸c˜ao, temos lim

θ→x

f(θ) =f(x). Desta forma, a ´ultima igualdade significa

ou seja, A´e uma primitiva de f.

No cap´ıtulo de integrais indefinidas vimos a Proposi¸c˜ao 1: se F ´e uma primitiva qualquer de f, ent˜ao existe uma constante k tal que

A(x) =F(x) +k.

Mas para x=atemos A(a) = Za

a

f(u)du=0 e, portanto,k= −F(a).

Para x = b temos A(b) = F(b) −F(a). Entretanto, A(b) = Zb

a

f(u)du, de onde conclu´ımos

Zb

a

f(u)du =

F(b) −F(a)que, na nota¸c˜ao original, ´e dada por

Zb

a

f(x)dx=F(b) −F(a),

como quer´ıamos.

Uma consequˆencia direta do TFC ´e dada por:

Zx

a

f(u)du=F(x) −F(a)_⇒

d dx

Zx

a

f(u)du

= d

dx(F(x) −F(a)) =F

′_{(x) −0⇒}

d dx

Zx

a

f(u)du

=f(x),

que ´e muito ´util no estudo das chamadas equa¸c˜oes diferenciais ordin´arias (EDO). Neste contexto, observemos que o extremo superior da integral ´e vari´avel. Portanto, na integral h´a duas vari´aveis: x eu. Nesta situa¸c˜ao, `as vezes chamamos a vari´avelude vari´avelmuda.

Exemplos.

Exemplo (1)CalculeR₀bxdxsendob > 0constante de duas formas diferentes: usando o TFC e usando diretamente a defini¸c˜ao.

Resolu¸c˜ao.

Primeiramente observemos que neste caso podemos calcular a integral usando geometria plana elementar, uma vez que o gr´afico def´e um segmento de reta e a ´area Aabaixo do gr´afico de fe acima do eixox, com 0_≤x_≤b, ´e um triˆangulo retˆangulo com base medindobe altura medindof(b) =b.Portanto,A= b2

2.

y

x

gráfico def y= ( ) =f x x

b 0

b

A

(i)Pelo TFC temosf(x) =xeF(x) = x₂2 (uma primitiva de f) sendo0_≤x_≤b. Logo,

Zb

0

xdx= x

2

2

b

0

= b

2

2 − 02

2 = b2

2 .

(ii)Utilizando defini¸c˜ao: fixemosn_∈N_{e tomemos a parti¸c˜aoP={x0, x1, . . . , xn}=0,}b

n, 2b

n, 3b

n, . . . , nb

y

x b

gráfico def y=x

n b

f x( 1) =x1

x1 0 2b

n

x2 3b

n

x3 xn

...

f x( 3) =x3

...

SejaAa ´area abaixo do gr´afico defe acima do eixox, com0_≤x_≤b. Logo,

A= Zb

0

f(x)dx= lim

|P|→0 n

P

i=1

f(xi)∆xi= lim n→₊∞

n

P

i=1

xi(xi−xi−1)

= lim n→₊∞

n

P

i=1

ib n

ib

n− (i−1) b n

= lim n→₊∞

n

P

i=1

ib

2

n2 =_n→lim₊∞ b2 n2

n

P

i=1

i

Mas a soma Pn i=1

ipode ser calculada. Para tanto, lembremos que(k+1)2−k2= (k+1+k) (k+1−k) =2k+1.

Logo, _

       

       

k=1 _{−→ 6}22₋₁2_=2.1+1

k=2 _{−→ 6}32₋₆₂2_=2.2+1

k=3 _{−→ 6}42₋₆₃2_=2.3+1

k=4 −→ 652−₆42=2.4+1

.. .

k=n −→ (n+1)2−₆n2=2.n+1

Somando as igualdades temos

(n+1)2−1=2(1+2+3+_{· · ·}+n) + (1+1+_{· · ·}+1)

| {z }

nvezes

⇒

n2+2n+1−1=2 _n

P

i=1

i

+n⇒

n

P

i=1

i= n

2_+n

2 ⇒

n

P

i=1

i= n(n+1) 2

Substituindo:

Zb

0

f(x)dx= lim n→+∞

b2

n2 n

P

i=1

i= lim n→+∞

b2_n(n+1)

2n2 =_n→lim+∞

b2_(n+1)

2n =n→lim+∞

b2 ₁₊ 1 n

2 =

b2

2 .

Exemplo (2)CalculeRb₀x2_{dxsendob > 0constante de duas formas diferentes: usando o TFC e usando diretamente} a defini¸c˜ao.

Resolu¸c˜ao.

Observe a ´area sob o gr´afico neste caso. N˜ao d´a para calcul´a-la utilizando f´ormulas de geometria plana elementar.

y

x

gráfico def y= ( ) =f x x2

b 0

b2

(i)Pelo TFC temosf(x) =x2_{eF(x) =} x3

3 (uma primitiva def) sendo 0≤x≤b. Logo,

Zb

0

x2dx= x

3 3 b 0 = b 3 3 − 03 3 = b3 3 .

(ii)Utilizando defini¸c˜ao: fixemosn_∈N_{e tomemos a parti¸c˜aoP}={x0, x1, . . . , xn}=

0,b_n,2b_n,3b_n, . . . ,nb_n . Escolhamos os n´umerosxi,1_≤i_≤n, nos extremos superiores dos subintervalos da parti¸c˜ao, ou seja,xi=i_nb.

y

x b

gráfico def y=x2

n b

f x( 1) =x12

x1 0 2b n x2 3b n x3 xn

...

f x( 3) =x32

...

SejaAa ´area abaixo do gr´afico defe acima do eixox, com0≤x≤b. Logo,

A= Zb

0

f(x)dx= lim

|P|→₀

n

P

i=1

f(xi)∆xi= lim n→+∞

n

P

i=1

(xi)2(xi−xi−1)

= lim n→+∞

n P i=1 ib n 2 ib

n− (i−1) b n

= lim n→+∞

n

P

i=1

i2b

3

n3 =_n→lim+∞ b3 n3 n P i=1 i2

Mas a soma Pn i=1

i2tamb´em pode ser calculada. Para tanto, lembremos que

(k+1)3−k3= (k+1−k)(k+1)2+ (k+1)k+k2

=k2+2k+1+k2+k+k2

=3k2+3k+1

Logo,                 

k=1 −→ 623−13=3.12+3.1+1 k=2 −→ 633−₆23=3.22+3.2+1 k=3 −→ 643−₆33=3.32+3.3+1 k=4 ₋→ 653−₆43=3.42+3.4+1

.. .

k=n ₋→ (n+1)3−₆n3=3.n2+3.n+1

Somando as igualdades temos

(n+1)3−1=3 12+22+32+_{· · ·}+n2

+3(1+2+3+_{· · ·}+n) + (1+1+_{· · ·}+1)

| {z }

nvezes

⇒

(n+1)3−1=3 _n P i=1 i2 +3 _n P i=1 i

+n_⇒

n

P

i=1

i2= (n+1)

3

− (n+1) −3n(n+1)₂

3 ⇒

n

P

i=1

i2= 2(n+1)

3

−2(n+1) −3n(n+1)

6 ⇒

n

P

i=1

i2=

(n+1)2(n+1)2−2−3n

6 ⇒

n

P

i=1

i2= (n+1) 2 n

2_+2n+1

−2−3n

6 ⇒

n

P

i=1

i2= (n+1) 2n

2_+n

6 ⇒

n

P

i=1

i2₌ n(n+1) (2n+1)

Substituindo:

Zb

0

f(x)dx= lim n→+∞

b3

n3 n

P

i=1

i2= lim n→+∞

b3_{n(n+1) (2n+1)}

6n3

= lim n→+∞

b3_{(n+1) (2n+1)}

6n2 =_n→lim+∞

b3 ₁₊ 1 n

2+ 1

n

6 =

b3

3 .

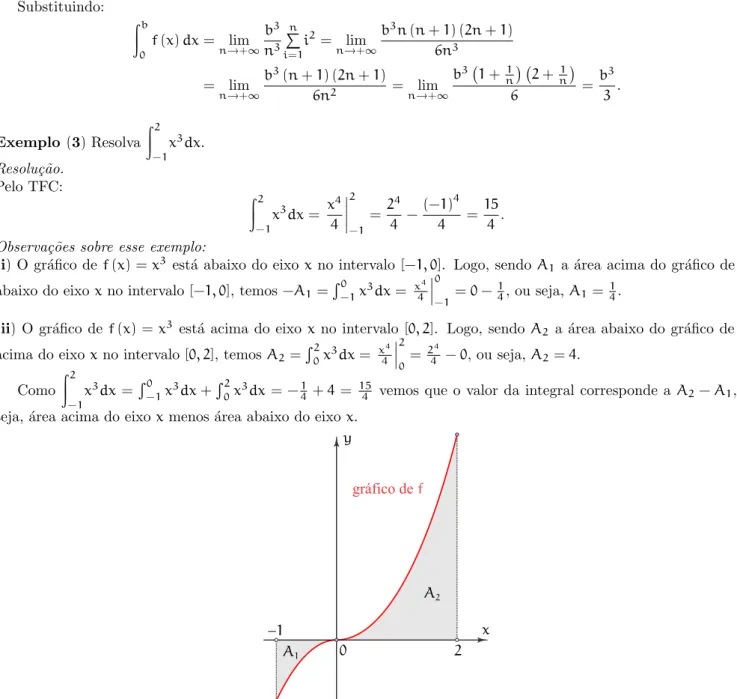
Exemplo (3)Resolva

Z2

−1

x3dx.

Resolu¸c˜ao.

Pelo TFC:

Z2

−1

x3dx= x

4

4

2

−1

= 2

4

4 − (−1)4

4 =

15 4 .

Observa¸c˜oes sobre esse exemplo:

(i)O gr´afico def(x) =x3_{est´a abaixo do eixox no intervalo[−1, 0]. Logo, sendo A}

1 a ´area acima do gr´afico def e abaixo do eixoxno intervalo[−1, 0], temos −A1=R₋₁0 x3dx= x

4

4

0

−1=0− 1

4, ou seja,A1= 1 4.

(ii)O gr´afico de f(x) = x3 _{est´a acima do eixox no intervalo [0, 2]. Logo, sendo A}

2 a ´area abaixo do gr´afico de f e acima do eixo xno intervalo [0, 2], temos A2=R₀2x3dx= x

4

4

2

0

= 24

4 −0, ou seja,A2=4.

Como

Z2

−1

x3_dx= R0

−1x3dx+

R2

0x3dx= − 1 4+4 =

15

4 vemos que o valor da integral corresponde a A2−A1, ou seja, ´area acima do eixo xmenos ´area abaixo do eixox.

y

x 2 A2

0

gráfico def

-1 A1

(iii)Se quis´essemos calcular essa integral utilizando diretamente a defini¸c˜ao de integral definida, precisar´ıamos de uma

express˜ao para a soma Pn i=1

i3_{. ´E um bom exerc´ıcio provar que}

n

P

i=1

i3₌

n(n+1) 2

2

.

Exemplo (4)Obter a ´area limitada pela curvay=x2_−x3_{e o eixo das abscissas.}

Resolu¸c˜ao.

A curvay= x2_−x3_{intersecta o eixo das abscissas em x= 0 ex=1 (basta resolver a equa¸c˜aox}2_−x3_{= 0, ou} seja,x2_{(1−x) =0).}

Fazendoy=f(x)podemos tra¸car com precis˜ao o gr´afico defpor meio de suas duas primeiras derivadas. y

x 0

gráfico def