10.26843/rencima.v11i3.2692 eISSN 2179-426X
Construindo o círculo na Geometria do taxi: uma proposta de
insubordinação criativa
Building the circle in taxicab Geometry: a creative insubordination proposal Raimundo Nonato Barbosa Cavalcante
Instituto Federal do Maranhão nonath.edms@gmail.com
https://orcid.org/0000-0001-9936-3757 Jobson de Queiroz Oliveira
Universidade Estadual do Ceará jobson.oliveira@uece.br
https://orcid.org/0000-0001-7777-7289
Resumo
A geometria é um ramo da Matemática cujos conceitos trabalham as formas, tamanho e posição de figuras relacionadas aos espaços, apresentando tipos diferentes. Nesse ramo alguns conceitos diferenciam as características do objeto, como o círculo, dependendo de qual tipo de geometria pretende-se trabalhar. O objetivo desse estudo foi apresentar a forma do círculo na geometria do táxi, desenvolvida por Hermann Minkowski, também baseada no plano cartesiano, utilizando o sistema de coordenadas cartesianas, mas com características próprias. O conteúdo não fazia parte do currículo escolar, assim, o pesquisador utilizou da Insubordinação Criativa, na busca em romper paradigmas curriculares, e introduziu o conceito de geometria do táxi. Para conduzir essa exploração, foram utilizadas oficinas como metodologia de ensino onde mostrou-se, através de atividades contextualizadas, as diferenças entre a distância na geometria euclidiana e na geometria do táxi, concluindo com a obtenção da figura do círculo a partir da definição já conhecida. Através das atividades, foram apresentados tópicos relevantes desse estudo despertando o aluno à reflexão acerca de conteúdos matemáticos já estabelecidos como possibilidade a novas descobertas e melhor compreensão da realidade.
Palavras-chave: Círculo. Geometria do Taxi. Insubordinação Criativa. Abstract
The Geometry is a branch of Mathematics whose concepts work the shape, size and position of figures related to space, presented different types. In this branch, some concepts differentiate the characteristics of the object, such as the circle, depending on what type of geometry it is intended to work with. The objective of this study was to present the circle shape in taxicab geometry, developed by Hermann Minkowski, as well based in cartesian plane which the cartesian coordinate system is used but with its own characteristics. The content was not part of the school curriculum, so the researcher used Creative
Insubordination in the quest to break curricular paradigms and introduced the taxicab geometry concept. For to conduct this exploration was used workshops how teaching methodology where it was shown, through contextualized activities, the differences between distance in Euclidean geometry and taxicab geometry, concluding with obtaining the figure of the circle from the definition already known. Through the activities, relevant topics from this study were presented, awakening the student to reflect on mathematical content already established as a possibility for new discoveries and a better understanding of reality.
Keywords: Circle. Taxicab Geometry. Creative Insubordination.
Introdução
Este trabalho é resultado de atividades que apresentaram aos alunos a geometria do táxi, de Hermann Minkowski (BOLTIANSKI, GOJBERG, 1973). Teve como objetivo levar o aluno, através da descoberta das propriedades dessa geometria, a confrontar suas semelhanças e diferenças com a geometria euclidiana, a identificar possibilidades e incentivá-lo a investigação matemática acerca do conteúdo de distâncias. Além disso levá-los a descobrir o círculo nessa geometria, tendo a Insubordinação Criativa como meio de instigação dos sujeitos envolvidos no desenvolvimento da atividade (Salazar e Fernández, 2017).
O trabalho desenvolveu-se com alunos das turmas do terceiro ano do Ensino Médio, em uma escola da rede estadual de educação, no estado do Ceará, em sessões didáticas (aulas) que envolveram feedback dos conteúdos de geometria analítica, especificamente da distância entre dois pontos, apresentação das propriedades da geometria do táxi e inferência da figura geométrica do círculo, sendo guiado por atividades realizadas no percurso dessa investigação.
O presente artigo divide-se em três partes. Na primeira é apresentada a Insubordinação Criativa no ensino da Matemática, onde discute-se o agir docente com subversão responsável. Aqui o docente, diante das questões de imposição curriculares de um programa a ser desenvolvido, busca se desvencilhar dos paradigmas impostos, conduzindo os alunos a novas abordagens e descobertas, fazendo-os refletir sobre o conteúdo apresentado no currículo, a aplicação prática e possibilidades que em se tratando da mesma temática os levem a tomar decisões diferentes.
Em seguida são apresentadas as origens e propriedades da geometria do táxi, onde se verifica as suas semelhanças e diferenças em relação à geometria euclidiana e logo depois aparece a intervenção pedagógica em sala de aula, quando o aluno é levado a conhecer essa nova geometria e apresenta-se, com a realização de atividades investigativas, o círculo nesse contexto. Na sequência são feitas as considerações finais e em seguida as referências utilizadas.
O estudo de Matemática no Ensino Médio é um desafio, tanto para o aluno quanto para o professor. Essa etapa do ensino é um tanto especial se levarmos em conta que estamos como atores do processo ensino-aprendizagem, diante de uma acirrada disputa pela atenção dos alunos, pois nessa etapa da vida encontram-se envoltos em muitos conflitos internos, definindo uma identidade em formação.
Para conseguir aproximar-se do aluno, o professor precisa, antes de tudo, buscar interagir com ele e compreender ao menos um pouco do mundo que o rodeia. Instigá-lo à curiosidade e levá-lo a enveredar pelo caminho da pesquisa, uma vez que o fazer matemática se torna algo útil, fugindo da mecanização do uso de fórmulas para a realização de cálculos e resolução de exercícios.
Uma das formas de resolver o problema que o aluno tem com a Matemática é buscar apresentá-la de forma dinâmica, podendo despertar seu interesse em estudá-la e reduzir com isso a aversão que ele tem da disciplina.
O espaço de interação entre os sujeitos que participam do cotidiano escolar, o “chão da escola”, é um laboratório fértil para o professor. Nesse momento de conquista do aluno pode-se fugir um pouco do programa da escola, destravar o currículo e adentrar em outros universos. Como argumenta Nuno Crato:
Mas faz parte da escola desviar-se de vez em quando do seu caminho sistemático e fazer uma incursão por temas novos, que podem estar ou não diretamente relacionados com os programas. Nesses desvios dão-se referências e abrem-se horizontes. Entusiasmam-se alguns alunos, despertam-se outros (CRATO, 2012, prefácio).
Nessa perspectiva o uso da geometria do táxi como princípio de partida para a investigação de como medimos distância traz para o aluno uma nova dinâmica do assunto abordado. Fugindo da tradicional apresentação desse conteúdo, mostrando as semelhanças e diferenças encontradas entre esta e a distância entre dois pontos da geometria euclidiana.
Para despertar a atenção do aluno, o professor deve também se abster do pensamento de que todo conteúdo matemático precisa, necessariamente, usar de situações problema que estão presentes no dia a dia dele. Isso nem sempre acontece. E ao partir para essa vertente, o professor que julga estar fazendo da Matemática algo interessante e de fácil apreensão ao aluno, corre o risco de frustrá-lo diante de situações em que a abordagem de conteúdos contextualizados de forma forçada prejudiquem a compreensão e, consequentemente o aprendizado.
Esse pensamento tem aparecido com bastante frequência no meio dos professores de Matemática. Nesse sentido, Costa e Allevato (2014) sobre as crenças dos futuros professores, destacam que:
Outro elemento que merece destaque nas crenças manifestadas pelos (futuros) professores, é a de que a Matemática ‘sempre’ se faz presente no dia a dia; de que serve para resolver problemas; e de que problemas são atividades ‘contextualizadas’, com enunciado, e que envolvem números a serem utilizados em cálculos. Ora, como ciência, ou seja, como corpo de conhecimentos, com seus
elementos e estrutura própria, a Matemática possui conteúdos que efetivamente não se aplicam a situações do dia a dia, no sentido imediato a que esses participantes se referiram em suas respostas. Ela possui conteúdos que estão a serviço da própria Matemática e/ou de outras áreas do conhecimento. A crença na natureza utilitária da Matemática deve ser superada pelos professores que irão se dedicar ou se dedicam ao seu ensino. (COSTA e ALLEVATO, REnCiMa, v. 5, n. 1, p. 21-36, 2014).
Ao falar de determinado assunto, e principalmente ter uma visão de como tal trabalho ou pesquisa pode ser trazido à realidade de jovens estudantes do Ensino Médio, o professor é desafiado. Há inúmeras possibilidades: o que fazer, como fazer, quais resultados esperar e principalmente a reação dos atores envolvidos na proposta.
Para a realização de um trabalho significativo é fundamental despertar o envolvimento na pesquisa. Aqui as armadilhas são evitadas. Ao não se ater ao utilitarismo da Matemática e forçar contextualizações desnecessárias, o docente precisa lançar mão de ferramentas que envolvam os alunos na resolução de problemas criativos e que os levem a novas descobertas, novos aprendizados.
E quando se trata de abordagens diferentes do habitual no universo do professor, o trabalho inicia-se apreensivo, porém ao se debruçar sobre ele, a experiência vai se tornando mais gratificante e cada resultado, progresso obtido, dá ânimo para continuá-lo, tanto para professores quanto para alunos.
Um conceito que se apresenta como meio de trabalhar a Matemática rompendo com o currículo fechado tradicional das escolas e proporcionando aquisição de aprendizado significativo à Insubordinação Criativa. Um conceito em que professores buscam ir além do que é imposto, rompendo as regras estabelecidas, mas que essa ruptura é benéfica, pois proporciona um aprendizado além do que se estava proposto.
Esse conceito surgiu, de acordo com Lopes e Jamarilo (2017) e Barbosa (2019) em pesquisas educacionais por volta de 1970, através de investigações da gestão escolar de diretores de escolas em Chicago. No campo da educação matemática o conceito foi difundido por Rochelle Gutiérrez, Celi Espasandin Lopes e Beatriz Silva D’Ambrosio, as últimas introduziram o conceito através de suas produções entre os educadores matemáticos brasileiros.
A Insubordinação Criativa proposta por essas autoras, de acordo com Barbosa (2019) ocorre quando há
ação de oposição ou desafio à autoridade, procedimentos ou diretrizes estabelecidas, quando estas se contrapõem ao bem do outro, mesmo que não intencional, por meio de determinações incoerentes, excludentes e/ou discriminatórias. A insubordinação criativa implica em ter consciência sobre quando, como e por que agir contra estas diretrizes ou procedimentos e é legitimada quando está centrada em práticas profissionais alicerçadas em bases éticas (BARBOSA, 2019. p. 3)
Desse modo, o professor pode se utilizar da insubordinação criativa para dar sentido a seu fazer pedagógico, desprendendo-se do engessamento do currículo e de paradigmas presentes no ensino de matemática, podendo ousar, mas tendo uma atitude de subversão responsável. É necessário criar possibilidades para o aluno aprender Matemática,
verificando que essa aprendizagem não está necessariamente vinculada à associação de conteúdo a um utilitarismo desejável, sendo que a matemática possui muitos ramos, dos quais uns são mais próximos a contextualizações e outros nem tanto.
Essa atitude de insubordinação do professor pretende dar sentido ao fazer pedagógico que não deve se ater a conceitos pré-estabelecidos. O ato de ensinar não deve ser pautado por um modelo fixo, como um conjunto de regras que devam ser seguidas para garantir resultados. Santos e Matos (2017), numa proposta de formação subversiva responsável a partir da insubordinação criativa vem coadunar com o exposto:
Nesse sentido, a formação docente que queremos tem em vista um profissional ético, crítico e reflexivo o qual ver o ensino como um ato pedagógico passível de transformação, pois como profissional tem consciência dos seus saberes e fazeres e sabe o momento de romper com alguns paradigmas para a tomada de decisão, no que se refere a necessária e responsável insubordinação criativa (SANTOS E MATOS 2017, REnCiMa, v. 8, n. 4, p. 11-30, 2017).
A atitude de insubordinação responsável traz ao docente novas perspectivas diante da sala de aula. Pode até utilizar em um primeiro momento do utilitarismo para buscar o envolvimento dos alunos conforme a atividade vai ocorrendo. Ele vai dando lugar à construção do conhecimento matemático abstrato, em que o aluno vai sendo levado a desenvolver seu raciocínio e a partir de suas descobertas se envolve e tem uma percepção positiva da Matemática.
Nesse contexto, trabalhando com um currículo de 3º ano do Ensino Médio em que a grade curricular trata o tema de distância como conteúdo da geometria analítica na perspectiva da geometria euclidiana, fazer uma abordagem na qual se estabelece outro conceito de distância e, a partir dele apresenta outras concepções através da aplicação no dia a dia do aluno, apresenta-se um processo de insubordinação criativa.
O professor desafia os procedimentos ou diretrizes estabelecidas ao propor o conceito de geometria do táxi com suas propriedades diferentes daquilo que foi estabelecido para o aluno desde o ensino fundamental. E, a partir de uso de problemas que fazem parte do dia a dia, o aluno é levado a fazer investigações a respeito do tema que o levará a um resultado inesperado: o círculo agora tem um formato que o aluno sempre viu como um quadrado.
Origens e propriedades da geometria do táxi
Da geometria analítica estudada no terceiro ano do Ensino Médio, dados dois pontos 𝐴(𝑥1, 𝑦1) e 𝐵(𝑥2, 𝑦2) distância euclidiana entre A e B é (IEZZI, 2013. p.6): 𝑑𝐴𝐵 = √(𝑥2− 𝑥1)2+ (𝑦2− 𝑦1)2
Tal forma de medir distâncias representa de fato a menor distância possível, mas em certos momentos, apesar de válida, não é, necessariamente, a mais adequada.
Suponha que nos encontramos em uma grande cidade. Essa cidade é planejada de tal forma que em seu plano as ruas estão traçadas verticalmente e horizontalmente, por
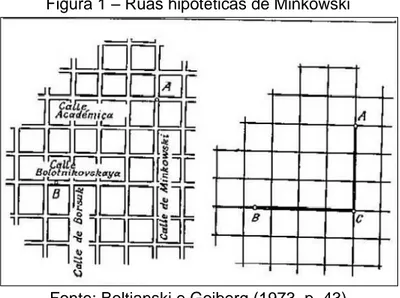
todo seu território, equidistantes, como no plano cartesiano, em que as ruas são as retas passando por pontos determinados pelas unidades das coordenadas, todas paralelas e perpendiculares entre si (Figura 1). Qual a melhor forma para ir do ponto A ao ponto B nessa cidade?
Figura 1 – Ruas hipotéticas de Minkowski
Fonte: Boltianski e Gojberg (1973, p. 43)
O matemático russo Hermann Minkowski escreveu e publicou um trabalho inteiro com várias métricas, nele estava contido a métrica que resolvia esse problema. A geometria dessa métrica ficou conhecida como a geometria do Plano de Minkowski.
Em 1952, uma exposição exibida no Museu de Ciência e Indústria de Chicago destacava tal geometria. Um pequeno livreto foi distribuído intitulado “Você vai gostar de geometria". Nas páginas deste livreto a geometria de Minkowski foi chamada de geometria do táxi (JANSSEN, 2007).
Assim, criou-se uma forma de encontrar as distâncias “reais” em um plano de ruas paralelas e ortogonais entre si, conhecida recentemente por Geometria Urbana, sendo assim denominada, porque as distâncias percorridas por um táxi, carro ou veículo qualquer pelas ruas aproximam-se melhor desta maneira de calcular distâncias do que no modo euclidiano. Uma vez que esses transportes precisam obedecer o trajeto das ruas para chegar ao seu destino, usando o plano cartesiano usual com um sistema de coordenadas ortogonais (x,y).
Sem dúvida alguma, tendo o plano da cidade, é possível traçar com uma régua o segmento AB e medir seu comprimento. No entanto, em nossa cidade, tal distância poderia ser real, porém inacessível, já que para deslocar-se pelo segmento AB seria necessário passar através de paredes das casas. Portanto, essa métrica ficou assim conhecida especialmente por considerar a distância entre dois pontos como uma distância na qual são considerados os traçados das ruas.
Assim, o menor percurso entre A e B é dado pela soma dos comprimentos, AC + CB, então deve-se considerar como a distância real entre os pontos A e B o comprimento ACB, apresentado na figura (fig. 1).
Além disso, não somente ACB é o único caminho de menor distância em oposição a considerarmos inicialmente a menor distância o comprimento do seguimento de reta AB. Aqui há uma série de outros caminhos reais de A até B como o mesmo comprimento de ACB, porém, caminho mais curto não há.
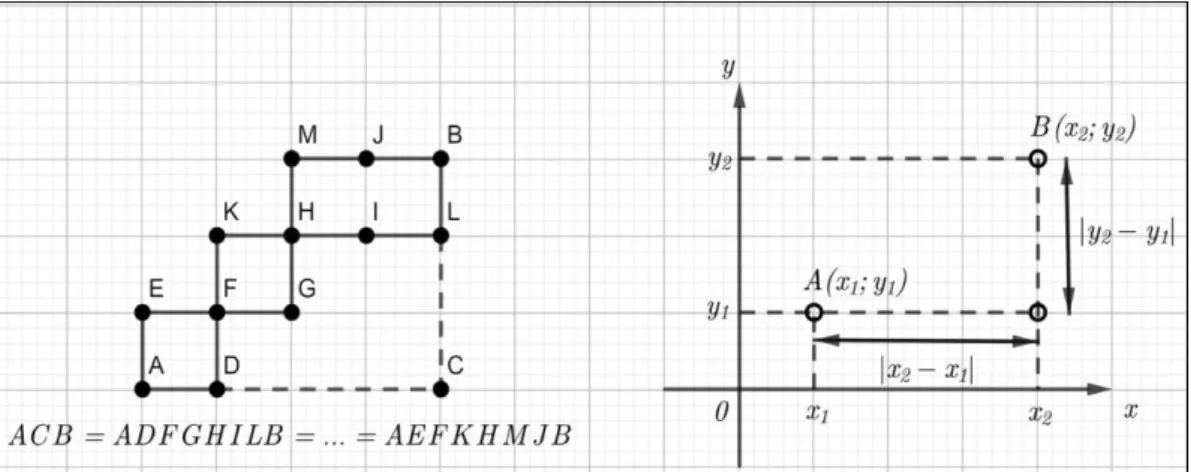
Introduzindo no plano da cidade um sistema de coordenadas, com um ponto fixado como origem e os eixos coordenados traçados sobre duas ruas reciprocamente perpendiculares, a distância real entre os pontos 𝐴(𝑥1, 𝑦1) e 𝐵(𝑥2, 𝑦2) dessa cidade, o
comprimento do segmento AB de acordo com a geometria adotada, é igual a 𝐴𝐵 = |𝑥2 − 𝑥1| + |𝑦2 − 𝑦1|
Tal geometria apresenta propriedades semelhantes às da geometria euclidiana: as distâncias são sempre não negativas, já que são dadas pela soma dos módulos; a distância entre A e B é zero se, e somente se, os pontos A e B coincidirem; É simétrica: a distância entre A e B é a mesma que a distância entre B e A; Satisfaz a desigualdade triangular; Se A e B estiverem na mesma rua horizontal ou a mesma rua vertical então tal distância é igual a medida da distância na geometria euclidiana entre A e B.
Porém, sobre outros aspectos ela se distancia bastante desta, se aplicarmos uma rotação ao segmento AB, ela pode alterar a distância entre dois pontos.
Se A = (0;0) e B = (1;1), a distância dAB= |0 − 1| + |0 − 1| = 2 . Girando o segmento em torno da origem em 45ºno sentido anti-horário, A permanecerá o mesmo, enquanto B se transformará em B’ que terá sua abscissa igual a 0 e a ordenada será a distância euclidiana entre A e B, ou seja, √2. Como B’ está na mesma reta vertical que A, a distância entre A e B na geometria do táxi será agora dAB = √2.
De tais propriedades deduz-se que a distância, outrora dada pelo comprimento de um segmento, agora pode ser dada por uma região do plano utilizando a soma dos comprimentos de seguimentos verticais e horizontais contidos nessa região. Assim temos mais de uma possibilidade para encontrar a distância 𝑑𝐴𝐵. Por exemplo, se 𝐴(2; 1), 𝐵(8; 6), 𝐶(8; 1) e 𝐷(2; 6), então, todo ponto P do retângulo ABCD satisfaz a 𝑑𝐴𝐵 = 𝑑𝐴𝑃 + 𝑑𝑃𝐵
Se os pontos A e B são pontos pertencentes a uma mesma reta vertical, ou seja, xA
= xB ou analogamente, a uma mesma reta horizontal, ou seja, yA = yB, tal retângulo vai
degenerar no segmento 𝐴𝐵̅̅̅̅, sendo, neste caso, a soma mínima entre os pontos A e B coincide com o segmento 𝐴𝐵̅̅̅̅, assim como na geometria euclidiana.
Conhecendo agora, como determinar distâncias “possíveis” entre dois pontos da cidade, e considerando que um círculo de centro O e raio r é o lugar geométrico dos pontos do plano que têm distância menor que ou igual a r de O.
Sendo círculo unitário o conjunto dos pontos cuja distância 𝑑𝑃𝑂 ≤ 1 e seja P(x,y) o conjunto dos pontos que satisfazem a desigualdade, descrevamos tal círculo na geometria do taxi. Como o ponto O possui coordenadas (0,0), segundo (2) a distância do ponto O ao ponto P, será igual 𝑂𝑃̅̅̅̅ = |𝑥 + 𝑦|
Fonte: Elaborado pelos Autores
Como a geometria do táxi traz uma noção de distância diferente daquela apresentada convencionalmente, então tal figura geométrica assume agora uma forma diferente do modo a qual estamos familiarizados.
Tal circunferência assume a forma apresentada na fronteira de um quadrado, com diagonais paralelas aos eixos coordenados. Sendo 𝑂 = (𝑥0; 𝑦0), a equação da circunferência de centro O e raio r é |𝑥 − 𝑥𝑜| + |𝑦 − 𝑦𝑜| = 𝑟
A distância na geometria do táxi não varia por translação, podemos considerar uma circunferência com centro O na origem do plano. Assim para qualquer ponto pertencente à fronteira do quadrado sua distância à origem de fato é r (HELLMEISTER, 2013).
Consequentemente, no plano apresentado da cidade o círculo unitário se determinará pela desigualdade |𝑥| + |𝑦| ≤ 1
Então, no plano dessa cidade tal círculo unitário é um quadrado.
Figura 3 – Círculo unitário
Fonte: Elaborado pelos autores
Tendo agora como base o círculo unidade, podemos determinar a distância entre dois pontos A e B quaisquer do plano, como indicado anteriormente.
Em sala de aula: construindo o círculo na geometria do táxi
A geometria do táxi vem sendo abordada em alguns trabalhos com aplicação na educação básica. Gusmão, Sakaguti e Pires (2017) e Leyvas (2019) trazem em suas pesquisas atividades realizadas nessa etapa da educação. Ambos partem do conceito de distância entre dois pontos da geometria euclidiana e depois inserem os conceitos da geometria do táxi. Os alunos são levados, através de atividades, a compará-las, compreender o novo conceito e sua aplicação.
O ensino do conteúdo de distância entre dois pontos faz parte do conteúdo da geometria analítica, apresentado em situações problema que consideram a menor distância
entre dois pontos dados. Sabe-se que esse tópico é a base do estudo da Geometria Analítica, mas que essa noção de distância varia de acordo com o objetivo a ser alcançado. Um dos objetivos desse trabalho foi fazer o aluno compreender outras abordagens, para isso, fez-se necessário romper com possíveis imposições do currículo, utilizar-se da subversão responsável e atuar com uma atitude de Insubordinação Criativa para trazer ao aluno a compreensão de um novo conceito.
Trazer ao contexto do ensino de Matemática uma aplicação que em um primeiro momento não parece ser usual, mostra ao aluno que a geometria do táxi, em alguns casos, aproxima-se mais da realidade do que a geometria euclidiana. Ao utilizar-se de elementos novos e introduzir um conceito muito presente no aprendizado de matemática, o círculo, e apresentá-lo de uma forma completamente diferente daquilo que se conhecia, mostra aos alunos diferentes possibilidades presentes na Matemática.
A construção do círculo na geometria do táxi se deu após o estudo do tópico de distância entre dois pontos do conteúdo de geometria analítica. Essa atividade foi realizada em forma de oficina. Fez-se um feedback da noção usual de distância d entre dois pontos. Dados dois pontos 𝐴(𝑥𝐴; 𝑦𝐴) e 𝐵(𝑥𝐵, 𝑦𝐵) encontremos a distância euclidiana entre os dois
pontos A e B.
Na figura 4 temos um triângulo ∆𝐴𝐵𝐶, retângulo em C. Observando que:
𝐴𝐶 = |𝑥𝐵 − 𝑥𝐴| , 𝐵𝐶 = |𝑦𝐵 − 𝑦𝐴| , |𝑥𝐵 − 𝑥𝐴|2 = (𝑥𝐵 − 𝑥𝐴)2 e |𝑦𝐵 − 𝑦𝐴|2 = (𝑦𝐵 − 𝑦𝐴)2
Fonte: Elaborado pelos Autores
Pelo teorema de Pitágoras:
𝑑 = 𝐴𝐵2 = 𝐵𝐶2+ 𝐶𝐴2
= √𝐵𝐶2+ 𝐶𝐴2
= √(𝑥𝐵 − 𝑥𝐴)2+ (𝑦𝐵 − 𝑦𝐴)2
Após a definição da distância entre dois pontos, o professor colocou uma situação-problema que envolveu uma atividade corriqueira dos jovens alunos, sujeitos envolvidos na atividade, o passeio do fim de semana no Parque da Cidade, um parque localizado nas margens de um riacho e uma famosa lanchonete da cidade conhecida especialmente pela venda de seus lanches fartos e baratos.
A situação colocada foi a seguinte: “Suponha que estejamos na cidade de Sobral, as avenidas Cleto Ferreira da Ponte e Dep. João Frederico Ferreira Gomes são os eixos cartesianos x e y, respectivamente, e a origem do plano cartesiano seja o Centro de Convenções denotado por C (0;0). Você deseja ir ao Parque da Cidade, lugar onde a galera se reúne aos fins de semana, situado no eixo das abscissas e denotado por A(500;0), mas você espera seus amigos na lanchonete Wandão, situada no eixo das ordenadas no ponto B(0;50). A unidade de medida é o metro. Utilizando as coordenadas apresentadas, na medição usual da geometria euclidiana, a que distância você se encontra do Parque da Cidade?”
Os alunos foram orientados a trabalhar em equipe, discutir a solução e apresentar o resultado obtido. A distância por eles encontradas foi 𝑑𝐴𝐵 = √252500 ≅ 502,5𝑚. Diante do resultado, o professor desenhou o plano hipotético na lousa e traçando o segmento AB indagou sobre a viabilidade deles seguirem aquele trajeto. Alguns alunos ficaram na dúvida, enquanto outros disseram que não, pois não havia rua que seguisse aquele sentido. Então o professor perguntou: Se houvesse essa rua, o que vocês fariam? Um dos alunos respondeu que seguiria essa rua, pois seria o menor caminho. Voltando-se para os outros alunos o professor pergunta se eles concordavam com o colega. Todos concordaram.
situação-problema, prosseguindo com o seguinte questionamento: Mas vocês percorrerão esse trajeto a pé como? Será que precisarão de táxi, Uber, carro ou irão a pé? Esse trajeto a maioria deles faz aos finais de semana, pois costumam ir de um ponto a outro a pé. Então o professor colocou uma hipótese a ser considerada pelo grupo: supondo que não haja outras ruas que deem acesso ao Parque da Cidade da Lanchonete Wandão, além das avenidas representadas nos eixos coordenados, quanto vocês andarão, em metros? Descrevam como será determinado esse trajeto.
O professor deu um tempo para que os alunos pudessem pensar e formular suas hipóteses para chegar à solução do problema e construir suas justificativas.
Os alunos, então, apresentaram algumas considerações: “Se saímos do Wandão, para ir ao Parque da Cidade, precisamos passar pelo Centro de Convenções, são 50 metros com mais 500 metros, fazendo um total de 550 metros.” Logo a distância passou a ser dada por 𝑑𝐴𝐵′ = 500 + 50 = 550𝑚 . Com base nesse resultado surgiu a seguinte indagação: as características apresentadas nas medidas de distâncias encontradas na primeira e segunda forma são iguais?
Agora, analisemos a distância d’ em que para chegar de A a B faz-se necessário prosseguir de A à C, com distância AC e depois de C a B, com distância CB, assim, d’ será dada por:
𝑑′= 𝑑𝐴𝐵 = (𝐴𝐶) + (𝐵𝐶)
= |(𝐴𝐶)| + |(𝐵𝐶)| = |𝑥𝐵 − 𝑥𝐴| + |𝑦𝐵 − 𝑦𝐴|
A distância apresentada em d’ é a medida de distância da geometria do táxi em que a medida de distância é a soma dos módulos da diferença entre as abscissas e da diferença entre as ordenadas (BOLTIANSKI, GOJBERG, 1973). Coube aqui observar as características dessa nova geometria, apresentada por Minkowski.
De posse dessa forma de medida de distâncias observaríamos agora a dinâmica do círculo utilizando essa métrica estabelecida com o intuito de estabelecer um conceito já conhecido de uma maneira nova e trazer aos alunos possíveis questionamentos inerentes ao campo da pesquisa em relação a característica do objeto apresentado, a forma do círculo.
Para estabelecer um trabalho voltado a apresentação dessas características novas nas concepções da geometria do táxi foi estabelecido a resolução de exercícios básicos. Nesse momento foram utilizados critérios mais informais para estabelecer o objeto de estudo, cabendo em outro momento discussões acerca das propriedades formais.
Foi escolhido criar um círculo de raio 3 para que as marcações no papel apresentassem uma melhor distribuição e fosse possível verificar o que estava acontecendo com um número maior de detalhes para que a visualização no papel já apresentasse algumas características e os alunos pudessem, ao serem questionados, apresentarem suas conclusões iniciais. Assim foi dado uma lista com as tarefas a serem realizadas por eles. Cada item deveria ser executado, e antes de passar para o próximo foi feito algumas
intervenções para perceber suas impressões. A atividade foi guiada pelos itens descritos a seguir:
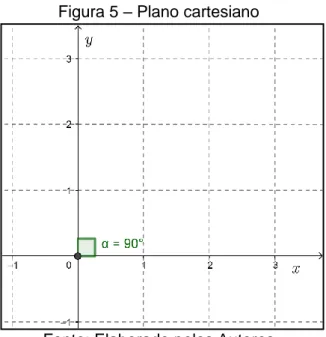
Dado o plano cartesiano
Figura 5 – Plano cartesiano
Fonte: Elaborado pelos Autores
a) Localizar no plano cartesiano os pontos dados, O (0;0) e cada ponto A (3;0), B(2;1), C(1;2), D(0;3), E(-1;2), F(-2;1), G(-3;0), H(-2;-1), I(-1;-2), J(0;-3), K(1;-2), L(2;-1).
b) Encontrar as distâncias entre a origem O (0;0) e todos os outros pontos dados.
Quadro 1 – Distâncias: origem aos pontos dados
Distâncias |𝑥2 − 𝑥1| + |𝑦2 − 𝑦1| 𝑂𝐴 ̅̅̅̅ |3 − 0| + |0| = 3 + 0 = 3 ⇒ 𝑂𝐴̅̅̅̅ = 3 𝑂𝐵 ̅̅̅̅ |2 − 0| + |1 − 0| = 2 + 1 = 3 ⇒ 𝑂𝐵̅̅̅̅ = 3 𝑂𝐶 ̅̅̅̅ |1 − 0| + |2 − 0| = 1 + 2 = 3 ⇒ 𝑂𝐶̅̅̅̅ = 3 𝑂𝐷 ̅̅̅̅ |0 − 0| + |3 − 0| = 0 + 3 = 3 ⇒ 𝑂𝐷̅̅̅̅ = 3 𝑂𝐸 ̅̅̅̅ |−1 − 0| + |2 − 0| = 1 + 2 = 3 ⇒ 𝑂𝐸̅̅̅̅ = 3 𝑂𝐹 ̅̅̅̅ |−2 − 0| + |1 − 0| = 2 + 1 = 3 ⇒ 𝑂𝐹̅̅̅̅ = 3 𝑂𝐺 ̅̅̅̅ |−3 − 0| + |0 − 0| = 3 + 0 = 3 ⇒ 𝑂𝐺̅̅̅̅ = 3 𝑂𝐻 ̅̅̅̅ |−2 − 0| + |−1 − 0| = 2 + 1 = 3 ⇒ 𝑂𝐻̅̅̅̅ = 3 𝑂𝐼 ̅̅̅ |−1 − 0| + |−2 − 0| = 1 + 2 = 3 ⇒ 𝑂𝐼̅̅̅ = 3 𝑂𝐽 ̅̅̅ |0 − 0| + |−3 − 0| = 0 + 3 = 3 ⇒ 𝑂𝐽̅̅̅ = 3 𝑂𝐾̅̅̅̅ |1 − 0| + |−2 − 0| = 1 + 2 = 3 ⇒ 𝑂𝐾̅̅̅̅ = 3 𝑂𝐿 ̅̅̅̅ |2 − 0| + |−1 − 0| = 2 + 1 = 3 ⇒ 𝑂𝐿̅̅̅̅ = 3
Fonte: Elaborado pelos Autores
c) Verifique que as distâncias entre O(0;0) e A’(2,5;0,5), B’(1,5;1,5), C’(0,5;2,5), D’(-0,5;2,5) E’(-1,5;1,5), F’(-2,5;0,5), G’(-2,5;-0,5), H’(-1,5;-1,5), I’(-0,5;-2,5),
J’(0,5;-2,5) K’(1,5;-1,5), L’(2,5;-0,5), também é 3.
Quadro 2 – Distâncias da origem a outros pontos dados
Fonte: Elaborado
pelo autor
d) Ligando os pontos A, A’, B, B’, C, C’, D, D’, E, E’, F, F’, G, G’, H, H’, I, I’, J, J’, K, K’, L, L’ qual figura geométrica obtemos?
e) A definição de circunferência nos diz que: sendo C um ponto no plano e r uma distância não nula, chama-se circunferência de centro C e raio r o conjunto dos pontos desse plano cuja distância ao ponto C é igual a r. Então qual a forma da circunferência no plano de Minkowski? E o círculo?
Após a realização da atividade e com as conclusões obtidas os alunos demonstram-se surpresos por verem que um determinado objeto matemático, com a mesma definição, pode ter diferentes representações, dependendo do contexto em que é apresentado. Passou-se a perceber o círculo, não pela figura em si, a qual todos conheciam desde o ensino fundamental. A atividade trouxe uma nova ideia de distância, a relação de cada uma com determinadas situações-problema específicas e a visualização de uma nova forma de círculo, sendo importante para além da figura conhecer a sua definição, essa não muda.
Conclusão
A compreensão de distância, conteúdo abordado na terceira série do Ensino Médio, é um dos assuntos que na Matemática pode se apresentar de diversas maneiras, em diferentes contextos, e dessa forma não pode ser expressa unicamente pelo uso da geometria euclidiana. Esse fato mostra que alguns conceitos precisam ser abordados junto aos alunos, mesmo que sejam contextos diversos do que se apresenta no currículo para possibilitar aquisição de competências e habilidades mais gerais e possibilite o indivíduo fazer julgamento e refletir acerca de situações problemas que sejam apresentadas a eles.
Distâncias |𝑥2 − 𝑥1| + |𝑦2 − 𝑦1| 𝑂𝐴′ ̅̅̅̅̅ |2,5 − 0| + |0,5 − 0| = 2,5 + 0,5 = 3 ⇒ 𝑂𝐴′̅̅̅̅̅ = 3 𝑂𝐵′ ̅̅̅̅̅ |1,5 − 0| + |1,5 − 0| = 1,5 + 1,5 = 3 ⇒ 𝑂𝐵′̅̅̅̅̅ = 3 𝑂𝐶′ ̅̅̅̅̅ |0,5 − 0| + |2,5 − 0| = 0,5 + 2,5 = 3 ⇒ 𝑂𝐶′̅̅̅̅̅ = 3 𝑂𝐷′ ̅̅̅̅̅ |−0,5 − 0| + |2,5 − 0| = 0,5 + 2,5 = 3 ⇒ 𝑂𝐷′̅̅̅̅̅ = 3 𝑂𝐸′ ̅̅̅̅̅ |−1,5 − 0| + |1,5 − 0| = 1,5 + 1,5 = 3 ⇒ 𝑂𝐸′̅̅̅̅̅ = 3 𝑂𝐹′ ̅̅̅̅̅ |−2,5 − 0| + |0,5 − 0| = 2,5 + 0,5 = 3 ⇒ 𝑂𝐹′̅̅̅̅̅ = 3 𝑂𝐺′ ̅̅̅̅̅ |−2,5 − 0| + |−0,5 − 0| = 2,5 + 0,5 = 3 ⇒ 𝑂𝐺′̅̅̅̅̅ = 3 𝑂𝐻′ ̅̅̅̅̅ |−1,5 − 0| + |−1,5 − 0| = 1,5 + 1,5 = 3 ⇒ 𝑂𝐻′̅̅̅̅̅ = 3 𝑂𝐼′ ̅̅̅̅ |−0,5 − 0| + |−2,5 − 0| = 0,5 + 2,5 = 3 ⇒ 𝑂𝐼′̅̅̅̅ = 3 𝑂𝐽′ ̅̅̅̅ |0,5 − 0| + |−2,5 − 0| = 0,5 + 2,5 = 3 ⇒ 𝑂𝐽′̅̅̅̅ = 3 𝑂𝐾′̅̅̅̅̅ |1,5 − 0| + |−1,5 − 0| = 1,5 + 1,5 = 3 ⇒ 𝑂𝐾′̅̅̅̅̅ = 3 𝑂𝐿′ ̅̅̅̅̅ |2,5 − 0| + |−0,5 − 0| = 2,5 + 0,5 = 3 ⇒ 𝑂𝐿′̅̅̅̅̅ = 3
Apresentando a geometria do táxi, também baseada no plano cartesiano, com características próprias, trazendo o comprimento de segmentos de reta como soma dos módulos das diferenças entre as abscissas e as ordenadas dos dois pontos que determinam tal segmento e mostrar diferenças entre a noção de distância euclidiana e dessa nova geometria, apresentado ao final o círculo, trouxe aos alunos a ideia de que há na matemática espaço para a criatividade e para a reflexão, não se tratando apenas de cálculos. Essa preocupação também está presente nos trabalhos de Gusmão, et. al (2017) e Leyvas (2018). Nesse caso o contexto de vivência dos alunos foi importante.
A Insubordinação Criativa foi um instrumento necessário ao professor para apresentar conteúdos diversos do currículo com criatividade, responsabilidade conforme as ideias presentes em Lopes (2017). Buscou-se ser subversivo responsável para que o resultado dessa insubordinação fosse um passo para garantir a aprendizagem do aluno e o permitisse refletir.
Trazer situações problemas a partir da vivência dos alunos, com utilização de espaços por eles conhecidos e trajetos percorridos, normalmente no fim de semana, trouxe suas atenções à resolução do problema apresentado, tendo uma participação ativa, embora em graus diferentes, de todos os participantes da oficina. O engajamento na realização das tarefas se deu de forma satisfatória.
O trabalho se desenvolveu bem, apesar dos alunos terem disponíveis apenas papel com as tarefas a serem realizadas, lápis e borracha para desenvolvimento dos cálculos e restringiu-se ao espaço da sala de aula. A projeção utilizando o software de geometria dinâmica GeoGebra foi utilizado ao final da investigação proposta a fim de possibilitar uma visualização melhor da formação do círculo, sendo que essa atividade foi mais intuitiva sem fazer uso de muitas formalidades devido ao tempo da sessão didática. Ficando essa formalização e aprofundamento da geometria do táxi para outras ocasiões.
Esse trabalho mostrou uma possibilidade de utilização de conteúdos diversos através da Insubordinação Criativa para fazer o aluno aprender matemática, utilizando situações problemas que os façam pensar, mas com o cuidado em não dar ao utilitarismo da matemática uma importância desnecessária, e sim fazer dessas situações um introdução para o estudo de propriedades de um conteúdo matemático novo a partir de conhecimentos pré-estabelecidos, confrontando-os e levando esses alunos a tornarem-se sujeitos pesquisadores, reflexivos.
Referências
BARBOSA, Josâne Geralda. Reflexões Sobre Beatriz Silva D’ambrosio e a Insubordinação Criativa. In: ENCONTRO BRASILEIRO DE ESTUDANTES DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA, 23., 2019. São Paulo, SP. Anais... São Paulo: Universidade Cruzeiro do Sul, Campus Anália Franco, 2019, p. 1-12.
BOLTIANSKI, Vladimir; GOJBERG, I. Ts; División de Figuras em Partes Menores. Moscú: Mir, 1973.
por (Futuros) Professores em Relação à Matemática e Seu Ensino. Revista de Ensino de Ciências e Matemática - RenCiMa. v. 5, n. 1 (2014).
CRATO, Nuno. Pela Honra do Espírito Humano. Prefácio. In: SÁ, Carlos Correia de; ROCHA, Jorge (editores); Treze Viagens Pelo Mundo da Matemática 2 ed.: Rio de Janeiro, SBM, 2012. (Coleção do Professor de Matemática)
GUSMÃO, Nathan Lascoski; SAKAGUTI, Fernando Yudi; PIRES, Liceia Alves. A geometria do táxi: uma proposta da geometria não euclidiana na educação básica. Educ. Matem. Pesq., São Paulo, v.19, n.2, pp. 211-235, 2017.
HELLMEISTER, Ana Catarina P. (coord.). Geometria em Sala de Aula. Rio de Janeiro: SBM, 2013. (Coleção do Professor de Matemática)
IEZZI, G. Fundamentos da Matemática Elementar 7: Geometria Analítica. 6 ed. São Paulo: Atual, 2013.
JANSSEN, Christina. Taxicab Geometry: Not the Shortest Ride Across Town (Exploring Conics with a Non-Euclidean Metric). Iowa: State University, 2007.
LEYVAS, José Carlos Pinto. Geometria euclidiana e do táxi: um problema concreto e os registros de representações semióticas. Revista de Educação Matemática, São Paulo, v. 16, n. 22, p. 252-269, mai./ago. 2019.
LOPES, Celi Espasandin. JAMARILO, Diana. ¿Qué Dicen las Escenas Acerca de los Processos de Insubordinación Creativa? LOPES, Celi Espasandin. JAMARILO, Diana. (Ed.) Escenas de la Insubordinacion Creativa en las Investigaciones en Educacíon Matemática en Contextos de Habla Espanhola. Estados Unidos da América: Lulu Press, 2017. p. 13-16.
SALAZAR, Jesús Victoria Flores; FERNÁNDEZ, Verônica Neira. Investigaciones Insubordinadas en Educación Matemática: Redefiniendo Nuestra Trayectoria. In: LOPES, Celi Espasandin y JAMARILO, Diana (eds.). Escenas de la Insubordinacion Creativa en las Investigaciones en Educacíon Matemática en Contextos de Habla Espanhola. Estados Unidos da América: Lulu Press, 2017. p. 111-117.
SANTOS, Maria José Costa dos & MATOS, Fernanda Cíntia Costa. A Insubordinação Criativa na formação contínua do pedagogo para o ensino da matemática: os subalternos falam?. Revista de Ensino de Ciências e Matemática - RenCiMa. Edição Especial - Insubordinação Criativa nas Pesquisas Qualitativas em Educação Matemática v. 8, n. 4 (2017).