COORDENAC¸ ˜AO DO CURSO DE P ´OS-GRADUAC¸ ˜AO EM F´ISICA
Tese de Doutoramento em F´ısica
Fases Geom´
etricas, Quantiza¸c˜
ao de Landau
e Computa¸c˜
ao Quˆ
antica Holonˆ
omica para Part´ıculas
Neutras na Presen¸ca de Defeitos Topol´
ogicos
Autor: Knut Bakke Filho
Orientador: Cl´audio Furtado
COORDENAC¸ ˜AO DO CURSO DE P ´OS-GRADUAC¸ ˜AO EM F´ISICA
Tese de Doutoramento em F´ısica
Fases Geom´
etricas, Quantiza¸c˜
ao de Landau
e Computa¸c˜
ao Quˆ
antica Holonˆ
omica para Part´ıculas
Neutras na Presen¸ca de Defeitos Topol´
ogicos
Knut Bakke Filho
Tese de Doutoramento realizada sob a orienta¸c˜ao do prof. Dr. Cl´audio Furtado e apresentada ao Departamento de F´ısica em complementa¸c˜ao aos requesitos para
obten¸c˜ao do t´ıtulo de Doutor em F´ısica. Jo˜ao Pessoa
Quero agradecer inicialmente ao professor Cl´audio Furtado pela confian¸ca depositada em mim e por estar sempre presente no desenvolvimento deste trabalho, diposto a discutir e tirar cada d´uvida minha. Sua vis˜ao cient´ıfica, postura e empenho em participar e ajudar os alunos s˜ao exemplos que quero seguir em minha carreira profissional.
Quero agradecer ao grupo de Teoria de Campos e Part´ıculas ao qual participei e pude assistir semin´arios e discuss˜oes que acrescentaram em muito em minha forma¸c˜ao. Quero agradecer tamb´em a p´os-gradua¸c˜ao pelos mini-cursos e col´oquios oferecidos durante meu per´ıodo inscrito no curso.
Quere agradecer ao professor Fernando Moraes, Carlos Romero, Eugˆenio e In´acio, aos quais pude sempre contar com o apoio para tirar d´uvidas essenciais no desenvolvimento deste e outros trabalhos, al´em de ter tido bons momentos de conversar sobre temas n˜ao relacionados ao trabalho. Quero agradecer ao professor Petrov que sempre nos ajudou fazendo a revis˜ao ortogr´afica de nossos artigos, al´em de participara no desenvolvimento de um de nossos trabalhos.
Quero agradecer ao companherismo de meus amigos Lincoln, Eduardo, Mauro Cabrunco, Marcelo (Mib), Janna´ıra, Marco Aur´elio, Jilvan e muitos outros que sempre estiveram pre-sentes para discutir e tirar d´uvidas, bem como nos maus momentos (quando a conta d´a errado ou artigo ´e rejeitado) quanto nos bons momentos (quando uma conta d´a certo ou um artigo ´e publicado), al´em das cacha¸cas, ´e claro. Quero agradecer a Seu Mariano (Seu Mam´a) por sempre estar em sua cantina com alegria fazendo nosso cafezinho.
Quero fazer tamb´em um agradecimento incomum, mas que deve ser manisfestado. Quero agradecer ao referee do artigo que escremos sobre a quantiza¸c˜ao de Landau. Gra¸cas a sua cr´ıtica pudemos ter a id´eia de fazer a quantiza¸c˜ao relativ´ıstica de Landau para part´ıculas neutra, o que nos gerou dois novos trabalhos.
Quero agradecer a minha noiva Roberta por ter me dado apoio e aguentado nesses anos, al´em de fazer todas as figuras inseridas nesta Tese. Quero tamb´em agradecer muito minha fam´ılia que sempre me deu suporte em todos os momentos.
Quero agradecer ao CNPq pelo apoio finaceiro concedido durante meu doutorado.
Neste trabalho estudamos inicialmente o surgimento de fases geom´etricas nas dinˆamicas quˆanticas relativ´ıstica e n˜ao-relativ´ıstica de uma part´ıcula neutra que possui momento de dipolo magn´etico e el´etrico permanente interagindo com campos el´etricos e magn´eticos ex-ternos na presen¸ca de defeitos topol´ogicos lineares. Para descrevermos defeitos topol´ogicos lineares usamos a aproxima¸c˜ao proposta por Katanaev e Volovich, onde defeitos lineares em s´olidos s˜ao descritos por elementos de linha que s˜ao solu¸c˜oes das equa¸c˜oes de Einstein no contexto da relatividade geral. Analisamos tamb´em a influˆencia de efeitos n˜ao-inerciais na dinˆamica quˆantica de uma part´ıcula neutra em dois tipos distintos de referenciais para os observadores: um ´e o referencial de Fermi-Walker e outro ´e um referencial girante. Vemos que a diferen¸ca entre dois referenciais est´a na presen¸ca/ausˆencia de efeitos de ar-rasto do espa¸co-tempo que ir´a influenciar diretamente na mudan¸ca de fase na fun¸c˜ao de onda da part´ıcula neutra. Em seguida, usamos nosso estudo de fases geom´etricas para fazer aplica¸c˜oes na Computa¸c˜ao Quˆantica Holonˆomica onde mostramos uma nova maneira de implementar a Computa¸c˜ao Quˆantica Holonˆomica atrav´es da intera¸c˜ao entre momen-tos de dipolo e campos externos e pela presen¸ca de defeimomen-tos topol´ogicos lineares. Outra aplica¸c˜ao para a Computa¸c˜ao Quˆantica Holonˆomica est´a baseada na estrutura de defeitos topol´ogicos em um material chamado grafeno. Na presen¸ca de defeitos topol´ogicos lin-eares, esse material apresenta duas fases quˆanticas de origens distintas: uma da mistura dos pontos de Fermi e outra da topologia do defeito. Para dar uma descri¸c˜ao geom´etrica para a origem de cada fase no grafeno usamos a Teoria de Kaluza-Klein, onde a dimens˜ao extra sugerida por esta teoria descreve os pontos de Fermi no grafeno. Portanto, a imple-menta¸c˜ao da Computa¸c˜ao Quˆantica Holonˆomica no grafeno est´a baseada na possibilidade de construir cones e anticones de grafite de tal maneira que se possa controlar os fluxos quˆanticos no grafeno. Na ´ultima parte deste trabalho estudamos a quantiza¸c˜ao de Lan-dau para part´ıculas neutras tanto na dinˆamica n˜ao-relativ´ıstica quanto na dinˆamica rela-tiv´ıstica. Na dinˆamica n˜ao-relativ´ıtica, estudamos a quantiza¸c˜ao de Landau na presen¸ca de defeitos em um referecial inercial e, em seguida, em um referencial n˜ao-inercial. Na dinˆamica relativ´ıstica, estudamos inicialmente a quantiza¸c˜ao de Landau no espa¸co-tempo plano em duas configura¸c˜oes de campos diferentes. Por fim, estudamos a quantiza¸c˜ao de Landau relativ´ıstica para part´ıculas neutras no espa¸co-tempo da desloca¸c˜ao c´osmica.
Palavras Chaves: Fases geom´etricas; defeitos topol´ogicos; tempo curvo; espa¸co-tempo curvo e com tor¸c˜ao; computa¸c˜ao quˆantica holonˆomica; quantiza¸c˜ao de Landau; efeito Aharonov-Casher; efeito He-McKellar-Wilkens; Efeito Mashhoon, Efeito Sagnac; fases quˆanticas de Anandan; referenciais locais; referenciais de Fermi-Walker; referen-ciais girantes; equa¸c˜ao de Dirac; aproxima¸c˜ao de Foldy-Wouthuyssen; spinores; grafeno; Teoria de Kaluza-Klein.
We start this work studying the appearance of geometric quantum phases as in the rel-ativistic as in the non-relrel-ativistic quantum dynamics of a neutral particle with permanent magnetic and electric dipole moment which interacts with external electric and magnetic fields in the presence of linear topological defects. We describe the linear topological defects using the approach proposed by Katanaev and Volovich, where the topological defects in solids are described by line elements which are solutions of the Einstein’s equa-tions in the context of general relativity. We also analyze the influence of non-inertial effects in the quantum dynamics of a neutral particle using two distinct reference frames for the observers: one is the Fermi-Walker reference frame and another is a rotating frame. As a result, we shall see that the difference between these two reference frames is in the presence/absence of dragging effects of the spacetime which makes its influence on the phase shift of the wave function of the neutral particle. In the following, we shall use our study of geometric quantum phases to make an application on the Holonomic Quantum Computation, where we shall show a new approach to implement the Holonomic Quan-tum Computation via the interaction between the dipole moments of the neutral particle and external fields and the presence of linear topological defects. Another applications for the Holonomic Quantum Computation is based in the structure of the topological defects in graphene layers. In the presence of topological defects, a graphene layer shows two distinct phase shifts: one comes from the mix of Fermi points while the other phase shift comes from the topology of the defect. To provide a geometric description for each phase shift in the graphene layer, we use the Kaluza-Klein theory where we establish that the extra dimension describes the Fermi points in the graphene layer. Hence, we can imple-ment the Holonomic Quantum Computation through the possibility to build cones and anticones of graphite in such way we can control the quantum fluxes in graphene layers. In the last part of this work, we study the Landau quantization for neutral particles as in the relativistic dynamics and non-relativistic dynamics. In the non-relativistic dynamics, we study the Landau quantization in the presence of topological defects as in an inertial as in a non-inertial reference frame. In the relativistic quantum dynamics, we start our study with the Landau quantization in the Minkowisky considering two different gauge fields. At the end, we study the relativistic Landau quantization for neutral particles in the Cosmic Dislocation spacetime.
Keywords: Geometric phases; topological defects; curved spacetime; cuverd space-time with torsion field, holonomic quantum computation; Landau quantization; Aharonov-Casher effect; He-McKellar-Wilkens effect; Mashhoon effect; Sagnac effect; Anandan quantum phases; local reference frame; Fermi-Walker reference frame; rotating frames; Dirac equation; Foldy-Wouthuyssen approach; spinors; graphene; Kaluza-Klein Theory.
O objetivo do trabalho desenvolvido nesta Tese de Doutorado ´e estudar o surgi-mento de fases quˆanticas geom´etricas tanto na dinˆamica quˆantica relativ´ıstica quanto na dinˆamica quˆantica n˜ao-relativ´ıstica de uma part´ıcula neutra na presen¸ca de defeitos topol´ogicos, a implementa¸c˜ao da computa¸c˜ao quˆantica holonˆomica para part´ıculas neu-tras usando fases geom´etricas quˆanticas e por fim estudar a quantiza¸c˜ao de Landau para part´ıculas neutras na presen¸ca de defeitos tanto no caso relativ´ıstico quanto no n˜ao-relativ´ıstico.
Essa Tese de Doutorado est´a dividida em trˆes partes: a primeira parte ´e dirigida para o estudo de fases geom´etricas quˆanticas na dinˆamica quˆantica de uma part´ıcula neutra com momentos de dipolo magn´etico e el´etrico permanentes interagindo com campos el´etrico e magn´etico externos na presen¸ca de defeitos topol´ogicos. Inciaremos com uma introdu¸c˜ao enfatizando o contexto hist´orico do desenvolvimento dos estudos sobre fases geom´etricas. O cap´ıtulo 1 destina-se para um breve introdu¸c˜ao a defeitos topol´ogicos, conceitos de goemetria diferencial e relatividade geral que ser˜ao os alicerces de nosso estudo. O cap´ıtulo 2 destina-se a uma breve introdu¸c˜ao sobre a dinˆamica quˆantica relativ´ıstica de part´ıculas neutras com momentos de dipolo magn´etico e el´etrico permanentes interagindo com um campo eletomagn´etico externo e a aproxima¸c˜ao de Foldy-Wouthuyssen para o limite n˜ao-relativ´ıstico da equa¸c˜ao de Dirac. Nos cap´ıtulos 3, 4 e 5 est˜ao nossos estudos sobre fases geom´etricas quˆanticas na presen¸ca de defeitos. No cap´ıtulo 3 estudaremos o surgimento de fases geom´etricas diante do espa¸co-tempo da corda c´osmica. No cap´ıtulo 4 estudaremos o surgimento de fases geom´etricas diante de um espa¸co-tempo que possui curvatura e h´a a presen¸ca de tor¸c˜ao que ´e conhecido como disloca¸c˜ao c´osmica. No cap´ıtulo 5 estudaremos o surgimento de fases geom´etricas em referenciais n˜ao-inercias, mas com o espa¸co-tempo sendo o da corda c´osmica.
Na segunda parte da Tese abordaremos a implementa¸c˜ao da computa¸c˜ao quˆantica holonˆomica para part´ıculas neutras na presen¸ca de defeitos topol´ogicos. Iniaremos essa parte da Tese com uma introdu¸c˜ao enfatizando o contexto hist´orico do desenvolvimento da computa¸c˜ao quˆantica holonˆomica e sua implementa¸c˜ao. Os cap´ıtulos 6 e 7 mostraremos nossos estudos sobre a implementa¸c˜ao da computa¸c˜ao quˆantica holonˆomica. No cap´ıtulo 6 mostraremos a implemeanta¸c˜ao da computa¸c˜ao quˆantica holonˆomica para part´ıculas neu-tas interagindo com campos externos na presen¸ca de defeitos. No cap´ıtulo 7 mostraremos uma vis˜ao geom´etrica para os fluxos quˆanticos no grafeno devido a presen¸ca defeitos atrav´es da Teoria de Kaluza-Klein e, em seguinda, discutiremos a implementa¸c˜ao da com-puta¸c˜ao quˆantica holonˆomica no grafeno usando esses fluxos quˆanticos.
Na terceira parte da Tese discutiremos a quantiza¸c˜ao de Landau para part´ıculas
tras. Nos cap´ıtulos 8, 9 e 10 mostraremos nossos resultados. No cap´ıtulo 8 come¸caremos estudando a quatiza¸c˜ao de Landau para part´ıculas neutras no limite n˜ao-relativ´ıstico na presen¸ca de defeitos topol´oligos. No cap´ıtulo 9, estudaremos a quanztiza¸c˜ao de Lan-dau para part´ıculas neutras no caso relativ´ıtico tanto na ausˆencia quanto na presen¸ca de defeitos topol´ogicos.
Por fim, mostraremos nossas conclus˜oes e as perspectivas deste trabalho. Durante o desenvolvimento desta Tese de Doutoramento, tivemos v´arios colaboradores e novamente deixamos nossos agradecimentos por esses trabalhos em conjunto. Nossos trabalhos foram divulgados com as seguintes publica¸c˜oes:
1. K. Bakke, J. R. Nascimento and C. Furtado,Geometric phase for a neutral particle in the presence of a topological defect, Phys. Rev. D 78, 064012 (2008); arXiv:hep-th/0803.3428.
2. K. Bakke, J. R. Nascimento and C. Furtado, Gravitational geometric phase in the presence of torsion, Eur. Phys. J. C 60, 501 (2009);64, 169 (2009).
3. K. Bakke and C. Furtado, Scalar Aharonov-Bohm effect in the presence of a Topo-logical Defect, preprint.
4. K. Bakke and C. Furtado, Abelian Geometric Phase for a Neutral Particle due the presence of Topological Defects, preprint.
5. K. Bakke and C. Furtado,Geometric phase for a neutral particle in rotating frames in a cosmic string spacetime, Phys. Rev. D 80, 024033 (2009).
6. K. Bakke and C. Furtado, Anandan Quantum Phase for a neutral particle with Fermi-Walker reference frame in the cosmic string background, preprint.
7. K. Bakke and C. Furtado,Holonomic quantum computation with Aharonov-Casher setup in the presence of topological defects, preprint.
8. K. Bakke and C. Furtado,Holonomic quantum computation with Anandan quantum phase for neutral particles and linear topological defects, preprint.
9. K. Bakke and C. Furtado, Holonomic quantum computation for electric dipole, preprint.
10. K. Bakke, A. Yu. Petrov and C. Furtado,Kaluza-Klein theory in graphene, preprint. 11. K. Bakke, C. Furtado and S. Sergeenkov, Holonomic quantum computation
associ-ated with a defect structure of conical graphene, EPL87, 30002 (2009).
12. K. Bakke, L. R. Ribeiro, C. Furtado and J. R. Nascimento, Landau quantization for a neutral particle in presence of topological defects, Phys. Rev. D 79, 024008 (2009); arXiv:hep-th/0810.3885.
13. K. Bakke and C. Furtado, Bound States for Neutral Particle in a Rotating Frame in the Cosmic String Spacetime, preprint.
15. K. Bakke and C. Furtado, Relativistic Landau-Aharonov-Casher quantization in topological defects spacetime, aceito para publica¸c˜ao no Int. J. Mod. Phys. D (2009).
Outros trabalhos desenvolvidos que n˜ao foram inclu´ıdos nesta Tese de Doutoramento foram
a. I. A. Pedrosa, K. Bakke and C. Furtado,Gaussian wave packet states of relic gravi-tons, Phys. Lett. B 671, 314 (2009).
b. K. Bakke, I. A. Pedrosa and C. Furtado,Geometric Phases and Squeezed Quantum States of Relic Gravitons, aceito para publica¸c˜ao no J. Math. Phys.
c. K. Bakke, L. R. Ribeiro and C. Furtado,Landau Quantization for an Induced Elec-tric Dipole in the Presence of Topological Defect, aceito para publica¸c˜ao no Central European Journal of Physics.
I
Fases Geom´
etricas Quˆ
anticas (FGQ) para Part´ıculas
Neu-tras na Presen¸ca de Defeitos
1
Introdu¸c˜ao 2
1 Defeitos Topol´ogicos 5
1.1 Introdu¸c˜ao a Defeitos Topol´ogicos . . . 5
1.2 Geometria Diferencial: uma breve introdu¸c˜ao . . . 10
1.3 Os Refereciais Locais . . . 17
1.4 A Derivada Covariante de um Spinor . . . 21
2 Dinˆamica das Part´ıculas Neutras 24 2.1 A Dinˆamica Relativ´ıstica de Particulas Neutras . . . 24
2.2 Aproxima¸c˜ao de Foldy-Wouthuysen . . . 26
2.3 Dinˆamica N˜ao-Relativ´ıstica para Part´ıculas Neutras . . . 28
3 FGQ no Espa¸co-Tempo da Corda C´osmica 30 3.1 Espa¸co-Tempo da Corda C´osmica e Configura¸c˜oes dos Campos Externos . 31 3.2 Dinˆamica Relativ´ıstica e Fases Geom´etricas Relativ´ısticas I . . . 33
3.3 Dinˆamica Relativ´ıstica e Fases Geom´etricas Relativ´ısticas II . . . 36
3.4 Dinˆamica N˜ao-Relativ´ıstica . . . 38
3.5 Fases Geom´etricas N˜ao-Relativ´ısticas I . . . 40
3.6 Fases Geom´etricas N˜ao-Relativ´ısticas II . . . 43
4 FGQ no Espa¸co-Tempo de uma Desloca¸c˜ao C´osmica 46 4.1 Fases Geom´etricas N˜ao-Abelianas Relativ´ısticas . . . 47
4.2 Fases Geom´etricas Quˆanticas N˜ao-Abelianas N˜ao-Relativ´ısticas . . . 53
4.3 Fases Geom´etricas Abelianas Relativ´ısticas . . . 58
4.4 Fases Geom´etricas Abelianas N˜ao-Relativ´ısticas . . . 61
5 FGQ em Referenciais N˜ao-Inerciais 62 5.1 Dinˆamica Relativ´ıstica com Referenciais Girantes na presen¸ca de Defeitos Topol´ogicos . . . 63
5.2 Dinˆamica N˜ao-Relativ´ıstica com Referenciais Girantes na presen¸ca de De-feitos Topol´ogicos . . . 67
5.3.1 Primeiro caso relativ´ıstico: intera¸c˜ao entre o momento de dipolo magn´etico e campo el´etrico radial . . . 73 5.3.2 Segundo caso relativ´ıstico: intera¸c˜ao entre o momento de dipolo
magn´etico e um campo magn´etico azimutal . . . 75 5.4 Dinˆamica N˜ao-Relativ´ıstica com Referenciais Transportados por
Fermi-Walker na presen¸ca de Defeitos Topol´ogicos . . . 77 5.4.1 Primeiro caso n˜ao-relativ´ıstico: intera¸c˜ao entre momento de dipolo
mang´etico e campo el´etrico radial . . . 77 5.4.2 Segundo caso n˜ao-relativ´ıstico: intera¸c˜ao entre o momento de dipolo
magn´etico e um campo magn´etico azimutal . . . 79
II
Computa¸c˜
ao Quˆ
antica Holonˆ
omica (CQH) na Presen¸ca de
Defeitos Topol´
ogicos
81
Introdu¸c˜ao 82
6 CQH para Part´ıculas Neutras 84
6.1 Implementa¸c˜ao de um conjunto universal de portas quˆanticas para um q-bit na configura¸c˜ao de Aharonov-Casher . . . 85 6.2 Implementa¸c˜ao de um conjunto universal de portas quˆanticas para um q-bit
na presen¸ca de um campo magn´etico azimutal . . . 89 6.3 Implementa¸c˜ao de um conjunto universal de portas quˆanticas para um q-bit
atrav´es da topologia de uma despira¸c˜ao . . . 91 6.4 Implementa¸c˜ao de um conjunto universal de portas quˆanticas para um q-bit
na presen¸ca de um campo magn´etico uniforme . . . 93 6.5 Implementa¸c˜ao de portas quˆanticas para dois q-bits . . . 95
7 Computa¸c˜ao Quˆantica Holonˆomica no Grafeno 98
7.1 Descri¸c˜ao geom´etrica dos fluxos no grafeno . . . 101 7.2 Implementa¸c˜ao de um conjunto de portas quˆanticas para um q-bit no grafeno104
III
Quantiza¸c˜
ao de Landau para Part´ıculas Neutras na
Pre-sen¸ca de Defeitos Topol´
ogicos
109
Introdu¸c˜ao 110
8 Quantiza¸c˜ao N˜ao-Relativ´ıstica de Landau 113
8.1 Quantiza¸c˜ao N˜ao-Relativ´ıstica de Landau na Presen¸ca de Defeitos Topol´ogicos113 8.2 Quantiza¸c˜ao N˜ao-Relativ´ıstica de Landau em Referenciais Girantes e na
presen¸ca de um Defeito Topol´ogico . . . 117
Gauge de Landau . . . 122
9.2 Quantiza¸c˜ao Relativ´ıstica de Landau no Espa¸co-Tempo Plano no Gauge Sim´etrico . . . 125
9.3 Quantiza¸c˜ao Relativ´ıstica de Landau na Presen¸ca de Defeitos Topol´ogicos . 129
Conclus˜
oes e Perspectivas
135
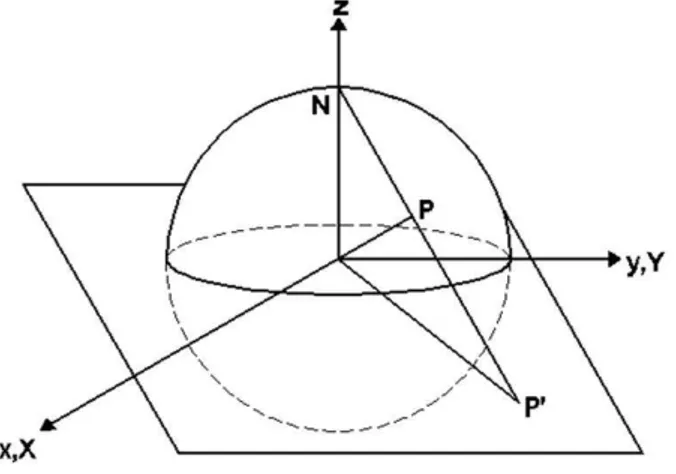
A Spinores na Relatividade Geral 141 A.1 A Esfera de Riemann . . . 141A.2 O Espa¸co de Spin . . . 143
A.3 ´Algebra Spinorial . . . 144
A.4 O spinor de Levi-Civita . . . 146
A.5 Base de di´adicas . . . 147
A.6 Conex˜ao entre tensores e spinores . . . 149
A.7 Forma spinorial da derivada covariante . . . 151
A.8 Matrizes de Dirac . . . 153
B Introdu¸c˜ao `a Computa¸c˜ao Quˆantica 155 B.1 Portas Quˆanticas para 1 q-bit . . . 155
B.2 Portas Quˆanticas para 2 q-bits . . . 157
B.3 Conjunto de Portas Universais . . . 158
C Dimens˜oes Extras: Teoria de Kaluza-Klein 160
1.1 Defeito Topol´ogico conhecido como desloca¸c˜ao lateral. A barra escura indica a dire¸c˜ao em que foi feita a desloca¸c˜ao. Note-se que a dire¸c˜ao da desloca¸c˜ao ´e prependicular ao eixo de simetria do defeito neste caso. . . 9 1.2 Defeito Topol´ogico conhecido como desloca¸c˜ao tipo h´elice. A barra escura indica a
dire¸c˜ao em que foi feita a deslaca¸c˜ao. Note-se que a dire¸c˜ao da desloca¸c˜ao ´e paralela ao eixo de simetria do defeito neste caso. . . 9 1.3 S´olido cristalino com simetria hexagonal. Os planos inseridos no hex´agonos mostram
o local do “corte” onde se pode remover ou inserir um setor para se produzir uma desclina¸c˜ao positiva ou negativa atrav´es dos processos de Volterra. . . 10 1.4 Defeito Topol´ogico conhecido como desclina¸c˜ao positiva. A forma¸c˜ao deste defeito ´e
realizada removendo um setor do plano com ˆangulo Φ/2πe “colando-se” as extremidades na figura 1.3. . . 10 1.5 Defeito Topol´ogico conhecido como desclina¸c˜ao negativa. A forma¸c˜ao deste defeito ´e
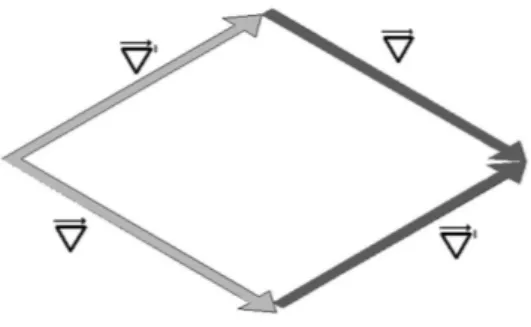
re-alizada cortando-se o hex´agono 1.3 em um dos locais mostrados pelos planos e inserindo-se um inserindo-setor no plano do hex´agono. . . 10 1.6 Transporte paralelo de um vetorV ao longo das dire¸c˜oes de vetoresAeB e retornando
a sua posi¸c˜ao inicial. Tem-se que ao retornar a posi¸c˜ao inicial o vetorV varia em rela¸c˜ao a sua configura¸c˜ao inicial emδV. . . 15 1.7 Representa¸c˜ao do operador comutador de duas derivadas covariantes. . . 16 4.1 Defeito Topol´ogico conhecido como desloca¸c˜ao espiral [98]. A forma¸c˜ao desse defeito ´e
realizada atrav´es de uma transla¸c˜ao sobre o plano-ρϕe “colando-se” as extremidades, o que promove a distor¸c˜ao de uma c´ırculo numa espiral. A barra escura indica a dire¸c˜ao do vetor de Burges. Note-se que o vetor de Burges est´a inserido no plano perpendicular ao eixo de simetria do defeito. . . 59 6.1 Representa¸c˜ao do qbit no sistema AC na presen¸ca de uma desloca¸c˜ao. Um feixe de
part´ıculas neutras incidentes ´e dividido em dois por um divisor de feixe, fazendo com que estes dois novos feixes passem por duas regi˜oes distintas. Na regi˜ao 1 consideramos que h´a apenas um campo el´etrico gerado por um capacitor de placas parelelas sem a presen¸ca de defeito topol´ogico, onde este campo ´e perpendicular a trajet´oria das part´ıculas. Na regi˜ao 2 consideramos que h´a um cristal s´olido com uma desloca¸c˜ao tipo h´elice representada pelo elemento de linha(6.3). Em cada uma das regi˜oes, a fun¸c˜ao de onda das part´ıculas neutras sofre uma mudan¸ca de fase. No final, os feixes recombinam-se. 87
feixe gerando dois novos feixes de part´ıculas neutras. Um dos feixes passa pela regi˜ao 1 onde h´a a presen¸ca de uma campo magn´etico uniforme, enquanto que o outro feixe passa pela regi˜ao 2 onde h´a a presen¸ca de um material s´olido contento uma desloca¸c˜ao. Em cada regi˜ao, a fun¸c˜ao de onda das part´ıculas neutras sofre uma mudan¸ca de fase diferente. Ao passarem por essas duas regi˜oes, os feixes recombinam-se. . . 94
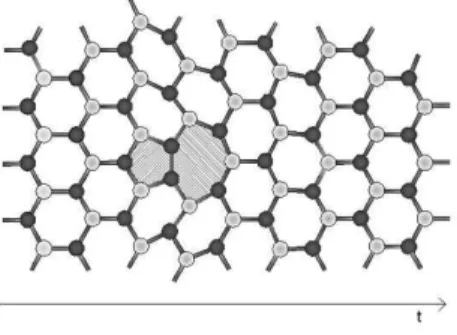
7.1 Estrutura planar de uma ´unica camada de grafite conhecida como grafeno. V´ertices em cinza e branco indicam as subredesAeB. . . 99 7.2 Porta quˆantica para um q-bit conhecida como porta de faseQ2 dada na express˜ao (7.39). Essa porta
quˆantica ´e implementada com um cone de gafeno constru´ıdo com dois setores removidos (cinza). Pode-se ver como os defeitos distorcem a rede do grafeno. A Pode-seta indica a direc¸c˜ao do movimento de um el´etron quando este passa em torno do defeito topol´ogico.. . . 106 7.3 Porta quˆantica para um q-bit conhecida como porta troca e mudan¸ca de faseQS dada na express˜ao
(7.40). Esta porta quˆantica ´e implementada com um cone de grafeno constru´ıdo com um setor removido e por um outro cone constru´ıdo com um setor inserido. O resultado do conjunto dos defeitos ´e idˆentico ao comportamento de multicones onde o fluxo atrav´es destes cones ir˜ao se cancela. A seta indica a orienta¸c˜ao do movimento de um el´etron que passa em torno do multicone. . . 107 A.1 Esfera de Riemann. . . 142 B.1 Esfera de Bloch. Proje¸c˜ao de um estado arbitr´ario para um q-bit|ψina esfera de Bloch. No p´olo norte
da esfera de Bloch localiza-se o estado|0ie no p´olo sul o estado|1i. Os ˆangulosθeϕconstituem os ˆ
angulos polar e azimutal, respectivamente. . . 156
Fases Geom´
etricas Quˆ
anticas (FGQ)
para Part´ıculas Neutras na Presen¸ca
de Defeitos
Nessas ´ultimas d´ecadas, o estudo do surgimento de fases geom´etricas em sistemas quˆanticos tornou-se um dos mais atrativos e importantes no entendimento do mundo quˆantico. O primeiro trabalho que tratou diretamente o aparecimento de fases geom´etricas quˆanticas data de 1956 feito por Pancharatnam [1]. Nesse trabalho, Pancharatnam de-scobriu uma mudan¸ca de fase em luz polarizada. J´a em 1959, Aharonov and Bohm [2] mostraram que a fun¸c˜ao de onda de um el´etron adquire uma fator de fase quando percorre uma trajet´oria ao redor de um fluxo magn´etico gerado por um solen´oide muito longo ou por um arranjo de dipolos magn´eticos, devido a presen¸ca de potenciais n˜ao-nulos: o po-tencial escalar Φ e o popo-tencial vetorA~(~r). Essa mudan¸ca de fase na fun¸c˜ao de onda ficou conhecido como efeito Aharonov-Bohm (AB)1, cuja express˜ao
φAB =
I
~
A·dr~ =qΦc, (1)
onde q ´e a carga do el´etron e Φc ´e o fluxo de campo magn´etico dentro do solen´oide. Contudo, o uso de fatores de fase para obtermos a fun¸c˜ao de onda exata de uma part´ıcula que interage com campos externos foi proposta em 1931 por Dirac [3] e, em 1980, Berry [4] mostrou que a fun¸c˜ao de onda exata para o efeito Aharonov-Bohm pode ser obtida aplicando a proposta do fator de fase de Dirac.
O termo fase geom´etrica quˆantica foi introduzido na Literatura a partir do trabalho produzido por Berry [5] em 1984, onde mostrou que a fun¸c˜ao de onda de uma part´ıcula adquire um fator de fase adicional `a fase dinˆamica do sistema durante uma evolu¸c˜ao adiab´atica que tem origem geom´etrica. Esse fator de fase geom´etrico adquirido durante uma evolu¸c˜ao adiab´atica ficou conhencido como fase de Berry. Simon [6] em 1983, inter-pretou as fases de Berry atrav´es de holonomias, ou seja, atrav´es do transporte paralelo de um vetor ou spinor ao longo de uma curva fechada. Tamb´em em 1984, Wilczek e Zee [7] propuseram um generaliza¸c˜ao das fases de Berry investigando o surgimento de fases geom´etricas n˜ao-abelianas. Contudo, em 1987, Aharonov e Anandan [8] mostraram que a fun¸c˜ao de onda de uma part´ıcula adquire um fator de fase durante uma evolu¸c˜ao c´ıclica sem necessitar da aproxima¸c˜ao adiab´atica. O estudo mais geral de fases de Berry foi realizado por Samuel e Bhandari [9] em 1988, onde a evolu¸c˜ao do sistema quˆantico con-siderada nem era unit´aria nem c´ıclica. Outros trabalhos que devem ser citados no estudo de fases geom´etricas s˜ao dados nas referˆencias [10, 11, 12, 13] e, para uma revis˜ao mais detalhada sobre os trabalhos citados nesta introdu¸c˜ao, al´em de discuss˜oes matem´aticas
1
Vamos considerar~=c= 1.
mais profundas sobre fases geom´etricas e aplica¸c˜oes em outras ´areas da F´ısica pode-se consultar as referˆencias [14, 15].
Ainda em 1984, Aharonov e Casher [16] desenvolveram um trabalho discutindo que situa¸c˜ao geraria um efeito Aharonov-Bohm para uma part´ıcula neutra. Dessa forma, eles consideraram um sistema onde part´ıculas neutras possuindo momento de dipolo magn´etico moviam-se ao redor de uma configura¸c˜ao de cargas el´etricas estacion´arias. Ent˜ao, dada uma distribui¸c˜ao linear de cargas e com o momento de dipolo magn´etico alinhado inicial-mente com esta distribui¸c˜ao de cargas, a fun¸c˜ao de onda da part´ıcula neutra adquire uma fase quˆantica topol´ogica dada por
φAC =
I
~µ×E~·dr~ =µλe, (2)
onde µ´e a proje¸c˜ao do momento de dipolo magn´etico ao longo da linha de carga e λe ´e a densidade linear de carga. A necessidade de termos o momento de dipolo magn´etico alinhado com a distribui¸c˜ao linear de cargas ´e para que n˜ao haja precess˜ao do momento de dipolo devido ao campo el´etrico, isto ´e, para que n˜ao haja for¸ca de Lorentz atuando no sistema. A fase quˆantica obtida ´e topol´ogica por n˜ao depender de um ponto do espa¸co para ser definida, ela ter´a o mesmo valor para qualquer trajet´oria fechada que a part´ıcula neutra percorrer. Esse efeito de surgimento de fase quˆantica dado pela express˜ao (2) ´e chamado de efeito Aharonov-Casher (AC) e sua observa¸c˜ao experimental foi descrita em sistema atˆomicos por Sangsteret al[17]. Portanto, h´a uma “dualidade” entre os efeitos AB e AC no sentido em que podemos trocar os pap´eis das part´ıculas carregadas e momentos de dipolos, isto ´e, λe→µem AB eµ→λe em AC. Por´em, devemos dizer que esses efeitos s˜ao rec´ıprocos, pois o efeito Aharonov-Bohm dual (DAB) foi demosntrado por Dowling
et al [18] usando a rela¸c˜ao de dualidade eletromagn´etica de Maxwell e, separadamente, por Furtado e Duarte [19] onde fizeram a an´alise da dinˆamica quˆantica de um monop´olo magn´etico em uma regi˜ao que existe um solen´oide el´etrico linear.
Em 1993, He e McKellar [20] e, em 1994, Wilkens [21] consideraram a existˆencia de monop´olos magn´eticos e trabalharam em um sistema onde uma part´ıcula neutra que possui um momento de dipolo el´etrico permanente move-se em um campo magn´etico produzido por monop´olos magn´eticos. De forma semelhante ao que foi feito por Aharonov e Casher, eles mostraram que se o momento de dipolo el´etrico estiver alinhado inicialmente com uma distribui¸c˜ao linear de monop´olos magn´eticos, a fun¸c˜ao de onda adquire uma fase quˆantica topol´ogica dada por
φHM W =
I
~
d×B~·dr~ =dλm, (3)
[23]. Observemos que o efeito HMW ´e rec´ıproco do efeito DAB, mas dual ao efeito AC. Podemos verificar essa dualidade fazendo ~µ↔d~eλe↔λm.
Uma das caracter´ısticas importante nas fases produzidas pelos efeitos AB, DAB, AC e HMW ´e que as essas fases s˜ao n˜ao-dispersivas, ou seja, elas n˜ao dependem da velocidade da part´ıcula neutra [24, 25]. Assim, esses efeitos s˜ao independentes da energia das part´ıculas e a fase observada ter´a o mesmo valor tanto no regime relativ´ıstico quanto no regime n˜ao-relativ´ıstico. Podemos ilustrar as rela¸c˜oes entre os efeitos AB, DAB, AC e HMW com o seguinte quadro:
AC(~µ, λe) ←→
dual HM W
~ d, λm
l rec´ıproco l rec´ıproco
AB(λe, ~µ) ←→dual DAB
λm, ~d
O tratamento relativ´ıstico e n˜ao-relativ´ıstico que unifica a intera¸c˜ao entre part´ıculas com momentos de dipolo magn´etico e el´etrico permanentes com o campo eletromagn´etico foi feito em 2000 por Anandan [26, 27], enquanto que uma an´alise detalhada de fases quˆanticas no limite n˜ao-relativ´ıstico desta intera¸c˜ao com campos el´etrico e magn´etico radiais foi feita em 2004 por Furtado e Lima Ribeiro [28].
Defeitos Topol´
ogicos
Em todo o desenvolvimento deste trabalho estaremos sempre adotando um espa¸co-tempo curvo, com a ausˆencia ou presen¸ca da tor¸c˜ao, como um pano de fundo. A inten¸c˜ao desse cap´ıtulo ´e fazer uma breve revis˜ao sobre os estudo de defeitos topol´ogicos em mat´eria condensada e sua liga¸c˜ao com a gravita¸c˜ao atrav´es da geometria diferencial e de conceitos de relatividade geral. Dessa forma, iniaremos com a defini¸c˜ao e classifica¸c˜ao de defeitos topol´ogicos em cristais s´olido. Em seguida, faremos uma breve introdu¸c˜ao `a geometria diferencial e aos conceitos b´asicos de relatividade geral tais como as defini¸c˜oes de derivada covariante de um vetor e um tensor, bem como a defini¸c˜ao dos referenciais locais dos observadores e a derivada covariante de um spinor no espa¸co-tempo curvo na ausˆencia ou presen¸ca de tor¸c˜ao. A revis˜ao feita neste cap´ıtulo n˜ao abrange os conceitos como o de variedades diferenci´aveis e fibrados para n˜ao deixarmos muito extensa essa revis˜ao. Essas discuss˜oes s˜ao extremamente bem realizadas em livros textos sobre relatividade geral tais como dados nas referˆencias [29, 30, 31, 32, 33, 34, 35, 36].
1.1
Introdu¸c˜
ao a Defeitos Topol´
ogicos
Nesta se¸c˜ao faremos uma breve introdu¸c˜ao a teoria de defeitos topol´ogicos em s´olidos, mais especificamente em cristais. A abordagem dessa se¸c˜ao ser´a simples e direta para que seja facilmente entendido o uso de defeitos topol´ogicos como pano de fundo no desenvolvi-mento deste trabalho.
Um cristal produzido em um laborat´orio nunca ´e perfeito. Ele sempre cont´em um grande n´umero de defeitos, cuja origem pode ser qu´ımica, el´etrica ou de car´acter estrutu-ral, isto ´e, ele pode ter em sua estrutura um excesso ou falta de el´etrons ou simplesmente sua simetria ´e quebrada em um determinado local. Para estudarmos defeitos topol´ogicos em s´olidos iremos considerar um cristal ideal. Um cristal ideal consiste de um arranjo peri´odico de ´atomos idˆenticos situados em pontos da rede cristalina
xn=n1a1 +n2a2+n3a3, (1.1)
onde ai s˜ao os vetores da rede e ni s˜ao n´umeros inteiros. Um exemplo simples ´e de uma rede c´ubica simples com ´atomos localizados a uma distˆanciaa um do outro
xn=a(n1aˆ1+n2aˆ2+n3ˆa3,), (1.2) com ˆai sendo um vetor unit´ario. Note-se que se pode descrever esse s´olido atrav´es da m´etrica Euclidiana δij = diag (+ + +). Agora, se for¸cas externas s˜ao aplicadas sobre o cristal, este ir´a sofrer deforma¸c˜oes e as posi¸c˜oes dos ´atomos na rede cristalina mudar˜ao do ponto xn para
xn →x′n =xn+un(x). (1.3)
Contudo, em um cristal real sempre existe imperfei¸c˜oes as quais denominamos de de-feitos. Os defeitos podem ser descritos atrav´es das deforma¸c˜oes na rede cristalina dadas pela express˜ao (1.3). Considerando o limite a → 0, pode-se estudar o cristal no limite do cont´ınuo e, assim, define-se o campo vetorial chamado deslocamento ui(x) atrav´es da express˜ao
x′i =xi+ui(x). (1.4)
Depois de uma deforma¸c˜ao ou distor¸c˜ao da rede cristalina, a distˆancia entre dois pontos vizinhos do material separados infinitesimalmente ´e dada por1
dx′i =dxi+∂juidxj. (1.5)
O comprimento entre esses dois pontos ser´a
dl′ = dl2+ 2ǫijdxidxj
1/2
, (1.6)
com dl = pdx2
i e onde tem-se que ǫij ´e um tensor sim´etrico chamado de tensor de
deforma¸c˜ao que ´e dado por
ǫij ≡ 1
2(∂iuj+∂jui+∂iul∂jul), (1.7) onde deve-se estabelecer que ∂jui <<1 para que este tenhamos uma aproxima¸c˜ao linear. Logo, pode-se reecrever o tensor de deforma¸c˜ao como [38]
ǫij ≡ 1
2(∂iuj+∂jui). (1.8)
Considerando-se um meio el´astico com for¸cas de curto alcance atuando sobre pontos vizinhos, pode-se definir a densidade de energia el´astica atrav´es da diferen¸ca dl′ −dl e,
desse modo, atrav´es do tensor de deforma¸c˜ao. Tomando-se as express˜oes paradl′ em (1.6),
1
Os ´ındices que se repetem nas equa¸c˜oes indicam uma soma sobre estes ´ındices que ´e conhecida como
conven¸c˜ao de Einstein. Por´em, apenas nesta se¸c˜ao ´e que n˜ao adotamos a soma de ´ındices iguais na forma
covariante para manter a nota¸c˜ao o mais pr´oxima poss´ıvel das referˆencias [38, 39]. A partir da pr´oxima
se¸c˜ao adotaremos a conve¸c˜ao de Eintein propriamente dita onde ´ındices covariantes e contravariantes
dl =pdx2
i e fazendo-se uma aproxima¸c˜ao para termos de ordem mais baixa, a densidade de energia el´astica pode se escrita como
e(x) = 1
2cijklǫijǫkl, (1.9)
ondecijkl´e chamado de tensor de elasticidade e ´e sim´etrico diante das permuta¸c˜oesi↔j,
k ↔l e ij ↔kl. Para um meio isotr´opico, o tensor de elasticidade ´e dado por [38]
cijkl=µ(δikδjl+δilδjk) +λ δijδkl, (1.10) com µeλsendo constantes conhecidas comoshear modulus e constante de Lam´e, respec-tivamente. Agora, se por um certa configura¸c˜ao o tensor de deforma¸c˜ao ǫij for alterado por um pequeno incremento δǫij, ent˜ao a densidade de energia el´astica ser´a alterada para
δe =cijklǫklδǫij. (1.11)
Assim, pode-se definir o tensor de tens˜ao como [38]
σij ≡
δe δǫij
=cijklǫkl. (1.12)
Para um meio isotr´opico, pode-se substituir a express˜ao (1.10) em (1.12) e obter
σij = 2µ ǫij +λ δijǫkk. (1.13) Agora, seja fi(x) uma densidade de for¸ca produzida por uma fonte externa que atua sobre um s´olido ou uma densidade de for¸ca interna n˜ao-el´astica distribu´ıda dentro do s´olido. O trabalho realizado por esta for¸ca externa sobre um dado elemento de volume do s´olido ´e dado por
w(x) =−fi(x) ui(x). (1.14) A for¸ca total que atua sobre o sistema ´e dada por
FT =
Z
[e(x) +w(x)]d3x, (1.15) ent˜ao, o estado de equil´ıbrio, quando h´a uma distor¸c˜ao na rede cristalina, pode ser obtido minimizando a energia total em rela¸c˜ao a varia¸c˜ao δui(x), isto ´e,
Z
[∂i(δuj)σij −fiδuj]d3x= 0. (1.16) onde pode-se reescrever o primeiro termo de (1.16) como
Z
[∂i(δujσij)−δuj∂iσij]dx3−
Z
fiδujdx3 = 0. (1.17) Aplicando o teorema de Gauss no primeiro termo de (1.17), tem-se uma integral de su-perf´ıcie. Dessa forma, a equa¸c˜ao (1.17) torna-se
Z
σijδuidSj−
Z
Considerando-se que a for¸ca externa ´e aplicada em um regi˜ao finita do s´olido, tem-se que
δui →0 no infinito, logo, pode-se descartar a integral de superf´ıcie. Dessa forma, tem-se que em um determinado ponto fixo do s´olido xque
∂iσij(x) +fi(x) = 0, (1.19) que ´e a equa¸c˜ao de Euler-Lagrange para a elasticidade linear [38]. Esta equa¸c˜ao d´a um sentido f´ısico para as componentes do tensor de tens˜ao: σi1, σi2, σi3s˜ao as trˆes componentes da for¸ca por unidade de ´area que atuam sobre um elemento de superf´ıcie dSi. Assim, as equa¸c˜oes (1.13) e (1.19) formam as equa¸c˜oes b´asicas para a teoria da elasticidade est´atica de pequenas deforma¸c˜oes [37, 38, 39], onde (1.13) corresponde a lei de Hook que relaciona o tersor de tens˜ao com o tensor de deforma¸c˜ao da rede e (1.17) corresponde a lei de Newton.
A conex˜ao da teoria da elasticidade com a geometria Riemanniana ´e feita quando ´e considerada transforma¸c˜oes infinitesimais que levam um ponto xµ′ para xµ no espa¸co-tempo
xµ′ =xµ−ξµ(x) (1.20)
ou seja, que transla¸c˜oes infinitesimais ξµ(x) sejam iguais aos deslacamentos u
i(x) (com o sinal invertido) no ponto x[38]. Desse modo, considrando x′ =y e tendo em vista que
ui(x) = ui(y(x)), pode-se escrever o tensor m´etrico gij(x) como
gij(x) =
∂yk
∂xi
∂yl
∂xj δkl ≈δij −∂iuj−∂jui =δij−2ǫij, (1.21) onde definimos em rela¸c˜ao ao tensor (1.8) diante da aproxima¸c˜ao linear, com ǫij(x) =
ǫij(y) e∂uj/∂xi =∂ui/∂yi. Com a express˜ao (1.21) pode-se, ent˜ao, descrever deforma¸c˜oes numa rede cristalina atrav´es do tensor m´etrico provindo da geometria diferencial. Com essa aproxima¸c˜ao linear pode-se descrever as deforma¸c˜oes na rede ou defeitos correspon-dendo a uma curvatura singular2, tor¸c˜ao ou com a ocorrˆencia de ambos. Essa formula¸c˜ao usando a geometria diferencial para a descri¸c˜ao de defeitos topol´ogicos foi desenvolvida por Katanaev e Volovich [37, 38, 39] e iremos fazer uma breve discuss˜ao no final da pr´oxima se¸c˜ao.
Passaremos agora para a classifica¸c˜ao dos defeitos topol´ogicos atrav´es do processos de Volterra. A descri¸c˜ao de Volterra para a forma¸c˜ao de defeitos topol´ogicos s˜ao gerados conceitualmente atrav´es de processos de “cortar e colar”. A classifica¸c˜ao dos defeitos que ser´a apresentada nesta se¸c˜ao est´a relacionada com a simetria de transla¸c˜ao da rede cristalina conhecida comodesloca¸c˜oes e `a simetria de rota¸c˜ao da rede cristalina, conhecida como desclina¸c˜oes.
Desloca¸c˜oes: S˜ao defeitos lineares associados `a simetria de transla¸c˜ao da rede cristalina. Em cristais, as desloca¸c˜oes devem satisfazer a invariˆancia translacional, ou seja, os ´atomos das duas superf´ıcies do corte podem ser alinhados apenas se o mento for uma opera¸c˜ao de simetria translacional da rede. Note-se que o desloca-mento m´ınimo numa rede cristalina ´e a distˆancia entre dois ´atomos adjacentes. As desloca¸c˜oes podem ser
2
Curvatura singular significa que s´o h´a um ponto no espa¸co onde o valor do tensor de curvatura ´e
a) Tipo lateral: s˜ao defeitos que resultam de transla¸c˜oes perpendiculares a um eixo ao longo das superf´ıcies de corte.
Figura 1.1: Defeito Topol´ogico conhecido como desloca¸c˜ao lateral. A barra escura indica a dire¸c˜ao em que foi feita a desloca¸c˜ao. Note-se que a dire¸c˜ao da desloca¸c˜ao ´e prependicular ao eixo de simetria do
defeito neste caso.
b) Tipo h´elice: s˜ao defeitos que resultam de transla¸c˜oes paralelas ao eixo definido pelas superf´ıcies de corte.
Figura 1.2: Defeito Topol´ogico conhecido como desloca¸c˜ao tipo h´elice. A barra escura indica a dire¸c˜ao em que foi feita a deslaca¸c˜ao. Note-se que a dire¸c˜ao da desloca¸c˜ao ´e paralela ao eixo de simetria do defeito
neste caso.
Desclina¸c˜oes: S˜ao defeitos associados `a simetria de rota¸c˜ao na rede cristalina. Pode-se classificar as desclina¸c˜oes em
b) Desclina¸c˜oes negativas: s˜ao desclina¸c˜oes que se obtem quando corta-se, desloca-se as extremidade em um certo ˆangulo e, em seguida, insere-se um determinado material nesse espa¸co. O ˆangulo pelo qual se insere um determinado material ´e chamado de
ˆ
angulo de acr´escimo.
Figura 1.3: S´olido cristalino com simetria hexagonal. Os
planos inseridos no hex´agonos
mostram o local do “corte”
onde se pode remover ou inserir
um setor para se produzir uma
desclina¸c˜ao positiva ou
nega-tiva atrav´es dos processos de
Volterra.
Figura 1.4: Defeito Topol´ogico conhecido como
de-sclina¸c˜ao positiva. A forma¸c˜ao
deste defeito ´e realizada
re-movendo um setor do plano
com ˆangulo Φ/2π e “colando-se” as extremidades na figura
1.3.
Figura 1.5: Defeito Topol´ogico conhecido como
de-sclina¸c˜ao negativa. A forma¸c˜ao
deste defeito ´e realizada
cortando-se o hex´agono 1.3 em
um dos locais mostrados pelos
planos e inserindo-se um setor
no plano do hex´agono.
Despira¸c˜oes: S˜ao defeitos associados `as simetrias de transla¸c˜ao e rota¸c˜ao. Pode-se obter esse defeito fazendo-se um corte no material, retirando-se ou inserindo-se um se-tor angular, mas antes de identificar as extremidades da superf´ıcie, faz-se uma transla¸c˜ao sobre um dos eixos (por exemplo o eixo z).
Portanto, nesta se¸c˜ao foi vista a correspondˆencia entre a forma¸c˜ao de defeitos topol´ogicos em redes cristalinas com a geometria diferencial e a teoria de Einstein-Cartan para a gravita¸c˜ao, al´em da classifica¸c˜ao de defeitos topol´ogicos. Nas pr´oximas se¸c˜oes faremos uma breve introdu¸c˜ao `a geometria diferencial e uma revis˜ao sobre alguns conceitos da teoria de Einstein-Cartan para a gravita¸c˜ao que ser˜ao essenciais no estudo de defeitos topol´ogicos.
O objetivo desta se¸c˜ao ´e revisar os conceitos b´asicos de gometria diferencial que s˜ao essenciais no estudo da teoria de Einstein-Cartan para a gravita¸c˜ao. Ser˜ao vistos a defini¸c˜ao de derivada covariante diante de um espa¸co-tempo curvo na presen¸ca de tor¸c˜ao, a defini¸c˜ao de tensor de tor¸c˜ao, do tensor de contor¸c˜ao e, por fim, a express˜ao para a derivada covariante na presen¸ca de tor¸c˜ao.
Sejam dois pontos do espa¸co-tempo xµ e yµ = xµ+ dxµ. Esses dois pontos est˜ao separados por um intervalo infinitesimal ds de tal forma que, em qualquer sistema de coordenadas, a distˆancia entre eles ´e sempre preservada e onde pode-se escrever esse intervalo infinitesimal como
ds2 =gµν(x) dxµdxν, (1.22)
onde as quantidades gµν(x) determinam todas as propriedades geom´etricas em qualquer sistema de coordenadas e constituem a m´etrica do espa¸co-tempo, isto ´e, as quantidades
gµν(x) s˜ao as componentes do tensor m´etrico G3. A express˜ao (1.22) ´e chamada de elemento de linha do espa¸co-tempo.
O tensor m´etrico possui as caract´eristicas de ser sim´etrico, gµν = gνµ, e que seu determinante seja n˜ao-nulo, isto ´e, g =|gµν| 6= 0. Ter seu determinante n˜ao-nulo permite que se possa definir uma inversa gµν atrav´es da rela¸c˜ao
gµνgνγ =gγβgβµ =δµγ, (1.23) e onde a simetria vinculada a gµν implica em quegµν tamb´em seja sim´etrico.
Diante do espa¸co-tempo descrito pelo elemento de linha (1.22), defini-se a derivada covariante de um vetor ou de um tensor como sendo um operador ∇ que atua como um operador de derivada partial,∂µ, de maneira que n˜ao depende do sistema de coordenadas. A derivada covariante ´e uma transforma¸c˜ao linear de um tensor (k, l) para um outro tensor (k, l+ 1) e que obedece a regra de Leibniz, ou seja,
1. Linearidade: ∇(T +V) = ∇T +∇V;
2. Regra de Leibniz: ∇(T ⊗V) =∇T ⊗V +T ⊗ ∇V.
Como a derivada covariante obedece a regra de Leibniz para o produto de vetorial de dois tensores T e V e deve ser independente do sistema de coordenadas, o operador
∇ deve ser escrito como a soma da derivada partial ∂µ mais um termo de corre¸c˜ao que corresponde a transforma¸c˜ao linear do sitema de coordenadas. Esse termo de corre¸c˜ao ´e chamado de conex˜ao afim e ´e dado por um conjunto de matrizes n ×n, onde n ´e a dimens˜ao do espa¸co-tempo. Em termos de suas componentes, a express˜ao mais simples para a derivada covariante ´e dada para um vetor V =Vνeˆ
ν, onde tem-se
∇µVν =∂µVν + ΓνµαVα, (1.24) onde o objeto Γν
µα representa nossa conex˜ao afim. Para obter as conex˜oes afim considera-se que a m´etrica permane¸ca considera-sempre constante, isto ´e, que a derivada covariante do tensor m´etrico seja nula
∇αgµν(x) = 0, (1.25)
3
isso implica na seguinte express˜ao
∂λgµν−Γβλµgβν−Γβλνgµβ = 0. (1.26) Sempre que a equa¸c˜ao (1.26) for satisfeita, a conex˜ao afim ´e dita ser uma conex˜ao com-pat´ıvel com a m´etrica. Ser´a com conex˜oes compat´ıveis com a m´etrica que iremos trabalhar em todo desenvolvimento de nosso trabalho. Para obter a express˜ao para a conex˜ao com-pat´ıvel com a m´etrica deve-se tomar permuta¸c˜oes c´ıclicas nos ´ındices da equa¸c˜ao (1.26):
∂µgνλ−Γβµνgβλ−Γβµλgµβ = 0, (1.27) e tamb´em
∂νgλµ−Γβνλgβµ−Γβνµgλβ= 0. (1.28) Tomando-se a combina¸c˜ao (1.27)+(1.28)-(1.26) tem-se
∂µgνλ + ∂νgλµ−∂λgµν − Γβµν+ Γβνµ
gβλ+
Γβλµ−Γβµλ gβν
+ Γβλν−Γβνλ gβµ = 0. (1.29)
Definindo os objetos abaixo
Tβλµ≡2Γβ[λµ]= Γβλµ−Γβµλ; Γβ(µν) = 1 2 Γ
β
µν + Γβνµ
, (1.30)
obtem-se que a conex˜ao compat´ıvel com a m´etrica Γ pode ser escrita em termos de suas componentes sim´etrica e antisim´etrica
Γβµν = Γβ(µν)+ Γβ[µν] =µνβ +Kβµν, (1.31) onde o primeiro termo da express˜ao (1.31) s˜ao os s´ımbolos de Christoffel definidos como
β
µν = 1 2g
βλ(∂
µgνλ+∂νgλµ−∂λgµν), (1.32) enquanto que o segundo termo de (1.31) ´e chamado de tensor de contor¸c˜ao4:
Kβµν = 1 2 T
β
µν−Tµ νβ −Tν µβ
. (1.33)
Observe-se que na express˜ao (1.30) foi definido um objeto Tβ
µν que ´e chamado de
tensor de tor¸c˜ao5. Note-se que o tensor de tor¸c˜ao ´e antisim´etrico nos dois ´ultimos ´ındices,
Tβ
µν = −Tβνµ, enquanto que o tensor de contor¸c˜ao ´e antisim´etrico nos dois primeiros ´ındices, Kβµν = −Kµβν. Com isso, a express˜ao para a derivada covariante de um vetor
(1.24) em um espa¸co-tempo curvo e na presen¸c˜ao de tor¸c˜ao fica
∇µVν =∂µVν +
ν
µα Vα+KνµαVα. (1.34)
4
Chama-se Kβ
µν de tensor por conveniˆencia, por´em o correto ´e cham´a-lo de componentes do tensor
de contor¸c˜ao. Da mesma forma deve-se chamarTβ
µν de componentes do tensor de tor¸c˜ao. 5
A nota¸c˜ao usada aqui ´e idˆentica `a referˆencia [40]. Essa escolha foi feita devido a defini¸c˜ao da conex˜ao
Contudo, ´e comum na literatura escrever o tensor de tor¸c˜ao em termos de trˆes com-ponentes irredut´ıveis [40]: A primeira ´e vetor tra¸coTµ e o segundo ´e o vetor axial Sν que s˜ao dados abaixo
Tµ =Tβµβ; Sα =ǫαβνµTβνµ; (1.35) e a terceira componente irredut´ıvel ´e o tensor qβνµ que satisfaz as condi¸c˜oes qβµβ = 0 e
ǫαβνµq
βνµ = 0. Dessa forma, o tensor de tor¸c˜ao poder´a ser escrito como
Tβνµ = 1
3(Tνgβµ−Tµgβν)− 1
6ǫβνµγS γ+q
βνµ. (1.36)
Essa decomposi¸c˜ao do tensor de tor¸c˜ao em suas componentes irredut´ıveis ser´a muito ´util para nosso trabalho quando estivermos estudando o surgimento de fases geom´etricas no espa¸co-tempo curvo e com tor¸c˜ao no cap´ıtulo 5.
Na express˜ao (1.34) foi definida a derivada covariante de um vetor, onde esta quantifica algo que est´a variando. Mas variando em rela¸c˜ao a que? A derivada covariante quantifica a taxa instatˆanea com a qual um vetor varia quando se move esse vetor de um ponto a outro do espa¸co em rela¸c˜ao a uma configura¸c˜ao na qual este vetor fosse mantido constante. Esse conceito de mover um vetor ao longo de uma curva, mantendo-o constante ao longo desta curva ´e conhecido na literatura como sendo o transporte paralelo de um vetor ao longo de uma curva [33]. Dessa forma, a derivada covariante de um vetor quantifica a taxa com a qual um vetor varia em rela¸c˜ao ao que este vetor seria transportado paralelamente.
Pode-se definir o transporte paralelo de um vetor V =Vνeˆ
ν ao longo de uma curva
xµ(γ) pelo requerimento que a derivada covariante deste vetor ao longo desta curva seja nula, isto ´e,
∂µVν + ΓνµαVα = 0. (1.37)
Com o conceito de transporte paralelo pode-se definir uma transforma¸c˜ao unit´aria chamada deholonomia. Considerando-se que n˜ao haja a presen¸ca de tor¸c˜ao para facilitar nossa discuss˜ao, holonomia ´e uma transforma¸c˜ao unit´aria aplicada sobre um vetor que descreve o transporte paralelo de um vetor ao longo de uma curva fechada. A express˜ao para a holonomia ´e obtida atrav´es do chamado propagador paralelo. O propagador par-alelo Pµ
ν(γ, γ0) ´e uma matriz que relaciona as componentes de um vetor em seu valor inicial Vµ(γ
0) com seu valor ap´os ser transportado ao longo de uma curvaγ:
Vµ(γ) =Pµν(γ, γ0) Vν(γ0), (1.38) onde a matriz Pµ
ν(γ, γ0) depende do caminho γ. Definindo-se
Aµν(γ) ={ναµ} dx α
dγ , (1.39)
pode-se reescrever a equa¸c˜ao (1.37) para o transporte paralelo de um vetor como
d dγ V
µ = dxα
dγ ∂αV
µ =Aµ
νVν. (1.40)
Desde que o propagador paralelo deve atuar sobre qualquer vetor, substituindo (1.38) em (1.40) tem-se
d dγ P
µ
Para resolver a equa¸c˜ao (1.41), deve-se primeiro integrar em ambos os lados para obter
Pµν(γ, γ0) = δµν +
Z γ
γ0
Aµβ(η) Pβν(η, γ0) dη, (1.42) ent˜ao, aplicando o m´etodo de intera¸c˜ao (onde tomamos o lado direito da equa¸c˜ao (1.42) e aplicamos diversas vezes) ou usando o mesmo procedimento da s´erie de Dyson [33], ´e obtida a seguinte express˜ao para o propagador paralelo6
Pµν(γ, γ0) =P exp
−
Z γ
γ0
Aµνdxν
, (1.43)
onde se pode ver claramente atrav´es das express˜oes (1.39) e (1.43) que a conex˜ao afim ´e que define uma maneira espec´ıfica de manter o vetor constante quando este ´e transportado de um ponto a outro numa curva, seja esta curva aberta ou fechada. Quando γ =γ0, ou seja, quando se tem uma curva fechada, a transforma¸c˜ao unit´aria (1.43) ´e chamada de holonomia.
Um outro ponto que se deve enfatizar ´e que quando o transporte paralelo de um vetor ´e realizado ao longo de uma curva, cuja express˜ao ´e
∂µVν +
ν
µα Vα = 0, (1.44)
tem-se uma curva chamadageod´esica7. A express˜ao para uma geod´esica ´e dada da seguinte forma
d2xµ
dτ2 +
ν
µβ
dxν
dτ dxβ
dτ = 0. (1.45)
Uma caracter´ıstica importante provinda do transporte paralelo de vetores surge quando dois vetores X e Y s˜ao transportados paralelamente ao longo de uma curva γ. Quando isso acontece tem-se que o produto interno entre esses dois vetores permanece constante ao longo do transporte paralelo, ou seja,
d
dγ (gµνX
µYν) =
d dγgµν
XµYν +gµν
d dγX
µ
Yν +gµνXµ
d dγY
ν
= 0, (1.46) onde foi usada a regra de Leibniz e considerado que d
dγ = dxα
dγ ∂α.
Tendo-se as defini¸c˜oes de derivada covariante e transporte paralelo vamos, ent˜ao, dis-cutir a curvatura. A curvatura ´e quantificada pelo tensor de Riemann, que depende da conex˜ao afim. Para obtermos a express˜ao para o tensor de Riemann iremos observar o transporte paralelo de um vetor V =V µeˆµ ao longo da dire¸c˜ao de um vetor A= Aµeˆµ, em seguida na dire¸c˜ao de um vetor B = Bµˆeµ, voltando ent˜ao ao longo da dire¸c˜ao de
A=Aµˆe
µ e B =Bµeˆµ para retornar ao ponto inicial, como mostra a figura 1.6.
6
N˜ao iremos mostrar cada passo para se obter a express˜ao para o propagador paralelo para n˜ao deixar
essa se¸c˜ao muito extensa. Para maiores detalhase sobre a obten¸c˜ao do propagador paralelo ver apˆendice
I da referˆencia [33].
7
Quando ´e considerada a presen¸ca da tor¸c˜ao, a curva gerada pela aplica¸c˜ao da derivada covariante
sobre o tensor m´etrico quando a conex˜ao ´e compat´ıvel com a m´etrica n˜ao ´e mais chamada de geod´esica,
Figura 1.6: Transporte paralelo de um vetorV ao longo das dire¸c˜oes de vetoresAeB e retornando a sua posi¸c˜ao inicial. Tem-se que ao retornar a posi¸c˜ao inicial o vetorV varia em rela¸c˜ao a sua configura¸c˜ao inicial emδV.
Dessa forma, ao ser transportado paralelamente ao longo das dire¸c˜oes dos vetoresA e
B e retornado ao ponto inicial, o vetor V varia em rela¸c˜ao a sua configura¸c˜ao dada por
δ Vµ =RµναβVνAαBβ, (1.47)
onde Rµναβ ´e conhecido na Literatura como tensor de Riemann ou tensor de curvatura [33] e possui a propriedade de antisimetria em seus dois ´ultimos ´ındices
Rµναβ =−Rµνβα. (1.48)
Para se obter a express˜ao para o tensor de Riemann, deve-se observar que a forma com que o vetor V varia em rela¸c˜ao a sua configura¸c˜ao inicial ´e dada pela derivada covariante deV em uma dada dire¸c˜ao. Desde que a derivada covariante de um vetor mede o quanto um vetor varia em rela¸c˜ao ao que este seria transportado paralelamente, pode-se calcular
δV atrav´es da diferen¸ca entre o transporte paralelo de V nas dire¸c˜oes de A e B e no retorno a sua posi¸c˜ao inicial. Essa diferen¸ca entre o transporte paralelo deV nas dire¸c˜oes deAeB e seu retorno ´e a defini¸c˜ao do operadorcomutador de duas derivadas covariantes, isto ´e,
[∇µ,∇ν]Vρ = ∇µ∇νVρ− ∇ν∇µVρ
(1.49) = ∂µΓρνβ −∂νΓρµβ+ Γ
ρ
µλΓλνβ −Γ ρ νλΓλµβ
Vβ −2Γλ[µλ]∇λVρ,
onde a express˜ao para o comutador de duas derivadas covariantes pode ser escrita em termos do tensor de Riemann e do tensor de tor¸c˜ao, ou seja,
[∇µ,∇ν]Vρ =RρλµνVλ−Tλµν∇λVρ (1.50) Dessa maneira, comparando as express˜oes (1.49) e (1.38), o tensor de Riemann deve ser escrito em rela¸c˜ao as conex˜oes afim, ou seja,
Rρλµν =∂µΓρνβ−∂νΓρµβ+ Γ ρ
µλΓλνβ−Γ ρ
νλΓλµβ. (1.51)
Figura 1.7: Representa¸c˜ao do operador comutador de duas derivadas covariantes.
tensor m´etrico. Com essa aproxima¸c˜ao linear Katanaev e Volovich desenvolveram uma formula¸c˜ao para descrever os defeitos topol´ogicos, no limite do cont´ınuo, atrav´es da ge-ometria diferencial. Na formula¸c˜ao de Katanaev e Volovich, os os defeitos topol´ogicos s˜ao produzidos por dois tipos de fonte: os defeitos gerados pela curvatura do espa¸co-tempo tem como fonte o tensor energia-momento e s˜ao chamados de desclina¸c˜oes enquanto que os defeitos gerados pela presen¸ca de tor¸c˜ao no espa¸co-tempo tem o momento angular de spin (cl´assico) como fonte e s˜ao chamados de desloca¸c˜oes. Portanto, para se obter o tensor m´etrico que corresponde a uma desloca¸c˜ao ou a uma desclina¸c˜ao ou ainda para a ocorrˆencia de ambas e que satisfa¸ca as equa¸c˜oes (1.13) e (1.19), quatro hip´oteses foram estabelecidas por Katanaev e Volovich [37] para resolver as equa¸c˜oes de Einstein e obter o tensor m´etrico
• Existem solu¸c˜oes que descrevem um meio com desloca¸c˜oes apenas, onde Rρλµν = 0 e Tρ
µν 6= 0.
• Existem solu¸c˜oes que descrevem um meio com desclina¸c˜oes apenas, onde Rρλµν 6= 0 e Tρ
µν = 0.
• Existem solu¸c˜oes que descrevem um meio sem desloca¸c˜oes e sem desclina¸c˜oes, ou seja, Rρλµν = 0 e Tρ
µν = 0.
• Existem solu¸c˜oes que descrevem um meio tanto com desloca¸c˜oes quanto desclina¸c˜oes, ou seja, Rρλµν 6= 0 e Tρ
µν 6= 0.
Assim, usando o princ´ıpio da m´ınima a¸c˜ao, esta formula¸c˜ao pode ser sintetizada atrav´es da a¸c˜ao de Einstein-Hilbert, onde a densidade Lagrangeana ´e dada por [37]
L =−κ
Z
ao longo de nosso trabalho. Na pr´oxima se¸c˜ao trabalharemos o restante das ferramentas matem´aticas junto com a defini¸c˜ao de referenciais locais.
1.3
Os Refereciais Locais
A necessidade de construirmos referenciais locais vem do fato que a defini¸c˜ao de part´ıcula no espa¸co-tempo curvo n˜ao ser un´ıvoca, por exemplo, um observador que es-teja em queda livre pode medir um n´umero de part´ıculas diferentes de outro observador que esteja acelerado [35]. Com isso, torna-se conveniente escolher um estado de v´acuo do qual o conceito de part´ıcula seja global em todo o espa¸co-tempo. Assim, a escolha natural para se definir o estado de v´acuo ´e o estado de v´acuo definido no espa¸co-tempo de Minkowisky, onde este estado de v´acuo ´e invariante dentro de grupo de Poincar´e e onde todos os observadores est˜ao localizados em referenciais inerciais. Dessa forma, a ausˆencia de part´ıcula para um observador implica na ausˆencia de part´ıcula para todos os outros e cada part´ıcula registrada por um observador inercial ´e definida como modos desse estado de v´acuo.
Para definir o spin no espa¸co-tempo curvo, recorre-se aos conceitos de teoria de cam-pos no espa¸co-tempo de Minkowisky, onde o spin ´e classificado de acordo com as trans-forma¸c˜oes infinitesimais de Lorentz
xa→x¯a = Λabxb = (δba+̟ab) xb, (1.53) onde ̟ab =−̟ba e |̟ab|<<1. No espa¸co-tempo curvo, as transforma¸c˜oes infinitesimais de Lorentz dependem do ponto onde s˜ao aplicadas Λa
b → Λab(x) e para n˜ao se peder a conex˜ao com o grupo de Poincar´e ou apenas com o grupo de Lorentz, as part´ıculas com spin devem ser definidas em cada ponto do espa¸co-tempo de modo que os observadores estejam localizados em referenciais inerciais.
Iremos ent˜ao descrever as leis da f´ısica da natureza na relatividade geral obedencendo o Princ´ıpio da Equivalˆencia. Com o Princ´ıpio da Equivalˆencia pode-se construir referenciais locais que s˜ao inerciais e onde estes se tranformam perante transforma¸c˜oes de Lorentz locais. Pode-se enunciar o Princ´ıpio da Equivalˆenica da seguinte forma [29, 31, 32, 33]
“Em todo ponto do espa¸co-tempo dentro de um campo gravitacional arbitr´ario ´e poss´ıvel escolher um sistema de coordenadas inercial local tal que, dentro de uma regi˜ao suficiente-mente pequena em torno do ponto em quest˜ao, as leis da natureza tomam a mesma forma como num sistema de coordenadas cartesiano desacelerado na ausˆencia da gravita¸c˜ao.”
O Princ´ıpio da Equivalˆencia estabelece que em qualquer ponto do espa¸co-tempo pode-se ter um sistema de coordenadas inercial local que satisfa¸ca as leis da relatividade especial. Dessa forma, considera-se uma part´ıcula que se move livremente dentro da influˆencia de for¸cas gravitacionais. De acordo com o Princ´ıpio da Equivalˆencia [29, 31, 32, 33] h´a um sistema de coordenadas em queda livre {ξa} cuja equa¸c˜ao de movimento ´e:
d2ξa
com dτ sendo o tempo pr´oprio da part´ıcula
dτ2 = −1
c2 ηabdξ
adξb. (1.55)
Nesse sistema de coordenadas em queda livre, o objetoηab´e definido como sendo o tensor m´etrico do espa¸co-tempo de Minkowisky.
Agora, suponha-se que ´e adotados um outro sistema de coordenadas qualquer {xµ}, este pode ser um sistema de coordenadas cartesiano no repouso do laborat´orio ou pode ser curvil´ıneo, ou acelerado, ou rotacionado, ou um outro qualquer desejado. As coordenadas em queda livre {ξa} s˜ao fun¸c˜oes de xµ e a equa¸c˜ao (1.54) torna-se:
d2ξa
dτ2 =
d dτ ∂ξa ∂xµ dxµ dτ = d dτ ∂ξa ∂xµ dxµ dτ + ∂ξa ∂xµ
d2xµ
dτ2
= ∂ξ a
∂xµ
d2xµ dτ2 +
∂ξa ∂xν∂xµ
dxµ dτ
dxν
dτ = 0. (1.56)
Multiplicando-se a equa¸c˜ao (1.56) por ∂xλ
∂ξa e levando-se em conta que
∂ξa
∂xµ
∂xλ
∂ξa =δ λ
µ⇒
d2xλ
dτ2 + Γ λ
νµ
dxµ
dτ dxν
dτ = 0, (1.57)
onde Γλ
νµ≡ ∂x λ ∂ξa
∂2ξa
∂xν∂xµ ´e a conex˜ao afim. O tempo pr´oprio dado em (1.55) pode tamb´em ser expressado em um sistema de coordenadas arbitr´ario:
dτ2 = −1
c2 gµνdx
µdxν, (1.58)
que pela equa¸c˜ao (1.55) resulta em
dτ2 = −1
c2 ηab
∂ξa
∂xµdx µ ∂ξb
∂xν dx
ν = −1
c2
∂ξa
∂xµ
∂ξb
∂xν ηabdx
µdxν. (1.59) Igualando-se (1.58) com (1.59), encontra-se uma rela¸c˜ao entre o sistema de coordenadas arbitr´ario e o referencial local em queda livre
gµν =
∂ξa
∂xµ
∂ξb
∂xν ηab, (1.60)
ou seja, pode-se escrever o tensor m´etrico dado para um sistema de coordenadas arbitr´ario em rela¸c˜ao um sistema de coordenadas locais que est´a em queda livre8.
Vamos, ent˜ao, estender nossa defini¸c˜ao de referencial local tomando um ponto qualquer do espa¸co-tempo e um certo sistema de coordenadas. Na vizinhan¸ca de um ponto X
num sistema de coordenadas arbitr´ario xµ temos que as coordenadas locais tornam-se
ξa→ξa(X). Ent˜ao, a rela¸c˜ao (1.60) fica:
gµν(X) =
∂ξa(X)
∂xµ
∂ξb(X)
∂xν ηab. (1.61)
8
Contudo, ´e poss´ıvel estender a rela¸c˜ao (1.60) para um sistema de coordenadas locais que n˜ao seja
inercial. Para isso basta que esse sistema continue obedecendo o Princ´ıpio da Equivalˆencia. No quinto
Portanto, se em todo ponto X tem-se um conjunto de coordenadas ξa(X) = ξa X que s˜ao locais em X e obedecem o Princ´ıpio da Equivalˆencia, o tensor m´etrico em qualquer sistema de coordenadas geral pode ser escrito em rela¸c˜ao ao sistema de coordenadas locais como
gµν(x) =eaµ(x)ebν(x)ηab, (1.62) onde
eaµ(X)≡
∂ξa X(x)
∂xµ
x=X
, (1.63)
s˜ao objetos que definem em cada ponto do espa¸co-tempo um referencial local. Note-se que foram fixadas as coordenadas inerciais locais ξa
X no ponto X, ent˜ao quando se muda as coordenadas gerais de xµ para x′µ, as derivadas parciais ∂ξaX(x)
∂xµ = eaµ(x) mudam de acordo com a regra:
ea
µ→e′aµ(x) =
∂ξa X(x)
∂xν
∂xν
∂x′µ =
∂xν
∂x′µ e a
ν(x), (1.64)
isto ´e, observa-se que os referenciais locais ea
ν(x) transformam-se como um vetor covari-ante e n˜ao como um tensor.
Tomada essa no¸c˜ao e defini¸c˜ao dos referenciais locais a partir do Princ´ıpio da Equivalˆencia, pode-se dar agora uma defini¸c˜ao em termos de uma base vetorial. Os refenciais lo-cais s˜ao constru´ıdos a partir dos elementos de uma base ortonormal n˜ao-coordenada [29, 30, 31, 32, 33, 35, 36]
ˆ
θa =eaµ(x) dxµ, (1.65)
cujos elementos ea
µ(x) definem os referenciais locais quando satisfazem a rela¸c˜ao (1.62) e s˜ao conhecidas com tetradas ou vierbein. As tetradas possuem uma inversa que satisfaz as seguintes rela¸c˜oes
eµ
a(x) eaν(x) =δµν; eaµ(x) e µ
b(x) = δab. (1.66) Portanto, com a defini¸c˜ao dos referenciais locais e sua inversa, iremos estabelecer que os ´ındices latinos indicar˜ao as componentes de vetores ou tensores nos referenciais locais enquanto que os ´ındices gregos indicar˜ao as componentes de vetores ou tensores num sistema de coordenadas geral, ou melhor, do espa¸co-tempo. Iremos utilizar essa nota¸c˜ao em todo o nosso trabalho.
Qualquer vetor ou tensor pode ser escrito em termos dos elementos da base n˜ao-coordenada (1.65). Por exemplo, vamos tomar as seguintes componentes de tensores9
Tµν =eµaeaνTab; Tab =eaµeνbTµν. (1.67) Vˆe-se, com a express˜ao (1.64), que os referenciais locais transformam-se como vetores. Qualquer mudan¸ca de base dever´a ser realizada da forma
ˆ
θa →θˆa′ = Λaa′(x) ˆθa, (1.68)
9
onde as matrizes Λa′
a(x) representam transforma¸c˜oes que dependem de cada ponto do espa¸co-tempo e deixam a forma canˆonica da m´etrica inalterada, ou seja,
ηa′b′Λaa′(x) Λbb′(x) = ηab. (1.69) Essas matrizes com ´ındices latinos promovem as chamadasTranforma¸c˜oes de Lorentz Lo-cais, enquanto que matrizes Λ com ´ındices gregos indicamTransfoma¸c˜oes de Coordenadas no espa¸co-tempo. Pode-se exemplificar as transforma¸c˜oes de Lorentz locais com
Ta′µ′b′ν′ = Λa ′
a
∂xµ′ ∂xµ Λ
b b′
∂xν
∂xν′ T
aµ
bν. (1.70)
Tendo-se a lei de transforma¸c˜ao em m˜aos, torna-se poss´ıvel definir a derivada covariante dos referenciais locais. Para uma base n˜ao-coordenada ˆθa, defini-se as componentes da conex˜ao um-forma como sendo ωa
b =ωµ ba dxµ como
∇µθˆb =ωµ ba θˆa. (1.71)
Ap´os alguns c´alculos, pode-se escrever a derivada covariante das componentes de um vetor dado no referencial local como
∇µVa=∂µVa+ωµ ab Vb. (1.72) Dessa forma, para um tensor podemos escrever a derivada covariante de suas componentes no referencial local como
∇µTab =∂µTab+Tcbωµ ca −Tacωµ bc . (1.73) Assim, tomando-se a express˜ao para a derivada covariante de um vetor num sistema de coordenadas geral, ou melhor, com ´ındices do espa¸co-tempo, e a express˜ao para a derivada covariante no refencial local (1.72) podemos obter a express˜ao para as componentes da conex˜ao um-forma em fun¸c˜ao das tetradas e das conex˜oes afins, ou seja,
ωµ ba (x) = −eνb∇µeaν =−eνb ∂µeaν −Γλµνeaλ
. (1.74)
Em geral essa express˜ao ´e muito boa para calcularmos as componentes das conex˜oes um-forma (1.74) quando se tem um espa¸co-tempo curvo sem tor¸c˜ao. Na ausˆencica de tor¸c˜ao, as conex˜oes afins Γλ
µν tornam-se os s´ımbolos de Christoffel que s˜ao facilmente cal-culados via equa¸c˜ao (1.32). Contudo, na presen¸ca de torc¸c˜ao, a express˜ao para a conex˜ao afim torna-se idˆentica a (1.31). Nessa situa¸c˜ao torna-se melhor calcular as conex˜oes um-forma bem como as componentes do tensor de tor¸c˜ao via equa¸c˜ao de estrutura de Maurer-Cartan [30, 36]
Ta =dθˆa+ωab∧θˆb, (1.75) onde o operador d indica a derivada exterior, o s´ımbolo ∧ indica o wedge product10,
Ta = Ta
µνdxµ∧dxν ´e chamada de tor¸c˜ao duas-forma e ωab = ωµ ba dxµ ´e uma conex˜ao um-forma. No geral, o termo ω a
µ b ´e chamado de conex˜ao de spin ou conex˜ao um-forma.
10
Owedge productentre duas um-formas ´e dado pordxµ
∧dxν =1 2(dx
µ
⊗dxν
−dxν