Análise de Sistemas no Domínio da Frequência
Introdução
O objetivo deste laboratório é familiarizar o aluno com a representação de sistemas no domínio da freqüência através da transformada de Laplace para a análise de sistemas no domínio do tempo contínuo.
Leitura - Bibliografia: Lathi - Capítulo 4.
Teorema da Derivação Real
A transformada de Laplace da derivada de uma função f(t) é dada por:
)
0
(
)
(
.
)
(
t
s
F
s
f
f
dt
d
L
onde f(0) é o valor inicial de f(t) calculado em t=0.
A generalização do teorema para o caso de derivada de ordem n de f(t), é obtida de modo similar e é dada pela seguinte equação:
1 2 2
1
)
0
(
)
0
(
.
....
)
0
(
.
)
0
(
.
)
(
.
)
(
n nn n
n n
f
f
s
f
s
f
s
s
F
s
t
f
dt
d
L
onde
1 2
)
0
(
),
0
(
),...,
0
(
),
0
(
n n
f
f
f
f
são as derivadas temporais sucessivas de f(t) avaliadas em t=0. Observe que as derivadas temporais são substituídas pelo operador ‘s’:dt
d
s
Da mesma forma que se estabelece equivalência entre domínios para operação de derivação, existe
também uma equivalência entre os domínios tempo e ‘s’ para operação de integração:
t
dt
s
01
.
Na transformada de Laplace, a notação ‘s’ refere-se a uma variável complexa:
s
j
.Exemplo 1:
- Saída: y(t)
- Condições iniciais:
posição inicial:
y
(
0
)
1
, velocidade inicial:y
(
0
)
0
, - Equação diferencial:
F
0
0
.
.
.
y
b
y
k
y
m
- Transformada de Laplace:
k
s
b
s
m
b
s
m
s
Y
s
s
Y
k
s
b
s
m
s
Y
k
y
s
Y
s
b
y
y
s
s
Y
s
m
.
.
.
)
(
1
)
(
).
.
.
(
0
)
(
.
)
0
(
)
(
.
.
)
0
(
)
0
(
.
)
(
.
.
2 2
2
Sinais e suas Transformadas de Laplace
Vimos que através do Teorema da Derivação Real, realizamos a transformação para o domínio s das equações diferenciais. No exemplo, foi mostrada a transformação de uma equação diferencial de um sistema dinâmico. Porém, note que o sistema não possuia nenhum sinal excitando o sistema. No exemplo, modelamos o sistema sem considerar força externa atuando sobre o sistema. Somente foi considerado um deslocamento inicial na direção da coordenada y.
Se por acaso, alguma força externa estivesse atuando sobre o sistema, este sinal seria considerado no somatório das forças. Sendo assim, necessitaríamos realizar a transformada de Laplace do sinal de excitação do sistema.
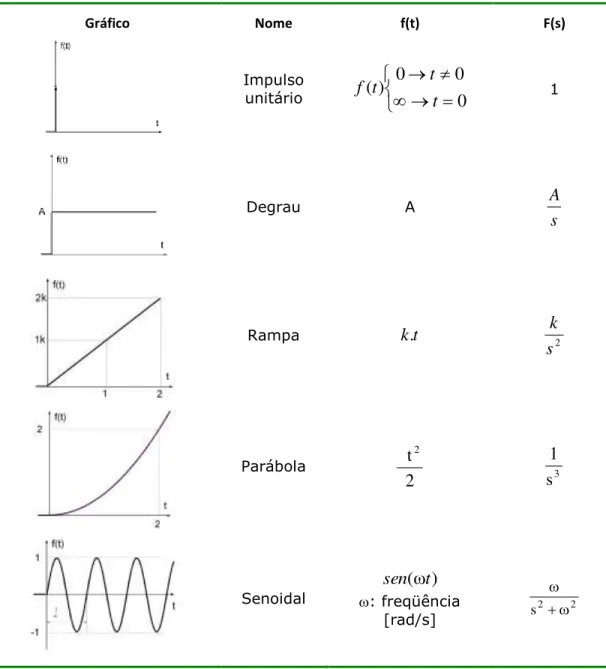
A seguir, é mostrado uma tabela com os sinais de entrada mais utilizados em sistemas físicos, relacionando com sua função temporal e a transformada de Laplace.
Gráfico Nome f(t) F(s)
Impulso
unitário
0
0
0
)
(
t
t
t
f
1Degrau A
s
A
Rampa
k
.
t
2s
k
Parábola
2
t
23
s
1
Senoidal
)
ω
(
t
sen
: freqüência [rad/s]
2 2
s
Exemplo 2:
- Entrada : Força constante de amplitude 10 N. u(t)=10
s
t
u
L
s
U
(
)
(
)
10
- Saída: y(t)
- Condições iniciais nulas:- Equação diferencial:
F
0
)
(
.
.
.
y
b
y
k
y
u
t
m
- Transformada de Laplace:
m
s
b
s
k
s
s
Y
s
s
Y
k
s
b
s
m
s
s
U
s
Y
k
s
Y
s
b
s
Y
s
m
.
.
1
.
10
)
(
10
)
(
).
.
.
(
10
)
(
)
(
.
)
(
.
.
)
(
.
.
2 2
2
Para encontrar y(t), deve-se determinar a Transformada Inversa de Laplace.
Transformadas de algumas funções
A transformada de Laplace de qualquer função transformável f(t) pode ser encontrada pela multiplicação de f(t) por
e
st e integrar o produto a partir det
0
atét
. A tabela abaixo mostra transformadas de algumas funções.f(t) para t0 F(s) f(t) para t0 F(s)
A
s
A
n ate
t
n
. 1
.
)!
1
(
1
na
s
)
(
1
t 12
s
t a n
e
t
.
. 1)
(
!
na
s
n
)!
1
(
1
n
t
nn
s
1
)
.
(
t
sen
2 2
s
n
t
1!
n
s
n
)
.
cos(
t
2 2
s
s
t a
e
.a
s
1
)
.
(
t
sen
e
at
2 2
)
(
a
s
t a
e
t
.
. 2)
(
1
a
s
e
cos(
.
t
)
at
2 2
) (
) (
a s
a s
Transformada Inversa de Laplace
A transformada inversa de Laplace possibilita encontrar a função temporal de uma reposta dinâmica de um sistema modelado no domínio complexo ‘s’. Alguns métodos podem ser aplicados na inversão da
função no domínio complexo para o domínio tempo. Os métodos mais simples baseiam-se na análise de tabelas de transformações. Porém, dependendo do grau da função F(s), requer-se fracioná-la, de maneira que a função total, por vezes de difícil solução, seja quebrada em parcelas com inversas mais simples. Esse método denomina-se Expansão por Frações Parciais.
)
(
...
)
(
)
(
)
(
)
(
s
F
1s
F
2s
F
3s
F
s
F
n
(
)
(
)
(
)
(
)
....
(
)
)
(
1 3 1 2 1 1 1 1s
F
L
s
F
L
s
F
L
s
F
L
s
F
L
t
f
n
)
(
...
)
(
)
(
)
(
)
(
t
f
1t
f
2t
f
3t
f
t
f
nExpansão por Frações parciais
O método de frações parciais de um sistema linear invariante no tempo, usando diretamente o sinal de
saída no domínio ‘s’, baseia-se no tipo de raízes do denominador da função. Dependendo das raízes, podem-se ter três métodos diferentes de obtenção da resposta temporal.
Serão mostrados os três métodos utilizando o exemplo 1 visto anteriormente.
- Saída: y(t)
- Condições iniciais:
posição inicial:
y
(
0
)
1
, velocidade inicial:y
(
0
)
0
, - Equação diferencial:
F
0
0
.
.
.
y
b
y
k
y
m
- Transformada de Laplace:
k
s
b
s
m
b
s
m
s
Y
s
s
Y
k
s
b
s
m
s
Y
k
y
s
Y
s
b
y
y
s
s
Y
s
m
.
.
.
)
(
1
)
(
).
.
.
(
0
)
(
.
)
0
(
)
(
.
.
)
0
(
)
0
(
.
)
(
.
.
2 2 2
1º. Caso : Função com raízes do denominador reais e distintas
Se m=1kg , b=52 N.s/m , k= 100 N.m , o sistema massa, mola, amortecedor apresentará uma resposta de saída dada pela seguinte equação:
100
.
52
)
50
.(
)
2
.(
2
50
100
.
52
52
)
(
22
s
s
s
B
s
A
s
B
s
A
s
s
s
s
Y
Determinando A e B, pode-se reescrever Y(s) como uma soma de duas frações. Assim para determinar A e B, substitui-se as raízes do denominador no numerador de Y(s) como mostrado abaixo:
)
50
.(
)
2
.(
52
A
s
B
s
s
2
04
,
1
50
1
.
04
,
0
)
(
s
s
s
Y
2
04
,
1
50
1
.
04
,
0
)
(
1 1s
L
s
L
t
y
t t
e
e
t
y
(
)
0
,
04
.
50.
1
,
04
2.Note que duas raízes reais geraram duas frações com inversas dadas por funções exponenciais.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Tempo [s]
y
(t
)
Tarefa 1 -Fração Parcial - raízes distintas
No MATLAB:
num = [1 52]; den = [1 52 100];
[R,P,K] = residue(num,den)
2º. Caso : Função com raízes do denominador reais iguais
Diminuindo o amortecedor, se m=1kg , b=20 N.s/m , k= 100 N.m , o sistema massa, mola, amortecedor apresentará uma resposta de saída dada pela seguinte equação:
100
.
20
)
10
.(
10
)
10
(
100
.
20
20
)
(
2 2
2
s
s
s
B
A
s
B
s
A
s
s
s
s
Y
Determinando A e B, pode-se reescrever Y(s) como uma soma de duas frações. Assim para determinar A, substitui-se a raiz do denominador no numerador de Y(s) como mostrado abaixo:
)
10
.(
20
A
B
s
s
Se
s
10
,s
20
A
B
.(
s
10
)
s10,A
10
Para determinar B, pode-se substituir qualquer valor de s na função, ou derivar a equação no seguinte formato:
10
)
10
.(
)
20
(
s
s
B
A
ds
d
s
ds
d
)
10
(
1
)
10
(
1
.
10
)
(
2
s
s
s
Y
)
10
(
1
)
10
(
1
.
10
)
(
1 2 1s
L
s
L
t
y
t te
e
t
t
y
(
)
10
.
.
10.
10.Note que duas raízes reais iguais apresentam a mesma exponencial, porém, um possui o termo t multiplicando a exponencial.
0 0.5 1 1.5
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 tempo [s] y (t )
Tarefa 2 - Fração Parcial – raízes múltiplas
Reproduzir o resultado acima utilizando os comandos do MATLAB vistos anteriormente. (ATENÇÃO: para operações de produto entre matrizes utilizar “.*”)
3º. Caso : Função com denominador com raízes complexas
Se m=1kg , b=12 N.s/m , k= 100 N.m , o sistema massa, mola, amortecedor apresentará uma resposta de saída dada pela seguinte equação:
2 2 2
8
)
6
(
.
)
8
6
)(
8
6
(
.
100
.
12
12
)
(
s
B
s
A
i
s
i
s
B
s
A
s
s
s
s
Y
Determinando A e B, pode-se reescrever Y(s) como uma soma de duas frações. Assim para determinar A e B, compara-se o termo s e o termo independente do numerador.
B
s
A
s
12
.
A
1
eB
12
2 2 2 2 2 2 8 ) 6 ( 8 . 75 . 0 8 ) 6 ( 6 8 ) 6 ( 12 ) ( s s s s s s Y
2 2 1 2 2 18
)
6
(
8
.
75
.
0
8
)
6
(
6
)
(
s
L
s
s
L
t
y
)
8
(
.
75
.
0
)
8
cos(
)
(
t
e
6.t
e
6.sen
t
y
t
tNote que as raízes complexas geram exponenciais com termos senoidais.
0 0.5 1 1.5
-0.2 0 0.2 0.4 0.6 0.8 1 1.2 y (t ) tempo [s]
Tarefa 3 - Fração Parcial – raízes complexas
Representação de Sistemas no Simulink
Os sistemas descritos através da transformada de Laplace podem ser representados através de blocos. Os diagramas de blocos facilitam a representação de sistemas com um grande número de equações
diferenciais, uma vez que podem ser simplificados ou arranjados de maneira organizada.
O sistema massa mola amortecedor do exemplo 2 é representado no MATLAB por blocos através da ferramenta Simulink.
No matlab digitesimulinkou utilize o atalho no programa.
Tarefa 4 - Simulink
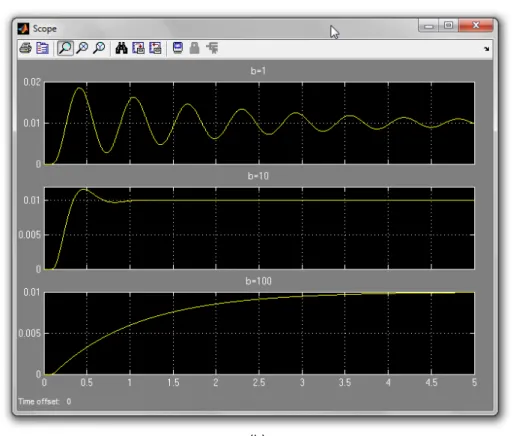
Monte o sistema abaixo utilizando as ferramentas de blocos do Simulink e simule o sistema do exemplo 2 para os valores de massa = 1, mola = 100 e variando o valor do amortecedor em b=1; 10; 100. Como sinal de entrada utilize um degrau de amplitude 1. Plote os 3 sistemas simultaneamente para observar o efeito do amortecimento no sistema. Apresente o resultado obtido para o professor.
(b)