UNIVERSIDADE FEDERAL DE OURO PRETO
Leandro Ribeiro Galvão
DISCRETIZADOR HEURÍSTICO PARA O
CONTEXTO DE CLASSIFICAÇÃO HIERÁRQUICA
Ouro Preto
UNIVERSIDADE FEDERAL DE OURO PRETO
Leandro Ribeiro Galvão
DISCRETIZADOR HEURÍSTICO PARA O
CONTEXTO DE CLASSIFICAÇÃO HIERÁRQUICA
Dissertação de Mestrado submetida ao Pro-grama de Pós-Graduação em Ciência da Computação da Universidade Federal de Ouro Preto como requisito parcial para a ob-tenção do título de Mestre.
Orientador:
Prof. Dr. Luiz Henrique de Campos Merschmann
Ouro Preto
Catalogação: www.sisbin.ufop.br
G182d Galvão, Leandro Ribeiro.
Discretizador heurístico para o contexto de classificação hierárquica [manuscrito] / Leandro Ribeiro Galvão. - 2016.
54f.: il.: grafs; tabs.
Orientador: Prof. Dr. Luiz Henrique de Campos Merschmann.
Dissertação (Mestrado) - Universidade Federal de Ouro Preto. Instituto de Ciências Exatas e Biológicas. Departamento de Computação. Ciência da Computação.
1. Distribuição (Probabilidades). 2. Classificação (Computadores). 3. Programação heurística. I. Merschmann, Luiz Henrique de Campos. II. Universidade Federal de Ouro Preto. III. Titulo.
Dedico este trabalho à minha mãe, que fez o possível e algumas vezes o que muitos pensavam
ser impossível para que eu pudesse realizar os meus sonhos. Dedico este trabalho também ao
Agradecimentos
Resumo
Diferentes tipos de problemas de classificação podem ser encontrados na literatura, cada qual possuindo seu nível de complexidade. Diversos algoritmos de aprendizado de má-quina requerem atributos discretos e nesses casos o pré-processamento da base de dados é necessário. Na literatura, os trabalhos apresentam diversos métodos de discretização, porém até o momento, não há nenhum método de discretização supervisionado projetado para ser utilizada em conjunto com classificadores hierárquicos globais.
Neste trabalho é proposto um método supervisionado de discretização capaz de lidar com bases do contexto de classificação hierárquica. Esse método corresponde a uma heu-rística, denominadaAgglomerative Discretization Heuristic for Hierarchical Classification - ADH2C, que foi projetada para ser utilizada em conjunto com classificadores hierárqui-cos globais.
A avaliação da qualidade da discretização realizada pela heurística ADH2C foi feita a partir de experimentos comparativos com métodos de discretização não-supervisionados Equal-Width (EW) eEqual-Frequency (EF). A qualidade da discretização foi medida por
meio do desempenho preditivo pelo classificador hierárquico Global Model Naive Bayes
(GMNB) utilizando-se 9 bases de dados de bioinformática pré-processadas pelos métodos de discretização EW, EF e ADH2C.
Os experimentos realizados neste trabalho mostraram que para a maioria das bases de dados utilizadas, o classificador GMNB alcançou o melhor desempenho preditivo (hF) quando utilizou as bases de dados pré-processadas pela heurística ADH2C. A melhora no desempenho preditivo do GMNB, utilizando as bases de dados pré-processadas pela heurística ADH2C, evidencia sua aplicabilidade no contexto de classificação hierárquica monorrótulo.
Abstract
Several classification tasks in different application domains can be seen as hierarchical classification problems. Many machine learning algorithms require discrete data. Then, it is mandatory the use of a discretization method. In order to be used together with global hierarchical methods, the use of the existing supervised flat discretization methods is not appropriate. For this reason, there has been used unsupervised discretization methods which ignores the class attribute.
In this work, we propose a supervised discretization method for hierarchical classifi-cation scenario. The proposed heuristic, known asAgglomerative Discretization Heuristic for Hierarchical Classification - ADH2C, is able to deal with hierarchical class structure and can be used with global hierarchical classifiers.
Experimental evaluation is performed through the preprocessing of 9 bioinformatics datasets. The hierarchical classification method Global Model Naive Bayes - GMNB, was adopted to measure the quality of the discretization. As far as we known, there is no supervised discretization method able to be used with hierarchical classification methods. Due to it, as baseline methods for experimental comparison, we adopted the unsupervised methods Equal-Frequency and Equal-Width.
Analyses of the experimental results showed that, for most of datasets, the GMNB classifier achieved higher predictive performance when they were preprocessed using ADH2C method. The proposed supervised discretization method has shown good performance in the hierarchical classification scenario and, therefore, can be used together with global hierarchical classification methods.
Sumário
Lista de Figuras ix
Lista de Tabelas x
1 Introdução 1
2 Discretização de Atributos 4
2.1 Equal-Width e Equal-Frequency . . . 6
3 Classificação Hierárquica 8 3.1 Abordagem por Classificação Plana . . . 9
3.2 Abordagem Local . . . 10
3.2.1 Abordagem Local por Nó . . . 10
3.2.2 Abordagem Local por Nó Pai . . . 11
3.2.3 Abordagem Local por Nível . . . 11
3.3 Abordagem Global . . . 12
3.4 Global Model Naive Bayes . . . 13
4 Heurística Proposta 15 4.1 Cálculo da Distância . . . 15
4.2 Heurística ADH2C . . . 18
Sumário viii
5.2 Avaliação da Heurística ADH2C . . . 28
5.2.1 Avaliação do Parâmetro w0 da Heurística ADH2C . . . 29
5.3 Resultados dos Experimentos . . . 29
6 Conclusão 35
Lista de Figuras
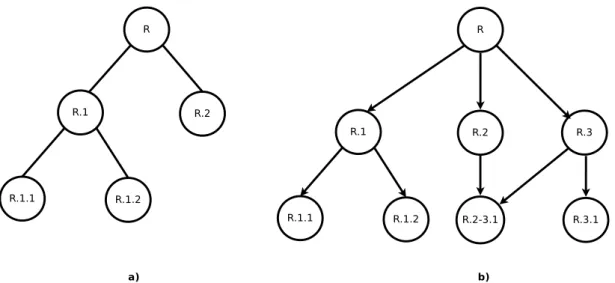
3.1 Estrutura hierárquica a) Árvore; (b) Grafo acíclico direcionado. . . 9
3.2 Abordagem por classificação plana. . . 10
3.3 Abordagem local por nó. . . 11
3.4 Abordagem local por nó pai. . . 12
3.5 Abordagem Local por Nível. . . 12
3.6 Abordagem global. . . 13
4.1 Hierarquia de classes. . . 16
Lista de Tabelas
2.1 Exemplo de discretização utilizando o método Equal-Width . . . 6
2.2 Exemplo de discretização utilizando o método Equal-Frequency. . . 7
4.1 Valores das distâncias entre classes utilizando-se w0=0,8. a) abordagem proposta em (Blockeel et al., 2002); b) abordagem proposta neste trabalho. 17 4.2 Fase de inicialização: a) atributo contínuo ordenado; b) criação de partições puras; c) agregação de partições adjacentes. . . 20
4.3 Soluções viáveis contendo a) 2 pontos de cortes; b) 4 pontos de cortes; c) 6 pontos de cortes. . . 22
5.1 Base de dados hierárquica multirrótulo . . . 25
5.2 Tabela de frequência das classes . . . 25
5.3 Base de dados com valores ausentes. . . 26
5.4 Base de dados após a substituição de valores ausentes. . . 27
5.5 Características da Base de Dados . . . 27
5.6 Valores médios de hF obtidos pelo GMNB após a discretização dos atribu-tos pela heurística ADH2C, . . . 30
Capítulo 1
Introdução
Os avanços tecnológicos nas últimas décadas propiciaram a geração e o armazenamento de grandes quantidades de dados associados a diferentes aplicações. A transformação desses dados em informações potencialmente úteis, válidas, novas e compreensíveis torna-se imperativa. No entanto, essa tarefa não é trivial, torna-sendo necessária a utilização de estratégias automatizadas para a análise dos dados (Han and Kamber, 2011). Um processo bastante utilizado para essa finalidade é o de descoberta de conhecimento a partir de
bases de dados (Knowledge Discovery from Data ou KDD), o qual é composto por três
etapas principais: o pré-processamento dos dados, a mineração de dados e a validação dos resultados.
O processo de discretização pode ser definido como uma etapa do pré-processamento de dados, cujo objetivo é transformar atributos contínuos em atributos discretos (Yang et al., 2005). Esse pré-processamento faz com que os valores contínuos de um atributo sejam organizados em partições, de modo que cada uma delas será representada por um valor discreto distinto no final do processo.
Os métodos de discretização podem ser categorizados como supervisionados ou não-supervisionados (Garcia et al., 2013). Os métodos que utilizam a informação presente no atributo classe durante o processo de discretização de um atributo são categorizados como supervisionados, enquanto que os métodos que desconsideram o atributo classe são categorizados como não-supervisionados.
1 Introdução 2
Naive Bayes (Richeldi and Rossotto, 1995; Chlebus and Nguyen, 1998). Desse modo, fica evidente a importância das técnicas de discretização como um pré-processamento da etapa de mineração de dados.
A classificação é uma tarefa de mineração de dados que busca identificar a classe de um determinado objeto a partir de suas características (Han and Kamber, 2011). Diferentes tipos de problemas de classificação podem ser encontrados na literatura, cada qual com o seu nível de complexidade (Silla Jr and Freitas, 2011). Em problemas de classificação plana, cada instância é associada a uma ou mais classes pertencentes a um conjunto finito de classes, sendo que não há qualquer tipo de relacionamento entre elas. Porém, existem problemas de classificação mais complexos, conhecidos como problemas de classificação hierárquica, nos quais as classes encontram-se organizadas em uma hierarquia.
Diversas áreas de pesquisa e aplicação, tais como categorização de textos (Qiu et al., 2011; Dollah and Aono, 2011), predição de funções de proteínas (Merschmann and Freitas, 2013; Valentini, 2014), classificação de gêneros musicais (Silla and Freitas, 2009b; Ariya-ratne and Zhang, 2012) e classificação de imagens (Binder et al., 2009; Kramer et al., 2012), já se beneficiaram com a utilização de técnicas de classificação hierárquica, uma vez que as classes a serem preditas encontravam-se naturalmente organizadas em uma hierarquia.
Os métodos de classificação hierárquica diferem na maneira de explorar a hierarquia de classes. Desse modo, tem-se as seguintes abordagens: abordagem por classificação plana, a qual ignora a hierarquia de classes e executa a predição considerando apenas as classes associadas aos nós folha da estrutura hierárquica; abordagens locais, caracterizadas pelo uso de múltiplos classificadores planos; e abordagem global, na qual um único classificador é treinado para predizer classes em qualquer nível da estrutura hierárquica.
Os métodos de discretização supervisionados disponíveis na literatura não foram proje-tados para levar em consideração os relacionamentos entre classes existentes em problemas de classificação hierárquica. Dessa forma, pesquisas na área de classificação hierárquica que necessitaram de atributos discretos, tais como (Silla and Kaestner, 2013), (Mersch-mann and Freitas, 2013) e (Ferrandin et al., 2013), utilizaram métodos de discretização não-supervisionados.
1 Introdução 3
para serem usados em conjunto com métodos de classificação hierárquica globais motivou o desenvolvimento desta pesquisa.
Os principais objetivos deste trabalho foram propor, implementar e avaliar um mé-todo de discretização supervisionado capaz de lidar com o relacionamento entre classes existente no problema de classificação hierárquica. O método aqui proposto corresponde a uma heurística que foi denominadaAgglomerative Discretization Heuristic for Hierarchical Classification - ADH2C.
Devido à inexistência de métodos de discretização supervisionados para o contexto de classificação hierárquica e dado que os métodos de discretização não-supervisionados EqualWidth e EqualFrequency vêm sendo utilizados em trabalhos de classificação hierár-quica, esses dois métodos não-supervisionados foram adotados como base de comparação com a heurística proposta neste trabalho.
Confirmando a hipótese levantada inicialmente, para a maioria das bases de dados uti-lizadas nos experimentos, o desempenho preditivo de um classificador hierárquico global, quando a base foi discretizada pela heurística ADH2C, foi superior àquele obtido quando
a mesma base de dados foi discretizada pelos métodos não-supervisionadosEqualWidth e
EqualFrequency.
Capítulo 2
Discretização de Atributos
O processo de discretização pode ser definido como uma etapa do pré-processamento de dados, cujo objetivo é transformar atributos contínuos em atributos discretos (Yang et al., 2005). Por exemplo, um intervalo contínuo [a, b] pode ser particionado em dois novos intervalos [a,c] e (c, b], sendoco ponto de corte adotado. Dessa forma, os valores contínuos contidos nesse intervalo serão divididos em dois grupos, os que pertencem à primeira partição e os que pertencem à segunda. A discretização também pode ser definida como um método de redução de dados, pois o conjunto de valores contínuos é reduzido à um subconjunto de valores discretos (Garcia et al., 2015).
Os métodos de discretização podem ser categorizados de acordo com diferentes crité-rios (Garcia et al., 2013). Um critério utilizado na categorização dos métodos de discre-tização está relacionada ao momento em que a discrediscre-tização é executada. O método de discretização é definido como estático quando a execução da mesma ocorre anteriormente à execução do algoritmo de aprendizagem. No entanto, se a discretização ocorre durante o processo de aprendizado, o método de discretização é conhecido como dinâmico. Os
métodos C4.5 (Quinlan, 1993) e ChiMerge (Kerber, 1992) são exemplos de métodos de
discretização dinâmico e estático respectivamente.
A quantidade de atributos acessados simultaneamente pelo método de discretização o caracteriza como uni-variado ou multi-variado. Os métodos que acessam apenas um buto por vez são conhecidos como uni-variado, enquanto que o acesso a mais de um atri-buto simultaneamente caracteriza o método como multi-variado. Além disso, os métodos de discretização multi-variados também podem discretizar um atributo por vez, levando em consideração a correlação existente entre os atributos da base de dados. Exemplos de método de discretização multi-variado podem ser encontrados nos trabalhos propostos
2 Discretização de Atributos 5
Principle - MDLP (Fayyad and Irani, 1993) é um exemplo de método de discretização
uni-variado, enquanto que o métodoMultivariate Discretization - MVD (Bay, 2001) é um
exemplo de método de discretização multi-variado.
A forma como as partições são construídas caracteriza os métodos de discretização em divisivos ou aglomerativos. Os métodos categorizados como divisivos iniciam o pro-cesso de discretização com apenas uma partição, contendo todos os valores contínuos do atributo e, em seguida, sucessivas subdivisões são executadas até que o critério de parada seja alcançado. De forma oposta, os métodos conhecidos como aglomerativos iniciam a discretização do atributo contínuo criando diversas partições iniciais e, por meio de fusões das partições, o processo de discretização é realizado. Há ainda métodos híbridos que executam fusões e subdivisões sobre o conjunto de partições de forma alternada durante todo o processo de discretização (Flores et al., 2007; Ching et al., 1995). Os métodos
CAIM (Kurgan and Cios, 2004), Chi2 (Liu and Setiono, 1995) e CADD (Ching et al.,
1995) são exemplos de métodos de discretização divisivo, aglomerativo e híbrido, respec-tivamente.
Outro critério utilizado na categorização dos métodos de discretização está relacio-nado ao númerok de partições a serem criadas ao final do processo de discretização. Os métodos que requerem a predefinição do número de partições a serem criadas são caracte-rizados como métodos diretos. Os métodos diretos também incluem em seu grupo métodos que executam a discretização em apenas um passo e métodos que adotam mais de um ponto de corte a cada etapa do processo. Em contrapartida, métodos de discretização ca-racterizados como incrementais executam diversas etapas de refinamento, iterativamente, do conjunto de partições até que seja atingido o critério de parada. O método Zeta (Ho and Scott, 1997) é um exemplo de método de discretização direto, enquanto que o método FUSINTER (Zighed et al., 1998) é um exemplo de método de discretização incremental.
Um método de discretização também pode ser caracterizado como supervisionado quando utiliza a informação presente no atributo classe durante o processo de discretiza-ção de um atributo contínuo. Por outro lado, os métodos não-supervisionados realizam a discretização de um atributo contínuo desconsiderando o atributo classe. Os métodos Equal-Width e Equal-Frequency (Li and Wang, 2002) são exemplos de métodos de
dis-cretização não-supervisionados. Já os métodos de disdis-cretização MDLP e ChiMerge são
exemplos de discretizadores supervisionados.
2.1 Equal-Width eEqual-Frequency 6
o número de pontos de corte gerados, o aumento na acurácia preditiva de classificadores e outros. Neste trabalho, os experimentos comparativos utilizaram um classificador na avaliação dos métodos de discretização adotados. Na Seção 2.1 serão apresentados os métodos de discretização não-supervisionadosEqual-Width eEqual-Frequency, que foram adotados como métodos de comparação nos experimentos realizados neste trabalho.
2.1
Equal-Width
e
Equal-Frequency
O método Equal-Width (EW) (Li and Wang, 2002) inicia o processo de discretização de
um atributo contínuo ordenando os valores contínuos do menor valor (Vmin) para o maior
valor (Vmax). Em seguida, os valores ordenados são particionados em k partições, sendo
k um parâmetro pré-definido pelo usuário. Todas partições terão o mesmo comprimento,
sendo ele definido pela Equação 2.1. O elemento de fronteira (Fi) de cada partição i é
obtido por meio da Equação 2.2.
A Tabela 2.1 fornece um exemplo de execução do método de discretização EW. Na primeira linha da tabela estão disponíveis os valores ordenados de um atributo contínuo. O método EW requer a predefinição do número de partições a serem criadas (na segunda linha é mostrado o valor adotado para k). Finalmente, na terceira linha da Tabela 2.1 é calculado o elemento de fronteira entre cada partição e os valores discretos obtidos são apresentados na quarta linha Tabela 2.1.
Comprimento= Vmax−Vmin
k (2.1)
Fi =Vmin+ (i×Comprimento) (2.2)
Tabela 2.1: Exemplo de discretização utilizando o método Equal-Width
Valores Contínuos Ordenados 5 8 10 13 21 23 30 40 44
Parâmetro k = 3
Variáveis Vmin = 5, Vmax = 44,
Comprimento= 13
Limites F1 = 5 + (1 ×13) = 18;
F2 = 5 + (2 × 13) = 31
2.1 Equal-Width eEqual-Frequency 7
O método Equal-Frequency (EF) (Li and Wang, 2002), assim como o método EW,
requer que os valores contínuos do atributo inicialmente sejam ordenados. Além disso, o número de partições a serem formadas também precisa ser previamente definido pelo
usuário. Diferentemente do que ocorre no método EW, no EF cada uma das k
parti-ções terá aproximadamente a mesma quantidade de elementos. Assim, dados n valores
contínuos distintos, cada partição terán/k valores contínuos. No entanto, múltiplas ocor-rências de um dado valor contínuo devem ser mantidas na mesma partição e, portanto,
nem sempre é possível produzir k partições com frequências (quantidade de elementos)
iguais.
A Tabela 2.2 fornece um exemplo de execução do método de discretização EF. Na pri-meira linha da tabela estão disponíveis os valores ordenados de um atributo contínuo. Na segunda linha da Tabela 2.2 é definido o número de partiçõesk, enquanto que na terceira linha são calculados os valores dos elementos de fronteira de cada partição. Finalmente, na última linha da Tabela 2.2, são apresentados os valores discretos obtidos.
Tabela 2.2: Exemplo de discretização utilizando o método Equal-Frequency.
Valores Contínuos Ordenados 5 8 10 13 21 23 30 40 44
Parâmetro k = 3
Qtde. de Valores por Partição 9/3, logo cada
partição terá 3 valores
Valores Discretos 1 1 1 2 2 2 3 3 3
Capítulo 3
Classificação Hierárquica
Na literatura, os trabalhos apresentam diversos problemas de classificação, sendo que a grande maioria deles corresponde ao problema de classificação plana. Em problemas de classificação plana as classes são independentes umas das outras, não possuindo nenhum tipo de relacionamento entre si. No entanto, existem problemas mais complexos em que as classes encontram-se relacionadas segundo uma estrutura hierárquica, tal como uma árvore ou um grafo acíclico direcionado (Direct Acyclic Graph - DAG). Esses problemas são conhecidos na literatura como problemas de classificação hierárquica (Freitas and de Carvalho, 2007).
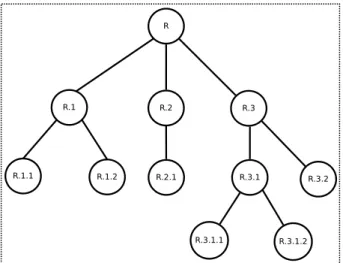
Os problemas de classificação hierárquica podem ser categorizados com base em qua-tros aspectos principais (Silla Jr and Freitas, 2011). O primeiro aspecto está relacionado ao tipo de estrutura hierárquica das classes. As classes podem estar hierarquicamente organizadas segundo uma árvore ou um DAG. A principal diferença entre essas estruturas está no número de pais que um dado nó (classe) pode possuir. Uma árvore restringe os nós (classes) a possuírem no máximo um nó (classe) pai. Já num DAG é possível que um determinado nó (classe) seja descendente de mais de um nó (classe) pai. A Figura 3.1 apresenta um exemplo de uma árvore e de um DAG. Nesses exemplos, as classes são representadas pelos nós e as arestas indicam a presença de um relacionamento entre elas.
O segundo aspecto diz respeito à profundidade na estrutura hierárquica na qual a classificação é realizada. Nos problemas de classificação hierárquica, a predição pode ser
mandatória em nós folha (Mandatory Leaf Node Prediction - MLNP) ou não-mandatória
em nós folha (Non-mandatory Leaf Node Prediction - NMLNP). O problema de predição
3.1 Abordagem por Classificação Plana 9
Figura 3.1: Estrutura hierárquica a) Árvore; (b) Grafo acíclico direcionado.
folha, a instância pode ser associada a qualquer nó da hierarquia de classes, seja ele nó folha ou não.
O terceiro aspecto está relacionado com a quantidade de classes (caminhos na hierar-quia de classes) que podem ser associados à uma dada instância. Esse aspecto define dois tipos de problemas: monorrótulo (Single Path of Labels) e multirrótulo (Multiple Path of Labels). O aspecto na sua forma mais restrita (monorrótulo) permite a predição de apenas uma classe, a qual está associada a somente um caminho da hierarquia de classes e, na sua forma menos restrita (multirrótulo), permite que múltiplas classes, envolvendo vários caminhos da hierarquia de classes, sejam preditas.
O último aspecto se refere à forma como a estrutura hierárquica é explorada pelo método de classificação. A estrutura hierárquica pode ser explorada segundo diferentes abordagens: abordagem por classificação plana, abordagem local e abordagem global. Nas próximas seções serão descritas cada uma dessas abordagens citadas anteriormente.
Neste trabalho, considera-se o cenário em que as classes estão hierarquicamente orga-nizadas segundo uma árvore e a predição é não-mandatória em nós folha, monorrótulo e segue a abordagem global.
3.1
Abordagem por Classificação Plana
3.2 Abordagem Local 10
Apesar de simples, essa estratégia tem a desvantagem de não conseguir levar em consideração as informações de relacionamento entre as classes. Além disso, o seu uso fica limitado aos problemas onde a classificação é mandatória nos nós folha. Na Figura 3.2 é apresentado um exemplo utilizando essa abordagem e a área delimitada pela linha tracejada destaca quais nós (classes) o classificador plano é capaz de predizer.
Figura 3.2: Abordagem por classificação plana.
3.2
Abordagem Local
A abordagem local explora a informação existente na hierarquia de classes segundo uma perspectiva local. A abordagem local subdivide-se em: abordagem local por nó, aborda-gem local por nó pai e abordaaborda-gem local por nível. A seguir serão apresentadas cada uma dessas abordagens.
3.2.1
Abordagem Local por Nó
Dentre as abordagens locais, a local por nó é a que possui a maior quantidade trabalhos publicados na literatura (Silla Jr and Freitas, 2011). Nessa abordagem, para cada nó da hierarquia de classes tem-se um classificador binário plano, o qual prediz se uma instância pertence ou não à classe com a qual ele está associado. O conjunto dos resultados de todos os classificadores binários será utilizado para compor a predição final.
3.2 Abordagem Local 11
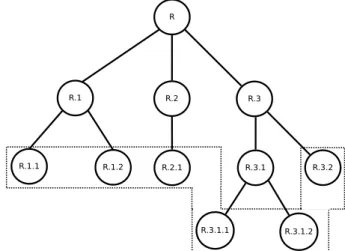
Nesse caso, algum método de correção de inconsistências precisa ser aplicado (Barutcuo-glu et al., 2006; Valentini, 2011). Na Figura 3.3, que ilustra a abordagem local por nó, os classificadores binários são representados pelos quadrados pontilhados.
Figura 3.3: Abordagem local por nó.
3.2.2
Abordagem Local por Nó Pai
Na abordagem local por nó pai treina-se um classificador multiclasse para cada nó (classe) pai da hierarquia, o qual deverá predizer, para uma determinada instância, uma classe associada a um dos nós filhos do nó em questão. Na Figura 3.4, que ilustra essa abordagem, os classificadores são representados pelos quadrados pontilhados.
Essa abordagem, quando utilizada seguindo a estratégia top-down, não produz resul-tados inconsistentes e, portanto, dispensa a utilização de métodos de correção de incon-sistências. Para ilustrar essa estratégia, considere a hierarquia da Figura 3.4. Suponha que uma instância de teste seja classificada como R.3 pelo classificador associado ao nó raiz (R). Desse modo, no primeiro nível hierárquico, o classificador associado ao nó da classeR.3será utilizado para classificar a instância em uma classe associada a um de seus nós filho (R.3.1 ou R.3.2) e, assim por diante, até que a instância seja classificada numa classe de um nível apropriado.
3.2.3
Abordagem Local por Nível
3.3 Abordagem Global 12
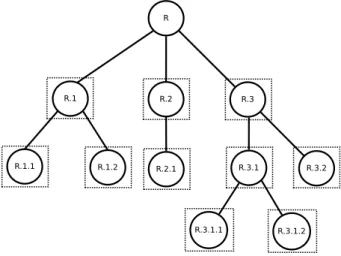
Figura 3.4: Abordagem local por nó pai.
pelas classes preditas em cada nível será utilizado para compor a predição final. De maneira similar ao que ocorre na abordagem local por nó, a predição final está sujeita a inconsistências. Sendo assim, a utilização de métodos de correção de inconsistências pode ser necessária. A Figura 3.5 apresenta um exemplo dessa abordagem, onde cada retângulo pontilhado representa um classificador multiclasse.
Figura 3.5: Abordagem Local por Nível.
3.3
Abordagem Global
3.4 Global Model Naive Bayes 13
de classes de uma só vez.
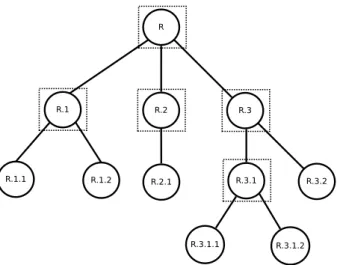
A Figura 3.6 ilustra a abordagem global. Nessa figura, o retângulo pontilhado repre-senta o classificador projetado para predizer classes em qualquer nível da hierarquia de classes.
Figura 3.6: Abordagem global.
Na literatura estão disponíveis diversos trabalhos propondo modificações em classifica-dores planos viabilizando a sua utilização no contexto de classificação hierárquica. Dentre eles destacam-se os seguintes trabalhos: HC4.5 (Clare and King, 2003) e HCL (Chen
et al., 2009) (versões modificadas do C4.5), Global Model Naive Bayes – GMNB (Silla
and Freitas, 2009a) (versão modificada doNaive Bayes),Clus-HMC (Blockeel et al., 2006; Vens et al., 2008) (baseado no método Predictive Cluster Trees) e o hAnt-Miner (Otero et al., 2009) (uma adaptação do algoritmoAnt-Miner).
O crescente interesse por parte dos pesquisadores pelos problemas de classificação hie-rárquica e a qualidade dos resultados obtidos utilizando-se métodos que utilizam a aborda-gem global reforçam a importância do desenvolvimento de técnicas de pré-processamento que possam ser aplicadas em conjunto com classificadores hierárquicos globais. O classi-ficador GMNB foi utilizado nos experimentos deste trabalho e, por isso, será descrito a seguir.
3.4
Global Model Naive Bayes
3.4 Global Model Naive Bayes 14
aos problemas de classificação hierárquica. Devido a isso, em (Silla and Freitas, 2009a) foi proposto o classificador hierárquico GMNB, uma adaptação do NB capaz de levar em consideração os relacionamentos entre as classes.
Assim como no classificador NB, dada uma nova instância X = {x1,x2,...,xm} para ser
classificada, ondex1,x2,...,xmcorrespondem aos valores dos atributos preditoresA1,A2,...,Am,
respectivamente, o classificador GMNB atribui a essa nova instância X a classe que tem maior probabilidade a posteriori P(Ci|X)α
Qn
k=1P(xk|Ci) × P(Ci).
A diferença com relação ao NB ocorre no cálculo das probabilidades condicionais e no cálculo das probabilidades a priori. No caso das probabilidades condicionais P(xk|Ci),
o classificador GMNB considera que qualquer instância que pertence à classeCi também
pertence a todas as suas classes ancestrais na hierarquia. Por exemplo, as instâncias associadas à classe R.3.1 serão contabilizadas no cálculo das probabilidades condicionais da própria classe R.3.1 (P(xk|R.3.1)) e da sua classe ancestral R.3 (P(xk|R.3)).
De forma análoga ao cálculo das probabilidades condicionais, para o classificador GMNB, o cálculo das probabilidadesa priori P(Ci), considera que qualquer instância da
classe Ci também pertence a todas as classes ancestrais de Ci na hierarquia. Utilizando
o mesmo exemplo anterior, as instâncias associadas à classe R.3.1 serão contabilizadas para o cálculo das probabilidades a priori de R.3.1 (P(R.3.1)) e de sua classe ancestral R.3 (P(R.3)).
A adaptação do NB proposta por Silla and Freitas (2009a) altera a forma como são calculadas as probabilidadesP(xk|Ci)eP(Ci), fazendo com que os relacionamentos entre
Capítulo 4
Heurística Proposta
Este capítulo apresenta a proposta de uma heurística para discretização supervisionada de atributos para o contexto de classificação hierárquica monorrótulo. Dado que a heu-rística proposta utiliza o conceito de distância entre partições para realizar o processo de discretização, a Seção 4.1 detalha esse conceito de distância utilizado pela heurística. Em
seguida, na Seção 4.2, a heurística proposta, denominada Agglomerative Discretization
Heuristic for Hierarchical Classification - ADH2C, é descrita.
4.1
Cálculo da Distância
Nos problemas de classificação hierárquica as classes associadas às instâncias encontram-se organizadas em uma estrutura hierárquica. Desse modo, considera-se que se uma instância está associada a uma classe X, então ela também pertence a todas as classes ancestrais de X, ou seja, ela está associada a todas as classes contidas no caminho percorrido na hierarquia para se alcançar a classeX.
Essa característica dos problemas de classificação hierárquica faz com que duas classes distintas possam ter maior ou menor semelhança (distância) dependendo da posição (grau de parentesco) das mesmas na hierarquia de classes.
Sendo assim, em (Blockeel et al., 2002) os autores apresentaram uma maneira para se calcular a distância entre duas classes pertencentes a uma estrutura hierárquica. Para tal, utilizaram vetores binários que determinam as classes que pertencem ao caminho hierár-quico entre o nó raiz e os nós que representam as classes entre as quais se deseja calcular a distância. Nesse vetor, cada posição representa uma classe da estrutura hierárquica.
4.1 Cálculo da Distância 16
posição do vetor binário está associada a uma classe contida no conjunto H ={R.1,
R.2, R.1.1 e R.1.2}, seguindo a ordem com que elas foram apresentadas nesse conjunto. Portanto, o vetor binário que representa a classe R.1.1é dado por v1 = [1; 0; 1; 0].
Dados os vetores binários v1 e v2 representando duas classes quaisquer (C1 e C2)
contidas em uma estrutura hierárquica, a Equação 4.1 fornece a distância entre as mesmas. Essa equação consiste basicamente na adaptação da distância Euclidiana tradicional para o contexto de classificação hierárquica.
distanciaˆ (C1, C2) =
v u u t
k
X
i=1
wi×(v1[i]−v2[i])2, (4.1)
ondek é número total de classes presentes na hierarquia de classes.
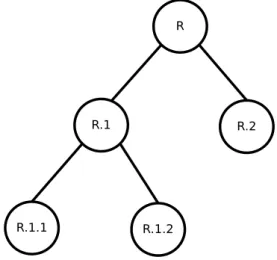
Figura 4.1: Hierarquia de classes.
O fator wi, presente na Equação 4.1, é responsável por ponderar a distância entre
classes de acordo com a profundidade em que as mesmas se encontram na hierarquia de classes. Ele é definido como wi = w
nivel(i)
0 , para 0 < w0 < 1, onde nivel(i) corresponde
ao nível hierárquico da classe representada na posição i do vetor binário (1 ≤ i ≤ k). O objetivo desse fator é atribuir pesos maiores para as classes contidas nos níveis menos profundos da hierarquia de classes.
Para exemplificar o cálculo da distância entre duas classes segundo a proposta de Bloc-keel et al. (2002), considere a hierarquia de classes presente na Figura 4.1 e as clas-ses C1 = R.1.1 e C2 = R.1.2. Os vetores binários que representam essas classes são
v1 = [1; 0; 1; 0] e v2 = [1; 0; 0; 1], respectivamente, cujas posições estão associadas
4.1 Cálculo da Distância 17
a distância entre as classes C1 e C2, calculada a partir da Equação 4.1, é dada por:
p
0,81.(1−1)2+ 0,81.(0−0)2+ 0,82.(1−0)2+ 0,82.(0−1)2 = 1,13.
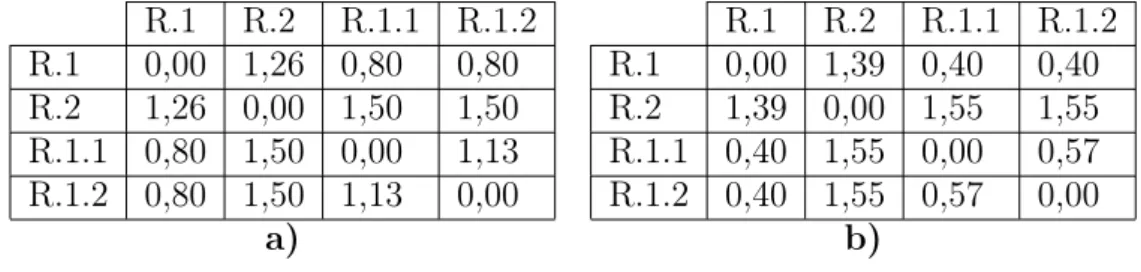
O cálculo de distância entre classes apresentado em (Blockeel et al., 2002) foi adaptado neste trabalho com o intuito de alterar o valor da distância entre duas classes da hierarquia. A adaptação proposta faz com que duas classes distintas, que não possuem classe(s) ancestral(is) em comum na hierarquia de classes, fiquem com uma distância maior do que aquela calculada da forma originalmente proposta em (Blockeel et al., 2002). Caso contrário, ou seja, se duas classes distintas possuem alguma classe ancestral em comum na hierarquia de classes, então a distância entre elas será menor do que aquela calculada a partir da proposta apresentada em (Blockeel et al., 2002). Um comparativo entre as duas abordagens é apresentado na Tabela 4.1, que mostra a distância para cada par de classes presentes na hierarquia representada na Figura 4.1. A Tabela 4.1(a) apresenta os resultados obtidos a partir da abordagem proposta em (Blockeel et al., 2002) e a Tabela 4.1(b) mostra os resultados alcançados utilizando-se a abordagem proposta neste trabalho.
Tabela 4.1: Valores das distâncias entre classes utilizando-se w0=0,8. a) abordagem
proposta em (Blockeel et al., 2002); b) abordagem proposta neste trabalho.
R.1 R.2 R.1.1 R.1.2 R.1 R.2 R.1.1 R.1.2
R.1 0,00 1,26 0,80 0,80 R.1 0,00 1,39 0,40 0,40
R.2 1,26 0,00 1,50 1,50 R.2 1,39 0,00 1,55 1,55
R.1.1 0,80 1,50 0,00 1,13 R.1.1 0,40 1,55 0,00 0,57
R.1.2 0,80 1,50 1,13 0,00 R.1.2 0,40 1,55 0,57 0,00
a) b)
A adaptação aqui proposta envolve apenas uma alteração nos vetores que representam as classes para as quais se deseja calcular a distância e, portanto, o cálculo continua sendo realizado utilizando-se a Equação 4.1. A alteração nos vetores foi realizada com intuito de se captar o grau de descendência entre as classes. Portanto, enquanto na proposta de Blockeel et al. (2002) o vetor que representa uma classe é binário, na proposta deste trabalho cada posição desse vetor armazenará um valor entre 0 e 1, calculado por meio da Equação 4.2. Considerando-se uma hierarquia contendo as classes do conjuntoH ={R.1,
R.2,R.1.1eR.1.2}, o valor dak-ésima posição do vetor que representa a classeCi é dado
por:
similaridade(Ci, Hk) = |⇑
Ci ∩ ⇑Hk |
|⇑Hk |
, (4.2)
4.2 Heurística ADH2C 18
Hk é a k-ésima classe da hierarquia de classes.
⇑(Ci)é o conjunto formado pela união das classes ancestrais de Ci e a própria classeCi.
⇑(Hk)é o conjunto formado pela união das classes ancestrais deHke a própria classeHk.
| ⇑(Hk) | é a quantidade de classes no conjunto ⇑(Hk).
Para exemplificar a adaptação proposta para o cálculo da distância entre duas classes
C1 e C2, considere novamente a hierarquia de classes presente na Figura 4.1 (H = {R.1,
R.2, R.1.1 e R.1.2}) e as classes C1 =R.1.1 e C2 = R.1.2. Utilizando-se a Equação 4.2
são calculadas cada uma das posições dos vetoresv1 ev2 , que representam as classesC1
eC2, respectivamente. Por exemplo, para se obter o valor da primeira posição do vetorv1
calcula-sesimilaridade(C1, H1), onde H1 =R.1(primeira classe que aparece no conjunto
H). Calculadosv1 = [1; 0; 1; 0,5] ev2 = [1; 0; 0,5; 1], aplica-se a Equação 4.1 para se obter
a distância entre as classesC1 eC2. Utilizando-se w0 = 0,8, a distância entre essas classes
é dada por: p
0,81.(1−1)2+ 0,81.(0−0)2+ 0,82.(1−0,5)2+ 0,82.(0,5−1)2 = 0,57.
A heurística proposta neste trabalho, descrita na Seção 4.2, utiliza a distância entre duas partições adjacentes para transformar atributos contínuos em atributos discretos. Se cada uma das partições para as quais se deseja calcular a distância contiver apenas uma instância, cada qual associada a uma classe, a distância entre as mesmas é calculada da maneira apresentada anteriormente, ou seja, computando-se a distância entre duas classes. No entanto, se a quantidade de instâncias em alguma dessas duas partições for superior a um, um novo procedimento, apresentado no Algoritmo 1, é realizado para permitir o cálculo de distância entre duas partições adjacentes.
Como pode-se observar no Algoritmo 1, o cálculo de distância entre duas partições adjacentes é realizado a partir da mesma Equação 4.1 utilizada para se calcular a distância entre duas classes. Portanto, a única diferença está no fato de que os vetores v1 e v2
utilizados nessa equação, que no Algoritmo 1 denominamosvi evi+1, respectivamente, ao
invés de representarem uma única classe, cada um deles representa todo o conjunto de classes de uma partição. Eles são computados somando-se os vetores de todas as classes contidas na partição (linhas 6 a 13).
4.2
Heurística ADH2C
4.2 Heurística ADH2C 19
Input: Partições adjacentes Pi ePi+1;
Output: Distância entre as partições adjacentes Pi e Pi+1;
Distância = 0; 1
− →vi = ∅; 2
−−→
vi+1 =∅;
3
for k= 1; k ≤Número de classes ; k+ + do
4
Hk ← classe k da hierarquia de classes;
5
for each Valor contínuo da partição i do 6
Cij ← classe associada ao valor contínuo j da partição i;
7
vi[k]+= similaridade(Cij, Hk);
8
end
9
for each Valor contínuo da partição i+ 1 do 10
C(i+1)j ←classe associada ao valor contínuo j da partição i+ 1;
11
vi+1[k]+= similaridade(C(i+1)j,Hk);
12
end
13
Distância += (wi × (vi[k] − vi+1[k])2);
14
end
15
return √Distˆancia; 16
Algoritmo 1: Pseudo-código da função Distância entre Partições Adjacentes.
dados, apresentado na Seção 4.1, para discretizar atributos contínuos de bases de dados utilizadas em problemas de classificação hierárquica monorrótulo. A heurística ADH2C, projetada para ser utilizada em conjunto com métodos globais de classificação hierárquica, é categorizada como supervisionada, estática, incremental, uni-variada e aglomerativa.
O Algoritmo 2 apresenta os passos da heurística ADH2C, que pode ser dividida em três fases principais: inicialização, construção das soluções candidatas e seleção da melhor solução.
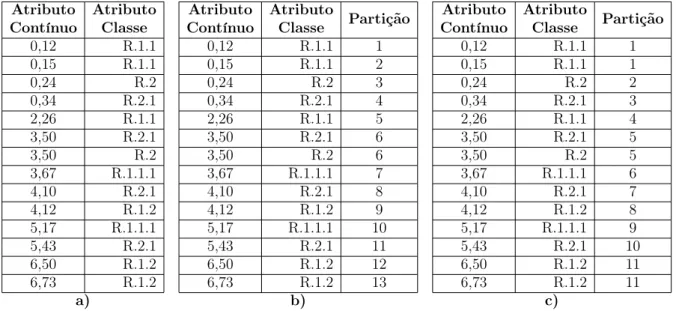
A fase de inicialização começa com a ordenação dos valores do atributo contínuo em ordem crescente (linha 1). Em seguida são criadas as partições puras, ou seja, cada valor (ou conjunto de valores) distinto do atributo contínuo é atribuído a uma partição (linha 2). Por fim, as partições adjacentes são avaliadas duas a duas e, sempre que todos os valores contínuos do par de partições estão associados a uma mesma classe, essas partições são fundidas (linha 3). A Tabela 4.2(a) apresenta um atributo contínuo de uma base de dados hipotética para o contexto de classificação hierárquica monorrótulo. As Tabelas 4.2(b) e 4.2(c) mostram os resultados obtidos após a execução da etapa de inicialização da heurística ADH2C sobre esse atributo contínuo.
4.2 Heurística ADH2C 20
Tabela 4.2: Fase de inicialização: a) atributo contínuo ordenado; b) criação de partições puras; c) agregação de partições adjacentes.
Atributo Contínuo Atributo Classe Atributo Contínuo Atributo Classe Partição Atributo Contínuo Atributo Classe Partição
0,12 R.1.1 0,12 R.1.1 1 0,12 R.1.1 1
0,15 R.1.1 0,15 R.1.1 2 0,15 R.1.1 1
0,24 R.2 0,24 R.2 3 0,24 R.2 2
0,34 R.2.1 0,34 R.2.1 4 0,34 R.2.1 3
2,26 R.1.1 2,26 R.1.1 5 2,26 R.1.1 4
3,50 R.2.1 3,50 R.2.1 6 3,50 R.2.1 5
3,50 R.2 3,50 R.2 6 3,50 R.2 5
3,67 R.1.1.1 3,67 R.1.1.1 7 3,67 R.1.1.1 6
4,10 R.2.1 4,10 R.2.1 8 4,10 R.2.1 7
4,12 R.1.2 4,12 R.1.2 9 4,12 R.1.2 8
5,17 R.1.1.1 5,17 R.1.1.1 10 5,17 R.1.1.1 9
5,43 R.2.1 5,43 R.2.1 11 5,43 R.2.1 10
6,50 R.1.2 6,50 R.1.2 12 6,50 R.1.2 11
6,73 R.1.2 6,73 R.1.2 13 6,73 R.1.2 11
a) b) c)
corte são definidos como a média dos valores localizados nas fronteiras das partições. Por exemplo, na Tabela 4.2(c), os valores 0.15 e 0.24 encontram-se na fronteira da partição 1 com a 2. Portanto, o primeiro ponto de corte do esquema de discretização para os dados representados na Tabela 4.2(c) é definido como(0.15+0.24)/2 = 0,195. Seguindo o mesmo raciocínio para o cálculo dos demais pontos de corte, temos a formação do conjunto de pontos de cortesP ={0,195; 0,29; 1,3; 2,88; 3,585; 3,885; 4,11; 4,645; 5,3; 5,965} que define esse esquema de discretização dos dados.
A execução da segunda fase do método requer que tenham sido produzidas pelo me-nos 4 partições na fase de inicialização. Desse modo, se essa restrição não for atendida, o processo de discretização é finalizado retornando o conjunto de pontos de cortes obtido na fase de inicialização (linha 5). Essa restrição garante que o critério de seleção da me-lhor solução candidata, o qual será explicado mais a frente, seja executado corretamente.
Supondo que tenham sido geradas N partições na fase de inicialização, sendo N ≥ 4, o
número de soluções candidatas geradas nessa segunda fase é igual N−1. Isso ocorre por-que a cada iteração realizada nessa fase (linhas 8 a 15), um par de partições adjacentes é fundido (linha 10) produzindo uma nova solução candidata (linha 12). Esse processo de fusões termina quando restar apenas uma partição.
4.2 Heurística ADH2C 21
A última fase de execução da heurística (linhas 16 a 34) é responsável pela seleção da solução (conjunto de pontos de cortes) que será apresentada como resultado final. Como cada solução candidata está associada à distância entre o par de partições adjacentes que ao serem fundidas deu origem à solução em questão, a seleção da solução final é realizada com base nessa distância.
Dentre as soluções candidatas obtidas na segunda fase, somente as denominadas so-luções viáveis serão consideradas no processo de escolha da melhor solução. Uma solução
S contendo N partições é considerada viável quando a distância associada à S é menor
do que aquelas associadas às soluções vizinhas, ou seja, soluções contendo N-1 e N+1 partições (linha 22). Identificadas as soluções viáveis, deve-se quantificar a qualidade de cada solução viável. A equação presente na linha 24 do Algoritmo 2 é utilizada para men-surar a qualidade de cada solução viável. Finalmente, a solução viável melhor avaliada é escolhida e o conjunto de pontos de cortes associado a ela é retornado como solução final (linha 31).
Caso não haja nenhuma solução viável (linhas 31 a 33), a heurística retorna como solução o conjunto de pontos de corte das partições geradas na fase de inicialização.
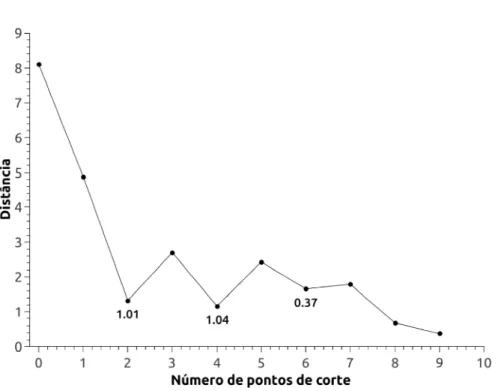
Para exemplificar esse processo de seleção da melhor solução, o gráfico da Figura 4.2 ilustra todas as soluções candidatas geradas pela segunda fase da heurística ADH2C para a base de dados presente na Tabela 4.2(a). Nesse gráfico, o eixo X representa o número
de pontos de corte de uma solução S e o eixo Y representa a distância entre o par de
partições adjacentes que foram fundidas para gerar essa soluçãoS. Portanto, cada ponto da curva plotada nesse gráfico representa uma solução candidata.
4.2 Heurística ADH2C 22
Número de pontos de corte
10
Figura 4.2: Soluções candidatas geradas a partir da execução da heurística ADH2C sobre a base de dados presente na Tabela 4.2(a).
Tabela 4.3: Soluções viáveis contendo a) 2 pontos de cortes; b) 4 pontos de cortes; c) 6 pontos de cortes.
Atributo Contínuo
Atributo
Classe Partição
Atributo Contínuo
Atributo
Classe Partição
Atributo Contínuo
Atributo
Classe Partição
0,12 R.1.1 1 0,12 R.1.1 1 0,12 R.1.1 1
0,15 R.1.1 1 0,15 R.1.1 1 0,15 R.1.1 1
0,24 R.2 2 0,24 R.2 2 0,24 R.2 2
0,34 R.2.1 2 0,34 R.2.1 2 0,34 R.2.1 2
2,26 R.1.1 2 2,26 R.1.1 2 2,26 R.1.1 3
3,50 R.2.1 2 3,50 R.2.1 2 3,50 R.2.1 4
3,50 R.2 2 3,50 R.2 2 3,50 R.2 4
3,67 R.1.1.1 2 3,67 R.1.1.1 2 3,67 R.1.1.1 4
4,10 R.2.1 2 4,10 R.2.1 2 4,10 R.2.1 4
4,12 R.1.2 3 4,12 R.1.2 3 4,12 R.1.2 5
5,17 R.1.1.1 3 5,17 R.1.1.1 3 5,17 R.1.1.1 5
5,43 R.2.1 3 5,43 R.2.1 4 5,43 R.2.1 6
6,50 R.1.2 3 6,50 R.1.2 5 6,50 R.1.2 7
6,73 R.1.2 3 6,73 R.1.2 5 6,73 R.1.2 7
4.2 Heurística ADH2C 23
Input: Atributo contínuo e respectivas classes;
Output: Pontos de corte do esquema de discretização;
Inicialização;
Ordenar os valores contínuos em ordem crescente; 1
Criar as partições iniciais de acordo com o valor do atributo contínuo; 2
Fundir partições adjacentes cujos elementos estão associadas a uma mesma classe; 3
Construção das soluções candidatas; if Número de partições < 4 then
4
returnPontos de corte das partições produzidas na fase de inicialização; 5
end
6
k = 1; 7
while Número de partições >1 do
8
Calcular a distância entre todos os pares de partições adjacentes; 9
Fundir o par de partições adjacentes que possuir menor distância; 10
Armazenar essa menor distância no vetor distância[k]; 11
Armazenar os pontos de corte do esquema de discretização resultante no vetor 12
candidatos[k];
Número de partições = Número de partições - 1; 13
k=k+ 1; 14
end
15
Seleção da melhor solução; if Min(−−−−−−→distância) > 1.0 then
16
returnPontos de corte das partições produzidas na fase de inicialização; 17
end
18
melhor = M IN_V ALU E;
19
for i= 2; i < k; i+ + do
20
anterior = distância[i−1]; atual = distância[i]; seguinte = distância[i+ 1]; 21
if (atual < anterior) and (atual < seguinte) then
22
maior = max(seguinte, anterior); 23
qualidade = anterior−atual maior +
seguinte−atual maior ;
24
if (qualidade≥melhor) then
25
melhor = qualidade; 26
id = i; 27 end 28 end 29 end 30
if melhor==M IN_V ALU E then
31
returnPontos de corte das partições produzidas na fase de inicialização; 32
end
33
return Pontos de corte da solução armazenada em candidatos[id]; 34
Capítulo 5
Experimentos Computacionais
Neste capítulo são apresentados os experimentos computacionais realizados para avaliar a heurística proposta neste trabalho. Inicialmente, as bases de dados utilizadas nos expe-rimentos e os pré-processamentos realizados nas mesmas são descritos na Seção 5.1. Em seguida, a medida de avaliação adotada nos experimentos é apresentada na Seção 5.2. Finalmente, os resultados computacionais são apresentados e discutidos na Seção 5.3.
5.1
Bases de Dados
Diversos trabalhos que abordam problemas de classificação plana estão disponíveis na literatura e, além disso, grande parte das bases de dados utilizadas nesses trabalhos estão publicamente disponíveis. No entanto, para classificação hierárquica, que é um tema de pesquisa mais recente, o cenário é diferente, fazendo com que a quantidade de trabalhos publicados e bases de dados disponíveis seja limitada.
No contexto de classificação hierárquica destaca-se o trabalho de Clare and King (2003), no qual foram utilizadas 12 bases de dados de bioinformática que tornaram-se
públicas1 e depois foram utilizadas em outros diversos trabalhos. As bases de dados
utilizadas em (Clare and King, 2003) contêm dados referentes a funções genéticas do genoma da levedura. Como 9 dessas 12 bases possuem atributos contínuos, elas foram adotadas nos experimentos realizados neste trabalho. Esses atributos incluem diversos tipos de dados da área de bioinformática, tais como: estrutura secundária da sequência, fenótipo, homologia, estatísticas da sequência e outros.
Essas 12 bases de dados utilizadas em (Clare and King, 2003) são multirrótulo, ou
5.1 Bases de Dados 25
seja, cada instância encontra-se associada a uma ou mais classes da hierarquia. Como este trabalho lida com o cenário monorrótulo (single path of labels), essas bases de dados foram transformadas para conter uma única classe por instância. Essa transformação foi realizada selecionando-se, para cada instância, a classe mais frequente na base de dados original. Em caso de empate na frequência das classes, seleciona-se de forma aleatória uma das classes.
O exemplo a seguir ilustra os passos executados para transformar uma base multir-rótulo em monormultir-rótulo. A Tabela 5.1 apresenta uma base de dados hipotética para o contexto de classificação hierárquica multirrótulo, na qual o símbolo@é responsável pela separação das classes associadas a uma dada instância.
Tabela 5.1: Base de dados hierárquica multirrótulo
ID Atributo F Atributo Classe
1 0,15 R.1.1@R.2.2
2 ? R.2@R.1.2
3 3,41 R.2@R.1
4 4,12 R.2.1@R.1.3
5 0,22 R.1.2@R.3
6 3,5 R.1.1@R.2
7 ? R.3.1@R.1
8 0,34 R.1.1.1@R.1.2
9 ? R.3.2@R.1.1.1
10 4,1 R.2@R.3.2
A Tabela 5.2 apresenta a frequência de cada classe da base de dados presente na Tabela 5.1. A tabela de frequência de classes foi gerada por meio da contagem do número de vezes que cada classe ocorre na base de dados.
Tabela 5.2: Tabela de frequência das classes
R.1 R.2 R.3 R.1.1 R.1.2 R.1.3 R.2.1 R.2.2 R.3.1 R.3.2 R.1.1.1
2 4 1 2 3 1 1 1 1 2 2
Assim como mencionado anteriormente, o processo de transformação ocorre escolhendo-se, dentre as classes associadas a uma dada instância, a de maior frequência. Em caso de empate, como ocorre para as instâncias 4 e 9 do exemplo apresentado na Tabela 5.1, escolhe-se aleatoriamente uma das classes da instância. A Tabela 5.3 apresenta a base de dados monorrótulo gerada a partir da execução desse processo de transformação sobre a base de dados presente na Tabela 5.1.
5.1 Bases de Dados 26
Tabela 5.3: Base de dados com valores ausentes.
ID Atributo F Atributo Classe
1 0,15 R.1.1
2 ? R.2
3 3,41 R.2
4 4,12 R.2.1
5 0,22 R.1.2
6 3,5 R.2
7 ? R.1
8 0,34 R.1.2
9 ? R.1.1.1
10 4,1 R.2
substituição dos valores ausentes de atributos nessas bases. O procedimento descrito a seguir foi adotado para a substituição dos valores ausentes. Dado um atributoF contendo um valor ausente associado à classeCj, esse valor ausente será substituído pela média de
todos os valores conhecidos deF associados à classe Cj. Caso não haja valores conhecidos
deF associados à classeCj, o valor ausente será substituído pela média de todos os valores
conhecidos de F associados à alguma classe descendente de Cj. Em último caso, quando
não é possível imputar o valor ausente utilizando um dos procedimentos anteriores, a média de todos os valores conhecidos do atributoF é utilizada como valor substituto.
Com o intuito de ilustrar os passos executados durante o pré-processamento, considere a base de dados incompleta presente na Tabela 5.3, na qual as instâncias 2, 7 e 9 possuem
valor ausente para o atributo F. Nesse exemplo, para cada uma dessas instâncias, uma
estratégia diferente é adotada para imputar o valor ausente do atributo.
A instância 2 está associada à classe R.2, a qual está associada a outras instâncias (3, 6 e 10) contendo valores conhecidos para o atributoF. Nesse caso, o valor ausente do atributo é substituído pela média dos três valores conhecidos (3,41; 3,5 e 4,1) das instâncias associadas à mesma classe (R.2) da instância contendo valor ausente do atributoF. Dessa forma, o valor do atributoF para a instância 2 é imputado como 3,67.
Para a instância 7, na qual o valor ausente esta associado à classe R.1, devido à inexis-tência de outras instâncias associadas a essa mesma classe, o valor ausente é substituído pela média dos valores conhecidos (0,15; 0,22 e 0,34) das instâncias associadas a classes descendentes da classe (R.1) associada à instância que contém valor ausente do atributo
F. Assim, o valor do atributo F para a instância 7 é imputado como 0,24.
5.1 Bases de Dados 27
outra instância da base de dados e nem é classe ascendente de qualquer outra classe
associada às instâncias com valores conhecidos do atributo F. Dessa forma, o valor
ausente é substituído pela média dos valores conhecidos do atributoF para as instâncias
da base de dados. Nesse caso, o valor do atributo F para a instância 9 é imputado
como 2,26.
A Tabela 5.4 apresenta a base de dados obtida após a execução do processo de impu-tação de valores ausentes sobre a base de dados presente na Tabela 5.3.
Tabela 5.4: Base de dados após a substituição de valores ausentes.
ID Atributo F Atributo Classe
1 0,15 R.1.1
2 3,67 R.2
3 3,41 R.2
4 4,12 R.2.1
5 0,22 R.1.2
6 3,5 R.2
7 0,24 R.1
8 0,34 R.1.2
9 2,26 R.1.1.1
10 4,1 R.2
As principais características das bases de dados utilizadas nos experimentos realizados neste trabalho são apresentadas na Tabela 5.5. Para cada base de dados é apresentado o seu número de atributos (contínuos e discretos), o número total de instâncias e o número de classes em cada nível da estrutura hierárquica.
Tabela 5.5: Características da Base de Dados
Base de dados # Atributos
Contínuos / Discretos # Instâncias # Classes/Nivel
CellCycle 77/0 3757 7/37/73/46/25/2
Church 26/1 3755 7/37/72/47/25/2
Derisi 63/0 3725 7/37/72/47/25/2
Eisen 79/0 2424 4/26/55/34/22/2
Expr 547/4 3779 7/37/72/47/26/2
Gasch1 173/0 3764 7/37/73/46/26/2
Gasch2 52/0 3779 7/37/73/46/26/2
Sequence 473/5 3919 7/37/73/47/26/2
5.2 Avaliação da Heurística ADH2C 28
5.2
Avaliação da Heurística ADH2C
Os experimentos executados neste trabalho permitiram a comparação da qualidade da discretização obtida por meio da heurística proposta com a de métodos de discretiza-ção não supervisionados comumente utilizados no contexto de classificadiscretiza-ção hierárquica. Devido a inexistência de métodos de discretização supervisionados que possam ser utili-zados em conjunto com métodos globais de classificação hierárquica, foram adotados nos experimentos comparativos realizados neste trabalho os métodos de discretização não-supervisionados Equal-Width eEqual-Frequency.
Os métodos de discretização Equal-Width eEqual-Frequency possuem o parâmetro k
que representa o número de intervalos discretos que devem ser gerados ao final do processo de discretização. Nos experimentos deste trabalho, os valores de k utilizados variaram de 5 até 20, em incrementos de 5 unidades. Além disso, em um segundo experimento o
parâmetro k dos métodos não supervisionados foi definido como o número de partições
geradas pela heurística ADH2C. As implementações dos métodos Equal-Width e
Equal-Frequency disponíveis na ferramenta W EKA (Hall et al., 2009) foram utilizadas nos experimentos realizados neste trabalho.
Após a discretização dos atributos das bases de dados a partir da heurística ADH2C e dos métodos utilizados como base de comparação, essas bases são utilizadas pelo
clas-sificador hierárquico Global Model Naive Bayes (GMNB) (Silla and Freitas, 2009b) e o
desempenho preditivo do mesmo é avaliado através da técnica 10-validação cruzada. Nessa técnica de avaliação a base de dados é dividida em 10 partições iguais, sendo 9 partes uti-lizadas no treinamento do classificador e a partição restante no teste do mesmo. Para tornar a comparação justa, todos os métodos de discretização utilizados neste trabalho receberam o mesmo conjunto de partições de treinamento e teste.
A medida de avaliação F-measure hierárquica (hF) foi adotada para mensurar o
de-sempenho preditivo do classificador GMNB. A medida hF é uma adaptação da tradicional F-measure amplamente utilizada na avaliação de classificadores em problemas de
classi-ficação plana. A hF é calculada por meio da equação hF = 2×hP×hR
hP+hR , onde hP e hR
representam a Precisão hierárquica e Revocação hierárquica, respectivamente.
Conside-rando Pi como sendo o conjunto contendo a classe predita para uma dada instância i e
suas respectivas classes ancestrais, eTio conjunto formado pela classe real da instânciaie
suas respectivas classes ancestrais, as medidas hP e hR são definidas como: hP =
P
i|Pi∩Ti|
P
i|Pi|
5.3 Resultados dos Experimentos 29
5.2.1
Avaliação do Parâmetro
w
0da Heurística ADH2C
A heurística ADH2C possui o parâmetrow0 que faz parte do fator de ponderação utilizado
no cálculo da distância entre partições. Esse parâmetro pode variar entre 0 e 1. Portanto, nos experimentos deste trabalho, w0 foi escolhido a partir de experimentos preliminares
onde variou-sew0 de 0,1 até 1,0.
A Tabela 5.6 apresenta o desempenho preditivo obtido pelo classificador GMNB uti-lizando as bases de dados pré-processadas pela heurística ADH2C variando o valor do
parâmetro w0. A primeira coluna da Tabela 5.6 contém o nome das bases de dados
utilizadas nos experimentos. A partir da segunda até a última coluna dessa tabela são
apresentados os valores médios de hF (com seus respectivos desvios-padrões entre
pa-rênteses) obtidos pelo classificador GMNB utilizando as bases de dados pré-processadas
pela heurística ADH2C. O parâmetro w0 adotado na execução da heurística ADH2C é
apresentado entre parenteses logo após a sigla da heurística. Além disso, para cada base de dados, o maior valor médio de hF está destacado em negrito.
A partir dos resultados apresentados na Tabela 5.6 observa-se que o classificador GMNB alcançou os melhores desempenhos preditivos ao utilizar as bases de dados pré-processadas pela heurística ADH2C utilizandow0 iguais a 0,7 e 0,8. Desse modo,
decidiu-se investigar também um valor intermediário, ou decidiu-seja, w0 = 0,75. A partir disso, como
w0 = 0,75foi o valor que propiciou o melhor desempenho para heurística ADH2C, ele foi
adotado nos experimentos deste trabalho.
5.3
Resultados dos Experimentos
A Tabela 5.7 apresenta o desempenho preditivo obtido pelo classificador GMNB utilizando as bases de dados pré-processadas pela heurística ADH2C e pelos métodos de discretização
não supervisionados Equal-Width e Equal-Frequency. A primeira coluna da Tabela 5.7
contém o nome das bases de dados utilizadas nos experimentos. A partir da segunda até a última coluna dessa tabela são apresentados os valores médios dehF (com seus respectivos desvios-padrões entre parênteses) obtidos pelo classificador GMNB utilizando as bases de
dados pré-processadas pelos métodos Equal-Width (EW), Equal-Frequency (EF) e pela
heurística ADH2C. Os métodos de discretização EF e EW requerem como parâmetro de
entrada o número de intervalos k a serem gerados. Desse modo, na Tabela 5.7, o valor
5.3
Resultados
dos
Exp
erimen
tos
30
Tabela 5.6: Valores médios de hF obtidos pelo GMNB após a discretização dos atributos pela heurística ADH2C,
ADH2C(0,1) + GMNB
ADH2C(0,2) + GMNB
ADH2C(0,3) + GMNB
ADH2C(0,4) + GMNB
ADH2C(0,5) + GMNB
ADH2C(0,6) + GMNB
ADH2C(0,7) + GMNB
ADH2C(0,8) + GMNB
ADH2C(0,9) + GMNB
5.3 Resultados dos Experimentos 31
médio de hF está destacado em negrito.
Os resultados computacionais obtidos foram submetidos ao teste estatísticoWilcoxon Signed-Rank Test (two sided test) para avaliar se a diferença no desempenho do clas-sificador GMNB ao utilizar as bases de dados pré-processadas pela heurística ADH2C e pelos métodos usados na comparação é estatisticamente significativa (Japkowicz and Shah, 2011). O teste estatístico foi aplicado utilizando-se um nível de confiança de 95%.
O teste estatísticoWilcoxon Signed-Rank Test foi executado para cada comparação, ou seja, entre cada um dos métodos não-supervisionados e a heurística ADH2C. O resultado desse teste é representado na Tabela 5.7 por meio dos símbolos+e−. O símbolo+indica que o resultado associado à heurística ADH2C foi estatisticamente superior ao resultado
associado ao método não-supervisionado em questão. De modo contrário, o símbolo −
indica que o resultado associado à heurística ADH2C foi estatisticamente inferior àquele associado ao método não-supervisionado utilizado na comparação. Além disso, nas duas últimas linhas da Tabela 5.7, é apresentada uma sumarização dos resultados do teste estatístico, ou seja, a quantidade de vezes em que a heurística ADH2C foi estatisticamente superior (linha +) ou inferior (linha −) ao método não-supervisionado representado na coluna correspondente.
A partir dos resultados apresentados na Tabela 5.7 observa-se que, para 7 das 9 bases de dados, o classificador GMNB alcançou o melhor hF médio ao utilizar as bases de dados pré-processadas pela heurística ADH2C. Além disso, para 6 bases de dados, a heurística apresenta desempenho estatisticamente superior a todos os demais métodos utilizados nas comparações. Vale ressaltar que, em apenas 1 das 9 base de dados, a heurística ADH2C apresentou desempenho estatisticamente inferior em relação a alguns métodos de comparação.
Os resultados mostrados nas duas últimas linhas da Tabela 5.7 confirmam a superi-oridade da heurística ADH2C em relação a cada um dos métodos não-supervisionados. Segundo os resultados dos testes estatísticos, em 6 comparações (com EW(5), EW(10), EW(15), EW(20), EF(5) e EF(10)), o desempenho do GMNB associado à heurística ADH2C foi superior àquele associado ao método não supervisionado para 6 bases de da-dos, inferior para apenas 1 base e igual para 2 bases. Em outras 2 comparações (com EF(15) e EF(20)), a superioridade da heurística se mantém para 5 bases de dados e um empate ocorre para as 4 restantes.
experi-5.3
Resultados
dos
Exp
erimen
tos
32
Tabela 5.7: Valores médios de hF obtidos pelo GMNB após a discretização dos atributos,
Bases EW(5)+
GMNB
EW(10)+ GMNB
EW(15)+ GMNB
EW(20)+ GMNB
EF(5)+ GMNB
EF(10)+ GMNB
EF(15)+ GMNB
EF(20)+ GMNB
ADH2C+ GMNB
CellCycle 15,41 (1,75) + 17,08 (1,37) + 18,96 (1,63) + 19,10 (2,03) + 20,83 (1,39) + 24,56 (2,69) + 26,03 (2,21) + 26,55 (2,12) + 34,43 (2,68)
Church 10,90 (1,01) + 11,85 (1,51) + 11,76 (1,41) + 12,63 (1,58) + 10,07 (1,25) + 11,57 (1,31) + 12,00 (1,63) + 13,14 (1,45) + 21,42 (1,49)
Derisi 8,92 (0,75) + 9,31 (1,28) + 9,69 (1,30) + 9,91 (1,14) + 9,36 (1,00) + 10,98 (1,20) + 11,73 (1,07) 11,52 (1,07) 12,41 (1,10)
Eisen 20,74 (2,35) 22,17 (1,42) 22,40 (1,27) 22,49 (1,97) 22,56 (1,33) 22,52 (2,10) 21,86 (2,23) 21,78 (1,70) 22,93 (1,75)
Expr 26,82 (1,69) + 29,62 (1,88) + 32,60 (1,49) + 34,46 (1,27) + 43,91 (1,39) + 45,82 (1,88) + 45,67 (2,35) + 45,54 (2,49) + 47,98 (2,19)
Gasch1 16,80 (1,47) + 18,36 (1,61) + 19,62 (2,27) + 19,36 (2,06) + 18,64 (1,97) + 21,75 (2,33) + 22,38 (1,51) + 22,85 (1,72) + 27,33 (2,61)
Gasch2 14,75 (1,17) + 16,10 (1,47) + 15,77 (1,32) + 16,61 (1,47) + 16,48 (1,70) + 17,59 (1,45) + 19,37 (1,90) + 19,69 (1,68) + 22,67 (2,67)
Sequence 24,02 (1,67)− 24,91 (1,47) – 24,05 (1,11)− 24,05 (1,26)− 21,39 (0,87)− 19,58 (1,03)− 18,83 (1,32) 18,75 (1,15) 18,23 (1,20) SPO 13,77 (1,43) 13,17 (1,19) 13,02 (1,63) 13,62 (0,85) 13,62 (1,41) 14,31 (1,25) 14,84 (1,37) 14,30 (0,78) 13,76 (1,37)
+ 6 6 6 6 6 6 5 5
5.3 Resultados dos Experimentos 33
mento, o número k de partições geradas pelos métodos EW e EF para cada atributo de
cada base de dados foi exatamente igual ao gerado pela heurística ADH2C. Para exem-plificar esse processo, suponha que a heurística ADH2C tenha gerado 6 partições para o
primeiro atributo da base de dados Church. Logo, os métodos EW e EF irão discretizar
o primeiro atributo dessa mesma base utilizando o parâmetro k igual a 6.
A Tabela 5.8 apresenta o desempenho preditivo obtido pelo classificador GMNB uti-lizando as bases de dados pré-processadas pela heurística ADH2C e pelos métodos EW e
EF. O parâmetrok adotado para os métodos EW e EF dependeu do número de partições
geradas pela heurística ADH2C para cada atributo de cada partição. A primeira coluna da Tabela 5.8 contém o nome das bases de dados utilizadas nos experimentos. A partir da segunda até a última coluna dessa tabela são apresentados os valores médios dehF (com seus respectivos desvios-padrões entre parênteses) obtidos pelo classificador GMNB utili-zando as bases de dados pré-processadas pelos métodos EW, EF e pela heurística ADH2C respectivamente. As duas últimas linhas da Tabela 5.8 apresentam uma sumarização dos resultados do teste estatístico, ou seja, a quantidade de vezes em que a heurística ADH2C foi estatisticamente superior (linha+) ou inferior (linha−) ao método não-supervisionado representado na coluna correspondente. Além disso, para cada base de dados, o maior valor médio de hF está destacado em negrito.
Tabela 5.8: Valores médios de hF obtidos pelo GMNB após a discretização utilizando
diferentes valores para o parâmetrok dos métodos EW e EF.
EW + GMNB EF + GMNB ADH2C + GMNB CellCycle 22,15 (2,83) + 29,64 (3,08) + 34,43 (2,68) Church 17,35 (2,21) + 17,85 (1.34) + 21,42 (1,49) Derisi 12,43 (0,90) 12,47 (1,19) 12,41 (1,10)
Eisen 21,26 (2,50) + 21,18 (1,82) + 22,93 (1,75)
Expr 38,81 (1,49) + 44,64 (2,53) + 47,98 (2,19)
Gasch1 20,69 (2,11) + 24,42 (2.32) + 27,33 (2,61) Gasch2 18,15 (1,48) + 21,03 (1.66) + 22,67 (2,67) Sequence 21,55 (1,21) - 18,87 (0,63) 18,23 (1,20)
SPO 13,89 (1,55) 13,65 (1,22) 13,76 (1,37)
+ 6 6
– 1 0
5.3 Resultados dos Experimentos 34
Capítulo 6
Conclusão
A presença de atributos contínuos em bases de dados, algo comum em diversos domínios de aplicação, pode afetar o processo de classificação. Existem algoritmos de classifica-ção que não conseguem lidar com atributos contínuos e outros que, apesar de lidarem, apresentam melhor desempenho preditivo quando todos os atributos da base são discre-tos. Desse modo, verifica-se a importância dos métodos de discretização, que permitem a transformação de atributos contínuos em discretos.
Diversos métodos de discretização podem ser encontrados na literatura para o cenário de classificação plana. Porém, até onde se tem conhecimento, ainda não existem propostas de métodos de discretização supervisionados projetados para serem usados em conjunto com métodos globais de classificação hierárquica.
Portanto, neste trabalho, um método heurístico de discretização supervisionado para bases de dados associadas ao contexto de classificação hierárquica monorrótulo é proposto e avaliado. A heurística proposta, denominadaAgglomerative Discretization Heuristic for Hierarchical Classification - ADH2C, foi projetada para ser utilizada em conjunto com métodos globais de classificação hierárquica.
A heurística ADH2C inicia o processo de discretização criando uma partição para cada valor (ou conjunto de valores) distinto(s) do atributo contínuo. A cada iteração um par de partições adjacentes é fundido e os pontos de corte das partições resultantes são armazenados. Ao final das iterações, o conjunto de pontos de corte melhor avaliado pela heurística é retornado como resultado final da discretização.