Cálculo das reações de engastamento perfeito de mísulas com variação parabólica
Calculation of the perfect cantilever reactions of corbels with parabolic variation
Thiago Junior Moreira Lima1, Maicon José Hilleshein2Resumo: As mísulas com variação parabólica são elementos estruturais que possuem variação da sua seção ao longo do comprimento, característica que permite a adaptação das peças à variação dos esforços. Esta pesquisa apresenta um método para determinar as reações de engastamento perfeito para estes elementos estruturais, as quais são essenciais para a resolução do Método dos Deslocamentos, conhecido pela sua vasta implementação computacional. As reações foram determinadas por meio do Método das Forças aliado a um método de integração numérica, Quadratura de Gauss, por sua resolução depender de integrais complexas decorrentes da divisão de polinômios, solúveis somente por meio de um método de integração numérica. Após serem determinadas, as reações de engastamento perfeito para 3 tipos de mísulas diferentes foram comparadas com bibliografia existente para validação do método. Além disso, avaliou-se o esforço cortante na determinação das reações de engastamento perfeito, que apresentou baixa influência. O processo foi realizado através de uma rotina de programação escrita em Fortran 90 que determina as reações de engastamento perfeito para qualquer tipo de mísula.
Palavras-chave: Mísula; método dos deslocamentos; reações de engastamento perfeito; método das forças; Fortran 90.
Abstract: Corbels with parabolic variation are structural elements which have variation of the section along their length, characteristic that allow adaptation of the elements to the stress variation. This research presents a method to determinate the perfect cantilever reactions to theses structural elements, which are essential to the resolution of Method of Displacement, known for its computer implementation. The reactions were determined by the Method of Forces allied with a numeric integration method, Gauss Quadrature, due to its resolution be dependent of complex integrals resulting from polynomials divisions, only solved by a numeric integration method. After being determined, the perfect cantilever reactions for 3 different corbels they were compared to existent bibliography for method validation. Furthermore, this research evaluated the shear stress on determination of the perfect cantilever reactions, which presented low influence. The process was done by a program routine written in Fortran 90 that determines the perfect cantilever reactions for any type of corbels.
Keywords: Corbels; method of displacement; perfect cantilever reactions; method of forces; Fortran 90. 1 Introdução
As mísulas são elementos estruturais muito comuns em obras com grandes vãos, como pontes, barracões, viadutos, etc. São barras que possuem variação de sua seção transversal ao longo de seu comprimento. Comumente, as mísulas são encontradas em estruturas que contêm grau de hiperestaticidade igual ou maior a um, devido a este fato, para determinação dos esforços solicitantes utiliza-se algum método de análise estrutural (Método das Forças, Método dos Deslocamentos, Método de Cross, etc), sendo o Método dos deslocamentos o mais utilizado, por sua fácil implementação computacional.
O Método dos Deslocamentos (MD) consiste na determinação do vetor de carga, composto pelas cargas nodais somadas às reações de engastamento perfeito, e os coeficientes de rigidez local das barras, com essas grandezas se monta um sistema de equações e permite calcular os deslocamentos nodais. A partir deles é possível determinar as reações de apoio e os esforços solicitantes da estrutura, essenciais para o dimensionamento estrutural.
Para a determinação das reações de engastamento perfeito em mísulas curvas, foco deste trabalho, será utilizado o Método das Forças (MF), onde os cálculos
dos coeficientes de flexibilidade e dos termos de carga recairão na resolução de integrais complexas advindas da formulação do princípio dos trabalhos virtuais.
A complexidade destas integrais é dada pela variação da seção ao longo do comprimento, ocorrem integrais de divisões de polinômios, as quais não podem ser resolvidas de forma analítica. Assim é necessária a utilização de ·métodos numéricos, neste trabalho será utilizado a Quadratura de Gauss.
Aliando as rotinas de computação com o processo de análise estrutural explicito neste trabalho, serão determinadas as reações de engastamento perfeito com baixo processamento computacional.
Quando o objetivo de um programa computacional é determinar a matriz de rigidez e as reações de engastamento perfeito de barras prismáticas há formulações analíticas prontas, porém ao se tratar de mísulas o mesmo não acontece, havendo pouco material pronto, e algumas poucas pesquisas sobre o assunto. Assim há a necessidade da criação de rotinas e formulações para o cálculo delas.
Para validação da rotina e formulação criadas neste trabalho será feito a comparação com outras bibliografias como Sussekind (1977) e Vilela (2008). Além disso será analisada a influência do esforço cortante nas reações de engastamento perfeito. 1 Graduando em Engenharia Civil, UNEMAT, Sinop, Brasil,
thiagomolima@hotmail.com
2 Mestre, Professor, UNEMAT, Sinop, Brasil,
2 Referencial Teórico
2.1 Mísulas
São barras com seção variável ao longo do seu comprimento, devido a isso possuem também a inércia variável ao longo da peça. Esse tipo de elemento estrutural permite aumentar a rigidez aonde a solicitação é maior, comumente o aumento da seção esta relacionado ao momento fletor elevado proximo aos apoios.
2.1.1 Classificação de mísulas
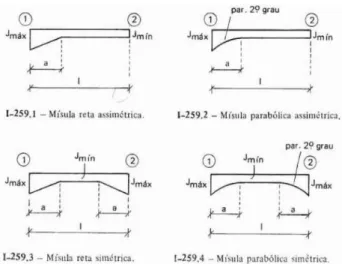
As mísulas podem ser classificadas de acordo com a variação de sua altura e com a simetria da peça. Em relação a sua altura, elas podem ser classificadas como reta ou parabólica, dependendo da forma a qual a curva da peça se aproxima.
Na Figura 1, referente ao Viaduto Machadinho, localizado em Natal, Rio Grande do Norte, pode-se observar o exemplo de uma mísula reta, em que há uma grande variação de seção proximo ao apoio.
Figura 1: Viaduto Machadinho em Natal. Fonte: http://nataltrip.com.br/_padrao/cartoes/car_19.jpg. Acesso
em outubro de 2015.
Na Figura 2 pode-se observar a ponte Rio-Niterói, nota-se a variação da seção com a forma semelhante a uma parábola de 2º grau.
Figura 2: Ponte Rio-Niterói. Fonte:
http://brasilconstrucao.com.br/?p=2098. Acesso em outubro de 2015.
As mísulas retas e parabólicas podem ser classificadas de acordo com a simetria caso ela exista ou não na peça, como mostrado nas figuras a seguir:
Figura 3: Classificação de mísulas em relação a simetria. Fonte: SUSSEKIND, 1973.
2.2 Teoria de Viga de Navier
Para determinação dos métodos de análise estrutural, em específico o das forças e o dos deslocamentos, se considera válida a Teoria da Viga de Navier que apresenta as seguintes hipóteses básicas, segundo Martha (2010):
Deslocamentos são pequenos em relação às dimensões da seção transversal.
Desprezam-se deformações por
cisalhamento (barras longas, isto é, comprimento é bem maior que a altura da seção)
Seções transversais permanecem planas e normais ao eixo da barra quando esta se deforma (Hipótese de Bernoulli).
Material tem comportamento elástico-linear (Lei de Hooke).
O material é isotrópico, ou seja, apresenta as mesmas propriedades para qualquer direção. 2.3 Princípio do Trabalho Virtual
Como em muitos outros métodos de análise estrutural, o Princípio do Trabalho Virtual (PTV) é baseado na conservação de energia. (HIBELLER, 2010).
Segundo Hibeller (2010), as cargas e deslocamentos de um corpo impedido de se mover devem atender respectivamente as condições de equilíbrio e de compatibilidade. Especificamente, as cargas externas e internas do corpo estão relacionadas para atender as condições de equilíbrio e os deslocamentos externos e internos estão relacionados para atender as condições de compatibilidade.
P
=
u
Equação 1 Onde::
P
Cargas externas;:
Deslocamentos externos;:
Deslocamentos internos;:
u
Cargas internas.Ainda segundo Hibeller (2010), a partir deste conceito pode se desenvolver o PTV de modo que ele possa ser usado para determinar o deslocamento em qualquer ponto de um corpo.
Para determinar o deslocamento em algum ponto qualquer é aplicada uma força imaginária ou virtual, de carga unitária, na mesma direção do deslocamento que se deseja encontrar, vale ressaltar que este caso é feito antes da aplicação das cargas reais da estrutura.
A aplicação desta carga virtual externa cria uma carga virtual interna, ambas também produzem deslocamentos virtuais e podem ser relacionadas pela equação 2. Aplicando as cargas reais, ocorrerão deslocamentos reais das forças virtuais previamente aplicadas, considerando somente a conservação de energia virtual, o trabalho virtual é igual ao externo, podendo escrever a seguinte equação:
u
dL
P
'
Equação 2Onde:
'
P
: a carga virtual externa unitária que age na direção de
;
: deslocamento externo provocado pelas cargas reais;u
: carga virtual interna que age sobre o elemento;dL
: deslocamento interno do elemento na direção deu
, provocado pelas cargas reais.Pode-se substituir a parte direita da equação 2, referente ao trabalho virtual interno, com as equações de energia de deformação decorrentes das tensões resultantes de esforços normais, cortantes, fletores e torsores.
Assim a equação pode ser reescrita como:
L s LL L
dx
GJ
tT
dx
GA
vV
f
dx
EI
mM
dx
AE
nN
P
0 0 0 0'
Equação 3 Em que::
,
,
,
m
v
t
n
São os esforços solicitantes na estruturaquando aplicada a carga virtual;
:
,
,
,
M
V
T
N
São os esforços solicitantes na estrutura quando aplicado as cargas reais.:
s
f
É o fator de forma para cisalhamento;:
I
Momento de inércia;:
J
Momento de inércia transversal;:
E
Módulo de elásticidade;:
G
Módulo de elasticidade transversal.2.4 Método das Forças
Segundo Martha (2010), o Método das Forças (MF) é um método clássico para resolução de estruturas hiperestáticas, e leva em consideração três condições básicas: as condições de equilíbrio, condições de compatibilidade e condições relacionadas ao material presente na estrutura. Seu processo é uma soma de soluções básicas que satisfazem as condições de equilíbrio, mas não as de compatibilidade, com a superposição dessas soluções básicas consegue-se reestabelecer as condições de equilíbrio.
A aplicação do método consiste primeiramente na escolha de um sistema principal isostático semelhante ao real, hiperestático, substituindo g reações de apoio, sendo esta váriavel o grau de hiperestaticidade, por uma carga unitária virtual de mesmo sentido. Analisam-se os casos relacionados às carregamentos externos e forças virtuais separadamente, assim determinando os deslocamentos na estrutura isostática.
Devido ao fato do deslocamento de um hiperestático ser igual a 0, considerando sua rigidez, pode-se somar os casos para reestabelecer a sua condição de deslocamento nulo pela seguinte equação de compatibilidade:
0
0
1 1 1 1 0 ) 1 ( 1 1 0 i j i i j i i i ij i ij iX
X
X
X
Equação 4 Onde::
iX
Hiperestáticos, sendo i o índice que varia de 1 a g;:
0 i
Termo de carga de rotação ou de deslocamento;:
ij
Coeficiente de flexibilidade podendo ser de deslocamento ou de rotação.Para a determinação destes deslocamentos se utiliza o conceito previamente apresentado para determinação, o PTV. Assim para determinação dos termos de carga e os coeficientes de flexibilidade temos as seguintes equações:
L i i s i i idx
GJ
T
t
GA
V
v
f
EI
M
m
EA
N
n
0 0
Equação 5
L i j i j s i j i jij
dx
GJ
t
t
GA
v
v
f
EI
m
m
EA
n
n
0
Equação 6i
n
,m
i,v
i,t
i: são os esforços solicitantes na estrutura com força unitária no caso i.j
n
,m
j,v
j,t
j: são os esforços solicitantes na estrutura com força unitária no caso j.Assim determinado os termos de carga e coeficientes de flexibilidade é possivel resolver a Equação 4 e encontrar os valores dos hiperestáticos.
2.5 Método dos Deslocamentos
É o método de análise estrutural mais utilizado em programações automáticas, devido ao seu amplo uso na computação, é considerado o método mais importante (SORIANO e LIMA, 2006).
De acordo com Martha (2010):
“O método dos deslocamentos tem como ideia básica determinar, dentro do conjunto de soluções em deslocamentos que satisfazem as condições de compatibilidade, qual solução faz com que as condições de equilíbrio também sejam satisfeitas.”
Segundo Soriano e Lima (2006) o MD possui a seguinte sistemática:
Escolha de um sistema principal em que os deslocamentos considerados como graus de liberdade da estrutura estejam restringidos. Esses deslocamentos são as incógnitas primárias a determinar (com sentidos positivos arbitrados)
Cálculo dos esforços de engastamento perfeito e combinação desses esforços, com sinais contrários com as forças externas diretamente aplicadas segundo os referidos deslocamentos, para obtenção das forças nodais combinadas.
Cálculo dos coeficientes de rigidez das barras e, a partir desses, obtenção dos coeficientes de rigidez da estrutura.
Montagem e resolução do sistema de equações de equilíbrio para determinação dos referidos deslocamentos.
Obtenção dos deslocamentos nodais incógnitos.
Cálculo dos esforços solicitantes na estrutura.
2.6 Reações de Engastamento Perfeito
Fazem parte da solução fundamental do método dos deslocamentos, consistem em reações de apoio para uma barra com as extremidades engastadas (deslocamentos e rotações restritas nas extremidades) resultantes da aplicação de uma solicitação externa (MARTHA 2010).
Para barras prismáticas há formulações analíticas prontas, pois, devido à uniformidade da inércia ao longo da peça, a mesma não influencia nos esforços, logo se considera apenas o comprimento e o carregamento aplicado na peça, como se pode observar na figura a seguir:
Figura 4: Reações de engastamento perfeito de barra prismática. Fonte: MARTHA, 2010.
Para mísulas não há formulação analítica de simples resolução, porém existem tabelas no livro Curso de Análise Estrutural III (SUSSEKIND, 1973), em que tendo o valor máximo e mínimo de inércia de uma peça, além do ponto da peça em que se inicia a inércia mínima é possivel encontrar as reações de engastamento perfeito para determinados carregamentos externos. Entretanto a formulação é pouco prática não é aplicável para qualquer relação de inércias e comprimentos.
2.7 Quadratura de Gauss
Devido à presença de integrais de divisão de polinomios no cálculo dos termos de carga e coeficientes de flexibilidades, é necessário a utilização de um método númerico para determinação destas integrais.
A Quadratura de Gauss, também conhecido como Método de Gauss-Legendre, é comumente aplicada em rotinas programadas e apresenta ótimo desempenho e precisão com baixo custo de processamento computacional (AZEVEDO, 2003). Este método consiste na avaliação de uma função cujo domínio deve estar transformado em coodernadas naturais no intervalo [-1;1] em n pontos de Gauss, determinado pela equação:
2
)
1
(
p
n
Equação 7Onde:
n
: É o numero de pontos de Gauss;p
: É o grau do polinômio.Com a quantidade de pontos de Gauss determinada, se retira de tabelas como Azevedo (2003) duas variáveis,
W
i, o peso que sera atribuído ao valor do ponto, eP
i, ponto em que será determinado o valor da equação analisada em coodernadas naturais. Assim o resultado da integral é encontrado pela seguinte equação:
nr ii i
f
P
W
dr
n
f
1 1
1
)
(
)
2.8 Coordenadas Naturais
São transformadas as coordenadas locais em naturais através das seguintes equações (AZEVEDO, 2003):
) ( )
( )
(
) ( )
( )
( )
( A iAj B iBj C iCj
i h x h x h x
x
Equação 9) ( )
( )
(
) ( )
( )
( )
( A iAj B iBj C iCj
i h y h y h y
y
Equação 10Em que:
i
y
,x
i:são as coordenadas locais nos determinados pontos A, B, C;
: é o intervalo de [-1;1];A
h
,h
B,h
C: são funções de forma determinadas pelas equações:)
1
(
2
1
)
(
A
h
Equação 11)
1
)(
1
(
)
(
B
h
Equação 12)
1
(
2
1
)
(
C
h
Equação 13Essas funções possuem o seguinte comportamento apresentado pela Figura 5:
Figura 5: Comportamento das curvas das funções de forma. Fonte: AZEVEDO, 2003.
Além disso, há a necessidade de multiplicação pelo jacobiano da transformação de coordenadas locais para naturais que é dado pela equação:
2
)
(
d dx
J i Equação 14
3 Metodologia
3.1 Mapeamento da Mísula
Para a análise de uma mísula qualquer, primeiramente é necessária a transformação de suas coordenadas locais em naturais.
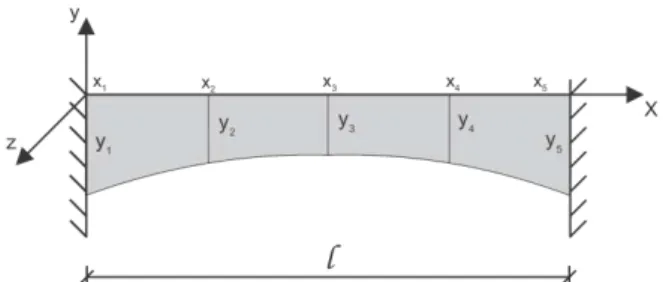
Foi utilizado como modelo uma mísula com suas seções determinadas em 5 pontos, em que não há a obrigatoriedade de simetria, pois a mesma é aproximada em curva pela rotina. O modelo pode ser visto na figura a seguir:
Figura 6: Mísula referenciada em coordenadas locais. Fonte: Arquivo pessoal, 2015.
Desta forma, pela utilização das funções de forma a mesma mísula é reescrita em coodernadas naturais, para que assim, a sua integração seja possível pela Quadratura de Gauss tendo a seguinte disposição:
Figura 7: Mísula referenciada em coordenadas naturais. Fonte: Arquivo pessoal, 2015.
A partir deste novo modelo é possível a determinação dos termos de carga e coeficientes de flexibilidade. 3.2 Pontos de Gauss
Para a resolução da Quadratura de Gauss foi determinado a utilização de 6 Pontos de Guass, esta escolha foi baseada em Rosebanch (2015), em que foi atrelado a 6 pontos de Gauss altíssima precisão para resolução de problemas com mísulas parabólicas.
Podem ser observados na Tabela 1 os
W
i e osP
ique serão utilizados.
Tabela 1. Pesos e Pontos referentes a Quadratura de Gauss com 6 Pontos De Gauss
Wi Pi0 -0,9324695142 0,1713244923 1 -0,6612093864 0,3607615730 2 -0,2386191860 0,4679139345 3 0,2386191860 0,4679139345 4 0,6612093864 0,3607615730 5 0,9324695142 0,1713244923
Fonte: Azevedo, 2003
3.3 Determinação das Reações de Engastamento Perfeito
Figura 8: Exemplo de mísula biengastada com carregamento genérico q(x). Fonte: Arquivo pessoal, 2015
Aplica-se o MF previamente apresentado, para se determinar as reações de engastamento perfeito, Como se trata de uma viga biengastada, onde não há presença de esforços horizontais, o seu grau de hiperestaticidade é igual à 2. Assim é necessário retirar 2 reações de apoio e criar dois casos com reações unitárias, a partir destas soluções se determinam os termos de carga e coeficientes de flexibilidade para somá-los e cumprir as condições de equilíbrio.
Desta forma, a equação de compatibilidade, apresentada pela Equação 4, é reescrita levando em conta o grau de hiperestaticidade da mísula apresentada.
0
0
2 22 1 21 20 2 12 1 11 10
X
X
X
X
Equação 17Aplicando os conceitos da Quadratura de Gauss nas equações5 e 6, e considerando apenas os esforços relacionados ao momento fletor e cisalhamento, elas ficam reescritas da seguinte forma:
i i nel j npi i i s i
i
J
w
GA
V
v
f
EI
M
m
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1 10
Equação 15 i i nel j npi i j i s j iij
J
w
GA
v
v
f
EI
m
m
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1 1
Equação 16 Onde:nel
: É o numero de elementos que a mísula esta dividida (2).npi
: É o número de Pontos de Gauss (6).Resolvendo-se o sistema, encontram-se os valores de
1
X
eX
2, que são os momentos de engastamento perfeito. Com estes momentos determinados podem-se determinar as outras reações da peça por meio de conceitos de isoestática, assim determinando as reações verticais de engastamento perfeito.3.4 Implementação Computacional
Com todo o processo previamente determinado, é possível a criação de um algoritmo em um compilador para o processo automático de cálculo, sendo necessária a informação apenas de parâmetros básicos como as coordenadas locais, largura da peça, módulo de elasticidade e carregamento externo. Que resultará sem esforço ao usuário as reações de
engastamento perfeito. Este processo pode ser visto no fluxograma apresentado pela figura 8.
Figura 9: Fluxograma do algoritmo. Fonte: Arquivo pessoal, 2015.
Todo o processo será automizado atráves de rotinas e sub-rotinas escritas em linguagem de computação Fortran 90, conhecida pelo uso extensivo em campos da matemática e engenharia e baixo uso de processamento computacional (ADAMS et al. 1992). 3.4 Tabelas Sussekind
Para efeito de validação da rotina programada e das considerações feitas, será feito a comparação dos resultados obtidos, com tabelas impressas no livro Curso de Análise estrutural vol. 3 de Sussekind, 1973. No entanto, Sussekind relaciona alguns parâmetros que devem ser previamente explicitados.
Para mísulas parabólicas assimétricas, como a apresentada pela figura 9, há uma relação direta entre as inércias nos pontos extremos da barra, A e B,
A B
I
I
/
que varia de 1,00 a 0,005 nas tabelas.Figura 10: Mísula parabólica assimétrica. Fonte: Arquivo pessoal, 2015.
Desta forma, para esta barra e para o seguinte esquema exemplificado na figura a seguir é possível determinar o momento de engastamento perfeito pelas equações 18 e 19.
12
2
1
ql
k
M
A
Equação 1712
2
2
ql
k
M
b
Equação 18Aonde:
1
k
ek
2são coeficientes de rigidez à rotação encontrados nas tabelas pela relaçãoI
B/
I
A. No caso de mísulas parabólicas simétricas, Figura 11, a relação é feita entre os pontos iniciais da barra e o seu centro, onde a inércia é menor. Como há semelhança entre os 2 lados da mísula, a tabela apresenta apenas o coeficientek
1 pois parak
2 a unica mudança é o sentido do momento, que é contrário.Figura 12: Mísula parabólica simétrica. Fonte: Arquivo pessoal, 2015.
4 Apresentação e Análise de Resultados
Foram feitas análises de 3 mísulas de diferentes formas, parabólica simétrica, parabólica assimétrica e reta assimétrica. Além disso, a primeira análise leva em conta apenas o esforço relacionado aos momentos fletores, ja ná segunda análise foi analisado também o esforço cortante.
4.1 Mísula Parabólica Simétrica
A figura 12 mostra o modelo de mísula que foi utilizado na sub-rotina para encontrar os valores das reações de engastametno perfeito e comparar com a tabela de Sussekind.
Figura 13: Exemplo de mísula parabólica simétrica. Fonte: Arquivo pessoal, 2015.
Foram utilizados os seguintes dados:
Comprimento de 10 metros;
Largura de 1 metro;
5 pontos em coodernadas locais;
2 sub-elementos;
Módulo de Elasticidade de 200 GPa
Alturas variáveis a partir de uma função parabólica de 2º grau, de forma que atenda a relação
I
B/
I
A de 1,000 a 0,005.Encontrado os momentos de engastamento perfeito pelo algoritmo, foi então determinado o coeficiente
k
1e comparado com a tabela de Sussekind como demonstrado na Tabela 2.
4.2 Mísula Parabólica Assimétrica
Da mesma forma e com os mesmos parâmetros utilizados pela mísula simetrica foram determinados os coeficientes
k
1 ek
2 a partir do modelo apresentado pela Figura 13.Figura 14: Exemplo de mísula parabólica simétrica. Fonte: Arquivo pessoal, 2015.
Foram então comparados os resultados obtidos com as tabelas como apresentado na Tabela 3
4.3 Mísula Reta
Para validação do método desenvolvido e sua capacidade de se adaptar a qualquer tipo de variação de altura, foram determinadas as reações de engastamento perfeito para a mísula reta na figura a seguir.
Figura 15: Exemplo de mísula reta. Fonte: Arquivo Pessoal, 2015.
Comparou-se os resultados obtidos com Sussekind e Vilela (2008), que desenvolveu um trabalho exclusivo com mísulas retas, obtendo os resultados da tabela 4.
IB/IA 1 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,12 0,10 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1(MF) 1,000 1,014 1,029 1,046 1,065 1,087 1,113 1,145 1,186 1,213 1,233 1,248 1,266 1,287 1,299 1,314 1,331 1,352 1,384 1,408 k1(S) 1,000 1,014 1,029 1,046 1,065 1,087 1,113 1,145 1,186 1,213 1,233 1,248 1,266 1,287 1,299 1,314 1,331 1,352 1,384 1,408
Tabela 2. Comparação entre coeficiente k1 obtido pela formulação do Método das Forças (MF) e por Sussekind (S) para mísula
parabólica simétrica.
4.4 Análise dos resultados
Observando os resultados obtidos nas tabelas 2, 3 e 4, aonde se tem os coeficientes encontrados pela formulação deste trabalho e os advindos de Sussekind (1973) e Vilela (2008). É possível afirmar a validade e competência do algoritmo desenvolvido por este trabalho.
4.5 Análise do efeito da cortante
Foram analisadas as mísulas previamente apresentadas nos Tópicos 4.1, 4.2 e 4.3, levando em conta o esforço cortante e momento fletor.
Devem ser levados em conta os parâmetros anteriormente apresentados e os seguintes relacionados ao esforço cortante:
Fator de forma igual a 1,20;
Módulo de elasticidade transversal de 76,92 GPa.
Os resultados obtidos podem ser observados nas Tabelas 5, 6 e 7.
Comparando as Tabelas que levam em consideração apenas o momento fletor, e as que consideram momento fletor e esforço cortante, pode-se observar a baixa influência, porém esta influencia é importante observar quando se pretende fazer um cálculo estrutural exato.
5 Conclusões
Nesta pesquisa desenvolveu-se um algoritmo capaz de determinar as reações de engastamento perfeito de mísulas parabólicas. Podendo ser levado em conta o efeito do esforço cortante.
A análise do programa é feita a partir dos dados inseridos, como coordenadas locais, módulo de elasticidade, largura da peça e carregamentos. Devido a sua propriedade de aproximar as coordenadas apresentadas à uma curva, a mesma formulação é capaz de determinar as reações de engastamento perfeito para barras prismáticas, mísulas retas e parabólicas simétricas e assimétricas.
IB/IA 1 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,12 0,10 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1(MF) 1,000 1,025 1,053 1,086 1,124 1,170 1,229 1,307 1,421 1,506 1,572 1,628 1,697 1,789 1,847 1,920 2,016 2,153 2,391 2,632 k1(S) 1,000 1,025 1,053 1,086 1,124 1,770 1,229 1,307 1,421 1,505 1,572 1,628 1,697 1,789 1,847 1,920 2,012 2,153 2,391 2,632 k2(MF) 1,000 0,983 0,963 0,941 0,916 0,887 0,852 0,808 0,748 0,707 0,676 0,651 0,622 0,586 0,563 0,536 0,503 0,458 0,389 0,327 k2(S) 1,000 0,983 0,963 0,941 0,916 0,887 0,852 0,808 0,748 0,707 0,676 0,652 0,622 0,586 0,563 0,536 0,504 0,458 0,389 0,327
Tabela 3. Comparação entre coeficientes k1 e k2 obtidos pela formulação do Método das Forças (MF) e por Sussekind (S) para
mísula parabólica assimétrica.
IB/IA 1 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,12 0,10 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1(MF) 1,000 1,021 1,045 1,073 1,105 1,144 1,192 1,256 1,349 1,416 1,469 1,513 1,567 1,638 1,683 1,739 1,812 1,916 2,094 2,274 k1(S) 1,000 1,018 1,043 1,071 1,110 1,146 1,193 1,255 1,348 1,416 1,469 1,513 1,571 1,638 1,683 1,739 1,812 1,916 2,095 2,274 k1(V) 1,000 1,021 1,045 1,073 1,105 1,144 1,192 1,256 1,349 1,416 1,469 1,513 1,567 1,638 1,683 1,739 1,812 1,916 2,095 2,274 k2(MF) 1,000 0,979 0,956 0,930 0,901 0,867 0,826 0,776 0,708 0,663 0,629 0,602 0,570 0,531 0,507 0,479 0,445 0,400 0,331 0,272 k2(S) 1,000 0,978 0,955 0,931 0,897 0,865 0,826 0,777 0,709 0,663 0,629 0,602 0,566 0,531 0,507 0,479 0,445 0,400 0,331 0,272 k2(V) 1,000 0,978 0,956 0,930 0,901 0,867 0,826 0,776 0,708 0,663 0,629 0,602 0,570 0,531 0,507 0,479 0,445 0,400 0,331 0,272
Tabela 4. Comparação entre coeficientes k1 e k2 obtidos pela formulação do Método das Forças (MF), por Sussekind (S) e
Vilela (V) para mísula reta. Fonte: Arquivo Pessoal, 2015.
Fonte: Arquivo Pessoal, 2015.
IB/IA 1 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,12 0,10 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1 1,000 1,014 1,029 1,046 1,065 1,087 1,113 1,145 1,186 1,213 1,233 1,248 1,266 1,287 1,299 1,314 1,331 1,352 1,384 1,408
Tabela 5. Coeficiente k1 considerado o efeito cortante para mísula parabólica simétrica.
Fonte: Arquivo Pessoal, 2015.
IB/IA 1 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,12 0,10 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1 1,000 1,025 1,053 1,085 1,123 1,170 1,228 1,305 1,420 1,504 1,570 1,626 1,695 1,787 1,845 1,918 2,014 2,150 2,389 2,630 k2 1,000 0,983 0,963 0,941 0,917 0,888 0,853 0,809 0,749 0,708 0,677 0,653 0,623 0,586 0,564 0,537 0,504 0,459 0,389 0,328
Tabela 6. Coeficiente k1 e k2 considerado o efeito cortante para mísula parabólica assimétrica.
Fonte: Arquivo Pessoal, 2015.
IB/IA 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,15 0,12 0,1 0,08 0,06 0,05 0,04 0,03 0,02 0,01 0,005 k1 1,000 1,021 1,045 1,072 1,105 1,143 1,191 1,255 1,347 1,414 1,467 1,511 1,565 1,636 1,681 1,737 1,810 1,914 2,092 2,271 k2 1,000 0,979 0,956 0,931 0,901 0,867 0,827 0,777 0,709 0,663 0,630 0,603 0,571 0,532 0,508 0,480 0,446 0,400 0,331 0,272
Tabela 7. Coeficiente k1 e k2 considerado o efeito cortante para mísula reta.
A comparação dos resultados obtidos pela formulação criada com bibliografia existente valida a eficácia do algoritmo. Além disso, observado o efeito do esforço cortante ele se mostrou ser de baixa influência para determinação das reações de engastamento perfeito. Por se inserir apenas parâmetros básicos, é possível encontrar as reações de engastamento perfeito para qualquer relação de inércia e curva, o que não é possivel pelas formulações ja existentes, pois as tabelas de Sussekind determinam valores apenas para certas relações de inércia.
Portanto, a utilização desta rotina é mais viável que formulações já prontas devido ao seu alto grau de liberdade de moldagem da curva, velocidade de determinação dos resultados e baixa utilização de capacidade processional do computador.
Agradecimentos
Agradeço a minha mãe, Fátima de Marco Lima (in memoriam), pelo amor imensurável e a vida que me proveu.
À minha família como um todo, pelo amor e paciência incondicional durante todos os anos de minha vida.
Ao amigo, irmão, Rafael “44/23” pelo companherismo
de 15 anos e constante suporte na jornada dessa vida.
À Emília pelo carinho e apoio incessantes em diversos períodos de minha vida, além de todo o auxílio diário no desenvolvimento deste trabalho.
Agradeço a Eric Francio Severo (in memoriam) pelo grande exemplo de amizade e felicidade que tive na minha vida, ao qual devo a metade do tesouro “One Piece” quando encontrá-lo.
Ao meu orientador, Maicon José Hilleshein pelo auxílio constante e indispensável para a realização desta pesquisa.
À Universidade do Estado de Mato Grosso –
UNEMAT por toda a estrutura existente para o curso de Engenharia Civil, além de todos os professores que poderam em auxiliar em minha formação.
Aos diversos colegas que fiz durante a graduação e me apoiaram durante a realização desta pesquisa, especialmente à Jamilly, Mateus, Raul, Fran, Mirian, Deisy, Daniele.
E a todos os outros que não foram citados, mas me apoiaram de alguma forma.
Referências
ADAMS, J. C.; BRAINERD W. S.; MARTIN B. T.; WAGENER J. L. Fortran 90 Handbook: Complete ANSI/ISO Reference. 1ª ed. New York: Mcgraw-Hill Book Company, 1992.
AZEVEDO, A. F. M. Método dos Elementos Finitos. 1ª. ed. [S.l.]: [s.n.], 2003.
HIBBELER, R. C. Resistência dos Materiais. 7ª. ed. São Paulo: PEARSON, 2010.
MARTHA, L. F. Análise de Estruturas: Conceitos e Métodos Básicos. 2ª. ed. Rio de Janeiro: Elsevier, 2010.
ROSENBACH, D. V.; HILLESHEIN, M. J. Cálculo da matriz de rigidez de mísulas com variação parabólica, 2015. 8p. Trabalho de conclusão de curso, Graduação em Engenharia Civil, Universidade do Estado de Mato Grosso, Sinop, MT.
SORIANO, H. L.; LIMA, S. S. Análise de Estruturas: Método das Forças e Método dos Deslocamentos. 2ª. ed. Rio de Janeiro: Ciência Moderna Ltda, 2006. SUSSEKIND, J. C. Curso de Análise Estrutural: Método das Deformações e Processo de Cross. 7ª. ed. Rio de Janeiro: Globo, v. 3, 1987.