Universidade Federal da Paraíba
Centro de Ciências Exatas e da Natureza
Departamento de Física
Dissertação
Gerando modelos de dois campos
escalares
Francisco Artur Pinheiro Alves Júnior
Jõao Pessoa
-2012-Universidade Federal da Paraíba
Centro de Ciências Exatas e da Natureza
Departamento de Física
Dissertação de Mestrado
Gerando modelos de dois campos
escalares
Francisco Artur Pinheiro Alves Júnior
Dissertação submetida ao Departamento de
Física da Universidade Federal da Paraíba,
sob orientação do professor Laércio Losano,
como parte dos requisitos para obtenção do
título de Mestre em Física.
João Pessoa
-2012-Agradecimentos
• Agradeço à Deus.
• Agradeço aos meu pais e familiares por todo apoio nanceiro e moral, em especial a minha mãe a meu irmão, Emanuel Abdalla, e a meu pai, e também ao Tio Hélder e à Tia Etiene.
• Agradeço à Ana Martins pelo apoio durante o curso de mestrado.
• Agradeço ao professor Laércio pela grande ajuda na confecção deste trabalho.
• Agradeço aos meus amigos da UFPB.
• Aos meus amigos da UFC.
• Aos meus amigos da Soparia e Lanchonete Zonna Sul.
"...Deixa eu te dizer um coisa que já sabe. O mundo não é um mar de rosas, é um lugar ruim e asqueroso. E não importa quão durão você é, ele te deixara de joelhos e manterá assim se permitir. E nem você nem eu, nem ninguém baterá tao forte quanto a vida. Mas isso não se trata de quão forte você pode bater, se trata de quão forte você pode ser atingido e continuar em frente, quanto pode continuar recebendo e continuar em frente. È assim que a vitória é conquistada! Agora se você sabe seu valor vá e conquiste!..."
Sumário
Agradecimentos i
1 Introdução 3
2 Teoria de Campos escalares 5
2.1 Modelo com um campo escalar . . . 5
2.1.1 Consideração sobre a energia. . . 6
2.1.2 Análise da estabilidade . . . 8
2.1.3 Estados BPS . . . 9
2.1.4 O modelo φ4 . . . 10
2.2 Modelos com dois campos escalares . . . 11
2.2.1 Modelo BNRT. . . 14
3 Gerando modelos de um campo 16 3.1 Método da deformação. . . 16
3.2 O Modelo seno-Gordon . . . 17
3.3 O Modelo p . . . 19
4 Gerando modelos de dois campos 22 4.1 Introduzindo o novo método . . . 23
4.2.1 Reproduzindo o BNRT . . . 25
4.2.2 Reproduzindo outros modelos polinomiais . . . 27
Abstract
We focus this work in scalar eld theory. We review the basic aspects of models containing one scalar eld, like the φ4, and the two scalars eld theory, like the BNRT. We still review the deformation procedure, in order to generate new soluble one eld models. The main result is concerned to a new procedure wich makes possible to generate new two eld models and its static solutions.
Resumo
Focamos este trabalho em teoria de campos escalares. Revisamos os aspectos básicos dos modelos contendo um campo, como o λφ4 e modelos contendo dois campos escalares, como o BNRT. Ainda, revisamos o procedimento de deformação, para gerar novos modelos solúveis com um campo escalar. Nosso principal resultado é um novo procedimento que possibilita a geração de modelos solúveis de dois campos escalares.
Capítulo 1
Introdução
Com a utilização dos campos escalares podemos modelar diversos fenô-menos na Natureza [1,2]. Isso é interessante pois insere esta linha de pesquisa em outras frentes de investigação da Física, como destacamos a seguir.
Em cosmologia, o campo escalar é usado para representar a energia es-cura, e assim tratar da expansão acelerada do Universo [3,4]. Em física de partículas, ele aparece como o campo de Higgs [5], responsável pela geração da massa das partículas fundamentais. Em matéria condensada, o campo es-calar pode aparecer através de defeitos topológicos, como um kink, espécie de zona separando duas fases distintas de um determinado sistema, como ocorre nas paredes de Bloch [6]. Outro tipo de defeito comum também aparecer em congurações do tipo vórtices, como no caso dos supercondutores [7]. Na química e na biologia, o campo escalar representa determinadas oscilações em cadeias poliméricas, como é o caso do DNA [8] e do polietileno. Neste caso, por exemplo, se consegue descrever congurações de twistons, que são ondas associadas ao movimento de rotação dos hidrogênios em cada unidade
Capítulo 2
Teoria de Campos escalares
Neste capítulo, discutimos as ferramentas utilizadas em teoria de campos escalares na descrição de defeitos. Tomamos como ponto de partida modelos com um campo escalar. Em seguida, revisamos aspectos básicos de teorias que envolvem dois campos escalares.
2.1
Modelo com um campo escalar
Em Teoria de Campos, os defeitos são representados pelas soluções es-táticas das equações de movimento. Para obter essas equações, recorremos ao formalismo Lagrangiano. A quantidade importante nesse tratamento é a ação S, que é a integral de uma densidade lagrangeana, L(φ, ∂µφ), no espaço-tempo (3+1). Assim
S =
Z
L(φ, ∂µφ)d~xdt. (2.1)
Do princípio da mínima ação temos a equação de Euler-Lagrange
∂µ
∂L ∂(∂µφ)
A densidade lagrangiana utilizada neste caso é dada por
L= 1 2∂µφ∂
µφ
−V(φ). (2.3)
Onde o primeiro elemento da lagrangiana contem o termo cinético, ∂φ ∂t
2 , e o termo gradiente, (∇φ)2. O outro é denominado termo potencial, que em geral é uma função não-linear do campo. Assim, a equação de movimento toma a forma
∂µ∂µφ+
d
dφV(φ) = 0. (2.4)
No espaço de (1+1) dimensional, rescrevendo equação anterior na forma
∂2φ
∂t2 −
∂2φ
∂x2 +
d
dφV(φ) = 0, (2.5)
que para soluções estáticas, φ =φ(x), se reduz a:
d2φ
dx2 =
d
dφV(φ). (2.6)
Um procedimento usual para solucionarmos a equação (2.5), consiste no método da quadratura, que nos leva as seguintes equações
dφ dx =±
p
2V(φ) + 2C (2.7)
onde C é uma constante determinada pelas condições de contorno. Para
estabelecer as condições de contorno para soluções do tipo defeito, devemos analisar sua energia.
2.1.1 Consideração sobre a energia
Recorrendo ao tensor momento-energia, dado por
Θµν =∂µφ∂νφ−δµνL, (2.8)
podemos vericar queC 6= 0pode conduzir à energia innita, como mostrado
A componenteΘ00fornece a densidade de energia do campo. Para soluções estáticas unidimensionais ela se reduz à
Θ00=ρ(x) = 1
2
dφ dx
2
+V(φ). (2.9)
Decorre então que a energia é
E =
Z +∞
−∞ dx " 1 2 dφ dx 2
+V(φ)
#
. (2.10)
Utilizando a condição V(φ)>−C,
E =
Z +∞
−∞
dx[2V(φ) +C]≥ −C
Z +∞
−∞
dx. (2.11)
Vemos que a energia diverge para alguns valores de C. Para evitar essa
divergência, tomamos C = 0. A energia ca então
E =
Z +∞
−∞
dx[2V(φ)]. (2.12)
Para que a integral acima convirja, devemos escolher congurações de campo que tenham uma densidade de energia concentrada em uma região nita.
Para encontrar congurações localizadas devemos impor que o campo é uniforme no innito e a solução estática vá assintoticamente para um dos mínimos do potencial. De uma maneira mais técnica, limx→+∞φ = v e
limx→−∞φ = ¯v, onde v e v¯ são vácuos e portanto V(v) = 0, V(¯v) = 0,
limx→±∞ dφ dx →0.
2.1.2 Análise da estabilidade
Em geral, defeitos topológicos são estruturas estáveis, por esse motivo devemos nos certicar que nossas soluções conseguem reproduzir essa carac-terística. Faremos, então, a análise da estabilidade linear.
Este procedimento consiste em fazer uma perturbação na solução estática da equação e vericar como ela se comporta. Seja φ0(x) a solução estática da teoria de campo cujo potencial é V(φ), e seja φ(x, t) = φ0(x) +f(x, t) a solução perturbada. Considerando somente os termos de primeira ordem em
f, da equação de movimento (2.5) temos que
− ∂ 2
∂t2f+
∂ ∂x2f =
d2V(φ =φ 0)
dφ2 f. (2.13)
Fazendo f(x, t) = Pηn(x) cos(ωnt), obtemos uma equação de autovalores semelhante a equação de Schrödinger independente do tempo, isto é,
− d 2η
n
dx2 +U(x)ηn(x) = ω 2
nηn, (2.14)
onde
U(x) =
d2V(φ)
dφ2
φ0(x)
. (2.15)
Se o potencial tipo mecânico quântico,U(x), fornecer só autovalores
não-negativos a solução é estável.
A análise da estabilidade pode ser simplicada pelo análise da forma da solução de autovalor nulo. Essa solução sempre existe para a equação de Schrödinger. Para demonstrar este fato, derivemos a equação de movimento em relação a x, que resulta em
d2 dx2 dφ dx − d 2V dφ2 dφ dx
= 0. (2.16)
Logo, φ′
(x) = dφdx é a autofunção de frequência nula, que representamos por
Uma função de onda sem nodos corresponde ao estado fundamental de um sistema. Se η0(x) não tiver nodos, então todos os outros estados devem assumir autovalores positivos, e portanto a solução é estável.
2.1.3 Estados BPS
Podemos obter as soluções topológicas sem resolver diretamente as equações de movimento. Existe um procedimento denominado BPS [12,13], que mostra como obter essas soluções por meio de equações de primeira ordem.
Supondo que exista uma função realW(φ), denominada super-potencial,
que possa ser usada para escrever o potencial da seguinte forma
V = 1 2W
2
φ, (2.17)
onde Wφ= dWdφ. Neste caso, a equação de movimento (2.5) é escrita como:
d2φ
dx2 =WφWφφ. (2.18)
Através de manipulações no funcional da energia podemos encontrar soluções que minimizam a energia da solução. Fatorando o funcional en-ergia do seguinte modo
E =
Z +∞
−∞ dx " 1 2 dφ dx 2 +1 2W 2 φ # , =
Z +∞
−∞ dx " 1 2 dφ dx ±Wφ
2 ∓ dφ dx dW dφ # , (2.19)
a energia é minimizada quando
dφ
dx =±Wφ. (2.20)
ordem, este método nos dá a possibilidade de calcular a energia do defeito, apenas utilizando o super-potencial, porque a energia minimizada é dada por
EBP S = Z ∞
−∞
dxdW
dx =|∆W|. (2.21)
Em seguida examinamos um modelo de um campo escalar.
2.1.4 O modelo
φ
4Introduziremos esse modelo através de um exemplo simples. Vamos imag-inar um material magnético unidimensional. A sua magnetização é devida ao alinhamento dos spins na cadeia [14]. Primeiro denimos um eixo, onde os spins podem se orientar em em duas direções possíveis, a favor contra o eixo. Podemos distinguir , assim, dois estados fundamentais para o sistema. Podemos representar a magnetização do material por uma campo φ(x).
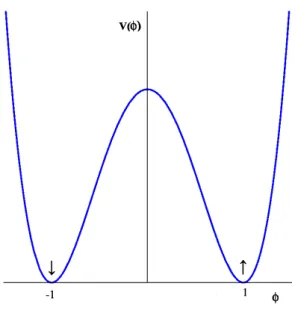
Utilizando a lagrangeana do campo escalar na situação estática com um potencial que possar reproduzir as simetrias que estão envolvidas. Assim, podemos tratar efetivamente o problema, considerando o potencial
V = 1 2(φ
2
−1)2, (2.22)
como ilustrado na gura (2.1). Este potencial possui dois estados fundamen-tais um deles é caracterizado por ter os spins "para cima", o outro tem os spins "para baixo".
As soluções estáticas, que caracterizam os defeitos devem satisfazer a equação (2.6), ou seja,
d2φ
dx2 = 2(φ 3
−φ). (2.23)
Outra maneira de introduzir o modelo é através do super-potencial W =
φ−φ3/3, de onde as equações de primeira ordem são:
dφ
dx =±Wφ=±(φ
2
Figura 2.1: O potencial do modeloφ4.
Ao solucionar a equação acima, obtemosφ(x) = ±tanh(x), veja g. (2.2). O
modo zero é dado porη0(x) =sech2(x), que não possui nodo, o que assegura a estabilidade da solução, veja a g (2.3). A energia do defeito é dada por
EBP S =|W(φ= 1)−W(φ=−1))|=
4
3 (2.25)
2.2 Modelos com dois campos escalares
Nesta seção, examinamos as características dos modelos com dois cam-pos escalares. Os modelos de interesse tem a densidade lagrangeana com a seguinte forma
L= 1 2∂µφ∂
µφ+ 1
2∂µχ∂
µχ
−V(φ, χ). (2.26)
No caso estático, φ=φ(x) e χ=χ(x), as equações para os campos em 1+1
Figura 2.2: As soluções tipo kink, em linha contínua, e anti-kink, em linha tracejada.
∂2φ
∂t2 −
∂2φ
∂x2 +
∂V
∂φ = 0, (2.27)
∂2χ
∂t2 −
∂2χ
∂x2 +
∂V
∂χ = 0. (2.28)
Para o caso estático, temos que
d2φ
dx2 =
∂V ∂φ,
d2χ
dx2 =
∂V
∂χ. (2.29)
Vamos nos restringir a potenciais super-simétricos, ou seja, que podem ser escritos através de um super-potencial W(φ, χ), da seguinte forma
V = 1 2W 2 φ + 1 2W 2
χ, (2.30)
onde Wφ= ∂W∂φ e Wχ= ∂W∂χ. As equações (2.26) tem a forma:
d2φ
dx2 =WφφWφ+WφχWχ, (2.31)
d2χ
Figura 2.3: O modo zero (2.26).
Essa escolha do potencial permite que encontremos soluções do tipo de-feito advindas de equações de primeira ordem. São os estados BPS, para modelos com dois campos. Para esses estados, a energia da solução estática é dada por
E = Z ∞ −∞ 1 2dx " dφ dx 2 + dχ dx 2
+Wφ2+Wχ2
#
. (2.33)
Através de um procedimento semelhante ao do caso de um campo, a energia pode ser reescrita como
E = Z ∞ −∞ 1 2dx " dφ dx ±Wφ
2
+
dχ dx ±Wχ
2#
+EBP S, (2.34)
onde a energia BPS é dada por
EBP S = Z ∞ −∞ 1 2dx Wφ dφ dx +Wχ
dχ dx
. (2.35)
Para minimizarmos a energia teremos que buscar congurações estáticas que satisfaçam as seguintes equações:
dφ
dx =±Wφ,
dχ
Neste caso, a energia do defeito pode ser facilmente calculada por
E =EBP S =|∆W|. (2.37)
A diculdade aqui é que não há procedimento geral para resolver um sis-tema de equações diferencias não-lineares acopladas. A seguir, apresentamos um exemplo, o modelo BNRT [15].
2.2.1 Modelo BNRT
O modelo é denido pela escolha do super-potencial na forma
W(φ, χ) = φ− 1
3φ
3
−rφχ2, (2.38)
de onde obtemos
Wφ = 1−φ2−rχ2, (2.39)
Wχ =−2rφχ. (2.40)
Utilizando (2.30), chegamos que o potencial é dado por
V(φ, χ) = 1
2 1−φ
2−rχ22+1
2r
2φ2χ2. (2.41)
Notamos que reproduzimos o potencial do modeloφ4 ao tomarmosχ= 0,
V(φ,0) = 1
2 1−φ
22. (2.42)
Por outro lado, para φ= 0 obtemos o potencial tipo χ4, dado por
V(0, χ) = 1
2 1−rχ
22 . (2.43)
As equações de primeira ordem são:
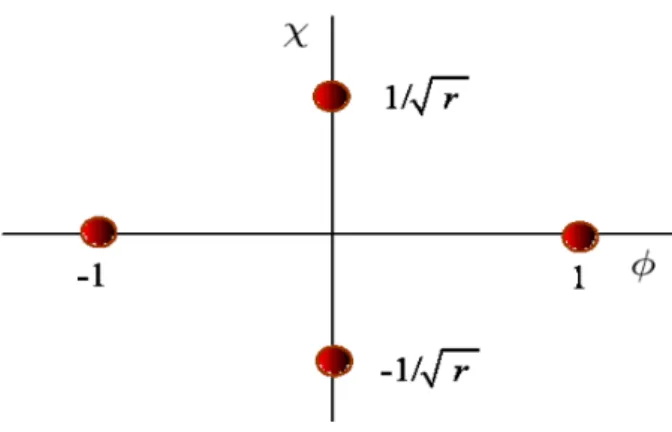
Figura 2.4: Os mínimos do potencial(2.40).
± dχ
dx =−2rφχ. (2.45)
Os pontos de mínimo do potencial são(±1,0)e(0,±1/√r), veja g. (2.4).
O modelo contém cinco setores topológicos, que estão entre os pares de mín-imos [(−1,0),(1,0)] e [(±1,0),(0,±1/√r)]. Apenas o setor correspondente
entre o par de mínimos localizados sobre o eixo χ é não topológico, pois
tem energia BPS nula. Usando o super-potencial (2.38) obtemos a energia:
EBP S = 4/3 no setor topológico que envolve os mínimos sobre o eixo φ, e
EBP S = 2/3nos demais setores topológicos.
Capítulo 3
Gerando modelos de um campo
Neste capítulo, apresentamos o método de deformação [10]. Em poucas palavras, ele é um procedimento que permite a construção de novos modelos de um campo escalar com suas soluções estáticas, partindo-se de um modelo de campo escalar com solução conhecida.
Um ponto importante do método é a possibilidade de obtermos soluções estáticas do novo modelo diretamente das soluções do modelo de partida, evitando assim que tenhamos que resolver as equações de campo, que são não-lineares e acopladas.
3.1
Método da deformação
Consideramos duas teorias de campos escalares distintas denidas pelas densidades lagrangianas,
L= 1 2∂µφ∂
µφ
−V(φ), (3.1)
Ld =
1 2∂µχ∂
µχ
Podemos encontrar as soluções do tipo defeito resolvendo as equações de primeira ordem associadas a cada modelo, que são respectivamente
dφ dx =±
p
2V(φ), (3.3)
dχ dx =±
q
2Ve(χ). (3.4)
A partir de função uma que relacione os dois defeitos, tal queφ =f(χ),
que seja inversível, diferenciável, e com derivada não nula em todos os pon-tos, podemos deformar um modelo no outro pela seguinte relação entre os potenciais
e
V(χ) = V(φ=f(χ))
(df /dχ)2 . (3.5)
Uma maneira elegante e simples de demonstrar essa armação é a partir das equações (3.3) e (3.4). Uma vez que φ = f(χ) podemos estabelecer a
seguinte relação entre a derivadas
dφ dx =
df dχ
dχ
dx ⇒ ±
p
2V(φ) =±
q
2Ve(χ)df
dχ. (3.6)
Quadrando ambos os lados da equação anterior, estabelecemos que
V(φ) =Ve(χ)
df dχ
2
⇒ Ve(χ) = V(φ=f(χ))
(df /dχ)2 . (3.7)
Portanto, o modelo denido pelo potencial deformado(3.7)terá soluções
estáticas χ(x) =f−1
(φ(x)), onde f−1 é a função deformadora inversa. Para ilustrar esse procedimento vamos considerar alguns exemplos.
3.2 O Modelo seno-Gordon
e
V(χ) = cos
2(χ)
2 , (3.8)
que caracteriza a nova teoria, como ilustrado na gura (3.1).
Figura 3.1: O potencial do modelo seno-Gordon e as soluções nos setores k =
0,±1.
Este potencial tem aplicações em problemas mecânicos, como nas os-cilações de uma ta elástica [18]; em matéria condensada, no movimento das paredes de Bloch em cristais [6]; e em física de partículas como um modelo para o estudo de mésons [19].
mapeamos o kink e o anti-kink do modeloφ4, nos kinks e anti-kinks presentes em cada setor topológico do modelo seno-Gordon,veja a gura (3.1).
3.3 O Modelo p
Outros modelos podem ser gerados a partir do modelo φ4. Aqui ilus-traremos esse procedimento utilizando a função f(χ) = χ1/p. Essa defor-mação tem aplicações no cenário das branas [16] e em certas classes de de-feitos globais [17].
Seguindo o procedimento de deformação chegamos no potencial do novo modelo,
e
V(χ) = p
2χ2
2 χ
−1/p
−χ1/p2. (3.9)
Vericamos que o modelo está associado ao seguinte super-potencial:
W(χ) = p
χ2−1/p
2−1/p −
χ2+1/p
2 + 1/p
. (3.10)
Para obter as soluções BPS, temos que resolver a equação diferencial
± dχ
dx =Wχ =p χ(χ
−1/p
−χ1/p). (3.11)
O parâmetro p é real e está relacionado com a não-linearidade do sistema.
Para os casos de interesse p é ímpar.
Ao invés de resolver a equação BPS (3.11), utilizamos a função defor-madora inversa,ou seja χ=φp, que fornece
χ(x) = tanhp(x). (3.12)
Figura 3.2: O potencial (à direita) e a solução (à esquerda), para p=3 em linha contínua, e para p=1 em linha tracejada.
Figura 3.3: O gráco do modo zero para p=3 e p=5. Ambos os casos não tem nodos.
mínimos na forma de um duplo-kink, veja a gura (3.2). Isto porque a segunda derivada do potencial em χ= 0 não é denida, assim esse mínimo
não é um vácuo do modelo.
η0p(x) = dχ
dx =psech(x) tanh
p−1
(x). (3.13)
Vericamos que p ímpar corresponde aos casos em que o modo zero não
apresenta nodo, portanto a correspondente soluções estática é estável, veja a gura (3.3).
Utilizando o super-potencial(3.10) a energia do duplo-kink é dada por
EBP S =|W(1,0)−W(−1,0)| =
4p
Capítulo 4
Gerando modelos de dois campos
No capítulo anterior, discutimos como criar novas teorias em modelos de um campo escalar. Um questionamento que pode ser colocado é referente à possibilidade de se construir teorias solúveis que envolvam dois ou mais campos, ou seja, como podemos criar novos modelos com vários campos escalares, que com soluções analíticas conhecidas?
Em se tratando de dois campos, existe uma maneira de concretizarmos essa ideia. A referencia [21] apresenta uma versão de deformação para dois campos, que consiste em escolher determinadas funções deformadoras para cada campo, sujeitas a um determinado vínculo. As soluções estáticas obtidas correspondem apenas a um setor topológico do potencial deformado.
4.1 Introduzindo o novo método
Como vimos anteriormente, alguns potenciais em modelos de dois campos são super-simétricos, isso possibilita a análise dos defeitos e suas propriedades via equações de primeira ordem. Para nosso estudo, tomaremos o super-potencial na forma
W(φ, χ) =
Z
dφf(φ)−rφχ2. (4.1)
Assim, o potencial associado é dado por
V = 1
2 f(φ)−rχ
22+ 2rχ2φ2, (4.2)
cujas soluções estáticas satisfazem:
dφ
dx =Wφ =f(φ)−rχ
2, (4.3)
dχ
dx =Wχ=−2rφχ. (4.4)
Para resolver esse sistema, derivamos novamente a primeira equação, obtendo
d2φ
dx2 =
df dφ
dφ dx −2r
2χdχ
dx
= df
dφ dφ
dx + 4rφ
f(φ)−dφ
dx
, (4.5)
ou de outra forma
d2φ
dx2 =
df
dφ−4rφ
dφ
dx + 4rf(φ). (4.6)
Assim, o sistema de equações (4.3)e (4.4)se desacopla para
rχ2 =f(φ)− dφ
dx, (4.7)
que é resolvida pela equação (4.6). O caso particular χ = 0 também é uma
órbita do modelo denido por (4.2), cuja solução é obtida diretamente de
dφ
Agora, desde que
dφ
dx =u1(φ), (4.8)
temos
d2φ
dx2 =
du1
dφ dφ
dx =u2(φ). (4.9)
Então a equação diferencial toma a forma:
df(φ)
dφ +
4φrf(φ)
u1(φ) −
4rφ+u2(φ)
u1(φ)
= 0. (4.10)
Esta equação pode ser solucionada utilizando o método do fator integrante, que leva a seguinte expressão
f(φ) =e−
R 4rφ u1(φ)dφ
Z
[4rφ+u2(φ)
u1(φ)
]e
R 4rφ′
u1(φ′)dφ′dφ+C
, (4.11)
onde C é uma constante.
4.2 Aplicações
Vamos escolher u1(φ) na forma u1 = k(φ−a)(φ+b), onde a, b e k são constantes reais. A solução (4.11) é escrita como
f(φ) = k(φ−a)(φ+b) +C(φ+b)−bα(φ−a)−aα, (4.12)
onde α = 4r
k(a+b). Uma vez que propomos uma forma para u1(φ), podemos gerar uma determinada classe de modelos, através de f(φ). Vamos mostrar
qual é a classe de teorias de dois campos geradas para nossa escolha deu1(φ). A solução da equação de primeira ordem (4.8) para o caso em questão é
φ(x) =
a−b
2 ±
b+a
2 tanh
k
2(a+b)x
. (4.13)
4.2.1 Reproduzindo o BNRT
O modelo BNRT, que foi apresentado no Cap.2, é um bom exemplo de aplicação para o nosso procedimento. Nele, f(φ) = 1−φ2 é obtido de (4.12) assim como as suas soluções estáticas são obtidas de (4.13) e (4.7), para as seguintes escolhas:
-Primeira escolha: C= 0, k=−1, a=b. A solução é dada pelo par
φ(x) =±tanh(x),
χ(x) = 0. (4.14)
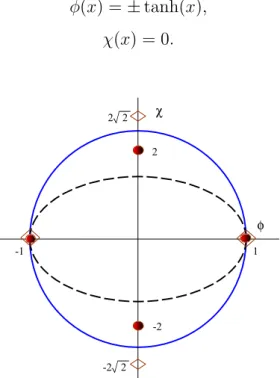
Figura 4.1: Órbitas do BNRT, reta (para a primeira escolha) e elípticas (para a segunda escolha), o caso r = 1/8 em linha contínua e o caso r = 1/4 em linha
tracejada. Os mínimos são representados por esfera(r= 1/4)e losango(r = 1/8).
-Segunda escolha: C = 1−2r, a=b = 1, k = 2r, com 0< r <1/2. A
solução é
φ(x) = ±tanh(2xr), χ(x) =±q1−2r
r sech(2rx).
onde 0< r <1/2. O que corresponde a órbita elíptica χ2 = 1−2r
r (1−φ2). Na gura (4.1), mostramos as órbitas conectando os mínimos φ = ±1,
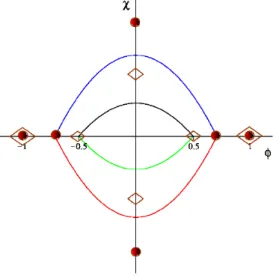
para as duas primeiras escolhas. Na gura (4.2) são apresentamos as órbitas conectando os mínimos nos demais setores topológicos corresponde à terceira escolha.
Figura 4.2: Órbitas do BNRT para b = 1, em linha cheia, e b = −1, em linha
tracejada.
-Terceiro escolha: a = 0, b =±1, C = 4rb, k = −4r, r = 1/4, nos leva
às seguintes soluções:
φ(x) = 1
2(−1±tanh(x/2)), (4.16)
χ(x) = ±p2(1±tanh(x/2)), (4.17)
para b = 1 correspondente à órbitaχ2 = 4(1−φ), e as soluções
φ(x) = 1 2
1±tanh(x 2)
, (4.18)
χ(x) = ±p2(1∓tanh(x/2)). (4.19)
4.2.2 Reproduzindo outros modelos polinomiais
Considerando o modelo polinomial descrito pelo super-potencial:
W(φ, χ) = φ−(1 +s)φ
3
3 + 1 5sφ
5
−rφχ2, (4.20)
o potencial é dado por
V(φ, χ) = 1
2(1−(1 +s)φ
2+sφ4
−rχ2)2+ 2r2φ2χ2, (4.21)
e seus mínimos são os seis pontos: (±1,0),(±1/√s,0) e (0,±1/√r). As
equações de primeira ordem são:
dφ
dx = 1−(1 +s)φ
2+sφ4
−rχ2, (4.22) dχ
dx = −2rφχ. (4.23)
Para reproduzir esse modelo, onde
f(φ) = 1−(1 +s)φ2+sφ4, (4.24)
na equação (4.13) escolhemos C =s ea =b, o que fornece
f(φ) =k(φ2−a2) +s(φ2−a2)−2r/k
, (4.25)
e tomando k =−r, obtemos
f(φ) = sφ4+ (−2sa2+k)φ2−ka2+sa4. (4.26)
Assim, para obter (4.24) de (4.26), temos duas possibilidades: a = ±1 ou
a =±1/√s. Para a primeira delas, o vínculo ér= 1−s, comr >0e s <1,
e as soluções são
φ(x) =±tanh((s−1)x), (4.27)
χ(x) = ±
r
s
1−ssech
2
Figura 4.3: Órbitas para o par de soluções (4.27),(4.28). Para s= 1/3, elipse
maior com os mínimos em esfera, e para s = 1/4 , elipse menor com os mínimos
em losangos.
cuja órbita é χ2 = s 1−s(φ
2−1)2.
Para a outra escolha, o vínculo é r = s −1,com r > 0 e s > 1, e as
soluções são
φ(x) =±√1
stanh
1−s
√
s x
, (4.29)
χ(x) =±p 1
s(s−1)sech
2
1−s
√
s x
, (4.30)
cuja órbita é χ2 = s s−1(φ
2−1/s)2.
Note que, os dois pares de soluções não ocorrem para os mesmos valores dos parâmetros de acoplamento, r e s. Nas guras (4.3) e (4.4), mostramos
Figura 4.4: Órbitas para as soluções para as soluções(4.29),(4.30). Paras= 2,
elipse maior com os mínimos em esfera, e paras= 4, elipse menor com os mínimos
Capítulo 5
Conclusão e comentários
Neste trabalho, revisamos alguns aspectos de teoria de campos para modelos que envolvem um e dois campos escalares. Fizemos uma revisão do método da deformação [10], procedimento que permite a geração de modelos de um campo escalar com suas soluções analíticas.
Além disso, apresentamos um novo método de deformação para modelos de dois campos, como uma alternativa ao procedimento introduzido em [21]. Nosso procedimento permite, através de determinadas escolhas de parâmet-ros, a obtenção das soluções estáticas em mais de um setor topológico do novo modelo.
Como ilustração, reproduzimos o modelo BNRT e suas soluções estáticas em todos os setores topológicos. Geramos ainda um novo modelo de dois campos escalares e suas soluções estáticas em alguns dos seus setores.
Referências Bibliográcas
[1] Dionisio Bazeia Filho, Campos escalares em ação, Tese Apresentada para o Concurso de Professor Titular - UFPB(2004).
[2] Roberto Menezes da Silva, Defeitos Globais em Teorias de Campos e Aplicações, Tese de Doutorado - UFPB (2007).
[3] A. Albrecht and P. Steinhardt, Cosmological Imprint of an Energy Com-ponent with General Equation-of-State, Phys. Rev. Lett. 80, 1582 (1998).
[4] S. Carrol, Quintessence and the Rest of the World ,Phys. Rev. Lett 81, 3067 (1998).
[5] P. Higgs, Spontaneus Symmetry Breakdown without Massless Bosons, Phys. Rev. 145, 1156 (1966).
[6] Marcos André Carara, Dinâmica das Paredes de Domínio: um estudo através da Impedanciometria, Tese de Doutorado - UFGRS (2001).
[7] A. Zee, Quamtum Field Theory in a Nut Shell, (Princeton University Press, Princeton, 2003).
[8] L. Yakushevich, Non-linear Physics of DNA, (Wiley, 2004).
[10] D.Bazeia, L. Losano, J. M. C. Malbuisson, Deformed Defects, Phys. Rev. D 66, 101701 (2002).
[11] R. Jackiw, Quantum meaning of classical eld theory, Rev. Mod. Phys. 49, 681 (1977).
[12] E.B. Bogomol'nyi, Stability Of Classical Solutions, Sov. J. Nucl. Phys. 24, 449 (1976).
[13] M.K. Prasad, An exact Classical Solution for The T'Hooft Monopole And The Julia-Zee Dyon, C. H. Somereld, Phys. Rev. Lett. 35, 760 (1975).
[14] T. C.Lubensky and P. M.Chaikin, Principles of Condensed Matter Physics, (Cambrigde University Press, 2000).
[15] D. Bazeia, M. J. dos Santos, and R. F. Ribeiro, Solitons in System of two Scalar Fields, Phys. Lett. A 208, 84 (1995).
[16] D. Bazeia, L. Losano, Deformed Defects with Aplication to Braneworlds, Phys.Rev. D 73 (2006).
[17] D. Bazeia, J. Menezes and R. Menezes, New Global Defect Structures, Phys. Rev. Lett. 91, 241601 (2003).
[18] D. Finkelsteint and C. W. Misner, Some New Conservation Laws, An-nals of Phsy. 6 230 (1959).
[19] T. H. R. Skyrmer, Particle States of a Qunatized Meson Field, Proc. R. Soc. Lond. A 262 237 (1961).