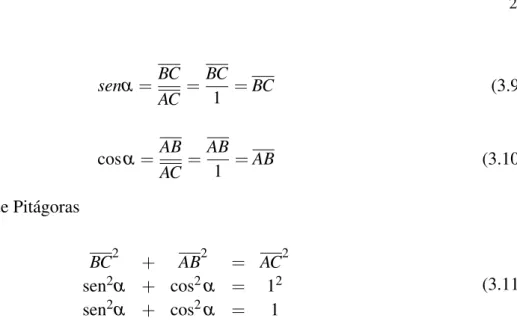Relações trigonométricas fundamentais

CENTRO DE CI ˆ

ENCIAS

DEPARTAMENTO DE MATEM ´

ATICA

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM MATEM ´

ATICA EM REDE

NACIONAL

ANT ˆ

ONIO ALMIR BEZERRA

RELAC

¸ ˜

OES TRIGONOM ´

ETRICAS FUNDAMENTAIS

RELAC

¸ ˜

OES TRIGONOM ´

ETRICAS FUNDAMENTAIS

Dissertac¸˜ao de Mestrado apresentada ao Pro-grama de P´os-Graduac¸˜ao em Matem´atica em Rede Nacional (PROFMAT) do Departamento de Matem´atica da Universidade Federal do Cear´a, como requisito parcial para obtenc¸˜ao do T´ıtulo de Mestre em Matem´atica. ´Area de

Concentrac¸˜ao: Ensino de Matem´atica

Orientadora: Profa. Dra. Maria Silvana Alcˆantara Costa

FORTALEZA

Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará

Biblioteca do Curso de Matemática B467r Bezerra, Antônio Almir

Relações trigonométricas fundamentais / Antônio Almir Bezerra. – 2014. 59 f. : il., enc.; 31 cm

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Departamento de Matemática, Programa de Pós-Graduação em Matemática em Rede Nacional, Fortaleza, 2014. Área de Concentração: Ensino de Matemática.

Orientação: Profª. Drª Maria Silvana Alcântara Costa.

`

A Deus, por sempre guiar meus passos para realizar com sucesso os meus objetivos.

A meus pais e irm˜aos que sempre foram minha base nesta caminhada, o meu muito obrigado por tudo `aquilo que me ensinaram e contribu´_ıram para as minhas realizac¸˜oes.

A meus amores Adriana Mendes de Brito Bezerra e Israel Levi Mendes Bezerra, esposa e _filho, pela dedicac¸˜ao, amor, apoio e incentivo constante sem o qual eu n˜ao estaria realizando este sonho.

Ao meu irm˜ao, Jo˜ao Batista Bezerra, que me acompanhou durante seis meses pelas estradas entre Juazeiro do Norte e V´arzea Alegre.

A minha orientadora Maria Silvana Alcˆantara pela con_fianc¸a e dedicac¸˜ao, por toda liberdade no desenvolvimento deste estudo e ter acreditado em meu potencial me conduzindo para esta realizac¸˜ao, obrigado pelas horas e apoio disponibilizados.

A todos meus professores do PROFMAT, pela arte de ensinar, por nos desa_fiar e acreditar em nossa capacidade de aprender sempre mais.

Neste trabalho apresentamos algumas relac¸˜oes trigonom´etricas fundamentais e suas demonstrac¸˜oes. Tais relac¸˜oes merecem destaque, pois s˜ao essenciais na resoluc¸˜ao de problemas nas diversas ´areas do conhecimento. Inicialmente_fizemos um breve hist´orico da Trigonometria destacando a sua importˆancia no contexto da Matem´atica. Em sequˆencia apresentamos as relac¸˜oes funda-mentais, dentre elas, enfatizamos as f´ormulas da adic¸˜ao de arcos, cujas demonstrac¸˜oes utiliza-mos ´area de_figuras planas, a lei dos cossenos e a lei dos senos. Al´em disso, mostramos como estas f´ormulas se relacionam com o Teorema da Corda Quebrada e o Teorema de Ptolomeu da Geometria Plana. Explorando a relac¸˜ao entre Trigonometria e Geometria Plana. Procuramos mostrar a importˆancia desta teoria no ensino m´edio motivando alunos e professores a buscar um maior interesse pelo conhecimento em Matem´atica.

The present research aims to present classic demonstrations of the fundamental relations of Tri-gonometry, with a simple approach, and exploring_flat shapes. The intention is to make such demonstrations better known and provide a highlight for Trigonometry, since they are essential in solving problems of everyday life. For this purpose, we made a historical highlighting of the importance of trigonometry in the mathematical context. Since we know Trigonometry is loosing its status and not being considered essential in basic education anymore, such demons-trations, associated with the_flat shapes, may be used as a model class. Therefore, we highlight the following fundamental relations: Basic Trigonometric relations, Derived Relations, Sine of the Sum and Difference of Two Arcs, Cosine of the Sum and Difference of Two Arcs, Double Arcs, Half Arc, Transformation in Product and Applications. For the demonstration ot these re-lations we used some area results, cosine law, Ptolemy’s theorem and the theorem of the broken chord Plane Geometry. We believe that Trigonometry is linked to the formation of these _flat shapes. Thus, such demonstrationas associated to these_flat shapes may serve to improve the Trigonometry teaching- learning and as motivator for students and teachers seeking to enhance their knowledge in mathematics.

Figura 2.1 Papiro de Rhind . . . 12

Figura 2.2 T´abua de Plimpton 322 . . . 12

Figura 2.3 Esquema de Ptolomeu . . . 14

Figura 2.4 Quadril´atero inscrito . . . 16

Figura 2.5 Circulo de raio unit´ario . . . 18

Figura 3.1 Angulo centralˆ . . . 20

Figura 3.2 Angulo inscritoˆ . . . 21

Figura 3.3 Angulo excˆentrico a uma circunferˆenciaˆ . . . 21

Figura 3.4 Triˆangulo retˆangulo . . . 22

Figura 3.5 Triˆangulo retˆangulo dividido . . . 23

Figura 3.6 Triˆangulo retˆangulo de hipotenusa unit´aria . . . 24

Figura 3.7 Triˆangulo retˆangulo de cateto adjacente unit´ario . . . 25

Figura 3.8 Triˆangulo retˆangulo de cateto oposto unit´ario . . . 27

Figura 3.9 Ciclo trigonom´etrico . . . 29

Figura 3.10 Ciclo trigonom´etrico e a reta . . . 29

Figura 3.13 ´Area de um triˆangulo em func¸˜ao do ˆangulo obtuso . . . 32

Figura 3.14 Triˆangulo qualquer e a Lei dos cossenos . . . 33

Figura 3.15 Triˆangulo obtuso e a Lei dos cossenos. . . 34

Figura 3.16 Triˆangulo inscrito . . . 35

Figura 4.1 Ciclo trigonom´etrico e o plano . . . 36

Figura 4.2 Circulo de raio unit´ario e o Retˆangulo . . . 37

Figura 4.3 Triˆangulo retˆangulos de lado unit´ario comum . . . 39

Figura 4.4 Triˆangulo retˆangulo de altura unit´aria . . . 41

Figura 4.5 Trap´ezio . . . 43

Figura 4.6 Triˆangulo is´osceles . . . 44

Figura 4.7 Triˆangulo retˆangulo inscrito . . . 46

Figura 4.8 Angulo excˆentrico e o seno da diferenc¸aˆ . . . 48

Figura 4.9 Quadril´atero inscrito de lados unit´arios . . . 49

Figura 4.10 Teorema de Ptolomeu . . . 51

Figura 4.11 Quadril´atero inscrito e o teorema de Ptolomeu . . . 52

1 INTRODUC¸ ˜AO. . . 11

2 UM BREVE HIST ´ORICO DA TRIGONOMETRIA . . . 12

2.1 A Trigonometria Grega . . . 13

2.2 A Trigonometria Hindu . . . 16

2.3 A Trigonometria na Europa . . . 18

3 DEFINIC¸ ˜OES E PRELIMINARES. . . 20

3.1 Angulo Central, Inscrito e Externo a uma Circunferˆenciaˆ . . . 20

3.2 Raz˜oes Trigonom´etricas no Triˆangulo Retˆangulo. . . 22

3.3 Area de um Triˆangulo Qualquer´ . . . 31

3.4 Lei dos Cossenos . . . 32

3.5 Lei dos Senos . . . 34

4 IDENTIDADES TRIGONOM ´ETRICAS E SUAS DEMONSTRAC¸ ˜OES. . . 36

4.1 Cosseno e Seno da Soma e da Diferenc¸a de dois arcos. . . 36

4.2 Arcos duplos e Arcos metades. . . 44

4.3 Teorema de Ptolomeu e o seno da diferenc¸a de dois arcos. . . 51

4.4 Teorema da Corda quebrada e o seno da diferenc¸a de dois arcos . . . 53

4.5 Transformac¸˜ao em produto . . . 55

5 CONSIDERAC¸ ˜OES FINAIS. . . 58

1 INTRODUC¸ ˜AO

Atualmente com as mudanc¸as no ensino de Matem´atica e consequentemente de Trigonometria na educac¸˜ao b´asica brasileira, tem-se aumentado o interesse de pesquisadores de Ensino da Matem´atica em debater esta problem´atica nas escolas e, at´e mesmo, nas Uni-versidades. “Al´em disso, h´a um interesse coletivo por este ramo da Matem´atica, como ´area de aprendizagem, pela sua contribuic¸˜ao na formac¸˜ao dos alunos e pela aplicac¸˜ao que tem em outras Ciˆencias, inclusive dentro da pr´opria Matem´atica” (EVES, 1992).

Com o intuito de tornar o Ensino de Trigonometria mais interessante constru´_ımos_fi -guras planas simples na tentativa de mostrar as demonstrac¸˜oes das identidades trigonom´etricas.

A ideia ´e desenvolver habilidades em Trigonometria, explorando “algumas relac¸˜oes fundamentais”, abordando a Geometria Euclidiana, tais como o Teorema de Ptolomeu, ´Areas de Triˆangulos, Lei dos Cossenos, que ´e utilizado tanto em Matem´atica como na F´_ısica. Te-oremas de Ptolomeu e Hiparco, que relacionam as diagonais e os lados de um quadril´atero inscrit´_ıvel, que nos d´a uma condic¸˜ao de relacion´a-los com relac¸˜oes de seno e cosseno da soma e da diferenc¸a de dois arcos, Arcos duplo e Triplo. Pois, seguem diretamente das relac¸˜oes fun-damentais acima citados. Para tal estudo_fizemos uma minuciosa pesquisa bibliogr´a_fica, e com o aux´_ılio de algumas construc¸˜oes procuramos detalhar a visualizac¸˜ao geom´etrica das relac¸˜oes fundamentais abordadas, possibilitando assim, demonstra-las.

Com a_finalidade de atender os objetivos, citados anteriormente, no capitulo 2 _fi -zemos um breve hist´orico da Trigonometria. J´a no cap´_ıtulo 3 apresentamos a teoria necess´aria para a compreens˜ao do trabalho. Fizemos algumas de_finic¸˜oes e apresentamos resultados envol-vendo semelhanc¸a de triˆangulos, a lei dos senos e a lei dos cossenos que ser˜ao utilizados no cap´_ıtulo seguinte. Pois com o auxilio das ´areas e resultados cl´assicos da Geometria Plana apre-sentamos as demonstrac¸˜oes das relac¸˜oes fundamentais e sua relac¸˜ao com o Teorema da corda Quebrada e o Teorema de Ptolomeu com as f´ormulas da adic¸˜ao de arcos.

2 UM BREVE HIST ´ORICO DA TRIGONOMETRIA

Conforme (EVES, 1992) o papiro de Rhind1 (Figura 2.1), uma das mais antigas

fontes da matem´atica eg´_ıpcia, data-se de 5.1650 a.c. Tamb´em conhecido como papiro de Ah-mes, esse papiro ´e um texto matem´atico na forma de manual pratico que cont´em 85 problemas, o mesmo foi adquirido no Egito, em 1858 numa cidade `a beira do Nilo, pelo egipt´ologo escocˆes A.Henry Rhind, sendo mais tarde comprado pelo museu Britˆanico. O papiro de Rhind foi pu-blicado em 1927 e ´e um rolo de papiro com cerca de0,30 m de altura e 5 m de comprimento. Este papiro esta atualmente no Bristish Museum, com excec¸˜ao de uns poucos fragmentos que est˜ao no Broklim Museum. APlimptom3222 (Figura 2.2) leva esse nome por se tratar de uma t´abula da colec¸˜ao G. A. Plimpton da universidade de Col´umbia e ter sido catalogada sob o nu-mero 322. Talvez a mais not´avel t´abula da matem´atica babilˆonica, a Plimpton 322 foi escrita no per´_ıodo babilˆonico antigo (aproximadamente entre 1900 e 1600 a.c).

Figura 2.1: Papiro de Rhind

Figura 2.2: T´abua de Plimpton 322

Etimologicamente a palavra trigonometria vem do grego trignom, “triangulo” e me-tron, “medida”. Esta ´area da matem´atica estuda as relac¸˜oes entre os ˆangulos e os lados do

triˆangulo. A trigonometria oportuniza ao matem´atico resolver problemas geom´etricos envol-vendo ˆangulos e distancias.

2.1 A Trigonometria Grega

Numa abordagem hist´orica da trigonometria ´e importantes destacar as descobertas e aplicac¸˜oes feitas pelos gregos nessa ´area da matem´atica. O povo grego usava-se da trigono-metria principalmente na resoluc¸˜ao de problemas sobre a astronomia. De inicio deve-se dar ˆenfase a_figura de um dos mais eminentes astrˆonomos gregos, o astrˆonomo Hiparco de Nic´eia, considerado o “Pai da trigonometria”, Hiparco viveu em torno de 140 a.c e assim como outros importantes matem´aticos gregos da antiguidade pouco se sabe sua vida. Segundo (EVES, 1992, p. 202)

E bem prov´avel que o mais eminente dos astrˆonomos da Antiguidade tenha sido Hi-parco, que viveu em torno de 140 a.C. Embora se tenham dados de um equin´ocio vernal registrado por Hiparco em Alexandria, no ano 146 a.C., suas observac¸˜oes mais not´aveis foram feitas no famoso observat´orio de Rodes, importante centro comercial. Hiparco era um observador extremamente cuidadoso e creditam-se a ele, em astro-nomia, feitos como a determinac¸˜ao da durac¸˜ao do mˆes lunar m´edio (o afastamento entre seu valor e aquele presentemente aceito n˜ao vai al´em de 1 ), um calculo acu-rado da inclinac¸˜aoda ecl´ıptica e a descoberta e uma estimativa da precess˜ao anual dos equin´ocios.

Hiparco, atrav´es de um estudo sistem´atico das relac¸˜oes entre o ˆangulo e o compri-mento da corda correspondente construiu uma tabela trigonom´etrica de cordas dos ˆangulos de 0◦a 180◦. Provavelmente a divis˜ao do circulo em 360◦teve origem a partir da tabela de cordas de Hiparco.

Atribui-se a Hiparco um tratado de doze livros, onde o astrˆonomo grego se dedicou a construc¸˜ao daquela que deve ter sido a primeira tabela trigonom´etrica. Para a montagem da tabela, Hiparco da interpolac¸˜ao linear, a mesma representou um grande avanc¸o na astronomia.

A trigonometria grega teve seu apogeu com Claudio Ptolomeu (150 d.C.) que in-fluenciado pela ideias de Hiparco, foi o autor da mais importante obra da trigonometria, no s´eculo II, em Alexandria. “Syntaxis Mathematic”, era uma obra composta de treze volumes, geralmente citada com titulo de traduc¸˜ao ´arabe “Almagesto” que em ´arabe signi_fica “A maior”, pois os ´arabes consideram a obra de Ptolomeu como a maior existente na ´epoca , na ´area da astronomia.

O objetivo doAlmagesto´e descrever matematicamente o funcionamento do sistema solar, tendo como base a teoria geocˆentrica, que supunha que a Terra era o centro do universo. Esta teoria foi substitu´_ıda no s´eculo XV pelo teoria heliocˆentrica de (teoria geocˆentrica, que seria substitu´_ıda j´a no s´eculo XV pela teoria heliocˆentrica do astrˆonomo e matem´atico polonˆes Nicolau Cop´ernico (1473 -1543). Nesta obra, Ptolomeu tamb´em apresenta seus c´alculos sobre a dimens˜ao da Lua e a distˆancia entre ela e o Sol.

circulo em 60 partes e utilizando 377/120 como a aproximac¸˜ao de pi, Ptolomeu n˜ao fez uso da express˜oes seno e cosseno para obter a tabela. Ele utilizou apenas as cordas e que pode ser considerado o pronuncio da relac¸˜ao fundamental sen2α+cos2α=1

Figura 2.3: Esquema de Ptolomeu

senα

2 =

AC

OA =

2AC

2OA=

AB

Diˆametro =

cdr(α)

120 (2.1)

Como Ptolomeu havia dividido a circunferˆencia em 60 partes, seu diˆametro ´e 120 ecrd(α) ´e o comprimento da cordaAB. NoAlmagestonenhuma tabela continha as “func¸˜oes” seno e cosseno, pois essa notac¸˜ao era feita usando a func¸˜ao corda do arco(α), denotada por crd(α). Na tabela de cordas de Ptolomeu existiam trˆes colunas: a primeira listando os arcos, a segunda o comprimento da corda correspondente a cada arco e a terceira que dava o aumento m´edio decrd(α)correspondente a um acr´escimo de um minuto emα. Ptolomeu desenvolveu a Trigonometria no d´ecimo e no d´ecimo primeiro cap´_ıtulo do primeiro livro do Almagesto, a tabela de cordas ´e apresentada no d´ecimo primeiro capitulo.

Deve-se ressaltar que a tabela de cordas de Ptolomeu teve como base a tabela cri-ada anteriormente por Hiparco e que todo esse c´alculo era do conhecimento de Hiparco. Para (EVES, 1992, p. 202)

Essencialmente, ent˜ao, a tabua de cordas de Ptolomeu fornece os senos dos ˆangulos de 0◦ a 90◦, com incrementos de 15. A maneira de se calcular os comprimentos dessas cordas, explicada ele suas tabuas e, ademais, que estava a par dos processos equivalentes a varias formulas hoje usadas na resoluc¸˜ao de triˆangulos esf´ericos retos.

Segundo, (MORGADO; WAGNER; CARMO, 2001) “[...] a Trigonometria foi uma criac¸˜ao da matem´atica grega. Ela surgiu devido `as necessidades da astronomia, a_fim de prever as efem´erides celestes e para ser utilizada na navegac¸˜ao e na geogra_fia”.

“O estudo dos triˆangulos esf´ericos na Matem´atica grega vinha sendo feito desde os ´ultimos pitag´oricos. O pr´oprio Euclides, que viveu em torno de 300 a.C., em um de seus trabalhos, os Fenˆomenos, estudou a geometria esf´erica. Aproximadamente em 20 a.C., Teod´osio compilou o que os gregos conheciam sobre o assunto em seu livro sobre a Esfera”. (MORGADO; WAGNER; CARMO, 2001)

Aristarco, segundo Arquimedes e Plutarco,”[...] em seu livro sobre as distˆancias do Sol e da Lua, baseando-se em observac¸˜oes, deduziu que a distˆancia da terra ao sol ´e maior do que 18 vezes e menor do que 20 vezes a distˆancia da terra `a lua”. (BOYER, 1974).

“Os erros cometidos por Aristarco devem-se aos dados experimentais que utilizou. Seus racioc´ınios dedutivos estavam corretos. Embora n˜ao tenhamos certeza de que utilizou Trigonometria, Apolˆonio de Perga, que viveu em torno de 200 a.C, um dos grandes matem´aticos gregos, achou, em seu Entrega R´apida, a aproximac¸˜ao 3,1416 paraπ, mais tarde utilizada pelos hindus, os quais exprimiam este valor como o quo-ciente 62832:20000. (MORGADO; WAGNER; CARMO, 2001, p. 101)

Na citac¸˜ao acima, se percebe que as raz˜oes trigonom´etricas foram utilizadas nas demonstrac¸˜oes do seno de pequenos ˆangulos.

Para (BOYER, 1974, p.109) Hiparco foi o primeiro a determinar com precis˜ao o nascer e o ocaso de v´arias estrelas, usando para isso uma tabela de cordas por ele calculada. Suas tabelas foram constru´_ıdas para serem usadas em Astronomia.

As principais contribuic¸˜oes de Hiparco em Astronomia foram `a organizac¸˜ao dos dados emp´ıricos babilˆonicos, a confecc¸˜ao de um cat´alogo de estrelas e a descoberta da pre-cess˜ao dos equin´ocios. ´E prov´avel que a divis˜ao do c´ırculo em 360otenha se originado com a tabela de cordas de Hiparco. Ele provavelmente seguiu a ideia do matem´atico grego Hipsiclo, o qual por sua vez havia dividido o dia em 360 partes, uma divis˜ao possivelmente inspirada na astronomia babilˆonica. (BOYER, 1974, p.109)

Podemos assim a_firmar, que Hiparco comparado a muitos matem´aticos gregos, foi essencial na construc¸˜ao da trigonometria.

Segundo (BOYER, 1974, p.111) “´e devido a Ptolomeu o qual cita v´arios resultados de Hiparco sobre Trigonometria e Astronomia, e a fragmentos de descric¸˜oes de seus trabalhos contidos nas obras de outros autores gregos”.

Morgado (MORGADO; WAGNER; CARMO, 2001, p. 102) a_firma que:

Figura 2.4: Quadril´atero inscrito

Segundo Morgado, “[...] Ptolomeu deduz usando as func¸˜oes seno e cosseno a ex-press˜ao para sen(α+β)e sen(α−β). Alem disso, demonstrou que sen2(α) +cos2(α) =1, ondeα eβ s˜ao agudos”.

Com as t´ecnicas expostas em seu livro, Ptolomeu decomp˜oe convenientemente triˆangulos em triˆangulos retˆangulo expondo dessa forma a Trigonometria at´e o renascimento. A trigonometria era usada pelos gregos em Astronomia. Eles nunca se preocuparam em utiliz´a-la em topografia, campo em que hoje ela tem emprego constante. A topogra-fia grega romana sempre recorreu somente a Geometria Euclidiana. (MORGADO; WAGNER; CARMO, 2001, p. 104) .

2.2 A Trigonometria Hindu

Com os hindus, “[...] a Trigonometria era um instrumento ´util e preciso para `a astronomia. No s´eculo V depois de Cristo, os astrˆonomos hindus abandonaram as tabelas de cordas e adotaram as de senos”. (BOYER, 1974)

[...] o matem´atico Aryabhata (476,?) passou a trabalhar com a corda AB em um c´ırculo de raio 3438( este n´umero ´e obtido supondo o comprimento da circunferˆencia 360.60 e usando 0 valor 3,14 paraπ. Com a mudanc¸a de raio, as tabelas de Ptolomeu n˜ao mais puderam ser utilizadas, sendo portando necess´ario refazˆe-las. A Trigonome-tria hindu era essencialmente aritm´etica, ao contr´ario da grega muito mais geom´eTrigonome-tria. (MORGADO; WAGNER; CARMO, 2001, p. 105).

Os ´arabes herdaram a Trigonometria dos gregos e hindus, adotando o ponto de vista aritm´eticos desses ´ultimos.

Introduziram para facilitar os c´alculos, a tangente, a cotangente, a secante e a cos-secante. Eles foram tamb´em indiretamente respons´aveis pelo uso da palavra seno cuja origem latina signi_fica bolsa, ba´_ıa.

[...] corda, em sˆanscrito, l´ıngua utilizada pelos antigos hindus, ´e jiva. Esta palavra foi usada sem modificac¸˜oes pelos ´arabes. No entanto, como em algumas outras l´ınguas, em ´arabe frequentemente se escrevem somente as consoantes das palavras, deixando as vogais ao cuidado da interpretac¸˜ao do leitor. Ora, a palavra sˆanscrita jiva tem as mesmas consoantes da palavra ´arabe Jaib3. Assim, foi natural que os tradutores de trabalhos matem´aticos, do ´arabe para o latim, e que desconheciam os sˆanscrito, supusessem que lidavam com tabelas de jaib, e traduziram esse termo pela palavra latina correspondente a sinus4. (MORGADO; WAGNER; CARMO, 2001, p. 105).

Como citamos, o interesse pela trigonometria entre gregos, hindus e ´arabes era mo-tivado por suas aplicac¸˜oes `a astronomia. A partir do Renascimento, ´epoca da expans˜ao mar´_ıtima europeia, que exigiu o desenvolvimento da cartogra_fia, a trigonometria passou a ser utilizada em Cartogra_fia e em topogra_fia.

[...] devido a necessidade de refazer todos os c´alculos da Astronomia posicional, com a adoc¸˜ao progressiva do sistema heliocˆentrico de Cop´ernico (1473-1543). Ali´as, seu livro, De Revolutionibus Orbium Celestium(1543) cont´em partes substanciais dedica-das a Trigonometria, as quais j´a tinham sido publicadedica-das independentemente em seu De Laeteribus et Angulis Triangulorum. Em ambos os trabalhos Cop´ernio demons-tra grande dom´ınio da Trigonometria. (MORGADO; WAGNER; CARMO, 2001, p. 105).

Com desenvolvimento da Navegac¸˜ao exigia mapas mais precisos e c´alculos mais exatos e numerosos de efem´erides5 astronˆomicas, para permitir a determinac¸˜ao da hora e da localizac¸˜ao durante as navegac¸˜oes.

Devemos citar, em primeiro lugar, George Peurbach(1423-1461), de Viena, que traduziu Almagesto diretamente do grego, comec¸ou a calcular tabelas de senos mais precisas exigida pelas aplicac¸˜oes. “[...] Com Regiomontano (1436-1476), o qual conhecia os trabalhos de trigonometria de Nasir Eddin e a partir deles, organizou a Trigonometria como uma parte da matem´atica independente da Astronomia”.

[...] com construc¸˜oes de tabelas trigonom´etricas, processo essencial para o progresso da Astronomia e da Matem´atica. A utilizac¸˜ao crescente da Trigonometria fez com que muitos outros matem´aticos constru´ıssem tabelas, como por exemplo, George Jo-aquim R´etico (1514-1576), Cop´ernico, Franc¸ois Vieta (1540-1603) e Bartolomeu Pi-tisco (1561-1613). A este ´ultimo devemos a Palavra Trigonometria6. R´etico fundiu as ideias de Cop´ernico e de Regiomontano com suas pr´oprias contribuic¸˜oes. (MOR-GADO; WAGNER; CARMO, 2001, p. 106).

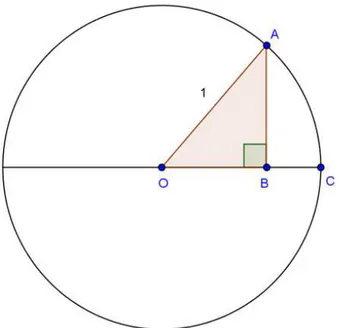
Regiomontano, faz uma exposic¸˜ao da trigonometria do triangulo retˆangulo num c´_ırculo (Figura 2.5) de raio igual a 1.

3_{Jaib: em ´arabe, significa bacia ou bolso.} 4_{Sinus: Origem do seno de um ˆangulo.}

Figura 2.5: Circulo de raio unit´ario

2.3 A Trigonometria na Europa

Na Europa, nesta ´epoca, estavam sendo descobertas e utilizadas v´arias identidades trigonom´etricas, como por exemplo, 2 cosα_·cosβ = cos(α+β) +cos(α−β), f´ormula in-troduzida pelo matem´atico ´arabe Ibn-Yunes (? 1008). A ˆenfase da Trigonometria comec¸ou a passar da soluc¸˜ao de triˆangulos para a investigac¸˜ao de relac¸˜oes funcionais. “A f´ormula citada acima ´e um exemplo das usadas na prostaf´erese, ou seja, substituic¸˜ao de produtos por somas” (BOYER, 1974, p. 211).

A prostaf´erese antecedeu os logaritmos como algoritimos para simpli_ficar c´alculos, e foi adotada por Tycho Brahe em seus c´alculos astronˆomicos. ´E muito prov´avel que a pros-taf´erese tenha sido o ponto de partida de Nepier em sua procura de um m´etodo (ou logaritmos) para efetuar, de maneira mais r´apida, os c´alculos longos e cansativos necess´arios na ´epoca.

Relata-se na historia um epis´odio pitoresco com o conhecimento que Vieta tinha da express˜ao para sen(nθ). Em 1593, o matem´atico belga Adriano Romano (1561-1615), desa_fiou os matem´aticos a resolverem a equac¸˜aox45−45·x43+945·x41−. . .−3795·x3+45·x=k

[...] o embaixador dos pa´ıses baixos da Franc¸a afirmou que n˜ao existiam matem´aticos franceses capazes de resolver este problema. O rei da Franc¸a, Henrique IV, convocou Vieta, o qual percebeu rapidamente que esta equac¸˜ao exprime sen(45·θ)em termos

de sen(θ), comk=sen(θ)·sen(45·θ)ex=2sen(θ). Vieta j´a sabia que a equac¸˜ao

podia ser decomposta em uma de grau 5 e duas de grau 3, ap´os o que ele a resolveu, para espanto de todos (BOYER, 1974, p. 213).

um gr´a_fico de dois per´_ıodos da func¸˜ao seno. ´E o primeiro aparecimento de uma func¸˜ao

trigo-nom´etrica usando o m´etodo dos indivis´_ıveis Robeval mostrou que

b

�

a

senx_·dx=cosb−cosa.

3 DEFINIC¸ ˜OES E PRELIMINARES

Uma das_figuras planas de grande relevˆancia ´e o triˆangulo, pois qualquer pol´_ıgono de n lados pode ser decomposto em triˆangulos. Tendo em vista este fato e sua relac¸˜ao com as func¸˜oes trigonom´etricas,_fizemos um breve estudo sobre esta_figura plana rica de informac¸˜oes. Apresentamos algumas de_finic¸˜oes e resultados sobre semelhanc¸a e congruˆencia, em seguida, de_finimos as func¸˜oes trigonom´etricas como raz˜oes entre as medidas dos lados de um triˆangulo retˆangulo com o intuito de apresentar as relac¸˜oes trigonom´etricas fundamentais.

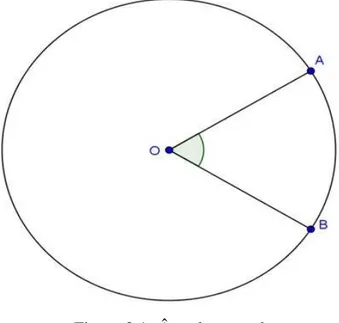
3.1 Angulo Central, Inscrito e Externo a uma Circunferˆenciaˆ

De_finic¸˜ao 3.1.1 ( ˆAngulo Central Relativo a uma circunferˆencia) Antes de apresentarmos a de_finic¸˜ao seguinte lembremos que ˆangulo ´e uma regi˜ao plana formada por duas semiretas com mesma origem cuja medida em radianos est´a entre zero e pi.

SejaA eB dois pontos de uma circunferˆencia de centro O. A semireta que passa

pelos pontos A e B divide o plano em dois semiplanos. Cada um destes semiplanos cont´em

uma parte da circunferˆencia as quais chamamos de Arcos determinados pelos pontosA eB e o segmento de retaAB ´e chamado corda AB. Se a corda AB for o diˆametro da circunferˆencia ent˜ao os arcos s˜ao chamados de semic´_ırculos, caso contr´ario, os arcos ser˜ao chamados dearco maior, que ´e o arco que_fica no mesmo semiplano que o centro do c´_ırculo, e o outro ´e chamado de arco menor. O ˆanguloAOBˆ que subentende o arco menor ´e chamado de ˆangulo central e a medida do arco menor ´e por de_finic¸˜ao a medida do ˆangulo central.

Figura 3.1: ˆAngulo central

Observe que na de_finic¸˜ao de ˆangulo inscrito, os pontos B e C determinam dois arcos. O arco que n˜ao contiver o v´erticeD do ˆangulo ´e chamado de arco correspondente ao ˆangulo inscrito dado.

Figura 3.2 ˆAngulo inscrito

De_finic¸˜ao 3.1.3 ( ˆAngulo excˆentrico a uma circunferˆencia) “Um ˆangulo excˆentrico a uma cir-cunferˆencia ´e um ˆangulo cujo v´ertice ´e um ponto exterior `a circir-cunferˆencia e seus lados inter-ceptam a circunferˆencia.”

Um ˆangulo excˆentrico a uma circunferˆencia ´e um ˆangulo cujo v´ertice ´e um ponto exterior `a circunferˆencia e seus lados intersectam a circunferˆencia como na_figura abaixo

Figura 3.3: ˆAngulo excˆentrico a uma circunferˆencia

De_finic¸˜ao 3.1.4 (Congruˆencia de Triˆangulos) Um triˆangulo ´e congruente a outro se, e so-mente se, ´e poss´ıvel estabelecer uma correspondˆencia entre seus v´ertices de modo que seus

la-dos congruentes aos lala-dos do outro e seus ˆangulos s˜ao ordenadamente congruentes aos ˆangulos do outro.

A congruˆencia entre triˆangulos ´e re_flexiva, sim´etrica e transitiva.

Definic¸˜ao 3.1.5 (Triˆangulos Semelhantes) Dizemos que dois triˆangulos s˜ao semelhantes se for poss´_ıvel estabelecer uma correspondˆencia biun´_ıvoca entre seus v´ertices de modo que ˆangulos correspondentes sejam iguais e lados correspondentes sejam proporcionais.

O caso de semelhanc¸a de triˆangulos que apresentamos abaixo ´e o caso onde os triˆangulos possuem ˆangulos iguais.

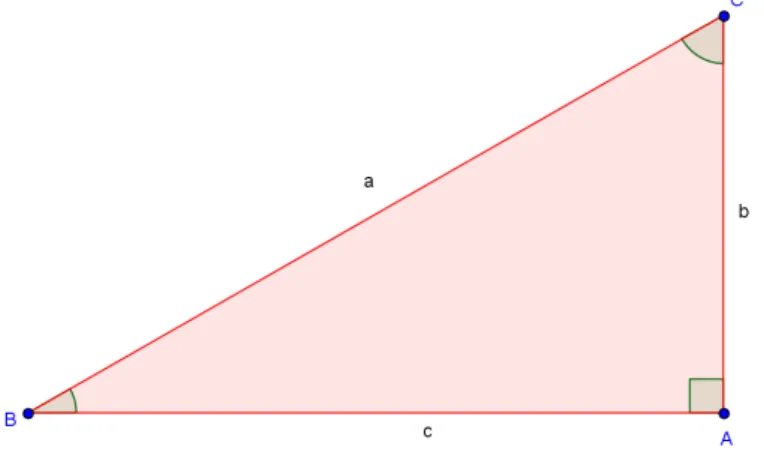
Considere um triˆanguloABC, retˆangulo emA. Denotaremos porθ eα as medidas dos ˆangulosACBˆ e ABC, respectivamente. Comoˆ θ eα s˜ao ˆangulos internos de um triˆangulo retˆangulo, ent˜ao s˜ao agudos e complementares. Seja AC =b a medida do lado oposto a α, AB=ca medida do lado adjacente ao ˆanguloα eBC=a, a medida do lado oposto ao ˆangulo reto, pela qual chamaremos, respectivamente, cateto oposto, cateto adjacente e hipotenusa.

Figura 3.4: Triˆangulo retˆangulo

3.2 Raz˜oes Trigonom´etricas no Triˆangulo Retˆangulo

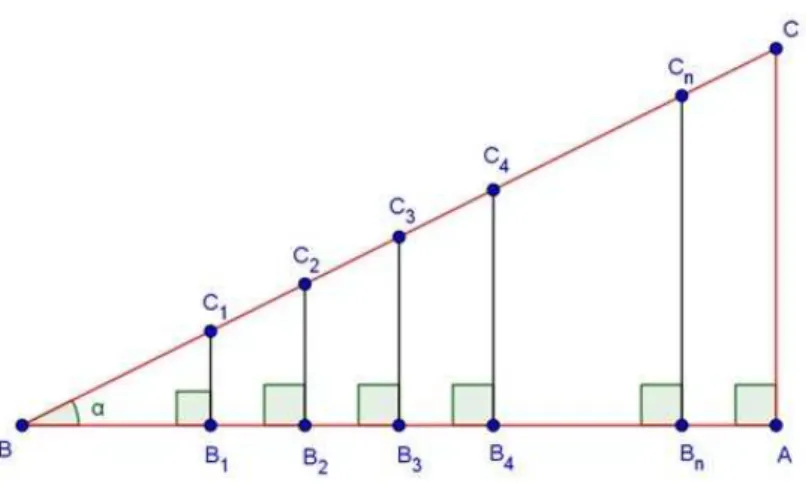
Figura 3.5: Triˆangulo retˆangulo dividido

Vejamos que os triˆangulos s˜ao semelhantes. Na semirreta BC marque os pontos C1,C2,C3, . . . ,Cn todos distintos, a partir destes, trace segmentos perpendiculares BC1, B2C2, B3C3,. . .,BnCnrelativos ao ladoAB. Assim, os triˆangulos constru´ıdosB1BC1,B2BC2,B3BC3,. . .,

BnBCnpossuem os ˆangulos agudos congruentes. Portanto,

B1C1 BC1

= B2C2

BC2

= B3C3

BC3

=. . .BnCn BCn

= BA

BC =

b

a (3.1)

As raz˜oes acima n˜ao dependem do comprimento dos lados dos triˆangulos, mas ape-nas da medidaα do ˆangulo. A raz˜ao acima ´e chamada de seno deα e denotamos por

senα =B1C1

BC1

=B2C2

BC2

=B3C3

BC3

=. . .BnCn BCn

= BA

BC =

b

a,0<α <

π

2 (3.2)

Similarmente, as raz˜oes:

BB1 BC1

=BB2

BC2

= BB3

BC3

=. . .BBn BCn

= BA

BC =

c

a,0<α <

π

2 (3.3)

B1C1 BB1

=B2C2

BB2

=B3C3

BB3

=. . .BnCn BBn

=AC

BA =

b

c,0<α <

π

2 (3.4)

que tamb´em n˜ao dependem da medida dos lados dos triˆangulos, mas somente, do ˆangulo α. Ent˜ao de_finiremos mais duas raz˜oes,

cosα = BA1

BC1

=BA2

BC2

= BA3

BC3

=BAn

BCn = BA

BC =

c

a,0<α <

π

2 (3.5)

tgα= A1C1

BA1 =

A2C2

BA2 =

A3C3

BA3 =

AnCn

BAn

= AC

BA =

b

c,0<α <

π

que s˜ao chamadas, respectivamente, de cosseno deα e tangente deα. Al´em das raz˜oes acima podemos de_finir mais trˆes raz˜oes paraα 0<α< π₂ , a saber

                    

sec α = 1

cosα

cotgα = 1

tgα

cossecα = 1

senα

(3.7)

as quais s˜ao chamadas respectivamente de secante de α, cotangente de α e cossecante de α. Observando o triˆangulo ABC acima e as de_finic¸˜oes das raz˜oes trigonom´etricas, conclu´_ımos facilmente que senθ =cosα,senα =cosθ etgθ =cotgα.

No que segue faremos demonstrac¸˜oes das principais identidades trigonom´etricas. Comec¸aremos pela relac¸˜ao fundamental da trigonometria.

Lema 3.2.1 SeABC ´e um triˆangulo retˆangulo emBent˜ao

sen2α+cos2α =1 (3.8)

ProvaComo vimos anteriormente, as de_finic¸˜oes das raz˜oes seno e cosseno de um ˆangulo n˜ao dependem das medidas dos lados do triˆangulo retˆangulo, mas somente do ˆangulo. Logo, pode-mos construir um triˆangulo retˆangulo cuja hipotenusaAC=1 , como na Figura 3.6.

assim,

senα = BC

AC =

BC

1 =BC (3.9)

cosα =AB

AC =

AB

1 =AB (3.10)

ent˜ao, pelo teorema de Pit´agoras

BC2 + AB2 = AC2

sen2α + cos2α = 12

sen2α + cos2α = 1

(3.11)

A tangente se relaciona com a secante e tamb´em com as raz˜oes seno e cosseno como mostramos abaixo

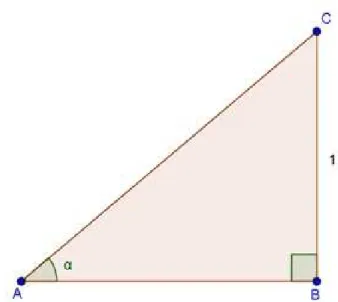
Lema 3.2.2 Se ABC ´e um triˆangulo retˆangulo em B ent˜ao

1+tan2α =sec2α e tanα = senα

cosα (3.12)

ProvaConsidereABCum triˆangulo retˆangulo emBeαa medida do ˆanguloBAC. Por semelhanc¸aˆ de triˆangulos podemos supor que a medida do ladoABvale 1, ou seja,AB=1 como na Figura 3.7.

por de_finic¸˜ao temos a tangente e a secante do ˆanguloα como as raz˜oes,

tgα = BC

AB =

BC

1 =BC (3.13)

cosα= AB

AC =

1

AC assim, AC=

1

cosα =secα (3.14)

por Pit´agoras e substituindo os valores acima

AB2 + BC2 = AC2

12 + tg2α + sec2α

1 + tg2α = sec2α

(3.15)

Mostraremos a segunda identidade usando a ´area do triˆanguloABC. Para isso, trace a alturahrelativa a hipotenusaAC=secα assim o triˆanguloABH ´e retˆangulo emHondeH ´e o p´e da alturah. Logo,AB=1 ser´a a hipotenusa do triˆanguloABHe pelo triˆangulo do lema 3.2.2 conclu´_ımos queh=senα. Ent˜ao, a ´area do triˆanguloABC ´e dada por

´

Area=A= AB·BC

2 =

AC_·h

2 (3.16)

substituindo os valores acima emA,

AB_·BC

2 =

AC_·h 2

1_·tgα

2 =

secα_·senα

2

tgα = secα_·senα

tgα = 1

cosα ·senα

tgα = senα

cosα

(3.17)

Mostraremos agora uma identidade equivalente para a cotangente.

Lema 3.2.3 SeABC ´e um triˆangulo retˆangulo emBent˜ao

cotg2α+1=cossec2α e cotg2α =cosα

senα (3.18)

Figura 3.8: Triˆangulo retˆangulo de cateto oposto unit´ario

temos,

tgα =BC

AB =

1

AB e senα =

BC

AC = (3.19)

assim

AB= 1

tgα =cotgα e =AC=

1

senα =cossecα (3.20)

Pelo teorema de Pit´agoras,

AB2+BC2=AC2 (3.21)

logo,

cotg2α+12=cossecα (3.22)

Para mostrarmos a segunda identidade traceh a altura relativa a hipotenusaAC =

cossecα. SejaH o p´e da alturah, logo o triˆanguloBHC ´e retˆangulo, sua hipotenusaBC=1 e h=senθ =cosα poisα eθ s˜ao complementares, ondeθ ´e a medida do ˆanguloACBˆ . Ent˜ao, a ´areaAdo triˆanguloABC ´e dada por

A= AB·BC

2 =

AC_·h

2 (3.23)

AB_·BC

2 =

AC_·h 2

cotgα_·1

2 =

cossecα_·cosα

2

cotgα = cossecα_·cosα

cotgα = 1

senα ·cosα

(3.24)

logo,

cotgα= cosα

senα (3.25)

Por enquanto, as func¸˜oes trigonom´etricas foram de_finidas para ˆangulos do intervalo

�

0,π₂�.Como esses ˆangulos podem ser medidos em radianos est˜ao naturalmente de_finidos o seno, o cosseno e a tangente de n´umeros reais no intervalo�0,π₂� . O pr´oximo passo ´e tentar estender estas func¸˜oes de modo que elas possam ser de_finidas para todos ou quase todos os n´umeros reais e que sejam mantidas as relac¸˜oes b´asicas

sen2x+cos2x=1 (3.26)

tgx= senx

cosx (3.27)

Figura 3.9: Ciclo trigonom´etrico

Observe que sex>0 ex>2_·π , ser´a necess´ario dar mais de uma volta emC, no sentido positivo, para atingirE(x), uma observac¸˜ao an´aloga vale para o caso de serx<0 . Seja como for,E(x) ´e um ponto bem de_finido deC. Por outro lado, dado um pontoPemC, ele ´e imagem pela func¸˜aoE de uma in_finidade de n´umeros reais, todos eles da forma

x+2·k·π,k∈Ze 0≤x≤2·π (3.28)

`

As vezes, se costuma exprimir este fato dizendo que x+2_·k_·π s˜ao as v´arias

determinac¸˜oes do arco����AP.

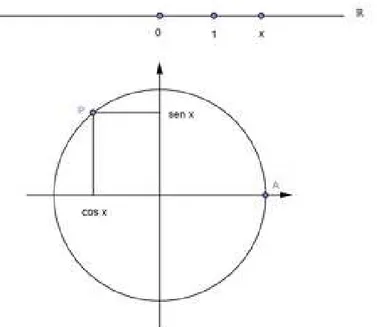
No sistema de coordenadas cuja origem ´e o centro deCe sendoA= (1,0)de_finimos

cosx = abscissa deP

senx = ordenada deP

tgx = senx

cosx,se cosx�=0

(3.29)

´

E claro que esta de_finic¸˜ao coincide com a anterior quando 0<x< π₂ al´em disso, permite escrevercos0=1 e sen0=0quandoP=A, cosπ₂ =0e senπ₂ =1.Ainda, como todo pontoP= (cosx,senx)deCest´a a uma distˆancia de 1 da origem, temos

sen2x+cos2x=1 (3.30)

A nova de_finic¸˜ao, portanto, estende a primeira e mant´em as relac¸˜oes b´asicas. Ob-serve quetgxn˜ao ´e de_finida parax= π₂+k.π(k inteiro), porque para estes valorescosx=0.

Podemos ent˜ao restringir o estudo destas func¸˜oes ao intervalo [0,2π] que corres-ponde ao estudo das coordenadas de um ponto que d´a exatamente uma volta no c´_ırculo tri-gonom´etrico. As func¸˜oes seno e cosseno, como coordenadas de um ponto, tˆem sinais que dependem do quadrante que se encontra na Figura abaixo.

3.3 Area de um Triˆangulo Qualquer´

SejaABCum triˆangulo. SeAB=ceAC=b, ent˜ao o valor da ´area do triˆanguloABC ´e

A= b·c·senθ

2 (3.31)

ProvaFaremos a demonstrac¸˜ao em dois casos. Considere o triˆanguloABCda Figura 3.12, com. Suponha que a medida do ˆangulo BACvaleˆ θ < π₂e b e cas medidas dos lados que formam o ˆanguloBACˆ .

Figura 3.12: ´Area de um triˆangulo em func¸˜ao do ˆangulo agudo

Sabemos que o triˆanguloADC ´e retˆangulo emD, logo pela de_finic¸˜ao da func¸˜ao seno podemos escrever

BD=AB_·senθ (3.32)

como a ´area do triˆanguloABC ´e dada por

A=AC·BD

2 (3.33)

ent˜ao, substituindoBD=AB_·rmsenθ na equac¸˜ao acima obtemos,

A= AC·AB·senθ

2 (3.34)

A= b·c·senθ

2 (3.35)

Figura 3.13: ´Area de um triˆangulo em func¸˜ao do ˆangulo obtuso

usando a de_finic¸˜ao do seno e sabendo queθ+α=π (suplementares), senα=senθ. Temos,

senα= BD

AB =

BD

c , assimBD=c·senα=c·senθ (3.36)

como a ´areaAdo triˆanguloABC ´e dada por

A=AC·BD

2 (3.37)

ent˜ao, fazendo BD=c.senα=c.senθ na equac¸˜ao acima obtemos

A=b.c.senθ

2 . (3.38)

Apresentaremos dois resultados que s˜ao de grande relevˆancia na geometria, a Lei dos Cossenos e a Lei dos Senos. Atrav´es destas provaremos algumas identidades trigonom´etricas.

3.4 Lei dos Cossenos

Teorema:Em um triˆangulo qualquerABC, vale a relac¸˜ao,

BC2=AB2+AC2−2·AB·ACcosθ (3.39)

Figura 3.14: Triˆangulo qualquer e a Lei dos cossenos

os triˆangulosABDeBDCs˜ao retˆangulos logo,

AB2 = BD2_+AD2

BC2 = BD2_+DC2 (3.40)

seDest´a entreAeC, ent˜aoAC=AD+DCque nos darDC=AC+AD. Subtraindo as equac¸˜oes acima teremos

BC2−AB2= (BD2+DC2)−(BD2+AD2)

BC2−AB2=DC2−AD2 BC2=AB2+DC2−AD2

(3.41)

substituindoDC=AC−ADemBC2=AB2+DC2−AD2

BC2=AB2+ (AC−AD)2−AD2 BC2=AB2+AC2−2_·AC_·AD+AD2−AD2

BC2=AB2+AC2−2_·AC_·AD

(3.42)

no triˆangulo retˆanguloADBtem-se queAD=AB·cosθ. Assim

BC2=AB2+AC2−2_·AC_·AB_·cosθ (3.43)

Figura 3.15: Triˆangulo obtuso e a Lei dos cossenos.

temos assimBDCeBDAtriˆangulos retˆangulos. Logo,

AB2=BD2+AD2

BC2=BD2+DC2 (3.44)

subtraindo as equac¸˜oes acima e substituindoDC=AC+AD

BC2−AB2 = (BD2+DC2)−(BD2+AD2)

BC2 = AB2+DC2−AD2

BC2 = AB2+ (AC+AD)2_−AD2

BC2 = AB2+AC2+2.AC_·AD+AD2−AD2

BC2 = AB2+AC2+2_·AC_·AD

(3.45)

como no triˆangulo retˆanguloBDA,AD=AB_·cos(π−θ) =−AB_·cosθ. Substituindo

AD=−AB_·cosθ emBC2=AB2+AC2+2_·AC_·AD (3.46)

conclu´_ımos,

BC2=AB2+AC2−2_·AC_·ABcosθ (3.47)

3.5 Lei dos Senos

Teorema:Em um triˆangulo qualquerABC, vale a relac¸˜ao

BC sen ˆA=

AC sen ˆB =

AB

ProvaSeja ABC um triˆangulo qualquer, inscrito numa circunferˆencia de raio R. Por um dos v´ertices B do triˆanguloABC.

tracemos o diˆametro correspondenteBA�e liguemosA�comCcomo na Figura abaixo,

Figura 3.16: Triˆangulo inscrito

sabemos que ˆA‘=Aˆ por determinarem na circunferˆencia a mesma corda BC, ou seja, inscrito na circunferˆencia. O triˆanguloA‘BC´e retˆangulo emCpor est´a inscrito numa semicircunferˆencia, ent˜ao

sen ˆA�₌ BC

BA� =

BC

2_·R (3.49)

analogamente fazendo o mesmo para os ˆangulos ˆBe ˆCteremos

sen ˆB� = AC

2_·R

sen ˆA� = AB

2_·R

(3.50)

conclu´_ımos,

BC sen ˆA=

AC sen ˆB =

AB

4 IDENTIDADES TRIGONOM ´ETRICAS E SUAS DEMONSTRAC¸ ˜OES

Neste cap´_ıtulo apresentaremos algumas demonstrac¸˜oes das f´ormulas da adic¸˜ao de arcos e sua relac¸˜ao com o Teorema da Corda Quebrada e o Teorema de Ptolomeu. Em sequencia arco duplo, transformac¸˜ao em produto da soma dos senos de dois arcos e a relac¸˜ao do teorema Ptolomeu e da corda quebrada com o seno e o cosseno da soma e da diferenc¸a de dois arcos.

4.1 Cosseno e Seno da Soma e da Diferenc¸a de dois arcos

Nesta sec¸˜ao, vamos deduzir as f´ormulas que calculam as func¸˜oes trigonom´etricas da soma e da diferenc¸a de dois arcos cujas func¸˜oes s˜ao conhecidas e para obter a primeira delas destacaremos a demonstrac¸˜ao normalmente usada para o caso do cosseno da soma,

cos(a+b) =cosa·cosb−sena·senb (4.1)

devemos lembrar que a distˆancia entre dois pontos do plano(x1,y1)e(x2,y2)´e dada por

d=

�

(x1−x2)2+ (y1−y2)2 (4.2)

consideremos ent˜ao no c´_ırculo unit´ario abaixo,

Figura 4.1: Ciclo trigonom´etrico e o plano

sejaB,QeR os pontos do ciclo associados aos n´umeros a,a+b e −b, respectivamente. Em relac¸˜ao ao sistemauOv, as coordenadas desses pontos s˜ao A= (1,0), B= (cosα,senα),Q=

d= �

(x1−x2)2_{+ (y1−y2)}2 _(4.3)

assim,

�

(cos(a+b)−1)2_{+ (sen(a+b)−0)}2₌�_{(cosa−cosb)}2_{+ (sena+senb)}2

(cos(a+b)−1)2_{+ (sen(a+b)−0)}2_{= (cosa−cosb)}2_{+ (sena+senb)}2 2−2_·cos(a+b) =2−2 cosa_·cosb+2_·sena_·senb

cos(a+b) =cosa_·cosb−sena_·senb

(4.4)

A demonstrac¸˜ao a seguir utilizaremos uma construc¸˜ao de um retˆangulo e um circulo de raio unit´ario. Para demonstrar o seno da diferenc¸a de dois arcos,

sen(α−β) =senα_·cosβ−senα_·cosβ (4.5)

Demonstrac¸˜ao:

Construa um Retˆangulo ABCD e considere o raio do c´_ırculo igual a 1, como na figura 4.2.

Figura 4.2: Circulo de raio unit´ario e o Retˆangulo

destacando os triˆangulosABE eAFG,na_figura acima, tomandoBAEˆ =β eFAGˆ =α. Assim, no triˆanguloAEF o ˆangulo EAFˆ =α−β . Teremos tamb´em, AB=cosβ,BE =senβ, pois AE=1 (visto no cap´_ıtulo 2),AG=cosα,GF =senα.

Como a ´area do retˆangulo ABCD pode ser determinada pela soma das ´areas dos

triˆangulos ABE,AEF,FCE e ADF .Para a ´area do triˆangulo AEF usaremos o teorema 3.3.

A= AB·BE

2 +

AE_·AF_·sen(α−β)

2 +

FC_·CE

2 +

FD_·DA

2 =AB·BC (4.6)

sabemos pela construc¸˜ao acima que

AG=FD,AE=AF =1,DA=FG=BC,FC=AB−AGeCE =FG−BE (4.7)

substituindo os valores conhecidos na ´area do retˆanguloABCDacima teremos

AB.BE

2 +

AE.AF.sen(α−β)

2 +

FC.CE

2 +

FD.DA

2 =AB.BC (4.8)

cosβ.senβ

2 +

1.1.sen(α−β)

2 +

(cosβ−cosα).(senα−senβ)

2 +

cosα.senα

2 =cosβ.senα

(4.9)

cosβ.senβ+sen(α−β) + (cosβ−cosα).(senα−senβ) +cosα.senα =2.cosβ.senα

(4.10)

ent˜ao,

sen(α−β) =senα.cosβ−senβ.cosα (4.11)

Vamos adiante prosseguir com mais uma construc¸˜ao e consequentemente apresentar outra demonstrac¸˜ao para o seno da diferenc¸a de dois arcos, demonstrada logo acima. Destaca-mos tamb´em, que esta mesma construc¸˜ao chegareDestaca-mos ao seno da soma de dois arcos.

Figura 4.3: Triˆangulo retˆangulos de lado unit´ario comum

Destacando o triˆangulo retˆangulo ABD e ABC. Chamaremos o ˆangulo BADˆ =

β e BADˆ =β . Assim, no triˆanguloADCo ˆangulo DACˆ =α−β. Aplicando as de_finic¸˜oes das raz˜oes trigonom´etricas nos triˆangulos retˆangulosABDeAB, teremos: BD=tgβ, AD=secβ, AC=secα e DC=tgα−tgβ. Sabemos que a ´area do triˆangulo ADC pode ser escrita pelo teorema 3.3 e pela de_finic¸˜ao da ´area de um triˆangulo da seguinte forma

A= DC.AB

2 =

AD.ACsen(α−β)

2 (4.12)

DC.AB=AD.ACsen(α−β) (4.13)

substituindo os valores dados acima

(tgα−tgβ).1=secβ.secα.sen(α−β) (4.14)

utilizando as de_finic¸˜oes de tangente e secante, teremos

senα

cosα −

senβ

cosβ =

1 cosβ.

1

cosα.sen(α−β) (4.15)

sen(α−β) =senαcosβ−senβcosα (4.16)

Agora utilizando a construc¸˜ao da_figura anterior apresentaremos outra demonstrac¸˜ao para o cosseno da diferenc¸a de dois arcos. Aplicando, a Lei dos Cossenos demonstrada no cap´_ıtulo 2, no triˆanguloADC. Sabemos tamb´em que esta mesma_figura encontramos o cosseno da soma de dois arcos.

Demonstrac¸˜ao:No triˆanguloADCda_figura anterior, sabemos que

DC2=AD2+AC2−2.AD.AC.cos(α−β) (4.17)

DC=tgα−tgβ (4.18)

AD=secβ (4.19)

AC=secα (4.20)

Substituindo os respectivos valoresDC,AD e ACna lei dos cossenos dada do triˆangulo ADC, teremos

DC2=AD2+AC2−2.AD.AC.cos(α−β) (4.21)

(tgα−tgβ)2=sec2β+sec2α−2.secβ.secα.cos(α−β) (4.22)

tg2α−2.tgα.tgβ+tg2β =sec2β+sec2α−2.secβ.secα.cos(α−β) (4.23)

tg2α−2.tgα.tgβ+tg2β =sec2β+sec2α−2.secβ.secα.cos(α−β) (4.24)

2.secβ.secα.cos(α−β) =sec2α−tg2α+sec2β−tg2β+2.tgα.tgβ (4.25)

sabemos quesec2α−tg2α =1e sec2β−tg2β =1 .Logo,

secβ.secα.cos(α−β) =1+tgα.tgβ (4.27)

1 cosβ.

1

cosα.cos(α−β) =1+

senα

cosα.

senβ

cosβ (4.28)

multiplicando ambos os membros porcosα.cosβ, teremos

cos(α−β) =cosα.cosβ+senα.senβ (4.29)

Utilizando uma nova construc¸˜ao, apresentaremos outra demonstrac¸˜ao daquela apre-sentada normalmente nos livros did´aticos para o seno da soma de dois arcos. Aplicando ´area de um triˆangulo e o mesmo pode ser feito para o cosseno da soma basta aplicar a Lei dos Cossenos no triˆangulo ADC.

Demonstrac¸˜ao: Construa um Triˆangulo Retˆangulo ADC e considere AB a altura relativa ao ladoDCigual a 1, como na_figura 3.14.

Figura 4.4: Triˆangulo retˆangulo de altura unit´aria

no triˆangulo ABC e ABD consideramos os ˆangulos α e β como indicado na _figura acima.

BD=tgβ ,AD=secβ , BC=tgα , AC=secα e DC=BC+BD (4.30)

substituindo estes valores na ´area do triˆangulo ADC pode ser determinada por

A=AC.AD.sen(α+β)

2 =

DC.BA

2 (4.31)

AC.AD.sen(α+β) =DC.BA (4.32)

secα.secβ.sen(α+β) = (tgα+tgβ).1 (4.33)

1.1.sen(α+β)

cosα.cosβ =

senα

cosα +

senβ

cosβ (4.34)

multiplicando ambos os membros porcosα.cosβ, teremos

sen(α+β) =senα.cosβ+senβ.cosα (4.35)

Vale lembrar que cada _figura constru´_ıda serve tanto para mostrar o seno como o cosseno da soma e da diferenc¸a de dois arcos. Aplicando novamente a lei dos Cossenos no triˆanguloADC como na demonstrac¸˜ao anterior deduziremos o cosseno da soma de dois arcos dada por

cos(α+β) =cosα.cosβ+senα.cosβ (4.36)

Construindo-se um trap´ezio vamos novamente deduzir o seno da soma de dois arcos dada anteriormente.

Figura 4.5: Trap´ezio

usando as de_finic¸˜oes das raz˜oes trigonom´etricas e analisando a construc¸˜ao da_figura conclu´_ımos facilmente que:

CD=AB=senα, BD=AC=cosα, DE=tgβ.BD,CE=CD+DE e BD=cosβ.BE (4.37)

sabemos que a ´area do trap´ezio ´e dada por:

´

Area do trapezio=

�

AB+CE

2

�

.BD (4.38)

e esta mesma ´area pode ser encontrada pela soma da ´area do triˆangulo ABC e BCE e para ´area do triˆangulo BCE usaremos o teorema 3.3, j´a para o triˆangulo ABC a de_finic¸˜ao comum da ´area de um triˆangulo.Assim,

AB.AC

2 +

BC.BE.sen(α+β)

2 =

�

AB+CE

2

�

.BD (4.39)

AB.AC+BC.BE.sen(α+β) =�AB+CE�.BD (4.40)

substituindo os valores,acima encontrados, na igualdade imediatamente acima. Teremos,

senα.cosα+1. BD

cosβ.sen(α+β) = �

senα+CD+DE�.BD (4.41)

senα.cosα+cosα

cosβ.sen(α+β) = �

senα.cosα+cosα

cosβ.sen(α+β) = (senα+senα+tgβ.cosα).cosα (4.43)

senα.cosα+cosα

cosβ.sen(α+β) = �

2.senα+senβ

cosβ.cosα �

.cosα (4.44)

multiplicando ambos os membros por cosβ e desenvolvendo encontraremos

cosβ.senα.cosα+cosα.sen(α+β) =2.senα.cosα.cosβ+senβ.cosα.cosα (4.45)

dividindo ambos os membros por cosα e desenvolvendo encontraremos

sen(α+β) =senα.cosβ+senβ.cosα (4.46)

4.2 Arcos duplos e Arcos metades

Destacaremos nesta sec¸˜ao a propriedade re_flexiva de triˆangulos congruentes. Para demonstrarmos o seno e o cosseno de um arco duplo que s˜ao dados por

sen(2.α) =2.senα.cosα e cos(2.α) =cos2α−sen2α

Demonstrac¸˜ao:Construa o triˆangulo is´osceles como o da Figura abaixo

O triˆangulo ADC e BDC s˜ao iguais. Observando o ˆangulo a do triˆangulo ADC retˆangulo conclu´_ımos facilmente que AD=DB=senα, AB=2.AD e CD=cosα,usando a de_finic¸˜ao de ´area de um triˆangulo. Podemos assim representar a ´area do triˆangulo ABC por

A=AC.BC.sen(2.α)

2 =

AB.CD

2 (4.47)

substituindo os dados acima em

AC.BC.sen(2.α)

2 =

AB.CD

2 (4.48)

1.1.sen(2.α)

2 =

2.AD.cosα

2 (4.49)

Agora neste mesmo triˆangulo is´osceles acima aplicaremos a lei dos cossenos para mostrarmos o cosseno do arco duplo. Destacando assim a lei

AB2=AC2+BC2−2.AC.BC.cos(2.α) (4.51)

substituindoAC=BC=1, AB=2.senα e CD=cosαna lei dos cossenos, encontraremos:

(2.senα)2=12+12−2.1.1.cos(2.α) (4.52)

4.sen2α =2−2.cos(2.α) (4.53)

2.sen2α =1−cos(2.α) (4.54)

sabemos quesen2α+cos2α=1, ent˜ao

2.sen2α=sen2α+cos2α−cos(2.α) (4.55)

cos(2.α) =cos2α−sen2α (4.56)

Apresentaremos outra construc¸˜ao para mostrar o seno do arco duplo que foi provado anteriormente. Para isso, construa o circulo como o da_figura 4.2.

Figura 4.7: Triˆangulo retˆangulo inscrito

de_finic¸˜ao dada no cap´_ıtulo 2 de ˆangulo inscrito conclu´_ımos que

ˆ

B= α

2 ,Cˆ=

β

2 (4.57)

pela lei dos Senos ´e de imediato que

AB=2.R.cos(Bˆ) (4.58)

AC=2.R.sen(Bˆ) (4.59)

pela construc¸˜ao,

BC=2.R (4.60)

AO=OC=R (4.61)

tomandoR=1 determinaremos a ´area do triˆanguloAOCem destaque na_figura.

A ´area do triˆanguloABC ´e o dobro da ´area do triˆanguloAOC. Pois, considerando a base do triˆanguloAOC, OC=Re a base do triˆangulo AOB,OB=R. Assim, tanto o triˆangulo AOCeAOBpossuem a mesma base e, por consequˆencia a mesma altura visto que o v´ertice que n˜ao est´a contido na base ´e o mesmo. Logo , a ´area do triˆanguloAOCser´a dada por

A= AO.OC.senα

2 =

AB.AC

4 (4.62)

substituindoα =2.Bˆ, AO=OC=1, AB=2.R.cosBeˆ AC=2.R.senBˆna igualdade acima

1.1.sen(2._Bˆ₎

2 =

2.cosBˆ.senBˆ

4 (4.63)

sen�2._Bˆ�_=2.senBˆ_.cosBˆ _(4.64)

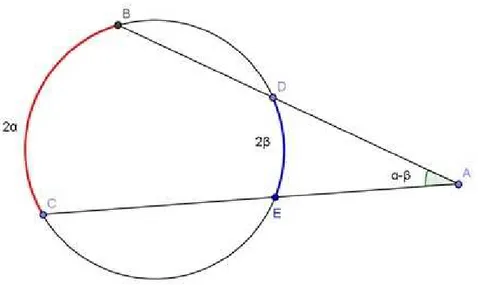
Figura 4.8: ˆAngulo excˆentrico e o seno da diferenc¸a

Consideraremos x =α e y =β , α+β = π₂ com α �= β. Pela construc¸˜ao P´e

excˆentrico exterior, PAtangente, PC ´e secante e contem o diˆametro da circunferencia. Sabe-mos tambem que o triˆangulo POA´e retˆangulo em e que o ˆangulo APOˆ =α−β. Pois, P ´e excˆentrico exterior. Como 2.β+ (α−β) = π₂ (complementares). Assim,

sen(α−β) =cos(2β) (4.65)

cos(α−β) =sen(2β) (4.66)

α eβ (4.67)

s˜ao complementares tamb´em.Por isso,senα =cosβe senβ =cosα. Usaremos o resultado do cosseno do arco duplo em

sen(α−β) =cos(2β) (4.68)

sen(α−β) =cos2β−sen2β (4.69)

sen(α−β) =cosβ.cosβ−senβ.senβ (4.70)

substituindocosβ =senα e senβ =cosα, resulta

sen(α−β) =senα.cosβ−senβ.cosα (4.71)

constatamos pela construc¸˜ao que s˜ao complementares

sen(α−β) =cos(2β) (4.72)

sen(α−β) =cos2β−sen2β (4.73)

sen(α−β) =cosβ.cosβ−senβ.senβ (4.74)

substituindocosβ =senα e senβ =cosα, resulta

sen(α−β) =senα.cosβ−senβ.cosα (4.75)

A demonstrac¸˜ao a seguir a para a tangente da metade de um arco que ´e dada por:

tg

�_α

2

� =

�

1−cosα

1+cosα, 0<α < π

2 (4.76)

Prova: Construa um quadril´atero inscrito ABDC e considere a medida do lado AB igual a medida ladoAC igual a 1, como na_figura 4.4.

Figura 4.9: Quadril´atero inscrito de lados unit´arios

Pela construc¸˜ao temos os triˆangulosABD e ACD inscritos e um de seus respecti-vos lados ´e o diˆametro da circunferˆencia. Por isso, s˜ao retˆangulos. FazendoBADˆ =CADˆ =

α e ADCˆ = ADBˆ =β , nos triˆangulos AEB e AEC congruentes BE =CE =senα.Pois,

AB=AC=1 (hipotenusa). Nos triˆangulosABD e ACDum de seus catetos ´e 1,assim conclu´_ımos queBD=CD=tgα.

BC2=BD2+DC2−2.BD.DC.cos(2β) (4.77)

BC2=AB2+AC2−2.AB.AC.cos(2.α) (4.78)

Igualando as equac¸˜oes acima

AB2+AC2−2.AB.AC.cos(2α) =BD2+DC2−2.BD.DC.cos(2β) (4.79)

12+12−2.1.1.cos(2α) =tg2α+tg2α−2.tgα.tgα.cos(2β) (4.80)

2−2.cos(2α) =2.tg2α−2.tg2α.cos(2.β) (4.81)

1−cos(2α) =tg2α.(1−cos(2.β)) (4.82)

mas,

2.α+2β =π eα+β = π

2 e cos(2.β) =−cos(2.α) (4.83)

substituindo,

1−cos(2α) =tg2α.(1+cos(2α)) (4.84)

1−cos(2α)

1+cos(2α) =tg

2_α

(4.85)

tgα= 2

�

1−cos(2.α)

1+cos(2.α) (4.86)

fazendo,

BADˆ =CADˆ = α

2 e ADCˆ =ADBˆ =

β

2 (4.87)

tgα

2 =

2

�

1−cosα

1+cosα (4.88)

4.3 Teorema de Ptolomeu e o seno da diferenc¸a de dois arcos

Ptolomeu, por meio de seu teorema, demonstrou propriedades que na trigonometria moderna seriam seno e cosseno da soma e da diferenc¸a de dois arcos e nesta sec¸˜ao enunciaremos o teorema de Ptolomeu com sua demonstrac¸˜ao e estabelecemos a relac¸˜ao que h´a entre o mesmo e a relac¸˜ao da soma e da diferenc¸a de dois arcos.

Teorema de Ptolomeu: ”O produto dos comprimentos das diagonais de um qua-dril´atero inscrit´_ıvel ´e igual a soma dos produtos dos comprimentos dos pares de lados opostos”.

Dado o quadril´ateroABCDtemos queAC.BD=AB.CD+BC.AD

Figura 4.10: Teorema de Ptolomeu

Demonstrac¸˜ao:

SejaABCD um quadril´atero inscrito em um circulo conforme a _figura acima, seja

AC.BD=AB.CD+BC.AD. Seja P um ponto sobre o prolongamento do lado CD tal que os

ˆangulos BACˆ e DAPsejam congruentes. Como o quadril´atero ABCD ´e inscrit´ˆ _ıvel ent˜ao os ˆangulosABCeˆ ADPˆ tamb´em s˜ao congruentes, assim os triˆangulos_∆ABCe_∆DAPs˜ao semelhan-tes. Com isso

AB

AD =

BC

DP =

AC

AP=⇒DP=

AD.BD AB

Como os ˆangulosBADeˆ CAPs˜ao congruentesˆ AB

AD= AC

APe os triˆangulos∆ABDe∆ACD

BD

CP =

AB

AC =⇒CP=

AC.BD.

AB (4.89)

MasCP=CD+DP, dessa forma

AC.BD

AB =CD+

AD.BD

AB ⇐⇒AC.BD=AB.CD+BC.AD (4.90)

A obra de Ptolomeu ´e basicamente astronˆomica, mas desperta o interesse dos ma-tem´aticos devido `as identidades trigonom´etricas que ele utilizou a_fim de reunir dados para a sua t´abua de corda (que ´e aproximadamente uma t´abua de senos).

Agora vamos apresentar uma demonstrac¸˜ao para o seno da diferenc¸a de dois arcos, vista anteriormente, usando o teorema de Ptolomeu.

Demonstrac¸˜ao:Construa um quadril´atero inscrito com um de seus lados sendo o diˆametro da circunferˆencia de raio igual a 1 como o da_figura 4.11.

Figura 4.11: Quadril´atero inscrito e o teorema de Ptolomeu

Os triˆangulosABD e ACDs˜ao retˆangulos e inscritos. Da´_ı, pela de_finic¸˜ao ou pela lei dos Senos nos triˆangulosABD e ACD, considerando DBˆ =2.α e CDˆ =2.β .

No triˆanguloACD,

AC=2.R.cosβ (4.91)

CD=2.R.senβ (4.92)

No triˆanguloABD,

BD=2.R.senα (4.94)

AD=2.R (4.95)

no triˆanguloBCDusando a lei dos senos,

BC=2.R.sen(α−β) (4.96)

substituindo os valores acima no teorema de Ptolomeu,

AC.BD=AB.CD+BC.AD (4.97)

2.R.sen ˆD.2.R.senβ+2.R.sen(α−β).2.R=2.R.cosβ.2.R.senα (4.98)

sen ˆD.senβ+sen(α−β) =cosβ.senα (4.99)

como,

ˆ

D+x= π

2, entao sen˜ Dˆ =cosα (4.100)

assim,

sen(α−β) =senα.cosβ−senβ.cosα (4.101)

4.4 Teorema da Corda quebrada e o seno da diferenc¸a de dois arcos

Nesta sec¸˜ao provaremos a f´ormula do seno da diferenc¸a de dois arcos utilizando o resultado da geometria plana conhecido como o teorema da corda quebrada o qual determina o ponto m´edio da corda quebrada.

Entende-se por corda quebrada a uni˜ao de duas cordasABeBC ondeA,BeC s˜ao pontos de uma circunferˆencia este resultado ´e mais uma das grandes ideias de Arquimedes.

Teorema 4.4.1 (Teorema da corda quebrada) Se AB e BC comp˜oem uma corda quebrada com AB<BC e se M´e o ponto m´edio do arco ABC, ent˜ao o p´e da perpendicularˆ Fsobre o lado ´e o ponto m´edio da corda quebrada.

do arcoABC e seja Fo p´e da perpendicular baixada sobre BC. Prolongue o segmento FBˆ at´e o pontoC‘, tal queFC=FC‘. Observe que os triˆangulosABM eMBC�s˜ao congruentes. De fato,o ˆanguloABMˆ =MBC, os arcos ˆˆ AM=MC. Logo,ˆ AM=MC=MC‘. Assim, os triˆangulos possuem seus lados iguais e podemos deduzir queBC‘=AB, portanto,

FC=FC‘= BF+BC‘=BF+AB (4.102)

FC=BF+AB (4.103)

Ent˜ao,F ´e o ponto m´edio da corda quebradaABC.

Figura 4.12: Corda Quebrada

Usaremos agora o teorema acima demonstrado para mostrar o seno da diferenc¸˜a de dois arcos. Para isso, observe a_figura acima e denote os arcos ˆAM=_MCˆ _{=2.α eBM}ˆ _=2.β. No triˆangulo BMC e MFC, usaremos de_finic¸˜ao das raz˜oes seno e cosseno e a lei dos senos,

respectivamente. Considerando, AM=MC=MC‘=1. Ent˜ao,

MF=senβ e FC=cosβ (4.104)

MC=2.R.senα =1, assim2.R= 1

senα =cossecα (4.105)

no triˆanguloBFM retˆangulo,FBMˆ =α ´e a metade do arco ˆMC(inscrito)

tgα = MF

BF =

senβ

BF , entao BF˜ = senβ

tgα (4.106)

neste triˆanguloα =C‘ ˆMB+β (teorema do ˆangulo externo).

usando a lei dos senos para o triˆangulo ABM,

AB=2.R.AMBˆ =2.R.sen(α−β) (4.107)

aplicando agora o teorema da corda quebrada e substituindo os valores acima

FC=BF+AB (4.108)

cosβ =senβ

tgα +2.R.sen(α−β) (4.109)

cosβ = senβ

tgα +

1

senα.sen(α−β) (4.110)

como,

tgα= senα

cosα (4.111)

cosβ = sen_senαβ cosα

+ 1

senα.sen(α−β) (4.112)

cosβ = senβ.cosα

senα +

1

senα.sen(α−β) (4.113)

multiplicando ambos os membros porsenα, resulta

senα.cosβ =senβ.cosα+sen(α−β) (4.114)

sen(α−β) =senα.cosβ−senβ.cosα (4.115)

4.5 Transformac¸˜ao em produto

O matem´atico francˆes Franc¸ois Vieta sistematizou o estudo da trigonometria esf´erica, at´e ent˜ao um amontoado de f´ormulas desconexas, e mostrou que

senα+senβ =2.sen

�_α +β 2 � .cos �_α −β 2 �

Por isso, nesta sec¸˜ao faremos uma demonstrac¸˜ao da soma dos senos de dois arcos. Com objetivo de mostrar geometricamente a soma de senos,

senα+senβ =2.sen

�_α +β

2

�

.cos

�_α

−β

2

�

(4.116)

Demonstrac¸˜ao:Construa a_figura 4.13.

Figura 4.13: Transformac¸˜ao em Produto

traceAC e OCformando os triˆangulos retˆangulosAEC e OCDe considere o raio do c´_ırculo igual a 1.

no triˆangulo retˆanguloOAB,

AB=senα (4.117)

OB=cosα (4.118)

no triˆangulo retˆanguloOCD,

OD=cosβ (4.119)

DC=senβ (4.120)

BD=EC,DC=BE (4.121)

no triˆangulo inscritoAFC, o ˆanguloFACˆ = α−₂β eAFCˆ =α+₂β pois s˜ao inscritos e pela lei dos senos

AC

sen(AFCˆ )=2.R (4.122)

no triˆangulo retˆanguloAECreto em E,

CAFˆ = α−β

2 , poise inscrito´ . (4.123)

sen�CAFˆ �=sen

� α−β

2

� = EC

AC e cos

�

CAFˆ �=cos

� α−β

2

� = AE

AC (4.124)

Mas, pela construc¸˜ao

EC=OD−OB e AE=AB+BE (4.125)

substituindo os valores acima em

AE=AB+BE (4.126)

AB+BE=AC.cos

� α−β

2

�

(4.127)

senα+senβ =2.R.sen(AFCˆ ).cos

� α−β

2

�

(4.128)

senα+senβ =2.1.sen

� α+β

2

�

.cos

� α−β

2

�

(4.129)

senα+senβ =2.sen

� α+β

2

�

.cos

� α−β

2

�

5 CONSIDERAC¸ ˜OES FINAIS

Neste trabalho procuramos fazer uma abordagem simples de algumas relac¸˜oes cl´as-sicas da Trigonometria usando resultados conhecidos da Geometria Plana.

Constru´_ımos_figuras com o intuito de despertar a criatividade. Criando um ambiente favor´avel `a busca de novos modelos de demonstrac¸˜oes, tornado o ensino mais prazeroso.

Embora, as demonstrac¸˜oes tenham um grande papel na resoluc¸˜ao de muitos proble-mas, est˜ao de certa forma deixada de lado. Visto que para muitos este processo de demonstrac¸˜oes ´e demorado, cansativo e at´e desnecess´ario.

Por isso, tanto no ensino b´asico quanto no ensino de graduac¸˜ao as demonstrac¸˜oes s˜ao deixadas a cargo do leitor. Vimos ao longo dos cap´_ıtulos, que muitas dessas relac¸˜oes fun-damentais s˜ao memorizadas apenas na resoluc¸˜ao de exerc´_ıcios.

Apesar desse tema est´a incorporado `as pr´aticas escolares e, at´e mesmo na formac¸˜ao de professores, sua forma aqui utilizada e suas generalizac¸˜oes para dimens˜oes superiores, s˜ao frequentemente utilizadas em demonstrac¸˜oes de problemas geom´etricos, pois as aplicac¸˜oes em outros contextos como no reconhecimento de cˆonicas, problema da trissec¸˜ao de um ˆangulo, nos complexos dentre outros ramos da matem´atica “constituem um campo rico de conex˜oes para raciocinar sobre o plano e o espac¸o” (WIKIP ´EDIA, 2013).

REFER ˆENCIAS

BASTOS, R. Notas sobre o ensino de geometria.Revista da APM, Lisboa, n. 94, 2007.

BOYER, C. B. Hist´oria da matem´atica. 7 ed. S˜ao Paulo: Edgard Bl¨ucher, 1974.

CARNEIRO, J. P.Reta de Euler e n´umeros complexos. 2013. Dispon´_ıvel em

<http://www.obm.org.br/export/sites/default/revista eureka/docs/artigos/reta euler.pdf>. Acesso em 25 jan. 2013.

DOLCE, O.; POMPEO, J. N.Fundamentos de matem ´atica elementar, 9: geometria plana.

Atual, 2005.

EVES, H.Hist´oria da Geometria. S˜ao Paulo: Atual Editora, 1992.

FILHO, M. F. d. A.Geometria anal´ıtica e ´algebra linear. Fortaleza, Premius Editora. 2001.

HEFEZ, A.; VILLELA, M. L. T. Polin ˆomios e equac¸˜oes alg´ebricas. Material da Disciplina de Polinˆomios e Equac¸˜oes Alg´ebricas do Mestrado Pro_fissional em Matem´atica-PROFMAT. Rio de Janeiro: SBM, 2012.

IEZZI, G. Fundamentos de matem´atica elementar: trigonometria. vol. 9. Atual, 1993.

MORGADO, A.; WAGNER, E.; CARMO, M. D. Trigonometria e n ´umeros complexos, 4a edic¸˜ao. [S.l]. Rio de Janeiro: Sociedade Brasileira de Matem´atica, 2001.

MORGADO, A.; WAGNER, E.; JORGE, M. Geometria ii. Livraria Francisco Alves, 1974.