Excesso de ruído no oscilador paramétrico ótico

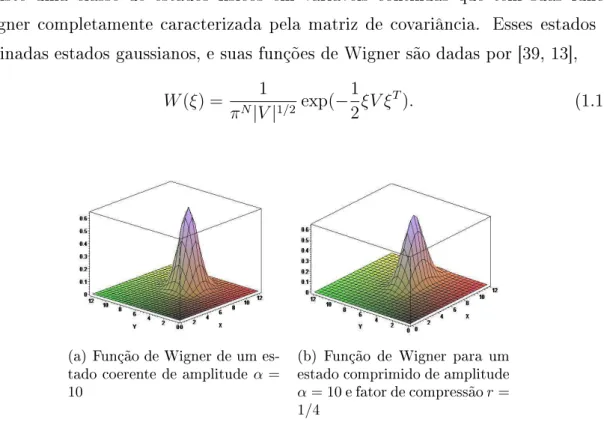
Instituto de Físia

Exesso de Ruído

no Osilador Paramétrio Ótio

Jnatas Eduardo da Silva César

Dissertação de mestrado apresentada ao

Instituto de Físiapara a obtenção

do título de Mestre emCiênias

Orientador: Prof. Dr. Marelo Martinelli

Bana Examinadora:

Prof. Dr. Marelo Martinelli (IF-USP)

Prof. Dr. Arnaldo Gammal (IF-USP)

Prof. Dr. Kaled Dehoum (UFF)

Agradeimentos

Dedio meus sinerosagradeimentos:

•

Agradeço ao Marelo Martinelli por sua orientação e por sua ajuda em vários as-petos relaionadosao experimento.

•

AgradeçoaoPaulo Nussenzveig pela orientação.

•

Agradeçoaos membros onvidados da bana examinadora Prof. Kaled Dehoum e Prof. Arnaldo Gammalpela leiturauidadosa desse texto.

•

Agradeço às pessoas do suporte ténio, espeialmente às seretárias Edi e Ivanei, aopessoal da eletrnia e serviços gerais, pois sem eles nosso trabalho seria

prati-amenteinviável.

•

Agradeçoaomeu amigoAntnioporompartilharomigo várias horasde trabalho nesse experimento.

•

Agradeço aos meus amigos Felippe, Rodrigo, Laério, Fábio e Paulo Valente por suas inúmeras e valiosas ajudas durante redação dessa dissertação e por tornarem

osmeus dias de onvivênia no laboratóriomuito mais agradáveis.

•

Agradeço aos meus ex-olegas de grupo Katiúsia e Alessandro por me passarem partede seus onheimentos emeajudaremnos primeirosmomentosnolabortório.

•

AgradeçotambémaminhanamoradaLayraeaosmeusamigosdeforadolabortório, João,Diego,Carlos,entreosoutrosqueometoainjustiçade nãoitar seusnomes,

porfazerem de São Paulo um lugar muito mais agradável de se viver.

Resumo

Apesar de ser um experimentobemonheido naliteraturarelaionada aoestudoda

informação quântia, o Osilador Paramétrio Ótio (OPO) operando aima do limiar

não forneeu sempre os resultados esperados por sua teoria, pois apresentava exesso de

ruídona fase de seus feixes, de origem desonheida.

Neste trabalho apresentamos de forma sistemátia a teoria padrão do Osilador

Pa-ramétrioÓtio noontexto quântio. Alémdisso, introduzimosum modelo ad-hopara

oexesso de ruído de fase doOPO que reproduz osresultados obtidos emnossos

experi-mentos.

Em nosso modelo, inserimos um ruído na fase de ada feixe do OPO proporional à

intensidadedosamposintraavidade. Esteruídoapresentaorrelaçõesnãoperfeitasentre

os feixes, omo foi demonstrado experimentalmente. Apesar de desonheidas a origem

desse exesso de ruído, temos indiações de que ele é ausado por entros expalhadores

Abstrat

In spite of the fat that the OptialParametri Osillator(OPO) is one of the most

known experiments related with quantum information researh, its experimental results

did not have a good agreement with the theory, in the above threshold regime, beause

of anunexpeted exess noise inthe phasequadrature onits beams.

In this work we sistematialy present the quantum theory of OPO. Moreover, we

introduean ad-ho modelforthe exess noise in the phasequadrature in the OPO that

reprodues our experimentaldata.

In ourmodel,the exessnoise inthe phasequadratureisproportionalofthe intensity

of eah OPO beam. This noise presents non-perfet orrelations among the elds, as is

experimentalyobserved. Despite oftheunknownoriginofthis exessnoise,wehavesome

Sumário

Introdução p.1

1 Coneitos preliminares em

Ótia Quântia p.5

1.1 Prinípio dainerteza. . . p.5

1.2 Matriz Densidade . . . p.7

1.3 Deomposição Espetral eQuantizaçãodo CampoEletromagnétio . . p.8

1.3.1 Quantizaçãodo Campo Elétrio . . . p.11

1.3.2 Estados de Fok . . . p.13

1.4 Proesso de medidae estados oerentes . . . p.14

1.4.1 Estados Coerentes . . . p.15

1.5 Quadraturas doCampoElétrio . . . p.18

1.5.1 Estados omprimidos . . . p.21

1.6 Espaço das freqüênias . . . p.23

1.6.1 Espetro de ruído . . . p.24

1.7 Equação Mestra . . . p.24

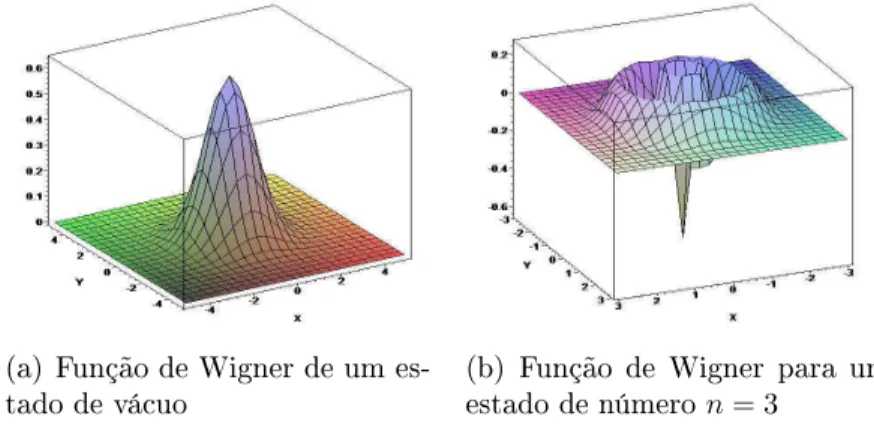
1.8 Espaço de Fase Quântio e Função de Wigner . . . p.25

1.8.1 Matriz de ovariânia eRelação de Inerteza . . . p.28

1.8.2 Estados Gaussianos . . . p.29

1.9 Equação de Fokker-Plank eEquação de Langevin . . . p.30

1.10.2 AutoHomodinagem . . . p.35

2 Emaranhamento p.39

2.1 Paradoxo EPR . . . p.39

2.2 Emaranhamento. . . p.41

2.2.1 Critériosde Emaranhamento. . . p.42

2.3 Positividade sob Transposição Parial . . . p.43

2.3.1 Apliaçãoem VariáveisContínuas . . . p.44

2.4 Somasde Variânias . . . p.45

2.4.1 Caso Tripartite . . . p.46

3 Osilador Paramétrio Ótio p.51

3.1 Desrição Quântia doOPO . . . p.52

3.2 Valores Estaionários . . . p.55

3.3 Flutuações Quântias Linearizadas . . . p.56

3.4 Espetro de ruído doOPO . . . p.59

3.5 FeixesGêmeos eEmaranhamentonoOPO . . . p.62

3.6 Exesso de Ruído no OPO . . . p.69

4 Experimento p.75

4.1 AparatoExperimental . . . p.75

4.1.1 Cavidade de ltro . . . p.75

4.1.2 OPO . . . p.77

4.1.3 Cavidades de análise . . . p.78

4.1.4 Deteção . . . p.79

4.2 Caraterização Experimental doExesso de Ruído . . . p.80

Conlusão e Perspetivas p.93

Referênias Bibliográas p.95

Introdução

Atualmente, o estudo da informação quântia é uma das prinipais áreas de

pes-quisaem físia, om vários artigos sendo publiados emrevistas de amplo impatoomo

Physial Review, Nature e Siene. O elemento prinipalpara o estudo da omputação

quântia é uma propriedade totalmente não trivial de sistemas quântios denominada

emaranhamento. O estudo da informação quântia aborda temas omo o próprio

pro-esso de omputação [1℄ e maneirasde se transferir os dados proessados para diferentes

loalidades [2℄.

Dizemos que um sistema quântio está emaranhado quando não podemos esrever a

função de onda total do sistema omo o produto das funções de onda de ada uma de

suas partes [3℄. Nesse aso as orrelações quântias podem ser muito mais fortes do que

orrelaçõeslássias[4℄.

O emaranhamentoé porsi só um grande objeto de estudo em físia,ele foi pela

pri-meiravez notadoemumtrabalhopubliado porEinsteinem1935[5℄omo um paradoxo

na teoria quântia. Nesse mesmo ano, Niels Bohr publiou um trabalho em resposta a

Einstein,mostrandoque oparadoxoapontado porEinstein eraapenas aparentee props

uma série de experimentos mentaisna tentativa de mostrar que a teoria quântia estava

orreta[6℄. Ainda nesse ano, Shrödinger unhou a paralavra emaranhameto [7℄ para

es-tados quântios que tinham a arateristia mostrada por Einstein. Ele onlui que o

emaranhamento é a araterístia dos sistemas quântios que rompe totalmente om a

idéiasda físialássia.

Em nossolaboratóriotrabalhamos om um sistemafísiohamadode Osilador

Par-métrioÓtio(OPO)apazdegerarfeixesdeluzintensosqueapresentamessaimportante

propriedade. O OPO onsiste de uma avidade Fabry-Perot onde é inserido um ristal

om suseptibilidade elétrianão-linearde segunda ordem,

χ

(2)

.

Inidimos naavidade doOPO um feixelaser intenso omfreqüênia

ω

0

denominado bombeio, então a partir do aoplamento desse feixe om o termo não-linear da

teremos que a soma das freqüênias dos feixes sinal e omplementar deverá ser igual a

freqüênia do feixe de bombeio

ω

0

=

ω

1

+

ω

2

. Quantiamente, podemos pensar nesse proesso omoa aniquilaçãode um fótondobombeioparaa riaçãode dois novosfótons

dos feixes sinal e omplentar.

É intuitivo pensar, devido ao proesso de onversão paramétria, que os feixes

bom-beiosinaleomplementarestejamfortementeorrelaionados,sendoessasorrelaçõestão

intensasqueesse feixespodemestaremaranhados. Oemaranhamentoentreosfeixessinal

eomplementarfoiprevistoteoriamentenoanode 1989[8℄,sendoaprinipal

araterís-tiaqueevideniaoemaranhamento,aompressãonoruídodasubtração dasamplitudes

e da soma dos ruídos de fase desses feixes, ou seja, as variânias dessas grandezas são

menores que a variâniada utuação dováuo.

A medidadaompressão doruído nasubtração das amplitudes foifeita já noano de

1987 na referênia [9℄, no entanto, a ompressão do ruído na soma das fases dos feixes

gêmeos sófoi medida reentemente pelonosso grupo [10, 11℄, omprovando o

emaranha-mentobipartiteentreosfeixessinaleomplementar. Alémdisso, oemaranhamentoentre

ofeixe de bombeioom osfeixes sinale omplementar foiprevisto tambémreentemente

pelonosso grupo[12℄. Noentanto,asmedidasfeitasaté hoje aindanão foramapazes de

omprovar essa propriedade entre os três ampos[13, 14℄.

O prinipal motivo para isso e também um dos prinipais motivos que impediu por

tantotempoaveriaçãodoemaranhamentobipartiteentreosfeixesgêmeos,éumexesso

de ruído presente na fasedesses feixe que até então tinha origem desonheida.

Portanto, a prinipal motivação para essa dissertação é introduzir um modelo para

esse exesso de ruído queajusta muito bemtodos osresultados obtidos pelonosso grupo

até hoje. Oprinipalingredientedonosso modelo paraoexesso de ruído éaintrodução

de um ruído de fase proporional à potênia intraavidade de ada feixe, onsiderando

orrelações não perfeitas entre esses ruídos. Ao que tudo india, esse termo de exesso

de ruído, que será introduzido nas equações do OPO, é gerado pelapresença de entros

espalhadoresdeluznoristaldevidoapresençadefnonsausadosporagitaçõestérmias

narede ristalina.

No primeiro apítulodessa dissertação introduzimos alguns oneitos de ótia

quan-tia quesão esseniais parao entendimento donosso trabalho. Esses oneitos vãodesde

a quantização do ampo elétromagnétio até distribuiçãode quase-probabilidade.

elétromagnétio. Noapítulo2falamos detalhadamentesobre emaranhamentoemétodos

para identiá-lo.

Já no apítulo 3, disorremos sobre o OPO, onde damos uma melhor noção de seu

funionamento a partir de prinípios quântios e mostramos as orrelações entre seus

feixes. Nomdesseapítulo,introduzimosonossomodeloteórioparaoexesso deruído

no OPO. O quarto apítulo da dissertação mostra os resultados de nosso experimento

orroborando om o nosso modelo para o exesso de ruído. Por m, apresentamos as

1 Coneitos preliminares em

Ótia Quântia

1.1 Prinípio da inerteza

Nameânialássiaoerrosobreumamedidadeorre simplesmenteporseonsiderar

queexisteumaertaimpreisãonoaparatodemedida. Noentanto,nameâniaquântia

ainerteza sobre uma medida é intrínsea àteoria, e deorre de que as grandezas físias

medidas no laboratório são auto-valores de operadores que atuam no espaço de Hilbert

[15℄. Dessa forma, a natureza quântia de muito sistemas físios só pode ser perebida

na análise minuiosa das inertezas relaionadas ao proesso da medida, pois os valores

médiosde muitas grandezas podem ser entendidos apenas usando afísia lássia.

A utuação sobre o valormédio de um operador

o

ˆ

édenida por

δ

o

ˆ

= ˆ

o

_{− h}

ˆ

o

_i

,

(1.1)

onde

h

ˆ

o

i

éamédiasobreafunçãodeondadosistemaesobreoutroselementosestatístios 1

.

Seguindo a desrição dada nareferênia [16℄, sabemos quepara qualquer operador

A

ˆ

eseu onjugadoHermitiano

A

ˆ

†

,

h

A

ˆ

A

ˆ

†

_{i ≥}

0

.

(1.2)

Denindo dois operadores Hermitianos

x

ˆ

e

y

ˆ

taisque

A

ˆ

=

δ

x

ˆ

+

λe

iθ

_δ

_y

_ˆ

₍

_{

_{λ, θ}

_{} ∈}

_R

₎

,

logo,

h

δ

x

ˆ

2

_i

+

λ

2

_h

δ

y

ˆ

2

_i

+

λ

_h

(cos

θ

_{

δ

x, δ

ˆ

y

ˆ

_{} −}

i

sin

θ

[

δ

x, δ

ˆ

y

ˆ

])

_{i ≥}

0

,

(1.3)

onde

[

,

]

é o omutador e

{

,

}

é o antiomutador. Para que a desigualdade (1.3) seja satisfeita

[

δ

x, δ

ˆ

y

ˆ

]

deveser igualazeroouaumnúmeroimagináriopuro,alémdisso, omo

1

_p

h

δ

x

ˆ

2

_{i −}

_λ

p

h

δ

y

ˆ

2

_i

2

_≥

₀

,ompletando quadradopodemosver que

h

(cos

θ

_{

δ

x, δ

ˆ

y

ˆ

_{} −}

i

sin

θ

[

δ

x, δ

ˆ

y

ˆ

])

_i

2

_≤

4

_h

δ

x

ˆ

2

_ih

δ

y

ˆ

2

_i

.

(1.4)

Como(1.4)temqueserválidaparatodoângulo

θ

devemosmaximizaroladoesquerdo dadesigualdade obtendo

|h{

δ

x, δ

ˆ

y

ˆ

_}i|

2

+

_|h

[

δ

x, δ

ˆ

y

ˆ

]

_i|

2

_≤

4

_h

δ

x

ˆ

2

_ih

δ

y

ˆ

2

_i

.

(1.5)

Noformalismolássio,asgrandezasfísiassãonúmerosreais,deformaqueamédiado

omutadorentreessasgrandezassempreénula. Portantonolimitelássioadesigualdade

(1.5) se reduziriaa

h

δx

2

_ih

δy

2

_{i ≥}

σ

_xy

2

,

(1.6)

onde,

σ

xy

=

1

2

h

δxδy

+

δyδx

i

. Classiamenteoanulamentode

σ

xy

éumaondiçãoneessária mas não suiente para a indepêndeiadas utuações[17℄.

JánaMeâniaQuântia, asgrandezas físiassão representadas poroperadores

Her-mitianos que atuam no espaço de Hilbert. Além disso, sabemos que dois operadores

Hermitianos que são onjugados não omutam entre si, omo, por exemplo, no aso dos

operadores posição

q

ˆ

e momento

p

ˆ

, onde o omutador entre eles é

[ˆ

q,

p

ˆ

] =

i

~

. Com isso, teremosque a desigualdade(1.5) se torna

∆ˆ

q

∆ˆ

p

_≥

r

1

4

~

2

₊

_σ

qp

,

(1.7)

onde denimos

∆

2

_o

_ˆ

₌

_h

_δ

2

_o

_ˆ

_i

. Quando

σ

qp

= 0

, ou seja, assumindo que só existem orre-laçõesquântias, enontramos aexpressão usual doPrinípiodaInerteza de Heisenberg

para posição e momento

∆ˆ

q

∆ˆ

p

_≥

1

2

~

.

(1.8)

Essa relação mostra que a posição e o momento de um objeto físio não podem ser

medidossimultaneamenteompreisãoinnita,independentementede quãoperfeito seja

1.2 Matriz Densidade

Na meânia quântia, para um sistema isolado, todaa informação físiaé dada por

um vetor de estado

|

ψ

(

t

)

i

, de formaque ovalormédio de um observavel

A

ˆ

é dado por

h

A

ˆ

_i

=

_h

ψ

(

t

)

_|

A

ˆ

_|

ψ

(

t

)

_i

.

(1.9)

Na prátia, um sistema isolado é muito difíil de se onstruir. Assim as medidas

realizadas em laboratório são médias sobre um onjunto funções de onda ponderadas

pormédias estatístias,que são obtidas pelarepetição sistemátia doexperimento. Com

isso, supondo que um sistema seja preparado em um onjunto de estados

|

ψ

n

i

, sob uma determinadaprobabilidadeestatístialássia

P

n

,ovalormédiode umoperador

A

ˆ

édado por

h

A

ˆ

_i

=

X

n

P

n

h

ψ

n

|

A

ˆ

|

ψ

n

i

.

(1.10)

Denindo agora o operadordensidade

ρ

ˆ

talque

ˆ

ρ

=

X

n

P

n

|

ψ

n

i h

ψ

n

|

,

(1.11)

então a médiadooperador

A

ˆ

poderá ser dada através da expressão

h

A

ˆ

_i

= tr

ρ

ˆ

A

ˆ

(1.12)

=

X

k

h

ψ

k

|

X

n

P

n

|

ψ

n

i h

ψ

n

|

A

ˆ

|

ψ

k

i

=

X

k

P

k

h

ψ

k

|

A

ˆ

|

ψ

k

i

.

Portanto,apartirdooperadordensidade podemosinorporartantoaestatístia

lás-sia quantoa estatístia quântia de sistemasfísios.

Estado puroe estadomistura: Seumoperadordensidadedeumsistemapodeser

esritoomo

ρ

ˆ

=

|

ψ

n

i h

ψ

n

|

, esse sitemaé denominadoomo puro. Ooperador densidade desse sistemaapresentará a propriedade

ρ

ˆ

2

_{= ˆ}

_ρ

.

Tendo em vista que

P

n

P

n

= 1

, quando a matriz densidade representa um estado puro,teremosque

tr

(ˆ

ρ

2

_{) = 1}

,aso ontrário,dizemosqueamatrizdensidaderepresenta

um estado tipomistura,e teremosque

tr

(ˆ

ρ

2

₎

_<

₁

Evolução temporal da Matriz densidade: A evolução temporal de um estado

quântio

|

ψ

i

genério é desrita pelaequação de Shröginger,

H

_|

_ψ

_i

₌

_i

_~

d

d

t

|

ψ

i

.

(1.13)

Portanto,derivando(1.11) emrelaçãoao tempo, eusando aequação de Shröginger,

vemos quea evolução temporaldamatriz densidade será dada por

d

d

t

ρ

(

t

) =

−

i

~

[

H

, ρ

(

t

)]

.

(1.14)

Essa equação é onheida na literatura omo equação de Von Neumann [16℄, apesar

de pareer om a equação de Heinsenberg, para a evolução temporalde operadoradores,

que édada por,

d

d

t

A

ˆ

=

i

~

[

H

,

A

ˆ

]

.

(1.15)

aequaçãodaevoluçãotemporalpara amatrizdensidade diferedaequaçãode Heisenberg

por um sinal, evideniando que a evolução temporal do operador densidade oorre no

mesmosentidoqueaevoluçãotemporalde vetoresdeestadonadesrição deShröginger,

enquantoaevoluçãotemporalparaoperadoresnadesriçãodeHeisenbergsedánosentido

ontrário.

1.3 Deomposição Espetral e Quantização do Campo

Eletromagnétio

As Equações de Maxwell no váuo para os ampos elétrio

E

e magnétio

B

, na presença das densidades de orrente

J

e arga

2

ρ

,são dadas por[18℄

∇ ×

E

+

_∂t

∂

B

= 0

,

(1.16)

∇ ×

B

₋

µ

0

ǫ

0

_∂t

∂

E

=

µ

0

J

,

(1.17)

∇ ·

E

=

_ǫ

1

₀

ρ,

(1.18)

∇ ·

B

= 0

,

(1.19)

Sabendo que o divergente de um rotaional é identiamente nulo, a equação (1.19)

2

nos informa queo ampomagnétio pode ser desrito por,

B

=

_{∇ ×}

A

,

(1.20)

onde otermo

A

é denominadopotenial vetor.

Substituindo a equação (1.20) em (1.16) e tendo emvista que

∇ × ∇

φ

= 0

, sendo

φ

um potenialesalar, vemos queo ampoelétrio será desritopor

E

=

_−∇

φ

₋

∂

∂t

A

.

(1.21)

Ao substituirmos as equações (1.20) e (1.21), dos ampos elétrio e magnétio em

termosdos potenialvetoreesalar, naequaçãode Maxwell(1.17) hegamosnaseguinte

expressão

∇

(

_{∇ ·}

A

)

_{− ∇}

2

A

+

1

c

2

∂

∂t

∇

φ

+

1

c

2

∂

2

∂t

2

A

=

µ

0

J

,

(1.22) onde foiusado a identidade

∇ × ∇ ×

A

=

∇

(

∇ ·

A

)

− ∇

2

_A

.

Através das equações de Maxwell vemos que os ampos elétrio e magnétio são

in-variantes sobre asseguintes transformaçõessobre os poteniaisvetor

A

e esalar

φ

,

A

=

A

′

_{− ∇}

Ξ

,

(1.23)

φ

=

φ

′

+

∂

∂t

Ξ

,

(1.24)

onde

Ξ

éumafunçãoesalarabitrária. Essetipodetransformaçãosobreospoteniais

pre-servaosvaloresdos amposelétriosemagnétios,sendodenominadasde transformações

de alibre.

Obtemos o alibre de Coulomb impondo que o potênial vetor obedeça à ondição

∇ ·

A

= 0

. Calulandoo divergente daequação (1.18)vemos queesse alibre nos fornee diretamente a equação de Poisson para o potenial elétrio

∇

2

_φ

₌

₋

1

ǫ

0

ρ

. Além disso

teremosque aexpressão (1.22) sereduz a

−∇

2

A

+

1

c

2

∂

∂t

∇

φ

+

1

c

2

∂

2

∂t

2

A

=

µ

0

J

.

(1.25)

PeloteoremadeHelmholtz[19℄qualquer equaçãode ampopode ser reesritaomoa

somade duas omponentes, uma om odivergenteigual azero e outraompontente om

o rotaional igual a zero, essas omponentes são denominadas ompenente transversal e

Além disso, o gradiente de um potênial esalar só tem a omponente longitudinal. F

a-zendo essa separação para a densidade de orrente,

J

=

J

T

+

J

L

, onde,

∇ ·

J

T

= 0

e

∇ ×

J

L

= 0

, eseparando a equação(1.25) emsuas omponentes transversais e longitudi-nais enontramos,

−∇

2

A

+

1

c

2

∂

2

∂t

2

A

=

µ

0

J

T

,

(1.26)

e

1

c

2

∂

∂t

∇

φ

=

µ

0

J

L

.

(1.27)

Portanto,quando não háorrenteelétria,vemos que (1.26)se reduz auma equação

de onda para o potenial vetor [20, 21℄,

∇

2

A

₋

1

c

2

∂

2

∂t

2

A

= 0

.

(1.28)

Podemos enontrar a solução dessa equação de onda expandindo o potenial vetor

numa série de Fourier e impondo uma ondição periódia de ontorno para um volume

V

=

L

3

doespaço, om issoteremosque

A

(

r

, t

) =

X

k

X

σ=1,2

e

k

σ

A

k

σ(

r

, t

)

,

(1.29)

onde,

A

k

σ

(

r

, t

) =

A

k

σ

e

i(

k

·

r

−

ωkt)

+

A

∗

k

σ

e

−

i(

k

·

r

−

ωkt)

.

(1.30)

Ovetordeonda

k

deneadireçãodepropagaçãodeumdeterminadomododoampo dentroda avidade, sendo quesuas omponentes são dadas por

k

x

=

2

π

L

ν

x

,

k

y

=

2

π

L

ν

y

,

k

z

=

2

π

L

ν

z

,

(1.31)

onde

{

ν

x

, ν

y

, ν

z

} ∈

Z

. A partir daequaçãode ondavemos quea freqüêniaangular

ω

k

se relaionaom o módulo dovetor de onda

k

por,

ω

k

=

ck

.

O vetor unitário

e

k

σ

é o vetor de polarização do ampo. Devido ao alibre de Cou-lomb o vetor de polarizaçãodeve ser perpendiular ao vetor de onda doampo, ou seja,

e

k

σ

·

k

= 0

. Além disso, os vetores de polarização são denidos de forma que um seja perpendiular ao outro,

e

k

σ

·

e

k

σ

′

=

δ

σσ

′

.

Pela expressão(1.21) vemos quena ausênia de orrentes

E

=

₋

∂

logo aexpressão para oampo elétrioserá

E

(

r

, t

) =

X

k

X

σ=1,2

e

k

σ

E

k

σ

(

r

, t

)

,

(1.33)

onde

E

k

σ

(

r

, t

) =

iω

k

A

k

σ

e

i(

k

·

r

−

ωkt)

−

A

∗

k

σ

e

−

i(

k

·

r

−

ωkt)

.

(1.34)

A partir de (1.20) temos que oampomagnétio é

B

(

r

, t

) =

X

k

X

σ=1,2

ˆ

k

_×

e

k

σ

B

k

σ

(

r

, t

)

,

(1.35)

onde

ˆ

k

=

k

/k

e

B

k

σ(

r

, t

) =

ik A

k

σ

e

i(

k

·

r

−

ωkt)

−

A

∗

k

σ

e

−

i(

k

·

r

−

ωkt)

.

(1.36)

Porm, temosque aenergiatotal doampo dentro daavidadede volume

V

=

L

3

é

H

₌

1

2

Z

d

V ǫ

0

E

(

r

, t

)

2

+

1

µ

0

B

(

r

, t

)

2

,

(1.37)

substituindoasexpressõesparaoampoelétrioeparaoampomagnétioenontraremos

quea energiatotal dos ampos pode ser esrita omo,

H

₌

_ǫ

₀

_V

X

k

σ

ω

_k

2

(

A

k

σ

A

∗

k

σ

+

A

∗

k

σ

A

k

σ

.

)

(1.38)

1.3.1 Quantização do Campo Elétrio

A Halmitonianaquantizada de um osilador harmnioé dada por

ˆ

H

₌

p

ˆ

2

2

m

+

1

2

mω

2

_q

_ˆ

2

_,

(1.39)

ondeosoperadoresdeposição

q

ˆ

emomento

p

ˆ

obedeemarelaçãodeomutaçãousual,

[ˆ

q,

p

ˆ

] =

i

~

. A partir desses operadores podemosdenir dois novosoperadores adimensionais

ˆ

a

=

r

1

2

m

~

ω

(

mω

q

ˆ

+

i

p

ˆ

)

,

ˆ

a

†

=

r

1

2

m

~

ω

(

mω

q

ˆ

−

i

p

ˆ

)

,

(1.40) queobedeem arelação de omutação

[ˆ

a,

a

ˆ

†

_{] = 1}

Inversamente teremos,

ˆ

q

=

r

~

2

mω

(ˆ

a

†

+ ˆ

a

)

,

p

ˆ

=

i

r

m

~

ω

2

(ˆ

a

†

−

a

ˆ

)

.

(1.41)

Substituindo(1.41) em(1.39), vemos quea halmitonianado osiladorharmnio poderá

ser esritaomo

ˆ

H

₌

1

2

~

ω

(ˆ

a

ˆ

a

†

_{+ ˆ}

_a

†

_ˆ

_a

_{) =}

_~

_ω

_(ˆ

_a

†

_ˆ

_a

₊

1

2

)

.

(1.42)

Apliandoosoperadores

ˆ

a

e

ˆ

a

†

naHamiltonianadoosiladorharmnioparaumdado

auto-estado

|

n

i

om um auto-valor

E

n

mostra-se que [15℄,

ˆ

a

_|

n

_i

=

√

n

_|

n

₋

1

_i

,

(1.43)

ˆ

a

†

_|

n

_i

=

√

n

+ 1

_|

n

+ 1

_i

.

(1.44)

Por esse motivo, denominamos

a

ˆ

†

e

a

ˆ

de operadores riação e aniquilação respeti-vamente. Para enontrarmos o resultado anterior foi neessário denir um estado

|

0

i

de mínima energiatalque,

ˆ

a

|

0

i

= 0

.

Dado(1.43) e (1.44)podemos deniro operador número

n

ˆ

= ˆ

a

†

_ˆ

_a

, talque,

ˆ

a

†

ˆ

a

_|

n

_i

= ˆ

n

_|

n

_i

=

n

_|

n

_i

.

(1.45)

Com isso, teremos que os auto-valores da hamiltoniana do osilador harmnio serão

dados por

H

_|

_n

_i

₌

_E

_n

_|

_n

_i

₌

_~

_ω

₍

_n

₊

1

2

)

|

n

i

.

(1.46)

A formanaqual foramapresentadas as hamiltonianasdoampoeletromagnétio e a

doosiladorharmnioquantizado (apresentados nas fórmulas(1.38) e(1.42)

respetiva-mente), sugere quea quantizaçãodo ampoeletromagnétio édada por

A

k

σ

→

r

~

2

ǫ

0

V ω

k

ˆ

a

k

σ

,

A

∗

k

σ

→

r

~

2

ǫ

0

V ω

k

ˆ

a

†

_k

_σ

.

(1.47)

Logo, existe um operador de riação e aniquilaçãopara ada modo e polarização do

ampo. Equivalentemente, poderíamoster feitoaquantizaçãodo ampoelétromagnétio

separando aspartes real eimagináriade

A

k

σ

nahamiltonianado ampoeletromagnétio lássio, e em seguida, identiando a parte real omo o operador posição e a parte

çõesde polarizaçãoa generalizaçãodarelação de omutação entre operadores de riação

eaniquilaçãoé

[ˆ

a

k

σ

,

ˆ

a

†

k

′

_σ

′

] =

δ

kk

′

δ

_σσ

′

(1.48)

Com isso, segue que a hamiltonianadoampoquatizado será dada por

ˆ

H

₌

X

k

σ

~

ω

k

(ˆ

a

†

k

σ

a

ˆ

k

σ

+

1

2

) =

X

k

σ

~

ω

k

(ˆ

n

k

σ

+

1

2

)

.

(1.49)

Portanto, para uma dada polarização, os modos do potenial vetor e dos ampos

elétriose magnétiosserão dados por,

A

k

σ(

r

, t

) =

r

~

2

ǫ

0

V ω

k

(ˆ

a

k

σ

e

i(

k

·

r

−

ωkt)

+ ˆ

a

†

k

σ

e

−

i(

k

·

r

−

ωkt)

);

(1.50)

E

k

σ(

r

, t

) =

iω

k

r

~

2

ǫ

0

V ω

k

ˆ

a

k

σe

i(

k

·

r

−

ωkt)

₋

a

ˆ

_k

†

_σ

e

−

i(

k

·

r

−

ωkt)

;

(1.51)

B

k

σ

(

r

, t

) =

ik

r

~

2

ǫ

0

V ω

k

ˆ

a

k

σ

e

i(

k

·

r

−

ωkt)

−

a

ˆ

†

k

σ

e

−

i(

k

·

r

−

ωkt)

_.

(1.52)

1.3.2 Estados de Fok

Os auto estadosda hamiltonianadoampoeletromagnétio são denominadoestados

de Fok ouestados número,

ˆ

H

_|

_n

_i

₌

_ω

_~

ˆ

a

†

ˆ

a

+

1

2

|

n

_i

=

ω

~

n

+

1

2

|

n

_i

.

(1.53)

Esses estados determinam o número de fótons para um modo do ampo om uma

erta polarização. Quando existem vários modos dentro de uma avidade o estado total

édado pelo produto externodos estadosde ada mododoampo,

|

n

k

1

1

, n

k

1

2

, n

k

2

1

, n

k

2

2

,

· · ·i

=

|

n

k

1

1

i |

n

k

1

2

i |

n

k

2

1

i |

n

k

2

2

i

=

|{

n

k

σ

}i

.

(1.54)

Um resultado fundamental da Meânia Quântia é que mesmo para o váuo, isto

é, quando o número de fótons é igual a zero, a energia do ampo não é nula. Assim

numa avidade ominnitos modospermitidostemosque aenergiamédia dosistemana

ausênia total de fótons é,

h{

0

k

σ

}|

H

ˆ

|{

0

k

σ

}i

=

X

k

σ

1

Apesar de experimentalmente ser muito difíil produzir estados onde o número de

fótons é disreto [22℄, a base de estados de Fok tem muita ultilidade por ser uma base

ortonormal, alémde ser auto-estado daHamiltonianadoampo elétromagnétio.

1.4 Proesso de medida e estados oerentes

Emumexperimentodeótiaquântiaadeteçãodoampoelétrioéfeitapordetetores

que são sensíveis a fótons por meio do efeito foto-elétrio, ou seja, o proesso de medida

se baseia no proesso pelo qual um fóton é aniquilado para que se produza um elétron,

gerando assim uma orrente medida [23℄.

Tomando somente um modo do ampo elétrio em uma determinada polarização, a

partir de (1.51), vemos que o ampo elétrio pode ser deomposto em uma parte om

freqüênia positiva

E

(+)

₍

_r

_{, t}

₎

e outraom freqüênia negativa

E

(

−

)

₍

_r

_{, t}

₎

.

E

(

r

, t

) =

E

(

−

)

(

r

, t

) +

E

(+)

(

r

, t

)

,

(1.56)

onde,

E

(

−

)

(

r

, t

) =

r

~

ω

2

ǫ

0

V

ˆ

a

†

e

−

i(

k

·

r

−

ωt)

_e

_E

(+)

₍

_r

_{, t}

_{) =}

r

~

ω

2

ǫ

0

V

ˆ

ae

i(

k

·

r

−

ωt)

_.

(1.57)

Classiamente essa separação é somente uma onvenção matemátia sem aarretar

nenhum signiadofísio,noentanto,nãopodemosonsiderar queomesmooorra

quan-tiamente, pois de fato, o operador não hermitiano

E

(+)

₍

_r

_{, t}

₎

é o responsável pela

ani-quilação dos fótons, e por onseguinte, pelo proesso de medida. Tendo isso posto, a

probabilidadede transição para queum fótonseja absorvidopelodetetorserá dadapor,

P

i

| h

f

|

E

(+)

(

r

, t

)

|

i

i |

2

,

(1.58)

oestado

|

f

i

representaoestadonalpara oqualoampoelétriofoiprojetado,enquanto oestado

|

i

i

representaoestadoiniialdoampo. Noentanto,essaprobabilidadedeveser ponderada pelaprobabilidade

P

i

estatístia de seenontrar o estadoiniial

|

i

i

.

Vendoque,

X

f

h

f

_|

E

(+)

(

r

, t

)

_|

i

_{i ∝}

X

f

h

f

_|

i

₋

1

_i

=

δ

f,i

−

1

,

(1.59)

medidadeve ser dada pelasoma de todos ospossíveisestados iniiais,de onde vem que

I

(

r

, t

) =

X

if

P

i

| h

f

|

E

(+)

(

r

, t

)

|

i

i |

2

=

X

if

P

i

h

i

|

E

(

−

)

(

r

, t

)

|

f

i h

f

|

E

(+)

(

r

, t

)

|

i

i

(1.60)

omo

P

f

|

f

i h

f

|

= 1

. Sabendoqueamatrizdensidadedosistemaé

ρ

=

P

i

P

i

|

i

i h

i

|

segue

I

(

r

, t

) = tr[

ρE

(

−

)

(

r

, t

)

E

(+)

(

r

, t

)] =

_h

E

(

−

)

(

r

, t

)

E

(+)

(

r

, t

)

_i

.

(1.61)

Com issoperebemosqueaintensidadedoampoéproporionalaooperadornúmero

ˆ

n

= ˆ

a

†

_ˆ

_a

, ou seja, a intensidade do ampo é proporional ao número de fótons que hega

nodetetor porunidade de tempo. Supondo que o estado iniialdo sistema sejao estado

de váuo,

|

0

i

, aintensidade medida será

I

(

r

, t

) =

_h

0

_|

E

(

−

)

(

r

, t

)

E

(+)

(

r

, t

)

_|

0

_i

= 0

(1.62)

omo esperado. Vale observar que, usando a teoria lássia a intensidade medida seria

igualao quadradodo operadorampo elétriototal, logo, para oestado de váuo

h

I

ˆ

_i

vac

=

_h

0

_|

E

(

r

, t

)

2

_|

0

_i

=

_h

0

_|

[

E

(+)

(

r

, t

) +

E

(

−

)

(

r

, t

)]

2

_|

0

_i

(1.63)

=

_h

0

_|

E

(+)

(

r

, t

)

E

(+)

(

r

, t

)

_|

0

_i

+

_h

0

_|

E

(

−

)

(

r

, t

)

E

(

−

)

(

r

, t

)

_|

0

_i

+

_h

0

_|

E

(+)

(

r

, t

)

E

(

−

)

(

r

, t

)

_|

0

_i

+

_h

0

_|

E

(

−

)

(

r

, t

)

E

(+)

(

r

, t

)

_|

0

_i

=

_h

0

_|

E

(+)

(

r

, t

)

E

(

−

)

(

r

, t

)

_|

0

_{i 6}

= 0

que é um resultado siamente inompatível, pois impliariaque mesmo para estado de

váuo osdetetores mediriamuma intensidade média diferente de zero.

1.4.1 Estados Coerentes

Como já foi exposto anteriormente, o operador

E

(+)

₍

_r

_{, t}

₎

éproporional aooperador

de aniquilação, então uma representação interessante para os estados do ampo elétrio

são os estados oerentes, que são auto-estados do operador de aniquilação [24℄. A luz

emitidapor um laser se aproximamuito de um estadooerente [25℄, assim sendo, vemos

queos estadosoerentes seaproximambastante de um estado lássio.

ˆ

apliando

h

n

−

1

|

e usandoas propridadesdo operador de aniquilação,segue que

√

n

_h

n

_|

α

_i

=

α

_h

n

₋

1

_|

α

_i

,

(1.65)

e usandoessa relaçãoreursivamenteenontramos,

h

n

_|

α

_i

=

α

n

√

n

!

h

0

|

α

i

.

(1.66)

Tendo em vista esse resultado, ao expandirmos

|

α

i

nos vetores do espaço de Fok, enontraremos

|

α

_i

=

X

n

|

n

_{i h}

n

_|

α

_i

,

=

_h

0

_|

α

_i

X

n

α

n

√

n

!

|

n

i

.

(1.67)

Aoimpormosaondiçãodenormalização

h

α

|

α

i

= 1

,enontramosquearepresentação doestado oerentena base dos estados de Fok é dada por,

|

α

_i

=

e

−

|

α

|

2

2

X

n

α

n

√

n

!

|

n

i

.

(1.68)

Apartirdisso, vemos queoestadooerenteapresentaumadistribuiçãode Poissonno

número de fótons

P

(

n

) =

_|h

n

_|

α

_i|

=

|

α

|

2n

n

!

e

|

α

|

2

.

(1.69)

de onde temos que o númeromédio de fótons éigual à variânia,isto é,

h

n

ˆ

_i

=

_h

α

_|

n

ˆ

_|

α

_i

=

_|

α

_|

2

(1.70)

e

∆

2

n

=

_h

α

_|

n

ˆ

2

_|

α

_{i − h}

α

_|

n

ˆ

_|

α

_i

2

=

_|

α

_|

2

.

(1.71)

Os estados oerentes formam uma base ompleta mas que não é ortogonal

apresen-tando aseguintepropriedade,

1

π

Z

queo produto interno entre dois estados oerentes é

h

β

_|

α

_i

=

e

−

|

α

|

2

₊

_|

_β

_|

2

2

+αβ

∗

,

(1.73)

onde ovalor absolutodoproduto interno é

|h

β

_|

α

_i|

=

e

−|

α

−

β

|

2

,

(1.74)

sendoque nolimite em que

|

α

−

β

| → ∞

osestados oerentes tendem aser ortogonais. Denindo o operadordesloamento omo em[24℄

D

(

α

) =

e

αˆ

a

†

−

α

∗

ˆ

a

.

(1.75)

eusando afórmulade Baker-Campbell-Hausdor,

e

A+ ˆ

ˆ

B

=

e

A

ˆ

e

B

ˆ

e

−

1

2

[ ˆ

A,

B]

ˆ

,

(1.76)

que pode ser usada quando

[ ˆ

A,

[ ˆ

A,

B

ˆ

]] = [ ˆ

B,

[ ˆ

A,

B

ˆ

]] = 0

, podemos esrever o operador desloamentoem ordemnormal, istoé, om as potênias de

ˆ

a

†

à esquerda das potênias

de

ˆ

a

,

D

(

α

) =

e

−

|

α

|

2

2

e

αˆ

a

†

e

α

∗

ˆ

a

,

(1.77)

ouem ordem antinormal, ouseja, om aspotêniasde

a

ˆ

†

àdireita das potêniasde

ˆ

a

,

D

(

α

) =

e

|

α

|

2

2

e

α

∗

_a

_ˆ

e

αˆ

a

†

,

(1.78)

Usando o operador desloamento em ordem normal podemos mostrar que estado

oerente pode ser obtido apliando-ono estadode váuo,

D

(

α

)

_|

0

_i

=

e

−

|

α

|

2

2

e

αˆ

a

†

e

α

∗

ˆ

a

_|

0

_i

=

_|

α

_i

.

(1.79)

É interessante notar que a evolução temporal do osilador harmnio forçado será dada

pelo operador desloamento vezes a evolução temporal do osilador harmnio simples

[26℄. Temos então que o estado oerente pode ser enontrado quando evoluimos

tempo-ralmenteo váuo omo ondição iniial para esse sistema.

Algumas propriedades importantes do operadordesloamento são,

D

(

α

)

†

aD

(

α

) =

a

+

α,

(1.80)

D

(

α

)

†

a

†

D

(

α

) =

a

†

+

α

∗

,

(1.81)

1.5 Quadraturas do Campo Elétrio

Como vimosna seção anterior podemosquantizar oampo elétriofazendo om que

os oeientes do potenial vetor para ada modo do ampo sejam relaionados om

os operadores riação e aniquilação do osilador harmnio. Para um únio modo do

ampoelétrioomfreqüênia

ω

quesepropaganadireção

z

eonsiderandoqueoampo elétrioémedidoemunidadesde

p

~

ω/

2

ǫ

0

V

,apartirdaequação(1.51)podemosesrever o operadorampoelétrio omo

ˆ

E

(

x, t

) =

i

ˆ

ae

i(kx

−

ωt)

₋

ˆ

a

†

e

−

i(kx

−

ωt)

=

X

ˆ

cos(

kx

₋

ωt

+

π/

2) + ˆ

Y

sin(

kx

₋

ωt

+

π/

2)

,

(1.83)

onde os operadores Hermitianos

X

ˆ

e

Y

ˆ

são denominados operadores de quadratura do ampoelétrio,e são denidos omo

ˆ

X

= ˆ

a

+ ˆ

a

†

,

Y

ˆ

=

₋

i

[ˆ

a

₋

ˆ

a

†

]

,

(1.84)

de forma que

[ ˆ

X,

Y

ˆ

] = 2

i,

(1.85)

portantoa relaçãode inerteza será

∆ ˆ

X

∆ ˆ

Y

_≥

1

.

(1.86)

Em(1.83)existe uma fasede

π/

2

para quepudéssemos denirosoperadores quadra-tura omo em (1.84). De fato, existe uma arbitrariedadede fase do ampo

eletromagné-tio, de forma quepodemos deniros operadores quadratura por,

ˆ

X

θ

= ˆ

ae

−

iθ

+ ˆ

a

†

e

iθ

,

Y

ˆ

θ

=

₋

i

[ˆ

ae

−

iθ

₋

a

ˆ

†

e

iθ

]

,

(1.87)

onde

Y

ˆ

θ

_{= ˆ}

_X

θ+π/2

é o operador onjugado de

X

ˆ

θ

. Essa arbitrariedadena fase é

ontor-nada quando levamos emonta a fase relativa de um ampoem relação a um ampo de

prova. Observamos que a relação de omutação e onseqüentemente a de inerteza são

independentes da fase

θ

, ouseja,

[ ˆ

X

θ

,

Y

ˆ

θ

] = 2

i,

∆ ˆ

X

θ

∆ ˆ

Y

θ

_≥

1

.

(1.88)

enontraremos

∆

2

_vac

X

θ

= 1 e ∆

2

_vac

Y

θ

= 1

.

(1.89)

Portanto,oestadodeváuoéumestadodemínimainerteza,pois

∆

vac

X

θ

_∆

vac

Y

θ

= 1

. Denimos então que o ruído de váuo sobre qualquer quadratura é hamado de ruído

padrão.

Como os valores médios dos operadores de quadratura são enontrados diretamente

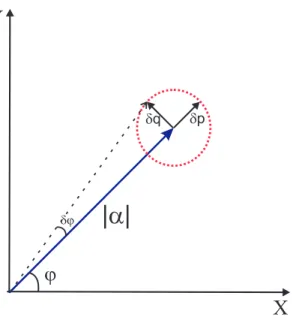
numa base de estados oerentes podemos representá-los num diagrama de Fresnel, g.

1.1, porém, a representação dos estados oerentes nesse diagramanão será dada por um

ponto, mas sim, por uma região devido ao prinípio da inerteza. O estado oerente

assimomo o váuo são estadosde mínima inerteza, ouseja, a inerteza sobre qualquer

quadraturaserá sempreigualaoruídopadrão. NodiagramadeFresnel oestadodeváuo

é representado por uma irunferênia de raio 1 entrada na origem, enquanto o estado

oerente é representado por essa mesma irunferênia só que agora desloada de uma

distâniaigual a

|

α

|

da origem.

Paraumestadooerenteemqueoauto-valordoampoelétrioé

α

=

|

α

|

e

iϕ

,podemos

assoiar omo quadraturas amplitude e fase respetivamente[27℄,

ˆ

p

= ˆ

ae

−

iϕ

+ ˆ

a

†

e

iϕ

,

(1.90)

ˆ

q

=

₋

i

[ˆ

ae

−

iϕ

₋

ˆ

a

†

e

iϕ

]

,

(1.91)

quando

h

p

ˆ

i ≫

1

, de onde temos que,

h

p

ˆ

_i

= 2

_|

α

_|

e

_h

q

ˆ

_i

= 0

.

(1.92)

O nome designado a essas quadraturas pode ser melhor entendido ao analisarmos a

gura1.1, de onde podemos verque,

δ

I

ˆ

=

h

p

ˆ

i

2

δ

p,

ˆ

(1.93)

δ

ϕ

ˆ

∼

=

2

h

p

ˆ

_i

δ

q.

ˆ

(1.94)

A partir das fórmulas aima vemos que a variânia do ruído de amplitude

∆

2

_p

_ˆ

vac

é proporional à intensidade média do feixe, enquanto a variânia do ruído de fase é

inversamente proporionalà intensidade média dofeixe.

Lembrando que o operador intensidade é dado por

I

ˆ

= ˆ

a

†

_ˆ

_a

e reesrevendo os

ope-radores riação e aniquilação omo

ˆ

a

=

α

+

δ

ˆ

a

e

ˆ

a

†

₌

_α

∗

₊

_δ

_ˆ

_a

†

Figura1.1: Representação doestado oerenteno diagrama de Fresnel. Oestado de váuo

seria representado pela mesma irunferêniasó que agora entrada na origem.

a equação (1.93) é valida quando fazemos

δa

†

_δa

_→

₀

. Apesar do operador Hermitiano

para afase não ser de fáilvisualisação[28, 21℄, é possível mostrarquenolimite de altas

intensidades do ampo elétrioa expressão(1.94) é válida, de onde se tem

[

δ

I, δ

ˆ

ϕ

ˆ

] = [ˆ

p,

q

ˆ

] = 1

.

(1.95)

Como os nossos detetores são sensíveis à intensidade dos feixes, experimentalmente

a medida do ruído padrão pode ser obtida medindodiretamente a variânia do ruído de

intensidade

∆

2

_I

_ˆ

de um estado oerente, oua partir de uma deteção balaneada,ou seja,

dividindoumfeixeemduaspartesdemesmaintensidade eemseguidasubtraindooruído

deadaparteealulandoavariâniadoresultado[11℄. Assim,apartirdaequação(1.93)

segue que,

∆

2

I

ˆ

= ∆

2

_vac

p

ˆ

_h

I

ˆ

_i

=

β

_h

I

ˆ

_i

.

(1.96)

Vimosnaseção 1.4.1 que avariânia doruído de intensidade da luzpoissoniana será

proporionalàintensidadedofeixe,onsequêniadofatodavariâniadonúmerodefótons

ser igual à médiado número de fótons desse feixe. Esse tipo de ruído é araterístio de

sistemas granulares, sendo por esse motivo denominado omo "shot noise". Assim, são

exemplosde "shotnoise"oruídogeradodevidoàolisãodeum feixede elétronsnoanodo

de uma válvula, oua utuação daesala de uma balançaprovoada pelaqueda de grãos

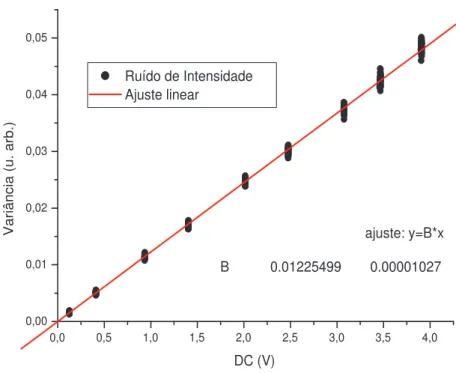
podemosmontarum gráode

∆

2

_I

_ˆ

× h

I

ˆ

_i

. Mantendoo jargãoempregado nolaboratório, hamaremos de alibração do"shot noise"a determinação do oeiente angular da reta

que ajusta os pontos medidos. Essa onstante de proporionalidade inlui já todos os

ganhos eletrnios empregados tanto na etapa de altafrequênia, empregada namedida

doruído,quandonaetapa de baixafrequênia,onde medimosa intensidademédia. Com

essamedidapodemosnormalizartodososvaloresderuídomedidosemnossoexperimento

pelo"shot noise".

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

0,00

0,01

0,02

0,03

0,04

0,05

ajuste: y=B*x

B

0.01225499

0.00001027

Variância (u. arb.)

DC (V)

Ruído de Intensidade

Ajuste linear

Figura1.2: Exemplo de alibração do "shot noise"usandoum feixe oerentede luz de 532

nm

É importante enfatizar que omo os nossos detetores medem somente a intensidade

doampo,portanto,amedidadoruídodeoutras quadraturas,quenãoseja aquadratura

amplitude,nãopode serfeitodiretamente. Sendoassim,devemosusar meiosalternativos

paramedir oruídode outrasquadraturas, osquaisserãoexpliados nas próximasseções.

1.5.1 Estados omprimidos

Outra lasse de estados de inerteza mínima são os estados omprimidos do ampo

eletromagnétio, esses estados são de natureza totalmente quântia [29, 30, 31℄. Um

que o produto das inertezas de ambas quadraturas respeite o prinípiodainerteza, ou

seja,

∆

X

θ

=

e

−

r

e ∆

Y

θ

=

e

r

.

(1.97)

Estados dessa natureza podem ser obtidos por uma transformação unitária sobre o

váuo e em seguida apliando ooperador desloamento,istoé,

|

α, ǫ

_i

=

D

(

α

)

S

(

ǫ

)

_|

0

_i

.

(1.98)

O operador

S

(

ǫ

)

édenominado operadorde "squeezing"ou ompressãoe é dado por

S

(

ǫ

) =

e

ǫ

∗

a

2

−

ǫa

†

2

_.

(1.99)

onde

ǫ

=

r

2

e

2iφ

,

r

édenominadofatorde ompressão ousqueeze,enquanto

φ

vaiindiar a quadratura de ompressãomáxima em relaçãoao argumento de

α

.

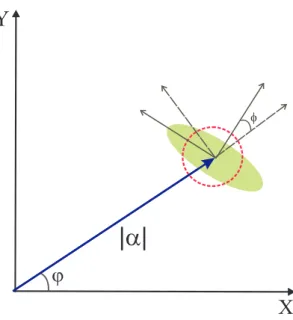
Nagura1.3vemosarepresentaçãodeumestadoomprimidonodiagramadeFresnel.

Figura 1.3: Representação de um estado omprimido no diagrama de Fresnel

Em(1.98)aso nãoapliquemosooperadordesloamentoriamosum estadohamado

de váuo omprimido. Diversos grupos em todo mundo produzem esse tipo de estado

prini-1.6 Espaço das freqüênias

Como vimos anteriormente, podemos reesrever os nossos operadores de riação e

aniquilaçãoomoo seu valormédio mais um termo de utuação, ouseja,

ˆ

a

(

t

) =

α

+

δ

ˆ

a

(

t

)

,

(1.100)

ˆ

a

†

(

t

) =

α

∗

+

δ

ˆ

a

†

(

t

)

.

(1.101)

Em nosso experimento os feixes tratados são monoromátios e intensos, om isso a

grande maioria dos fótons se enontram em uma freqüênia ótia

ω

, denominada banda entral, mas também apresentam utuações om um número pequeno de fótons em

freqüênias

ω

±

Ω (Ω

≪

ω

)

, ompondoas bandaslaterais. Sendo assim, afísiado nosso sistemapode ser mais failmenteentendida no domíniodas freqüênias, então, tomando

atransformada de Fourierdo operadorde aniquilaçãotemos [16℄

a

(Ω) =

Z

dte

iΩt

₍

_α

₊

_δ

_ˆ

_a

₍

_t

₎₎

_,

(1.102)

=

αδ

(Ω) +

δ

ˆ

a

(Ω)

.

(1.103)

Denimosa transformada de Fourier sobre ooperadorde riação omo

δ

ˆ

a

†

(Ω) = [

δ

ˆ

a

(Ω)]

†

.

(1.104)

A relação de omutação entre os operadores de riação e aniquilação no domínio

temporalédadapor

δ

ˆ

a

(

t

)

, δ

ˆ

a

†

₍

_t

′

₎

=

δ

(

t

₋

t

′

₎

,portantonodomíniodas freqüêniasessa

relaçãode omutação será dada por

δ

ˆ

a

(Ω)

, δ

ˆ

a

†

(Ω

′

)

= 2

πδ

(Ω

₋

Ω

′

)

.

(1.105)

Assim, tomando atransformandade Fourierdos operadores dequadratura dadosnas

equações (1.87)teremos que

δ

X

ˆ

θ

(Ω) =

e

−

iθ

δ

ˆ

a

(Ω) +

e

iθ

δ

ˆ

a

†

(

₋

Ω)

,

(1.106)

δ

Y

ˆ

θ

(Ω) =

₋

i

[

e

−

iθ

δ

a

ˆ

(Ω)

₋

e

iθ

δ

ˆ

a

†

(

₋

Ω)]

.

(1.107)

Pelahermitiidadedos operadores de quadratura nodomíniotemporalsegue,

h