Modelando o emprego regional a partir do modelo GVAR: uma análise dos dados brasileiros

(1)

ESCOLA DE ECONOMIA DE SÃO PAULO

MÁRIO SEGANTI ATHAYDE JR.

MODELANDO O EMPREGO REGIONAL A PARTIR DO MODELO GVAR: UMA ANÁLISE DOS DADOS BRASILEIROS

SÃO PAULO 2016

(2)

Dissertação apresentada à Escola de Economia de São Paulo da Fundação Getulio Vargas, como requisito para a obtenção do titulo de Mestre em Economia.

Campo de conhecimento: Econometria

Orientador: Prof. Dr. Emerson F. Marçal

SÃO PAULO 2016

(3)

Athayde Junior, Mário Seganti.

Modelando o emprego regional a partir do modelo GVAR : uma análise dos dados brasileiros / Mário Seganti Athayde Junior. - 2016.

117 f.

Orientador: Emerson Fernandes Marçal

Dissertação (MPFE) - Escola de Economia de São Paulo.

1. Modelos econométricos. 2. Econometria. 3. Cointegração. 4. Mercado de trabalho – Brasil. 5. Pessoal - Dispensa. I. Marçal, Emerson Fernandes. II. Dissertação (MPFE) - Escola de Economia de São Paulo. III. Título.

(4)

Dissertação apresentada à Escola de Economia de São Paulo da Fundação Getulio Vargas, como requisito para a obtenção do titulo de Mestre em Economia. Campo de conhecimento: Econometria

Data de aprovação:

__ / __ / ____

Banca examinadora:

____________________________________ Prof. Dr. Emerson F. Marçal (Orientador) FGV-EESP

____________________________________ Prof. Dr. Rogério Mori

FGV-EESP

____________________________________ Prof. Dr. Diogo de Prince Mendonça

(5)

Ao Professor Dr. Emerson Fernandes Marçal, por ter aceitado a orientação, profissionalismo e pela ajuda demonstrada durante a realização deste trabalho. Ao Professor Dr. Diogo de Prince Mendonça, pelo apoio e colaboração.

A Beatriz Aline Zimmermann, pelo apoio e comentários quanto às ferramentas relacionadas a econometria espacial.

A Thiago Stravos, aluno do mestrado acadêmico, pela ajuda quanto à utilização das ferramentas para manipulação das bases de dados.

Aos meus pais, Mário (in memorian) e Francisca, pela minha criação, e pelos conselhos ao longo de minha vida.

A Juliana Bonomi, Stella Melaragno, Kátia Bosognini e Fábio Sousa, pela atenção e pelo apoio.

(6)

(7)

O objetivo deste trabalho será contribuir para o estudo da econometria espacial através da utilização do conceito de modelagem da interdependência regional. A interdependência regional é uma área de estudo cuja pesquisa ainda apresenta muitas frentes a serem exploradas. Para o propósito deste trabalho será utilizado o modelo GVAR (Global Vector AutoRegressive), proposto por Pesaran et al.

O trabalho analisará a aplicação, a dados brasileiros, dos conceitos econométricos do GVAR produzido por pesquisadores alemães, sobre dados daquele país, e utilizados no artigo “Regional Unemployment Forecasts with Spatial Interdependencies”, por Schanne, Wapler eWeyh (2008).

O modelo de GVAR utilizado inicialmente testará a existência de cointegração entre as séries históricas de admissão e de demissão de trabalhadores nas 27 unidades federativas (UF) do Brasil. Em seguida, o modelo será utilizado como ferramenta para a previsão da taxa de ocupação do mercado de trabalho.

Os resultados obtidos indicam que a existência das denominadas “unidades dominantes” acaba exercendo um significativo efeito em termos de econometria espacial, para os dados utilizados neste estudo.

Palavras-chave: interdependência regional; econometria espacial; GVAR; matriz de pesos.

(8)

The goal of this work will be to contribute to the study of spatial econometric by using the concept of modeling for regional interdependence. Regional interdependence is a field of study whose research also has many fronts to explore. For the purpose of this work will be used the GVAR model (Global Vector AutoRegressive), proposed by Pesaran et al.

The work will examine the application, to Brazilian data, of GVAR econometric concepts produced by German researchers on data of that country, and used in the paper "Regional Unemployment Forecasts with Spatial Interdependencies", by Schanne, Wapler and Weyh (2008).

The model GVAR used initially tests the existence of cointegration between the historic series of admission and dismissal of workers in 27 units (UF) of Brazil. Then, the model will be used as a tool for forecasting labor market occupancy rate. The results indicate that the existence of so-called "dominant units" ends up playing a significant effect in terms of spatial econometrics, for the data used in this study. Keywords: regional interdependence; spatial econometrics; GVAR; weight matrix

(9)

Gráfico 1: Função Resposta ao Impulso Generalizada - choque positivo nas

admissões no estado de São Paulo...42

Gráfico 2: Função Resposta ao Impulso Generalizada - choque positivo nas demissões no estado de São Paulo...43

Gráfico 3: Função Resposta ao Impulso Generalizada - choque positivo da PI no estado de São Paulo...44

Gráfico 4: Função Resposta ao Impulso Generalizada - choque positivo da TJR no estado de São Paulo...45

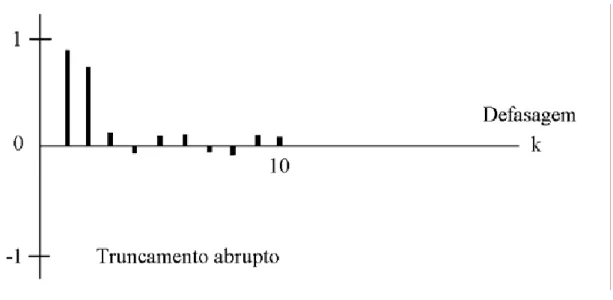
Gráfico A1: Valores das autocorrelações significativos nos períodos iniciais de defasagem e truncamento posterior...57

Gráfico A2: Valores das autocorrelações significativos decaindo de forma extremamente devagar segundo padrões de decaimento...57

Tabela 1: Elasticidade – choque positivo nas admissões...33

Tabela 2: Elasticidade – choque positivo nas demissões...34

Tabela 3: Elasticidade – choque positivo na produção industrial...35

Tabela 4: Elasticidade – choque positivo na produção industrial (Estado de São Paulo como unidade dominante)...36

Tabela 5: Elasticidade – choque positivo da taxa de juros real 37

Tabela 6: Elasticidade – choque positivo da taxa de juros real (Estado de São Paulo como unidade dominante)...38

Tabela 7: intervalo de confiança, a 90%, p/ a mediana do Perfil de Persistência...39

(10)

Tabela 10: Vetores de Cointegração...72

Tabela 11: admissões, por UF... 88

Tabela 12: demissões, por UF...96

Tabela 13: Matriz de Vizinhança, por UF...104

Tabela 14: produção industrial brasileira...105

Tabela 15: taxa de juros real...111

Figura A1: Geração de série temporal Yt...45

Figura A2: Associação de modelo à série de observações Yt...45

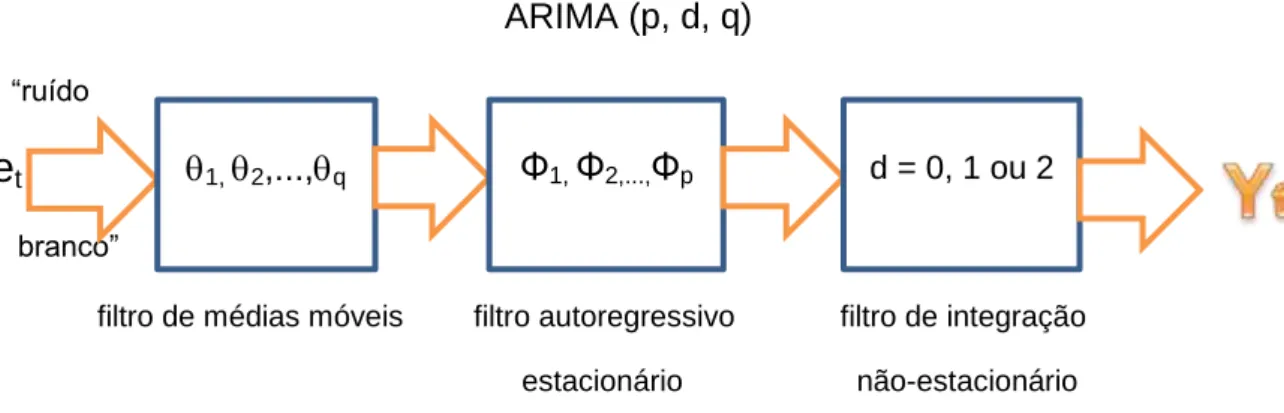
Figura A3: Filtros de médias móveis, autoregressivo e de integração não-estacionária...47

(11)

1) Introdução...12

2) Parte teórica...14

2.1) Vetor de Correção de Erros (VEC)...14

2.2) Perfil de Persistência (PP)...16

2.3) Função Resposta ao Impulso Generalizada...17

3) GVAR – Conceito e aplicações...19

4) GVAR – Estudo de caso...21

5) Solução do modelo GVAR...26

6) Base de dados...29 7) Resultados...30 8) Conclusões...46 9) Bibliografia...49 10) Anexos...51 10.1) Revisão Teórica.………...51 a) Séries temporais...51

b) Previsão com Metodologia Box-Jenkins...52

c) Função de Autocorrelação...56

d) Vetores Autoregressivos (VAR)...60

e) VAR(p)...66

f) Cointegração...68

(12)

10.3) Definições Estatísticas...81 10.4) Definições para a planilha de resultados...84

(13)

1) Introdução

A econometria espacial é uma área relacionada às ciências econômicas que pode oferecer meios de melhor compreensão de atividades relacionadas, por exemplo, ao nível de emprego de uma determinada região e como esta variável pode estar vinculada à distribuição física dos entes econômicos ali existentes.

Em termos econômicos, a modelagem da interdependência regional se mostra aplicável em função do conceito que atividades econômicas relevantes desenvolvidadas em uma determinada região são significativamente influenciadas por outras regiões contíguas ou próximas, o que indicaria a existência de dependência espacial.

A modelagem da interdependência regional pode ser avaliada como um processo que, por utilizar o conceito de dependência espacial, apresentar-se-ía como instrumento de previsão mais robusto do que a abordagem via séries temporais. O objetivo deste trabalho é verificar como a aplicação de conceitos de econometria espacial, considerando a proximidade física entre unidades geográficas, pode influenciar níveis de contratação e demissão de mão-de-obra no Brasil. Além disto, se as técnicas estudadas permitem que seja possível avaliar o nível de emprego esperado.

A inspiração deste trabalho partiu da pesquisa realizada por estudiosos alemães sobre a aplicação do GVAR nos índices regionais de desemprego daquele país, “Regional Unemployment Forecasts with Spatial Interdependencies”, por Schanne,

Wapler e Weyh (2008).

Este trabalho se propõe a utilizar os conceitos do GVAR (Global Vector AutoRegressive) a uma realidade brasileira.

O GVAR é uma ferramenta econométrica que utiliza o conceito de espaço para a obtenção de resultados que permitam avaliar interações macroeconômicas globais. M. Hashem Pesaran é um dos econometristas que mais trabalhou esta ferramenta. Para a execução do trabalho foram coletados dados nacionais referentes à admissão e demissão de empregados, obtidos através do CAGED (Cadastro Geral

(14)

de Empregados e Desempregados), instrumento gerenciado pelo Ministério do Trabalho e Emprego do Governo Federal. Os dados estão segregados pelas 27 unidades federativas (UF).

Para poder utilizar o conceito de econometria espacial foi apurada a matriz de vizinhança relativa às 27 UF, elemento essencial quando da apuração de um GVAR.

Também foram apurados dados nacionais relativos à produção industrial e à taxa de juros real da economia, de forma que estas duas variáveis fossem consideradas variáveis globais no modelo.

O capítulo 2 desenvolve uma revisão conceitual sobre vetor de correção de erros (VEC), Perfil de Persistência e Função Resposta ao Impulso Generalizada.

O capítulo 3 discute o modelo GVAR e sua relação com econometria espacial.

O capítulo 4 apresenta o estudo de caso alemão, inspiração para este trabalho.

O capítulo 5 apresenta a solução matemática do GVAR.

O capítulo 6 apresenta a base de dados utilizada, e de que forma tais dados foram trabalhados.

No capítulo 7 os resultados do modelo são avaliados, considerando-se o resultado dos Perfis de Persistência e da elasticidade apurada das variáveis de admissão e demissão em relação a choque aplicados ao modelo.

O capítulo 8 apresenta as conclusões do trabalho.

O capítulo 9 a bibliografia utilizada.

O capítulo 10 apresenta os anexos, incluindo uma revisão conceitual sobre séries temporais, Modelo Box-Jenkins, vetores autoregressivos (VAR), cointegração, e Causalidade de Granger.

(15)

2) Parte teórica

2.1) Vetor de Correção de Erros (VEC)

A existência de cointegração tem implicações para a especificação de modelos VAR. Se as variáveis são cointegradas o modelo VAR deve ser especificado e estimado como um modelo de correção de erro, em que as mudancas nas variáveis dependem de desvios em relação a um equilíbrio de longo prazo, definido pela relação de cointegração.

Consideremos, por exemplo, a relação entre consumo de bens não duráveis (C) e a renda disponível (RD) expressa na forma de um VAR(1).

C

t

= θ

0

+ θ

1

C

t - 1

+ Ф

1

RD

t - 1

+ e

t

(1)

RD

t

= δ

0

+ δ

1

C

t - 1

+ α

1

RD

t - 1

+ u

t

2

RD

t – 1 (5)

Desta forma, as variações em C e RD (ou as correções em C e RD) dependem da magnitude do desvio do sistema em relação ao seu equilíbrio de longo prazo no período anterior. Os choques et e ut conduzem a desvios de curto prazo da

(16)

trajetória de equílibrio de cointegração. Há, então, uma tendência a uma correção de volta ao equilíbrio.

Em outras palavras, a ideia por traz da correção de erros é que sistemas cointegrados têm um equilíbrio de longo prazo, isto é, a média de longo prazo da combinação linear das duas séries. Se ocorre um desvio em relação ao equilíbrio de longo prazo, uma ou as duas séries ajustam para restaurar o equilíbrio.

(17)

2.2) Perfil de Persistência (PP)

Ao passo que a Função Resposta ao Impulso mostra o efeito de um choque sobre uma variável específica, o Perfil de Persistência, como definido por Lee e Pesaran (1993), e Pesaran e Shin (1996), apresenta os efeitos de amplos choques sobre as relações de cointegração.

No caso das relações de cointegração os efeitos dos choques tenderão a desaparecer. Portanto, os aspectos gráficos dos Perfis de Persistência geram informação valiosa sobre a velocidade de convergência das relações de cointegração em direção a seus estados de equilíbrio.

Perfis de Persistência devem tender a zero quando o horizonte de previsão tende ao infinito, caso o vetor em consideração seja um vetor de cointegração válido. Para tanto é necessária a definição do horizonte de previsão.

O horizonte aplicado neste estudo foi de 40 períodos, seguindo o valor sugerido por Smith e Galesi (2014) para o modelo em Matlab do GVAR utilizado .

Definição:

PP(



’

ji

z

it

;



t

, n) =



’

ji

W

i

A

n



A’

n

W’

i



ji

(6)



’

ji

W

i

A

0



A’

0

W’

i



ji

n = 0, 1, 2, ...

sendo que:





’

ji é a j-ésima relação de cointegração na i-ésima unidade da federação (j =

1, 2,..., ri);

 n é o número de períodos do horizonte;





é a matriz de covariância de



t;

 An são matrizes de coeficientes relativos à parte estocástica de um MA;

(18)

2.3) Função Resposta ao Impulso Generalizada

O processo de cálculo do GVAR envolve a análise da aplicação de choques sobre as variáveis do modelo e análise dos resultados obtidos. Tais choques são aplicados através da utilização da Função Resposta ao Impulso, ou Generalised Impulse Response Functions (GIRF).

Uma Função de Resposta ao Impulso mensura o perfil temporal do efeito de choques, em um determinado ponto do tempo, sobre os esperados valores futuros das variáveis.

Em um sistema dinâmico é o resultado obtido quando tal sistema é defrontado com um breve sinal de entrada. De forma mais genérica, trata-se da reação de qualquer sistema dinâmico em resposta a alguma mudança externa. Em termos econométricos, segundo Bueno (2012), um modelo VAR não permite identificar todos os parâmetros da forma estrutural, a não ser que se imponham restrições adicionais.

Diferentemente dos modelos univariados o VAR busca responder qual a trajetória de uma série, dado um choque estrutural. Por trajetória avalia-se quando um choque afeta uma série.

Em um modelo multivariado a não estacionariedade emerge ou se verifica quando um dos autovalores da matriz de coeficientes está sobre ou fora do círculo unitário. No modelo univariado os autovalores se confundem com as raízes da equação característica, ao passo que no modelo multivariado isto não chega a ocorrer estritamente.

Se o processo é estacionário a incerteza da previsão é limitada, mesmo para previsões de longo prazo. Isto implica que o erro de previsão mais distante tem um limite bem definido.

Contudo, processos integrados têm erro de previsão indeterminado quando o horizonte se eleva. Uma maneira triangular de decompor os resíduos é a Decomposição de Cholesky.

(19)

GIRF(x

t

; u

ilt

, n) = E(x

t+n

|u

ilt

= √

ii,ll

, I

t-1)

− E(x

t+n

|I

t−1

)

(7)

sendo que:

 It−1 é a informação definida no momento t-1;





ii,ll é a diagonal da matriz de variância-covariância

Σ

u, correspondente à

l-ésima equação da i-l-ésima unidade federativa;

(20)

3) GVAR – Conceito e aplicações

Pesaram e Chudik (2010) analisaram a extensão do conceito de GVAR (Global Vector AutoRegressive) para o de IVAR (Infinite Dimensional Vector AutoRegressive).

Para tanto, observaram que a teoria econométrica do VAR não obtém uma boa performance quando defrontada com aplicações empíricas nas quais a dimensão do modelo e o número de observações das séries temporais são grandes

Sem a imposição de restrições os parâmetros do VAR não podem ser estimados, de forma consistente, nos casos em que tanto a dimensão (N) quanto o número de séries temporais (T) são grandes, uma vez que em tais casos o número de parâmetros desconhecidos cresce na ordem de N2.

Análises mais profundas sobre o IVAR foram executadas para o caso no qual uma das variáveis, ou as unidades de seção transversal do IVAR, são dominantes ou preponderantes. Tais análises demonstraram ser tecnicamente complexas.

Pesaran e Chudik (2010) propõe uma solução alternativa para a questão da dimensionalidade, baseada em uma classificação, a priori, das unidades em “próximas” e “não próximas”. Os coeficientes correspondentes às unidades “não próximas” são restringidos a desaparecer no limite, quando N

→

∞

, ao passo que os efeitos nas proximidades são mantidos sem restrições.

Eles demonstram que as propriedades do modelo IVAR dependem, de forma significativa, da extensão da dependência em seção transversal entre as unidades em estudo. Nas situações nas quais as dependências são fracas (na formulação apresentada pelo estudo) os pesquisadores definiram que o modelo IVAR desagrega-se para regresões individuais que podem ser ser estimadas de forma consistente.

Também foi analisado o caso em que a seção transversal das unidades são fortemente correlacionadas. Contudo, sua análises são restritas a situações nas quais a fonte de forte dependência na seção transversal é externa ao modelo e originada de um conjunto finito de fatores exógenos. Para este caso em questão foi

(21)

proposto um estimador de mínimos quadrados aumentados o qual é demonstrado ser consistente e assintoticamente normal.

Os estudos realizados pela dupla indicaram que a unidade dominante influencia as demais variáveis no modelo IVAR, direta e indiretamente, sendo que seus efeitos não se extinguem mesmo na situação em que a dimensão do modelo tende ao infinito. Ou seja, o fato de haver uma unidade dominante demonstra ser fator decisivo na utilização do modelo, apesar de o cenário apresentar um grande número de demais unidades.

Os efeitos da unidade dominante, tais como das unidades em sua proximidade, podem ser estimados de forma consistente pelo cálculo de regressões de mínimos quadrados aumentados que incluam funções defasagem da unidade dominante. Pesaran e Chudik analisaram modelos IVAR com uma unidade dominante, e assumiram que esta unidade dominante é conhecida a priori. Modelos com mais de uma unidade dominante e como identificá-las não foram tratados.

(22)

4) GVAR – Estudo de caso

Ao considerarmos o cenário brasileiro verificamos que, após a crise econômica internacional de 2008, o governo federal aplicou medidas macroeconômicas de natureza anticíclicas, com o objetivo de que os reflexos da crise fossem minimizados, dentro do possível, na economia interna.

Desta forma, no período entre 2008 e 2012 o crescimento econômico e as taxas de desemprego não apresentaram grandes sobressaltos. Contudo, a partir de 2013 passa-se a observar quedas relevantes no nível de atividade econômica e, por sua vez, crescimento nos índices de desemprego, conforme o gráfico abaixo, que exibe a a evolução da taxa de desemprego pelo critério PNAD do IBGE:

A elevação dos índices de desemprego gera questões relacionadas a como reduzir o impacto desta realidade sobre as famílias e sobre a demanda agregada, em virtude da queda de rendimento verificada sobre o consumo.

(23)

Segundo Oliveira e Carneiro (2001), a forma de como tratar a questão sobre a escolha da política de empregos mais adequada envolve as políticas tidas como ativas, que procuram incentivar diretamente a criação de postos de trabalho e a possibilidade de inserção do trabalhador naqueles postos desocupados, e outras consideradas passivas, que atuam na oferta de trabalho, procurando reduzi-la ou mesmo aliviando os problemas do desemprego por meio de pagamentos de benefícios aos desempregados.

Logo, a forma como projeta-se a evolução do nível de desemprego mostra relevância ao poder impactar de qual maneira pretende-se aplicar políticas de emprego: ativa ou passiva.

A modelagem da interdependência espacial, via GVAR, é uma técnica econométrica que coloca em destaque a questão da proximidade territorial e sua influência sobre as relações econômicas existentes.

O fator essencial que agregará as relações espaciais é a matriz de vizinhança, que definirá a ponderação espacial sobre as unidades federativas deste estudo. A forma como tratar a proximidade espacial pode ser realizada de duas maneiras:

 Regiões são conectadas mais intensamente quanto menor a distância entre elas. Desta forma, a utilização de uma função exponencial inversa, na qual temos a distância d entre as localidades i,j, pode ser aplicada para a geração dos pesos wi,j:

o

w

i,j

= e

-di,j, se i ≠ j

o

w

i,j

= 0,

se i = j

Nesta abordagem o peso é positivo para qualquer distância, embora ele convirja para zero conforme as distâncias tornam-se maiores.

 A segunda maneira de criar a matriz de vizinhança é através do conceito de dicotomia: há contiguidade (valor “1”), ou não há contiguidade (valor “0”) entre as fronteiras. No nosso estudo esta foi a opção utilizada para a ponderação da matriz de vizinhança.

(24)

A dinâmica das taxas de emprego e desemprego, em mercados de trabalho regionais, é conhecida por ser interdependente espacialmente.

Modelos GVAR geram um vínculo entre os mercados de trabalho local e do entorno e, desta forma, podem ser úteis quando analisando e prevendo taxas de emprego e desemprego, mesmo se elas são não estacionárias ou possuem tendência integrada.

Em seu estudo, Schanne, Wapler e Weyh (2008) projetam os níveis de desemprego para 176 distritos de mercado de trabalho em uma base mensal. Em função de seus pequenos tamanhos, uma forte interdependência espacial existe entre estas unidades regionais. Para poder contabilizar estes cenários, assim como considerar a heterogeneidade do desenvolvimento regional em relação ao tempo, foram aplicadas diferentes versões do modelo GVAR espacial univariado.

Quando comparando a precisão da previsão do modelo GVAR com aquela dos métodos de séries de tempo univariadas constata-se que que o modelo espacial de fato performa melhor ou, pelo menos, da mesma forma. Sendo assim, o modelo GVAR espacial proporciona uma aproximação complementar, ou alternativa, aos métodos comumente usados em previsão regional que não consideram interdependência regional.

No estudo em questão é utilizado o Índice de Moran, que consiste em uma medida de autocorrelação espacial a partir do produto dos desvios em relação à média. A abordagem GVAR pode ser brevemente sumarizada como uma abordagem em 2 passos. No primeiro, modelos regionais de pequena escala são estimados condicionais ao resto do mundo. Estes modelos caracterizam variáveis domésticas e médias ponderadas de seções transversais de variáveis externas que são, também, tratadas como fracamente exógenas.

i,t

+ u

i,t (8)

onde:

 yi,t é o elemento da variável dependente do vetor Yt que corresponde à

unidade da federação i no momento t;





i,t representa a média condicional determinística do processo de geração

de dados de yi,t;

 ui,t é um distúrbio estocástico distribuído de forma independente;

 y*i;t = ∑𝑁𝑗=1wI,j yj,t (com wi,i = 0) corresponde ao valor ponderado sobre os

elementos do vetor Yt que não correspondem à unidade da federação i e N

é o número de unidades da federação;





i,l, com l = 1,…, L são os parâmetros que descrevem a correlação espacial

dentro do painel i;





i,0 representa a autocorrelação especial contemporânea;





I,l, com l = 1,…, L representa o processo de autocorrelação espaço-tempo.

Ao analisarmos a aplicabilidade do GVAR sobre o mercado de trabalho verificamos que a teoria econômica fornece várias explicações em relação à conectividade de mercados de trabalho regionais (impacto de um polo industrial, disseminação de conhecimento de uma região especializada em pesquisa). Contudo, todas as explicações têm em comum que a intensidade destas interrelações depende da proximidade geográfica, ou seja, se elas possuem contiguidade de vizinhança ou se encontram-se a maiores distâncias.

O modelo de GVAR mencionado acima permite verificar algumas das premissas e restrições que são feitas nas análises econométricas espaciais:

(26)

 O limitado grau de dependência temporal no espaço;

 A homegeneidade dos processos determinísticos e estocásticos.

Em relação à questão da homogeneidade, ao assumir-se que os coeficientes são homogêneos há uma vantagem no processo, pois os coeficientes estimados convergirão para um número reduzido de períodos. Entretanto, ao assumir-se que um processo homogêneo determina o desenvolvimento de todas as regiões em análise, este procedimento pode não adequadamente capturar as heterogeneidades regionais.

Desta forma, previsões mais precisas, que englobem as heterogeneidades regionais, poderiam ser obtidas por estimações específicas para cada unidade federativa.

(27)

5) Solução do modelo GVAR

Embora a estimação do modelo seja feita em uma base região a região, o modelo GVAR é resolvido para todo o conjunto de variáveis, considerando que toda as variáveis são endógenas para o sistema, como um todo.

Após a estimação dos modelos VECM individuais, para cada unidade federativa, os correspondentes modelos VARX* são recuperados.

Partindo-se de um modelo VARX*(pi, qi) ele será apresentado na seguinte forma:

xit = ai0 + ai1t + Φi1 xi,t−1 +...+ Φipi xi,t-pi +

Λ

i0 x*it +

Λ

i1 x*i,t−1 + ... +

Λ

iqi x*i,t-qi + uit (9)

defina-se zit por:

it−pi

+ u

it (10)

onde:

Ai0 = (Iki, −

Λ

i0), Aij = (Φij,

Λ

ij) para j = 1,..., pi

Podemos utilizar as matrizes de peso Wi, definidas pelos pesos wij em função da

contiguidade existente entre as unidades federativas, para obter a identidade

z

it

=W

i

x

t (11)

t-pi

+ u

+ u

t, (13) onde: G0 = ( 𝐴𝑜𝑜𝑊𝑜 𝐴1𝑜𝑊1 ⋮ 𝐴𝑁𝑜𝑊𝑁 ), Gj = ( 𝐴𝑜𝑗𝑊𝑜 𝐴1𝑗𝑊1 ⋮ 𝐴𝑁𝑗𝑊𝑁 ) para j = 1, ..., p, a0 = ( 𝑎𝑜𝑜 𝑎1𝑜 ⋮ 𝑎𝑁𝑜 ), a1 = ( 𝑎𝑜1 𝑎11 ⋮ 𝑎𝑁1 ), ut = ( 𝑢𝑜𝑡 𝑢1𝑡 ⋮ 𝑢𝑁𝑡 )

e p = max pi entre todos os i. De forma geral, p = max(max pi, max qi).

(30)

6) Base de dados

A base utilizada foram os dados de admissões e demissões disponibilizados pelo Cadastro Geral de Empregados e Desempregados (CAGED) do Ministério do Trabalho, segregados por cada uma das 27 unidades federativas (26 estados e o distrito federal).

A janela de análise foi mensal, compreendendo o período de maio/1999 a dezembro/2015 (199 observações).

Para a utilização do GVAR, das estatísticas de autocorrelação espacial e as estimações do modelo, é necessária a definição de uma matriz de vizinhança na qual sejam atribuídos pesos espaciais (W). Tal matriz tem por objetivo a captura de toda autocorrelação espacial em referência ao fenômeno em estudo.

A matriz de pesos utilizada nesse trabalho refere-se à matriz geográfica de contiguidade por convenção rainha (critério “Queen”). Esta matriz considera, no caso em estudo, as fronteiras que cada unidade federativa possui em relação às demais unidades, adotando-se um critério binário, ou seja, peso “1” para os casos em que a respectiva unidade tem fronteira comum, e peso “0” para os casos em que não há fronteira comum.

Os elementos de sua diagonal principal são iguais a zero, pois nenhuma unidade federativa é contígua a si própria.

Como a matriz de vizinhança é utilizada em cálculos de indicadores de análise exploratória ela será normalizada por coluna, de forma que a soma dos ponderadores de cada coluna seja igual a um. Ou seja, as UF’s terão pesos iguais, independende de seu desenvolvimento econômico, por fazerem fronteira com a UF em questão.

(31)

7) Resultados

A análise dos resultados indicou que o modelo conseguiu calcular GVAR’s estáveis (todos os autovalores são < 1) para todas as UF’s.

Este cálculo foi executado após a aplicação de testes de raiz unitária e utilizando modelos VARX* a partir de modelos VECMX* estimados.

Ordem de defasagem (lag order) calculada para o GVAR: 2, para X e X*.

Em todos os casos ocorreu cointegração. O intervalo de confiança utilizado para o cálculo dos Perfis de Persistência foi de 90%, conforme tabelas 7 a 9.

Para a execução do objetivo deste trabalho é realizada, após o cálculo do GVAR pelo modelo, uma análise dinâmica que envolve a simulação de choques sobre as variáveis. Tal simulação é obtida através da utilização da Função Resposta ao Impulso Generalizada (GIRF, em inglês) acumulada. No modelo do GVAR utilizado um choque corresponde à aplicação de uma unidade de erro padrão (standard

error).

Tendo sido geradas pelo modelo GVAR as funções GIRF, sobre os resultados obtidos foi calculada uma função elasticidade, de forma que possa ser avaliada qual a magnitude dos choques. Esta função elasticidade é definida como a relação entre a função GIRF acumulada de determinada UF sobre a função GIRF acumulada da UF de referência.

Logo, considerando-se o objetivo de avaliar a resposta das demais regiões a choques aplicados a cada uma das unidades da federação os seguintes tipos de choque foram aplicados:

 Choque positivo na variável “Admissões” em cada uma das 27 unidades federativas (Tabela 1);

 Choque positivo na variável “Demissões” em cada uma das 27 unidades federativas (Tabela 2);

 Choque positivo na variável global “Produção Industrial” (Tabela 3);

 Choque positivo na variável global “Produção Industrial”, considerando o estado de São Paulo como unidade dominante (Tabela 4);

(32)

 Choque positivo na variável global “Taxa de Juros Real” (Tabela 5);

 Choque positivo na variável global “Taxa de Juros Real”, considerando o estado de São Paulo como unidade dominante (Tabela 6).

Para a definição de unidade dominante foi utilizado o estado de S. Paulo, em função de ser a principal unidade econômica do país.

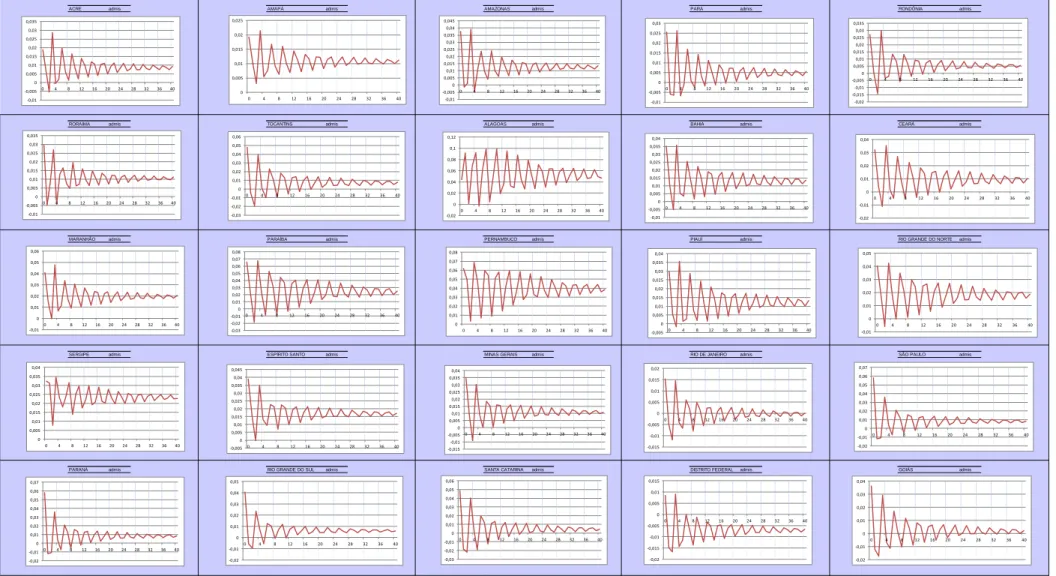
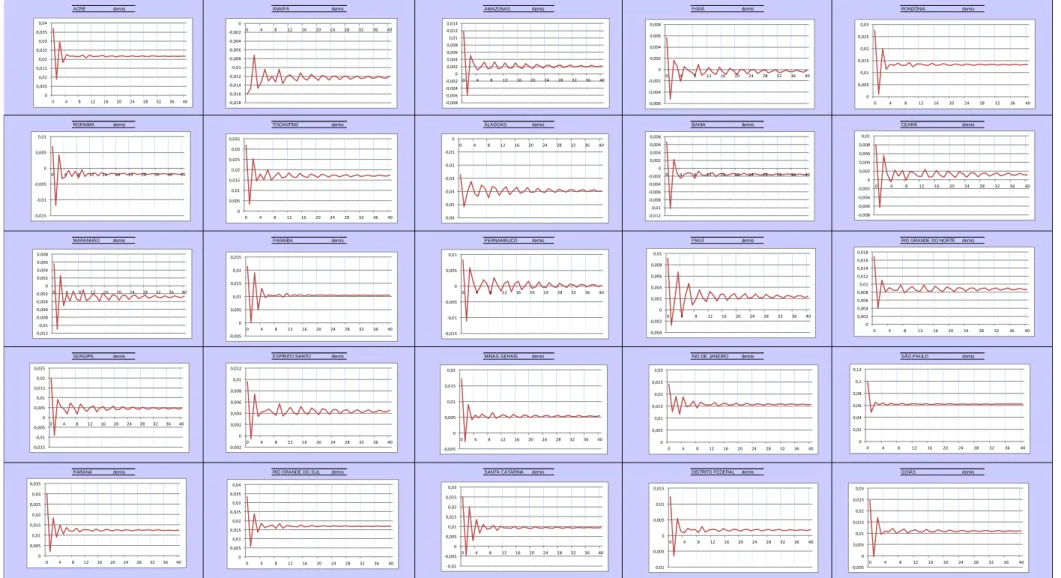
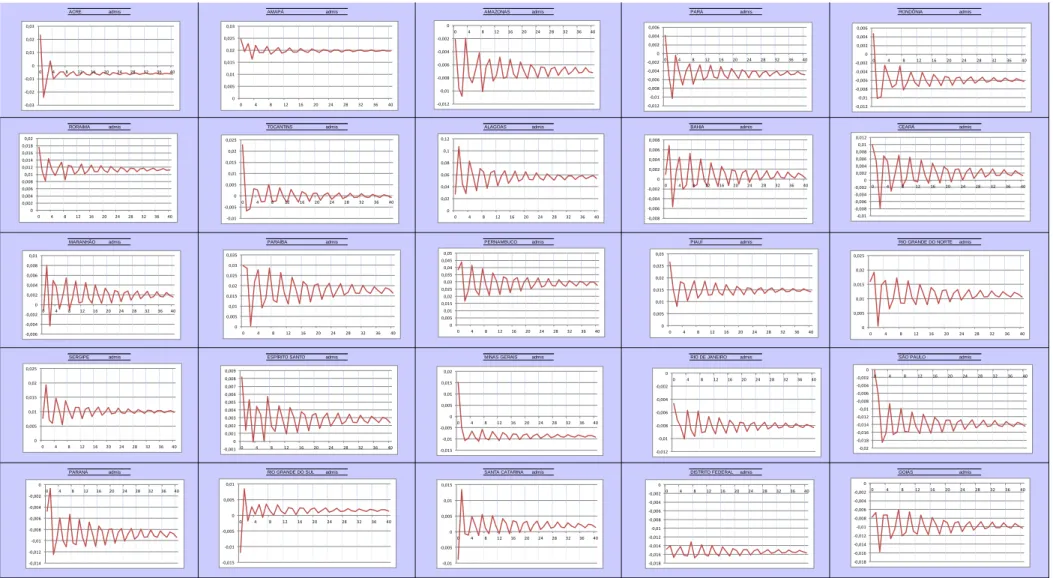
A análise dos gráficos gerados pelos Perfis de Persistência, conforme pode ser visualizado através dos gráficos 1,2,3 e 4, indica que os perfis, após 40 impulsos, tendem a zero, ou valores muito próximos de zero, o que indica que o vetor de cointegração em análise pode ser considerado válido.

Os Perfis de Persistência indicam com qual magnitude as relações de cointegração retornam ao seu estado de equilíbrio. Para a análise dos Perfis de Persistência foi utilizado o estado de São Paulo como amostra.

Observando-se os resultados obtidos através do modelo de GVAR, e as elasticidades calculadas, as seguintes inferências foram obtidas:

 Choques positivos na variável “admissão” (Tabela 1) provocaram impactos positivos na maior parte das UF.

 Choques positivos aplicados na variável “admissão” (Tabela 1) por cada um dos estados, sobre o Distrito Federal (DF), resultam que, das 52 elasticidades calculadas na tabela (duas variáveis * 26 UF), em 9 casos há elasticidades negativas. Nos demais casos a elasticidade resultante foi positiva. Deve ser observado que o DF possui a característica de que parte representativa de sua massa de assalariados é formada por servidores públicos que apresentam estabilidade funcional, ou seja, estão menos impactados por variações no nível de emprego do país.

 Choques positivos na variável global “Produção Industrial” (Tabela 3) produziram impactos positivos no nível de admissão em 23 UF, ou seja na ampla maioria. Este resultado está alinhado com o conceito que crescimento na atividade econômica gera impacto positivos no mercado de trabalho.

 Ainda em relação à Tabela 3, observamos que algumas UF apresentam valores de elasticidade acima de 1 para o choque positivo da variável global

(33)

“Produção Industrial” sobre o nível de admissões. Estes resultados, comparados com a magnitude das elasticidades obtidas nos demais cenários de simulação de choques, podem indicar que esta variável é a que apresenta sinais de maior relevância entre as analisadas.

 Choques aplicados na variável global “Produção Industrial”, considerando o estado de São Paulo como unidade dominante (Tabela 4), produziram resultados consistentes em termos de impulso, pois observa-se um amplo impacto em termos de aumento nas admissões pelo país, em função de um choque positivo sobre tal variável. Este resultado corrobara a questão que, sendo São Paulo o estado de maior atividade econômica do país, impactos positivos nos seus níveis de atividade estão associados a crescimento de atividade em outras regiões do país.

 Por outro lado, ao analisarmos o resultados da Tabela 4 não é possível inferir que a interdependência regional tenha sido um fator preponderante no cenário analisado, pois a grande maioria das UF apresentou uma elasticidade positiva, independente da distância ao estado de São Paulo.

 Choques aplicados na variável global “Taxa de Juros Real” (Tabela 5) produziram resultados negativos no nível do emprego na maioria das UF (16 x 11), o que indica que, de fato, taxas de juros reais elevadas contraem o nível da demanda agregada e elevam o nível de desemprego.

 Choques aplicados na variável global “Taxa de Juros Real”, considerando o estado de São Paulo como unidade dominante (Tabela 6), produziram resultados dispersos, de forma que não se pode concluir que tal variável tenha influência relevante sobre as taxas de admissão e demissão.

(34)

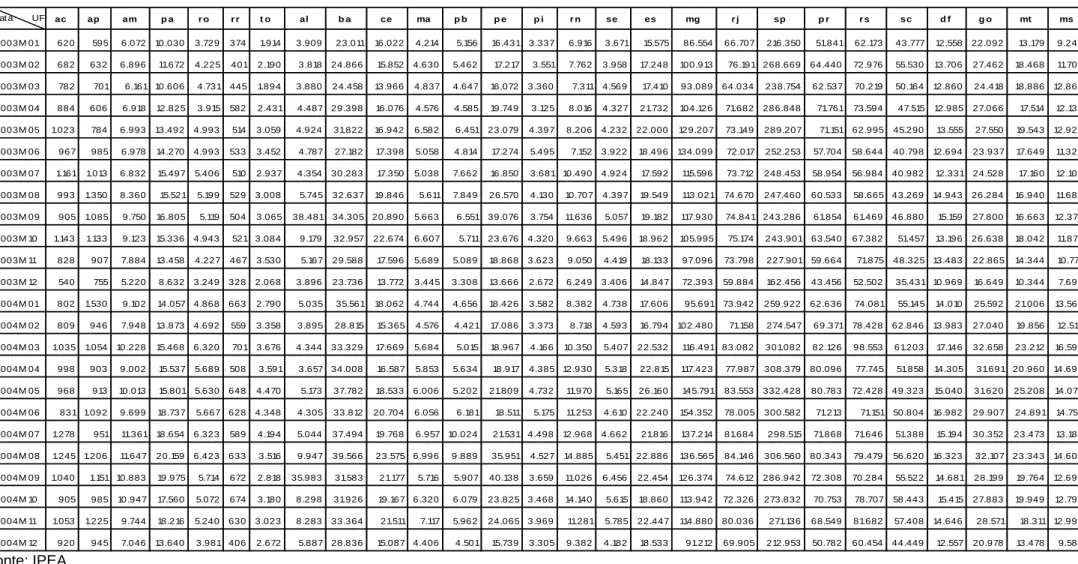
Tabela 1: Elasticidade – choque positivo nas admissões

Fonte: autor ac ap am pa ro rr to al ba ce ma pb pe pi rn se es mg rj sp pr rs sc df go mt ms adm 1 0,086270 0,330110 0,170649 0,340026 0,050936 0,152577 1,256582 0,191266 0,101621 0,206435 -2,835417 -0,133027 0,179195-0,829932 0,166514 0,213620 1,549597 0,135963 0,575169 0,580139 4,387541-0,085444 0,122032 0,175428-0,170837 -2,082139 dem 1 0,003722-0,089691 1,008303 0,090697 0,258363 0,085419 0,037338-0,000819 0,411427-0,065135 0,648134 0,142842 0,484193-0,030773 -0,041751 -0,203005 -0,008019 0,191288 0,262251-0,021838 0,127556 0,361488 0,043440 0,176881 0,229752-0,114913 adm -0,116049 1 0,105552 0,209624 0,294941 0,144687 0,031605 0,944149-0,041854 0,175742 0,275354 2,554661 0,199269 0,042122-7,259552 0,082495 0,273198 0,636327-0,002876 0,718432 0,852862 -3,324090 0,098125 0,212342 0,166047 0,073231-3,704963 dem 0,137744 1 0,226750 1,510087 0,220058 0,747887-0,085723 0,002337 0,131477-0,607845 0,223574 0,868282 0,214444 0,185730-0,403993 -0,087046 0,200978-0,395688 -0,261373 -0,704088 0,323526 0,906738 0,178986 0,239153 0,021599 0,087142 0,168224 adm -0,585558 0,034021 1 0,261817 0,086884 0,075404 0,470578 1,794897 0,483783 0,278378 0,220540 -2,355587 0,009441 0,302561 2,404436 0,366943 0,171912 2,331140 0,292996 0,857939 1,105697 12,949430 0,104251 0,172960 0,191744-0,349720 0,710352 dem 0,280065 0,020815 1 1,628564-0,030865 -0,434023 -0,029454 0,057376 0,164604 1,000955-0,029217 0,309994 0,041208 0,449692 0,011712-0,145149 -0,174493 -0,199538 -0,044173 -0,211512 -0,177530 0,611844 0,098444-0,235445 0,197003 0,225283-0,054885 adm 0,215289-0,048596 0,279504 1 0,344035 0,056663 0,124101 1,166421 0,199838 0,346748 0,039552 -2,405191 -0,189262 0,161355-0,015810 0,300856 0,212039-0,607983 0,165766 0,330159 0,812919 8,878703-0,140766 0,212433 0,329195-0,417256 -1,456481 dem 0,093037 0,138301 0,086858 1 0,036243 0,242142 0,077644 0,010806 0,078711 0,059068 0,108580 0,139919 0,045803 0,094073-0,089176 -0,025030 0,010486-0,050831 -0,013041 -0,116687 0,085666 0,118914 0,048770 0,012617 0,096732 0,143552 0,022388 adm 0,234320 0,200079 0,261430 0,230475 1 0,125588 0,136268 1,510507 0,257436 0,089834 0,263542 -0,839926 -0,107537 0,177721-3,254783 0,186650 0,302066 0,708327 0,242297 0,368451 0,831214 4,070728 0,118277 0,215867 0,185862-0,023779 -4,038688 dem 0,165410 0,171224 0,464693-0,150530 1 0,538758 0,005156-0,026199 -0,037322 0,415408 0,140784 0,216975-0,012304 -0,023705 -0,221227 0,024645 0,262263-0,110530 0,216575-0,037947 0,166236 0,148525 0,172782 0,296182 0,053667 0,177176 0,394667 adm 0,528045 0,322038 0,124375 0,013263 0,463440 1 0,091784 1,537483-0,010733 0,354811-0,023987 -3,817193 0,411074 0,122006-9,085055 0,292370 0,369674 3,764435-0,234964 0,704219 1,034482 9,830805 0,150855 0,318451 0,584361 0,092512-1,952756 dem 0,000860 0,071034 0,267044 0,646182 0,066942 1 0,007353-0,004353 0,079223-0,101936 0,014101 -0,007450 0,053207 0,047658-0,113156 0,000886 0,064215 0,111007-0,078460 0,042076 0,039144 -0,018566 0,044132 0,091049-0,028477 0,069871 0,043771 adm -0,326234 -0,009444 0,282912 0,325297 0,217876 0,060851 1 1,675564 0,453599 0,260467-0,114892 -1,128496 -0,216980 0,326851-7,116946 0,240115 0,115227 0,888239 0,266373 0,522628 1,029380 6,187492 0,033545 0,234827 0,260136-0,361233 -3,161393 dem 0,124462 0,073437-0,106300 0,815600 0,084338-0,070525 1 0,006722 0,288985 0,397420-0,221368 -0,445103 -0,004713 0,458040-0,708865 -0,081613 0,158913 0,217874 0,253332 0,070516 0,369291 -0,684329 -0,083331 0,178750 0,500034-0,034929 0,131950 adm -0,274786 -0,064365 0,414011 0,174576 0,045764 0,058076 0,284196 1 2,920910 0,759339 0,101203 -1,916895 -0,667668 0,513810 1,313938 0,714008-0,087490 7,296563 0,646878 3,466038 0,781354 3,506577-0,022889 0,295027 0,013644 0,601515-4,084767 dem -0,931613 -0,026683 -2,036812 -1,398164 -0,289187 -1,091219 0,090809 1 1,334907 1,213505-0,302257 -4,184572 -0,020748 0,335387 0,807254 0,162654-0,597130 1,857491 0,756480-2,073071 -0,918270 -2,052910 1,580600 1,051077 0,679062 0,893157-2,198338 adm -0,026021 0,005625 0,089989 0,017157 0,061326 0,033036 0,097271 0,832940 1 0,125627 0,049428 -0,209453 -0,048302 0,068964 0,726355 0,154358 0,009386 2,826377 0,183988 0,886530 0,221182 1,591589-0,039681 0,077482 0,040549 0,046038-0,574130 dem -0,051973 0,031667-0,028559 0,076485-0,039006 -0,000519 0,089319 0,062155 1 0,751380 0,004025 -0,350980 0,068261 0,075856-0,144812 -0,021615 0,147450 0,015191-0,030704 0,074108-0,042857 0,042954 0,125673 0,048583 0,072057 0,079507-0,043617 adm -0,081697 0,080851 0,180356 0,107036 0,042799 0,092838 0,089563 0,834727 0,442444 1 0,153631 7,154170 0,110735 0,180244-6,916371 0,209920 0,074075-0,541112 0,126867 0,640741 0,583616 0,614330-0,046426 0,124072 0,113619 0,207522-0,497811 dem -0,019044 0,017986-0,078607 0,167403 0,044133 0,057282-0,030260 0,012989 0,032898 1 0,029832 -0,069028 0,111410 0,022430 0,133979 0,007028 0,006161 0,099344 0,040816-0,144758 -0,073710 -0,006932 0,110353-0,001556 -0,024817 -0,012849 -0,065548 adm -0,337342 -0,010620 0,213624 0,174861 0,133422 0,025514 0,154350 1,507363 0,130605 0,149691 1 2,703345-0,108889 0,270119 1,492302 0,131792 0,088180 0,417515 0,251389 1,316185 0,964582 0,261140-0,057466 0,157841 0,034270 0,107874-3,631130 dem 0,074124 0,005894-0,072722 0,895817 0,031730-0,212107 0,011515-0,005903 0,052251 0,183707 1 0,633933 0,070682 0,294637 0,299747-0,116818 -0,028212 -0,284875 0,072449-0,192937 0,338521 0,068547-0,087411 -0,001180 0,212097 0,054053-0,009194 adm -0,069743 0,078328 0,164234 0,007678 0,046174 0,086482 0,101420 1,035965 0,411976 0,390755 0,197377 1 0,347170 0,138174-1,936276 0,180002 0,082213 2,278184 0,184956 1,659437 0,228696 0,338706 0,041382 0,097387 0,143620 0,177225-2,336957 dem -0,177801 0,132512-0,460187 0,415213 0,420540 0,919087-0,294861 0,047608 0,117769 0,239204 0,084256 1 0,422344-0,282473 0,174282 0,160102 0,147633 0,426966 0,298487-1,603975 -0,300299 0,765946 0,740241 0,185544-0,270121 0,003576-1,004381 adm -0,449856 0,136996 0,275455 0,003346 0,102807 0,161462-0,033948 2,882639 1,255971 0,564244 0,261488 2,050363 1 0,314663-3,682878 0,404497 0,040795 2,972051 0,255333 2,644087 0,496241 4,135924-0,006902 0,100306 0,369611-0,007722 -4,693581 dem -0,153369 0,158999-0,667014 0,595538 0,087830 0,785092-0,162090 0,067727-0,017582 -0,171180 0,111662 -0,577431 1 0,441194 0,089911 0,176938-0,025943 0,572827 0,082654-0,049948 -0,234159 -1,068981 0,407501-0,007900 -0,205001 -0,018281 -0,413500 adm -1,250005 0,028467 0,376922 0,134852 0,153440 0,042375 0,141449 2,343663 0,213569 0,372332 0,218174 3,704739-0,268860 1-5,240858 0,411190-0,016847 -2,125383 0,337940 0,823998 0,736366 -1,404528 0,232852 0,197847 0,129073 0,103492-6,840619 dem -0,108280 0,046680 0,144827 0,516531 0,016182 0,077491 0,145397 0,050115 0,179741 0,581354 0,133352 -0,228677 0,266342 1 0,006059-0,083819 0,046156 0,184214-0,008308 -0,152315 0,015271 -0,412978 0,029825-0,053545 0,106577-0,011656 -0,231711 adm -0,069369 0,045281 0,152070 0,038789 0,025567 0,047247 0,119826 0,648223 0,310095 0,433540 0,188943 3,061811 0,061318 0,130393 1 0,128170 0,083625 1,118676 0,167851 1,227741 0,245617 -0,583954 -0,003573 0,095952 0,072238 0,186978-2,594631 dem -0,013841 0,001004-0,671817 -0,049471 0,123755-0,283379 -0,052671 0,040271-0,053393 1,581672 0,198876 0,490552-0,076375 -0,371948 1-0,009786 0,134370 0,093906 0,307313-0,276730 -0,217462 0,579957 0,249604 0,144228-0,008689 0,008903 0,247574 adm -0,037664 0,057393 0,182946 0,085668 0,035070 0,065637 0,163797 0,967974 0,222232 0,102575 0,010508 -5,437029 0,204672 0,153593-2,033033 1 0,195252 2,598111 0,192193 1,554006 0,306611 2,105286 0,284192 0,047522-0,076126 0,362700 0,847630 dem -0,074381 0,042121-0,673118 -0,657517 0,003340 0,133233 0,023323 0,057111 0,350126-0,033720 -0,076766 -1,004193 0,165878-0,265184 -0,017954 1 0,191721 0,158666 0,121219-0,028164 0,007585 -0,497875 0,390929 0,033316 0,128013 0,161779-0,410994 adm 0,057758 0,189784 0,072072 0,064368 0,213376 0,100641 0,150150 1,024816 0,091001 0,078341-0,002937 2,560719-0,119458 0,052750-2,264540 0,214501 1 6,532007 0,048053 1,141573 0,684558 2,324388 0,033032 0,217128 0,175819-0,091973 3,554558 dem -0,083231 0,101012-0,150523 -0,392831 0,145509 0,264680 0,053853-0,009606 0,254245-0,140368 -0,084887 -0,011648 -0,016267 0,022239-0,144826 0,142492 1 0,786202 0,030203-0,046672 0,241009 -0,646598 -0,025812 0,263124-0,005231 -0,077797 -0,377604 adm -0,111521 0,054688 0,123797 0,080826 0,147410 0,082325 0,001790 0,905979 0,377811 0,130331 0,164613 3,533140-0,090813 0,154988 0,927136 0,160925 0,221330 1 0,321477 0,740480 0,469386 -1,360177 0,246477 0,355916 0,297349 0,163915-0,825744 dem -0,277186 0,009168-0,274980 -0,201264 0,048139 0,084832 0,143344 0,004280 0,230184 0,374685-0,125563 -1,127858 0,022411 0,241701-0,297286 0,073650 0,220264 1 0,305697-0,071951 0,238858 -1,370791 -0,227766 0,136698 0,147005-0,042782 -0,136560 adm 0,197631-0,000758 0,107680 0,054925 0,103314 0,001410 0,156883 0,412597 0,152825 0,008166 0,250430 1,417376-0,039131 0,097211 1,218482 0,099367 0,052930 1,075151 1 0,000827 0,291928 2,855953-0,033593 0,159631-0,149414 0,076971-1,117119 dem -0,098690 -0,006438 -0,348008 -0,434838 0,112152-0,142553 0,081320-0,002172 -0,028343 0,064979 0,050931 -0,074364 0,001996-0,114550 -0,007094 0,093475 0,160695 0,241652 1-0,350107 0,205675 -0,845385 -0,098512 0,213603 0,177051-0,043897 -0,017556 adm -0,094269 0,018531 0,147724 0,073588 0,134940 0,060606 0,093688 0,724290 0,227052 0,065236 0,139263 1,468031-0,026151 0,128325-0,966682 0,163133 0,144462 1,352606 0,446633 1 0,619252 0,171730 0,271355 0,238009 0,157955 0,183521-1,169444 dem 0,126149-0,035927 -0,168103 0,061705 0,070888-0,297630 0,223267-0,013889 0,009076 0,620745-0,101399 -0,265518 0,021280 0,156243-0,204200 0,019537 0,118363 0,437331 0,318574 1 0,353356 -0,325194 -0,069375 -0,018311 0,219359 0,011539 0,436985 adm -0,026608 0,038164 0,180901 0,076833 0,127872 0,097420-0,066698 0,310233 0,086125 0,080770 0,176032 2,013751-0,019508 0,152858-0,798484 0,174115 0,140339 0,820775 0,284975 0,591687 1-0,164423 0,541091 0,254769 0,306478 0,358950-1,222673 dem 0,080997 0,016975-0,267783 0,185700 0,029821-0,079657 0,064586 0,049775 0,260719 0,110409 0,180228 0,350584-0,045214 0,030166 0,008382-0,088624 0,013198 0,005069 0,129933-0,013819 1 0,046459 0,032647 0,154238 0,114172 0,234472 0,542950 adm 0,074446 0,026268 0,072260 0,016040 0,026493 0,088463-0,298688 -0,452988 -0,192638 -0,037200 -0,106496 1,496083 0,130309 0,112916 1,221074 0,129850 0,101846-0,448079 -0,025021 0,433599-0,979108 1 1,057920 0,079387 0,413589 0,200437-1,609936 dem 0,179532 0,118325-0,250258 0,257638 0,154963 0,254959 0,084170-0,021764 0,057428 0,190037 0,126537 -0,198057 0,032661-0,127568 -0,301076 -0,018649 0,217993 0,468578 0,109704 0,032691 0,347655 1 0,393394 0,266702 0,053382-0,072554 -0,065804 adm -0,052582 0,057200 0,083770 0,018045 0,073301 0,089744-0,222752 -0,156554 -0,112989 -0,018220 -0,054202 0,852734 0,121395 0,115558-0,413098 0,126173 0,125884 0,176081 0,020379 0,329466-0,676773 -1,314931 1 0,109885 0,352111 0,095236-0,564135 dem 0,186113 0,124994-0,251753 0,353670 0,145154 0,393412-0,040270 0,031624 0,312267 0,601824 0,018141 0,031261 0,088169-0,241261 -0,196531 -0,002538 0,237916 0,184607-0,066615 -0,155214 0,096356 0,929578 1 0,196486-0,078016 -0,013733 0,150142 adm 0,585392 0,090612 0,089192 0,091723 0,182435 0,118099 0,101662 0,767783 0,055150 0,153906 0,030059 0,454253-0,193349 0,139114-0,642994 0,094861 0,137428 2,237856 0,248660-0,452406 0,640075 0,898692 0,176830 1 0,043010 0,046666 0,648251 dem -0,138270 0,033580-0,065451 -0,261650 0,093799 0,054463 0,100478 0,004827 0,069418-0,309491 -0,085495 -0,213755 -0,051250 -0,020947 -0,076763 0,026480 0,085421 0,154756 0,196718-0,528375 0,146251 -0,451408 -0,071284 1 0,315721-0,009376 -0,168753 adm 0,186163 0,000917 0,153889 0,138292 0,108217 0,119702-0,231036 0,847005 0,259656 0,154390 0,079400 0,108098 0,017110 0,161052 0,042024 0,162101 0,078947 1,829796 0,067619 0,141512 0,514123 2,813821 0,290005 0,269175 1 0,006141-0,830667 dem 0,110930 0,045070 0,258673 0,560945 0,006563-0,548908 0,355951 0,026941 0,178877 0,739350-0,038125 -0,134729 -0,076552 0,312993-0,137070 -0,066781 0,065974-0,025159 0,243929 0,374772-0,059113 0,244604-0,266406 -0,102306 1 0,176313 0,027492 adm -0,208480 0,037774 0,315364 0,285390 0,258409 0,110475-0,074176 0,642810 0,167346 0,224026 0,138425 -1,775406 -0,097286 0,218991 0,424938 0,320615 0,118620 0,677654 0,168288 0,463688 0,575658 4,520500 0,205938 0,175004 0,391337 1-0,649509 dem 0,198183 0,069142 0,262404 0,928412 0,042935 0,320234-0,035185 0,052445 0,358665 0,125703 0,110664 -0,282604 -0,026546 -0,002036 0,025270 0,143551 0,012959 0,210737 0,094826 0,565756-0,101762 0,345759 0,108030-0,070641 0,146182 1 0,115731 adm -0,006756 0,030794 0,194432 0,132212 0,161867 0,101711-0,074829 0,721938 0,242787 0,137104 0,127809 0,682130-0,032367 0,165026-1,054116 0,222682 0,141955 1,108547 0,253113 0,410798 0,672273 1,072906 0,353992 0,265634 0,387690 0,296542 1 dem 0,140980 0,012770 0,266353 0,206015 0,004455-0,429251 0,164870 0,043159 0,297623 0,538268 0,043581 0,120993-0,054293 0,186906 0,272740-0,161862 0,060239 0,297512 0,205339 0,583186 0,092266 -0,464051 -0,285681 -0,104568 0,099191 0,348815 1 go mt ms rj sp pr rs sc df pe pi rn se es mg to al ba ce ma pb ac ap am pa ro rr

(35)

Tabela 2: Elasticidade – choque positivo nas demissões

Fonte: autor ac ap am pa ro rr to al ba ce ma pb pe pi rn se es mg rj sp pr rs sc df go mt ms dem 1 0,177099 3,125860 1,950139-0,242518 0,469331 0,071197-0,026634 0,230290-1985,899854 0,203794 0,049904 0,103942 0,952502 0,042855 0,211481-0,030872 0,018306 0,125029 0,348509 0,363171 0,064945-0,093958 0,321054 0,053103 0,385735-0,019978 adm 1-0,036329 1,453787 0,322758 0,464155 0,239282 0,190281 0,153818 0,061183 0,364512 0,056281 0,078300 0,070745 0,310588 0,310525-0,043724 0,260643-0,073114 0,319823 0,025981 0,098434 0,019640 0,141703-0,025752 0,152993-0,090103 0,107481 dem 0,101772 1-0,879064 -1,249694 0,204028 0,378991-0,035696 -0,027556 0,255947-1530,142566 0,085818 0,094961 0,103109 1,445713-0,035308 0,035933 0,913359 0,042546-0,101081 -0,196939 0,191792 0,280643 0,147667 0,358690 0,083228 0,027130-0,053322 adm 0,038755 1 0,854669 0,669512 0,241771 0,294576 0,164878 0,013345-0,032933 -0,336572 0,204223 -0,974935 0,196503 0,031074 0,189626 0,043311 0,682129-0,196106 0,140001-0,009745 0,497769-0,053257 0,059461 0,118186 0,103073 0,154881 0,238906 dem 0,313942 0,028273 1 3,420831-0,110988 -0,798396 -0,045422 -0,017631 0,108217 -383,472594 0,011608 0,018089-0,046913 0,948496-0,023449 0,027338-0,204824 -0,037604 -0,186582 0,035444-0,000575 0,055102-0,044883 -0,065605 0,192519 0,129780 0,068446 adm 0,354163 0,023900 1 0,404286 0,127884 0,394019 0,291089 0,256736-0,208195 -0,095982 0,232244 0,120382 0,223302 0,485661 0,560254 0,116576 0,231717-0,276247 0,658987 0,297557 0,475322-0,034148 0,096440-0,003723 0,317515 0,237686 0,327831 dem 0,068567 0,121750 0,235012 1 0,028200 0,187014 0,077759-0,002136 0,133762 -137,718719 0,098430 0,017712 0,014107 0,111240-0,005300 0,030106 0,097872-0,006051 -0,006694 -0,003610 0,064816 0,093658 0,020032-0,005712 0,084684 0,127208 0,015060 adm 0,210908 0,137251 0,965337 1 0,282168 0,309286 0,295019 0,117752-0,033466 -0,185450 0,173993 0,299907 0,077136 0,326591 0,152314 0,143155 0,363945-0,311784 0,441228 0,141124 0,276537-0,022562 -0,099375 0,187755 0,274955 0,126762 0,232243 dem 0,074663 0,090891 0,509143-0,920663 1 1,537930 0,147630-0,011036 -0,019292 -523,120463 0,109717 0,076869 0,050793 0,305289 0,077805 0,052085 0,601991-0,007409 0,367313 0,215340 0,170886 0,081420 0,169326 0,328975 0,070020 0,077557 0,023023 adm 0,590843 0,065268 0,756274 0,399680 1 0,406620 0,342756 0,081569 0,069387 -0,009657 0,147866 -1,195011 0,125455 0,225568 0,458149 0,030337 0,551922-0,066850 0,499762 0,407455 0,312021-0,019434 0,268186 0,139015 0,171974 0,003912 0,163582 dem 0,042066 0,058425 0,245795 0,094505 0,044716 1 0,014008-0,006551 0,004230 -242,499089 0,012721 0,018708 0,053068 0,170198-0,015587 0,020554 0,152150 0,008061-0,072867 -0,027584 0,026926 0,004543 0,057309 0,094385-0,027672 0,095439-0,011322 adm 0,100212 0,293084 0,210514 0,490450 0,354830 1 0,204417-0,055644 0,085933 -0,499126 -0,018098 -2,011000 0,439005 0,077261-0,204181 0,160408 0,715692-0,429881 -0,033845 -0,173120 0,245962-0,011964 0,385624 0,311468 0,541660 0,639977 0,450720 dem 0,074159-0,046282 0,417637-1,251409 0,088164-0,210521 1 0,026813 0,387965 1425,743166-0,053833 -0,027471 -0,055384 -0,689159 -0,042530 0,071936 0,077631 0,072780-0,119609 0,275917 0,113871 0,291017-0,117836 -0,132770 0,393352 0,007983 0,106663 adm 0,197426-0,037273 0,122528 0,396733 0,184635 0,102709 1 0,119433 0,290224 -0,156123 -0,014925 0,663686 0,046612 0,552440 0,125339 0,099726 0,319425-0,077474 0,316164 0,450206 0,266548-0,007182 0,017865 0,135777 0,355895 0,112537 0,250959 dem -0,028715 -0,269314 -3,50825212,208656-0,474023 -7,871622 0,295087 1-0,807418 7268,440048-0,286909 0,106613 0,122106 4,152944 0,509656-0,013402 0,330464 0,848364 1,315801-0,627452 0,982617-0,088776 0,135829-0,157558 -0,000447 1,048871 0,451568 adm 0,467568-0,205157 -1,467268 0,164184-0,072368 0,100615 0,541928 1 3,286604 0,271908 0,033699 6,986236 0,291756 0,858361 0,894367 0,057735 0,129952 0,102064 0,393038 0,838735 0,400781 0,285981-0,418530 -0,366595 0,238712 0,616378 0,230099 dem 0,022148 0,016567-0,634705 0,391157-0,026886 -0,046220 0,050133 0,026585 1 754,540837 0,056056 0,032684-0,006338 0,105890 0,022334 0,087677 0,042819 0,084237 0,046564-0,023457 0,117911 0,045904 0,083052 0,070228 0,024378 0,102968 0,045117 adm 0,093741-0,010165 -0,524069 0,116479 0,029650 0,066798 0,188199 0,182203 1 0,047835 0,014163 0,973491 0,156930 0,177422 0,198212-0,007854 0,092735 0,014001 0,099784 0,302003 0,076944 0,062599-0,092884 -0,070211 0,060811 0,103158 0,101318 dem 0,021963 0,034555-0,354523 0,261014 0,046279 0,020223-0,010589 0,011310 0,078927 1 0,026728 0,079124 0,084724 0,219794 0,086362 0,037643 0,078315 0,035395 0,137025 0,020805 0,038083 0,040609 0,070011 0,101747-0,016215 0,025387-0,004243 adm 0,076957 0,065933 0,102063 0,136324-0,020322 0,253924 0,169944 0,094533 0,232014 1 0,153340 0,698026 0,272064 0,337339-0,048768 -0,011691 0,113811-0,008228 0,080873 0,137268 0,230922-0,000530 -0,152387 0,026798 0,126015 0,216736 0,099744 dem 0,076319 0,149684-0,010366 -2,093045 0,077494 1,032241-0,089663 -0,007536 0,553511 -219,818575 1 0,003066 0,035278-0,433616 0,079760 0,009940 0,126611-0,100342 0,383814-0,043500 0,172593 0,275909-0,025945 -0,020330 0,201267-0,027180 0,054524 adm 0,121958 0,135868 0,155400 0,473807 0,133233 0,353534 0,098354 0,074786-0,119981 -0,182196 1 0,708958 0,109046 0,567227 0,568696 0,032240 0,263470 0,200653 0,532047 0,212415 0,466162-0,024376 -0,031536 0,017020 0,090200 0,177593 0,082383 dem 0,109830 0,319920-2,211160 2,354277 0,376017 0,873625-0,051980 0,020861 0,424661 3305,611040 0,073381 1 0,170975 2,281814 0,120032 0,124246 0,868756 0,215435 0,767369 0,168724 0,402564-0,023848 0,496502 1,199373-0,319168 0,276472-0,184199 adm 0,077658 0,067177 0,032436 0,203813 0,001491 0,261244 0,165297 0,137348 0,334997 0,657038 0,180085 1 0,430491 0,374067 0,567092 0,032810 0,085203-0,050752 0,173896 0,382137 0,252036 0,026844-0,066205 -0,052608 0,127715 0,252743 0,077114 dem 0,098641 0,164517-1,314922 -1,337011 -0,005850 0,456455-0,009082 0,106458 0,219267 2572,008873 0,007640 0,145378 1 0,608792-0,011058 0,234724 0,027654 0,280278 0,196719 0,003906 0,055427 0,193027 0,247998 0,279310-0,146057 0,228002 0,032039 adm 0,123155 0,084349-0,206539 0,385963 0,003313 0,415082 0,188713 0,041319 0,941849 0,432911 0,165158 3,174573 1 0,683391 0,115748 0,162689 0,039433-0,040210 0,175004 0,553347 0,061404 0,027540-0,029560 -0,070974 0,254029 0,307753 0,195933 dem 0,082483 0,074661-0,149896 -1,397972 0,015729 0,024352 0,149246 0,024457 0,345916 1295,517081 0,130142 0,043325 0,193424 1-0,011715 0,056620-0,019817 0,090547-0,070068 0,039024 0,048882 0,170638 0,009042 0,007157 0,107794 0,003576 0,052118 adm 0,292720-0,081418 0,878078-0,170656 0,098817 0,220727 0,202612 0,096755 0,101391 -0,827977 0,294839 0,544665 0,101744 1 0,498627 0,132787 0,303312 0,197206 0,641673 0,163778 0,240553 0,029854 0,153614 0,126487 0,225124 0,359714 0,189873 dem 0,018620 0,046160-1,304206 1,557301 0,188006 0,471722-0,088197 0,044497 0,090222 218,704473 0,265313 0,030870-0,025742 -0,731205 1-0,001286 0,336593-0,007784 0,850821 0,141963 0,296314 0,256544-0,023213 -0,010881 0,045812 0,035773 0,011596 adm 0,077366 0,036404 0,099197 0,129140 0,002600 0,215834 0,119688 0,132079 0,234441 0,573675 0,201265 1,963148 0,231279 0,356298 1-0,010835 0,081280 0,024794 0,194692 0,292031 0,268651-0,007185 -0,134110 -0,066988 0,059900 0,179123 0,025893 dem 0,049723-0,068720 -0,747356 1,193279 0,004233-0,398191 0,044261 0,080932 0,344646 179,666913-0,033312 0,050058 0,074530 0,357465 0,024116 1-0,032740 0,149239 0,211793 0,075183 0,086462 0,034313 0,205253-0,035039 -0,063772 0,429700-0,066665 adm -0,000948 -0,067722 -0,002728 0,088820 0,026561 0,129828 0,185461 0,156492 0,228121 -0,015166 0,047988 0,252112 0,165091 0,205474 0,176559 1-0,002236 -0,157801 0,153279 0,565806 0,160149 0,060527 0,141738-0,104929 0,137038 0,664845 0,328044 dem -0,015291 0,056968-0,817681 -0,449212 0,190196 0,182763 0,105672 0,003876 0,272049 554,230012 0,003422 0,032574 0,038865-0,162887 0,041306 0,093434 1 0,183058-0,087531 0,070373 0,034460 0,163306 0,151621 0,128805 0,032737 0,055793 0,022098 adm 0,172527 0,100553 0,128629 0,072760 0,244861 0,131262 0,262634-0,002670 0,211315 0,231950 0,134253 -0,037421 0,100570 0,315691 0,375235 0,073261 1 0,317268-0,116946 0,360738 0,185313 0,009215 0,225988 0,034903 0,071635 0,193655 0,147595 dem 0,048727 0,039127-1,486621 -3,663688 0,043714 0,312447 0,187923 0,052368 0,242284 1361,233973-0,132971 0,040657 0,110523 0,922360 0,022127 0,056194 0,234716 1 0,268090 0,087862 0,072201 0,262216-0,028059 0,020940 0,037458 0,090398 0,110164 adm 0,134265 0,060349-0,838299 -0,036256 0,157508 0,055820 0,191993 0,025421 0,429892 -0,285281 0,164940 0,088557 0,071159 0,320911 0,316015 0,040661 0,495940 1 0,322768 0,471834 0,395249 0,121693 0,149664 0,276494 0,397675 0,248988 0,503577 dem 0,034191-0,004002 -0,223327 0,841612 0,154200-0,214347 0,123758 0,017015 0,078725 925,241226-0,004960 0,030725 0,029708 0,411417 0,060797 0,075785 0,238286 0,235529 1 0,252956 0,088545 0,255012-0,008018 0,211294 0,053747 0,043236 0,035983 adm 0,028494 0,010326-0,565739 -0,124337 0,125490 0,009595 0,203787 0,083212 0,179389 0,441864 0,122856 -0,193051 0,044098 0,094672 0,377383 0,027567 0,143720 0,160615 1 0,410639 0,279361-0,018763 -0,015484 0,110508 0,085465 0,180182 0,145332 dem 0,071209-0,055568 -0,058971 -0,199655 0,137469 0,323759 0,223476 0,009248 0,147099 808,505896 0,022920 -0,004462 0,062559 0,193992 0,083275 0,113518-0,020158 0,174311-0,054912 1 0,158175 0,388661-0,103645 -0,268279 0,267859-0,011512 0,155535 adm 0,062577 0,045496-0,582595 -0,005298 0,153457 0,042245 0,261195 0,044626 0,252322 -0,010876 0,136670 -0,362611 0,077931 0,242251 0,343842 0,105536 0,318050 0,471307 0,438560 1 0,551444 0,100577 0,162476 0,160623 0,304147 0,369652 0,679244 dem 0,075977 0,136948-0,307809 0,955918 0,113264 0,388979 0,133802 0,028571 0,303915 119,150107 0,164874 0,023510-0,003046 0,020232 0,110913 0,007765 0,378973 0,101462 0,174358 0,201787 1 0,308136-0,082014 -0,083618 0,115558-0,002206 0,105160 adm 0,070059 0,112787-0,376982 0,012203 0,154405 0,032772 0,242745 0,078995 0,227430 -0,155807 0,143000 -1,037960 0,063476 0,249427 0,302106 0,129146 0,442183 0,326424 0,387341 0,557284 1 0,301383 0,399790 0,165716 0,491115 0,515003 1,028087 dem 0,016759 0,125126-1,491278 1,812973 0,183361 0,474542 0,080539 0,002463 0,448231 -796,994766 0,194554 0,036652 0,088376-0,085472 0,116269 0,125281 0,501183 0,039953 0,451414 0,274140 0,315938 1 0,344260 0,495436 0,006997 0,034783-0,001099 adm 0,132015-0,076524 -0,483544 -0,065707 0,071923-0,063017 0,052597 0,035978 0,384951 -0,178872 -0,091147 -1,237325 -0,000404 0,024424-0,209179 0,133331 0,247931 0,214322-0,018366 -0,176043 0,016646 1 1,094774-0,077146 0,531761 0,383966 0,634003 dem 0,008607 0,071609-1,484527 3,154397 0,231213 0,029453 0,063503 0,005250 0,320176-1146,596275 0,102100 0,083788 0,051598 0,480809 0,052027 0,206040 0,673476 0,055794 0,261792 0,152457 0,333929 0,052672 1 0,247662-0,158549 0,087974-0,020298 adm 0,113567-0,025974 -0,057111 -0,094394 0,106475-0,038336 0,070148 0,020400 0,247588 -0,271855 -0,024113 -1,269115 0,030403 0,047038-0,071041 0,152716 0,301597 0,207834 0,100172 0,036231 0,088227 0,652075 1 0,027832 0,479014 0,364493 0,650743 dem 0,038197 0,044350-0,559700 -0,490446 0,109983 0,033051 0,099130 0,022677 0,118585 -664,887038 -0,009254 0,016629-0,000465 0,539194 0,002109 0,002824 0,566202 0,237555 0,151436 0,029494 0,051758 0,218027-0,018482 1 0,154490-0,051593 0,036376 adm 0,034926 0,153699-0,062131 0,122066 0,199380 0,053438 0,275720 0,139390 0,138490 -0,958862 0,132412 -0,418570 0,070496 0,117771 0,223577-0,038361 0,964470 0,172252 0,257016 0,178800 0,427158-0,012752 0,143831 1 0,449211 0,005610 0,285800 dem 0,038339-0,041952 0,049999 0,760035 0,006627 0,814167 0,130822 0,020633 0,108154 939,600788 0,118376 -0,058102 -0,079254 0,110928 0,033484-0,035085 -0,192017 -0,013467 -0,061422 0,177558-0,019955 0,220801-0,287559 -0,455795 1-0,031690 0,167624 adm 0,121699 0,068229-0,227131 0,168253 0,101297-0,011327 0,186214 0,053101 0,249289 -0,345310 -0,022980 -0,742101 0,132410 0,233615 0,110456 0,062973 0,373957 0,006637 0,229290 0,018452 0,310476 0,130335 0,265075 0,285228 1 0,317279 0,436809 dem 0,081872 0,011700 1,673932 2,298938-0,014794 0,637458 0,041557 0,033109 0,018304 726,453171 0,058143 0,006815 0,005106-0,742422 0,028469 0,109044-0,146224 -0,017758 0,112598 0,013354 0,227178-0,096627 -0,059702 -0,456377 0,117126 1 0,049432 adm 0,193004 0,049093-0,330332 0,223829 0,223657 0,196461 0,215468 0,154633 0,090064 -0,114094 0,069760 -0,563531 0,095549 0,384822 0,216411 0,165002 0,260160-0,045436 0,424796 0,136499 0,467485 0,074487 0,114374 0,084272 0,455188 1 0,490327 dem 0,016445-0,104548 0,636647 1,177390 0,087655 1,089706 0,123467 0,041411 0,064849 972,321514 0,046125 -0,076422 0,017688 0,260408 0,058051-0,139161 -0,061517 0,048340-0,110689 -0,020767 -0,182332 0,199357-0,168134 -0,761767 0,329928-0,191095 1 adm 0,097887 0,088046-0,359267 0,080463 0,154482 0,035941 0,214017 0,058848 0,231842 -0,209000 0,091991 -0,841011 0,084670 0,280989 0,240188 0,132606 0,389231 0,281184 0,383486 0,524517 0,639171 0,139859 0,234592 0,239334 0,538212 0,580472 1 go mt ms rj sp pr rs sc df pe pi rn se es mg to al ba ce ma pb ac ap am pa ro rr