Introdução à Pesquisa Operacional Fundamentos

Introdução à Pesquisa Operacional

2

Introdução à Pesquisa Operacional



Descrição:

 Técnicas e métodos matemáticos empregados para

auxiliar a tomada de decisões em sistemas organizacionais.



Emprego:

 Problemas que necessitam da especificação

quantitativa da forma de execução de operações e atividades.



Objetivo:

 Identificação da melhor solução possível (solução

Características Gerais



Maximização ou minimização de uma função

numérica.



Problema de Programação Linear (PPL):

 Alocação ótima de recursos para atender a um

objetivo.

 Recursos expressos por variáveis.

 Existência de restrições aos valores possíveis

para os recursos.

 Relações entre variáveis → funções lineares

Descrição Matemática



Conjunto de m restrições lineares (=, <=, >=)

em n variáveis.



Expressão:

Restrições a_i1x₁ + a_i2x₂ + … + a_inx_n {=, <=, >=} b_i,

i = 1,..,m

Variáveis x_j >= 0, j = 1,..,n

Método Gráfico

1)

Determinar a região de viabilidade

1) Restrições como igualdades

2) Identificar, mediante teste, o semi-plano

correspondente



Calcular o vetor gradiente grad(z)

1) Calcular as derivadas parciais em relação a cada

variável

Método Gráfico

3)

Deslocar a reta-objetivo no sentido de grad(z)

para maximização (ou -grad(z) para

minimização), até encontrar o ponto da região

de viabilidade que satisfaz ao problema.

4)

Determinar as coordenadas do ponto como a

10

Solução Gráfica: Construindo o conjunto de possibilidades

Conjunto

de Possibilidades

12

2

x

1

2

x

Solução Gráfica: Definindo as Curvas de Nível do Objetivo

L

x

x

L

x

x

+

=

⇒

=

−

+

1 2

2

1

4

4

Para cada valor de L tem-se uma reta no plano (x2

vs x1).

Dado um valor de L é possível traçar um lugar

geométrico (uma reta) onde as várias

12

Solução Gráfica: Desenhando as Curvas de Nível do Objetivo

1

x

2

x

0

5

=

L

7

=

L

9

=

L

Solução Gráfica: Reunindo os componentes e resolvendo

Conjunto

de Possibilidades

12

2

x

13

=

L

A solução



Que características permitiram a solução?

 O conjunto de possibilidades era convexo.

 Um conjunto é convexo quando toda

combinação convexa de dois elementos dele pertence a ele.

 Uma combinação convexa de dois elementos,

x e y é um terceiro elemento z tal que: z=a.x+(1-a).y onde 0 ≤ a ≤ 1.

 É possível definir combinação convexa de n

Valores p/ Restrição 1

Casos onde a solução não existe



_{Conjunto de Possibilidades é vazio}

Não há solução compatível



_Exemplo:

2

x

16

Conjunto de Possibilidades

Casos onde a solução não existe



_{A solução é ilimitada}

Caso de Infinitas Soluções

Conjunto

de Possibilidades

2

x

As soluções são

combinações lineares dos pontos

extremos

Método Simplex



Forma:

– z = Min{c

1x1 + c2x2 + … + cnxn},

 s.a ∑a_ijx_j = b_i,  j = 1...n,  i = 1...m,

 b_i>= 0,

● x

O Método Simplex

1)

Selecione para entrada na base a variável

não-básica com custo relativo que melhore o

valor da função objetivo. Se não houver, a

solução já é ótima.

2)

Selecione para saída da base a variável

básica com menor valor da razão b

/a

, com a

j

> 0. Se não houver a

> 0, o PPL tem

solução ilimitada.

Forma Canônica



Existe uma submatriz identidade de ordem m

→ as variáveis associadas compõem uma

solução viável básica

(SVB).



As variáveis são divididas em dois grupos:

 Variáveis básicas (ou dependentes)

 Variáveis não básicas (ou independentes)



Premissas:

 Valores iniciais das variáveis não básicas: 0

 Valores iniciais das variáveis básicas: o valor da

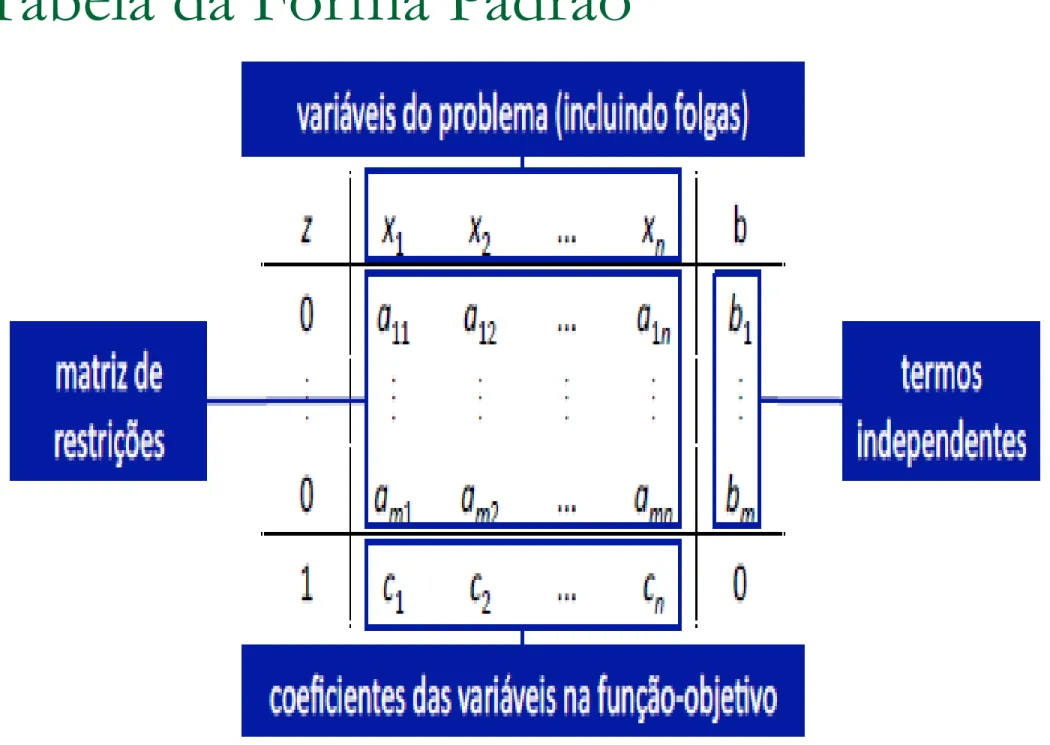
Modelo Padrão

Todo modelo de programação linear pode ser posto na forma padrão que não é limitativa.

Um problema de minimização, por exemplo, pode ser resolvido pela maximização do negativo da

função objetivo.

Restrições de ≥ podem ser multiplicadas por -1 para se tornarem restrições padrão.

Variáveis que possam assumir qualquer valor e não apenas valores positivos podem ser

Técnica de Resolução

 Passo 1: Introduzir as variáveis de folga; uma para cada

desigualdade.

 Passo 2: Montar um quadro para os cálculos, colocando os

coeficientes de todas as variáveis com os respectivos sinais e, na última linha, incluir os coeficientes da função objetivo transformada.

 Passo 3: Estabelecer uma solução básica inicial, usualmente

Técnica de Resolução

 Passo 4: Como próxima variável a entrar na base, escolher

a variável não básica que oferece, na última linha, a maior contribuição para o aumento da função objetivo (ou seja, tem o maior valor negativo).

 Se todas as variáveis que estão fora da base tiverem

coeficientes nulos ou positivos nesta linha, a solução atual é ótima.

 Se alguma dessas variáveis tiver coeficiente nulo, isto

significa que ela pode ser introduzida na base sem

26

Técnica de Resolução

 Passo 5: Para escolher a variável que deve deixar a base,

deve-se realizar o seguinte procedimento:

 a) Dividir os elementos da última coluna pelos

correspondentes elementos positivos da coluna da variável que vai entrar na base. Caso não haja elemento algum

positivo nesta coluna, o processo deve parar, já que a solução seria ilimitada.

 b) O menor quociente indica a equação cuja respectiva

variável básica deverá ser anulada, tornando-se variável não básica.

 Passo 6: Usando operações válidas com as linhas da matriz,

transformar o quadro de cálculos de forma a encontrar a nova solução básica. A coluna da nova variável básica deverá se tornar um vetor identidade, onde o elemento 1 aparece na linha correspondente à variável que está sendo anulada.

Operação na Tabela Canônica

Problema Dual





"A cada modelo de programação linear,

contendo coeficientes a

ij

, b

e c

, corresponde

um outro modelo, denominado Dual, formado

por esses mesmos coeficientes, porém

Exemplos

 _{1) PRIMAL}  Max L = 4 x

1 +x2

 s. a 9x

1 + x2 ≤ 18

 3x

1 +x2 ≤ 12

 x

1 e x2 ≥ 0

 DUAL Min D = 18y₁ +12y₂  s. a 9y

1 + 3y2 ≥ 4

 y₁ +y₂ ≥ 1

 y

1 e y2 ≥ 0

 2) PRIMAL

 Max P = 5 x₁ + 2x₂

 s. a x

1 ≤ 3 y1 x2 ≤ 4 y

2

 x

1 + 2x2 ≤ 9 y3

 DUAL Min D = 3y

1 + 4y2 + 9y₃

 s.a. y

1 + y3 ≥ 5  y

•

“Processo de elaboração de um

modelo

de um

sistema

real (ou hipotético) e a

condução de experimentos

com a

finalidade de

entender

o comportamento

de um sistema ou

avaliar

sua operação”

•

(Shannon, 1975)

•

“O princípio básico é simples. Analistas

constroem

modelos do sistema

de interesse,

escrevem programas

destes modelos e utilizam

um computador para inicializar o comportamento

do sistema e submetê-lo a diversas políticas

operacionais. A melhor política

deve ser

selecionada.

”

•

(Pidd, 2000)



_{Captura o comportamento do}

_{sistema real}

_{Permite a análise pela pergunta:}

●

_{“E se...?”}



_{Capaz de representar}

_{sistemas complexos}

_de

natureza

dinâmica e aleatória



_{Limitações:}

– Podem ser de construção difícil

– Não há garantia do ótimo



_Sistemas

_dinâmicos

_{: os estados se}

alteram com o tempo



_Sistemas

_discretos

_{: os atributos dos}

estados só mudam no tempo discreto



_{Determinística}

_ou

_Estocástica

 _{Analisar um novo sistema antes de sua implantação}

 _{Melhorar a operação de um sistema já existente}

 _{Compreender melhor o funcionamento de um sistema}

 _{Melhorar a comunicação vertical entre o pessoal de}

operação

 _{Confrontar resultados}

 _{Medir eficiências}

Quando Simular?

Problema Ferramentas Resultados

Planilhas

Calculadora

Lápis e Papel

Geração de Números Aleatórios

●

Métodos Congruentes

– _{A maioria dos métodos usados hoje em dia}

são variações do chamado Método

Congruente Linear, cujos pontos básicos foram propostos por Lehmer em 1951. Neste método os números aleatórios,

44

Gerador de Números Aleatórios

● Na formula anterior, a é o termo multiplicativo, c é o termo

aditivo.

● Se c≠0, o gerador é chamado de misto (pouco usado na

atualidade porque os números gerados tendem a ter problemas para passar os testes de aleatoriedade).

● Se c = 0, o gerador é chamado de multiplicativo.

● Se a = 1, o gerador é chamado de aditivo.

● Um dos requisitos é que a sequência seja intuitivamente

aleatória. Então deve-se escolher as constantes a e m tais que:

– _{1.A sequência seja intuitivamente uma amostra de}

números uniformes[0,1)

– _{2.Para uma semente, toda a sequência gerada se}

Engenheiro de Produção

Jr

Março 2010

 As técnicas de simulação são ferramentas muito utilizadas

na gestão de operações, entretanto, apresentam como

DESVANTAGEM

 (A) a impossibilidade de testar cenários diferentes para um

mesmo problema operacional.

 (B) a necessidade de interferência direta nos sistemas

reais, afetando as operações do dia a dia.

 (C) a inadequação para estudar situações complexas do

mundo real com grande quantidade de variáveis.

 (D) o uso de abordagens iterativas e de tentativa e erro que

Engenheiro de Produção

Junior

Edital 2008

 Dentre as finalidades da simulação, destaca-se:

 (A) descrever o comportamento de sistemas de forma

consistente e rápida.

 (B) impedir que variáveis dinâmicas mudem de estado, o que

geraria um novo sistema.

 (C) otimizar sistemas não convergentes.

 _{(D) reproduzir o comportamento de qualquer tipo de sistema,}

inclusive os não estruturáveis.

 (E) simplificar variáveis em sistemas complexos, reduzindo a

 _{(A) f(XN, XN-1, K, L) = K.XN + L, tem-se a congruência mista.}  (B) f(XN, XN-1, K, L) = K.XN / L, tem-se a congruência mista.

 (C) f(XN, XN-1, K, L) = K.(XN + L), tem-se a congruência multiplicativa.  _{(D) f(XN, XN-1, K, L) = K.XN + L.XN-1, tem-se a congruência mista.}

Analista de Pesquisa Operacional 2010

As técnicas de simulação são muito importantes em uma grande variedade de projetos quando estes apresentam cálculos muito complexos ou experimentos reais muito dispendiosos. Na base da simulação, tem-se a necessidade de geração de números pseudoaleatórios, quando as duas principais preocupações são: (1) um possível número deve ter a mesma probabilidade de ocorrer que qualquer outro dentre os demais possíveis números e (2) deve existir independência entre as ocorrências, isto é, a probabilidade de ocorrência de um número não deve ser afetada pelas eventuais ocorrências dos demais possíveis números.

 Um serviço de atendimento, que se inicia às 9 h, tem uma única fila

para atendimento por um único servidor. O intervalo (em minutos) entre a chegada de dois clientes é uma variável aleatória uniformemente distribuída entre 0 e 4, e o tempo (em minutos) de atendimento pelo servidor é uma variável aleatória distribuída uniformemente entre 5 e 10. No quadro a seguir, é apresentado o resultado de uma simulação com essas variáveis.

 Por exemplo, o primeiro cliente chega às 9 h 2 min, é atendido

durante 5 min e, portanto, sai do sistema às 9 h 7 min. O segundo cliente chega 1 min após a chegada do primeiro cliente, e o servidor irá consumir 10 min em seu atendimento. O cliente que aguardará na fila mais tempo para ser atendido irá esperar

 _{(A) 13 min (B) 14 min (C) 15 min (D) 16 min (E) 17 min}

Analista de PO 2010

CLIENTE INTERVALO ATENDIMENTO

1 2 5

2 1 10

3 1 6

Definições

●

Teoria da Decisão

–

_{Estudo dos paradigmas subjacentes à}

decisão e seus fundamentos analíticos.

●

Decisão

–

_{Processo que leva, direta ou}

Tipos de Decisão

● Programadas ou Estruturadas

– _{Decisões adotadas para problemas bem}

compreendidos, altamente estruturados, rotineiros, repetitivos e passíveis de adoção de procedimentos e regras sistemáticos.

– _{Ambiente usual: nível operacional.}

● Não Programadas ou Não Estruturadas

– _{Decisões adotadas para problemas não bem}

compreendidos, mal estruturados, singulares e

inadequados para adoção de procedimentos e regras sistemáticos.

Condicionantes da Decisão

●

decisão em condições de certeza

– _{ocorre quando há total conhecimento de todos}

os estados da natureza do processo decisório.

●

decisão em condições de risco

– ocorre quando não são conhecidas as

Condicionantes da Decisão

● decisão em condições de incerteza ou em

condições de ignorância

– ocorre quando não se obtiveram informações e dados

sobre as circunstâncias do processo decisório ou em relação à parcela dessa situação.

● decisão em condições de competição ou em

condições de conflito

– _{ocorre quando a estratégia e a situação em si do}

Situações de

Método de Daft para

Modelo Racional

●

Monitoramento do ambiente de decisão

Definição do problema

●

Especificação dos objetivos da decisão

Diagnóstico do problema

●

Desenvolvimento de soluções alternativas

Avaliação das alternativas

●

Escolha da melhor alternativa

56

Modelos de Tomada de Decisão

●

Racionalidade Limitada – Método de

Simon:

– _{Ambiente restrito em informações e capacidades de}

processamento.

– _{Construção de modelos simplificados → Limitação}

da Racionalidade.

– _{Participação racional e consciente, em ambiente}

com alternativas parcialmente racionais, em virtude da seleção de critérios de avaliação.

– _{Decisões satisfatórias, mas não ótimas.}

– _{Processos de decisão intuitivos, com emprego de}

Teoria dos Jogos

Componentes Básicos

 _{É composto de:}

 _{jogadores (N): aqueles que tomam decisões}

 estratégias (C_i): possível ação do jogador

 funções de utilidade (u_i): retorno auferido pelo jogador

quando o conjunto de jogadores emprega a estratégia C = {C_i}_iЄN



G = ( N,{C

}

,{U

(C)}

)

Teoria dos Jogos

Vantagens

 _Fiani

 _{Entendimento teórico do processo de decisão de agentes}

que interagem, a partir da compreensão da lógica da situação na qual se encontram

 _{Desenvolvimento da capacidade de raciocinar}

estrategicamente, explorando todas as possibilidades de interação (inclusive as não-intuitivas)

 _{Habilidade para descrever não só atores individuais e}

Teoria dos Jogos

Representação Matricial

• _{Combinação de estratégias determina o retorno de}

A B C

A (2, 2) (0, 0) (-2, -1)

B (-5, 1) (3, 4) (3, -1)

Jogador 1

Jogador 2

Retorno para

Jogador 1 Retorno para Jogador 2 Estratégias do

Jogador 1

Teoria dos Jogos

Dúvida

–

_{Como os jogadores vão se comportar}

diante de determinado jogo, ou seja,

Teoria dos Jogos

Equilíbrio de Nash

–

_{Ponto em que nenhum jogador pode}

aumentar seu retorno alterando,

unilateralmente, sua estratégia

Teoria dos Jogos

Teorema Geral do Equilíbrio (Nash,

1951)

–

_{Para todo jogo finito na forma}

estratégica, existe ao menos um

equilíbrio de Nash,

puro

ou

misto

Teoria dos Jogos

Ótimo de Pareto

–

_{É um ponto tal que nenhum}

jogador consegue aumentar seu

próprio retorno (mudando

unilateralmente de estratégia) sem

prejudicar algum outro jogador.

»

Medida de eficiência na

Teoria dos Jogos

Classificação

–

_{Muitas formas de classificação – exemplos:}

_{Cooperativos x Não-Cooperativos}

_coalizões



_{Estáticos x Dinâmicos}

_{adoção variável de estratégias e funções objetivo}



_{Soma-Zero x Soma-Não Zero}

Teoria dos Jogos

Jogos de Soma-Zero



_{Caso abordado nos trabalhos iniciais}



_{Situações em que dois indivíduos estão}

em oposição pura entre si, ou seja, o

ganho de um jogador

é sempre

a perda do

outro

.



_{Solução intuitiva}

_{Única, com a maximização do retorno para}

cada jogador

Teoria dos Jogos

Dominância

L M R

T -2 -1 4

B 3 2 3

Jogador 1

Jogador 2

Existência de estratégia E1 para a qual o retorno é

Teoria dos Jogos

Ponto de Sela

A

B

D

A

12

-1

0

C

5

2

3

D

-16

0

-1

Jogador 1

Jogador 2

Um resultado é um ponto de sela se for, ao

mesmo tempo, menor ou igual a qualquer valor de sua linha e maior ou igual que qualquer valor em

Teoria dos Jogos

Jogo Estratégico Misto

Γ

_{= ( N,}

∆

_(C

_i

_{), U}

_{(c) )}

_{A estratégia (e a distribuição}

de probabilidades) deve ser escolhida de tal forma que o

retorno seja o mesmo, independentemente da

estratégia do outro jogador

_{O objetivo é provocar ao}

oponente a maior perda (ou, ao menos, o menor ganho)

C D

A 4 0

B -5 3

1/4 3/4

Retorno com a estratégia A = 1/4(4) + 3/4(0) = 1

Teoria dos Jogos

Jogos de Soma Não-Zero



Também chamado de não estritamente

competitivo

_{Retornos não obrigatoriamente opostos} ⇒

margem à cooperação entre agentes

A B

A 5, 4 2, 0

Teoria dos Jogos

Teorema do Minimax (Von Neumann)



_{Todo jogo de soma-zero onde os agentes}

empregam estratégias mistas possui um

ponto de equilíbrio – solução ou valor do

jogo

_{Possibilidade de várias soluções com}

Definições – PERT-CPM

 PERT – Program Evaluation and Review

Technique

 CPM – Critical Path Method

● Técnicas de planejamento e controle de projetos

● Empregam os conceitos de grafos (redes) para

Construção da Rede

● Nós: atividades

● Arcos: relações de precedência

Perguntas Relevantes

●

Tempo requerido para completar o projeto

Identificação das atividades-gargalo

– críticas para não haver atrasos na execução

Caminho Crítico

● Caminho:

– qualquer rota seguindo os arcos, de INÍCIO até

FIM.

● Comprimento do Caminho:

– _{soma das durações das atividades sobre o}

caminho.

Programação de Atividades

● Determinação dos Tempos de Início e de Término de uma

Atividade

● Emprego de 4 variáveis:

– _{ES (Earliest Start): tempo inicial mais cedo}

– _{EF (Earliest Finish): tempo final mais cedo}

– _{LS (Last Start): tempo inicial mais tarde}

Regras de Programação de Atividades

●

Regra do ES = maior EF das atividades

precedentes

●

Regra do EF=ES + Duração D

●

Regra do LF = menor LS das atividades

sucessoras

Cálculo de Folgas em Atividades

● Comentários Gerais

– _{ES: calculado de INICIO para FIM (forward pass)} – _{LF: calculado de FIM para INICIO (backward pass)}

– _{LF – EF = LS – ES = folga na execução da atividade }

atraso na atividade sem comprometer a duração do caminho crítico

Incerteza na Duração de uma Atividade

●

Existência de fatores de variação



inserção de

incertezas sobre a duração de cada atividade.

●

Versão original PERT: 3 tipos de estimativas

–

Mais provável (m)

Otimista (o)

–

_{Pessimista (p)}

Aproximações para a

Duração de Atividades

●

Média = (o + 4m + p)/6

●

Variância = [(p-o)/6]

●

Possibilidades Adquiridas:

–

Construção do cenário de pior

caso

–

Probabilidade de ocorrência de

Probabilidade de Ocorrência de

Cenário

●

Caminho Crítico Médio

– _{Caminho crítico em que a duração de cada}

atividade é a duração média

– _{Atividades estatisticamente independentes}

●

Duração total do projeto

–

_{distribuição normal}

– Cálculo do número de desvios padrão de

Modelo CPM

●

Objetivo: controlar os custos do projeto.

– _{Ideia básica: se colocarmos mais recursos na}

execução de uma atividade, conseguiremos fazê-la mais rapidamente, embora

aumentando o seu custo.

●

Cada atividade possui 2 estimativas de

Relação entre Custos/Durações

Normal e Acelerado

 Relação linear entre modelos normal e acelerado

 Custo incremental: tangente do ângulo k

 Objetivo: diminuir a duração do projeto minimizando o