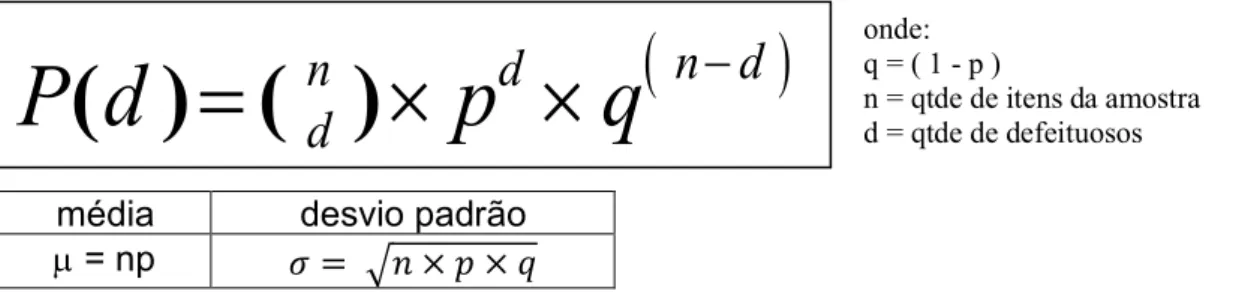CONTROLE ESTATÍSTICO DO PROCESSO

(1)

CONTROLE ESTATÍSTICO DO PROCESSO

ATRIBUTOS

Nesta metodologia a avaliação é feita através da constatação da existência ou não do defeito. Essas cartas são

excludentes, pois a unidade defeituosa exclui a possibilidade de ser perfeita e, exaustivas pois não existe outra

alternativa a não ser “bom” ou “ruim”.

Quando utilizar controle por atributos?

• Quando a utilização de uma escala contínua for impossível ou então economicamente inviável.

Ex.: existência ou não de manchas numa peça pintada.

• Quando o número de características a controlar em cada unidade for muito elevado.

Ex.: total de defeitos em um conjunto montado.

• Quando houver condições para utilização de calibradores tipo “P - NP”

Desta forma os produtos poderão ser considerados “bons” ou “ruins”, em relação à quantidade de defeitos

constatados na amostra ou então nas unidades apresentadas.

Dependendo do objetivo a ser alcançado podemos utilizar 4 tipos de gráficos por atributos, a saber:

ATENÇÃO!

Cuidados a serem tomados nos critérios de năo conformidades

a) Superfície deve ser isenta de falhas

Ø

O que é falha ?

Þ

_{Como medi-la ?}

b) A pintura deve estar conforme padrão e sem manchas visíveis

Ä

Com que grau de conformidade ?

i

Como medi-la ?

$

Visível por quem ?

(2)

m.a.perissinotto –

CEPA

.

-

2 GRÁFICO DA FRAÇÃO DEFEITUOSA

Carta... “p”

GRÁFICO DO NÚMERO DE DEFEITUOSAS

Carta... “np”

GRÁFICO DO NÚMERO DE DEFEITOS POR UNIDADE

Carta...“u”

GRÁFICO DO NÚMERO DE DEFEITOS POR AMOSTRA

Carta... “c”

LEMBRETE PARA SELECIONAR UMA CARTA DE ATRIBUTO:

UNIDADES NÃO

CONFORME

NÃO CONFORMIDADES

( DEFEITOS )

“p”

“u”

Mais

complexa,

adapta-se

a

porcentagem e pode ser usada com

tamanho de amostra variável.

( PROPORÇÃO )

“np”

“c”

Simples, mas exige tamanho de amostra

constante.

(3)

GRÁFICO DA FRAÇÃO DEFEITUOSA ( p )

Carta... “p”

Conforme estudos matemáticos trata-se de uma Distribuição Binomial, onde a probabilidade de encontrarmos “ d ” defeituosas em uma amostra de fração defeituosa “ p ” , será:

A Distribuição Binomial se aproxima da Distribuição Normal, quando os valores de “n” são grandes.

Um tamanho de amostra “grande”, pode significar um longo período de operação do processo, para minimizar esse problema se adota, para definição do tamanho de amostra, um dos dos conceitos:

Conceito Fraco ®_np³_{5 Conceito Forte}®_np³₈

Na variável amostral obtemos:

fração defeituosa média

desvio padrão

_{𝑛" =}

∑ %

&

ð

Q = Qtde de amostras

𝑝 =

𝑑

_{𝑛 → 𝑝 ̅ =}

_{∑ 𝑛}

∑𝑑

_{𝜎 = -}

𝑝̅ × (1 − 𝑝̅)

𝑛"

A construção das cartas “ p ” , obedece o princípio das cartas variáveis, com os limites de ± 3 s_.

CÁLCULO DOS LIMITES

ATENÇÃO:

Se a variação do tamanho das amostras for mantido dentro de ± 25% do tamanho médio das amostras o cálculo dos limites será único para todas as amostras, caso contrário, para as amostras fora desse percentual deverão ter seus limites recalculados

(

)

P d

( ) ( )

=

_d

n

_´

p

d

_´

q

n d

-onde: q = ( 1 - p )

n = qtde de itens da amostra d = qtde de defeituosos

média

desvio padrão

µ

= np

𝜎 = 3𝑛 × 𝑝 × 𝑞

𝜎

5

= -

𝑝̅ × (1 − 𝑝̅)

_𝑛

5

𝑳𝑺𝑪 = 𝒑: + 𝟑 × -

𝒑:(𝟏 − 𝒑:)

_𝒏:

𝑳𝑴 = 𝒑:

𝑳𝑰𝑪 = 𝒑: − 𝟑 × -

𝒑:(𝟏 − 𝒑:)

_𝒏:

onde:

ni = valor da amostra considerada, ou seja as amostragem que

(4)

(5)

ATENÇÃO

IDENTIFICAR NO GRÁFICO QUAIS OS PONTOS DE ATENÇÃO

( idêntico aos “semancóis” do CEP-V7 e CEP-V8)

CÁLCULO DOS PARÂMETROS DA CARTA “ p “

(pág. anterior)

1

A) B) C)

2

A) B) C) D)

3

A) B)-

C)-

4

A)- B)-

𝑳𝑺𝑪 𝒐𝒖𝑳𝑰𝑪 = 𝒑: ± 𝟑 × -𝒑: × (𝟏 − 𝒑:)_𝒏

𝒄𝒐𝒏𝒔𝒊𝒅𝒆𝒓𝒂𝒅𝒐=

5

n=

352

𝟑 × K

𝒑:×(𝟏L𝒑:)

𝟑𝟓𝟐 =

0,0306

𝑳𝑺𝑪 = 0,0684

DATAS:

8

𝑳𝑰𝑪 = 0,0072

6

n=

𝟑 × K𝒑:×(𝟏L𝒑:)= _{𝑳𝑺𝑪 =}

DATAS: 𝑳𝑰𝑪 =

7

n=

𝟑 × K𝒑:×(𝟏L𝒑:)=

𝑳𝑺𝑪 =

8

n=

𝟑 × K𝒑:×(𝟏L𝒑:)=

𝑳𝑺𝑪 =

𝒑: =∑ 𝒅_{∑ 𝒏 =} % 𝒑ç𝒔 𝑶𝑲 = (𝟏 − 𝒑:) 𝒏: =∑ 𝒏_{𝑸 =}

𝒑: × (𝟏 − 𝒑:) = 𝒑: × (𝟏 − 𝒑:)

𝒏: = -𝒑: × (𝟏 − 𝒑:)

𝒏: = 𝟑 × -𝒑: × (𝟏 − 𝒑:)𝒏: =

𝑳𝑴 = 𝒑: =

𝑳𝑺𝑪 = 𝒑: + 𝟑 × -𝒑: × (𝟏 − 𝒑:)_𝒏: =

𝑳𝑰𝑪 = 𝒑: − 𝟑 × -𝒑: × (𝟏 − 𝒑:)_𝒏: =

(6)

CEPA

.

-

6

EXEMPLOS:

1- Um procedimento de controle de qualidade foi planejado para garantir um máximo de 10% de itens defeituosos na produção. A cada 15 minutos uma amostra de 60 peças é retirada e em havendo mais de 15% de defeituosos, para-se a produção para verificações. Qual a probabilidade de uma parada?

a) Itens defeituosos → p = 0,1 ( 10%)

b) Itens não defeituosos → q = (1-p) = 0,9 ( 90%)

c) Amostra → n = 60 peças

Havendo mais de 15% de 60, ou seja, havendo mais de 9 (LSC) peças defeituosas interrompe-se a produção.

É preciso verificar a aproximação da binomial pela normal, então

:

np>5

è

60*0,1 = 6

aplica-se a aproximação.

Para haver mais de 9 peças defeituosas

:

2- Em um 𝐺𝐶 𝑝, com amostragem n=50, obteve-se LSC= 0,3697 e LIC=0,0303, qual a probabilidade de aprovação de um lote

com fração defeituosa de 0,40?

1º passo:

Calculamos o desvio padrão do novo lote -

2º passo:

Calculamos Z, para na tabela encontrarmos Pz –

𝑍

Z

=

𝐿𝑆𝐶 − 𝜇

_𝜎

Z

=

9 − 6

2,32379 =

2,32379 = 1,29

3 𝜇

Z

= 𝑛𝑝 → 60 × 0,1 = 6

𝜎

Z

= 3𝑛 × 𝑝 × 𝑞 → 360 × 0,1 × 0,9 → 35,4 = 2,324

𝑍

Z

= 1,29 → 𝑝𝑜𝑟 𝑡𝑎𝑏𝑒𝑙𝑎 → 𝑃

n

= 0,0985 → 9,85%

0,4 0,3697

𝜎 = -

𝑝̅ × (1 − 𝑝̅)

_𝑛

= -

0,40 × (1 − 0,40)

₅₀

= -

0,4 × 0,60

₅₀

= 0,0693

(7)

CARTA DO NÚMERO DE DEFEITUOSOS - (np)

CARTA.... “np”

A carta ( np ) é semelhante a carta “ p ” , somente modifica a escala das ordenadas. Essa modificação se dá com a multiplicação dos valores por “n”.

A escolha, de utilização, da carta “ np ” , se dá quando:

a) for mais significativo ou mais simples relatar o número total de defeituoso, ou

b) por qualquer motivo se deseja manter o tamanho da amostra ( n ) constante

CÁLCULO DOS LIMITES:

𝒑 =

𝒅

_{𝒏 → 𝒏𝒑 = 𝒅}

𝒑: =

∑ 𝒅

_{∑ 𝒏}

𝒏𝒑: =

∑ 𝒅

_𝑸

𝝈 = 3𝒏𝒑:(𝟏 − 𝒑:)

Q = Qtde de amostras

𝑳𝑺𝑪 = 𝒏𝒑: + 𝟑 × 3𝒏𝒑:(𝟏 − 𝒑:)

𝑳𝑴 = 𝒏𝒑:

𝑳𝑰𝑪 = 𝒏𝒑: − 𝟑 × 3𝒏𝒑:(𝟏 − 𝒑:)

onde:

d = número de defeituosas na amostra n = Qtde de itens da amostra p = fração defeituosa da amostra

onde:

S_{d = Total de defeituosas de toda a amostragem}

S_{n = Total de peças da amostragem (Q x n)}

(8)

m.a.perissinotto -

CEPA

-

8

Média = LSC = LIC =

Amostra 6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

6

2

Número (np)

2 5 4 3 3 6 5 0 7 5 4 1 2 3 6 3 8 4 4 4 6 4 2 3 7

Fração (p, u)

Data 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Tamanho Médio da Amostra 62 / Frequência 1 hora

0

1

2

3

4

5

6

7

8

9

10

11

(9)

CÁLCULO DOS PARÂMETROS DA CARTA “np”

(pág. anterior)

1

𝒏𝒑: =∑ 𝒅_{𝑸 =}

2

𝒑: =∑ 𝒅_{∑ 𝒏 =}

3

% de pçs OK =

4

𝒏𝒑: × (𝟏 − 𝒑:)

5

3𝒏𝒑: × (𝟏 − 𝒑:)

6

𝟑 × 3𝒏𝒑: × (𝟏 − 𝒑:)

7

𝑳𝑴 = 𝒏𝒑: =

𝑳𝑺𝑪 = 𝒏𝒑: + 𝟑 × 3𝒏𝒑:(𝟏 − 𝒑:) =

8

𝑳𝑰𝑪 = 𝒏𝒑: − 𝟑 × 3𝒏𝒑:(𝟏 − 𝒑:)=

ATENÇÃO

IDENTIFICAR NO GRÁFICO QUAIS OS PONTOS DE ATENÇÃO

( idêntico aos “semancóis” da CEP-V)

EXEMPLO:

1-Utilizando um

𝐺𝐶 𝑛𝑝

, com 25 amostras de 50 itens cada amostra, obteve-se

∑ 𝑑 = 325

. Calcular os

limites de controle.

𝑝̅ =

∑ 𝑑

_{∑ 𝑛 =}

_{25 × 50 =}

325 _{1250 = 0,26 → 𝑛𝑝̅ = 50 × 0,26 = 13}

325

𝐿𝑆𝐶 = 13 + 3 × 313 × (1 − 0,26) → 13 + 3 × √13 × 0,74 → 13 + 3 × 3,10 → 13 + 9,10 → 22,3

𝐿𝑆𝐶 = 𝑛𝑝̅ + 3 × 3𝑛𝑝̅ × (1 − 𝑝̅)

𝐿𝐼𝐶 = 𝑛𝑝̅ − 3 × 3𝑛𝑝̅ × (1 − 𝑝̅)

(10)

CEPA

.

-

10 CARTA DO NÚMERO DE DEFEITOS POR UNIDADE-(u)

Carta.... “u”

Nas cartas anteriores a orientação era para produtos “bons” ou “ruins”, com uma determinada característica de controle. Agora a orientação é encontrar os números de defeitos nas unidades do produto.

Uma unidade de produto pode apresentar mais de um defeito.

Exs.:

-quantidade de defeitos em cada 10 metros de fio ( isolação fina ) -quantidade de defeitos em uma placa de vidro ( bolhas )

-quantidade de defeitos em cada unidade pintada ( automóvel )

Portanto a unidade de produto pode ser peça, comprimento, área, etc., ou seja, a orientação é avaliar com que frequência ocorrem os defeitos em cada unidade do produto considerado.

Segundo os matemáticos trata-se de uma Distribuição de Poisson, também chamada “lei dos eventos raros”, a ocorrência do evento surge com grande número de oportunidades porém com pequena probabilidade.

Lembrete:

CÁLCULO DOS LIMITES:

𝒖 =

_𝒏

𝒄

onde: c = número de defeitos por unidade

n = tamanho da amostra

𝒖: =

_{∑ 𝒏}

∑ 𝒄

onde: S_{c = número total de defeitos de todas as amostras} S_{n = número total de produtos inspecionados} Média amostral → n" =∑ n_Q

𝐷𝑒𝑠𝑣𝑖𝑜 𝑃𝑎𝑑𝑟ã𝑜 → 𝜎 = -𝑢"_𝑛"

A

TENÇÃO:

Se a variação do tamanho das amostras for mantido dentro de ± 25% do tamanho médio das amostras o cálculo dos limites será único para todas as amostras, caso contrário, para as amostras fora desse percentual deverão ter seus limites recalculados

𝜎

₅

= -

_𝑛

𝑢"

5

𝑳𝑺𝑪 = 𝒖: + 𝟑 × -

𝒖:

_𝒏:

𝑳𝑴 = 𝒖:

𝑳𝑰𝑪 = 𝒖: − 𝟑 × -

𝒖:

_𝒏:

onde:

ni = valor da amostra considerada, ou seja as amostragem que estiverem acima ou abaixo dos 25% do tamanho

(11)

Amostra

8 8 9 8 8 7 7 8 8 8 7 8 9 9 8 8 4 8 ₁₂ ₁₂ ₁₆ 8 4 4 8

##

Número (

c

)

8 ₁₇

₁₈

₁₅

₂₃

9 ₁₉

6 ₁₄

₁₇

₁₃

₁₅

₁₆

₂₂

₁₃

₁₀

₁₄

9 ₂₃

₂₁

₅₁

₃₁

3

8 ₁₂

##

Fração (

u

₎

1,00

2,13

2,00

1,88

2,88

1,29

2,71

0,75

1,75

2,13

1,86

1,88

1,78

2,44

1,63

1,25

3,50

1,13

1,92

1,75

3,19

3,88

0,75

2,0

1,5

Data

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Tamanho Médio da Amostra = 8 cxs / Frequência = Diária Média = LSC = LIC =

CARTA u

0,00

1,00

2,00

3,00

4,00

5,00

1

(12)

CEPA

.

-

12 CÁLCULO DOS PARÂMETROS DA CARTA “u”

(pág. anterior)

1

A) B)

2

A) B) C)

3

𝑳𝑴 = 𝒖: =

𝑳𝑺𝑪 = 𝒖: + 𝟑 × -𝒖:_{𝒏: =}

4

𝑳𝑰𝑪 = 𝒖: − 𝟑 ×

-𝒖: 𝒏: =

5

𝒏𝟏,𝟐𝟓%= 𝒏: × 𝟏, 𝟐𝟓 = 𝒏𝟎,𝟕𝟓= 𝒏: × 𝟎, 𝟕𝟓 =

6

𝑳𝑺𝑪 𝒐𝒖𝑳𝑰𝑪 = 𝒖: ± 𝟑 × -_𝒏 𝒖:

𝒄𝒐𝒏𝒔𝒊𝒅𝒆𝒓𝒂𝒅𝒐=

7

n=

4

𝟑 × K

𝒖:

𝟒=

2,119

𝑳𝑺𝑪 =

4,114

DATAS:

17, 23, 24

𝑳𝑰𝑪 =

(-0,12)

= 0

8

n=

𝟑 × K𝒖:= 𝑳𝑺𝑪 =

DATAS: 𝑳𝑰𝑪 =

9

n=

𝟑 × K𝒖:= 𝑳𝑺𝑪 =

DATAS: 𝑳𝑰𝑪 =

ATENÇÃO

IDENTIFICAR NO GRÁFICO QUAIS OS PONTOS DE ATENÇÃO

EXEMPLOS:

1- Para a elaboração de um 𝐺𝐶 𝑢 , optamos por 25 amostras, com amostragem média de 110 peças (bomba de vácuo), para

facilitação dos cálculos, nenhuma das amostras “fugiu” dos limites de 25% da amostragem média. O total de defeitos encontrados foi de 498. Calcular os limites da carta.

1º passo: Calcular o nº médio de defeitos por unidade e o desvio padrão do processo:

2º passo:

Calcular os limites de controle:

𝑢" =_{∑ 𝑛 =}∑ 𝑐 _{25 × 110 =}498 _{2750 = 0,181 → 𝜎 =}498 -𝑢"_{𝑛" =}-0,181

110 = 0,041

𝐿𝑆𝐶 = 𝑢" + 3 × K𝑢"𝑛" = 0,181 + 3 × 0,041 = 0,304 𝐿𝐼𝐶 = 𝑢" − 3 × K𝑢"𝑛" = 0,181 − 3 × 0,041 = 0,058 𝒖: =_{∑ 𝒏}∑ 𝒄

=

𝒏: =∑ 𝒏_𝑸 =

𝒖:

(13)

CARTA DO NÚMERO DE DEFEITOS POR AMOSTRA-(c)

CARTA... “c”

A carta “c” é semelhante à carta “u” , porém exige tamanho de amostras “n”, constante.

Nesta carta a orientação é para o número de defeitos na amostra.

Lembrete:

CÁLCULO DOS LIMITES:

𝑁ú𝑚𝑒𝑟𝑜 𝑚é𝑑𝑖𝑜 𝑑𝑒 𝐷𝑒𝑓𝑒𝑖𝑡𝑜𝑠 → 𝒄" =

∑ 𝒄

_𝑸

onde: Sc = somatório de defeitos de todas as amostras Q = qtde de amostras

𝐷𝑒𝑠𝑣𝑖𝑜 𝑃𝑎𝑑𝑟ã𝑜 → 𝝈 = √𝒄"

𝑳𝑺𝑪 = 𝒄" + 𝟑 × √𝒄"

𝑳𝑴 = 𝒄"

(14)

m .a .pe ri ss in o tto - C E P A 14 T a m a n h o m é d io d a a m o s tr a = 1 r o lo /d ia A m ost ra 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO 1 ROLO N úm er o (

c

) 9 15 11 8 17 11 5 11 13 7 10 12 4 3 7 2 3 3 6 2 7 9 1 5 8 ## Fr açã o ( p, u) D at a 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 LM L S C L IC

CA

RT

A

c

(15)

CÁLCULO DOS PARÂMETROS DA CARTA “c”

(pág. anterior)

1

𝒄" =∑ 𝒄_{𝑸 =}

2

√𝒄 :=

3

𝟑 × √𝒄" =

4

𝑳𝑴 = 𝒄" =

𝑳𝑺𝑪 = 𝒄" + 𝟑 × √𝒄" =

5

𝑳𝑰𝑪 = 𝒄" − 𝟑 × √𝒄" =

ATENÇÃO

IDENTIFICAR NO GRÁFICO QUAIS OS PONTOS DE ATENÇÃO

EXEMPLOS:

1- Em um 𝐺𝐶 𝑐, com 25 amostras de 08 itens, obtemos 1393 defeitos. Calcular os limites de controle.

1º passo: Calcular o nº médio de defeitos e em seguida o desvio padrão:

2° passo:

Calcular os limites

2 - Na inspeção de uma linha de embalagens metálicas, na verificação de latas amassadas, optou-se por “𝐺𝐶 𝑝", obtendo-se: 𝑛" =

1385 𝑒 𝑝̅ = 0,025 , com 𝐿𝑆𝐶_’= 0,038 𝑒 𝐿𝐼𝐶_’= 0,012.

Analisar a situação nas amostragens: 𝑛_”•= 𝟐𝟎𝟓𝟎, 𝑑 = 21, 𝑒 𝑛_–—= 𝟓𝟓𝟎, 𝑑 = 28.

𝑐̅ =

”˜™˜_–—

= 55,72 → 𝜎 = √𝑐̅ → 𝜎 = 355,72 = 7,46

𝐿𝑆𝐶 = 𝑐̅ + 3 × √𝑐̅ → 55,72 + 3 × 7,46 = 78,11

𝐿𝐼𝐶 = 𝑐̅ − 3 × √𝑐̅ → 55,72 − 3 × 7,46 = 33,32

𝑛”•→ 𝑝̅ =_{2050 = 0,01 → 𝜎}21 ”•= -0,025 × 0,975₂₀₅₀ = 0,0034 →𝐿𝑆𝐶_{𝐿𝐼𝐶 → 0,025 š}+_{− 3 × 0,0034 ›}0,035_{0,015 → 𝑂𝐾}

𝑛" = 1385 ›× 1,25_{× 0,75 š}1731₁₀₃₈

(16)

CEPA

.

-

16

Exercícios:

1- Uma fábrica de refrigerante, constatou após análise da carta “GC np” de 25 amostras de n=50 encontrou um total de 190 embalagens rejeitadas ( amassadas, riscadas, etc.).

a) Quais os limites de controle?

2- Na produção de geladeiras a empresa necessita conhecer o número de defeitos por unidade produzida. Após o levantamento de 20 amostras, obteve-se na aplicação de “GC u”,com os resultados: LSC=5,24 e LIC=0,76 Na amostra “n15” o resultado foi n= 4, c= 21. Essa unidade está dentro ou fora dos limites?

3- No controle de envase em latinhas de cerveja, utilizando a “GC p”,qual o desvio padrão do processo, após 20 amostras, com os seguintes resultados:

4- Numa fábrica de retrovisores a empresa definiu implantar carta “GC c”,com 25 amostras de 50 itens cada uma. Para obtermos um LSC= 22, qual deve ser o valor de “c barra”?

∑ 𝑛 = 108 𝑒 ∑ 𝑐 = 324

(17)

Nome:_______________________________________NºT:_

EXERCÍCIO:

(1)- No monitoramento de uma fabricação de PCI, optou-se por "𝑮𝑪 𝒖",com 26 amostras de 𝑛" = 52, com ∑ 𝑐 = 2704. Calcular

os limites de controle.

(2)- Em uma determinada linha de produção, o setor de qualidade precisa saber a quantidade de defeitos na amostra. Para isso

implantou-se um “𝑮𝑪 𝒄 ", no final de 26 amostras obteve-se 516 defeitos.

Qual a % de peças entre a média e 𝑐 = 20?

(3) Um determinado fabricante, quer saber a quantidade de defeitos por unidade fabricada. Na inspeção final de 20 amostras com 5

bicicletas obteve ∑ 𝑐₅= 193. Calcular os limites de controle.

(4)- Quais os limites de controle, para um “𝑮𝑪 𝒏𝒑",com ∑5¦–§_5¦” 𝑛𝑝₅= 482, com 50 itens em cada amostra?

(5)- A diretoria da empresa definiu, no envase de latinhas de cerveja, com a utilização do “GC p”,no mínimo 99% das latinhas dentro dos limites especificados. Para que isso aconteça qual deve ser o desvio padrão do processo?

¤ 𝑛 = 8750