UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO
Análise cinemática e dinâmica do salto
vertical
DISSERTAÇÃO DE MESTRADO EM ENGENHARIA MECÂNICA
Beatriz Teixeira de Almeida
Professor José Morais (orientador) Professor José Xavier (co-orientador)
UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO
Análise cinemática e dinâmica do salto
vertical
Beatriz Teixeira de Almeida José Joaquim Lopes Morais (orientador)
José Cardoso Xavier (co-orientador)
Dissertação apresentada à Universidade de Trás-os-Montes e Alto Douro para obtenção do grau de Mestre em Engenharia Mecânica, realizada sob orientação científica do Professor Doutor José Joaquim Lopes Morais e coorientação científica do Professor Doutor José Cardoso Xavier.
iii
v
Agradecimentos
Foram cinco anos fantásticos nesta Universidade de Trás-os-Montes e Alto Douro e a realização desta dissertação é o culminar da vida de estudante e sem várias pessoas este percurso não tinha sido concluído.Ao Professor José Morais e Professor José Xavier por me terem sugerido um tema tão interessante e cativante, por toda a ajuda que me deram durante o desenvolvimento desta dissertação, e por todo o tempo que despenderam para chegarmos a este momento.
Aos meus pais e à minha irmã, o maior agradecimento de todos, por sempre me apoiarem mesmo nos momentos mais difíceis, nunca desistirem mesmo quando estava de mau humor e os deixava a todos chateados, não tenho palavras para vos agradecer tudo o que me deram.
À minha família e aos meus padrinhos por estarem comigo desde sempre e conseguirem animar-me com qualquer coisa, por terem estado em todos os momentos mais importantes dos meus 23 anos e que continuem sempre.
Ao meu namorado José Vieira, por estares sempre lá, por me ouvires e acreditares sempre que eu ia conseguir, por tudo o que temos conseguido nestes anos, és o meu grande apoio.
Aos meus amigos e amigas que me ajudaram e apoiaram durante estes anos, quero que seja sempre assim.
Ás minhas amigas, Xana, Catarina, Joana, por sempre me ouvirem quando eu mais precisava, pelas saídas todas, por estes anos todos que vos aturo e por último por partilharem comigo a aventura que é realizar uma dissertação de mestrado.
Sara e Nuno, obrigada por este último ano, por poder falar com vocês, sobretudo por todos os jantares que tivemos e que vamos continuar a ter.
vii
Resumo
Atualmente o conhecimento do corpo humano passa pelo estudo biomecânico do movimento, para conhecer os esforços internos que desenvolve e os esforços externos a que está submetido. A biomecânica do movimento beneficiou do desenvolvimento de outras áreas científicas, nomeadamente das técnicas experimentais. A biomecânica coexiste e também contribui decisivamente para outras áreas, como a medicina, o desporto e a ergonomia, tentando recriar, analisar e simular o movimento humano para melhorar a qualidade de vida do ser humano.Este trabalho incide sobre o problema de dinâmica inversa do salto vertical. Esta tarefa motora é particularmente interessante para a validação de modelos biomecânicos, incluindo os parâmetros inerciais, os modelos de contato entre o pé o solo, os modelos de ativação e ação muscular, e os algoritmos de controlo e otimização empregue nos problemas de dinâmica direta.
Esta dissertação tem como objetivo desenvolver três algoritmos de cinemática e de dinâmica inversa de sistemas multicorpo, aplicados ao salto vertical, baseados em coordenadas cartesianas absolutas, em coordenadas relativas e em coordenadas naturais. Esses algoritmos foram desenvolvidos em ambiente Python e Excel.
ix
Abstract
Nowdays the understanding of the human body goes through the biomechanical study of the movement, in order to identify the internal efforts that are developed and the external efforts that are submited. The biomechanichs of the movement benefits from the developments of other cientific areas, namely from experimental technics. The biomechanichs coexists with and contributes decisively to other areas, like medicin, sports and ergonomy, trying to recreate, analyse and simulate the human movement to improve the quality of life.This work focuses on the inverse dynamic problem of the vertical jump. This motor task is particularly interesting for validating biomechanic models, including the inertial parameters, the contact models between the foot and the ground, the muscule activation and action models, and the control and otimization algorithms used in direct dynamic problems.
The objective of this dissertation is to develop three algorithms of kinematic and inverse dynamic analyses of multibody systems, applied to vertical jump, based on absolute cartesian cordinates, relative coordinates and natural coordinates. These algorithms where developed in Python and Excel.
xi
Nomenclatura
k j a , - Aceleração da rótula
k,j ; k a - Aceleração do segmentok; kA - Matriz de transformação do segmento k;
k j r
F , - Forças resultantes na articulação
k,j ; , ( )
t
f k j - Função motora da articulação
k, j ;I- Matriz identidade; k
I - Momento de inércia central do segmento k;
k,j - Articulação entre o segmento ke o segmento j ; km - Massa do segmento k; M – Matriz de massa;
k j
n , - Momento resultante na articulação
k,j ;k
P - Matriz de peso do corpo k;
q- Acelerações generalizadas;
q
- Coordenadas generalizadas;d
Q - Matriz das forças diretamente aplicadas;
q- Velocidades generalizadas;
k j
r , - Coordenadas da articulação
k,j ;k
r - Coordenadas do centro de massa do segmentok; R- Matriz de rotação ortogonal;
kj k
s , - Posição da articulação
k,j no referencial do corpo k; lk k
s , - Posição da articulação
l,k no referencial do corpo k; k j v , - Velocidade da rótula
k,j ; k v - Velocidade do segmentok; n - Multiplicadores de Lagrange k - Ângulo absoluto do segmento k;
k ,j
xii
k ,j
- Aceleração angular da articulação
k,j ;- Aceleração angular do segmento k;
k ,j
- Velocidade angular da articulação
k,j ;k
- Velocidade angular do segmento k.
k
xiii Índice Agradecimentos ... v Resumo ... vii Abstract ... ix Nomenclatura ... xi CAPÍTULO 1 ... 1 Introdução ... 1 CAPÍTULO 2 ... 3 Revisão bibliográfica ... 3 2.1. Introdução... 3
2.2. Segmentos anatómicos e sistemas de referência ... 3
2.3. Movimentos básicos entre os segmentos anatómicos no plano sagital ... 6
2.4. Propriedades inerciais do corpo humano ... 8
2.5. Métodos experimentais em biomecânica do movimento humano ... 11
2.6. Aplicações da biomecânica do movimento humano ... 12
2.7. Métodos analíticos e numéricos em biomecânica do movimento humano .. 13
2.8. Análise e modelação do salto vertical ... 14
2.9. Conclusões ... 16
CAPÍTULO 3 ... 19
Cinemática e dinâmica de mecanismos planos... 19
3.1 Introdução... 19
3.2 Posição de um sólido em movimento plano: coordenadas cartesianas absolutas ... 19
3.3 Posição de um sólido em movimento plano: coordenadas naturais ... 21
3.4 Campos cinemáticos de um sólido em movimento plano ... 27
3.5 Equações de Newton-Euler para o movimento plano do sólido ... 31
3.6 Princípio das potências virtuais para o movimento plano do sólido ... 33
3.7 Cinemática de mecanismos planos ... 38
3.7.1 Coordenadas generalizadas ... 39
3.7.2 Equações de constrangimento, jacobiano e análise de posição ... 42
3.7.3 Análise das velocidades ... 45
3.7.4 Análise das acelerações ... 45
3.8 Dinâmica inversa de mecanismos planos ... 46
xiv
3.8.2 Método dos multiplicadores de Lagrange ... 48
3.9 Conclusões ... 51
CAPÍTULO 4 ... 53
Análise cinemática do salto vertical ... 53
4.1 Introdução ... 53
4.2 Modelo anatómico para o salto vertical ... 53
4.3 Algoritmo 1: coordenadas relativas ... 56
4.3.1 Coordenadas, velocidades e acelerações generalizadas ... 56
4.3.2 Equações de constrangimento ... 56
4.3.3 Análise de posição ... 57
4.3.4 Análise das velocidades ... 59
4.3.5 Análise das acelerações ... 60
4.3.6 Estrutura do algoritmo ... 61
4.4 Algoritmo 2: coordenadas cartesianas absolutas ... 62
4.4.1 Coordenadas, velocidades e acelerações generalizadas ... 62
4.4.2. Equações de constrangimento geométrico ... 63
4.4.3. Equações de constrangimento motor ... 64
4.4.4. Agrupamento das equações de constrangimento ... 64
4.4.5. Jacobiano dos constrangimentos ... 65
4.4.6. Análise de posição ... 66
4.4.8. Análise das acelerações ... 68
4.4.9. Estrutura do algoritmo ... 68
4.5 Algoritmo 3: coordenadas naturais ... 69
4.5.1. Coordenadas, velocidades e acelerações generalizadas ... 70
4.5.2. Equações de constrangimento geométrico ... 71
4.5.3. Equações de constrangimento motor... 72
4.5.4. Agrupamento das equações de constrangimento ... 74
4.5.5. Jacobiano dos constrangimentos ... 75
4.5.6. Análise de posição ... 77
4.5.7. Análise das velocidades ... 77
4.5.8. Análise das acelerações ... 79
4.5.9. Estrutura do algoritmo ... 81
4.6 Apresentação e discussão dos resultados ... 82
4.7 Conclusões ... 88
xv
Análise dinâmica inversa do salto vertical ... 91
5.1 Introdução ... 91
5.2 Propriedades inerciais do modelo anatómico para o salto vertical ... 91
5.3 Algoritmo 1: coordenadas relativas ... 92
5.3.1 Determinação dos esforços articulares: método 1 ... 92
5.3.2 Determinação dos esforços articulares: método 2 ... 95
5.3.3 Estrutura do algoritmo ... 96
5.4 Algoritmo 2: coordenadas cartesianas absolutas ... 97
5.4.1 Determinação dos multiplicadores de Lagrange ... 97
5.4.2 Determinação dos esforços articulares ... 98
5.4.3 Estrutura do algoritmo ... 98
5.5 Algoritmo 3: coordenadas naturais ... 99
5.5.1. Determinação dos multiplicadores de Lagrange ... 99
5.5.2. Determinação dos esforços articulares ... 103
5.5.3. Estrutura do algoritmo ... 105
5.6 Movimento do centro de massa ... 106
5.7 Apresentação e discussão dos resultados ... 107
5.8 Conclusões ... 111
CAPÍTULO 6 ... 113
Conclusões ... 113
Bibliografia ... 115 Anexo 1 – Funções motoras ... I Anexo 2 – Esforços articulares ... V Anexo 3 – Código dos ALGORITMOS C2 e D2 ... XIII
xvi
Índice de Figuras
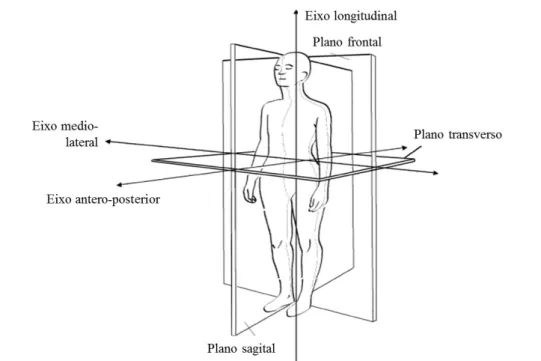
Figura 2.1 – Segmentos anatómicos, posição anatómica e posição fundamental (adaptado de Hamill e Knutzen, 2008)………..…4 Figura 2.2 – Planos e eixos cardinais do corpo humano (adaptado de Knudson, 2007)...5 Figura 2.3 – Movimentos básicos no plano sagital: flexão e extensão (adaptado de
Tozeren, 2000)………...7
Figura 2.4 – Movimentos básicos no plano frontal: abdução e adução (adaptado de
Tozeren, 2000)………...7
Figura 2.5 – Movimentos básicos no plano transversal: rotação interna e externa
(adaptado de Tozeren, 2000)……….8
Figura 2.6 – Método da imersão para o braço (adaptado de Drillis et al, 1964)………...9 Figura 2.7 – Método da plataforma de reação (adaptado de Drillis et al, 1964)………....10 Figura 2.8 – Método de libertação rápida (adaptado de Drillis et al,
1964)………...…….10
Figura 2.9 – Estratégia de salto vertical com impulso contrário (adaptado de Kim S. et
al,2014)………15
Figura 2.10 – Estratégia de salto vertical a partir da posição agachada (adaptado de
Bastian et al, 2013). ………15
Figura 3.1 – Posição de um sólido com movimento plano, em coordenadas cartesianas
absolutas……….……….20
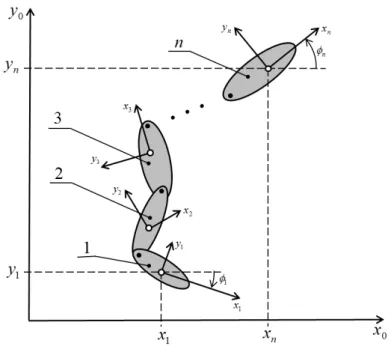
Figura 3.2 – Posição de um sólido em coordenadas naturais. ………22 Figura 3.3 – Relação entre as coordenadas naturais e as coordenadas cartesianas
absolutas. ………....26
Figura 3.4 – Forças exteriores que atuam num sólido, reduzidas no centro de massa…32 Figura 3.5 – Campo de velocidades virtuais dum sólido em movimento plano………..34 Figura 3.6 – Binário associado ao momento P
i
n ………...…….37
Figura 3.7 – Mecanismo plano em cadeia simples aberta, com elementos interligados
por rótulas. ……….……….39
Figura 3.8 – Coordenadas relativas num mecanismo plano em cadeia simples aberta, com elementos interligados por rótulas. ……….40
xvii
Figura 3.9 – Coordenadas cartesianas absolutas num mecanismo plano em cadeia
simples aberta, com elementos interligados por rótulas. ………...….41
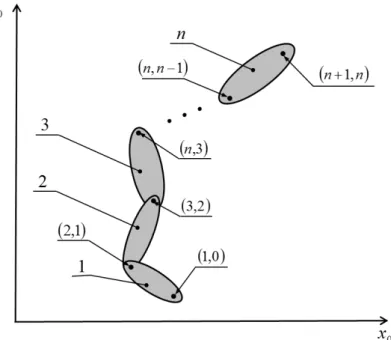
Figura 3.10 – Coordenadas naturais num mecanismo plano em cadeia simples aberta, com elementos interligados por rótulas. ………..…..……42
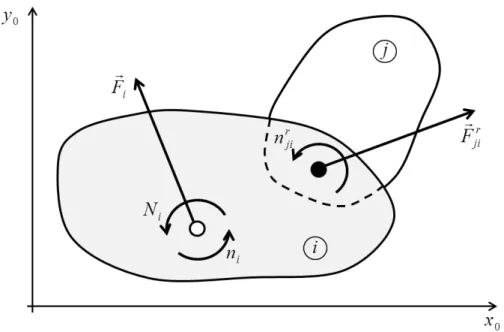
Figura 3.11 – Esforços exteriores que atuam num elemento de um mecanismo: forças exteriores m i d i i F F F ; momentos das forças exteriores em relação ao centro de massa, m i d i i N N N ; momentos exteriores, m i d i i n n n ; esforços de reação, r ji F e r ji n ………....47
Figura 4.1 – Modelo biomecânico na posição anatómica de referência: segmentos, rótulas, referenciais locais e referencial global. ……….………….…...54
Figura 4.2 – Medição da orientação relativa de segmentos anatómicos adjacentes…....55
Figura 4.3 – Rótulas
j, i e
k, j do segmento j .………...…….58Figura 4.4 – Fluxograma do ALGORITMO C1. ………..…….….61
Figura 4.5 – Rótula
k,j , entre os segmentos k e j .………..………….…63Figura 4.6 – Fluxograma do ALGORITMO C2. ………...….69
Figura 4.7 – Segmentos anatómicos, rótulas e pontos básicos, no plano sagital: coordenadas naturais. ………..70
Figura 4.8 – Constrangimento de corpo rígido, para o segmento j ………...…71
Figura 4.9 – Constrangimento motor associado à rótula
k, j , entre os segmentos k e j .………...……….73Figura 4.10 – Fluxograma do ALGORITMO C3. ……….81
Figura 4.11 – Configuração do modelo biomecânico em diferentes instantes da fase de impulso (ALGORITMO C1). ……….82
Figura 4.12 – Ordenada do centro de massa (yCM), obtida pelo ALGORITMO C1 e obtida por Anderson e Pandy (1999). ……….…………83
Figura 4.13 – Posição do centro de massa durante a fase de impulso, determinada pelo ALGORITMO C1 e pelo ALGORITMO C2: (a) abcissa, xCM; (b) ordenada, yCM…….84
Figura 4.14 – Trajetórias do centro de massa durante a fase de impulso, identificadas pelo ALGORITMO C1 e pelo ALGORITMO C2. ………...….84
Figura 4.15 – Velocidade do centro de massa durante a fase de impulso, determinada pelo ALGORITMO C1 e pelo ALGORITMO C2: (a) CM x v ; (b) ordenada, vCMy …..….86
xviii
Figura 4.16 – Componente segundo y da velocidade do centro de massa ( CM y
v ), obtida
pelo ALGORITMO C1 e obtida por Anderson e Pandy (1999). ………..…….86
Figura 4.17 – Aceleração do centro de massa durante a fase de impulso, determinada pelo ALGORITMO C1 e pelo ALGORITMO C2: (a) CM x a ; (b) ordenada, aCMy ...……87
Figura 4.18 – Componente segundo y da aceleração do centro de massa ( CM y a ), obtida pelo ALGORITMO C1 e obtida por Anderson e Pandy (1999). ………..……..88
Figura 5.1 – Diagrama de corpo livre do segmento j .………..………..93
Figura 5.2 – Fluxograma do ALGORITMO D1: método 1. ………..……96
Figura 5.3 – Fluxograma do ALGORITMO D1: método 2. ………..…96
Figura 5.4 – Fluxograma do ALGORITMO D2. ………...……….99
Figura 5.5 – Forças diretamente aplicadas nos segmentos j e k.……….102
Figura 5.6 – Fluxograma do ALGORITMO 3. ………..……..105
Figura 5.7 - Força de apoio, determinada pelo método 1 e pelo método 2, do ALGORITMO C1: (a) 1,0 x F ; (b) Fy 1,0 .………108
Figura 5.8 - Força de apoio, determinada pelo método 2 do ALGORITMO C1 e pelo ALGORITMO C2: (a) 1,0 x F ; (b) ordenada, Fy 1,0 . ………..109
Figura 5.9 - Força de apoio, determinada pelo método 2 do ALGORITMO C1 e por Anderson e Pandy (1999): (a) 1,0 x F ; (b) ordenada, Fy 1,0 .………110
Figura 5.10 – Trajetória do centro de massa na fase de impulso (ALGORITMO C1) e na fase de voo. ………...……111
xix
Índice de Tabelas
Tabela 4.1 – Geometria dos segmentos anatómicos e articulações……….55 Tabela 5.1 – Propriedades inerciais dos segmentos anatómicos.………92
1
CAPÍTULO 1
Introdução
A biomecânica do movimento tem como objetivo a descrição e modelação do movimento do corpo humano, procurando conhecer as limitações e patologias motoras do corpo humano e desenvolver para elas as soluções mais adequadas. Um exemplo recente das aplicações da biomecânica do movimento é o desenvolvimento de exoesqueletos para melhorar a qualidade de vida das pessoas paraplégicas (Knudson, 2007). A biomecânica do movimento tem contribuído para diferentes áreas da vida humana, como a medicina, a reabilitação, a ergonomia, o desporto e a indústria do entretenimento.
Os problemas de biomecânica do movimento podem ser classificados em dois grandes grupos: os problemas diretos e os problemas inversos. Os problemas diretos consistem na simulação do movimento humano, sendo as grandezas cinemáticas que descrevem o movimento do corpo determinadas através de algoritmos de controlo ótimo, que simulam a atividade cerebral e muscular. Nos problemas inversos as grandezas cinemáticas são conhecidas à partida, e as incógnitas são os esforços articulares resultantes (Manal et al, 2004; Vilà, 2012).
Quer para os problemas de dinâmica direta, quer para os problemas de dinâmica inversa, é necessário conhecer as características geométricas e as propriedades inerciais dos segmentos anatómicos. Em geral, os parâmetros inerciais são obtidos a partir de tabelas antropométricas, juntamente com modelos de regressão ou modelos geométricos para a personalização dos modelos biomecânicos do movimento (Peyer et al, 2006).
O salto vertical é uma tarefa motora complexa, que requer a sincronização e a coordenação de inúmeros músculos e articulações (Kim et al, 2011). Trata-se de uma tarefa motora particularmente adequada para a validação de modelos biomecânicos, nas suas mais variadas vertentes: fiabilidade das propriedades inerciais, validação de
2
modelos de contato entre o pé e o solo, validação de modelos da acção muscular, entre outras. No salto vertical há a distinguir duas estratégias diferentes (Kim et al, 2011): o salto com movimento de impulso contrário (countermovement) e o salto a partir da posição agachada. A primeira dessas estratégias é mais eficiente, dado que permite atingir uma altura máxima do centro de massa entre dois a quatro centímetros mais elevada. Em qualquer uma das estratégias de salto anteriores temos ainda que considerar os membros superiores imobilizados ou não.
Neste trabalho o salto vertical é analisado bidimensionalmente, no plano sagital. Os movimentos relativos dos segmentos anatómicos neste plano são a flexão e a extensão, em praticamente todas as articulações do corpo humano; de salientar que para o caso particular do pé, os movimentos a considerar são a flexão plantar e a dorsiflexão (Hamill J. et al, 2008). A partir do trabalho de Anderson e Pandy (1999) escolheu-se um modelo biomecânico constituído por seis rótulas e por seis segmentos anatómicos: pé anterior, pé posterior, perna, coxa, pélvis e HAT (head-arms-trunck). Foi efetuada uma análise inversa, para três tipos de coordenadas generalizadas: coordenadas relativas, coordenadas cartesianas absolutas e coordenadas naturais. Para essa análise foram utilizados dois softwares, o Excel e o Python.
Este trabalho está dividido em seis capítulos, sendo o primeiro capítulo esta introdução. No segundo capítulo é feita uma revisão bibliográfica relacionada com os aspetos gerais da biomecânica do movimento incluindo a análise e modelação do salto vertical no plano sagital. O terceiro capítulo é uma síntese da cinemática e da dinâmica de mecanismos planos, principalmente para os mecanismos cinematicamente definidos, contendo os fundamentos teóricos que são necessários para o presente trabalho. No quarto capítulo são apresentados o modelo biomecânico e os três algoritmos construídos para a análise cinemática, assim como os resultados obtidos. O quinto capítulo contém aos algoritmos para a análise de dinâmica inversa do modelo biomecânico, assim como os resultados obtidos. Por último, no sexto capítulo, apresentamos as principais conclusões
3
CAPÍTULO 2
Revisão bibliográfica
2.1. INTRODUÇÃO
Neste Capítulo serão apresentados os aspetos gerais da biomecânica do movimento. Assim será apresentada uma breve revisão bibliográfica onde se pretende dar a conhecer os sistemas de referência, os movimentos básicos entre os segmentos anatómicos nos planos cardinais, as propriedades inerciais, os métodos experimentais utilizados para determinar as propriedades inercias, as inúmeras aplicações da biomecânica e por fim os métodos numéricos e analíticos utilizados no estudo da biomecânica do movimento.
2.2. SEGMENTOS
ANATÓMICOS
E
SISTEMAS
DE
REFERÊNCIA
O corpo humano pode ser dividido anatomicamente em cabeça, pescoço, tronco e membros (Figura 2.1). No tronco inclui-se o tórax e o abdómen, enquanto os membros compreendem dois membros superiores (ou torácicos) e dois membros inferiores (ou pélvicos). Nos membros superiores podemos distinguir o braço, o antebraço e a mão (Figura 2.1); por sua vez, nos membros inferiores podemos distinguir a coxa, a perna e o pé (Figura 2.1). Os segmentos anatómicos que acabamos de mencionar estão ligados entre si por articulações, que permitem o seu movimento relativo por acção muscular, dentro de certos limites funcionais (Rohen et al, 1989).
4
Figura 2.1 – Segmentos anatómicos, posição anatómica e posição fundamental (adaptado de Hamill e Knutzen, 2008).
Na biomecânica do movimento o corpo humano é considerado como um mecanismo em cadeia aberta, constituído por corpos rígidos que estão ligados entre si por articulações (Silva e Ambrósio, 2004). Cada um desses corpos rígidos corresponde a um dos segmentos anatómicos da anatomia geral do corpo humano, que foram referidos no último parágrafo. Por vezes adotam-se modelos biomecânicos mais simplificados, agrupando segmentos anatómicos num único corpo rígido, como é o caso do segmento HAT (head-arms-trunk) usado por alguns autores (Koopman et al, 1995; Anderson e Pandy, 1999).
Para descrever os movimentos articulares, entre segmentos anatómicos adjacentes, é necessário definir uma posição de referência do corpo humano. Em geral são adotadas duas posições de referência: a posição anatómica ou a posição fundamental, que estão ilustradas na Figura 2.1 (Hamill e Knutzen, 2008). Na posição anatómica, o corpo está numa postura ereta, com a cabeça voltada para a frente, com os braços ao lado do tronco e as palmas das mãos voltadas para a frente, e com as pernas juntas e os pés voltados para a frente. A posição fundamental é semelhante à posição anatómica, mas com as palmas das mãos voltadas para o tronco.
Para a descrição do movimento é também prática habitual associar planos e eixos de referência à posição de referência anatómica ou à posição de referência
5
fundamental do corpo humano (Figura 2.2). Esses planos e eixos de referência contêm o centro de massa do corpo, na posição de referência. Os planos de referência (ou planos cardinais) são o plano sagital, o plano transverso e o plano frontal; os eixos de referência são o eixo médio lateral, o eixo ântero-posterior e o eixo longitudinal (Hamill e Knutzen, 2008; Palastanga et al, 2012). O plano frontal divide o corpo nas partes anterior e posterior; o plano transverso divide o corpo nas partes superior e inferior; por último, o plano sagital divide o corpo na metade direita e na metade esquerda (Hamill e Knutzen, 2008; Palastanga et al,2012).
Um dos métodos empregues para caracterizar a orientação de cada segmento anatómico durante a execução de uma tarefa motora, bem como para descrever os movimentos relativos entre os segmentos ligados por uma dada articulação, é o método das coordenadas cartesianas (absolutas ou relativas), que se baseia na definição prévia de um sistema local de coordenadas, solidário com cada segmento anatómico (Anderson e Pandy, 1999; Quental et al, 2012). A diversidade de referenciais locais que têm vindo a ser usados por diferentes autores dificulta a comunicação e a comparação de resultados. Por esta razão, o Comité de Normalização e Terminologia (Standardization
and Terminology Committee) da Sociedade Internacional de Biomecânica (International Society of Biomechanics) elaborou uma proposta de normalização dos referenciais
locais (Wu et al, 2002; Wu et al, 2005).
6
Outro método que tem vindo a ser usado cada vez mais frequentemente na biomecânica do movimento, para definir a posição do corpo humano, é o método das coordenadas naturais (Silva e Ambrósio, 2004, Czaplicki, 2007). Este método utiliza pontos e vetores fixos em cada segmento anatómico para quantificar a sua posição no espaço, proporcionando uma associação direta aos dados cinemáticos recolhidos experimentalmente (Czaplicki, 2007).
2.3. MOVIMENTOS BÁSICOS ENTRE OS SEGMENTOS
ANATÓMICOS NO PLANO SAGITAL
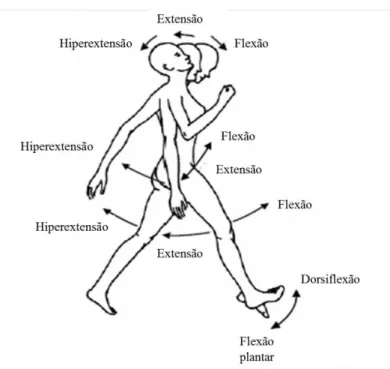
Para a modelação e análise biomecânica do movimento humano é essencial conhecer os movimentos relativos básicos entre os segmentos anatómicos, a partir da posição anatómica fundamental (Tozeren, 2000; Hamill e Knutzen, 2008). A flexão e a extensão são os movimentos básicos que ocorrem no plano sagital (Figura 2.3). Estes dois movimentos ocorrem em praticamente todas as articulações do corpo humano: nos dedos dos pés, no tornozelo, no joelho, na anca, no tronco, no ombro, no cotovelo, no punho e na mão. A flexão é caracterizada pela rotação entre dois segmentos adjacentes que provoca a diminuição do ângulo entre eles (a partir da posição anatómica fundamental); a extensão é o movimento que contraria a flexão, provoca o retorno à posição de referência (Figura 2.3). Além dos movimentos básicos referidos, há ainda a considerar, no plano sagital, os movimentos de hiperflexão e de hiperextensão, ou seja, quando o movimento de flexão se prolonga para além do normal e quando o movimento de extensão ultrapassa a posição de referência, respetivamente (Figura 2.3). De salientar que no caso particular do pé, a extensão e a flexão tomam o nome de flexão plantar e dorsiflexão (Figura 2.3). A flexão plantar ocorre quando o pé se movimenta no sentido inferior (e aumenta o ângulo relativo entre o pé e a perna), enquanto a dorsiflexão é o movimento do pé na direção da perna (o que diminui o ângulo relativo formado entre esses dois segmentos).
Os movimentos básicos no plano frontal são a abdução e a adução (Figura 2.4). O movimento de abdução consiste no afastamento do segmento anatómico em relação ao plano sagital, por exemplo, o movimento dos braços ao afastarem-se do tronco. A
7
Figura 2.3 – Movimentos básicos no plano sagital: flexão e extensão (adaptado de Tozeren, 2000).
adução é o movimento de aproximação do segmento anatómico ao plano sagital, por exemplo, o retorno dos braços para junto do tronco. Além disso, há ainda a ter em conta os movimentos de hiperabdução e hiperadução (Hamill e Knutzen, 2008; Palastanga et al,2012).
8
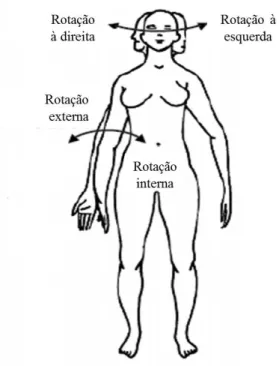
Os dois últimos movimentos básicos, rotação interna e rotação lateral, ocorrem no plano transversal (Figura 2.5). O movimento de rotação interna, ou medial, é o movimento do segmento anatómico em torno do eixo longitudinal em que a superfície anterior do segmento se move na direção do plano sagital enquanto a superfície exterior se afasta do plano sagital. O movimento de rotação lateral, ou externa, ocorre no sentido oposto ao movimento de rotação interna, ou seja, a superfície anterior do segmento afasta-se do plano sagital, enquanto a superfície exterior se movimenta na direção do plano sagital (Hamill e Knutzen, 2008; Palastanga et al,2012).
2.4. PROPRIEDADES INERCIAIS DO CORPO HUMANO
A antropometria dedica-se ao estudo da forma, das dimensões e da distribuição da massa (centros de massa e tensor de inércia) dos segmentos do corpo humano. Os resultados da antropometria são fundamentais para a ergonomia, para a prática clinica, para as próteses e ortóteses, para o desporto e para todas as áreas de intervenção da biomecânica do movimento (Hatze, 2005).
Figura 2.5 – Movimentos básicos no plano transversal: rotação interna e externa (adaptado de Tozeren, 2000).
9
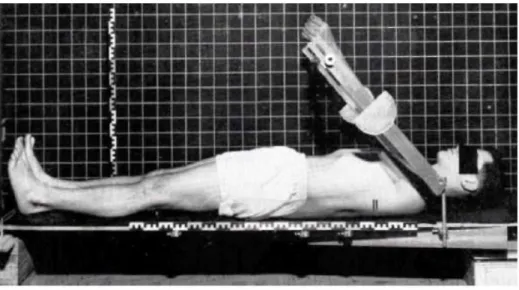
Para a determinação dos parâmetros inerciais (massa, centro de massa, momentos de inércia e produtos de inércia) dos segmentos anatómicos têm vindo a ser empregues vários métodos. Nos primeiros trabalhos foram efectuadas medições em cadáveres, tendo mais tarde sido efetuadas medições em pessoas vivas. Entre as técnicas iniciais usadas in vivo, contam-se a técnica de imersão em água (Figura 2.6) para medir o volume e estimar a massa do segmento anatómico, conhecida a massa volúmica média dos tecidos (Drillis et al, 1964). A plataforma de reação (Figura 2.7) e o método de libertação rápida (Figura 2.8) foram outros métodos usados nos primeiros trabalhos de medição das propriedades inerciais do corpo humano (Drillis et al, 1964). Mais recentemente, emergiram as técnicas baseadas em imagem, como a ressonância magnética nuclear, o varrimento por raios gama, a tomografia computorizada, a absorção de raios-X (DEXA) ou a fotogrametria (Norton et al, 2002; Dumas et al, 2007; Mei et al, 2009; Peyer et al, 2010). Esta última técnica tem a vantagem de evitar a exposição a radiações ionizantes, mas apresenta a limitação de permitir aceder apenas à geometria global do corpo humano (Dumas et al, 2007; Wicke, 2009; Peyer et al, 2010). Através dos métodos mencionados anteriormente foram construídas tabelas antropométricas e modelos de regressão (lineares e não lineares, com as dimensões dos segmentos e as suas características inerciais, que ainda são utilizadas atualmente na biomecânica do movimento humano, apesar das limitações decorrentes das amostras em
10
Figura 2.7 – Método da plataforma de reação (adaptado de Drillis et al, 1964).
Figura 2.8 – Método de libertação rápida (adaptado de Drillis et al, 1964).
que se baseiam os dados (Drillis et al, 1964; Peyer et al, 2006). Os modelos de regressão assumem que as propriedades de inércia dos segmentos anatómicos podem ser determinadas a partir de uma relação (linear ou não linear) com outras grandezas antropométricas, como a massa total do corpo, a altura total do corpo ou o comprimento do segmento. A personalização do modelo requer a determinação de grandezas antropométricas do corpo (massa e altura) ou dos segmentos anatómicos (comprimento, perímetro ou outra).
11
Outra abordagem na identificação dos parâmetros inerciais segmentares consiste na utilização de modelos geométricos, assentes na associação de formas geométricas regulares aos segmentos anatómicos e na determinação da densidade dos tecidos. Estes modelos geométricos têm sido desenvolvidos com vários níveis de complexidade e representam de forma mais precisa as diferenças de morfologia entre os indivíduos. Destacam-se o modelo de Hanavan (com 15 segmentos), o modelo de Yeadon (com 11 segmentos) e o modelo de Hatze (com 17 segmentos). A personalização destes modelos requer a recolha de um conjunto de dimensões antropométricas ou, mais recentemente, a utilização da ressonância magnética nuclear, do varrimento por raios gama (Zatsiorsky e Seluyanov, 1983), da tomografia computorizada e da absorção de raios-X (Mei, 2009) ou da fotogrametria (Gittoes et al, 2009).
2.5. MÉTODOS EXPERIMENTAIS EM BIOMECÂNICA DO
MOVIMENTO HUMANO
No estudo experimental da biomecânica do movimento humano são empregues diversas técnicas experimentais e equipamentos não invasivos, como plataforma de forças, imagem vídeo, sensores inerciais e eletromiografia, entre outros (Payton e Bartelett, 2008). A plataforma de forças é o equipamento mais utilizado em laboratórios biomecânicos para medir a força exercida entre o pé e o solo durante o movimento, através de sensores piezoeléctricos (Cross,1998; Payton e Bartelett, 2008).
A imagem vídeo, aliada à plataforma de forças, é outra das técnicas de uso corrente em biomecânica (Gruen A.,1997). Nesta técnica são utilizadas câmaras de alta velocidade, de luz branca ou de infravermelhos, para a reconstrução de superfícies e a determinação da trajetória de pontos do corpo, usando técnicas de videogrametria (Gruen A.,1997). A videogrametria utiliza marcadores de pele, refletores ou emissores de luz, colocados em pontos anatomicamente característicos, para quantificar o movimento dos segmentos anatómicos. O principal problema associado à utilização desses marcadores é o movimento local da pele em relação aos ossos subjacentes (Bonci et al, 2014). Recentemente foi proposto um novo sistema de medição que emprega uma única câmara e dispensa a utilização de marcadores (Schmitz et al, 2015).
12
As unidades de medida inerciais são cada vez mais usadas na análise cinemática do movimento humano, sobretudo porque são sistemas de medida portáteis, não estando a sua utilização confinada ao laboratório como acontece com os sistemas baseados em imagem. As unidades de medida inerciais combinam acelerómetros para a medição da aceleração de pontos anatómicos, com giroscópios para medir aceleração angular dos segmentos anatómicos e magnetómetros para determinar a orientação no espaço dos segmentos anatómicos (Kun, 2010; Chen, 2013; Arsenault, 2014). Estes sensores têm sido usados no estudo dos padrões do caminhar humano (Steins et al, 2014), no estudo dos mecanismos de controlo da postura ereta (Ma et al, 2015) e na análise biomecânica de outras tarefas motoras (Music et al, 2008).
A eletromiografia permite conhecer quais os músculos que são ativados durante o movimento, assim como a sua intensidade e duração, através da atividade elétrica de cada músculo (Morgan, 2014). Os dados obtidos por eletromiografia são particularmente importantes nos problemas de biomecânica direta (Anderson e Pandy, 1999)
2.6. APLICAÇÕES DA BIOMECÂNICA DO MOVIMENTO
HUMANO
O estudo da biomecânica do movimento é fundamental para diversas áreas, como o desporto, a reabilitação, a medicina, a ergonomia, a segurança nos transportes e o entretenimento. Relativamente ao desporto a biomecânica estuda as limitações do corpo humano, permitindo conhecer a relação do desportista com o equipamento utilizado durante a prática de uma atividade, diminuir o risco de lesões e melhorar o desempenho do desportista (Knudson, 2007).
Na reabilitação e na medicina, o conhecimento dos esforços mecânicos durante o movimento, aliado ao conhecimento das propriedades mecânicas dos tecidos, leva ao desenvolvimento de novos equipamento (como próteses e ortóteses), de novas terapias preventivas e de reabilitação, assim como ao desenvolvimento de métodos cirúrgicos (Knudson, 2007; Firmani et al, 2009). Atualmente já existem exoesqueletos capazes de
13
aumentar a performance da locomoção ou até mesmo assistir na locomoção e na reabilitação de indivíduos paraplégicos (Knudson, 2007; Firmani et al, 2009).
A ergonomia estuda a postura e os movimentos corporais aliados aos fatores ambientais e à informação que rodeia o ser humano, permitindo tornar o ambiente mais seguro, saudável e eficiente. Os problemas da biomecânica estão diretamente relacionados com a ergonomia, ou seja, com a postura, a movimentação de cargas excessivas e diferentes atividades ocupacionais. Além disso, a ergonomia e a biomecânica também se encontram relacionadas com a segurança nos transportes (Lima et al, 2015).
Atualmente a biomecânica é também utilizada na área de entretenimento e realidade virtual. De facto, a utilização de tecnologia diretamente relacionada com a biomecânica, como a análise de movimento e dados cinemáticos, permite criar personagens de animação mais reais (Lee S.H.,2008).
2.7. MÉTODOS
ANALÍTICOS
E
NUMÉRICOS
EM
BIOMECÂNICA DO MOVIMENTO HUMANO
Os problemas de dinâmica inversa são os mais comuns na literatura científica (Koopman et al, 1995; Manal et al, 2004; Vilà, 2012). Esses problemas requerem o conhecimento prévio das grandezas cinemáticas e das propriedades inerciais do corpo humano. Na construção de modelos biomecânicos do movimento são usadas tabelas antropométricas, ou então são efectuadas medições directas nos indivíduos que participam no protocolo experimental (ver secção 2.5). O objetivo central da dinâmica inversa é a determinação dos esforços articulares, numa determinada tarefa motora (Koopman et al, 1995; Manal et al, 2004; Vilà, 2012).
A dinâmica direta procura determinar o movimento de um corpo em função das ações internas e externas, sem necessidade de realizar medições experimentais cinemáticas ou dinâmicas. O aspeto central dos problemas de dinâmica direta reside na simulação do comando cerebral através de modelos de otimização da ativação e ação muscular, com o apoio da eletromiografia para a identificação dos músculos ou grupos musculares mais relevantes para o movimento (Manal et al, 2004; Vilà, 2012). Porém, a
14
eletromiografia não permite determinar a força exercida por um músculo, sendo que para isso necessário utilizar métodos de otimização para a modelação da ação dos músculos.
Um dos problemas ainda em aberto na dinâmica direta do movimento humano é a modelação do contacto do pé com o solo (Manal et al 2004; Vilà, 2012). O método dos elementos finitos não linear foi utilizado por Antunes et al (2011) para analisar detalhadamente o modelo do pé humano a três dimensões. Este método é bastante útil no estudo biomecânico, atendendo à estrutura anatómica complexa do pé. Jung Y. et al (2014) utilizaram um novo método para determinar as forças de contacto plantar. Para isso desenvolveram modelos para estimar a força de contacto na planta do pé quando apenas são conhecidas as grandezas cinemáticas das articulações. A plataforma de forças, tal como explicado na secção 2.5, permite a medição das forças exercidas entre o pé e o solo, sendo informação utilizada na validação dos modelos de dinâmica inversa ou até mesmo como dados de entrada para o modelo biomecânico (Wu et al, 2010).
2.8. ANÁLISE E MODELAÇÃO DO SALTO VERTICAL
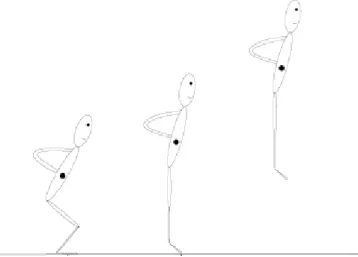
O salto vertical é uma tarefa motora complexa que requer uma coordenação rápida e harmonizada dos segmentos anatómicos, das articulações e dos músculos. O movimento de salto vertical compreende duas fases: a fase de impulso (enquanto os pés estão em contato com o solo) e a fase de voo (quando o pé deixa o solo). O objetivo fundamental é atingir a maior altura possível; isso depende diretamente da velocidade do centro de massa do ser humano quando o pé deixa o solo (Babic et al, 2007; Domire et al, 2007).
Atualmente as estratégias de salto mais estudadas são o salto com movimento de impulso contrário (countermovement) e o salto a partir da posição agachada. O salto vertical com impulso contrário (Figura 2.9) é caracterizado por se iniciar a partir da posição vertical seguido da rápida flexão dos joelhos e quadris antes do movimento ascendente. O movimento de impulso contrário provoca uma maior velocidade do centro de massa e, consequentemente, um aumento da altura do salto, conforme está representado na Figura 2.9. O instante do início de subida, após o movimento de descida
15
inicial, é um instante crítico no salto vertical dado que os momentos nas articulações atingem nesse instante os valores mais elevados, o que condiciona de forma positiva a altura do salto (Kim et al, 2011). Na estratégia de salto vertical a partir da posição agachada (Figura 2.10) a altura do salto aumenta com a profundidade de agachamento inicial (Kim S. et al, 2014: Domire Z. et al, 2007). Comparando as duas estratégias de salto, o salto com impulso contrário permite ao ser humano atingir alturas superiores, numa média de 2 cm a 4 cm, devido à energia elástica armazenada, aos reflexos de estiramento e aos músculos que são ativados durante o movimento (Kim Y-K. et al, 2011).
Figura 2.9 – Estratégia de salto vertical com impulso contrário (adaptado de Kim S. et al,2014).
Figura 2.10 – Estratégia de salto vertical a partir da posição agachada (adaptado de Bastian et al, 2013).
16
O movimento dos braços tem um papel importante no salto, podendo oscilar ou permanecer parados. A sua oscilação contribui para um melhor desempenho no salto, uma vez que provoca o aumento da velocidade do centro de massa. Além disso, provoca o aumento da energia cinética e potencial no instante em que o ser humano deixa o solo (Lees et al, 2006).
Foram propostos diferentes modelos biomecânicos para o estudo do salto vertical, especialmente para compreender a força dos músculos, a sua coordenação e a oscilação dos braços. Os modelos utilizados no estudo podem ir desde os mais simples, com apenas uma articulação e um músculo, até aos mais complexos, com múltiplas articulações e músculos. Estes modelos biomecânicos necessitam de métodos de controlo e de otimização, para identificar a velocidade máxima e a altura máxima do centro de massa (Domire et al, 2007).
2.9. CONCLUSÕES
A biomecânica do movimento tem tirado partido dos contributos de outras áreas, como a anatomia, a fisiologia, a eletrónica, a tecnologia vídeo e as ciências da computação. A biomecânica do movimento tem também contribuído de forma decisiva para outras áreas, nomeadamente para o desporto, a prática clínica e cirúrgica, a ergonomia, a segurança nos transportes e o entretenimento. Desta forma, a biomecânica tem tido impacto na melhoria da qualidade de vida do ser humano.
Os problemas de biomecânica do movimento podem ser classificados em duas grandes classes: os problemas de dinâmica inversa e os problemas de dinâmica direta. O método da dinâmica inversa é o mais utilizado em biomecânica, para a determinação dos esforços articulares a partir do conhecimento prévio das características inerciais dos segmentos anatómicos e das grandezas cinemáticas que descrevem o seu movimento. Este método é independente do tipo de coordenadas utilizadas para definir a configuração geométrica instantânea dos modelos biomecânicos: coordenadas relativas, absolutas ou naturais.
O salto vertical é uma tarefa motora particular, mas cujo estudo é fundamental para alguns aspetos da biomecânica do movimento, nomeadamente para a validação de
17
modelos matemáticos de contacto pé/solo, de controlo da ação muscular e das próprias propriedades inerciais.
19
CAPÍTULO 3
Cinemática e dinâmica de mecanismos
planos
3.1 INTRODUÇÃO
Neste capítulo vamos apresentar uma síntese da cinemática e da dinâmica de mecanismos planos, com especial destaque para os mecanismos cinematicamente definidos. Esta síntese tem um duplo objetivo: por um lado, apresentar a notação que será mais tarde empregue na análise cinemática e dinâmica do modelo biomecânico do salto vertical que é objeto de estudo neste trabalho; por outro lado, deduzir alguns resultados que serão necessários para a análise do referido modelo biomecânico.
3.2 POSIÇÃO DE UM SÓLIDO EM MOVIMENTO PLANO:
COORDENADAS CARTESIANAS ABSOLUTAS
Consideremos um sólido
S
i que se move no planox
0y
0 de um referencial
O
,
i
0,
j
0,
k
0
, que designamos por referencial absoluto ou global, conforme está ilustrado na Figura 3.1. Para definir a posição do sólido em cada instante, comecemos por escolher arbitrariamente um sistema de coordenadas
C
ii
ij
ik
i
,
,
,
solidário com o sólido, ao qual chamamos referencial local. É evidente que o vetor de posição do ponto genéricoP
i do sólido é (Figura 3.1):P i i P i
r
s
r
(3.1)20
Figura 3.1 – Posição de um sólido com movimento plano, em coordenadas cartesianas absolutas.
Designemos por
r
i a matriz coluna com as coordenadas do pontoC
i no referencialglobal e por iP i
s
a matriz coluna com as coordenadas do pontoP
i no referencial local,respetivamente (Figura 3.1): i i i y x r e P i i P i i P i i y x s (3.2)
Então, as coordenadas absolutas do ponto
P
i (isto é, as coordenadas deP
i noreferencial global) são (Figura 3.1):
P i i P i i i i i i i i P i P i y x y x y x cos sin sin cos (3.3)
Esta equação pode ser escrita de modo mais compacto, recorrendo à notação matricial (Haug, 1989; Sabana, 1994): P i i P i r A s r i i (3.4)
21
Na última equação (ou na equação 3.3) usamos as coordenadas locais do ponto
i
P para identificar esse ponto. Assim sendo, a equação 3.4 mostra que a posição de um sólido fica completamente caraterizada pelas funções
x
i
t
,y
i
t
e
i
t
. Designamos estas funções por coordenadas cartesianas absolutas do sólido, sendo conveniente arrumá-las numa matriz coluna (Haug, 1989; Shabana, 1994): t t y t x t q i i i a i (3.5)
Posto isto, tem sentido designar a equação 3.4 (ou a equação 3.3) por equação de transformação (das coordenadas generalizadas do sólido para as coordenadas cartesianas globais do ponto genérico do sólido).
3.3 POSIÇÃO DE UM SÓLIDO EM MOVIMENTO PLANO:
COORDENADAS NATURAIS
Em alternativa às coordenadas cartesianas absolutas, a posição de um sólido pode ser definida pelas coordenadas absolutas de dois quaisquer dos seus pontos,
M
i1 e2
i
M
, escolhidos arbitrariamente e designados por pontos básicos (Figura 3.2):
t y t x t r i i i 1 1 1 e
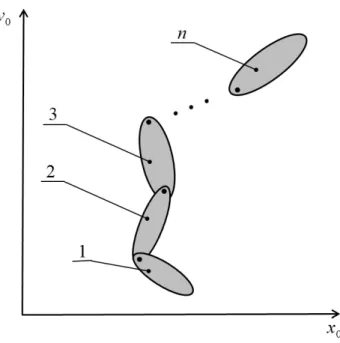
t y t x t r i i i 2 2 2 (3.6)Designamos as funções anteriores por coordenadas naturais do sólido, que agrupamos na seguinte matriz das coordenadas generalizadas naturais do sólido (Jalón e Bayo, 1994):
t y t x t y t x t q i i i i n i 2 2 1 1 (3.7)22
Figura 3.2 – Posição de um sólido em coordenadas naturais.
Ao contrário das coordenadas cartesianas absolutas, que são independentes entre si para um sólido livre, as coordenadas naturais de um sólido devem satisfazer sempre a seguinte equação de constrangimento (Figura 3.2):
2 1 2 2 0 i i i r L r (3.8)
sendo L i Li constante ao longo do tempo. Esta equação de constrangimento exprime
analiticamente a condição de indeformabilidade do sólido e adquire o seguinte aspeto na notação matricial
0 2 1 2 1 2 i i i T i i r r r L r (3.9)ou, usando explicitamente as coordenadas generalizadas naturais,
2 1
2
2 1
2 20 i i i i i x y y L x (3.10)23
Vamos agora obter as coordenadas cartesianas absolutas do ponto genérico
P
i ,a partir das coordenadas naturais do sólido, isto é, vamos obter a chamada equação de transformação para as coordenadas generalizadas naturais. Para isso, é conveniente introduzir o sistema de coordenadas local auxiliar
M
i1,
i
i
,
j
i
,
k
i
, a partir dos pontos básicosM
i1 e2
i
M
(Figura 3.2). Da geometria da figura é evidente que P i i P i
r
r
1
(3.11)Por outro lado, podemos exprimir assim o vetor
iP
(Jalón e Bayo, 1994): i i i P i uL u k L 2 1
(3.12)sendo u1 e u2 constantes ao longo do tempo, para um dado ponto
P
i . Além disso,temos (Figura 3.2): 2 1 i i i r r L (3.13)
As equações 3.11 a 3.13 constituem o ponto de partida para a obtenção da equação de transformação para as coordenadas generalizadas naturais. Comecemos então por projectar a equação 3.12 no referencial local auxiliar,
Mi ii ji ki
, , , 1 : 2 1 2 1 0 0 0 0 u u L L L u L u y x i i i i P i P i (3.14)
Esta equação pode ser invertida para determinarmos as constantes u1 e u2:
P i P i i i y x L L u u 1 0 0 1 2 1 (3.15)
24 P i i P i L u (3.16)
onde os índices
P
ei
são empregues para realçar o facto das constantes u1 e u2 dizerem respeito ao pontoP
i .Regressemos agora às equações 3.11 a 3.13, para escrevermos a seguinte equação vetorial:
2 1
2 1 2 1 1 i i i i i i P i r u r r u k r r r (3.17)Projetando esta equação no referencial global,
O,i0,j0,k0
, obtemos a seguinte equação matricial:
2 1
2 1 2 1 1 i i i i i P i r u r r u Rr r r (3.18)sendo R a matriz de rotação ortogonal,
10 01 R (3.19)
A equação 3.18 pode ainda ser escrita da seguinte forma equivalente:
2 1 2 1 2 1 1 i i P i r r R u I u R u I u r (3.20)ou, de forma expandida (Jalón e Bayo, 1994),
2 2 1 1 1 2 1 2 2 1 2 1 1 1 i i i i P i P i y x y x u u u u u u u u y x (3.21)
25
Esta equação pode ser escrita numa notação simbólica, mais condensada, conforme se segue: n i P i P i U q r (3.22)
A última equação, complementada com a equação 3.16, constitui a equação de transformação entre as coordenadas naturais do sólido e as coordenadas cartesianas absolutas do ponto Pi. Chamamos a atenção para o facto de o ponto Pi ser
identificado pelas suas coordenadas
x
iP e P iy
no referencial local auxiliar (Figura 3.2 e equação 3.15).As coordenadas cartesianas absolutas e as coordenadas naturais, sendo formas distintas de definir a posição de um sólido, estão relacionadas entre si. Comecemos por obter as componentes no referencial global dos versores
i
i
e
j
i
, do referencial local auxiliar (Figura 3.3 e equação 3.13):
i i i i i i i i L j y y i x x L L i 0 1 2 0 1 2 e
i i i i i i L j x x i y y j 0 1 2 0 1 2 (3.23)A partir daqui obtemos a matriz de rotação do referencial local auxiliar (3.3 e 3.4):
1 2 1 2 1 2 1 2 1 i i i i i i i i i i x x y y y y x x L A (3.24)
Se designarmos por
i o ângulo entre os versoresi
i
e
i
i
(Figura 3.3), que é constante ao longo do tempo, então a matriz de rotação do referencial local
Ci ii ji ki
, , , é:
26
Figura 3.3 – Relação entre as coordenadas naturais e as coordenadas cartesianas absolutas.
i i i i i i A A cos sin sin cos (3.25)
Para definir a posição do referencial
Ci ii ji ki
, , , resta-nos determinar as coordenadas de Ci a partir das coordenadas naturais do sólido. Para isso usamos a equação 3.22 (ou 3.21), n i i i U q r (3.26)
sendo os elementos da matriz i
U
dados pela equação 3.16 (ou 3.15),
i i i L
u
(3.27)Em resumo, as equações 3.24 a 3.27 permitem-nos obter as coordenadas cartesianas absolutas ( a
i
q ) a partir das coordenadas naturais ( n
i
q ).
27
3.4 CAMPOS
CINEMÁTICOS
DE
UM
SÓLIDO
EM
MOVIMENTO PLANO
Por definição, a velocidade do ponto genérico do sólido (
P
i) é a derivada emordem ao tempo do vetor de posição
r
iP
(Figura 3.1): dt r d v P i P i (3.28)ou, em notação matricial,
P i P i P i P i y x r v (3.29)
Derivando em ordem ao tempo a equação 3.3, obtemos a relação entre a velocidade do ponto
P
i e a velocidade do pontoC
i (v
i
ouv
i ): P i i P i i i i i i i i i P i P i y x y x y x cos sin sin cos 0 1 1 -0 (3.30)ou, de forma mais compacta,
P i i i i i P i v RA s v (3.31)
A equação 3.31 é a versão matricial da bem conhecida equação vetorial do campo das velocidades de um sólido (Huston, 1990; Angels, 1997):
P i i i P i
v
s
v
(3.32)sendo i a velocidade angular do sólido,
0 0 k k i i i
(3.33)Derivando em ordem ao tempo a equação 3.30, obtemos imediatamente a seguinte relação entre a aceleração do ponto
P
i (a
iP
) e a aceleração do ponto
C
i (a
i
28 P i i P i i i i i i i P i i P i i i i i i i i i P i P i y x y x y x y x cos sin sin cos cos sin sin cos 0 1 1 0 2 (3.34)
Esta equação pode ainda ser escrita de forma mais compacta, como se segue, P i i i i P i i i i i P i a R A s A s a 2 (3.35)
sendo
a
iP ea
i as matrizes coluna com as componentes P ia
ea
i
, respetivamente, no sistema de coordenadas, P i P i P i y x a e i i i y x a (3.36)A equação 3.35 é a representação matricial da conhecida equação vetorial do campo das acelerações de um sólido, para o movimento plano (Huston, 1990; Shabana, 1994):
P i i P i i i P i
a
s
s
a
2
(3.37)onde i a aceleração angular do sólido,
0 0 k k i i
(3.38)Pela equação 3.30 vê-se que o campo das velocidades de um sólido fica completamente determinado quando se conhecem em cada instante as funções xi
t ,
tyi e
i
t
, ou seja, a matriz das velocidades generalizadas absolutas (Haug, 1989):
t t y t x t q i i i a i (3.39)De igual forma, a equação 3.34 mostra que o campo das acelerações de um sólido é completamente determinado pela seguinte matriz das acelerações generalizadas absolutas (Haug, 1989):
29
t t y t x t q i i i a i (3.40)Nesse sentido, quando o movimento plano de um sólido é descrito em coordenadas cartesianas absolutas (ver secção 3.2), as equações 3.30 e 3.34 são as equações de transformação das velocidades a
i
q e das acelerações qia do sólido, respetivamente, nas
velocidades viP e nas acelerações P i
a do ponto genérico Pi .
Quando se opta por descrever o movimento plano de um sólido com coordenadas naturais (ver secção 3.3), as velocidades e as acelerações generalizadas do sólido são (3.7):
t y t x t y t x t q i i i i n i 2 2 1 1 (3.41) e
t y t x t y t x t q i i i i n i 2 2 1 1 (3.42)É claro que estas velocidades (3.41) e acelerações generalizadas (3.42) não são independentes entre si, em virtude do constrangimento de corpo rígido que as coordenadas naturais têm que satisfazer em cada instante (3.8 a 3.10). As equações de transformação das velocidades e das acelerações generalizadas do sólido obtêm-se imediatamente derivando em ordem ao tempo a equação de transformação 3.22 (Jalón e Bayo, 1994): n i P i P i U q v (3.43) e