UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA HIDRÁULICA E AMBIENTAL PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL
JULIANA ALENCAR FIRMO DE ARAÚJO
ANÁLISE DO RISCO AMBIENTAL EM RIOS MEDIANTE
APLICAÇÃO DE UM MODELO MATEMÁTICO BIDIMENSIONAL
DIFUSO CONSIDERANDO A INFLUÊNCIA DE ONDAS DE CHEIA
ANÁLISE DO RISCO AMBIENTAL EM RIOS MEDIANTE
APLICAÇÃO DE UM MODELO MATEMÁTICO BIDIMENSIONAL
DIFUSO CONSIDERANDO A INFLUÊNCIA DAS ONDAS DE CHEIA
Tese submetida à Coordenação do Curso de Pós-Graduação em Engenharia Civil, área de concentração em Recursos Hídricos, da Universidade Federal do Ceará, como parte dos requisitos para a obtenção do título de Doutor.
Área de Concentração: Recursos Hídricos.
Orientador: Prof. Dr. Raimundo Oliveira de Souza.
Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará
Biblioteca de Pós-Graduação em Engenharia - BPGE
A689a Araújo, Juliana Alencar Firmo de.
Análise do risco ambiental em rios mediante aplicação de um modelo matemático bidimensional difuso considerando a influência de ondas de cheia / Juliana Alencar Firmo de Araújo. – 2015.
121 f. : il. color. , enc. ; 30 cm.
Tese (doutorado) – Universidade Federal do Ceará, Centro de Tecnologia, Departamento de Engenharia Hidráulica e Ambiental, Programa de Pós-Graduação em Engenharia Civil: Recursos Hídricos, Fortaleza, 2015.
Área de Concentração: Recursos Hídricos.
Orientação: Prof. Dr. Raimundo Oliveira de Souza.
1. Recursos hídricos. 2. Análise de riscos. 3. Água - Qualidade. I. Título.
Dedico essa conquista aos meus pais, Nelson e Iany, à minha sogra, Ana Cleide, e ao meu esposo, Paulo Roberto, pelo amor incondicional, e por serem minha fonte de inspiração e de alegria a cada dia.
A Deus, em primeiro lugar e acima de tudo, por todo seu amor, zelo e cuidado comigo e todos que me cercam. Por nunca me abandonar e por todas as bênçãos que Ele vem derramando na minha vida.
Aos meus pais, Nelson e Iany, que acreditaram no meu propósito e me estimularam das mais diversas formas durante toda essa caminhada. Por me ensinarem os verdadeiros valores da vida e pelo esforço realizado para minha educação.
Ao meu esposo, Paulo Roberto, sempre conselheiro e amigo. Agradeço, acima de tudo, pela sua paciência e compreensão. Por todo seu amor, amizade, carinho, companhia e incentivo nessa fase, e em vários momentos da minha vida.
A toda minha família, que como meus incentivadores, acreditaram que meu esforço e dedicação serviriam para eu completar a minha formação profissional.
Ao orientador e amigo, professor Raimundo Oliveira de Souza, pelos conselhos, ensinamentos e disponibilidade durante os últimos 10 anos. Por sempre acreditar no meu potencial, e nunca permitir que as dificuldades do processo atingissem meus objetivos. Obrigada por me apoiar em mais uma conquista, e sempre me servir como exemplo, contribuindo para o meu crescimento pessoal e profissional.
Ao meu orientador no exterior, professor Mark T. Brown, cujos ensinamentos repassados foram fundamentais para que esse trabalho fosse possível.
A todos os professores do Departamento de Engenharia Hidráulica e Ambiental (DEHA/UFC), pela contribuição acadêmica, profissionalismo e dedicação. Por colaborarem, direta ou indiretamente, com ensinamentos valiosos que formaram a base necessária ao desenvolvimento deste trabalho.
Aos membros da banca de qualificação, professores Dr. Raimundo Oliveira de Souza (orientador), Dr. John Kenedy de Araújo, e Dra. Carla Freitas de Andrade, pelas sugestões pertinentes para o aprimoramento desta tese.
importantes contribuições no final deste trabalho.
Aos funcionários do Departamento de Engenharia Hidráulica e Ambiental (DEHA/UFC), por toda atenção e apoio prestado. Em especial às funcionárias Shirley Gomes, Edineuza Firmino e Terezinha.
À Coordenação do Curso de Pós-Graduação em Recursos Hídricos, na pessoa do professor Dr. Francisco de Assis Sousa Filho, por toda experiência, ensinamento e atenção.
À Universidade Federal do Ceará (UFC), juntamente com o governo, por proporcionar uma ótima oportunidade de estudar e contribuir para o desenvolvimento da ciência.
À Universidade da Flórida (UF) por proporcionar uma oportunidade ímpar de participar do estágio de doutorado em Gainesville, e contribuir para o desenvolvimento científico desta pesquisa.
À Coordenadoria de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), pelo suporte financeiro com a manutenção de bolsa de auxílio, tanto para o desenvolvimento desta pesquisa como pelo suporte no estágio no exterior (PDEE – Programa de Doutorado no País com Estágio no Exterior).
Aos colegas de turma de doutorado, com quem cursei as disciplinas, e com quem pude aprender muito no decorrer dos trabalhos desenvolvidos. Em especial aos amigos: Raquel, Rejane, Flávia, Socorro, Jacqueline, Samíria, Wictor, Diego, Samuelson e Cleiton.
A todos os amigos americanos e brasileiros que fiz durante o estágio de doutorado.
RESUMO
A presença de componentes físicos, químicos e biológicos nos rios, associada à dinâmica fluvial presente nestes ecossistemas, permite a existência de processos extremamente complexos, fazendo com que sua descrição através de modelos matemáticos se torne uma missão desafiadora. Isto implica na necessidade de se estabelecer um conjunto de simplificações criteriosas, de modo a se ter resultados que venham descrever esses processos com um grau de realismo. A utilização de modelos matemáticos para avaliar as questões de
lançamento e assimilação de poluente em um corpo d’água é uma ferramenta de suma
importância, em virtude da complexidade dos processos determinantes nas questões da qualidade de água. Esses modelos tomam como base, os fundamentos do princípio de conservação de massa, conjuntamente com a lei de Fick para transporte de poluente. Por outro lado, este tipo de análise acaba por desenvolver modelos ditos determinísticos, onde não há qualquer possibilidade de avaliar as incertezas inerentes nos mais diversos fenômenos que se desenvolvem nos corpos hídricos. Para contornar estes inconvenientes, algumas pesquisas têm lançado mão de uma metodologia com base na teoria fuzzy. Esta teoria, que se fundamenta na representação matemática de alguns parâmetros, na forma de funções de pertinência, e tem a vantagem de permitir uma avaliação das incertezas em qualquer processo físico, sem a necessidade de uma base de dados tão consistente. Este trabalho tem como objetivo analisar as relações entre campos de concentração de um poluente e escoamento transiente composto de ondas de cheia em rios naturais, mediante a aplicação de um modelo bidimensional de transporte de massa, na sua forma fuzzy, de modo que campos de risco ambiental possam ser estudados. Para atingir os objetivos, as equações diferenciais de transporte de massa, bem como as equações da hidrodinâmica, foram tratadas nas suas formas fuzzy e solucionadas mediante a aplicação do método das diferenças finitas. Os resultados foram obtidos com o uso de um programa computacional, em linguagem FORTRAN, que permitiu a realização de várias simulações para diferentes cenários. Os resultados mostraram que a presença da onda difusa nos modelos de transporte tem um comportamento bem diferente do modelo da onda cinemática, mostrando, assim, que estudos mais detalhados são sempre necessários para conclusões definitivas para estes problemas relacionados com a qualidade de água.
ABSTRACT
The presence of physical, chemical and biological components in rivers, associated with fluvial dynamics in these ecosystems, enables the existence of extremely complex processes, making your description using mathematical models a challenging task. This implies the need to establish a set of insightful simplifications, in order to get results that may describe these processes with a degree of realism. The use of mathematical models to evaluate the release and assimilation of polluting matters into a water body is a most important tool, due to complexity of the determining processes on issues of water quality. These models are based on the fundamentals of mass conservation principle amongst Fick's law for polluting transport. On the other hand, this type of analysis generate deterministic models where there is no possibility to evaluate the inherent uncertainties in various phenomena developed in water bodies. To overcome these drawbacks, some research has made use of a methodology based on fuzzy theory. This theory is based on mathematical representation of some parameters in the form of membership functions, and has the advantage of allowing an assessment of uncertainty in any physical process, without the need of a database so consistent. This work aims to analyze the relations among pollutant concentration and transient flow fields compound by flood waves in natural rivers, through the application of a two-dimensional model of mass transport, in its fuzzy form, so that fields of environmental risk may be studied. To achieve the goals, the differential equations of mass transport, as well as the hydrodynamics equations, were treated in its fuzzy forms and solved by applying the finite difference method. The results were obtained using a computer program in FORTRAN language, allowing the achievement of various simulations for different scenarios. The results indicated that the presence of diffused wave in the transport models have a very different behavior of the kinematic wave model, thus showing that more detailed studies are needed to reach definitive conclusions for these problems related to water quality.
Figura 2.1 – Conjunto difuso na forma triangular ... 25
Figura 3.1 – Volume de controle ... 38
Figura 3.2 – Forças que atuam sobre a massa fluida ... 40
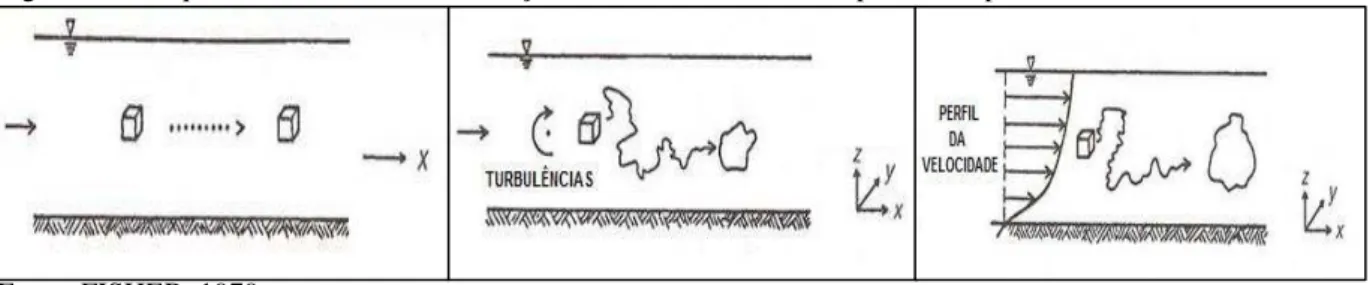
Figura 4.1 – Esquema dos fenômenos adveção, difusão turbulenta e dispersão ... 55
Figura 4.2 – Esquema do balanço de massa em um volume de controle ... 57
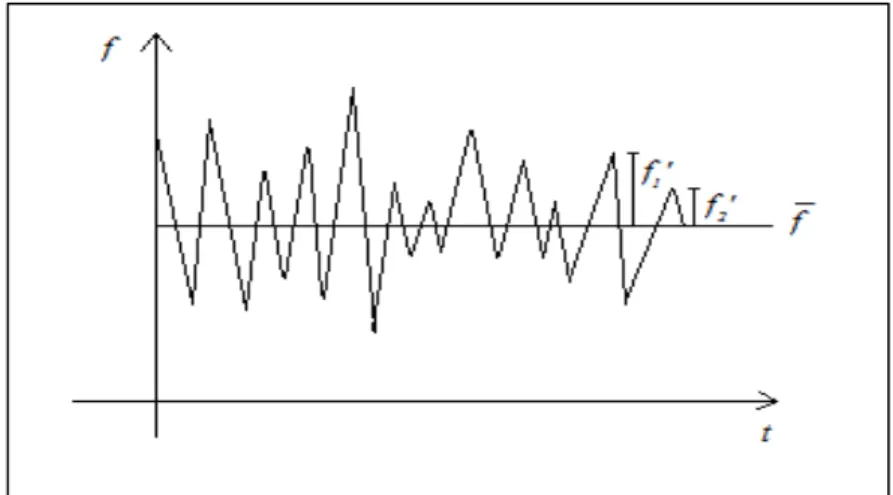
Figura 4.3 – Esquema da flutuação da função instantânea em torno da média ... 60
Figura 4.4 – Classes de enquadramento e respectivos usos e qualidade da água ... 65
Figura 5.1 – Representação gráfica do risco e garantia ... 79
Figura 6.1 – Aproximação por diferenças finitas ... 81
Figura 6.2 – Grade computacional ... 82
Figura 6.3 – Esquema numérico para solução da equação da onda cinemática ... 83
Figura 6.4 – Esquema numérico para solução da equação da onda difusiva... 85
Figura 6.5 – Esquema numérico para solução da equação do transporte de poluentes ... 89
Figura 6.6 – Fluxograma do modelo computacional completo ... 92
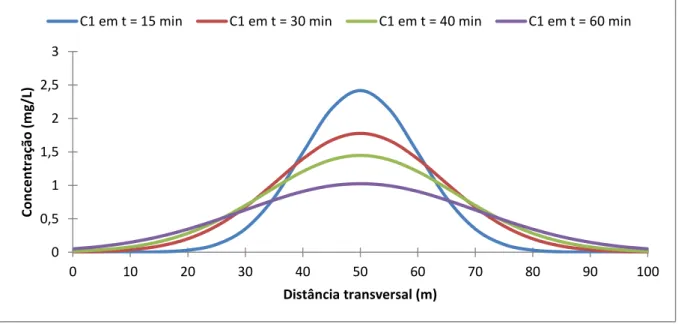
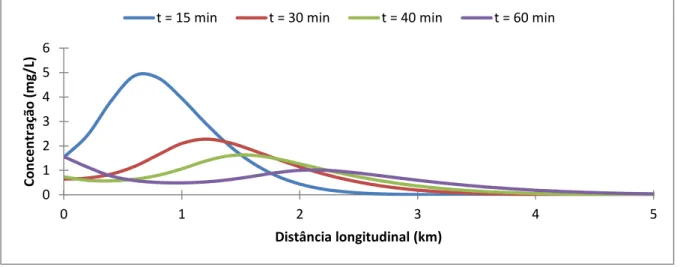
Figura 7.1 – Concentrações com maior grau de pertinência na seção longitudinal em diferentes tempos, sem ondas. ... 95
Figura 7.2 – Concentrações com maior grau de pertinência na seção transversal em diferentes tempos, sem ondas ... 96
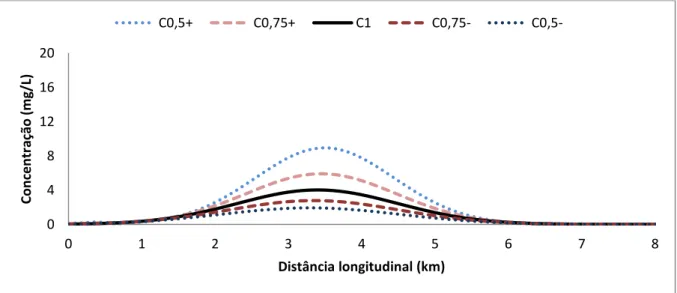
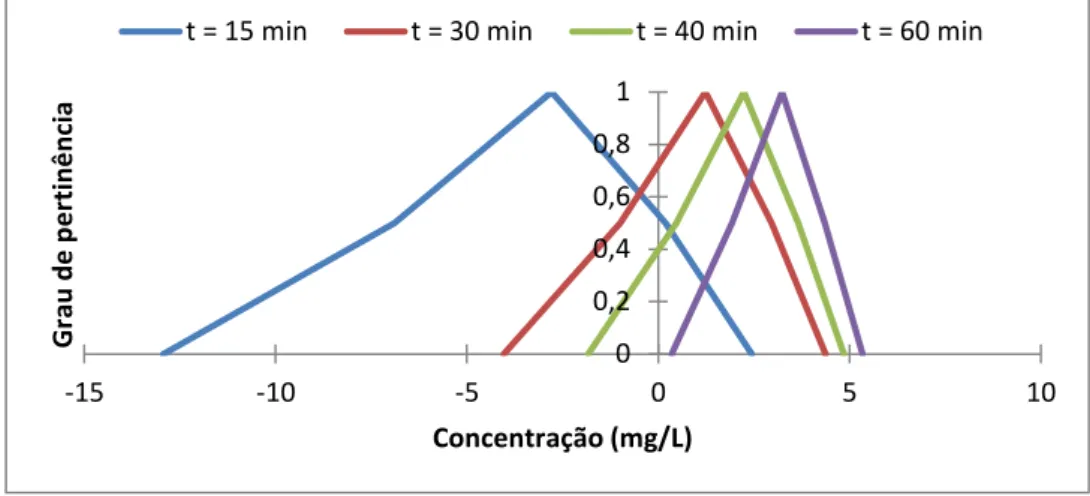
Figura 7.3 – Concentrações com diferentes graus de pertinência na seção longitudinal em t = 15 min, sem ondas... 97
Figura 7.4 – Concentrações com diferentes graus de pertinência na seção longitudinal em t = 30 min, sem ondas... 97
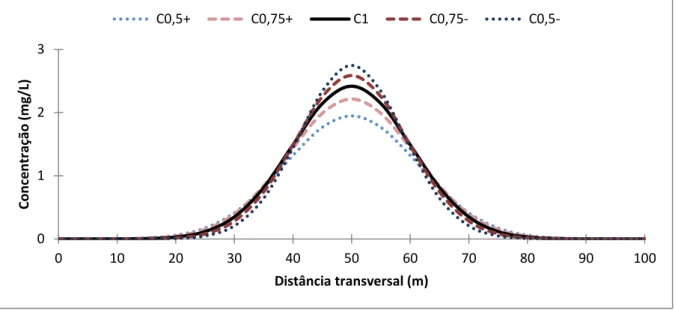
Figura 7.5 – Concentrações diferentes graus de pertinência na seção transversal para t = 15 min, sem ondas... 98
Figura 7.9 – Risco na seção longitudinal em diferentes tempos, sem efeito de ondas.. ... 100 Figura 7.10 – Garantia na seção longitudinal em diferentes tempos, sem efeito de ondas. ... 101 Figura 7.11 – Risco na seção transversal em diferentes tempos, sem efeito de ondas... ... 101 Figura 7.12 – Vazões na seção longitudinal para diferentes tempos, sob a influência da
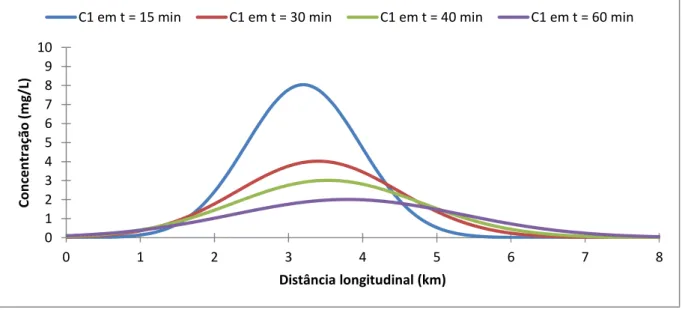
onda cinemática ... 102 Figura 7.13 – Concentrações na seção longitudinal para diferentes tempos, sob a
influência da onda cinemática ... 103 Figura 7.14 – Risco na seção longitudinal para diferentes tempos, sob a influência da
onda cinemática ... 103 Figura 7.15 – Concentrações na seção transversal para diferentes tempos, sob a influência
da onda cinemática ... 104 Figura 7.16 – Risco na seção transversal para diferentes tempos, sob a influência da onda
cinemática ... 104 Figura 7.17 – Vazões na seção longitudinal para diferentes tempos, sob a influência da
onda difusiva. ... 105 Figura 7.18 – Concentrações na seção longitudinal para diferentes tempos, sob a influência
da onda difusiva. ... 106 Figura 7.19 – Risco na seção longitudinal para diferentes tempos sob a influência da onda
difusiva ... 106 Figura 7.20 – Concentrações na seção longitudinal em t = 40 min, sem efeito de ondas e
sob a influência da onda cinemática e da onda difusiva ... 107 Figura 7.21 – Risco na seção longitudinal em t = 40 min, sem efeito de ondas e sob a
influência da onda cinemática e da onda difusiva ... 108 Figura 7.22 – Garantia na seção longitudinal em t = 40 min, sem efeito de ondas e sob a
influência da onda cinemática e da onda difusiva ... 108 Figura 7.23 – Concentrações na seção transversal para t = 30 min, sem efeito de ondas e
sob a influência da onda cinemática e da onda difusiva. ... 109 Figura 7.24 – Risco na seção transversal em t = 20 min, sem efeito de ondas e sob a
LISTA DE TABELAS... 10
CAPÍTULO 1 - CONSIDERAÇÕES INICIAIS... 14
1.1 Objetivos da pesquisa... 17
1.1.1 Objetivo geral... 17
1.1.2 Objetivos específicos... 17
1.2 Organização do trabalho... 18
CAPÍTULO 2 – TEORIA DOS CONJUNTOS DIFUSOS... 19
2.1 Conjuntos difusos (conjuntos fuzzy)…….... 21
2.2 Conjuntos nível h, difusos normal e convexo... 23
2.3 Números difusos…………... 24
2.4 Representação L-R de um número difuso... 26
2.5 Operações aritméticas em intervalos... 27
2.5.1 Adição... 27
2.5.2 Subtração... 28
2.5.3 Multiplicação... 28
2.5.4 Divisão………... 29
2.6 Princípio da extensão... 30
CAPÍTULO 3 – MECÂNICA FLUVIAL……….. 35
3.1 Dedução da equação de Saint-Venant…...………... 37
3.1.1 Equação da continuidade... 38
3.1.2 Equação da quantidade de movimento... 40
3.2 Modelo da onda cinemática... 46
3.3 Modelo da onda difusiva... 48
3.4 Aplicação da teoria fuzzy nos modelos... 52
4.1 Lei de Fick…………...... 56
4.2 Princípio da conservação de massa... 57
4.3 Equações do transporte de poluentes... 59
4.3.1 Equação da difusão molecular... 59
4.3.2 Equação da difusão advectiva... 59
4.3.3 Equação da difusão turbulenta... 60
4.4 Equação do transporte de poluentes fuzzificada... 64
4.5 Classificação dos rios segundo a qualidade de suas águas... 65
CAPÍTULO 5 – ANÁLISE DE RISCO... 70
5.1 Risco e incertezas... 71
5.2 Análise de risco... 72
5.3 Risco fuzzy... 76
5.4 Cálculo do risco fuzzy... 77
CAPÍTULO 6 –FORMULAÇÃO NUMÉRICA E ASPECTOS COMPUTACIONAIS... 80
6.1 Formulação numérica para solução do modelo da onda cinemática... 83
6.2 Formulação numérica para solução do modelo da onda difusiva... 85
6.3 Formulação numérica para solução do modelo de transporte de poluentes... 87
6.4 Aspectos computacionais... 91
6.5 Cenários de simulação... 93
6.5.1 Cenário 1: Escoamento permanente (sem efeito de ondas de cheia)... 93
6.5.2 Cenário 2: Escoamento sob efeito da onda cinemática... 93
6.5.3 Cenário 3: Escoamento sob efeito da onda difusiva... 93
CAPÍTULO 7 – ANÁLISE E DISCUSSÃO DOS RESULTADOS... 94
7.1 Cenário 1 - Escoamento permanente (sem efeito de ondas de cheia)... 95
7.2 Cenário 2 - Escoamento sob efeito de onda cinemática... 102
CAPÍTULO 1
1 CONSIDERAÇÕES INICIAIS
A presença de componentes físicos, químicos e biológicos nos rios associada à dinâmica fluvial presente nestes ecossistemas permite a existência de processos extremamente complexos, fazendo com que sua descrição através de modelos matemáticos se torne uma missão desafiadora. Isto implica a necessidade de se estabelecer um conjunto de simplificações criteriosas, de modo a se ter resultados que venham descrever esses processos com um grau de realismo.
A utilização de modelos matemáticos para avaliar as questões de lançamento e
assimilação de poluente em um corpo d’água é uma ferramenta de suma importância, em
virtude da complexidade dos processos determinantes nas questões da qualidade de água (CHAPRA, 1997).
A formulação de um modelo matemático para descrever as interações físicas químicas e biológicas em um sistema aquático vem sendo realizada com mais frequência após o desenvolvimento de sistemas computacionais, considerando esta complexidade citada anteriormente.
Quando se estuda qualidade de água mediante a aplicação de modelos matemáticos, dois tipos de modelos podem ser considerados. O primeiro, conhecido como modelo determinístico, trata da solução de problemas onde não há necessidade de análise de incertezas. Neste caso, estudo de risco não pode ser considerado com esta classe de modelos. O outro tipo de modelo, chamado de modelo estocástico, trata de problemas onde análise de incerteza precisa ser realizada. Os modelos estocásticos, no entanto, necessitam de um banco de dados consistente para sua aplicação.
Atualmente, para contornar estas dificuldades de bancos de dados, surgiu uma teoria que permite que análise de incertezas possa ser realizada com a necessidade de bancos de dados tão consistentes. Esta teoria, chamada de teoria fuzzy, tem se tornado uma ferramenta consistente na análise de problemas de qualidade de água.
alguns problemas, soluções exatas nem sempre são necessárias, assim, uma solução aproximada, porém rápida, pode ser útil numa tomada de decisão preliminar, ou como estimativa inicial em uma técnica numérica para poupar custos computacionais, ou em inúmeras situações onde os valores de entrada para o sistema são vagos, ambíguos ou desconhecidos.
1.1 Objetivos da Pesquisa
1.1.1 Objetivo Geral
Analisar a relação entre campos de concentração e ondas de cheia em rios naturais, mediante a aplicação de um modelo bidimensional de transporte de massa na sua forma fuzzy,
de modo que campos de risco ambiental possam ser estudados.
1.1.2 Objetivos Específicos
Desenvolver um modelo de transporte de massa bidimensional aplicado em rios de grandes dimensões;
Fuzzificar o modelo desenvolvido de modo que campos de concentração com diferentes graus de pertinência possam ser calculados;
Desenvolver modelos de onda cinemática e onda difusa que possam ser aplicados separadamente neste corpo hídrico;
Fuzzificar os modelos de ondas de cheia de modo que sejam incorporadas as incertezas do processo;
Formular uma metodologia para calcular o risco e a confiabilidade ambiental deste corpo hídrico para diferentes cenários de lançamento;
Desenvolver um programa computacional em linguagem Fortran que permita a obtenção de resultados provenientes das equações diferenciais que compõem o modelo integrado;
1.2 Organização do trabalho
Esta tese foi organizada em oito capítulos. O capítulo 1 descreve sua introdução, os objetivos da pesquisa e como o documento foi organizado.
O capítulo 2 apresenta os principais fundamentos da teoria fuzzy. Neste capítulo estão descritas as principais definições, assim como as operações e técnicas de operações aritméticas da teoria fuzzy.
O capítulo 3 apresenta a fundamentação da mecânica fluvial. Aqui são mostradas as formulações da continuidade, quantidade de movimento, onda cinemática e difusiva. No final do capítulo, as formulações são transformadas em funções de pertinência mediante aplicação da teoria fuzzy.
O capítulo 4 apresenta os fundamentos do transporte de poluentes. Aqui as equações de transporte são deduzidas a partir da lei de Fick e princípio da conservação de massa. Em seguida, essas equações são formuladas para seu uso nos estudos de qualidade de água em rios. No final do capítulo, as formulações são transformadas em equações diferenciais fuzzy
mediante a transformação dos principais parâmetros do modelo em parâmetros fuzzy.
O capítulo 5 apresenta os fundamentos da análise de risco. Neste capítulo são mostradas as diversas faces que compõem a metodologia para o cálculo do risco fuzzy. A função marginal é definida e mostrada, assim como o mecanismo de operação e as formulações do cálculo dos índices do risco e da confiabilidade fuzzy.
O capítulo 6 apresenta a formulação numérica e os aspectos computacionais desenvolvidos ao longo da pesquisa. Neste capítulo são mostrados os conceitos e fundamentos da teoria do método das diferenças finitas, com os seus mais diversos esquemas numéricos para soluções de equações diferenciais. Este método é usado na solução das diversas equações diferenciais fuzzy que compõem o estudo em questão.
O capítulo 7 apresenta uma análise e discussão dos resultados. Neste capítulo são mostrados os vários resultados obtidos a partir do programa computacional sendo, sendo para tal, mostrado em uma sequência composta pelos vários cenários que compuseram o estudo.
CAPÍTULO 2
2 TEORIA DOS CONJUNTOS DIFUSOS
A incerteza pode ser pensada como sendo o inverso da informação. A informação sobre um particular problema de engenharia pode ser imprecisa, incompleta, fragmentada, incerta, vaga, contraditória, ou deficiente de alguma forma (KLIR & YUAN, 1995). Quanto mais complexo é um sistema, mais imprecisa ou inexata é a informação que se tem para caracterizá-lo. Além disso, uma maior precisão implica em altos custos.
A gradual evolução da palavra incerteza usando a teoria da probabilidade foi desafiada primeiramente em 1937 por Max Black com seus estudos em imprecisão, e posteriormente coma introdução dos conjuntos difusos ou conjuntos fuzzy por Zadeh (1965).
O trabalho de Zadeh teve uma profunda influência no pensamento sobre a incerteza já que este desafiou não só a teoria da probabilidade como única representação da incerteza, mas também os próprios fundamentos nos quais a teoria da probabilidade foi baseada: lógica binária clássica (KLIR & YUAN, 1995).
A lógica fuzzy tem se mostrado adequada no tratamento de termos incertos, subjetivos e vagos (BARROS & BASSANEZI, 2006). De forma mais objetiva e preliminar, pode-se definir lógica fuzzy como sendo uma ferramenta capaz de capturar informações vagas, em geral descritas em uma linguagem natural, e convertê-las para um formato numérico, de fácil manipulação pelos computadores (TANAKA, 1997).
O principal benefício da teoria de sistemas difusos adicionado a um modelo dinâmico é aproximar o comportamento do sistema onde não existem funções analíticas ou numéricas, ou seja, sistemas complexos. Alternativamente, a teoria dos conjuntos difusos pode ser utilizada na avaliação de sistemas mais convencionais, menos complexos. Para alguns problemas, soluções exatas nem sempre são necessárias, assim, uma solução aproximada, porém rápida, pode ser útil numa tomada de decisão preliminar, ou como estimativa inicial em uma técnica numérica para poupar custos computacionais, ou em inúmeras situações onde os valores de entrada para o sistema são vagos, ambíguos ou desconhecidos.
2.1 Conjuntos difusos (Conjuntos fuzzy)
A teoria dos conjuntos fuzzy (ZADEH, 1965; ZIMMERMANN, 1985) é um método matemático usado para caracterizar e quantificar a incerteza e imprecisão nos dados e relações funcionais. Conjuntos difusos são especialmente úteis quando o número de dados não é suficiente para caracterizara incerteza por meio de medidas padrão da estatística envolvendo a estimativa de frequências.
A ideia proposta por Lotfi Zadeh sugere que definir a função de pertinência é a chave para a tomada de decisão quando há incerteza. De acordo com Ganoulis (1994) o conceito central da teoria dos conjuntos difusos é a função de pertinência que representa numericamente o grau em que um elemento pertence a um conjunto. Se um elemento pertence a um conjunto difuso em algum grau, o valor da sua função de pertinência pode ser qualquer número entre 0 e 1. Quando a função de pertinência de um elemento pode ter apenas os valores 0ou1, a teoria dos conjuntos se reduz à teoria clássica dos conjuntos.
Um conjunto difuso consiste em um conjunto de pares ordenados que contém o elemento () e seu valor de pertinência~()
F . Formalmente, um conjunto F ~
é chamado
fuzzy em um universo, se ela consiste de pares ordenados tais que:
]} 1 , 0 [ ) ( ; : )) ( , {( ~ ~ ~
F F
F
Em contraste com as regras básicas de probabilidade, na teoria dos conjuntos difusos, as regras a seguir são definidas na forma de axiomas para avaliar a função de pertinência da uniãoA~B~ e da intersecçãoA~B~dos conjuntos difusosA~eB~. Para cada dois conjuntos difusosA~ e B~pertencentes ao universo, temos:
)) ( ), ( ( ) ( ; ~ , ~ ~ ~ ~ ~
A B má x A B
B
A
)) ( ), ( min( ) ( ; ~ , ~ ~ ~ ~ ~
A B A B
B
A
Outra regra básica na teoria dos conjuntos difusos é de complementação.A~Cé um
complemento de conjunto difusoA~, quando:
A AC
~
~ 1
Diferente da abordagem probabilística, as regras de união, interseção e complementação na teoria dos conjuntos fuzzy não implica necessariamente que:
AC e A AC
A~ ~ ~ ~
Como é o universal ou referencial ou “sempre o evento certo” e é o conjunto vazio, que se identifica como "evento sempre impossível". Isso significa que:
0 ) ( 1
) (
;
2.2 Conjuntos nível h, difusos normal e convexo
Para cada elementopertencente aA~, está associado um nível hde pertinência. Inversamente, consideram-se todos os elementos tendo o mesmo nível de pertinênciah. Assim, o conjunto de nível h de um conjunto difusoA~, é definido como o conjunto ordinário de todos os elementos cujo valor de pertinência éhou superior, ou seja:
]} 1 , 0 [ ; );
) ( , {( )
(h ~ h h
A
A
Um conjunto difuso normal é aquele em que pelo menos um valor de existe,
tal que()1. Em outras palavras, o valor máximo da função de pertinência é a unidade.
Um conjunto difuso convexo é aquele onde para cada número real a, b, c e com
c b
a , aplica-se que:
)) ( ), ( ( )
( ~ ~
~ b mín a c
A A
A
2.3 Números difusos
Um número difusoX~ é um caso especial de conjuntos difusos, tendo as seguintes propriedades (KAUFMANN & GUPTA, 1985; 1988): a) É definido no conjunto dos números reais , ao invés de um conjunto de propriedades linguísticas; b) A sua função de pertinência atinge sempre o valor máximo de 1, ou seja, é um conjunto difuso normal; c) A sua função de pertinência é unimodal, logo consiste em uma parte crescente e decrescente; d) Uma aritmética completa está disponível para combinar números difusos, além disso, as funções multidimensionais de números difusos podem ser definidas e calculadas. Assim, a análise de incerteza, as previsões do modelo e análise de risco e confiabilidade fuzzy podem ser realizadas.
Um número difuso ou fuzzy pode ser formalmente definido como:
]} 1 , 0 [ ) ( ; : )) ( , {( ~
~
~
x x x x
X X X
As funções de pertinência podem ter diferentes formas, dependendo do conceito que se deseja representar e do contexto em que serão utilizadas. Podem ser definidas a partir da experiência do usuário, mas comumente são utilizadas funções de pertinência padrões como de forma triangular, trapezoidal e gaussiana.
Segundo Galvão& Valença (1999), as formas gráficas mais comuns de se representar um conjunto difuso são a triangular e trapezoidal. Nesse estudo serão adotados conjuntos difusos na forma triangular.
O número fuzzy triangular (NFT) é uma associação de funções de pertinência lineares de cada lado do pico. Pode ser caracterizado por três números reais: dois valores onde a função de pertinência alcança zero, e o outro alcança o valor unitário. Assim, A~ (a,b,c)
Figura 2.1 – Conjunto difuso na forma triangular.
Fonte: Elaborado pela autora.
A função de pertinência de um NFT é definida como (CHENG, 1999; HSIEH & CHEN, 1999):
; ,
0 ) (
~ x se x a
A
; ,
) (
~ se a x b
a b
a x x
A
; ,
) (
~ se b x c
b c
x c x
A
. ,
0 ) (
~ x se x c
A
Segundo Li et al. (2007), um NFT pode ser considerado como um valor aproximado de intervalo com uma função de pertinência. Dentro do intervalo, diferentes valores numéricos correspondem a diferentes graus de pertinência ou confidência. Supõe-se que
1 ) (
~ x
A
corresponde ao valor mais provável e ~(x)0
A
2.4 Representação L-R de um número difuso
A função de pertinência de um número difuso pode ser descrita matematicamente por meio de duas funções estritamente decrescentes L e R (DUBOIS & PRADE, 1980).
Para um número difuso convexo, a parte de uma função de pertinência a esquerda do
pico pode ser expressa em termos da variável adimensional (xm x)/x1como a função L. A
parte correspondente à direita do pico é expressa em termos da variável adimensional
2 / ) (xxm x
como a função R.
0 ,
0 ,
2 2
1 1
~
x e x x x
x x R
x e x x x
x x L
m m
m m
X
Pelo uso da notação L-R, um número difusoX~é simbolicamente expresso como:
LR m x x x
2.5 Operações aritméticas em intervalos
O cálculo difuso é extensão das operações realizadas em intervalos de números reais.
2.5.1 Adição
Um intervalo é definido como um par ordenado em colchetes como:
} :
{ ] ,
[a1 a2 a a1 a a2
A
Onde,
1
a é o limite esquerdo e
2
a é o limite direito deA.
Tomando dois intervalos [ , ]
2 1 a a
A eB[b1,b2], a soma do intervalo é dada por:
] ,
[a1 b1 a2 b2 B
A
C
Operações com números difusos podem ser realizadas considerando seus intervalos de nível h, e depois aplicaras operações correspondentes em intervalos. De modo geral, tomando dois números difusos ̃ e ̃eseus correspondentesintervalosde nível h:
̅ [ ] e ̅ [ ]
Define-se a soma de dois números difusos como sendo:
̃ ̃ ̃
Logo, considerando o nível h temos:
̅ ̅ ̅ [ ] [ ]
Em caso de números fuzzy triangulares a operação é simples:
2.5.2 Subtração
Tomando dois intervalos ̅ [ ] e ̅ [ ]. O intervalo oposto de ̅ é a imagem espelhada de ̅ tendo o ponto 0 como origem, ou seja:
̅ [ ]
Assim, a diferença entre os intervalos ̅ e ̅ é:
̅ ̅ ̅ ̅ ̅ [ ]
Define-se o oposto de um número difuso ̃ como sendo:
̅ [ ]
Logo, considerando o nível h temos:
̅ ̅ ̅ ̅ ̅ [ ] [ ]
Em caso de números fuzzy triangulares:
̃ ̃ ̃
2.5.3 Multiplicação
O produto de dois intervalos ̅ [ ] e ̅ [ ] é dado pela simples relação:
̅ ̅ ̅ [ ]
Define-se o produto de dois números fuzzy ̃ e ̃ como sendo:
̃ ̃ ̃
Logo, considerando o nível h temos:
Em caso de números fuzzy triangulares:
̃ ̃ ̃
Vale ressaltar que o produto de dois números fuzzy triangulares não é necessariamente outro número fuzzy triangular.
2.5.4 Divisão
Tomando dois intervalos ̅ [ ] e ̅ [ ]. O intervalo inverso de ̅ é definido como sendo:
̅ [ ]
Assim, a razão entre os intervalos ̅ e ̅ é:
̅ ̅
̅ ̅ ̅ [ ]
Define-se o inverso de um número difuso ̃ como sendo:
̅ [
]
Logo, considerando o nível h temos:
̅ ̅ ̅ ̅ ̅ [
] [ ]
Em caso de números fuzzy triangulares:
̃ ̃
̃ ( )
2.6 Princípio da extensão
O princípio da extensão de Zadeh (1965) é utilizado para estender operações típicas dos conjuntos clássicos, promovendo a extensão de conceitos matemáticos não-difusos em difusos. Usando esse princípio, que é uma ferramenta básica da aritmética difusa, é possível operar ponto a ponto em conjuntos difusos. Pode-se descrever o princípio da extensão da seguinte forma (JAFELICE, 2004):
O grau de pertinência de um valor do contradomínio é definido diretamente pelo grau de pertinência de sua pré-imagem.
Quando um valor do contradomínio é mapeado por vários domínios, o seu grau de pertinência é obtido pelo valor máximo dos graus de pertinência dos valores de entrada.
Sejam dois conjuntos arbitrários X e Y e f uma função de um conjunto X para um conjunto Y, isto é:
A função f é determinística e pode ser estendida para uma situação de conjunto difuso. Logo, seja ̃ um conjunto difuso em X com função de pertinência ̃ . A imagem de ̃ em Y é o conjunto difuso ̃com função de pertinência dada pelo seguinte princípio de extensão:
̃ ̃ ;
Chongfu (1996) demonstrou um método avançado para calcular a liberação, exposição
e as consequências dos perigos naturais urbanos, através da avaliação de risco difuso. Foi
considerado cálculo para um terremoto, onde foi discutida a maneira de calcular o risco fuzzy
de um terremoto, a intensidade local, reações individuais, e as perdas de uma cidade. O
método proposto mostrou ser útil para qualquer tipo de perigo natural em que a abordagem
probabilística convencional é insuficiente ou complexa.
Lee & Wen (1997) aplicaram duas abordagens de programação objetiva fuzzy (FGP) à
gestão da qualidade da água em uma bacia hidrográfica do rio Tou-Chen em Taiwan, para
resolver problemas de otimização multiobjetiva envolvendo informações vagas e imprecisas.
O caso de estudo demonstrou a capacidade das duas abordagens FGP funcionarem
adequadamente na gestão da qualidade da água em uma bacia hidrográfica.
Dubois & Prade (1998) introduziram a noção de conjuntos difusos como uma
ferramenta para modelagem de conjuntos com limites mal definidos ou flexíveis. Os autores
reconhecem que os conjuntos difusos são uma ferramenta importante na engenharia de informação com o objetivo de “tapar os buracos” existentes entre o conhecimento originado pelo homem, e dados numéricos.
Chang et al. (2001) apresentaram um estudo comparativo usando três técnicas de
avaliação fuzzy para avaliar as condições de qualidade da água em comparação com os
resultados gerados por procedimentos convencionais, como o índice de qualidade da água
(IQA). Com base em um conjunto de dados coletado sem estações de amostragem, foi
realizado um estudo de caso para o sistema fluvial Tseng-Wen em Taiwan para demonstrar
seus potenciais de aplicação. Os resultados indicaram que as técnicas podem harmonizar com
sucesso discrepâncias inerentes e interpretar condições complexas.
Liou et al. (2003) propuseram um modelo de indicadores para avaliar as tendências na qualidade do rio usando uma teoria de conjuntos difusos de dois estágios para condensar de
forma eficiente os dados monitorados. As funções de pertinência do índice de poluição do rio
padrão (IPR) foram construídas como distribuições lineares. As variáveis normalizadas foram
construídas com base na extensão da convergência da média-c fuzzy (MCF). As somas
ponderadas dos graus de similaridades derivadas das extensões da MCF foram usadas para
construir um índice global alternativo, o índice de qualidade do rio (IQR). Concluiu-se que o
resultando em uma abordagem mais sistemática. O modelo proposto neste trabalho é uma
nova idéia criativa no índice de avaliação ambiental, pois fornece um modelo menos
subjetivo, mais sensível e mais eficiente para avaliar a qualidade e as mudanças na qualidade.
Vieira et al. (2004) demonstraram toda a versatilidade e adequabilidade do uso da teoria dos conjuntos difusos (TCD) nas áreas de recursos hídricos e meio ambiente através da caracterização de danos de inundação, benefícios e riscos econômicos difusos, relações custo/benefício, quantificação de impactos ambientais, indicação de níveis de pertinência de impactos negativos (deterioração ambiental), bem como os riscos ambientais difusos.
Ocampo-Duque et al. (2006) propuseram uma metodologia baseada em sistemas de
inferência fuzzy para avaliar a qualidade da água. O potencial de aplicação do índice difuso foi
testado com dados coletados do rio Ebrona Espanha por duas diferentes agências de proteção
ambiental. Os resultados concordaram com relatórios oficiais e opiniões de especialistas sobre
os problemas de poluição na área estudada. Assim, este método surge como uma ferramenta
adequada e alternativa para o desenvolvimento de eficazes planos de gestão de água, embora
na avaliação global das águas européias haja a necessidade de usar componentes bióticos, e
não somente o monitoramento químico das redes como foi utilizado pelos autores.
Karmakar & Mujumdar (2006) desenvolveram um modelo de otimização difusa denominado modelo de alocação de cargas residuais difusas cinzentas – GFWLAM para a gestão do sistema fluvial abordando as incertezas envolvidas na fixação das funções de
pertinência para diferentes objetivos da Agência de Controle da Poluição e descarregadores.
Os níveis de remoção de fraccionais ótimos dos poluentes são obtidos sob a forma de
números em intervalos, o que aumenta a flexibilidade e aplicabilidade no processo de tomada
de decisão à medida que o decisor recebe uma gama de soluções ideais para a fixação do
esquema de decisão final. De um modo geral, é adaptável em vários sistemas ambientais onde
um uso sustentável e eficiente do ambiente é de interesse.
Icaga (2007) propôs um modelo de índice para avaliação da classificação da qualidade
da água superficial usando lógica fuzzy. As classes de qualidade convencionais foram
transformadas em formas contínuas. Os valores de concentração dos diferentes parâmetros de
qualidade foram acrescidos usando regras fuzzy, e por fim, o índice foi desenvolvido após a
defuzzificação dosvalores somados. A aplicação prática e viabilidade do modelo proposto
Turquia. Concluiu-se que o poder do método depende da capacidade de integrar diferentes
tipos de observações de qualidade.
Dahiya et al. (2007) aplicou a teoria dos conjuntos difusos para a tomada de decisão
na avaliação da qualidade físico-química da água subterrânea para fins de consumo. Foi
aplicada a regra difusa em um modelo de otimização em amostras de água subterrânea
coletadas, e analisa dos16 diferentes parâmetros físico-químicos de qualidade da água, sendo
essa abordagem difusa aplicada em 10 destes. Concluiu-se que mais da metade das fontes de
água se enquadraram na categoria "desejável" ou "aceitável"parafins de consumo, assim, estas
podem ser avaliadas de maneira mais logística, e os resultados sobre a classificação da
qualidade da água pode ser descrito comum nível de confiança de pertencimento de amostras
específicas para qualquer categoria bem definida de água potável.
Li et al. (2007) simularam relações difusas e imprecisas na modelagem de qualidade
da água do rio utilizando a aritmética fuzzy. Foi estabelecido um modelo bidimensional difuso
de qualidade da água para súbita descarga poluente cujos parâmetros de qualidade da água
foram definidos como números fuzzy triangulares simétricos. As concentrações de poluentes
foram obtidas por meio da técnica do corte-α e operações aritméticas de números triangulares
difusos. Os resultados do estudo revelaram que é possível em teoria, e confiável em cálculo, a
aplicação de números fuzzy triangulares para a simulação da qualidade da água do rio.
Lermontov et al. (2009) propuseram a criação de um novo índice de qualidade da água
com base na lógica fuzzy, o índice de qualidade de água fuzzy (IQAF). O desempenho do
índice proposto foi avaliado por meio da comparação com diversos índices de qualidade da
água (IQA’s) sugeridos na literatura, e utilizando dados de levantamentos hidrográficos do rio
Ribeira do Iguape, São Paulo. Esta metodologia incorpora o fator peso na esfera qualitativa ao
longo das regras na inferência. O índice mostrou uma boa correlação com o IQA
tradicionalmente calculado no Brasil podendo ser utilizado como uma ferramenta alternativa
para na gestão ambiental de tomada de decisão.
Rehana & Mujumdar (2009) desenvolveram um modelo de alocação de cargas
residuais difusas imprecisas para a gestão da qualidade da água de um sistema fluvial sujeito a
uma crescente incerteza. Foi realizada a simulação de Monte-Carlo para avaliar o risco difuso
impreciso da baixa qualidade da água, considerando as variáveis de entrada como imprecisas.
sujeito a incertezas e dados perdidos em uma variável hidrológica. Além disso, com modelos
apropriados de distribuição espacial e temporal do poluente num corpo hídrico, essa
metodologia pode ser utilizada para reduzir o risco, no qual os parâmetros de qualidade da
água estão sujeitos a erros.
Janssen et al. (2010) desenvolveram um método para a avaliação das incertezas em modelos baseados em regras fuzzy é proposta, combinando a avaliação das incertezas na estrutura do modelo, nos dados de entrada e nos parâmetros. Num modelo exemplo, cada um destes três possui o potencial para dominar incerteza agregada, apoiando a relevância de uma abordagem incerteza ampla. A contribuição relativa das diferentes incertezas para a incerteza total pode fornecer um resultado útil levar para a redução da incerteza.
Peche & Rodríguez (2012) desenvolveram uma metodologia baseada na lógica fuzzy
para o projeto e a posterior avaliação de índices de qualidade ambiental (IQA) permitindo a concepção de índices específicos para avaliar a qualidade de diferentes perspectivas em qualquer compartimento ambiental. A metodologia foi aplicada a um estudo de caso simplificado, a fim de ilustrar a sua aplicação prática: a concepção e avaliação de um índice de qualidade físico-química do solo num local particular.
Jayawardena et al. (2014) basearam seu estudo na utilização de uma abordagem lógica
fuzzy. A confiabilidade e a robustez da abordagem foram demonstradas com previsões de descarga diárias e de 6 horas, de 4 rios em 3 países com contrastantes climatológicos, características geográficas e de uso da terra. Foram usados tanto sistemas de inferência fuzzy
CAPÍTULO 3
3 MECÂNICA FLUVIAL
O escoamento em canais fluviais apresenta diversas características dinâmicas que se tornam responsáveis pelas qualidades atribuídas aos processos fluviais (CHRISTOFOLETTI, 1981).
Um modelo matemático tendo como base a segunda lei de Newton e o princípio da conservação das massas é conhecido como modelo hidrodinâmico quando todos os termos responsáveis pelo movimento do fluido no canal são representados pela equação do movimento. O conjunto de equações diferenciais resultantes desta combinação é conhecido como equação de Saint Venant. Esses modelos têm sido utilizados por várias décadas nos estudos de propagação de ondas de cheia, e é possível encontrar na literatura um rico material propondo diferentes abordagens para o tratamento destas equações (SHEN & YEN, 1984).
3.1 Dedução da equação de Saint-Venant
A combinação da equação da continuidade (princípio da conservação de massa) com a equação da conservação da quantidade de movimento é conhecida como equação da onda dinâmica, ou equações de Saint-Venant. Essas equações descrevem a propagação de uma onda de cheia, onde variáveis de controle (i.e. velocidade, vazão, área e profundidade) variam com o tempo e posição. Assim, o movimento de uma onda de cheia representa um escoamento não permanente e não uniforme.
Existem diferentes maneiras de deduzir estas equações. Tendo em vista o melhor entendimento e simplicidade do processo de formulação, foi adotado o método do volume de controle (V.C.). No entanto, segundo Sturm (2001), algumas considerações devem ser assumidas: i) escoamento em águas rasas; ii) declividade do canal pequena; iii) fundo do canal estável; iv) escoamento unidimensional; e, v) resistência de atrito de fundo é a mesma tanto no escoamento não permanente como no escoamento permanente.
3.1.1 Equação da continuidade
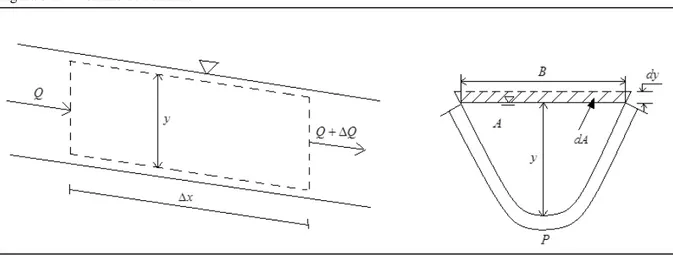
A equação da continuidade é obtida através da aplicação do princípio da conservação das massas em um volume de controle de comprimento xem um trecho do rio, conforme ilustrado na figura 3.1.
Figura 3.1 – Volume de controle.
Fonte: Elaborado pela autora.
Pelo princípio da conservação de massa, o balanço de massa fluida de entrada no volume de controle pela seção de montante em um intervalo de tempo t e saída no volume de controle pela seção de jusante em um intervalo de tempo té igual à variação temporal da massa fluida no interior deste volume. Matematicamente, este princípio é representado pela seguinte formulação:
t x t A t
x x Q Q
t
Q
(3.1)
Vale ressaltar que contribuições laterais não serão consideradas neste estudo.
Onde:
Massa específica da água [ML3];
Q Vazão média no interior do canal natural [L3T1];
t
Intervalo de tempo relativo ao volume de controle [T];
x
Comprimento do volume de controle [L];
Simplificando a equação (3.1) temos: t x t A t x x Q t Q t
Q
Dividindo por
xt
:t A x Q
Considerando o escoamento de fluido incompressível ( constante):
t A x Q 0 x Q t A (3.2)
Esta é a equação da continuidade, onde as variáveis de controle são a vazão e a área.
Outra maneira de apresentar a equação (3.2) é considerando o canal retangular. Logo:
y B A
0 t y B x Q (3.3) Onde:
B Largura do canal [L ; ]
y Profundidade do canal [L . ]
3.1.2 Equação da quantidade de movimento
A equação da quantidade de movimento é deduzida a partir da aplicação da 2ª lei de Newton em um volume de controle, conforme ilustrado na figura 3.2.
Figura 3.2 – Forças que atuam sobre a massa fluida.
Fonte: Elaborado pela autora.
As forças que atuam sobre o volume de controle da figura 3.2 são a componente das forças de pressão hidrostática
FP1eFP2
, e a força de atrito nas paredes e fundo ( fa).a m f F
FP1 P2 a
a x A x
P h
A o
dt dv x A x
P h
A o
Dividindo todos os termos por x:
dt dv A P
x h
A o
(3.4)
Lembrando que a velocidade é dada em função do tempo e espaço, ou seja:
) , (xt v
Pela regra da cadeia: dt t v dx x v dv
Dividindo todos os termos por t:
t v dt dx x v dt dv Assim: x v v t v dt dv a
Substituindo na equação tem-se:
x v v t v A P x h
A o
Dividindo todos os termos pela área (A):
x v v t v A P x h o x v v t v x h A P
o
Do conceito de raio hidráulico,
P A
Rh , é possível reescrever a equação acima.
Assim: x v v t v x h Rh
o
Do conceito de peso específico, g, e colocando em evidência, é possível reescrever a equação acima. Assim:
x v v t v g x h Rh
o 1
x v v t v g x h Rh o 1 (3.5)
Considerando o escoamento permanente e não uniforme tem-se que o termo
t v é nulo. Assim: x v v g x h Rh o 1 g v h x Rh o 2 2
H x Rh o (3.6) Onde: o Tensão de cisalhamento de fundo [ML1T2]; Peso específico do fluido[ML2T2];
h
R Raio hidráulico[L];
h Cota da superfície livre do canal em relação a uma referência definida [L];
x Distância ao longo do canal[L];
g Aceleração da gravidade [LT2];
v Velocidade média do fluido no volume de controle [LT1];
H Energia total do escoamento no volume de controle [L].
Sabendo que a declividade da linha de energia (Sf ) é dada pela tangente do ângulo formado entre a linha de energia e o eixo positivo de x. Logo:
x H S tg f x H Sf
Voltando para equação (3.6) tem-se:
f hh o f
R S
(3.8)
Logo, é possível verificar que a equação (3.7) pode ser gerada a partir da equação do movimento. Entretanto, essa equação não permite o cálculo das velocidades. Para isso, há necessidade de relacionar as velocidades com a tensão de cisalhamento através de uma formulação empiríca que foi formulada por Chézy:
2 v o
Para transformarmos a proporcionalidade em uma igualdade, se faz necessário acrescentar uma constante que depende da rugosidade das paredes do canal. Assim:
2
'v k
o
(3.9)
Onde:
'
k Coeficiente de proporcionalidade.
Substituindo (3.9) em (3.7):
f
h S
R v
k' 2
' 2
k S R v h f
' k
S R v h f
f
h S
R k
v
'
vC Rh Sf
(3.10) Onde:
'
k
C
Elevando (3.10) ao quadrado:
f
h S
R C v2 2
h f R C v S 2 2 (3.11)
Combinando as equações (3.11) e (3.8):
h o h f R R C v S
2
2
(3.12)
Admitindo agora o escoamento não permanente e não uniforme, e combinando as equações (3.12) e (3.5) tem-se:
t v g x v g v x h R S h o f 1
Lembrando que h yztem-se:
t v g x v g v x z x y R S h o f 1
(3.13)
Sabendo que a declividade de fundo (So) é dada pela tangente do ângulo formado entre a cota do canal (z) e o eixo positivo(x) tem-se:
x z S tg o x z So
Substituindo em (3.13):
t v g x v g v x y S
Sf o
1 0 1
Sf So
0 o
f g S
S g x y g x v v t v (3.14)
Esta é a equação da quantidade de movimento para rios e canais naturais.
A equação (3.14) pode ser escrita em função da vazão e da área. Assim:
A Q
v
02 2
g Sf So
x y g A Q x A Q t Ou:
02 o f S S A g x y A g A Q x t Q (3.15)
Os métodos hidrológicos para propagação de cheias estão baseados em simplificações das equações de Saint-Venant.
A propagação de uma onda de cheia em um corpo hídrico é um processo físico de alta complexidade. Uma onda representa uma variação em um escoamento, tal como uma
mudança na vazão ou no nível da superfície d’água. Este fenômeno pode ser ocasionado por
uma chuva intensa ou pelo rompimento em uma estrutura de controle qualquer, a jusante do corpo hídrico.
Dentro de um contexto de modelos, as ondas de cheias podem ser classificadas como: onda dinâmica, onda gravitacional, onda difusa e onda cinemática, de acordo com o número de elementos considerados no modelo.
Os modelos para estudo de onda de cheia podem ser usados para descrever a transformação de chuva torrencial em escoamento superficial sobre uma bacia hidrográfica, ou produzir uma hidrógrafa do escoamento e, então considerar esta hidrógrafa como dado de entrada na extremidade a montante de um rio (CHOW, 1988; HENDERSON, 1966).
3.2 Modelo da onda cinemática
As ondas cinemáticas são oriundas da equação de Saint-Venant levando em consideração apenas o termo gravitacional e o termo de atrito na equação de movimento. Logo, a equação geral do movimento (3.15) se reduz à equação abaixo:
0 Sf g So g
o
f S
S
Na sua formulação, há a necessidade de se introduzir uma equação de estado que relacione a área da seção transversal com a vazão. Para este trabalho foi utilizada a equação de Manning. 2 / 1 3 / 2 f h S R n A
Q
2 / 1 3 / 2 o h S R n A
Q
2 / 1 3 / 2 3 / 2 o S P A n A
Q
Isolando o termo da área, A, tem-se:
2 / 1 3 / 2 3 / 5 o S P n Q
A
5 / 3 5 / 3 2 / 1 3 / 2 Q S P n A o Assim:: Q
A
Como a área pode ser dada em função da vazão, ou seja, A f(Q):
t Q Q t A
1
Substituindo na equação da continuidade (3.2):
0 1 x Q t Q Q
Dividindo todos os termos por (Q1):
0 1
1
x Q Q t Q 0 1 x Q Q t Q
Esta equação pode ser reescrita da seguinte maneira:
0 ) ( x Q Q K t Q (3.16) Onde:
Q Vazão do corpo hídrico [L3T1];
Parâmetro geométrico do rio definido por:
5 / 3 2 / 1 3 / 2 o S nP
n Coeficiente de rugosidade de Manning;
P Perímetro molhado [L]; o
S Declividade do fundo do canal [L/L];
) (Q
K Celeridade da onda [LT1]definida por:
1
) (Q Q K
A equação da onda cinemática é uma equação não linear. Esta equação diferencial é resolvida mediante o método das diferenças finitas usando para tal um esquema explícito com linearização da celeridade, K(Q). A solução numérica será abordada no capítulo 6, e consiste em obter os valores das funções em um número de pontos através da substituição das derivadas da função que aparecem na equação diferencial por expressões aproximadas.
3.3 Modelo da onda difusiva
As ondas difusas são oriundas da equação de Saint-Venant, levando em consideração a aceleração causada pela variação da pressão ao longo do rio, além do termo gravitacional e de atrito, na equação do movimento.
Logo, a equação geral do movimento (3.15) se reduz à equação abaixo:
0
g A Sf So
x y A g
0 o f S S x y x y SSf o
(3.17)
Da equação de Manning:
2 / 1 3 / 2 f h S R n A
Q
Elevando ao quadrado e isolando o termo da declividade da linha de energia tem-se:
f
h S
R n A
Q 2 4/9 2 2 2 9 / 4 2 2 Q R A n S h f 2 2 1 Q k
Sf
k Parâmetro de transporte que depende das características do canal definido por: 2 9 / 4 2 2 n R A
k h
3 / 2 h R n A
k
A expressão (3.18) foi substituída na equação (3.17). Assim:
x y S k Q o 2 2
Derivando com relação ao tempo:
x
y t k Q t 2 2 t x y k t k k Q t Q k Q 2 4 2 2 2 2 t x y k t k Q t Q k Q 2 3 2 2 2 t y x t x y t k k Q t Q k Q 2 3 2 2 2 2 (3.19)
Substituindo na equação da continuidade (3.3):
0 t y B x Q x Q B t y 1
Substituindo em (3.19):
2 2 3 2 2 1 1 2 2 x Q B x Q B x t k k Q t Q k Q (3.20)
Pela regra da cadeia tem-se que:
Pela equação da continuidade: x Q t A Assim: dA dk x Q t k (3.21)
Da equação de Manning tem-se:
2 / 1 3 / 2 f h S R n A
Q
k R n A S Q h f 2/3 2
/ 1
(3.22)
Da equação (3.22) é possível verificar que:
2 / 1 1 f S dQ dk (3.23)
Substituindo (3.22) em (3.20):
2 2 2 / 3 3 2 2 1 2 2 x Q B t k S Q Q t Q S Q Q f f 2 2 2 / 3 1 2 2 x Q B t k Q S t Q Q
Sf f
2 2 2 / 1 2 x Q BS Q t k S t Q f f
Substituindo (3.21) na equação acima tem-se:
2 2 2 / 1 2 x Q BS Q x Q dA dk S t Q f f
dA dQ S dA dQ Q k dA dk f
1/2
1 Logo: 2 2 2 / 1 2 / 1 2 1 x Q BS Q x Q dA dQ S S t Q f f f
Assim, a formulação final da onda difusiva pode ser escrita na forma:
2 2 2 x Q BS Q dA dQ x Q t Q o
(3.24)
Seja a celeridade da onda difusa definida por:
dA dQ t
x
( , )
E seja o coeficiente de difusão aparente da onda definido por:
o S Q t x D 2 ) , (
A equação final da onda difusiva pode ser expressa da seguinte maneira:
2 2 ) , ( ) , ( x Q t x D x Q t x t Q
3.4 Aplicação da teoria fuzzy nos modelos
Através do princípio da extensão, as equações (3.16) e (3.24) foram transformadas em equações na forma fuzzy, significando que todos os parâmetros e variáveis de controle passam a ser apresentadas na forma de funções de pertinência dentro de um grau de confiança calculado a partir das simulações.
Para expressar as variáveis na forma fuzzyé necessário colocar o sinal til “~” sobre as
mesmas. Desta maneira, têm-se as seguintes formulações:
3.4.1 Modelo de onda cinemática fuzzificada
0 ~ ) ( ~ ~
x Q Q K t Q
Onde:
Q~ Função de pertinência para a vazão;
) ( ~
Q
K Função de pertinência para a celeridade.
2 2~ ~ 2
~ ~
~ ~ ~
x Q
S B
Q
x Q
A d
Q d
t Q
o
Onde:
0 ~
S Função de pertinência para a declividade de fundo.
A~ Função de pertinência para área transversal do rio.
Lamberti & Pilati (1996) usaram modelos da onda dinâmica para estudar a propagação de ondas em canais naturais com base nas equações de Saint Venant, verificando sua aplicação em tempo real de previsão. Os autores fizeram uma transição entre os modelos da onda dinâmica e cinemática, verificando assim vários aspectos de influência de parâmetros hidráulicos e hidrológicos na propagação das ondas de cheias.
Yulianti et al. (1999) estudaram as condições de lançamentos de agentes poluentes, provenientes de fontes difusas, e seus efeitos na qualidade de água de uma bacia hidrográfica. A metodologia usada consistiu em introduzir incertezas, através do método de Monte Carlo, de forma a permitir uma avaliação da sensibilidade da bacia devido a estas incertezas, e em relação aos dados de entrada.
Leon et al. (2001) desenvolveram um modelo para estudar qualidade de água distribuída considerando um sistema de lançamento difuso e elementos como sedimentos e
nutrientes presentes no corpo d’água. O estudo ainda se encontrava em fase de
desenvolvimento e a aplicação de sistemas de informações geográficas pode produzir um avanço na solução desta classe de problema de qualidade de água.
Kashefipour & Falconer (2002) desenvolveram estudos para medir o coeficiente de dispersão longitudinal em canais naturais usando dados medidos em vários rios americanos. Os autores estabeleceram uma equação baseada em parâmetros hidráulicos do canal e em sua geometria. Os resultados encontrados apresentaram boa aproximação com os dados medidos.
parâmetros de entrada sobre os de saída são mais significativos em situações especiais, como baixos valores de coeficiente de rugosidade de Manning e / ou uma inclinação do leito mais acentuada das características de uma hidrógrafa, entre vários outros fatores.