Utilização do método de rayleigh-ritz para encontrar soluções para o modelo da viga de euler-bernoulli / Use of rayleigh-ritz method to find solutions for euler-bernoulli beam model

(1)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761

Utilização do método de rayleigh-ritz para encontrar soluções para o

modelo da viga de euler-bernoulli

Use of rayleigh-ritz method to find solutions for euler-bernoulli beam

model

DOI:10.34117/bjdv6n4-234

Recebimento dos originais: 16/03/2020 Aceitação para publicação: 16/04/2020

Anderson Donay Martins

Graduado em Licenciatura em Matemática Instituição: Universidade Federal de Pelotas (UFPel)

Endereço: Campus Capão do Leão, Caixa Postal 354 - 96001-970, Pelotas - RS, Brasil E-mail: andersondmm@hotmail.com

Alexandre Molter Doutor em Engenharia Mecânica

Instituição: Universidade Federal de Pelotas (UFPel)

Endereço: Campus Capão do Leão, Caixa Postal 354 - 96001-970, Pelotas - RS, Brasil E-mail: alexandre.molter@yahoo.com.br

Claudio Zen Petersen Doutor em Engenharia Mecânica

Instituição: Universidade Federal de Pelotas (UFPel)

Endereço: Campus Capão do Leão, Caixa Postal 354 - 96001-970, Pelotas - RS, Brasil E-mail: claudiopetersen@yahoo.com.br

RESUMO

Neste trabalho o Método de Rayleigh-Ritz é utilizado para resolver o problema da viga de Euler-Bernoulli, considerando a situação onde a carga distribuída está em forma triangular. É apresentado o funcional de energia potencial total e as condições essenciais e não essenciais de contorno do problema, bem como duas alternativas de solução: a equação de Euler-Lagrange que remete a resolver uma equação diferencial de quarta ordem e o Método de Rayleigh-Ritz, que transforma o problema em uma resolução de um sistema algébrico. O Método de Rayleigh-Ritz é escolhido para a resolução pelo fato de que nem sempre é possível resolver a equação diferencial resultante de forma exata e, quando necessário, o método é muito eficiente para encontrar soluções aproximadas. Em seguida, o método é aplicado e o sistema algébrico resultante é resolvido através do método da Eliminação de Gauss, na qual obtém-se soluções consistentes para o problema.

(2)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 Palavras-chave: Rayleigh-Ritz, Euler-Bernoulli, Eliminação de Gauss.

ABSTRACT

The Rayleigh-Ritz Method is used to solve the Euler-Bernoulli beam problem, considering a triangular distributed load. The total potential energy functional and the essential and nonessential boundary conditions of the problem are presented, as well as two solution alternatives: the Euler-Lagrange equation, which refers to solving a fourth-order differential equation and the Rayleigh-Ritz Method, that turns the problem into a resolution of an algebraic system. The Rayleigh-Ritz method is chosen for the resolution because sometimes it is not possible to solve the resulting differential equation exactly and, when necessary, the method is very efficient in finding approximate solutions. After, the method is applied and the resulting algebraic system is solved by the Gaussian Elimination, in which satisfactory solutions to the problem are obtained.

Keywords: Rayleigh-Ritz, Euler-Bernoulli, Gaussian Elimination.

1 INTRODUÇÃO

Em algumas áreas da engenharia são utilizadas estruturas como vigas, treliças, placas, entre outras, que possuem propriedades necessárias para a construção, como por exemplo, de prédios, aviões e navios. Essas estruturas estão sujeitas a cargas de tração, torção, flexão e de outros tipos, conforme citado por Rodrigues (2014). Elas precisam ser projetadas para suportar essas forças (embora leves deformações sejam inevitáveis), permitindo que possam exercer suas funções sem problemas.

Esse trabalho está concentrado nas flexões dos elementos do tipo vigas. Conforme Mascia et al. (2008), as vigas são definidas como estruturas lineares que podem ser dispostas horizontalmente ou inclinadas, com um ou mais apoios (móvel ou fixo) ou engastes.

O método utilizado é o Método de Rayleigh-Ritz (MRR) no qual é obtida uma solução para o modelo da viga de Euler-Bernoulli (biapoiada) com rigidez de flexão constante, ou seja, mesmo material e mesma secção transversal em todo o domínio. O MRR foi utilizado por Hauser et al. (2014) para resolver um problema de valor de contorno, no qual o domínio foi dividido em n intervalos e foi proposta uma solução linear em cada intervalo, e conforme n tendesse ao infinito, a solução obtida tenderia a solução do problema. Neste trabalho tem-se uma proposta diferente, no qual são propostas soluções no lineares para a situação da carga triangular.

(3)

Além da utilização do MRR para resolver o problema da flexão de vigas, o trabalho tem como objetivo analisar a eficácia do MRR para obter soluções aproximadas, fornecendo a possibilidade de solução através de um custo computacional muito menor.

2 METODOLOGIA

De acordo com Soriano (2009), um funcional é definido como “uma função de funções sob a forma de equação integral e que resulta em um número real quando essas funções são arbitradas. ” Os funcionais de um problema estão diretamente relacionados com a equação diferencial e as condições iniciais e de contorno que o modelam. Essa equação relacionada com o funcional pode ser encontrada minimizando o funcional (ou seja, considerando a taxa de variação do funcional como nula). Além disso, os funcionais são necessários para a utilização do MRR e no caso da viga biapoiada, o funcional utilizado é o funcional de energia potencial total. Esse funcional já é conhecido da literatura, inclusive citado por Sousa (2017), entretanto neste trabalho é considerado o funcional com apenas a carga distribuída, sem considerar cargas concentradas. Assim, chega-se a equação do funcional J do problema como: (1) 2 0 ( ) 2 L xx EI J u  _ u pu dx_  



,

Onde L é o comprimento da viga, u(x) é a função que descreve o deslocamento transversal, p(x) é a função que descreve a carga distribuída, E é o módulo de Young (constante que depende do material) e I é o momento de inércia da área (constante que depende do formato e dimensões da secção transversal da viga).

Quando se tenta achar a solução de um modelo matemático pode ocorrer de ser impossível obtê-la de forma exata ou uma representação em forma analítica, no entanto na maioria das situações não é necessária uma solução exata para o problema, sendo admissível uma solução aproximada, e isso pode ser feito através de métodos numéricos ou aproximações da solução, na qual substitui-se a equação diferencial por um sistema algébrico. Nos métodos numéricos obtém-se a solução em pontos isolados do domínio, enquanto que pelos métodos de aproximação da solução obtém-se uma solução analítica próxima da solução exata (ou até a própria solução exata). A grande vantagem de trabalhar

(4)

com sistemas algébricos é que é possível utilizar softwares para resolvê-los, e assim obter a solução de sistemas enormes em questão de segundos (e com uma boa precisão).

Para resolver esse problema de forma analítica, uma das opções é utilizar as equações de Euler-Lagrange do funcional, que são equações diferenciais já conhecidas que possuem a mesmas soluções que minimiza o funcional, entretanto mudando a natureza do problema. Assim, ao invés de minimizar um funcional é necessário resolver uma equação diferencial de ordem igual ao dobro da ordem da derivada de maior ordem do funcional. Conforme Campos (2017), considerando k como o integrando do funcional (1) e n a maior ordem das derivadas, chega-se a equação diferencial

(2)

 

0 1 0 j j n j j j j d k d u dx dx     _     _     



,

Que no caso do funcional de energia potencial total, resulta em

(3) ( ) 0

xxxx

EI u p x  ,

Com as condições essenciais de contorno (0)u u L( )0 devido as extremidades fixas e as condições não-essenciais de contorno u_xx(0)u_xx( )L 0 devido aos momentos fletores nulos nas extremidades. No geral, pode-se obter a solução integrando quatro vezes a expressão p x( ) /

 

EI , que dependendo da funcção p x considerada, pode ser bem ( ) complicado de efetuar essa integração (as quatro constantes arbitrárias são encontradas com a utilização das condições de contorno).

A outra possibilidade é o MRR, que nada mais é do que um método no qual se encontra uma solução analítica aproximada para o problema. O MRR consiste em substituir

( )

u x por uma função com um formato definido, e ao invés de encontrar uma função que minimize o funcional, encontram-se as constantes dessa função que minimizam o funcional.

(5)

A carga triangular consiste em uma carga que aumenta ou diminui linearmente conforme percorre o comprimento da viga. É fácil de ver que a carga pode ser expressa como uma função de primeiro grau, e nesse caso especifíco toma-se ( )p x  p x_o , onde a carga é nula em x0 e possui o valor de em. Ao integrar quatro vezes uma função linear é obtido um polinômio de grau 5, e consequentemente, a solução exata assume o seguinte formato: (4) 2 3 4 5 0 1 2 3 4 5 ( ) u x a a xa x a x a x a x ,

onde a a a₀, ₁, ₂, a₅ são constantes a determinar.

Da mesma forma que propondo um polinoˆmio de grau 5 chega-se a solução exata, também é possível propor um outro tipo de solução, por exemplo, um polinômio de grau 4. Neste caso, a solução obtida corresponde ao polinômio de grau 4 que mais se aproxima da solução exata. Cabe ressaltar que um erro é introduzido, contudo ocorre um ganho computacional, pois tem um coeficiente a menos para calcular e, consequentemente, um sistema com uma equação e uma variável a menos. Para efeito de comparação, com o propósito de mostrar a eficácia do MRR, o problema é resolvido pelas duas propostas de solução.

2.1 SOLUÇÃO POLINOMIAL DE GRAU 4

A solução aproximada proposta assume a forma

(5)

2 3 4

0 1 2 3 4

( )

u x a a xa x a x a x

Onde a a a₀, ₁, ₂, a₄ são constantes a determinar. As condições essencias de contorno,também devem ser satisfeitas pela solução aproximada. Então, utilizando a condição essencial de contornou(0)0 tem-se quea₀ 0. Por outro lado, utilizando a

(6)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 condição essencial de contornou L( )0, tem-se que



2 3



1 2 3 4

a   a La L a L , de acordo com Soriano (2009), e consequentemente,

(7)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 (6)



2 3



2 3 4 2 3 4 2 3 4 ( ) u x   a L a L a L x a x a x a x .

Tomando a equação (1) e substituindo por e por, obtém-se o funcional

(7)



₂



2



₂

 

₃ ₂





₄ ₃



2 3 4 0 2 3 4 0 0 ( ) 2 6 12 2 L L EI J u 



a  a x a x dx



p x a_ x Lx a x L x a x L x _dx

Efetuando as derivadas parciais do funcional em relção as constantes e igualando-as a zero, tem-se: (8)

























2 3 2 2 3 4 0 2 0 2 3 4 2 2 2 3 4 0 3 0 2 3 4 5 3 2 2 3 4 0 4 0 ( ) 2 2 6 12 0 ( ) 6 2 6 12 0 ( ) 12 2 6 12 0 L L L J u EI a a x a x p x Lx dx a J u EI a x a x a x p x L x dx a J u EI a x a x a x p x L x dx a  _ _        _ _ _    _ _ _ _ _ _ _ _  _ _ _   _ _   _     _   



Após o cálculo dessas integrais e algumas manipulações algébricas, obtém-se o sistema algébrico (09) 3 2 0 2 3 4 3 2 0 2 3 4 3 2 0 2 3 4 2 3 4 24 3 3 45 5 20 45 72 12 p L a a L a L EI p L a a L a L EI p L a a L a L EI  _ _ _      _ _ _          .

(8)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 Reescrevendo o sistema na forma matricial, segue que

(10) 2 2 ₃ 2 0 3 2 4 2 3 4 1 1 2 3 8 / 15 24 20 45 72 10 L L a p L L L a EI L L a           _            _{ } _ _  

Aplicando as operações entre as linhas do método da Eliminação de Gauss, obtém-se o sistema com matriz diagonal superior da forma

(11) 2 2 ₃ 2 0 3 2 4 2 3 4 1 0 2 1/ 15 24 0 0 2 1 L L a p L L L a EI L a           _            _{ } _  _  

Aplicando a retrosubstituição chega-se aos valores dos coeﬁcientes:

(12) 3 2 0 0 4 4 2 , 24 48 p L p L L a a EI EI    (13) 3 2 0 0 0 3 2 3 2 2 48 360 45 p L p L p L La L a EI EI EI      _ _     E (14) 2 3 3 2 0 0 0 0 2 2 2 2 3 4 45 48 24 240 p L p L p L p L a L L a EI EI EI EI       _ _ _ _      

(9)

Substituindo os valores nos coeﬁcientes da solução proposta em (6), chega-se a solucão aproximada por polinomio de gra 4 da forma:

(15) 4 3 2 2 3 4 0 0 0 0 7 2 ( ) 360 240 45 48 p L p L p L p L u x x x x x EI EI EI EI    

2.2 SOLUÇÃO POLINOMIAL DE GRAU 5

Utilizando a proposta de solução feita em (4) é encontrada a solução exata do problema. Assim como no caso anterior, a solução proposta deve satisfazer as condições essenciais de contorno. Da condição (0)u 0, segue que a₀ 0. . Da condição ( )u L 0,

segue que



2 3 4



1 2 3 4 5

a   a L a L a L a L , e então, a proposta de solução é reescrita como:

(16)



2 3 4



2 3 4 5

2 3 4 5 2 3 4 5

( )

u x   a L a L a L a L x a x a x a x a x

Aplicando a função proposta em (16) e substituindo ( )p x por p x na fórmula do 0( ) funcional descrita em (1), segue que

(17)







 



2 2 3 2 3 4 5 0 3 2 4 2 2 5 3 2 6 4 2 0 2 3 4 5 0 ( ) 2 6 12 20 2 L L EI J u a a a x a x dx p a x Lx a x L x a x L x a x L x dx        _        _



Calculando as derivadas parciais e igualando-as a zero, obtém-se um sistema de 4 equações, na qual a solução fornece os coeficientes da solução polinomial de grau 5. As derivadas parciais do funcional em relação a a a a e 2, 3, 4 a são dadas por 5

(10)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 (18)

























2 3 3 2 2 3 4 5 0 2 0 2 3 4 4 2 2 2 3 4 5 0 3 0 2 3 4 5 5 3 2 2 3 4 5 0 4 0 3 4 2 3 4 5 ( ) 2 2 6 12 20 0 ( ) 6 2 6 12 20 0 ( ) 12 2 6 12 20 0 ( ) 20 2 6 12 L L L J u EI a a x a x a x p x Lx dx a J u EI a x a x a x a x p x L x dx a J u EI a x a x a x a x p x L x dx a J u EI a x a x a x a  _ _ _ _ _ _ _ _ _     _ _ _ _ _ _ _ _ _     _ _  _      _    _ _ _ 





5 6





6 4 2



5 0 0 20 0 L a x p x L x dx            _ _      _ _ 



Calculando as integrais e fazendo simplificações algébricas, obtém-se o sistema (já escrito na forma matricial) como

(19) 2 3 2 2 3 3 3 0 2 3 4 2 3 5 1 2 3 4 5 8 / 15 1 2 3 4 10 24 20 45 72 100 16 35 84 140 200 a L L L a L L L p L a EI L L L a L L L           _      _                    

Efetuando as operações de linha do processo da Eliminação de Gauss, chega-se ao sistema com a matriz diagonal superior da forma:

(20) 2 3 2 2 3 3 3 0 2 3 4 3 5 1 2 3 4 5 1/ 15 0 2 3 1 24 0 0 2 5 1/ 5 0 0 0 a L L L a L L L p L a EI L L a L           _      _              _       

Aplicando a retrosubstituição, chegam-se aos valores dos coeﬁcientes a a a e ₂, ₃, ₄ a : ₅

(21) 3 3 0 0 5 5 , 120 120 p L p L a a EI EI   

(11)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 (22) 3 2 3 0 0 4 4 2 5 0 120 24 p p L L a L a EI EI    _ _     (23) 3 2 3 0 0 0 3 3 3 120 360 36 p p L p L a L L a EI EI EI      _ _     E (24) 2 3 3 0 0 0 2 2 2 3 5 0 36 120 24 p L p p L a L L a EI EI EI       _ _ _ _      

Substituindo esses valores na solucão proposta em (16), conclui-se que a solução para o problema é dada por:

(25)





4 2 3 5 4 2 3 5 0 0 0 0 7 ( ) 7 10 3 360 36 120 360 p L p L p p u x x x x L x L x x EI EI EI EI       3 RESULTADOS NUMÉRICOS

Considerando uma viga de liga de aço, com secção quadrada de lado 1m e comprimento de 20m, com carga distribuída de acordo com a relação p x( )500x (em N/m). De acordo com Hibbeler (2006), o módulo de Young do aço é de

9

200G Pa200 10 Pa. Segundo Beer et al. (2011), o momento de inércia da secção quadrada (considerando a como a medida do lado) é dado por

4 2 1 12 12 a I   Kg m .

Assim, substituindo os valores na equação (15), segue que a solução aproximada de grau 4 é dada por

(12)

Braz. J. of Develop.,Curitiba, v. 6, n.4,p.19846-19858 apr. 2020.ISSN 2525-8761 (26) 5 6 2 7 3 7 4 28 16 1 ( ) 10 10 10 10 0 3 3 8 u x   x  x   x   x 

Substituindo os valores na equação (25), segue que a solução exata é

(27)





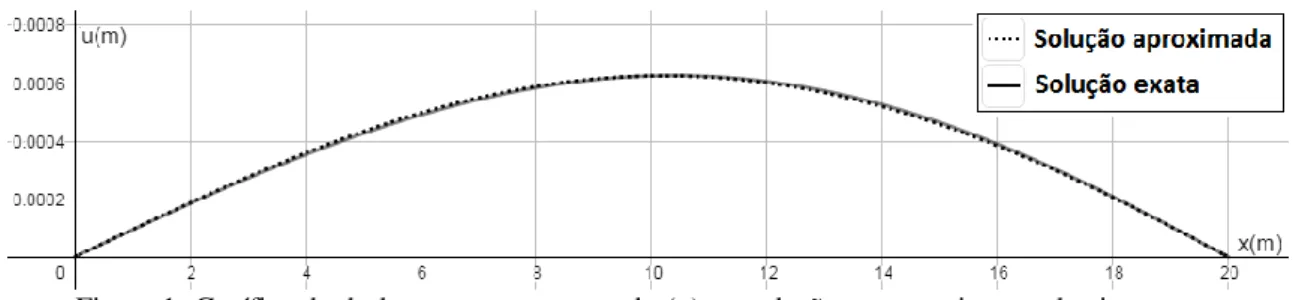
9 3 5 1 ( ) 10 1120000 4000 3 0 12 u x   x x  x 

Na figura 1, estão expostos os gráficos das duas soluções, sendo o gráfico pontilhado referente a solução aproximada e o gráfico contínuo referente a solução exata.

A tabela 1 mostra os deslocamentos transversais em alguns pontos da viga (com arredondamento em 8 casas decimais).

É interessante notar que a viga sofre mais deslocamentos na metade da direita do que na metade da esquerda, o que é esperado, pois a carga é maior conforme se aproxima da extremidade direita da viga. Com auxílio computacional, nota-se que o maior deslocamento na solução aproximada ocorre em aproximadamente x10, 22193025 com deslocamento de 4

6, 2537 10  , e na solução exata ocorre em aproximadamente

10,38659234

x com deslocamento de 4

6, 2613 10 

(13)

Tabela 1- Comparação entre a solução exata e a aproximada

Posiçaõ(x) Soluçaõpol.degrau4 Soluçaõpol.degrau5 Desvio relativo

2, 5 2, 3174 ×10−4 2, 2815 ×10−4 1, 5735% 5, 0 4, 3281 ×10−4 4, 2578 ×10−4 1, 6511% 7, 5 5, 7080 ×10−4 5, 6531 ×10−4 0, 9711% 10, 0 6, 2500 ×10−4 6, 2500 ×10−4 0, 0000% 12, 5 5, 8643 ×10−4 5, 9192 ×10−4 0, 9275% 15, 0 4, 5781 ×10−4 4, 6484 ×10−4 1, 5123% 17, 5 2, 5361 ×10−4 2, 5720 ×10−4 1, 3958% 4 CONCLUSÃO

O MRR se mostrou um método bem eficaz para resolver o problema proposto, tanto obtendo a solução exata quanto uma solução aproximada. No caso da solução aproximada, o desvio absoluto foi menor que um décimo de milímetro para todos os pontos da viga, evidenciando uma grande vantagem do MRR, que é a possibilidade de buscar soluções aproximadas muito próximas da solução exata. Isso leva a considerações do que é mais relevante, se é a minimização do erro cometido quando se aproxima a solução ou se é o ganho computacional adquirido.

Para trabalhos futuros, pretende-se elaborar um programa que ajude na resolução de problemas mais complexos, que envolvam propriedades do material (e do formato) não homogêneas ao longo da estrutura, cargas dinâmicas (vibrações) ou domínio bidimensional. Para isso, pretende-se acrescentar o Método dos Elementos Finitos para resolver o modelo.

AGRADECIMENTOS

Os autores agradecem a Universidade Federal de Pelotas e ao Programa de Pós-Graduação em Modelagem Matemática pelo apoio e oportunidade.

REFERÊNCIAS

Beer, F.P.; DeWolf, J.T.; Johnston, E.R.; Mazurek, D.F. (2011), ”Mecânica dos Materiais”, 5a. edição, AMGH Editora Ltda., Porto Alegre.

Campos, C.A.L. (2017), ”Algumas Aplicações de Cálculo Variacional: de Braquistócrona a Desigual- dade de Hardy-Sobolev”, Dissertac¸a˜o de Mestrado, Unicamp.

Hauser, E.B.; Rodrigues, D.S.; Rodrigues Y.E. (2014). ”O Método de Rayleigh-Ritz aplicado a um Problema de Deflexão de Viga utilizando o Matlab”, Proceeding Series of

(14)

the Brazilian Society of Applied and Computational Mathematics, Vol. 2, N. 1. DOI:10.5540/03.2014.002.01.0071.

Hibbeler, R.C. (2006), ”Resistência dos Materiais”, 5a. edição, Pearson Prentice Hall, 2006. Mascia, N.T.; Rodrigues, R.B.; Souza, M.F.S.M. (2008), ”Sistemas estruturais de edificac¸o˜es e exem- plos”, Unicamp.

Rodrigues, L.E.M.J. (2014), ”Fundamentos da Engenharia Aerona´utica com Aplicações ao Projeto SAE-AeroDesign: Estabilidade e Estruturas”, 1a. edição, Edição do Autor, Salto.

Soriano, H.L. (2009), ”Elementos Finitos - Formulação e Aplicação na Estática e Dinâmica das Estru- turas”, 1a. edição, Ciência Moderna, Rio de Janeiro.

Sousa, C.M.L. (2017), ”Determinação de Deslocamentos em Trelic¸as Planas via Método da Energia”, Trabalho de Concluão de Curso, UEPB.