Afin de donner à cette thèse une certaine unité, nous avons présenté uniquement nos travaux liés aux biosystèmes, avec un bref rappel de quelques travaux antérieurs en théorie du management (Chapitre 1), dont nous avons ensuite appliqué certains résultats à l'étude de biosystèmes spécifiques. - les systèmes. Nous commençons par une courte note dans laquelle nous présentons les différentes activités et travaux et sujets de recherche. La plupart de nos travaux sur les systèmes halieutiques et épidémiologiques sont présentés dans les chapitres 2 et 3.
Nous avons choisi de détailler certaines parties qui n'apparaissent pas dans les articles proposés ou qui ne sont pas publiées. Nous terminerons en présentant quelques perspectives et projets de recherche que nous comptons développer. En annexe nous présentons sept articles qui contiennent les preuves et les détails techniques des résultats présentés dans les chapitres 1, 2 et 3.
Stabilisation de syst`emes non lin´eaires en temps continu
Saberi, Kokotovic et Sussmann ([87]) dérivent un contrôle stabilisateur à partir d'une fonction de Lyapunov stricte V(x) pour (1.3). Cependant, il n’existe pas de méthode systématique pour construire de telles fonctions de Lyapunov. L’intérêt de notre approche est que pour des classes très larges de systèmes, y compris les systèmes mécaniques, il est plus facile de construire une fonction de Lyapunov large qu’une fonction stricte.
Ferfera, une condition suffisante pour une stabilisation globale par contrôle régulier pour les systèmes non affines contrôlant la forme (1.1), généralisant la condition bien connue de Jurdjevic-Quinn pour les systèmes affines contrôlant (cf. [59]). On peut le résumer ainsi : s'il existe une fonction de classe C∞ V : IRn→IR définie positive et propre telle que. Pour les systèmes non affines contrôlant la forme générale (1.1), où ˙V(x) n’est plus linéaire inu, la principale difficulté est de prouver l’existence d’une rétroactionu(x) conduisant à ˙V(x )≤0.
Stabilisation de syst`emes non lin´eaires discrets
Stabilisation par retour d’´etat estim´e par observateur
Étant donné une rétroaction stabilisante x7 → u(x) en fonction de l'état, que se passe-t-il si, au lieu d'appliquer la rétroaction d'état u(x), nous appliquons la rétroaction d'état estimée u(ˆx). Pour les systèmes non linéaires il existe peu de résultats sur ce problème (cf. [33]).
Stabilisation de syst`emes non lin´eaires stochastiques
Notons également que l'approche stochastique de l'étude des systèmes contrôlés permet de prendre en compte les perturbations aléatoires auxquelles est soumis un système déterministe (erreurs de modélisation, bruit dans les variables du système). Enfin, [11] donne l'analogue discret du résultat de [12] pour les systèmes stochastiques discrets de la forme Nous donnons ici quelques applications de la théorie du contrôle à des systèmes qui modélisent l'évolution dans le temps de populations soumises à l'exploitation humaine.
Nous n'avons pas utilisé les résultats existants pour ces systèmes, mais avons construit un nouvel observateur pour cette classe de systèmes. Sinon, la plupart des méthodes classiques de synthèse d'observateurs pour les systèmes non linéaires utilisent des techniques de linéarisation autour du point d'équilibre et créent ainsi des serveurs ob - locaux. Un observateur local n'a pas beaucoup d'intérêt pratique pour les systèmes qui nous intéressent, c'est pourquoi nous avons essayé de construire un observateur global, dont nous développerons la construction plus loin dans ce chapitre.
Estimation de stock pour une pˆecherie
Mod`ele discret structur´e en ˆage
2.2) Etant donné que la dernière classe comprend les individus âgés de n, ainsi que les individus âgés de plus de n (s'ils existent), il faut ajouter les individus qui étaient n au temps k et sont encore en vie au temps k+. 1 ce qui donne. L'âge 1 est supposé être l'âge d'entrée dans la phase d'exploitation : les individus peuvent être chassés à partir de l'âge 1. Le nombre de nouveau-nés qui survivent jusqu'à l'âge 1 correspond à ce qu'on appelle le recrutement.
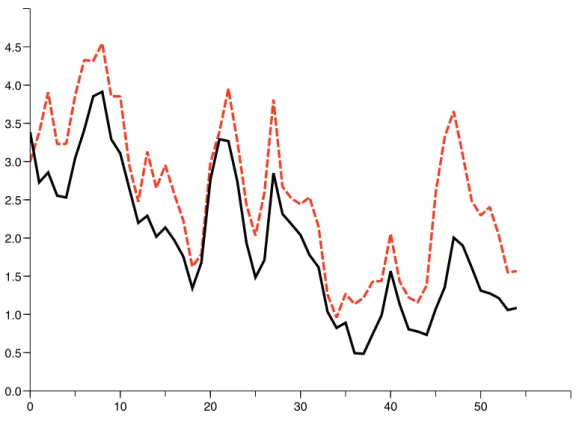
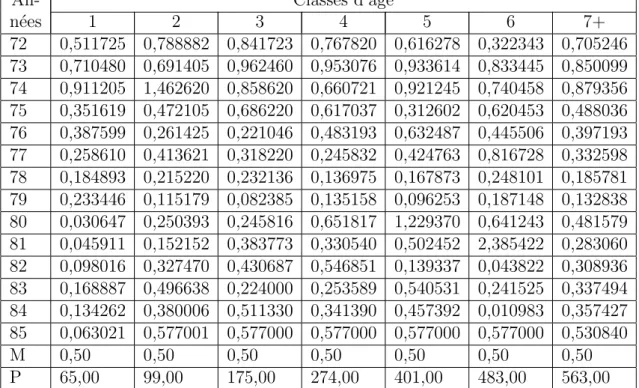
Si nous désignons le poids individuel moyen des poissons de la classe d’âge i par wi, alors nous pouvons exprimer la biomasse totale capturée Y(k) comme suit. La figure 2.1 donne les estimations pour la classe d'âge 2, calculées par l'observateur, avec deux conditions initiales prises au hasard. Captures en millions d'individus par tranche d'âge (Divisions 34.1.3 et 34.3.1) et captures totales en milliers de tonnes.
Mod`eles structur´es en ”stades”
Ces données proviennent du rapport IECS [2] et ont été reproduites et utilisées dans [100]. Les mesures se réfèrent aux captures entre 1946 et 2000, le rapport du CIEM donne également des estimations de mortalité par pêche et de biomasse pour chaque classe, dont nous reproduisons une partie (voir tableau 2.3) en ajoutant une colonne pour les captures totales (voir [100] pour le tableau complet) . Pour le taux de mortalité naturelle (hors pêche), nous avons pris les valeurs [100], à savoir M1 = M2 = 0,2 et pour le taux de passage de la classe des immatures à la classe des matures p = 0,1.
Bien que les données fournissent les captures pour chacune des deux classes, nous utilisons uniquement le total des captures pour l'observateur sans distinguer les individus. Les figures 2.2 et 2.3 permettent de comparer les estimations du CIEM avec celles données par l'observateur (2.15). On obtient la même forme, mais avec une légère surestimation par l'observateur (surtout pour les immatures), qui peut être due aux valeurs de Mi et pchoisies.

Stabilisation d’un mod`ele continu de pˆeche
Cette méthode a l'avantage de fournir un résultat global ; de plus, la fonction Lyapunov considérée permet de stabiliser le système par un effort de pêche variable et explicitement calculable. Nous montrons également comment répondre à la variation de l'effort de pêche [80] pour stabiliser le système au point d'équilibre non trivial. Si les hypothèses H1, H2, H3 et H4 sont remplies, alors X∗ est un point d’équilibre globalement asymptotiquement stable pour le système (2.16).
Si les hypothèses H1, H2, H3 et H4 sont satisfaites, on peut construire un effort de pêche qui dépend de l'état du système X(t) (feedback) de la forme E(X) = ¯E+u(X ) tel que X∗ est un point d’équilibre globalement asymptotiquement stable pour le système (2.16) bouclé avec E(X). On peut aussi stabiliser le système (2.16) en agissant sur la vitesse de variation de l'effort de pêche, ce qui revient à avoir une stratégie qui consiste à dire : pêcher plus ou pêcher moins selon l'état du système. L'effortE devient donc une autre variable d'état et le système est contrôlé en agissant sur ˙E la dérivée de E et non plus directement sur E.
La prise en compte des h´et´erog´en´eit´es
Les mod`eles multi-groupes
Par la suite, ce modèle introduit par Jacquez a été baptisé par Hyman et al. Enfin, il existe des porteurs infectieux asymptomatiques qui jouent un rôle dans la transmission de la maladie. Dans l'article [26] (ci-joint) nous avons donné un résultat de stabilité qui nous a permis d'étudier un système constitué de n groupes de systèmes SIS, en particulier nous avons donné une preuve plus simple du résultat de Lajmanovich et Yorke [64] .
Dans [51] (article ci-joint), nous avons étudié le modèle (3.4) avec une fonction démographique ϕ(S), qui est plus générale qu'un simple recrutement constant Λ, et nous introduisons des classes de maladies latentes (elles ne transmettent pas la maladie ). Nous avons également pris en compte les modèles d’infectivité différentielle de DI (modèles d’infectivité différentielle), présentés dans la figure 3.2. Nous avons ensuite déterminé le caractère dissipatif de ces systèmes (existence d'un compact positivement invariant et absorbant), calculé R0 le taux de reproduction de base, étudié l'existence de points d'équilibre, prouvé la stabilité asymptotique globale du DFE (équilibre sans maladie) et Nous avons surtout prouvé la stabilité asymptotique globale de l’équilibre endémique lorsqu’il existe pour le modèle SP (3.5).

Les mod`eles `a pathog`enes comprenant des souches multiples . 37
Ce travail a fait l'objet de la publication [49] (ci-jointe) dans laquelle nous avons présenté un nouveau modèle prenant en compte la structure par âge des parasites Plasmodium et incluant différentes souches du parasite. Le modèle que nous avons proposé et étudié est décrit par le système ci-dessous. Le paramètre u est un nombre positif qui peut prendre la valeur 0 ou 1 notamment et donc notre modèle permet de considérer à la fois le cas où l'on prend en compte le terme −β x m dans l'équation ˙m et seulement le cas où on néglige ce terme terme.
Ce modèle généralise les modèles existants dans la littérature et permet d'étudier, entre autres, l'infection par le VHB pour laquelle nous disposons de données liées au Sénégal. Prenant en compte ces données ainsi que plusieurs études expérimentales et statistiques (OMS, CDC, National Institute of Health, etc.) qui montrent clairement l'influence de l'âge au moment de l'infection sur l'évolution de la maladie, nous avons proposé une dynamique modèle avec cinq classes de sujets sensibles (0-1 mois, 1-6 mois, 7-12 mois, 1-5 ans et > 5 ans), deux divisions de sujets infectés de manière latente (ne transmettant pas l'infection) et deux divisions de sujets infectieux (symptomatiques). infectieuse) et infectieuse chronique). Le modèle présenté par le diagramme 3.5 s'inscrit bien dans la classe des systèmes (3.10) avec.

L’h´et´erog´en´eit´e et les temps de s´ejours
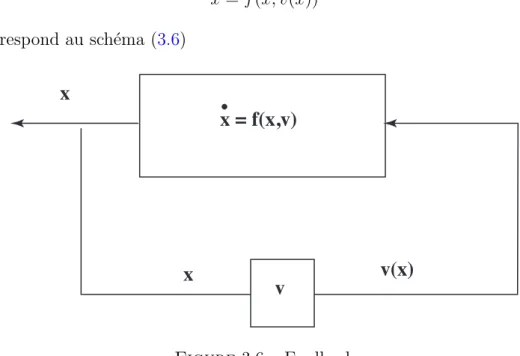
Une condition nécessaire et suffisante pour la réductibilité d'un système d'équations fonctionnelles à un système d'équations différentielles ordinaires est donnée par Fargue [27]. Si l'on veut prendre en compte ce retard dans (3.11), cela revient à introduire un retard sur v(x) dont la fonction de densité de probabilité est h, le système devient un système intégré egro-différentiel. Cette répartition est réalisée par le système de chaînes linéaires représenté par le schéma 3.7.
L’étude des propriétés (3.17) peut donc être dérivée de l’étude du système suivant. Les propriétés (3.19) peuvent être comprises à partir des propriétés du système d'équations différentielles. L'utilisation de l'approche expliquée ci-dessus nous a permis d'étudier dans [50] le système de retard suivant, qui modélise l'attaque des cellules saines par le parasite.
L’h´et´erog´en´eit´e spatiale
The first classx0 consists of pre-recruits, i.e. eggs, larvae and juveniles. This proves the global asymptotic stability of EE in the positive ordinal for the system (2.1). In this section we will describe a method to prove the global stability of the endemic equilibrium.