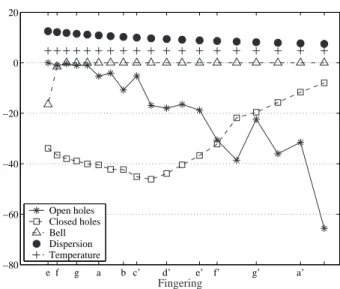
Le premier concerne l’impact qualitatif de la non-linéarité sur les fréquences de lecture et le timbre, en se concentrant sur la courbe d’impédance d’entrée. Dans la première, nous adoptons l’approche linéaire, en nous concentrant sur l’inharmonicité des fréquences de résonance pour résoudre un problème de précision de la clarinette.
Introduction
Generalities on the clarinet
Definitions
Inharmonicity and sound production
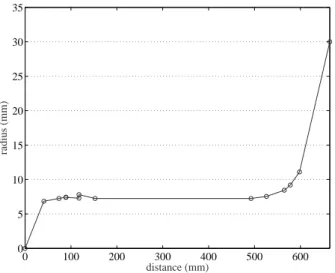
The tone holes are numbered from 1 to 24 in order of decreasing distance from the mouthpiece, the 24th being the register hole. For input impedance measurements, the nozzle is replaced by a 77 mm long cylindrical tube.
Method and approximation
Length correction and inharmonicity produced by a small perturbation
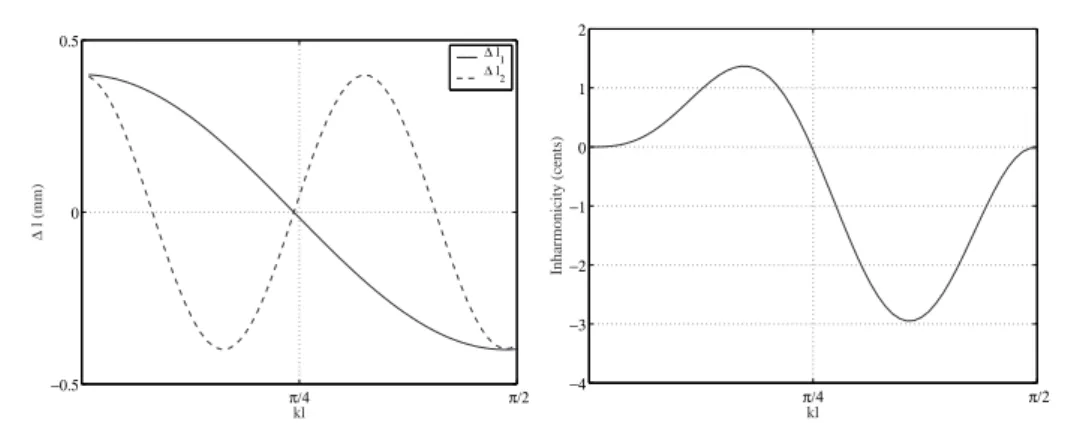
- Length corrections: definition
- Inharmonicity of the resonance frequencies
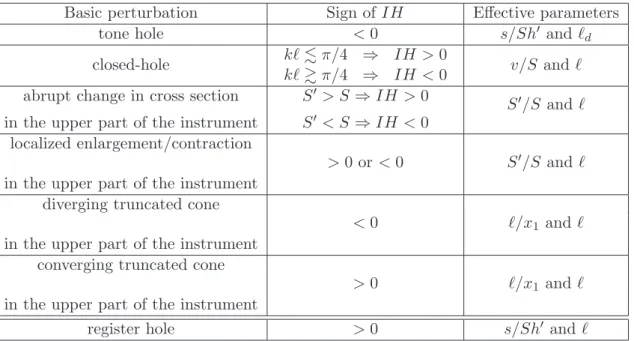
- Length corrections and inharmonicity formulae for acoustic basic
- Other effects: radiation, dispersion and temperature
- Theoretical analysis of a clarinet resonator
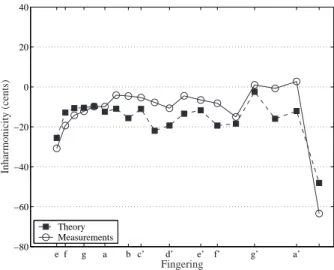
- Comparison between theory and measurements
- Discussion and conclusions
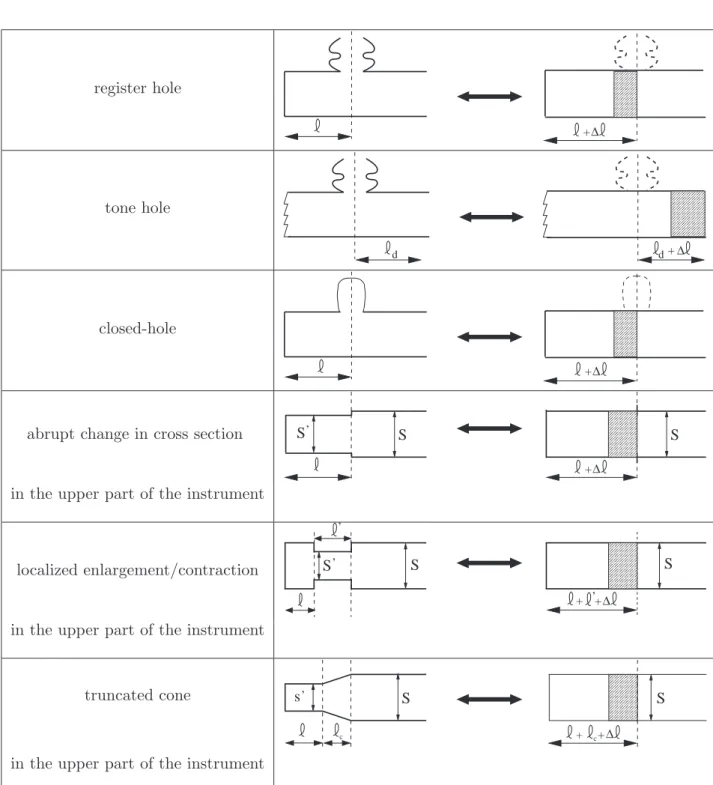
The expression first order length corrections refers to length corrections extended to first order in the ratio of the length correction to the wavelength. Consider a localized expansion (or contraction) of length `0 located at a distance' from the effective input in a cylindrical air column and let α =S0/S be the ratio of the cross-sectional area of the expansion (or contraction) to the one of the main tube.
Optimization of the location of the register hole and tuning corrections
Assumptions
Formulation of the optimization problem
Criterion functions
IHregandIHpert the inharmonicities associated with the register hole and the perturbation respectively, a criterion function can be written as. Moreover, another criterion function has also been investigated by minimizing the function defined as . 1.47), for which the minimum is reached when the inharmonicity associated with the inserted perturbation is of the same magnitude as the register hole deviation and in the opposite direction.
Results and discussions
Register hole location
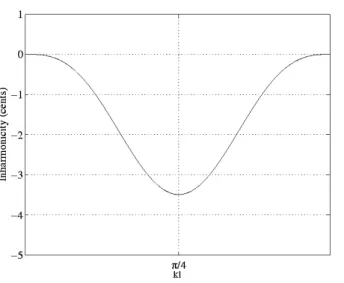
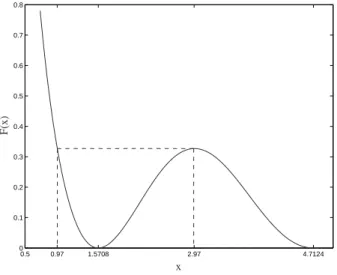
As expected, the maximum deviation appears at the beginning of the register and is almost equal to a quarter tone. Above `/L= 0.2041, the maximum value of the frequency shift increases linearly with the location of the log hole.
Adjustements of natural frequencies by means of small changes of
The optimization variables used for the narrow turbulence case (see Table 1.2) are the top edge radius of our model R0, the top angle θ and the location point. Thus, no enhancement can be made to compensate for the effect of the register hole, except for tones at the bottom of the scale.

Conclusion
Γn partie imaginaire de la pulsation de résonanceωn Φin fonction propre associée à la valeur propre kn ω pulsation de l'onde. Pour chaque formulation, nous fournissons la solution du problème basée sur la fonction de Green qui vérifie les conditions aux limites du problème.

Position du probl`eme
Le modèle le plus simple utilisé pour calculer les oscillations de la clarinette repose généralement sur des équations qui s'appliquent à l'entrée de l'instrument. A noter qu'ici les coefficients de la caractéristique polynomiale du roseau sont des coefficients dimensionnels. Le résonateur doit être linéaire et seule la connaissance de l'impédance d'entrée est requise.
Etablissement des ´equations du r´esonateur avec amortissement
Les extensions asymptotiques de (1.6) au premier ordre des rapports `v/r et `t/r donnent respectivement l'impédance et l'accès de la ligne. Par rapport à (1.10), les effets visco-thermiques dans le guide sont proportionnels à la racine carrée de la fréquence de l'onde. Le facteur α possède une partie réelle qui reflète l'affaiblissement de l'amplitude des ondes lors de la propagation et une partie imaginaire qui correspond au phénomène de dispersion (variation de la vitesse des ondes en fonction de la fréquence).
Pr´esentation de deux formulations du probl`eme de propagation
Formulation avec condition de type Neumann `a l’entr´ee
L'impédance à fréquence nulle est généralement faible (à noter qu'elle doit être recherchée avec un autre modèle d'écoulement dans la canalisation) et a peu d'influence sur le comportement dynamique du modèle, puisque ce sont les pics d'impédance de forte amplitude qui participent à l'auto- oscillation. Ce choix correspondra simplement à faire une décomposition de l'impédance d'entrée Ze(ω) lorsque l'on recherche une décomposition modale des auto-oscillations. La condition de Neumann (1.21) exprime que la paroi (fictive) au point x= 0 est parfaitement rigide et que tout le flux U entre par conséquent dans le résonateur : l'impédance de paroi Z est infinie.
Formulation avec condition absorbante `a l’entr´ee
Ceci permet d'écrire en tenant compte des relations de continuité pour le corps P(x) et sa dérivée spatiale. 1.20) Le choix d'une condition de type Neumann en entrée impose. En résumé, notre première formulation, dite formulation avec condition de type Neumann en entrée, est écrite. Maintenant l'accès A est défini selon la normale entrante (voir figure C.1) ; c'est donc l'opposé de l'accès aux entrées classique :. 1.29) L'accès conventionnel a une partie réelle positive s'il correspond à un milieu passif, absorbant, et négative dans le cas où l'extrémité fournit de l'énergie.
Solutions int´egrales du probl`eme de propagation
En particulier, le choix d'une fonction de Green répondant aux mêmes conditions aux limites que la pression souhaitée permet de simplifier le calcul de (1.30), la seconde intégrale devient nulle. Dans la suite nous écrivons pour chaque formulation le problème de Green associé ainsi que la solution de chacun des problèmes selon la fonction de Green. La fonction de Green G(x;e x0) utilisée répond au problème de valeurs limites non homogènes1 suivant.
Conclusion
Probl`eme de Green et la solution ´el´ementaire
La fonction de Green g(x,t|x0,t0) est la solution élémentaire d'un problème et traduit l'effet au point x au moment d'une impulsion émise en x0 à un instant précédent t0. Le premier principe reflète le fait que changer les positions de l'émetteur et du récepteur et changer les temps de transmission à -t0 ne modifie pas la fonction Greeng(x, t|x0,t0). La seconde affirme qu'un effet doit être précédé d'une cause et qu'on ne peut pas « ressentir ».
Modes propres : d´efinitions dans le domaine fr´equentiel
Modes de r´esonance
Deux principes essentiels sont vérifiés par les fonctions de Green : la relation de réciprocité et le principe de causalité.
D´eveloppement de la fonction de Green sur les modes propres avec condition
Calcul des modes propres
D´eveloppement modal
D’après (2.8) les pôles sont situés au dessus de l’axe réel, de sorte que le théorème des restes donne La fonction de Green correspondante dans le domaine temporel, obtenue par transformation de Fourier inverse de (2.10) par intégration par la méthode des résidus (voir encadré), est donnée par . Pour rendre le modèle plus réaliste, nous décidons d'attribuer à chaque amplitude modale gm(t) un facteur d'amortissement γm, qui correspond à la valeur de l'amortissement pour la fréquence du mode.

D´eveloppement de la fonction de Green sur les modes de r´esonance
- Solution compacte dans le domaine fr´equentiel
- Calcul des pˆoles
- Position des pˆoles
- Calcul des r´esidus
- Fonction de Green d´ecompos´ee sur les modes
- Cas d’une terminaison active
- Validation de la forme d´ecompos´ee
Le calcul de la transformée de Fourier inverse de (2.23) se fait à l’aide du théorème des résidus (la variable ω est un nombre complexe) et nécessite le calcul des pôles que nous présentons dans la section suivante. Le calcul de l'expression de la fonction de Green dans le domaine temporel se fait en appliquant le théorème des résidus (voir encadré 2.2.2). Le transfert de (2.34) à (2.31) conduit à l’expression dans le domaine temporel de la fonction de Green, décomposée en fonction des modes de résonance du problème.
Mise sous forme d’´equations diff´erentielles des auto-oscillations
Probl`eme avec condition de Neumann `a l’entr´ee
Finalement, nous arrivons à une formulation de problème sous la forme d'un système constitué d'une infinité d'équations différentielles du second ordre non linéaires et couplées. Notons qu'en posant y= ˙p on aurait pu écrire directement des équations différentielles du premier ordre, ce qui conduit à écrire le problème sous la forme d'un système dynamique, où chaque pn est remplacé par le couple (pn, yn). En multipliant les deux côtés de l'équation par l'un des modes Φq, puis en intégrant sur le domaine [0;`], les propriétés d'orthogonalité des modes Φm conduisent au système th.
Probl`eme avec condition parfaitement absorbante `a l’entr´ee
L'équation (2.58) montre que le couplage non linéaire modifie les termes d'inertie (¨p) et de dissipation (˙p) et que la non-linéarité implique des termes quadratiques et cubiques. Enfin, notons que, comme convenu, l'annulation des termes B et C dans (2.50) et (2.58) souligne que l'écriture du problème avec la condition d'absorption est bien une version linéaire du problème. th initial, le système est placé sous forme diagonale dans le régime linéaire.
Discussions
Le début de ce chapitre est consacré à préciser les conditions initiales de chaque formulation qui garantissent l’unicité de la solution. La stabilité du système et les conditions d'auto-oscillations sont recherchées et une expression analytique du signal de pression en régime transitoire est proposée par une méthode disruptive. Formulation avec conditions de Neumann en entrée L'expression exacte de la fonction de Green du système est écrite.
R´eduction `a un mode : un oscillateur de Van der Pol
Approche de la dynamique du mod`ele au seuil d’oscillation
La stabilité locale du point fixe (au sens de Lyapunov) est obtenue en analysant le système dans sa version linéaire au voisinage du point fixe (on regarde la dynamique tangente au point fixe). Nous écrivons le système linéarisé dans sa base propre et nous intéressons au signe de la partie réelle des valeurs propres. On peut faire vérifier au système (3.16) les conditions d’application du théorème.
Approche de la solution au seuil d’oscillation
Pour les solutions non triviales, ρP F 6= 0, la correction de la fréquence de l'oscillation est donnée par Le résultat (3.36) révèle un phénomène non linéaire typique : la dépendance en amplitude de la résolution. La correction de la fréquence d'oscillation pendant le régime transitoire est obtenue par intégration par rapport au temps (3.32), ce qui conduit à.
Simulations num´eriques
En supposant qu'à l'instant initial θ(t0 = 0) =θ0, la correction de fréquence se produit en régime transitoire. 3.41). L'approche analytique suppose une pulsation ωconstante, tandis que les termes non linéaires agissent également sur la fréquence d'oscillation. On remarque que lorsqu'on s'éloigne du seuil d'oscillation, la fréquence d'oscillation n'est plus correctement estimée par le calcul analytique.

R´esonateur multimodes - Simulations num´eriques
Comportement du syst`eme
Comparaison entre la solution de la formulation de l'état de Neumann et la fonction de Green (2.35). Ces deux effets garantissent que l’ajout d’un composant améliore la description de la solution. 3.13 – Influence sur le spectre de puissance de l'ajout d'un composant lors de la décomposition de la solution – formulation avec condition de Neumann en entrée.

Convergence et confrontation de la m´ethode avec l’´equilibrage har-
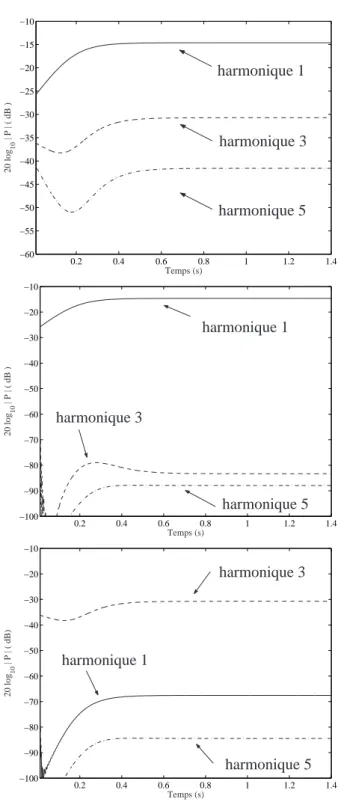
On voit que les évolutions temporelles d'une harmonique dans le spectre sont clairement corrélées à celles d'une composante de la décomposition. L'importance d'une telle mesure est qu'elle est indépendante de la description du signal (temporel ou fréquentiel) choisi. Enfin, il ressort de la figure 3.18 que les deux formulations convergent rapidement, et qu'une estimation correcte de la solution est obtenue à partir de N=8 composantes pour les deux formulations.
Discussions
This appendix describes the calculations that lead to the following expression for the frequency of the played tone. In the limit that R → ∞, the frequency of the played tone fc approaches the frequency when the hole is closed. Equation (E.12) can be transformed in the time domain, leading to a solution corresponding to the successive reflections of the Green's function in infinite space at the two boundaries.
Putting the expression in the frequency domain (E.12) into equation (E.5) leads to the modal expansion of the time domain expression. To calculate the solution based on the initial conditions, using equation (E.66) at t= 0, the following result is obtained:.
![Fig. 3.19 – R´egime permanent. Comparaison avec les r´esultats fournis par ´equilibrage har- har-monique (EH), pris dans [53]](https://thumb-eu.123doks.com/thumbv2/1bibliocom/467219.71776/115.892.236.614.283.892/fig-egime-permanent-comparaison-esultats-fournis-equilibrage-monique.webp)