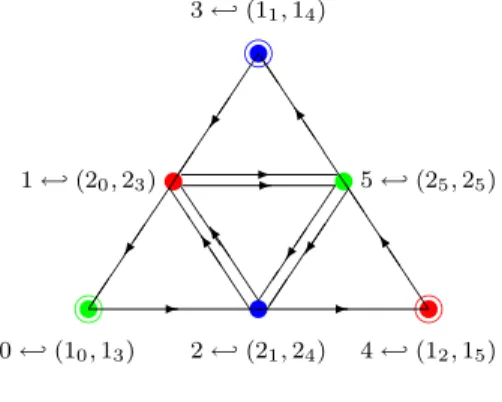
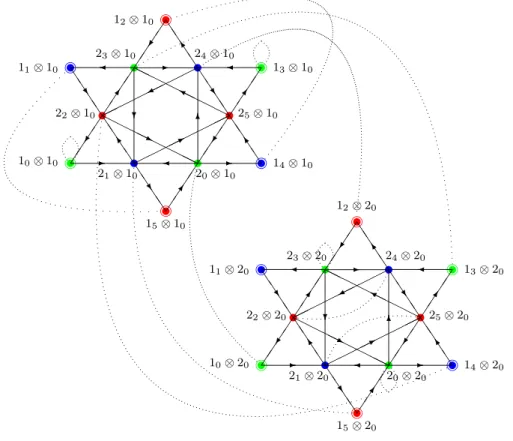
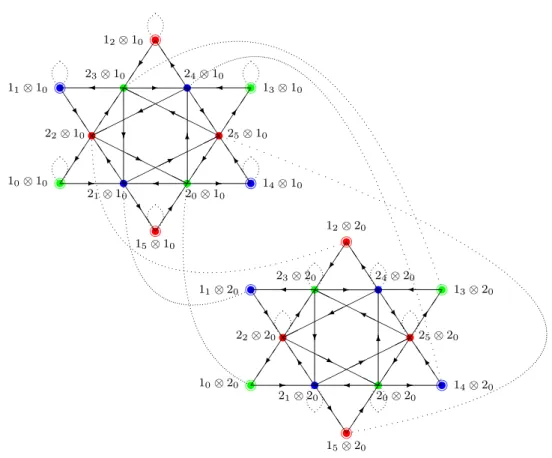
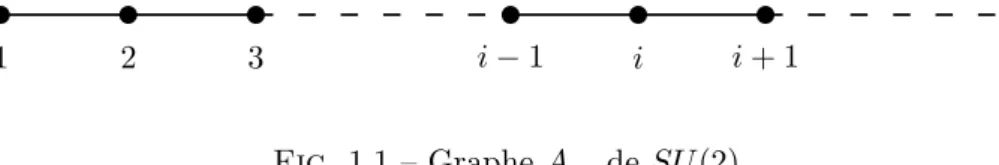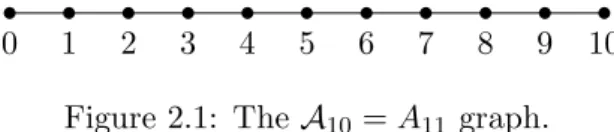La seconde est une algèbre associative (mais pas nécessairement commutative) de dimension finie, l'algèbre de symétrie quantique Oc(G). Pour cet exemple on construit l'espace B à partir de l'algèbre de graphes A2, du coproduit et des deux algèbres de caractères associées.
Notions sur les graphes et graphes ADE
Graphes bi-orient´es et leur classification
Les autres valeurs propres de A peuvent être exprimées en fonction de κ comme λ= 2 cos(mπκ ) (éventuellement avec multiplicité), où les nombres m sont appelés exposants de Coxeter. Correspondance de Mc-Kay Les sommets des diagrammes affines (A(1)ℓ , D(1)ℓ , Eℓ(1)) sont en biunivoque avec les représentations irréductibles des sous-groupes du groupe US( 2 ) , et la composante de Perron-Frobenius de ces sommets est égale à la dimension des représentations irréductibles (irreps) : c'est la correspondance classique de Mc-Kay [51].
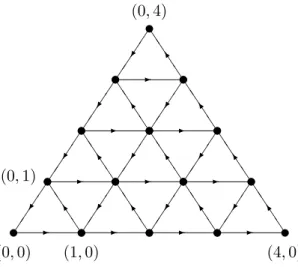
Produit de repr´esentations irr´eductibles et graphes A
- Cas classique
- Cas quantique
- Alg`ebre de graphe et matrices N i
- G comme module sur A (G) : matrices F i (ou E a )
On associe une matrice Ni à chaque nœud de sorte que (Ni)jk=Nijk donne les constantes de structure de l'algèbre. Propriété 1 L'espace vectoriel G est un module sur l'algèbre définie par le graphe A(G), l'action de A(G) sur G est la suivante.
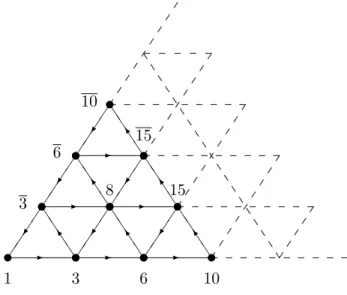
La big`ebre de Hopf faible B associ´e a un graphe ADE
- L’espace vectoriel des triangles admissibles
- Big`ebre faible B
- Projecteurs minimaux centraux, unit´es et counit´es
- Alg`ebres de caract´eres pour B et B b
- Cellules d’Ocneanu
SU(2) (étiqueté par les sommets du graphe A∞), ou pour les représentations irréductibles du graphe du groupe quantique SU(2)q, avec q la racine de l'unité. De même, les caractères de l'algèbre semi-simple (Bb,ˆ◦) sont les éléments ˇ̟x;∈ B définis comme.
Le graphe d’Ocneanu Oc(G)
D´efinition
Nous verrons que cette propriété des connexions permet d'obtenir l'ensemble complet des cellules dans l'exemple A2 SU(2) (mais aussi pour environ A1 SU(3)) à partir de la valeur de la connexion des cellules de base. De même que pour les matrices Ni et Fi, la compatibilité avec le produit (1.43) nécessite que les matrices Ox donnent une représentation fidèle de l'algèbre Oc(G).
G comme module sur Oc(G) : matrices S x
On obtient alors l'algèbre des graphes Oc(G), que l'on notera aussi Oc(G) et dont la multiplication est donnée par. Notons que même dans les cas où u G n'a pas d'auto-fusion, l'action est bien définie : la multiplication 1.a existe toujours (codée par le graphe G, c'est-à-dire `, c'est-à-dire par l'opération génératrice, le graphe A( G)).
Relations entre A (G) et Oc(G)
Fonctions de partition
Relations entre A(G) et Oc(G) 23 En définissant les matrices (dO×dO)Veij telles que (Veij)xy =Wfxyij, les conditions de compatibilité [63],[64] stipulent que ces matrices doivent satisfaire l'algèbre de fusion quadratique. La matrice Ve11 est l'identité, tandis que les matrices Ve21 et Ve12 correspondent respectivement aux deux matrices adjacentes d'un graphe de OcneanuOc(G):. 1.55) Ainsi, les données du graphe d'Ocneanu (des matrices O1 et O1′) permettent d'obtenir les matrices Ve21 et Ve12, et en utilisant (1.54) puis (1.53) d'obtenir les matrices Veij, et donc les coefficients Wfxyij définissant fonctions générales de partition.
Définition 5 On définit les matrices toriques généralisées comme les matrices dA×dA données par la relation (Wxy)i,j =Wxyij. L'action est bien définie et permet d'obtenir des formules compactes pour les expressions de fonctions de partition invariantes modulaires et généralisées.
Relations de compatibilit´e alg´ebrique
La double base correspondante ˆeI (représentée par des doubles triangles horizontaux avec un tilde) est une base du double espace Bb. Pour un graphe G du système SU(2), les composantes du vecteur de Peron-Frobenius normalisé définissent les dimensions quantiques des sommets σ de G : ce sont des nombres quantiques [n]q=qdim(σ) .
Un exemple de sym´etries quantiques des graphes du syst`eme SU (2), les graphe
L'espace vectoriel B est muni de la structure algébrique définie par le produit vertical défini par l'équation (1.23). Il faut identifier les éléments de base rr, rl, lr, ll} avec les unités matricielles correspondant aux blocs B0 et B1.
Cette propriété est vérifiée pour chacune des entrées de la table de multiplication (voir [19]). Enfin nous mentionnerons seulement que l'espace B possède également un antipode S défini par la commutation simultanée des étiquettes supérieure et inférieure, droite et gauche des diagrammes de distribution de base.
Pour l'espace dualBbla, la situation est similaire, mais nous sommes partis d'une base différente, la base duale. Les unités matricielles que nous avons construites pour Bb sont naturellement liées aux éléments de la base horizontale, et les blocs sont définis par la longueur horizontale x = 0 ou 1.
Alg`ebre de fusion et alg`ebre de sym´etries quantiques
Le coproduit de l'identité de l'action peut être écrit explicitement sur les éléments de base. Les transformations entre les éléments de la base de longueur i=x= 1, c'est-à-dire les cellules de SU(3), qui correspondent aux cellules de base, sont les suivantes. Ainsi, nous avons obtenu la valeur des cellules de base pour le graphe A1 de la famille SU(3).
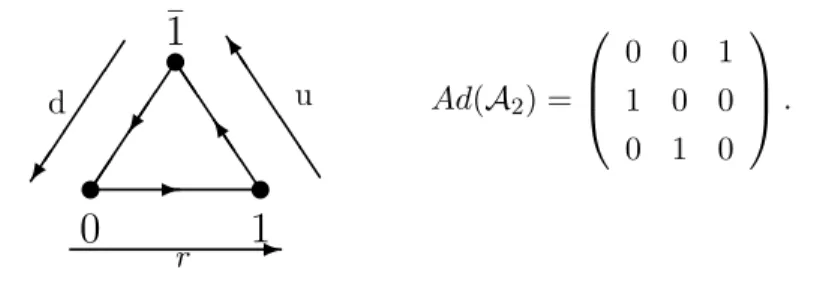
CFT and graphs
Steps of the resolution
We start with the double fusion equations (2.6), which are matrix equations involving the double annular matrices Vi j, of size dO ×dO, with coefficients (Vi j)xy. Note that these coefficients can also be encoded in matrices Wxy, of size I×dI, with coefficients (Wxy)i j= (Vi j)xy. When there are no defective lines (x = y= 0), we must recover the modular invariant of the theory, therefore W00=M.
From the modular invariant to graphs
- Determination of toric matrices W x0
- Determination of double toric matrices W xy
- Determination of the Ocneanu algebra O x
- Determination of the higher ADE graph G
- Comments
If not, a discussion similar to that for the previous items allows to determine the new toric matrices. For SU(n) there are n−1 generators f of the fusion algebra, and thus 2(n−1) generators of the quantum symmetry algebra. In the degenerate case, the determination of the double toric matrices Wxy from equation (2.16) is not easy, since some coefficients are still free.
Examples
The E 6 case of c su(2)
Une représentation matricielle 20 × 20 de l'algèbre de symétrie quantique est donnée par les matrices Os. Ce sont des matrices à 4 × 4 dimensions qui forment une représentation à 4 dimensions de l'algèbre de symétrie quantique. Une représentation matricielle 24×24 de l'algèbre de symétrie quantique est donnée par les matrices Os.
Mais les matrices Sx peuvent aussi être obtenues en réalisant l'algèbre des symétries quantiques. Ce sont des matrices 2×2 qui donnent une représentation de l'algèbre des symétries quantiques.
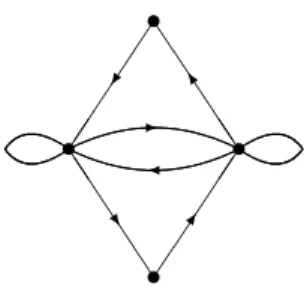
The E 9 case of su(3)
The vector space of the graph E9 is a module over the operation of the left-right graph algebra of the graph A9, encoded by the ring matrices FEi. Other aspects and properties of the graph E9 and its algebra of quantum symmetries (semisimple structure of the connected quantum groupo¨ıd, semisimple structure of Oc(E9) itself, quantum dimensions and quantum mass) are presented in [6]. , 25, 9]. The vector space spanned by the nodes of M9 is also a module under the operation of the graph algebra E9.
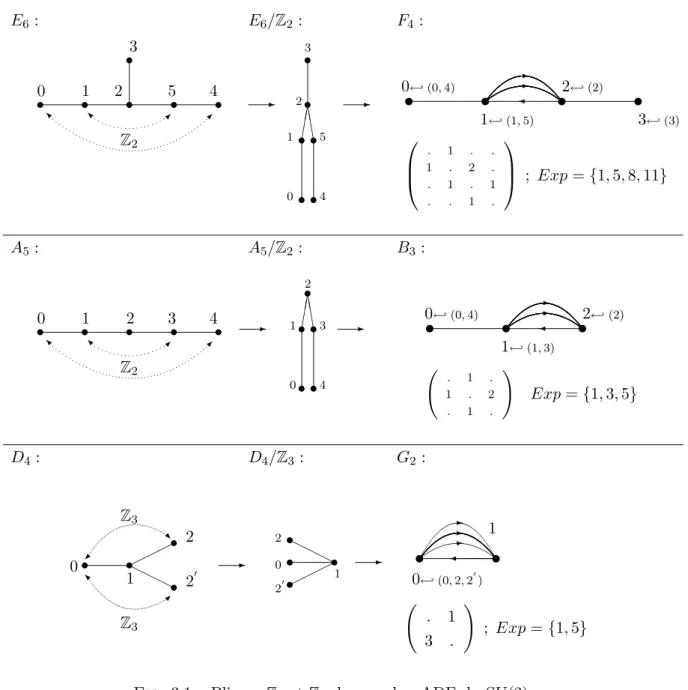
Pliage des graphes ADE, fonctions de partition et propri´et´es modulaires
La première section contient des considérations générales sur les méthodes et les résultats liés aux graphes non uniformément connectés du système SU(2). Notez que dans le processus menant à l'obtention de graphes non simples (par exemple, B3 à partir de A5), nous n'avons pas dupliqué le point de transformation fixe (point 2 de A5). La fonction de partition d'un graphe non simple construit avec le quotient du graphe ADE n'est invariante que sous l'action d'un sous-groupe congruent de type Γ0(2) ou Γ0(3) du groupe modulaire.
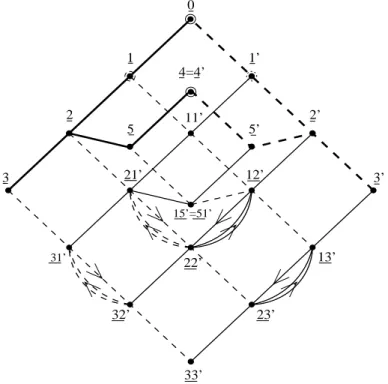
La m´ethode de scission modulaire et les sym´etries quantiques des
Si le graphe de symétrie quantique est en effet non simplement lacé, alors un graphe de Coxeter-Dynkin non simplement lacé avec la même norme que G (pas nécessairement Glui même) apparaît comme un sous-graphe de module de Oc (G). Sinx correspond à la variété des matrices toriques, et si notre graphe de symétrie quantique est (exclusivement) simplement lacé, alors. Si nx correspond au coefficient de l'équation (3.2), et si notre graphe de symétrie quantique autorise des sous-graphes non simplement lacés, alors.
Le cas F 4
Ces matrices sont les constantes de structure de l'algèbre (voir [25]) et elles peuvent être calculées à partir des relations de récurrence du graphe Oc(F4) comme suit. L'opération de Oc(F4) sur F4 est codée par les matrices Sx, qui sont des matrices à 4×4 dimensions qui forment une représentation à 4 dimensions de l'algèbre de symétrie quantique. La liste des matrices donnant l'opération de Oc(F4) sur F4 est la même que celle présentée pour la réalisation non triviale de l'équation d'algèbre de symétrie quantique 3.11.
Le cas B 3
Les matrices Fi sont des matrices 3x3 obtenues à partir des relations de récurrence codées par le graphe A5, avec générateur F1 = Ad(B3) et unité F0 = I3. B3 est un module sur le graphe Oc(B3), l'action de Oc(B3) sur B3 est codée par les constantes de structure (Sx)ab. Les matrices Sx sont des matrices de dimension 3×3, et sont calculées à partir des relations de récurrence codées par le graphe Oc(B3) (deux copies des relations de récurrence du graphe A5) avec g´ générateurs chiraux S1+=S1−=Ad( B3) et les unités S0+ = S0− =I3.
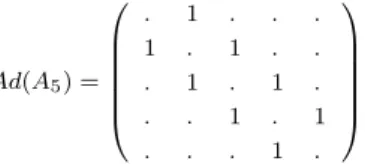
Le cas B 4
Les matrices Fi sont des matrices de dimension 4x4 obtenues à partir des relations de récurrence codées par le graphe A7. Comme dans l'exemple précédent, l'identification de la fonction de partition ZB4 avec le graphe non simplement lacé B4. Mais comme dans le cas B3, il s'avère que le graphe de la famille de Coxeter numéro huit, D5, est aussi un module sur A7 et Oc(B4).
Le cas g´en´eral B n
L'espace vectoriel généré par cet ensemble de matrices est de dimension r= 2×(2n−1)−1, et la dimension de l'algèbre de symétrie quantique est dimOc(Bn) = 2×( 2n−1). L'algèbre de symétrie quantique est réalisée sous la forme Oc(Bn) =A2n−1⋊ Z2, les étiquettes de la figure 3.10 correspondent à la notation des éléments de base i±, ou id désignent les sommets du graphe A2n−1. Le graphe de symétrie quantique est le graphe de multiplication de Cayley avec des générateurs gauche et droit, chaque partie chirale étant composée de l'union de deux graphes disjoints de type A2n-1.

Le cas G 2
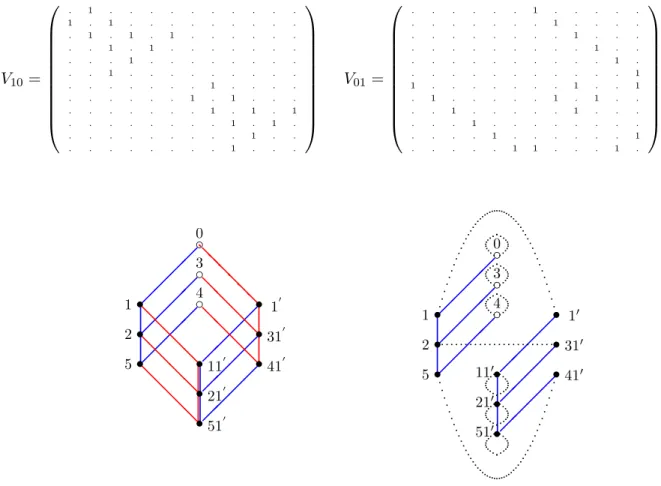
Ces deux matrices sont les matrices d'adjacence des parties chirales gauche et droite du graphe d'Ocneanu. Une représentation 9×9 de l'algèbre de symétrie quantique est donnée par les matrices Ox qui sont calculées à partir des relations de récurrence du graphe Oc(G2) et en fonction des deux générateurs O1⊗0 =V10 et O0⊗1 =V01 comme suit. Une représentation 16×16 de l'algèbre de symétrie quantique est donnée par les matrices Ox qui sont calculées à partir des relations de récurrence du graphe Oc(G2).
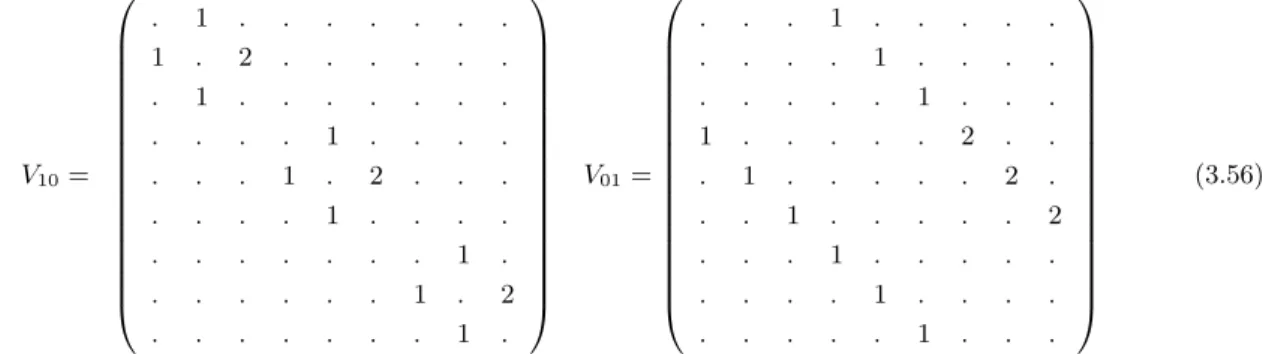
Un exemple non-simplement lac´e du syst`eme SU (3)
Dans l'ordre choisi, les matrices d'adjacence V10 et V01 correspondent aux générateurs droit et gauche de l'algèbre de symétrie quantique. La résolution de cette équation permet de calculer de manière relativement simple les symétries quantiques d'un invariant modulaire, à savoir l'ensemble des matrices toriques, le graphe d'Ocneanu et une réalisation mathématique de l'algèbre de symétrie quantique Oc(G) . Dans des cas ordinaires (simplement connexe), on sait relier, à toute théorie conforme invariante modulaire, deux algèbres en dualité (plus précisément, un groupoïde quantique) dont les algèbres de caractères s'identifient à l'algèbre de fusion, d'une part, et aux l'algèbre des symétries quantiques, d'autre part.