In the Jaynes-Cummings-Gaudin model that we will consider in this paper, the set equilibrium point level is a compact pinched torus with a size of 2 m. In Section 2, we recall the definition of the Jaynes-Cummings-Gaudin model and basic facts about its integrability. It is then easy to see that all first-order terms in the extensions of the Hamiltonians Hj.
From the previous discussion, the normal flows on the singular torus are given by the Hamiltonian flows associated with the generatorsKjandLjdefined in terms of the conserved Hamiltonians in equations. Let al (resp.. θl) denote the time variable of the normal flow generated by Kl(resp.). We now want to accurately indicate the relationship between these solitonic formulas and the linearized flows near the equilibrium point.
There is a significant connection between the Ck components of the C cone and the currents associated with the Kyon Hamiltonians of the critical collector. S(I) of the tangent cone with that based on the normal coordinates presented in Section 3. This shows that we are actually describing a 2m-dimensional subspace (over R) of the tangent space at the equilibrium point.
In reality, C(E¯j) is not exactly zero, due to the subleading terms included in the determinantD1.
Motivation
To check that this is indeed true, we need to know the asymptotic expression for C(λ) when |Xj| → ∞ for any j ∈ I. 33) and the asymptotic expressions cf. If the typical value of theXj scales like X, the ratio of these subleader terms over the dominant one scales like X−2. The leading behavior for C(λ) is now given by eq. 35) where the setI is replaced by the complementary setI (in which all indices are replaced by i→¯i).
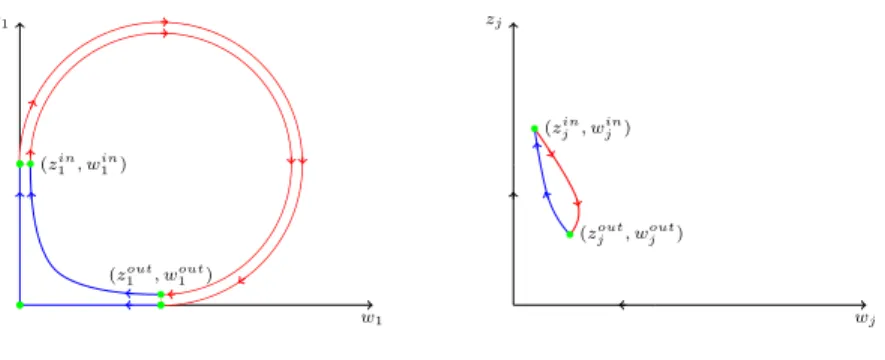
3, it is possible to use these large solitonic trajectories to construct periodic trajectories, at least for regular tori close to the singular. The motion starts from a position (z1in, win1 ≃0) on the expanding manifold and returns to a position (z1out≃0, w1out) on the contracting manifold. At the same time on the jth>1 component there is an induced movement from (zjin, winj ) to (zjout, woutj.
Periodic flows
Diagonal case
The first is the large solitonic motion generated by α1K1+β1L1 during a time course 2T, which gives a relation between (zin1, win1) → (zout1, wout1) as explained in section 7. This part of the trajectory is complemented by an additional effect of the flow α1K1 +β1L1 during a time course τ relating (zout1 , wout1 ) → (zin1 , win1 ) to obtain a closed path. This last part of the analysis lies exclusively in the domain of validity of the normal forms.
The quantity 2T +τ is the total time it takes to run once along the closed path, that is, the period of the movement.
Non diagonal case
Action variables and symplectic invariants
The form Ωreg contains all the regularized symplectic invariants of San V˜u Ngoc [4], calculated here on the singular fiber. Regarding the action H(1), we see that it has the unique property of being singular when c1=K1+iL1→0, but it remains regular whencj =Kj+iLj →0, j6= 1. To get an indication of its global definition , we can consider the example of the 3-spin model and the motion of the separated variables in the soliton solution (see Appendix 9) corresponding to the limiting motion generated by H(1) on singular fiber.
Thus, the corresponding points (µk, λk) belong to different planes in the representation of the spectral curve covering the complex plane. The important ingredient here is the identification of the Bj cycles by the movement of the divisor of the correct soliton solution. A full analysis of this motion has not yet been established, but using the asymptotic expressions for determinants given in section 10, it is possible to show that if time t1 goes to −∞, we have one separate variableλ have +1 located at E¯ 1, and another one, λ−1, at E1.
As t1 goes to +∞, there is one discrete variable λ+i located at E1 and one λ+j located at E¯1. It is established that the other remaining separate variables, m−2 of type λ+ and m−1 of type λ−, occupy the same sets of points in the complex plane in both limits t1 → −∞ and t1 → ∞ due to the periodicity conditions of equation (47). The difficult task remains to show that this possibly complex motion of separate variables can be continuously deformed into one of the cycles of Bj. An alternative approach would be to use the Picard-Fuchs equations for the action variables as in [7].

Monodromy
Eliasson's theorem allows an easy description of this stratification in a local neighborhood of the equilibrium point. In this case, the rank of the momentum map drops tor = 2m−2 and the equation of this stratum is Kj = Lj = 0. Monodromy is defined in the open set of the regular values of the moment map.
Following up the transformation of the action integrals H(j) defined in the previous section along such a non-trivial path would also lead to an interpretation of the monodromy within the framework of the Picard-Lefschetz theory as in [12]. Consider the point U : (z1=δ, w1= 0) on the expanding manifold and the path of the flow starting at that point. As shown before [4, 5], the symplectic invariants are associated with the Liouville foliation in the vicinity of the singular torus.
In the neighborhoods U and U', the study of the symbolic diffeomorphism is thus reduced to the study of the commutative diagram. This implies that the matrix is diagonal, and since it is an element of GLm(Z), it is of the form Aik =ζiδij, ζi=±1. The rank-preserving remarks of the momentum map impose restrictions on the form of the Taylor expansions of these functions.
One can push the argument and show that smoothness of the map in limitc1→0 gives. The initial dynamical model can be recovered by adding the phase of the oscillator coordinates ¯b, b to the separated variables. HamiltoniansHj for the reduced model are obtained by writing that the points (λk, µk) belong to the spectral curve.
Using the Poisson bracket equation (70), the equation of motion of the variable λk with respect to Hi. The choice of sign here plays a crucial role in describing the different layers of the level set. In particular, recalling eq.(69), this means that one of the separated variables, say λ1, is frozen at the value E, provided ¯bb6= 0.
We then consider the remaining complex roots of the spectral polynomial where no discrete variables are frozen. Note that the last term on the right-hand side is necessary to adjust the terms for degree+ 1 and nin λ between the two sides of the equation. As we have seen, the general solution of the Hamiltonian evolution on the critical torus, Eq.
In the following discussion, however, only the homotopy class of the trajectory will be important.