Temperature0
The number of nucleotides in the barrel is N − 10, since the stem always consists of two segments. This indicates that the entropy gain provided by opening the hairpin contributes to lowering the free value. The role of loop stiffness can be tested by hanging the loop value.
10 8 Monte Carlo steps, while the rosses involve only 4 10 8 Monte Carlo steps
So we must integrate e − βH s over all the variables of the stem except the first.
The expression for Z (r) allows us to calculate the average value of r versus T, which is a measure of the opening of double-stranded DNA. Where N is the number of monomers, { α N }, the general loop variables, and H N , the loop Hamiltonian. To construct the hairpin partition function, we will start from the reduced loop partition function made by N.
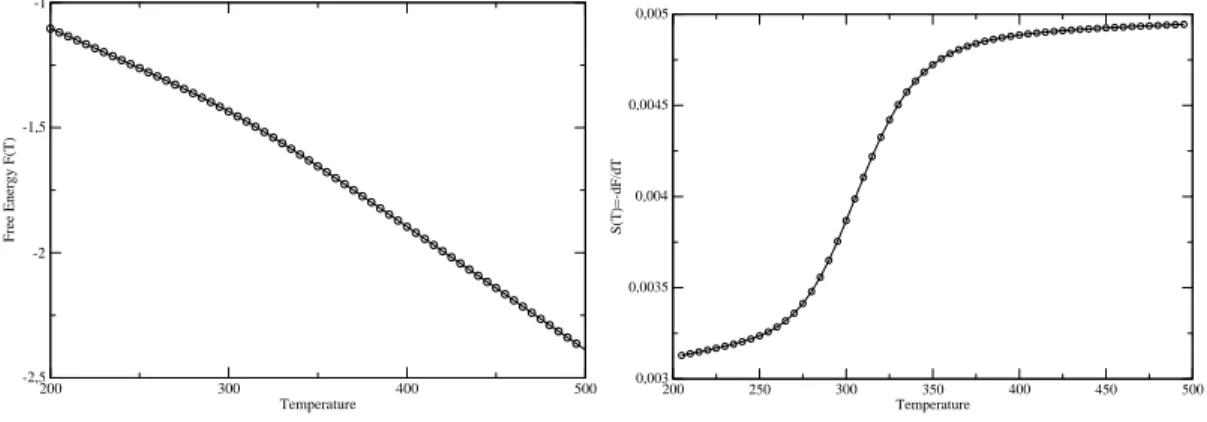
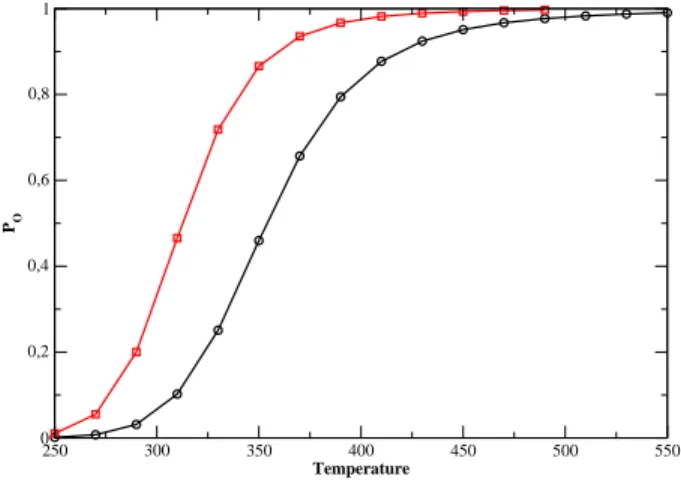
The same process is repeated if we add a third base pair in the stem. We see a change in the slope of the free energy around 310 K, which could be
Z r max
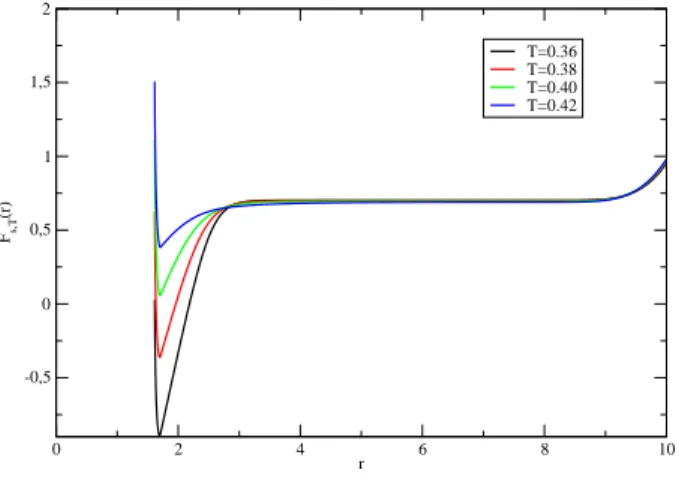
To get an initial idea of the hairpin's behavior, it is useful to start. For the Kratky-Porodhain model the penalty is energetic, while for the FRC very low values of r reduce the value again. This form of the urve F(r) justifies the image of the two-state system that we have.
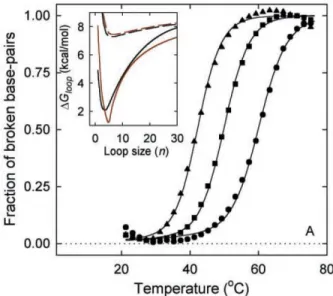
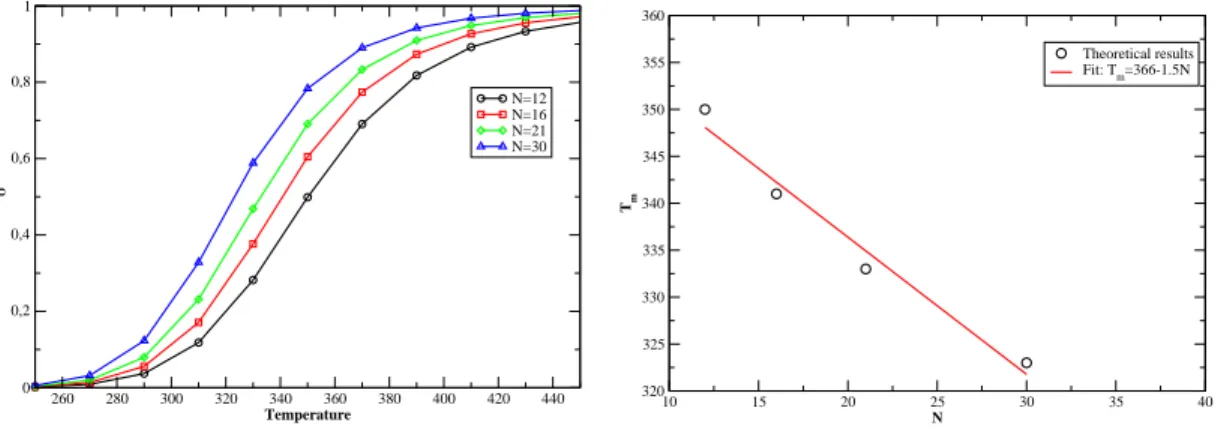
We see that the stem tends to open at lower temperatures in the presence of the loop. To further study the details of the cycle, we now present the results. Disrete Kratky-Porod hain If we hang the loop pattern, it is inter-.
End-to-end distance r0,001
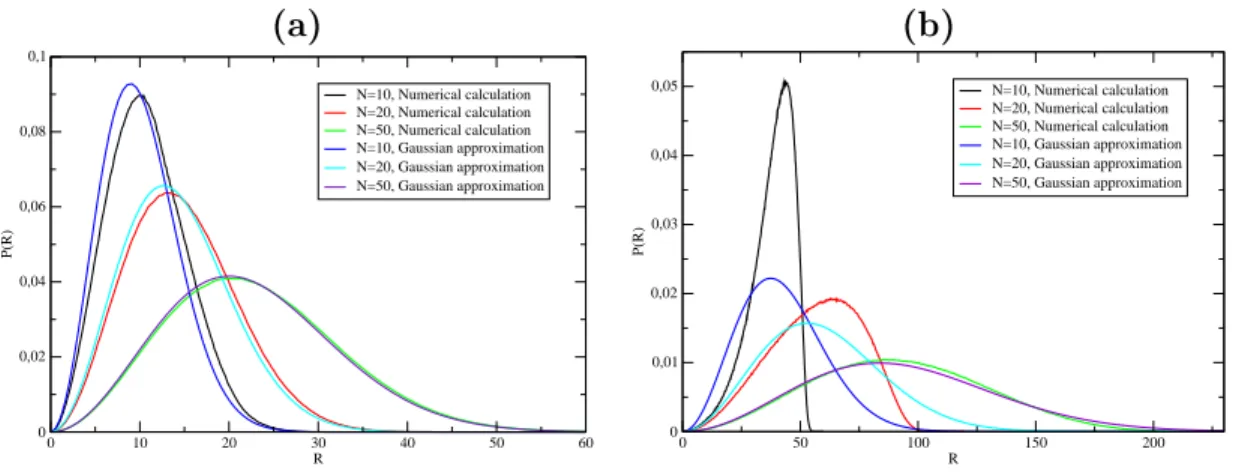
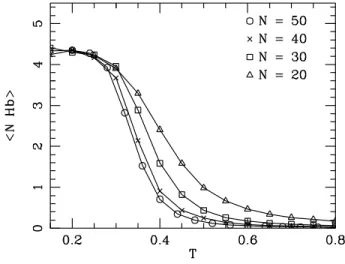
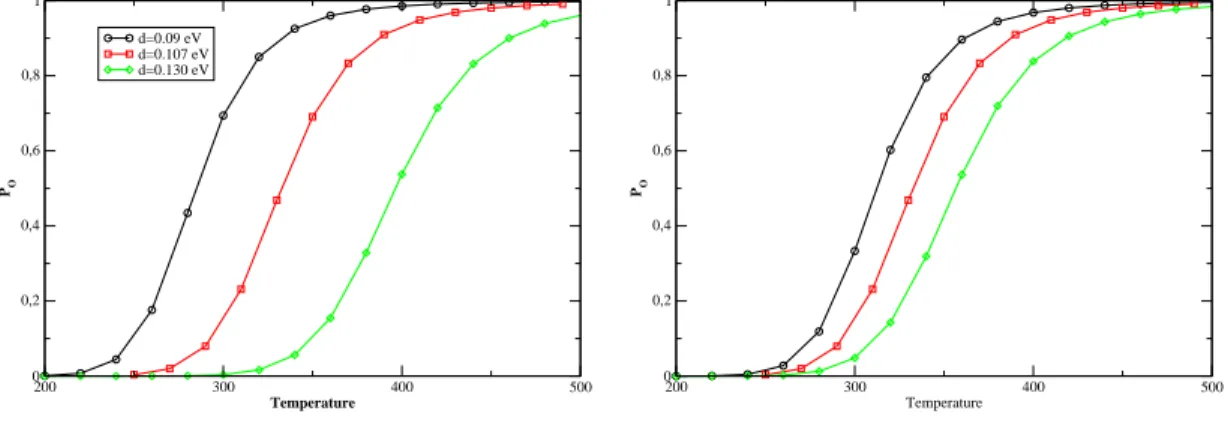
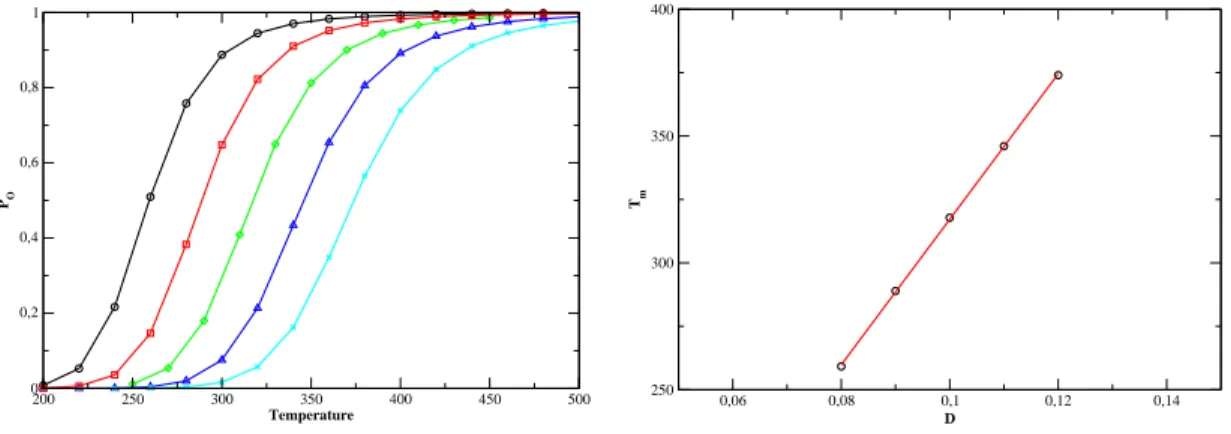
However, for |=0.0040eV.Å− 2 we get something quite surprising. the evolution of T m as a function of N is not monotonic. the chance of forming small loops, which are necessary to form hydrogen bonds in the stem, is very small. To see this eats,Fig. probability distribution of the Kratky-Porodhain for different loop lengths and for. large enough to allow the system to overcome the free energy barrier represented. Secondly, if we hang the value of k, we achieve the stiffness of the. The onguration is more stable for larger values of k and the equilibrium is shifted toward higher temperatures.
The value of ρ has a smaller value. melting proles because we consider them to be short stems such as a five base pair stem. This differs from eet ρ on double-stranded DNA. Helies of large ρ values lead to a large increase in entropy when some regions are included. As we increase the width of the Morse potential, we also increase the width of the first well of free energy, which represents
Thus, the lost information is more stable and. the same inuence of parameters in T m as in long dsDNA with a square. The parameters are as follows-. inuene of ǫ as well as inuene of D in fusion proles with Kratky-. Furthermore, the eet of ǫ is comparable to the eet of θ in FRC,. the larger the value of ǫ, the smaller T m.
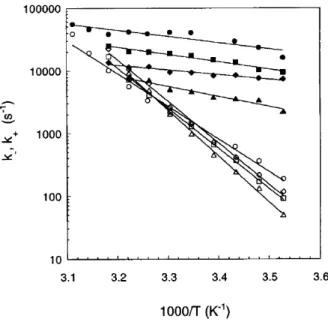
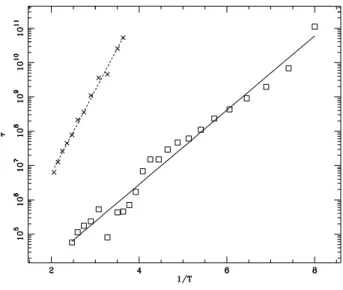
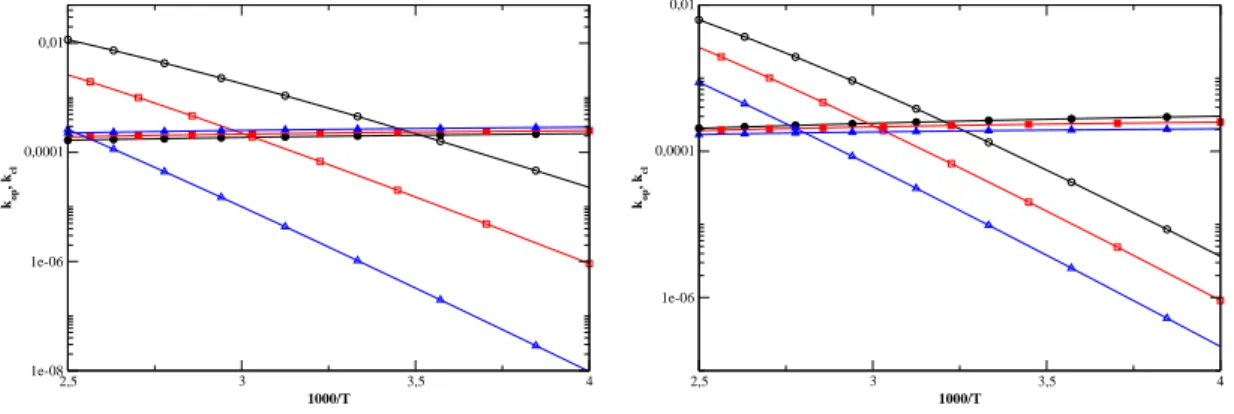
Therefore, when we increase the stiffness, the hairpin is subject to liners from the loop portion which tend to destabilize it. The ethers of the length of the loop and of the θ angle of the FRC model are shown. 5.23), which shows the kinetic constants k op and kcl versus temperature in a semi-log plot.
The variation of k op and k cl with other parameters. indicate the notions that we have drawn from the study of N and θ. 5.24) a variation of D and k has little effect on the loss rate. because loss is mostly governed by the entropy of the loop. Open and lost symbols represent the frequency of opening and losing, repeatedly. the variation of D and k significantly inuences the opening, which is controlled by.
Therefore, it increases E and slows down the opening. we notice only a very small eat on E. This seems surprising because K enters. in an energetic term in the stem and therefore we expect it to play a role. but we anticipate this discussion by noting that the link is along the. This entropy gain is smaller as k increases due to the relative motions of. the elements of the stem are more restricted.
With the FRC model, we see a change in loop parameters. The open and lost symbols represent the level of open and loss. energy is now positive, which agrees with some experimental results. understand, because due to the ǫ-term in the Hamiltonian of the Kratky-Porod chain, there is now no energy for loss.
Temperature300
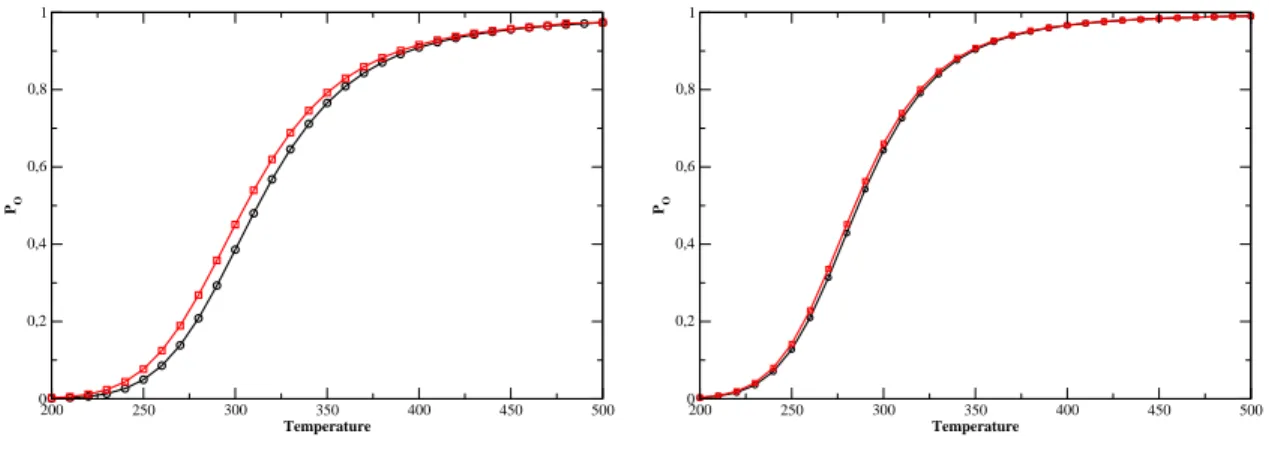
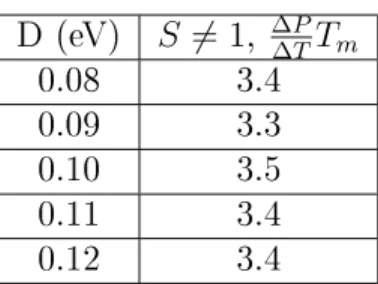
Nevertheless, as the following table shows, the width of the transition is not significantly affected by the variation of D. This shows us that the depth of the Morse potential serves as the tting of the. Furthermore, the width of the transition is slightly reduced by the slope of α and axis. the smaller the width of the Morse potential, the smaller the width.
Right: evolution of the establishment temperature with α. 5.33) gives the evolution of the fusion prole as a function of k. It is interesting to see the eet of the function S in the ase of Kratky-Porod. The next table gives the variation of the transition width with and without the S function.
Temperature290
As disproved for FRC ase, this is due to the fat with which the stem. For the FRC model, it is not possible to quantitatively compare only theoretical results and experimental results, because first we. As for the FRC model, the opening kinetics is independent of the change.
This problem of the broad melting was also encountered in the first studies of the double. For a long double helix (or within the limit of an innit, double-stranded DNA), the problem was solved by introducing the non-linear. Its purpose is to increase the entropy of the molten part of the helix with respet to.
Temperature-0,8
Due to the presence of l 0, the approximation of the previous two integrals is non-trivial. Now go easy from end to end of the distance of the throat using the fat. Finally, we give the result of the radius rotation exas as well as its value in .