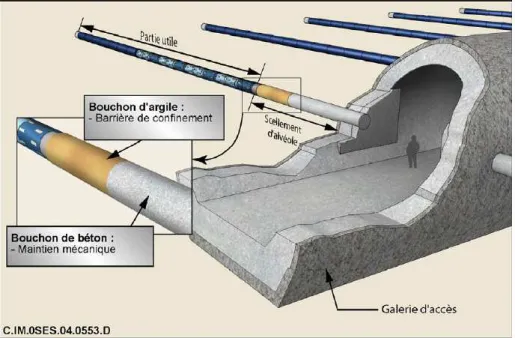
Nous nous intéressons dans cette thèse à l'évaluation des paramètres de transport de solutés dans un milieu poreux à faible perméabilité, d'un point de vue théorique et appliqué, en relation avec le stockage de déchets nucléaires à vie longue en couche géologique profonde. Dans le premier paragraphe, nous présentons le contexte général du projet de thèse.
Contexte g´ en´ eral
Traditionnellement, on distingue trois types de gestion des déchets HAVL, correspondant aux trois domaines de la loi de 1991 (cf. section 1.1.3) : entreposage en surface, transmutation-incinération, entreposage en profondeur sur site. Cette loi prévoit des recherches et des études liées aux déchets radioactifs de haute activité (HA) et de moyenne activité à vie longue (MA-VL) et renforce la position d'Andro en tant que responsable de la gestion durable de l'ensemble des déchets radioactifs produits par la France.

Contexte scientifique
Dans ces délais, les colis rouilleront et des radionucléides seront rejetés dans la décharge. Il est donc essentiel de pouvoir estimer la propagation des radionucléides en cas de rejet dans le milieu géologique.
Mod` eles physiques et math´ ematiques
Définition 1.3 (Perméabilité) La notion de perméabilité quantifie l'influence de la géométrie de la matrice solide sur la vitesse d'écoulement des fluides dans la roche. Définition 1.4 (Conductivité hydraulique) La conductivité hydraulique K du milieu poreux est définie comme le rapport entre la perméabilité et la viscosité de l'eau.
Pr´ esentation du probl` eme inverse
Un des objectifs de la thèse consiste donc dans le développement d'un outil numérique d'estimation des paramètres de transport (problème inverse) à l'échelle métrique. Les outils développés dans la partie identification des paramètres sont ici réutilisés.
Plan du m´ emoire
Avant de présenter la résolution numérique des équations d'écoulement et de diffusion-convection, il convient de définir ce qu'on appelle par problème direct : on dit résoudre un problème le direct (par opposition au problème inverse, cf. section 3.1) lorsque l'on recherche . Puis nous expliquons le fonctionnement de la plateforme Alliances et du code Traces et nous terminons en présentant le problème que nous considérons et en exposant les résultats numériques du problème direct.
Les ´ equations d’´ etat
Nous revenons dans ce chapitre sur ces équations et présentons les modèles numériques associés. Le chapitre est organisé comme suit : d'abord on rappelle les équations d'état puis on présente les schémas numériques qui ont servi à la discrétisation.
Discr´ etisation des ´ equations
Brezzi [10], Farhloul & Serghini Mounim [49] pour la formulation EFMH des équations de convection et de diffusion et enfin Roberts & Thomas [85] pour une vision globale du problème. On rappelle ici les grandes lignes de la méthode EFDG pour la partie hyperbolique.
Plateforme de calcul Alliances
Le modèle de données Alliances se compose des éléments (entités) suivants. Meshes and Fields qui regroupent des méthodes et des données pour importer et échanger des meshes et des champs entre modules.
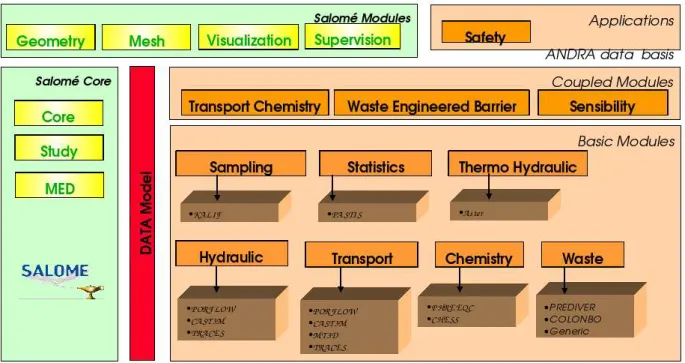
Impl´ ementation
Généralement, les différents arguments qui posent problème sont définis à l'avance, notamment pour plus de lisibilité du script.
Position du probl` eme
Les résultats du code seront considérés (comme pour la norme "parcelle") comme des mesures pour le problème d'identification. Nous n'avons traité que le cas 2D alors que la géométrie du problème réel est en 3D (axisymétrique).

R´ esolution du probl` eme
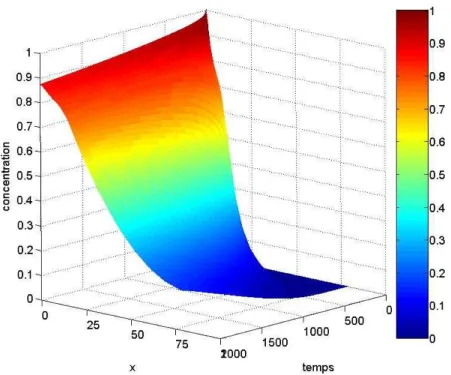
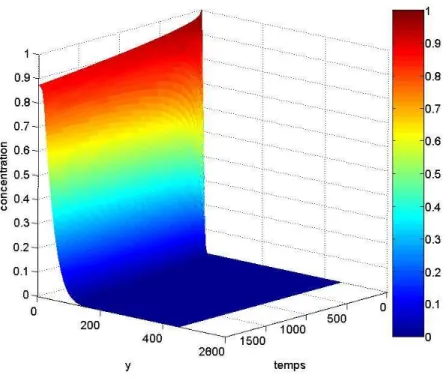
Dans l'équation (1.6), on prend le terme source Qnul et on part d'une concentration de 1mol/m3 dans la zone d'injection Ω2, que l'on laisse évoluer sur 1000 jours (un pas de temps d'une demi-journée). Le résultat est visible sur la figure 2.10 : la concentration a légèrement diminué dans le colis, mais a tout de même atteint le bord droit du domaine. Ces résultats concordent bien avec la physique et ce à quoi on pourrait s'attendre.
Avant de présenter des méthodes de résolution de problèmes inverses, il convient de définir ce qu'on appelle un problème inverse : on dit qu'un problème inverse est une solution (par opposition à un problème direct, voir chapitre 2) quand on veut déterminer les paramètres de porosité ω et diffusion D dans l'équation (1.6 ) connaissant les conditions initiales et les valeurs limites et de concentration.

Introduction
La même méthode s'applique dans le cas de strates géologiques en milieu naturel [26] où un zonage horizontal peut être envisagé (cf. figure 2.4). La modélisation des écoulements et des transports en milieu poreux autour du stockage nécessite la connaissance des paramètres physiques des différentes couches géologiques. Parmi ces paramètres, la porosité et la diffusion ne sont pas directement accessibles par des mesures, c'est pourquoi nous devons résoudre un problème inverse pour les identifier.
De manière théorique et pratique, la question se pose toujours de savoir si les mesures sont suffisantes pour estimer les paramètres que l'on recherche et quelle est l'incertitude.
Etude th´ eorique du probl` eme inverse
Les questions de stabilité et d'identifiabilité sont donc au cœur de l'estimation des paramètres et sont étroitement liées au choix de la paramétrisation. Ce procédé devient d'autant plus coûteux que le nombre de paramètres est important. On procède de la même manière que dans la section précédente pour obtenir le gradient de la fonction de coût par rapport aux paramètres à identifier.
Comme nous l'avons déjà souligné dans la section 3.2.2, la méthode des états conjoints prouve son efficacité lorsque le nombre de paramètres devient grand.

Etude num´ erique du probl` eme inverse
Dans le cas de la méthode de Newton, Bk est exactement la matrice hessienne ∇2Jk. Dans l'optique d'utiliser des méthodes quasi-Newton à mémoire limitée, nous avons essayé l'algorithme de minimisation M1QN3 de Gilbert & Lemar´echal [54] de l'INRIA. Dans le chapitre précédent, nous avons vu comment calculer efficacement le gradient continu en utilisant la méthode de l'état adjoint.
Nous allons voir ici comment calculer numériquement le gradient de la fonction de coût.
G´ en´ eralit´ es sur le calcul des d´ eriv´ ees
En effet, dans notre cas nous devons calculer la dérivée de la fonction J(K) par rapport à aK, où K = (ω, D)∈RN. Pour mieux approximer la dérivée, on pourrait utiliser la formule des différences finies centrées au lieu de (4.4), c'est-à-dire que la courbe en bas à gauche donne l'évolution de la différence relative entre le taux d'accroissement et la dérivée.
Nous avons vu au chapitre 3 que la méthode des états adjoints permettait d'obtenir le gradient de la fonction de coût en résolvant seulement deux systèmes d'équations aux dérivées partielles.

Diff´ erentiation automatique du code par Tapenade
Les principales difficultés résident dans la (possible) non dérivation de certaines fonctions et la gestion de la mémoire par le code assistant. Pour obtenir ces valeurs lors de l'exécution du code clé (puis du code commun) il existe plusieurs options. Cette méthode nécessite N intégrations (la longueur de K) du code tangent et une intégration du code direct.
Si l'on prend la structure du code TRACES (voir section 2.4.1), comme architecture du code TRACES ajouté, on a un schéma similaire au schéma 2.2.

Du point de vue num´ erique
Conclusion
G´ en´ eralit´ es
R´ esultats num´ eriques
L'évolution des paramètres au cours des itérations ainsi que la fonction de coût et le gradient sont représentés sur la Figure 5.2. L'évolution des paramètres au cours des itérations ainsi que la fonction de coût et le gradient sont représentés sur la Figure 5.7. L'évolution des paramètres au cours des itérations ainsi que la fonction de coût et le gradient sont représentés sur la Figure 5.8.
L'évolution des paramètres au cours des itérations ainsi que la fonction de coût et le gradient sont présentés sur la figure 5.9.
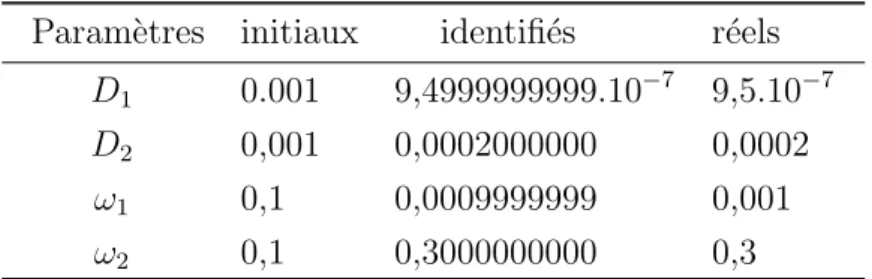
Conclusion des tests
Dans le chapitre 3, nous nous sommes intéressés à l'estimation de paramètres connaissant la géométrie exacte du domaine. Ces tests sont très importants car le nombre et la position exacte des sous-domaines sont inconnus en pratique. Concernant les données (synthétiques), pour les observations nous avons utilisé les valeurs de concentration générées avec le zonage exact du domaine dans les cas sans bruit et avec bruit.
Pour le bruit nous avons également utilisé le bruit généré avec le zonage exact du domaine.
Introduction
On cherche ici, à partir d'une configuration géologique modifiée, à trouver la bonne configuration géologique (celle qui a permis de générer directement les données synthétiques du problème) en identifiant les paramètres qui supportent ces zones. En regroupant ensuite les coefficients identifiés selon les isovaleurs, nous aurons la configuration souhaitée.
Etude num´ erique
L'évolution de la fonction de coût et du gradient est représentée sur les figures 6.23 et 6.24. Les évolutions de la fonction de coût et du gradient sont présentées dans les figures 6.27 et 6.28. L'évolution de la fonction de coût et du gradient est représentée sur les figures 6.31 et 6.32.
L'évolution de la fonction de coût et du gradient sont présentés dans les figures 6.35 et 6.36.
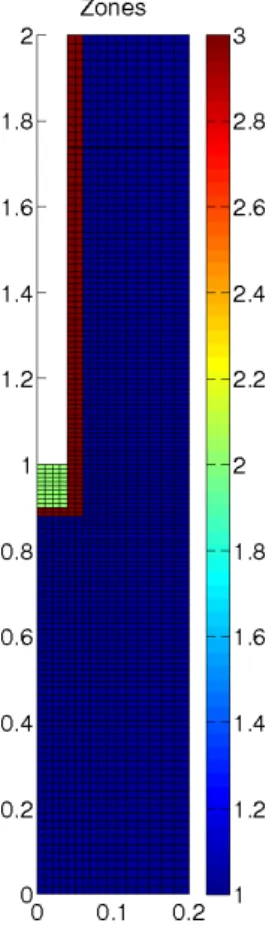
Conclusion des tests
Dans cette thèse nous nous intéressons à différents aspects de l'identification de paramètres dans un milieu poreux saturé. Le zonage, dans le cas test "réel" (proche de l'expérience DIR), a pris en compte la zone endommagée par le forage. Le réglage des outils a d'abord été effectué dans des zones fixes, puis, dans un deuxième temps, l'identification des zones a été effectuée.
Nous avons obtenu des résultats très satisfaisants à la fois dans l'estimation des paramètres et dans l'identification des zones avec des données bruitées et non bruitées, ce qui est là encourageant.