Elle est plus pragmatique car son but est de décrire à moindre coût le comportement de la matière qui nous entoure, constituée d'un grand nombre de fermions. Ceci est intéressant car une partie de la vue à un seul corps reste intacte, décrite en termes d’excitations de trous de particules. Après variation, on obtient des équations de type champ moyen parfaitement équivalentes à l'équation de Schrödinger (au sein de l'hypothèse de Kohn-Sham), c'est-à-dire prenant en compte les corrélations, avec un hamiltonien également fonctionnel, de la densité fermionique totale .
Au cours des dernières décennies, la théorie de la fonctionnelle de la densité a connu de nombreux succès dans l’étude des systèmes électroniques (tels que les atomes, les molécules, les agrégats et les solides). Il s'agira d'un chapitre très général, qui expliquera le problème exact qui a motivé mon travail de thèse : les approximations inhérentes à la théorie fonctionnelle de la densité n'éliminent pas un effet non physique appelé auto-interaction. , ce qui est particulièrement gênant pour la description des rayonnements. , et les méthodes actuellement utilisées pour annuler cet effet ne sont pas satisfaisantes dans le cas dynamique. Pour cela nous proposerons un nouveau formalisme dynamique sans auto-interaction, résultant de la généralisation au cas dépendant du temps du schéma SIC exact et d'une méthode de propagation numérique (chapitre 2).
La théorie fonctionnelle de la densité (plus tard DFT) est devenue, au cours des dernières décennies, un outil théorique largement utilisé pour la description et l'analyse des propriétés électroniques des systèmes physiques et chimiques, en particulier pour les systèmes contenant un grand nombre d'électrons [6,5 ]. Une approximation supplémentaire, beaucoup plus simple à propager numériquement, découle naturellement de la localisation spatiale d'un des ensembles d'orbitales.
La théorie de la fonctionnelle de la densité
L'approximation adiabatique de densité locale et le problème d'auto-intéraction. 29
Notons qu’il n’est pas nécessaire d’imposer la conservation de la norme, comme dans le cas stationnaire, car elle est déjà contenue sous la forme de l’intégrale d’action. Toute la puissance de la DFT est qu'elle permet de prouver (à l'exception de l'hypothèse de Kohn-Sham3) que cette expression peut s'écrire sous la forme d'une fonctionnelle universelle. La théorie de la fonctionnelle de densité dépendante du temps (ci-après TD-DFT) est basée sur la stationnarité de l'intégrale d'action quantique (1.2).
Par conséquent, la forme de l’intégrale d’action (1.21) contient bien la conservation de la norme de chacune des orbitales à un corps. On voit dans la forme obtenue (1.31) que le résultat ne dépend que localement de la densité, c'est-à-dire qu'on a UXLDA[](r) = UXLDA[(r)]. Mais, de la même manière que dans le cas stationnaire, l’expérience numérique montre que la validité de la LDA ne se limite pas à.
L’investigation des limites de la LDA dans le cas dynamique en est encore à ses balbutiements. La conservation de la normalisation des orbitales monoélectroniques est matérialisée sous la forme de l'intégrale d'action SIC.

Lois de conservation
Sur la localisation spatiale et ses conséquences
Il s’agit de la généralisation au cas dépendant du temps des 2 ensembles de formalisme SIC présentés en 1.3.1 (notés par la suite 2 ensembles de TDSIC). Car (2.7) montre clairement que la forme de la correction SIC résultante (donc du potentiel résultant) n'est pas hermitienne dans tout l'espace de Hilbert ( ^USIC 6= ^USICy). Nous commençons par un ensemble d'orbitales diagonales f'i(t)g et recherchons la transformation unitaire ^(t) qui satisfait la condition de symétrie (2.11).
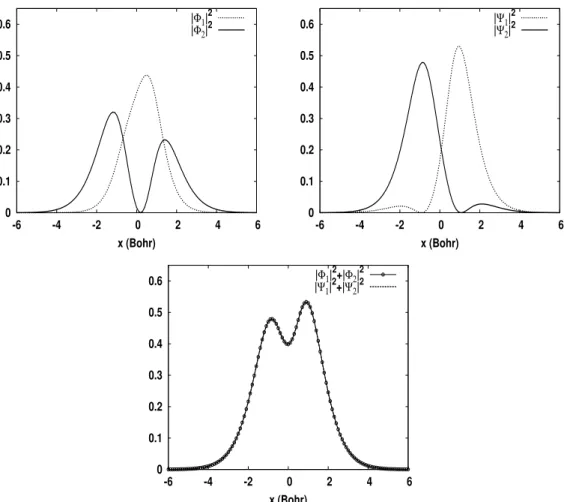
Nous avons souvent soutenu que les orbitales satisfaisant la condition de symétrie (2.11) sont spatialement très localisées (en général, bien plus que les 'i-orbitales diagonales). Evolution de la valeur relative de '(variance spatiale des orbitales diagonales) par rapport à (variance spatiale des orbitales localisées), en fonction du temps. En observant la forme de la condition de symétrie (2.11), il n’est pas clair que la transformation unitaire qui la satisfait produise nécessairement des orbitales spatialement hautement localisées.
Enfin, nous faisons varier l'expression obtenue par t et fixons le résultat à 0, nous donnant la condition pour localiser la forme. On remarque que la structure du résultat (2.29) est proche de la structure de la condition de symétrie (2.11), qui est réécrite dans la représentation fjr)g. Si tel est le cas, cela fournirait un argument formel clair pour prouver que la condition de symétrie produit des orbitales localisées.
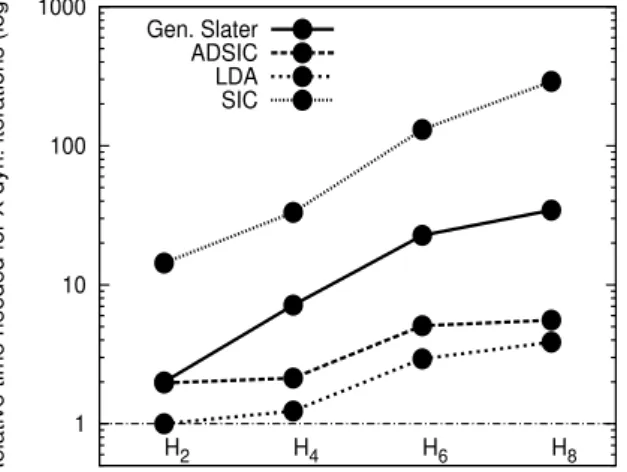
Ceci permet de déduire que dans un calcul stationnaire les orbitales qui satisfont à la condition de symétrie doivent toujours rester très localisées. Il a été proposé par Giannoni et al en 1976 [70] dans le cadre du formalisme Hartree-Fock [71] et dans l'esprit de son approximation adiabatique, et par Domps et al en 1998 [72] dans le cadre de la DFT. Nous n'avons pas le choix du critère de placement : ce doit être la condition de symétrie (malgré son coût numérique plus important que les autres critères de placement).
Nous avons vu que la forme du projecteur de correction de SIC (2.7) impose sa non-localité, c'est-à-dire Cela semble justifier fondamentalement l’introduction de fonctionnelles de densité à un électron j j2 dans le cadre DFT. Ce formalisme est tout à fait cohérent avec l'idée de base de la DFT, dans le sens où il permet de déduire que l'énergie SIC résultante peut s'écrire sous la forme d'une fonction (implicite).
![Figure 2.1 - Potentiel v ext + U LDA [] résultant d](https://thumb-eu.123doks.com/thumbv2/1bibliocom/464046.69649/57.892.310.620.128.359/figure-potentiel-résultant-résolution-modèle-électrons-correction-représentée.webp)
Formalisme dépendant du temps
Approximation Generalized SIC-Slater et lois de conservation
Premières considérations sur l'intérêt de ce formalisme
Dans le cas où cela dépend du temps, ils peuvent fortement perturber les économies d'énergie. Le résultat étant nouveau tant pour le cas stationnaire que pour le cas dépendant du temps, commençons par présenter le cas stationnaire. Comme ce potentiel n'est que légèrement non local (en raison de la forte localisation spatiale de - cf. 2.3.3), nous concluons que le potentiel UapproxSIC doit être une très bonne approximation locale de ^USIC.
Cette sensibilité n'a plus sa place dans le cadre du formalisme OEP-SIC Généralisé et l'approche (3.13) en découle naturellement. Puisque, en raison de la forte localisation spatiale de , OEP-SIC généralisé est une excellente approximation locale du potentiel non local ^USIC (2.7) et que ^UGS est une très bonne approximation de OEP-SIC généralisé, nous concluons que cela doit être également une très bonne approximation locale de ^USIC - nous le vérifierons numériquement au chapitre 4. Utilisation de la localisation de. simplifions-le d'abord à VAppprox = 1. On ne néglige plus les variations de UapproxSIC j) autour de ULDA[j j2]j), comme auparavant pour l'approximation DC, même si cette dernière doit rester petite.
Mais cet observable n’est que très insensible à la correction KLI dans le cadre du formalisme Général OEP-SIC. Pour les mêmes raisons que dans le cas stationnaire, il s’agit a priori d’une bonne approximation locale du potentiel à 2 ensembles TDSIC (2.7). Voyons maintenant si, comme dans le cas stationnaire, l'exploitation de notre localisation spatiale nous permet de simplifier davantage les choses.
On voit qu'il a la même forme que le potentiel GS obtenu dans le cas stationnaire et qu'il ne contient pas explicitement d'effets mémoire (pas d'intégrale temporelle). Pour les mêmes raisons que dans le cas stationnaire, il s’agit a priori d’une approximation locale pertinente du potentiel à 2 ensembles TDSIC (2.7). Nous obtenons finalement la variation temporelle de l'énergie SIC (2.2) en lien avec une propagation GS.
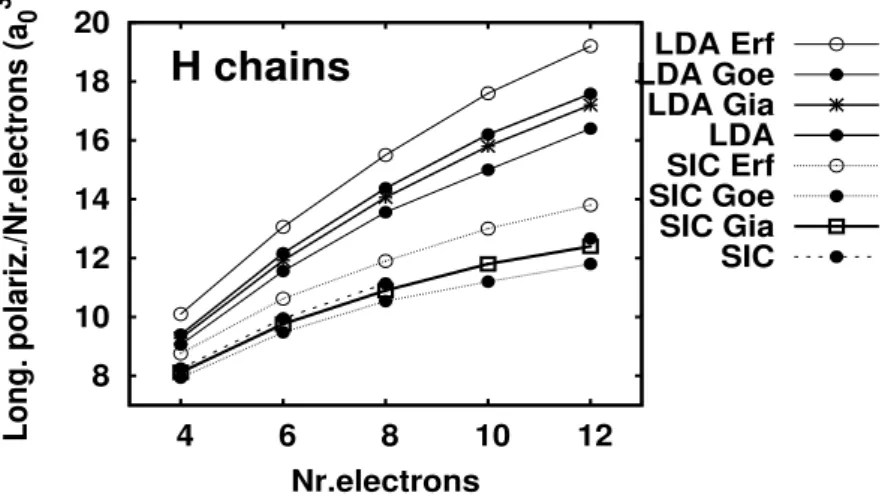
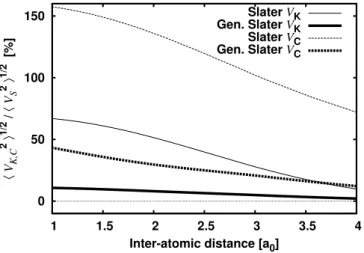
Ceci est encore plus vrai dans le contexte du formalisme OEP-SIC généralisé, car le VK correspondant est proche de zéro. Dans le cas de l'état stationnaire, nous étudierons l'amélioration produite par GS et deux ensembles SIC sur des observables difficiles à décrire avec les approches traditionnelles SIC-Slater/KLI : surfaces d'énergie potentielle et polarisations. Ensuite, dans le cas dépendant du temps, nous testerons les lois de conservation et la description de l'ionisation.
Méthode numérique
Polarisabilités et surfaces d'énergie potentielle
Excitation dans le régime linéaire et lois de conservation
Excitation dans le régime non-linéaire et ionisation
Après de nombreux tests, nous avons choisi d'utiliser la minimisation de la somme des variances spatiales des orbitales. Cependant, pour le formalisme SIC exact, la satisfaction de la condition de symétrie est cruciale pour assurer l'hermiticité de l'hamiltonien (dans le sous-espace occupé) et donc l'orthonormalité. Dans le cas SIC exact dépendant du temps, la vérification de la condition de symétrie est cruciale pour assurer l'hermiticité de l'hamiltonien (uniquement dans le sous-espace occupé) et donc la préservation de l'orthonormalisation.
Ceci interdit, pour ce formalisme, une itération avec la condition de localisation (4.8) au lieu de la condition de symétrie. Mais la détérioration de la condition de symétrie pourrait détériorer la vérification estimée des lois de conservation. Si on impose Ei = kri2, c'est à dire un potentiel scalaire de la forme kri, on a ça.
Dans le cas général, le LDA ne reproduit pas la courbure du PES proche de l'équilibre, ce qui conduit à de faibles fréquences de vibration atomiques. On voit que la violation totale de la conservation d'énergie et l'instabilité du moment dipolaire apparaissent très rapidement dans le cadre d'une propagation SIC-Slater traditionnelle, à partir de 20 fs, soit seulement 10 fois la période d'oscillation. Le panneau inférieur gauche de la figure 4.15 montre l'évolution temporelle du moment dipolaire dans la direction X.
Nous avons vu que le formalisme TD-DFT est le plus important pour atteindre cet objectif. La question, dans le cas dépendant du temps, d'un formalisme SIC exact (sans approximation) qui satisfasse aux lois de conservation, y compris la préservation de l'orthonormalité, et qui soit numériquement manipulateur reste une question ouverte. Cependant, elle n'est que faiblement non locale, ce qui est une conséquence de la localisation spatiale caractéristique de , que nous avons justifiée par l'approximation semi-classique.
C'est la méthode présentée page 51 (^hSIC est remplacé par ^hGS pour la propagation GS). Nous avons vu que dans le cas SIC exact dépendant du temps, la vérification de la condition de symétrie est essentielle pour assurer l'hermiticité de l'hamiltonien (uniquement dans le sous-espace occupé) et donc la préservation de l'orthonormalisation. D’un autre côté, la détérioration de la condition de symétrie pourrait également dégrader la vérification approximative des lois de conservation.
Rappelons que ce terme vient de la contrainte de normalisation imposée en minimisation énergétique. En rapportant tous les résultats précédents dans l'action (B.4), on obtient (on note =.. B.11) La stationaryisation est directe et donne 1.