l’équation de Vlasov

Thèse

Articles dans revues à comité de lecture

Actes de colloques avec comité de lecture

Rapports/prépublications

Introduction

Alors il existe une partition Ω = Ω1 ∪Ω2∪ · · · de Ω telle que la densité supérieure Dj+ de Ωj est égale à αjD+ pour chaque j. Il découle de la définition d'une densité supérieure que si Ω = Ω1∪Ω2∪ · · · est une partition finie ou infinie de Ω, alors.

Preuve du Théorème 1.1

Soit Ω := (ωk)k∈Z une famille de nombres réels ken (1.1), et H un espace de Hilbert de dimension finie. Puisque la dernière expression ne dépend pas de r, y et est un O(1/R) lorsque R → ∞, le lemme suit.

Le cas des différences divisées

Le point clé est que nous pouvons nous débarrasser du dernier terme de (2.9) où il n’y a pas d’état de trou grâce à la positivité de f. On peut également remarquer que l'on obtient le même temps que le temps obtenu par la méthode de filtrage de paramètre α= 1/2. Les méthodes de division considérées ici sont basées sur la décomposition H = T + U de l'hamiltonien (2.2).

Notons que cette définition est cohérente avec la périodicité et que l'on est toujours dans le cas scalaire. Notez que nous pouvons utiliser une implémentation de type FFT sur ce cadre de maillage uniforme avec des conditions périodiques. Notez que nous pouvons adapter des versions locales pour les splines [29], ce qui peut être important pour la parallélisation.

On peut également considérer l'équation de Vlasov-Poisson sans faire de fractionnement.

Preuve du Corollaire 1.4

Si Dj+ >0 pour certains j, alors choisissez une séquence d'intervalles bornés (Imj) satisfaisant |Imj | → ∞et. Récemment, dans [92], une première preuve basée sur les séries de Fourier a été donnée dans le cas où le domaine est un carré grâce à un test de type Hautus.

Introduction

Grâce à une décomposition adaptée, nous pouvons supprimer les termes dans lesquels il n'y a pas de déviation spectrale (comme dans [65]) et ainsi obtenir l'inégalité d'observabilité souhaitée. Le temps d’observation et les constantes impliquées dans l’inégalité peuvent être expliqués, mais nous n’avons pas pu atteindre le temps optimal avec cette méthode.

Une nouvelle inégalité d’Ingham

Nous développons ensuite l'approche d'Ingham en établissant de nouveaux théorèmes d'Ingham adaptés à cette situation. À cet égard, nous établissons un cas d'inégalité de type Ingham où la position de l'intervalle joue un rôle dans la détermination du temps optimal, ce qui n'est généralement pas le cas.

Introduction

La méthode des deux réseaux Nous pouvons également retrouver une observabilité uniforme en modifiant les conditions initiales. Pour la suite, nous rappellerons la preuve de résultats d'observabilité uniforme multiples obtenus par la méthode du multiplicateur.

L’inégalité directe par la méthode des multiplicateurs

Autres méthodes Il existe également d'autres moyens pour trouver une observabilité uniforme : l'ajustement de Tychonoff [43], qui consiste à ajouter un terme qui agit à l'intérieur du domaine et disparaît lorsque la taille du maillage tend vers zéro, en ajoutant un terme de viscosité (voir [91] dans le cas de problèmes de stabilisation), à partir des données analytiques initiales [76]. La méthode des multiplicateurs consiste à établir des identités pour les solutions considérées pour lesquelles une observabilité uniforme est dérivée.

L’observabilité uniforme par la méthode des multiplicateurs . 30

La méthode des deux grilles En traduisant les relations (3.15) en séries de Fourier, grâce à l'expression (3.6), on obtient pour j = 0,. Application à la méthode à deux grilles Le résultat principal concernant l'application à la méthode à deux grilles peut être formulé comme suit.

Inégalité directe par une approche de type Ingham

A propos de l’optimalité

Nous verrons également que dans certaines situations (pour une inégalité simplifiée) le moment optimal peut dépendre de la position de l'intervalle. Nous recherchons maintenant les cas où la position de l'intervalle joue un rôle dans le temps d'observation optimal. L'inégalité (3.26) est une généralisation de (3.24), mais elle semble plus compliquée à obtenir que (3.25), nous essaierons donc ici uniquement d'étudier sous quelle condition sur I l'inégalité (3.25) est vérifiée.

Preuve d’un théorème de type Ingham

D'une part les méthodes PIC (Particle in Cell) et d'autre part les méthodes basées sur le réseau d'espace des phases (méthodes eulériennes ou semi-Lagrange). C'est une sorte de compromis entre les méthodes purement Euler (volumes finis/différences finies), qui se limitent généralement aux conditions CFL (généralement le déplacement doit être inférieur à une grille), et les méthodes PIC, qui ne passent pas par la projection dans l'espace des phases. phase. Notons également que les méthodes semi-lagrangiennes ont été initialement développées et sont largement utilisées dans les simulations climatiques (voir [108] pour une revue).

La forme générale

Le système de Vlasov-Poisson 1D × 1D

Le modèle centre-guide

Plusieurs travaux existent sur ce sujet dans le cadre de la solution numérique de l'équation de Vlasov et s'appuient généralement sur [113]. D’un autre côté, il existe désormais une littérature bien développée sur la construction de schémas d’ordre supérieur pour les ODE basées sur des partitions. Comme pour le cas de dimension finie, il existe de nombreux travaux sur l'analyse des conditions d'ordre pour le fractionnement (voir notamment les références incluses).

Structure de Poisson

LA,LB],LB],LB où [ , ] est défini comme la parenthèse de Lie des deux opérateurs, les conditions d'ordre algébrique des coefficients ci et di peuvent être simplifiées, et on parle de méthodes de Runge Kutta Nyström (RKN) ( voir [12] pour une revue). Les systèmes différentiels du second ordre de la forme y(t) =¨ g(y(t)), g:Rn → Rn sont un cas particulier important. Nous allons maintenant voir comment dériver les relations d'ordre de manière élémentaire, jusqu'à l'ordre 4 inclus, sans utiliser ce cadre abstrait qui nécessite la manipulation d'opérateurs de Lie de dimension infinie agissant sur les espaces de Banach.

Conditions d’ordre ≤ 4 et caractéristiques

Nous avons donné la formule de la dérivée quatrième, mais celle-ci ne sera pas utile pour obtenir les conditions d'ordre ≤4. Grâce à toutes ces relations précédentes, on obtient les conditions de commande pour order4 sous forme abrégée. Grâce à la relation (2.7) on soupçonne que pour un ordre ≥5 les conditions d'ordre seront différentes de celles pour RKN (il y aura plus de coefficients pour le système de Vlasov-Poisson).

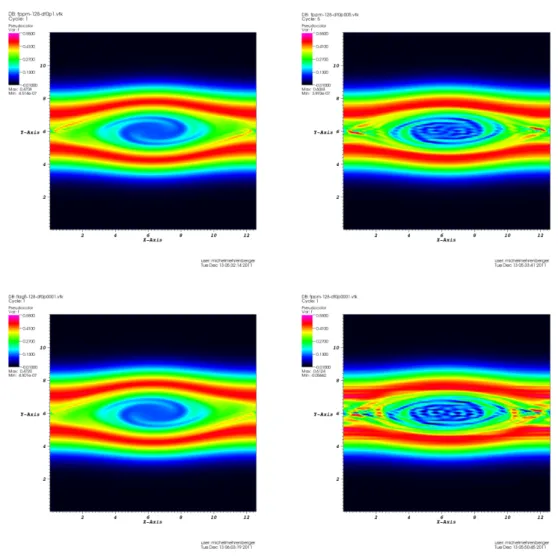
Résultats numériques

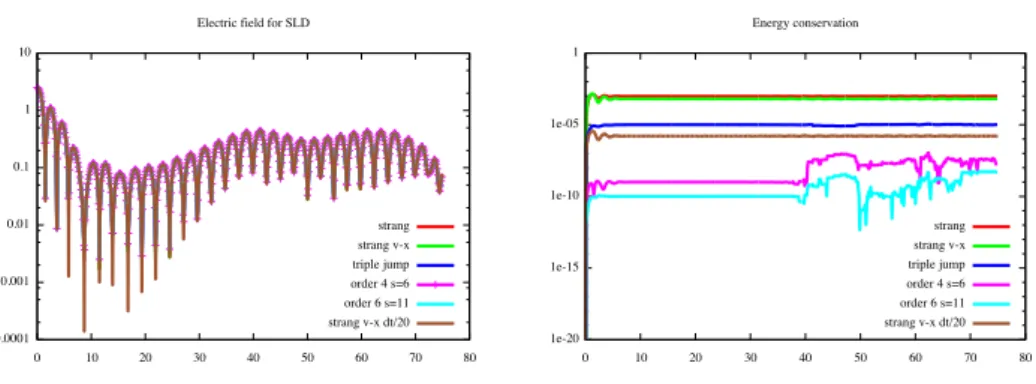
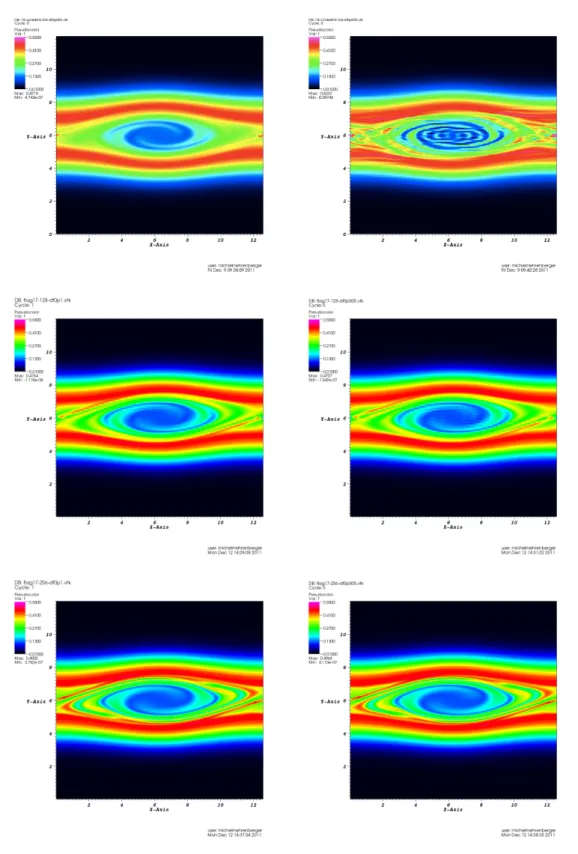
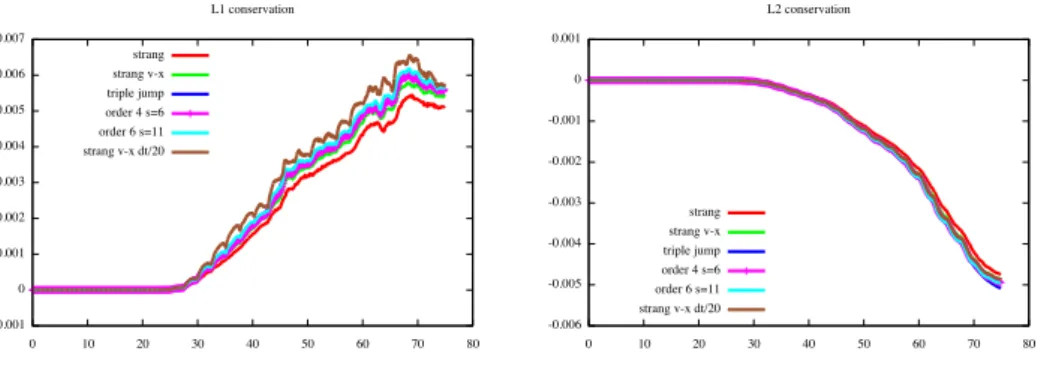
Pour ces différentes divisions, les figures 3.1 et 3.2 montrent l'évolution dans le temps de l'énergie électrique Ee(t) = R2π/k. Néanmoins, on voit clairement dans la figure 3.1 l'avantage d'utiliser des schémas d'ordre élevé dans le temps pour la conservation de l'énergie ; cela a déjà été souligné dans [112], mais les coefficients optimisés de Blanes et Moan [13] donnent des résultats encore meilleurs. On voit alors que pour un temps de simulation donné, la division d'ordre élevé avec les coefficients optimisés donne le meilleur résultat.

Principe d’une méthode semi-Lagrangienne

L'entier N permet de fixer une discrétisation dans l'espace et le nombre réel ∆t permet de fixer la discrétisation dans le temps. Il est également possible que les valeurs fn,k,j ne correspondent pas forcément à des valeurs précises, mais plus généralement à des degrés de liberté. Toutes ces définitions restent valables pour les séries périodiques (une fois que l'on définit gj+α, pour j = 0,.

Valeurs ponctuelles

Valeurs moyennes

D’une reconstruction à l’autre

Lien entre les deux reconstructions

Schémas homogènes

Lagrange LAG(2d + 1)

Splines SPL(d)

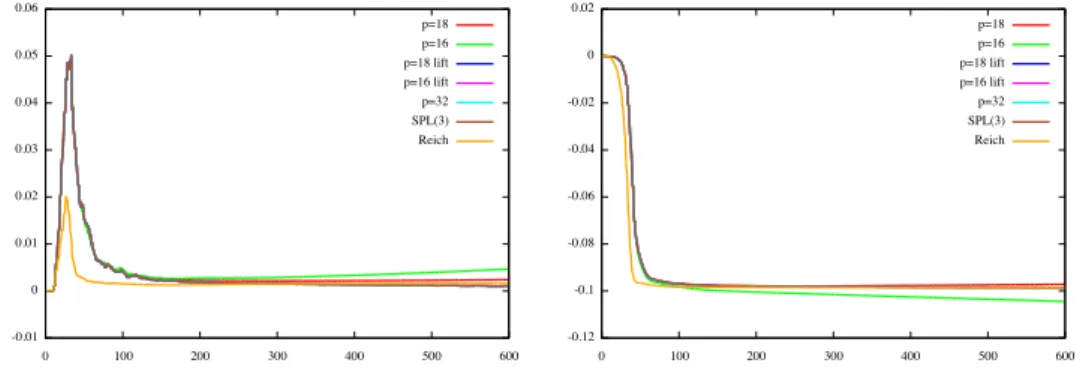
Les différences à p = 16 et p = 18 sont observées sur un temps plus long lorsque la procédure de correction n'est pas utilisée : cela se voit principalement dans l'énergie totale. La quasi-interpolation utilisée dans [93] permet une meilleure préservation de la positivité, mais au prix d'une diffusion beaucoup plus importante (norme L2). Figure 4.2 – Evolution temporelle de la norme L1 def (à gauche) et de la norme L2 f (à gauche), pour p = 16,18 avec ou sans correction (correction = hausse), p = 32, méthode SPL(3)) et interpolation quasi -Reich avec correction.

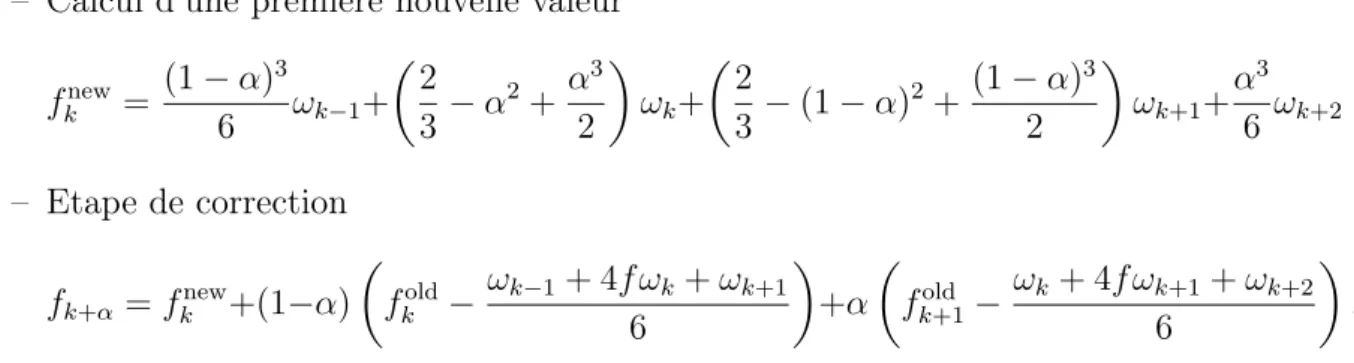
Hermite

Galerkin discontinu GD(d+1)

Schémas de Lagrange

Les splines cubiques

La stabilité pour les interpolettes

Stabilité de schémas homogènes vectoriels

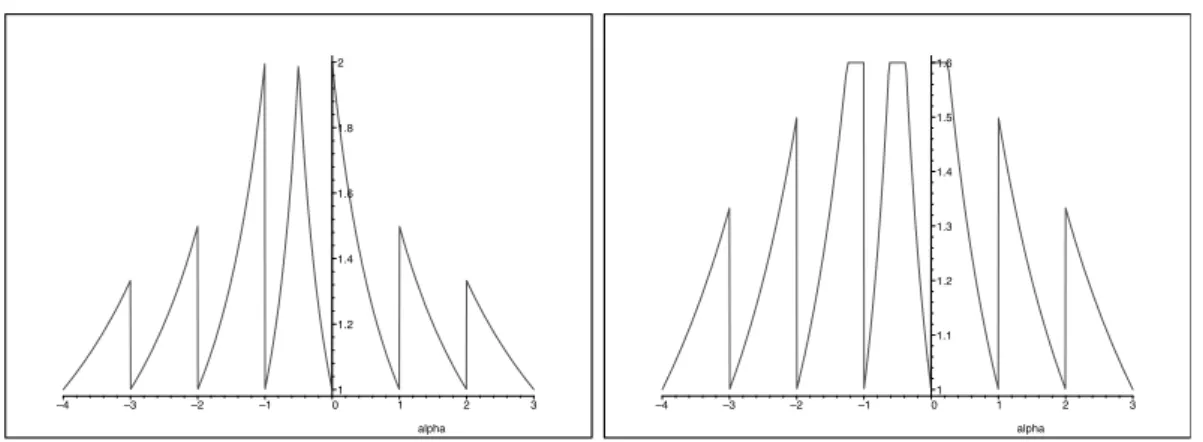
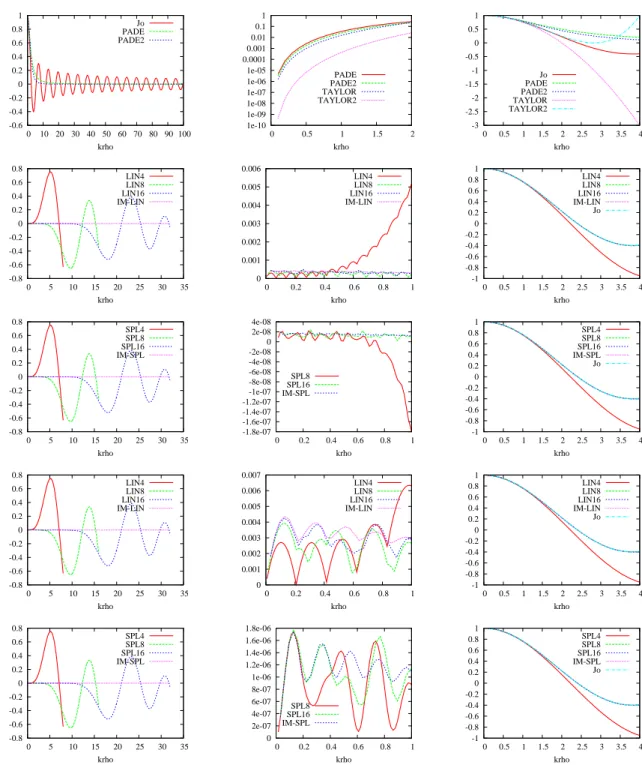
Maintenant, si nous diagonalisons la matrice Aˆk avec Aˆk = Pk∆kPk−1, alors récursivement nous avons fˆkn = Pk(∆k)nPk−1fˆk0. Le facteur d'amplification (1−ρ(ω)) de ces méthodes est présenté dans la figure 4.4 pour des valeurs sélectionnées de ω = k/N en fonction du déplacement α ∈ [0,1]. A noter que l'interpolation de type éléments finis est instable pour une puissance supérieure ou égale à 3 (voir Q3 et Q4).

Le cadre du volume fini

Le flux semi-Lagrangien

On fait alors le changement de variable y = X(tn, t, xi+1/2), pour passer de l'intégrale en temps à l'intégrale en espace.

Intégrateur exponentiel

Pour les schémas semi-lagrangiens, on peut également utiliser des approximations de vent contraire au lieu de PPM dans la reconstruction. Notez qu'il s'agit d'un point crucial dans [6] ; un schéma non linéaire est dérivé : une approximation centrale est utilisée si la solution est régulière, et une approximation d'un ordre de moins si la solution n'est pas régulière. On peut alors constater que, lorsque les pas de temps ne sont pas trop petits, la norme L2 diminue généralement pour un schéma semi-lagrangien avec une reconstruction centrée des dérivées (comme les splines cubiques, PPM) et cela peut empêcher les oscillations parasites observées. dans le cas de volumes finis.

Résultats numériques

De plus, les auteurs classent ce type de méthode dans [89] sous les schémas semi-lagrangiens de type différences finies (et volumes non finis) et présentent ce type de schéma en introduisant une fonction H satisfaisante. Nous considérons maintenant la généralisation des méthodes semi-lagrangiennes au cas de l'advection générale sans divergence. Ainsi, comme dans le cas d'une méthode semi-lagrangienne ponctuelle, l'algorithme des méthodes conservatrices se compose de deux étapes principales : le calcul des courbes caractéristiques et l'étape de reconstruction.

Calcul des courbes caractéristiques

A partir de (2.8) et notant [xj, xj+1] le maillage dans lequel (xi −αi) tombe, on écrit la reconstruction linéaire de an. 2.12) Reste maintenant à déterminer l'indice j. Méthodes Runge-Kutta On peut également utiliser des techniques classiques telles que les méthodes Runge-Kutta (RK) pour l'intégration de (2.6). Notez que bien que nous utilisions des méthodes Runge Kutta d’ordre supérieur, nous ne pouvons pas avoir plus d’ordre deux dans le temps puisque nous résolvons (2.6) au lieu de (2.3).

Étape de reconstruction

Limiteurs de pente

Définir les extrêmes Nous devons d'abord définir les limites gmin, gmax où nous voulons conserver la solution. Ainsi, nous proposons de simplifier la définition des extrêmes comme suit : nous remplaçons gminparmin(goldi, gmin) et gmax par max(goldi, gmax). Ainsi les extrêmes positifs sont préservés et dans le cas d’une advection constante les extrêmes globaux sont également préservés.

Principe de la méthode

Nous avons ensuite ajouté le filtre suivant qui tend à privilégier la dérivée de la reconstruction la plus diffusive si l'erreur entre les deux reconstructions est trop grande. Nous comparons la reconstruction GLV avec le PSM pour mieux corriger la formule PPM0 gj−1/2,m= ¯g. Ensuite, les branches des caractéristiques aux points gaussiens xbj,` ≈X(tn;tn+1, xj,`), `= 0, sont calculées numériquement.

Simulations du modèle centre-guide

Milieu droit : évolution temporelle du premier mode de Fourier kφk=0.5(t)kL2 En bas à gauche : évolution temporelle du changement kE(t)kL2. Dans le cadre de la résolution numérique de l'équation de Vlasov, la méthode de transport est généralement liée au calcul du champ : la résolution de l'équation de Poisson, équation de Maxwell. Nous nous intéressons ici à la résolution numérique de cet opérateur en présentant et en comparant différentes méthodes numériques.

Décomposition dans une base

Dans un champ magnétique uniforme, les particules décrivent une trajectoire en spirale et la projection sur un plan perpendiculaire est un cercle. L'opérateur de moyenne gyromap traduit alors en théorie gyrocinétique l'idée de faire la moyenne de la fonction de répartition des particules autour d'un cercle de rayon caractéristique (rayon de Larmor ρ), qui représente le mouvement de rotation très rapide des particules autour des lignes de champ.

Expression en Fourier

Approximation de Padé et autres variantes

Approximation linéaire et par splines cubiques

Comparaison des méthodes

Résultats numériques

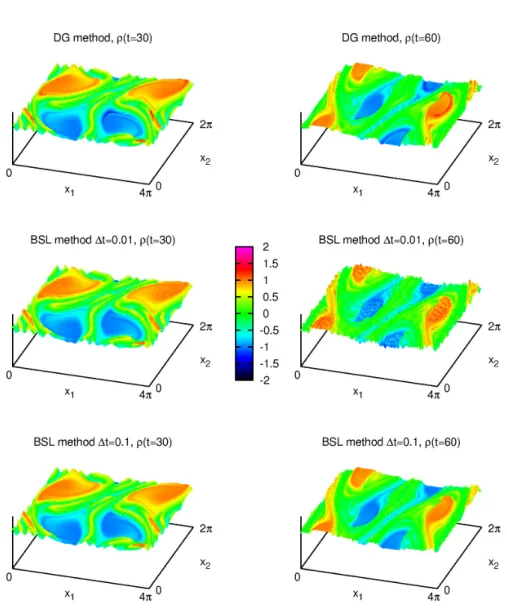
Nous avons donc la représentation DG de f sous la forme f(x, y) =. 2.1) Nous représentons maintenant f dans l'espace de Fourier par 3.3) Grâce à la propriété de divergence nulle, les propriétés satisfont à la propriété de conservation de masse. Nous dériverons ici une condition de divergence discrète sur le terrain, dépendant de la méthode semi-lagrangienne utilisée, pour que cette dernière soit satisfaite à l'ordre 1 en temps.

Méthodes semi-Lagrangiennes 2D en arrière

Conservation de la masse Considérons maintenant une fonction arbitraire sur le réseau à l'instant tn. La masse de la fonction de base au temps tn sur une grille uniforme est. Cette fois nous n’avons pas M(tn) = M(tn+1) en général, cette valeur dépend largement de la manière dont les propriétés sont approximées.

Méthode semi-Lagrangiennes conservatives splittées

Illustration numérique

Mehrenberger, Convergence of classes of high-order Pollagrange schemes for the Vlasov equation, Math. Mehrenberger, Convergence of an adaptive semi-Lagrange scheme for the Vlasov-Poisson system, Numerische Mathematik no. Seal, A positivity-preserving high-order discontinuous Galerkin scheme for the Vlasov-Poisson equations, J.