Méthodes itératives pour la résolution d’équations matricielles

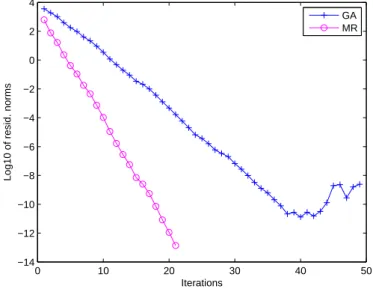
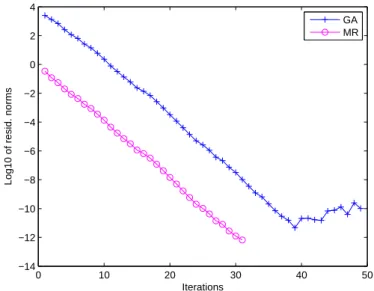
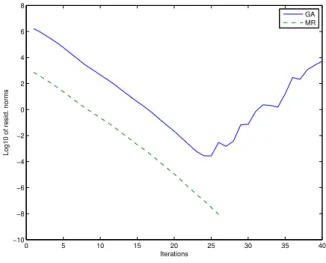
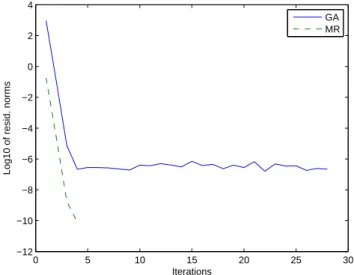
Méthode itérative de résolution de l'équation de Riccati, lors du congrès international de la Société Marocaine de Mathématiques Appliquées (SM2A), organisé à Marrakech en 2012. Nous présentons deux méthodes de projection itérative sur les sous-espaces de Krylov étendus globaux.

Introduction

Matrices particulières

Norme de Frobenius

Formule de Sherman-Morrison Woodbury

Inverse généralisée d’une matrice

La décomposition en valeurs singulières (SVD)

Approximation de rang inférieur

Le produit de Kronecker et le -produit

Méthodes de Krylov

Sous-espace de Krylov par blocs
Sous-espace de Krylov étendu par blocs
Sous-espace de Krylov étendu global
Algorithme d’Arnoldi étendu global

Plus précisément, en supposant que la matrice A est inversible, le sous-espace de Krylov étendu par blocs associé à (A, V) est donné par [36, 102]. Par construction, la matrice Vm est orthonormée, ce qui signifie que les matrices V1, V2, Vm forment une base orthonormée de l'espace de Krylov étendu Kme(A, V).

Contrôlabilité et l’observabilité

Pour les petites équations matricielles de Lyapunov, il existe plusieurs méthodes dans la littérature, telles que l'algorithme de Bartels-Stewart [11], Hessenberg-Schur [45]. Une caractéristique commune à toutes ces méthodes de projection est que les approximations Xm de la solution exacte de l'équation de Lyapunov sont données sous forme factorisée, Xm = ZmZmT avec Z une matrice de rang inférieur.

Solution exacte de l’équation de Lyapunov

Méthode de Galerkin

L’algorithme de la méthode Arnoldi étendue globale pour résoudre l’équation de Lyapunov peut être résumé comme suit.

Méthode de minimisation du résidu

Méthodes itératives pour résoudre le problème réduit

LSQR global

L'utilisation de la procédure globale de bi-diagonalisation de Lanczos permet de trouver des approximations Yk de la solution exacte YmM R du problème de minimisation réduite (2.16) à chaque itération. Ensuite la solution du problème de minimisation (2.16), par la méthode LSQR globale (Gl-LSQR), permet de donner une solution approchée de la solution exacte YmM R du problème (2.16).

La méthode du gradient conjugué globale préconditionné

Par conséquent, l’algorithme global de gradient conjugué préconditionné est obtenu en appliquant le préconditionneur (2.27) à l’équation normale associée à l’opérateur matriciel défini par (2.28). Notons que le calcul de la norme du résidu R(XmM R) à chaque itération m nécessite uniquement la connaissance de YmM R sans avoir à construire la solution approchée XmM R.

Exemples numériques

Exemple 1

Exemple 2

Conclusion

Dans ce chapitre, nous présentons une nouvelle méthode de résolution des grandes équations matricielles de Sylvester. Les équations matricielles de Sylvester jouent un rôle important dans de nombreuses théories : automates, traitement du signal, restauration d'images, filtrage, réduction de modèle en théorie du contrôle, calcul du contrôle optimal en contrôle quadra-linéaire. La grande équation matricielle de Sylvester est ensuite projetée sur ces sous-espaces de Krylov.

La solution de l'équation matricielle peut être exprimée en fonction de la solution de l'équation projetée et des matrices orthogonales construites à partir des sous-espaces de Krylov. Cette écriture, qui réduit l'équation de Sylvester à la solution d'un système linéaire de taille ns×ns, n'offre en réalité que peu d'avantages en termes de résolution, qu'elle soit directe ou itérative.

Méthode de type Galerkin

Méthode de minimisation du résidu

Dans cette section, nous nous intéressons à la résolution de l'équation de Sylvester en utilisant la méthode de projection sur des sous-espaces de Krylov étendus avec la condition de minimisation du résidu MR (résiduel minimum). Soit Vm et Wm des matrices orthonormées construites en appliquant simultanément m itérations de l'algorithme d'Arnoldi étendu par blocs à des paires de matrices (A, E) et (BT, F), respectivement.

Méthodes pour résoudre le problème de minimisation réduit

La méthode directe basée sur la formulation de Kronecker
Méthode de Hu et Reichel
La Méthode LSQR globale
La méthode du gradient conjugué globale préconditionné

Dans les sous-sections suivantes, nous présentons d’autres méthodes efficaces pour résoudre le problème de minimisation (3.11). Nous révélons dans cette partie la méthode de Hu et Reichel (voir [57]) pour résoudre le problème réduit (3.11). La méthode de Hu et Reichel est résumée dans l'algorithme suivant : Algorithme 3 Algorithme de Hu-Reichel pour résoudre le problème (3.14).

Le problème réduit (3.14) peut également être résolu en utilisant la méthode LSQR globale ou la méthode du gradient conjugué global préconditionné. Dans cette section, nous discutons de la méthode PGCG (Global Gradient Conjugate) préconditionné pour résoudre le problème de minimisation réduite (3.11).

Forme factorisée de l’approximation de la solution

L’algorithme GA-LRSE

L’algorithme MR-LR-Sylvester

Résolution de l’équation de Stein non symétrique

Méthode de Galerkin

Dans cette section, nous rappellerons l'approche de Galerkin pour résoudre la grande équation de Stein non symétrique. XmGA = VmYmGAWTm, (3.35) où Vm, Wm sont des matrices orthogonales produites en appliquant simultanément m itérations de l'algorithme d'Arnoldi étendu par blocs à des paires de matrices (A, E) et (BT, F), respectivement. Puisque les matrices Vm et Wm sont orthogonales, il est plus facile de montrer que YmGA ∈R2mr×2mr est une solution de taille réduite de l’équation de Stein.

La résolution de l'équation de Stein réduite (3.36) peut être obtenue par une méthode directe, par exemple la méthode de Hessenberg-Schur [33]. 63] Soit YmGA la solution exacte de l'équation réduite de Stein (3.36) et XmGA = VmYmGAWTm la solution approchée de l'équation (3.32).

Méthode de minimisation du résidu

Exemples numériques

Tests numérique pour l’équation de Sylvester

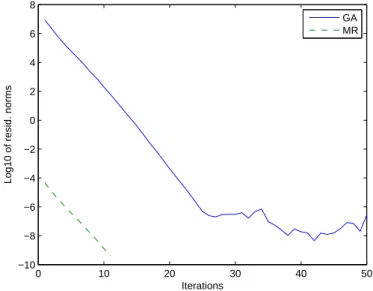
A noter que le problème de minimisation réduite (associé à la méthode de minimisation résiduelle MR) est résolu par la méthode itérative globale LSQR (Gl-LSQR). Pour ce test, nous avons choisi r = 2 et le problème de minimisation réduite a été résolu par la méthode des moindres carrés directs basée sur le produit de Kronecker (dans la section 3.4.1). Le problème de minimisation de taille réduite est résolu par la méthode de Hu et Reichel.

Le problème de minimisation réduite a été résolu par les moindres carrés directs, le LSQR global (Gl-LSQR), le gradient conjugué préconditionné global (GPCG) ou la méthode de Hu-Reichel (HR). Dans cet exemple, nous comparons notre méthode MR (GPCG) avec deux autres méthodes qui font référence dans la littérature : l'approche GA et la méthode ADI de rang le plus bas (Lr_ADI) [ 21 , 23 ].

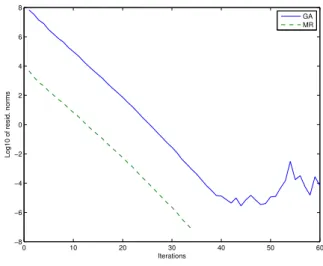
Figure 3.1: Résultat pour l’exemple 1.1.

Tests numérique pour l’équation de Stein non symétrique

Conclusion

Le calcul de la solution de l'équation algébrique de Riccati est souvent utilisé dans divers domaines, tels que les problèmes de calcul de contrôle linéaire quadratique (QLQ) suivants. La solution de l'équation de Riccati est liée au calcul des sous-espaces invariants de la matrice hamiltonienne associée H. De nombreuses méthodes numériques ont été proposées pour résoudre l'équation de Riccati (4.4), on peut citer en premier, et pour les petits problèmes l'approche aux valeurs propres consiste dans le calcul des sous-espaces invariants de la matrice hamiltonienne H, comme les méthodes de type Lanczos ou la méthode de Newton.

Par exemple, dans l'article de Heyouni et Jbilou [55], nous cherchons à construire une solution XmGA approchée de la solution X de l'équation de Riccati (4.4) sous la forme. Notre approche consiste à rechercher la solution approchée XmM R de la solution X de l'équation de Riccati (4.4) sous la forme.

Méthode de Galerkin

Méthode de minimisation du résidu

Nous proposons une nouvelle méthode de type projection sur un sous-espace de Krylov étendu avec une condition de minimisation résiduelle au lieu de la condition de Galerkin. Le but de cette méthode MR est de réduire la norme du résidu sur Kem(AT, CT). Le théorème suivant transforme le problème de minimisation de grande taille (4.11) en un problème de minimisation de petite taille.

Soit Vm une matrice orthonormée construite en appliquant l'algorithme d'Arnoldi étendu par blocs aux couples (AT, CT). Soit V1RC la décomposition QR de CT, et Vm la matrice orthogonale construite en appliquant l'algorithme d'Arnoldi étendu par blocs à (AT, CT).

Résolution du problème de minimisation réduit

Ψ(Y) :=ATF(Y)BT +BF(Y)A+ETYBF(Y)BT +BF(Y)BTYET Nous allons résoudre numériquement l'équation matricielle non linéaire (4.16) par la méthode de Newton, donc la dérivée Fréchet non linéaire mapper Ψ(Y) à Y. Nous allons construire une séquence de matrices Yk d'approximations de la solution exacte Y de l'équation Ψ(Y) = 0.

Méthode de MINRES globale

La matrice bloc Vk est F-orthonormale par construction, ce qui signifie que les matrices V1, .., Vk forment un système orthonormé au sens du produit scalaire de Frobenius, soit hVi, VjiF =δi,j, 1 ≤ i, j ≤ k. On commence par choisir le premier terme X0 ∈ Rn×n et en notant R0 le résidu correspondant : R0 =C − M(Z0), on construit les itérations Zk telles que l'on a. Si l'on note R1 la matrice k×k obtenue en éliminant la dernière ligne ˜Rk, le vecteur yk est calculé en résolvant le système triangulaire R1yk=gk.

A l'étape K, le résidu Rk = C − M(Zk) obtenu par la méthode globale MINRES vérifie les deux identités suivantes. A chaque redémarrage, la dernière approximation calculée est choisie comme terme initial de l'algorithme global MINRES.

Forme factorisée de la solution approchée

Algorithme GA-CAREs

Algorithme MR-CAREs

Exemples numériques

Exemple 1

Dans tous les tests effectués dans la section ci-dessous, la matrice A est issue de la discrétisation de l'opérateur. La taille de la matrice construite est n=n20, où n0 est le nombre de points de grille dans chaque direction.

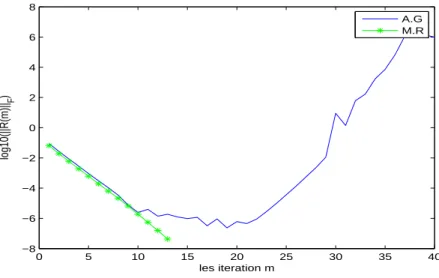
Exemple 2

Exemple 3

Conclusion

On peut associer l’équation de Riccati non symétrique (5.1) à la matrice M, qui a la forme suivante. La solution de l'équation (5.1) est liée au calcul des sous-espaces invariants de la matrice Hasociée. La méthode peut être coûteuse lors de la résolution de l'équation de Sylvester par des méthodes directes.

Dans ce chapitre, nous considérons des équations matricielles de Riccati non symétriques (NARE) de grande taille, où le membre de droite est écrit comme le produit de deux matrices de bas rang. Dans ce chapitre, nous proposons deux nouvelles méthodes pour la solution numérique de l'équation de Riccati non symétrique (NARE) de grande taille.

La méthode de Newton-Krylov par blocs

L'algorithme suivant décrit le processus de la méthode Newton-Kleinman pour résoudre l'équation de Riccati non symétrique. À chaque itération de l'algorithme de Newton-Kleinman, nous résolvons l'équation matricielle de Sylvester avec le deuxième terme donné comme produit de deux matrices de bas rang. Ici, nous avons utilisé des sous-espaces de Krylov étendus par blocs (ou des sous-espaces de Krylov étendus par blocs) pour résoudre la grande équation matricielle de Sylvester (5.8).

La méthode est définie comme suit : On applique d'abord l'algorithme d'Arnoldi amélioré par blocs (ou algorithme d'Arnoldi par blocs) à (Ak, Lk) et (DkT, Mk) à l'étape m, il génère des matrices orthonormées Vm,k et Wm,k colonnes dont sont les bases orthonormées du sous-espace de Krylov engendrées respectivement par les blocs Km(Ak, Lk) et Km(DTk, Mk). On obtient donc que la matrice Zm est la solution de la petite équation de Silvester suivante.

Solution approchée de rang inférieur de NAREs

Cette annotation permet de trouver des méthodes qui donnent des approximations "faibles" de la solution de l'équation LrNARE. Soit Ym la solution exacte de l’équation NARE réduite (5.17) obtenue à l’itération m de l’algorithme d’Arnoldi étendu par blocs. Soit Xm la solution approchée obtenue par itération de l'algorithme d'Arnoldi étendu par blocs, et soit X la solution de l'équation LrNARE (5.14).

Alors l'erreur X−Xm est une solution de l'équation algébrique de Riccati non symétrique perturbée suivante. Nous donnons maintenant le résultat d’une restriction de la norme de l’erreur X−Xm au pasm de l’algorithme d’Arnoldi étendu en blocs.

Figure 5.1: Les valeurs singulières de la solution non négative minimale de l’équation NAREs

Applications à la théorie de transport

Après avoir discrétisé cette équation intégro-différentielle, le problème peut être exprimé sous la forme de l'équation matricielle non symétrique de Riccati suivante. Nous appliquons ensuite la méthode d’Arnoldi étendue à l’équation NARE (5.28) pour obtenir des solutions approximatives de bas rang. Notons qu'en appliquant la méthode ci-dessus, nous utilisons des opérations "matrice-vecteur" de la forme A−1v et D−Tv.

Puisque les matrices A et D impliquées dans l’équation algébrique non symétrique de Riccati (5.28) sont la somme d’une matrice diagonale et d’une matrice de bas rang, nous pouvons utiliser la formule de Sherman-Morrison-Woodbury pour calculer A−1u et D− 1u , où u∈Rn. 5.34) Cette formule réduit le temps de calcul et réduit également l'espace mémoire.

Résultats numériques

Xu, Alternative linearized implicit iteration methods for minimal nonnegative solutions of nonsymmetric algebraic Riccati equations, Nr. Meini, On the solution of Riccati algebraic equations arising in fluid sequences, Linear Algebra Appl pp.

Wei, A Modified Newton Method for Solving Nonsymmetric Algebraic Riccati Equations Appearing in Transport Theory, IMA J. Lu, Solution Form and Simple Iteration of the Nonsymmetric Algebraic Riccati Equation Appearing in Transport Theory, SIAM J.