Dans le premier chapitre, nous présenterons la formulation mathématique du problème du forgeage mécanique et les principales équations de sa discrétisation par la méthode des éléments finis. Parallèlement, nous présenterons le modèle de déformation élastique des presses à forger et montrerons comment nous l'avons intégré dans le logiciel Forge3®.
M ODÈLES DE RAIDEUR DES PRESSES DE FORGEAGE
- Approche actuelle standardisée
- Approche du projet NETTFORM
- Approche du projet IMPRESS
- Outils flottants dans Forge3 ®
Le modèle proposé est celui de la matrice de flexibilité ou de rigidité (voir équations et (I.3) et (I.4)). Pour prendre en compte la raideur en compression, nous choisissons la méthode de la matrice de flexibilité (cf.
F ORMULATION DU PROBLÈME MÉCANIQUE
- Équations d’équilibre et de conservation de la masse
- Lois rhéologiques
- Conditions aux limites mécaniques
- Formulation faible
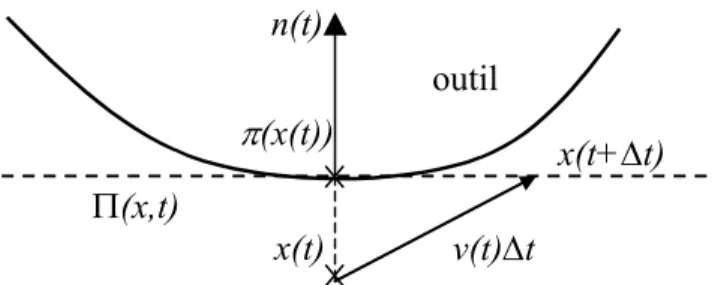
Le développement de la plasticité d'un matériau standard associé est décrit par la loi de Prandtl-Reuss. Sur la base de la description de la vitesse de l’outil flottant (I.5), nous appliquons la même chose.
F ORMULATION DU PROBLÈME DISCRET
- Discrétisation temporelle et contact incrémental
- Discrétisation spatiale
- Modèle de presse
- Linéarisation des équations discrètes
- Implémentation dans Forge3 ®
Avec ces notations on obtient la composante linéaire de la vitesse de presse vO (cf. Un autre aspect du problème est la forme de la matrice de rigidité de la presse.
V ALIDATION PAR RAPPORT AU CAS ANALYTIQUE
La figure I.12a montre l'évolution de la vitesse du train inférieur soumis à un déplacement vertical. Une comparaison entre la vitesse calculée lors de la simulation et la vitesse de la solution analytique est également présentée.
C ONCLUSION
Cette méthode peut également être qualifiée de globale, car elle consiste à résoudre le système linéaire dans son ensemble, mais dans les données distribuées, les vecteurs et les matrices sont partagés par différents processeurs. Le même code s'exécute à la fois séquentiellement et en parallèle, et la solution est la même (sauf pour les erreurs d'arrondi).
S TRATÉGIE S.P.M.D
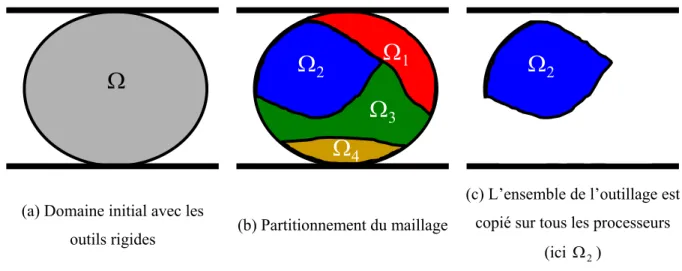
De cette manière, chaque processeur peut effectuer l'analyse des contacts indépendamment des autres (Figure II.2). Analyse des contacts réalisée indépendamment par chaque transformateur avec tous les outils (ici deux simples pieux plats). La description des outils rigides est lue par chaque processeur comme dans le cas monocorps.
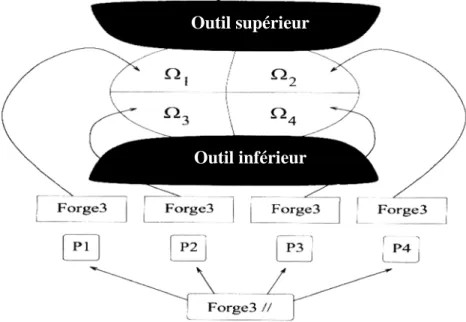
P ARTITIONNEMENT
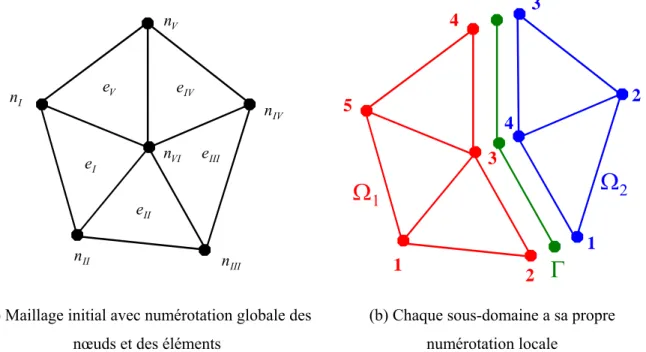
Partitionnement du maillage
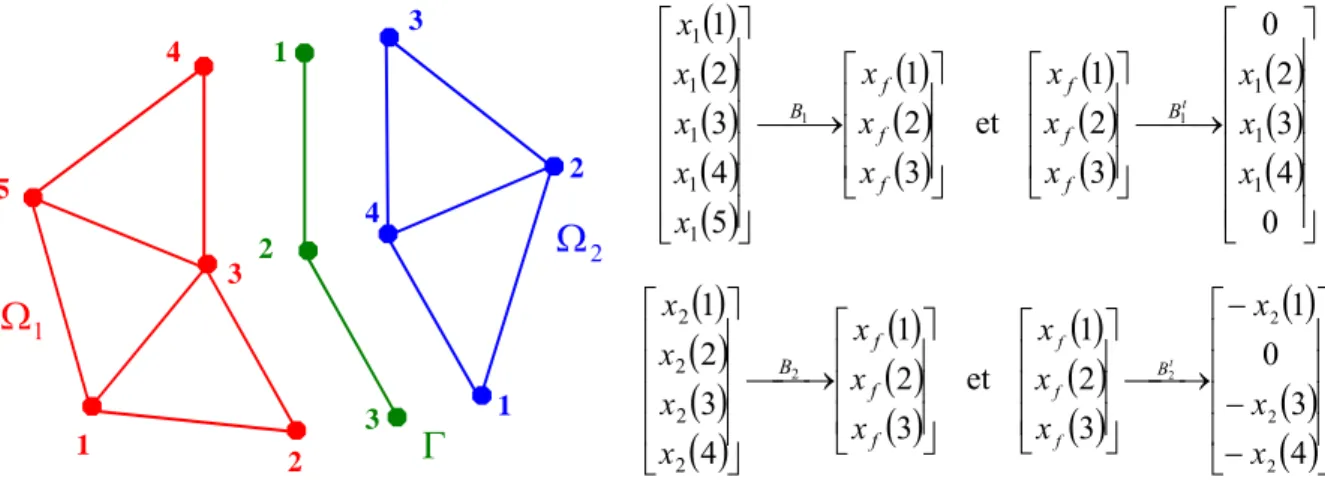
Pour plus de détails sur l'algorithme parallèle de création d'éléments de contact, nous renvoyons le lecteur à [Barboza 2004]. a) L'un des corps est considéré. Ainsi, dans le sous-domaine Ω1 (à gauche et en rouge) le vecteur interface. a) Réseau initial avec le nombre global de nœuds et d'éléments. On modifie la couleur du quadrilatère visité afin de minimiser une fonction de coût qui prend en compte le nombre d'éléments par couleur (charge processeur) et le nombre de communications, soit le nombre de faces séparées par des éléments de couleurs différentes.
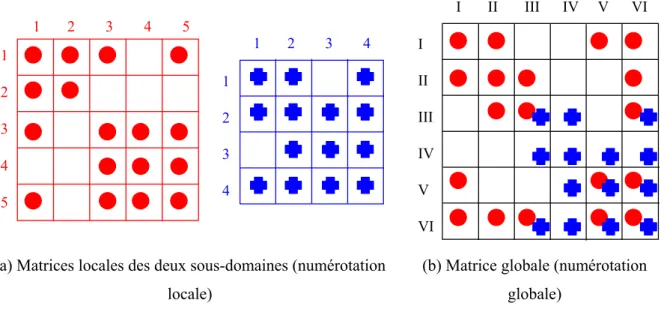
Partitionnement des vecteurs et de la matrice
Il existe ainsi cinq configurations possibles de couleurs voisines (Figure II.5a et b) en fonction de la couleur de l'élément considéré. En prenant l'exemple de la partition présentée sur la figure II.4, les deux matrices locales construites sur chaque sous-domaine sont représentées sur la figure II.6a. L'application de cette stratégie à l'exemple de deux sous-domaines donne la matrice globale de la figure II.6b.
M ÉTHODE DE RÉSIDU MINIMAL
A chaque itération k de la méthode, on détermine le vecteur descendant wk et le scalaire αk pour calculer la solution à l'itération suivante xk+1. Enfin, nous déterminons la direction de descente optimale wk+1 pour réduire E()rk+2 de. On le recherche dans le plan formé par les directions rk+1 et wk, avec le paramètre d'optimisation de descente βk.
P ARTICULARITÉS PARALLÈLES
- Produits matrice-vecteur
- Produits scalaires
- Calculs des normes infinies des vecteurs
- Algorithme parallèle
- Prise en compte de la raideur de presse
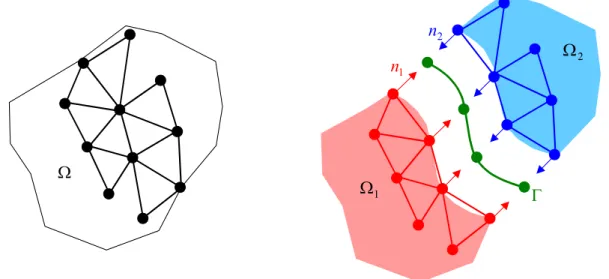
Étant donné que les vecteurs globaux sont partagés entre les processeurs, le résultat du produit scalaire global doit être calculé comme la somme des contributions des sous-domaines. Dans le cas plus général d'une partition multi-domaines, les contributions des nœuds d'interface sont sommées aussi souvent que le nombre de sous-domaines auxquels appartiennent ces nœuds. Échange des données d'interface entre des sous-domaines adjacents pour collecter des contributions au produit vectoriel matriciel.
P RINCIPE DE BASE
Le problème à résoudre consiste alors à trouver les solutions locales x1 et x2 du système (III.1) en tenant compte des conditions (III.2) et (III.3). Les problèmes locaux (III.1) sont bien énoncés si l'une des deux inconnues, x ou ∂x ∂n, est fixée sur l'interface. La plupart des méthodes de décomposition de domaines consistent donc à effectuer des itérations sur l'une des conditions (III.2) ou (III.3).
M ÉTHODE DU COMPLÉMENT DE S CHUR
La taille du problème (III.9) correspond exactement au nombre de degrés de liberté de l'interface. Ce système (III.9) est résolu par une méthode itérative, utilisant à chaque itération, le calcul des solutions locales exactes (III.5). Puisque nous utilisons une méthode itérative pour résoudre le système (III.9), il est nécessaire de réaliser des produits à partir de la matrice complémentaire de Schur S.
M ÉTHODE FETI
La troisième équation de (III.15) reflète fidèlement la condition de continuité des solutions à travers l'interface (III.2). En injectant les solutions des deux premières équations dans la troisième (on suppose que les matrices Ki sont non singulières), on obtient le problème condensé à l'interface. Le problème condensé à l'interface (III.16) est résolu par une méthode itérative, telle que la méthode du gradient conjugué ou la méthode du minimum résiduel.
M ÉTHODE PRIMALE - DUALE
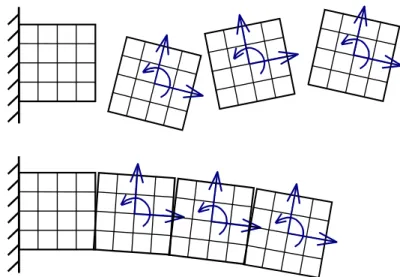
Lorsque le gradient (III.18) est nul, les valeurs de xi de part et d'autre de l'interface sont les mêmes. Le problème localisé à l'interface (III.26) et (III.28) à résoudre est présenté sous la forme. A noter que la partie du vecteur frontière wv correspondant aux vitesses apparaît dans le deuxième terme, comme dans la méthode dual (III.19), et représente des conditions aux limites de type Neumann.
P RECONDITIONNEMENT
Méthode du complément de Schur
En effet, contrairement au système (III.4) de la méthode primaire où l'on résout le problème de type Dirichlet avec les inconnues de l'interface bloquée (les données) pour trouver un vecteur S(i)vf, pour trouver un vecteur ( ) p . La contribution d'un sous-domaine au gradient du problème d'interface est le flux de la solution du problème de Dirichlet local. La résolution du problème de Neumann (III.37) nécessite la factorisation et la conservation de la matrice locale Ki.
Méthode FETI
De plus, l'utilisation de ce préconditionnement pour la solution du problème condensé aux interfaces implique une augmentation du coût des calculs à chaque itération comparable à la solution du problème de Dirichlet. Ce préconditionneur est basé sur la définition (III.7) de la matrice complémentaire de Schur. Au lieu de préconditionner avec le complément de Schur complet comme dans (III.10)-(III.12), on approche la matrice locale S(i) par K(iff) et le préconditionnement s'écrit sous la forme .
Méthode primale-duale
Kff de la matrice locale Ki correspond aux degrés de liberté bloqués aux interfaces, mais cette fois ce sont les vitesses d'interface. Le système à résoudre pour supposer est similaire au système (III.31) et s'écrit ainsi. Ainsi, le gradient préconditionné QDN−1g est organisé comme dans (III.35) en deux parties : le saut des solutions locales yi sur l'interface pour le gradient de vitesse et la collection des vecteurs supplémentaires qi pour la partie pression.
P ROBLÈME DES MODES RIGIDES
- Extraction des modes rigides
- Problème hybride aux interfaces
- Méthode itérative projetée
- Méthode primale-duale
En utilisant la matrice K+ on résout le système (III.57) m fois avec une colonne Rj de la matrice R, j=1,K,m comme deuxième membre. Ce système, écrit pour m sous-domaines flottants sous Nproc, est une généralisation du problème d'interface condensé de la méthode FETI (III.16). Dans le cas mixte, l'analogue de l'équation (III.63) de la méthode FETI est la solution spécifique xi+ du problème en présence de modes rigides.
S OLUTION DU PROBLÈME CONDENSÉ AUX INTERFACES
Méthode OrthoDir préconditionnée
La méthode de résolution du problème global selon la méthode du complément de Schur (III.9) est la suivante. Calculez le champ local wk dans le sous-domaine Ωi et c'est la solution au problème de Dirichlet. Construire les contributions sik nécessite néanmoins un échange de données, ainsi que le calcul du coefficient de descente ρk et du coefficient de conjugaison γk.
Méthode OrthoDir projetée
Initialisation : définition de la direction de descente initiale w0 égale au gradient prédit préconditionné. Initialisation : Calculer le produit w0 avec la matrice complémentaire de Schur dual D comme le saut des vecteurs xi0+ à travers les interfaces. Calculez le gradient qui est le produit de sem+1 avec la matrice complémentaire de Schur double D.
Méthode OrthoDir projetée de la méthode primale-duale
Initialisation : calculer le nouveau gradient comme le produit de la direction de descente w0 par la matrice M. Initialisation : calculer le vecteur z0 qui est la projection du vecteur Mw0+ (III.129)-(III.130), suivi du préconditionnement étape et reprojection. Suivez les étapes de projection du vecteur Mwk+ (III.129)-(III.130), préconditionnement et reprojection pour trouver le vecteur zk.
C ONCLUSION
On pourrait citer ici la méthode FETI à deux niveaux [Farhat et al. 2000a], où le choix du concepteur (III.69) est plus compliqué que celui présenté dans ce travail. Pour cette première expérimentation de méthodes de décomposition de domaines, nous nous sommes limités à une étude assez basique, qui reste néanmoins un défi passionnant. Dans ce chapitre nous présentons quelques cas de tests assez simples, qui ont néanmoins permis de valider les équations du chapitre précédent et même d'évaluer le comportement des trois méthodes de décomposition de domaine.
É CRASEMENT D ’ UNE BARRE LONGUE
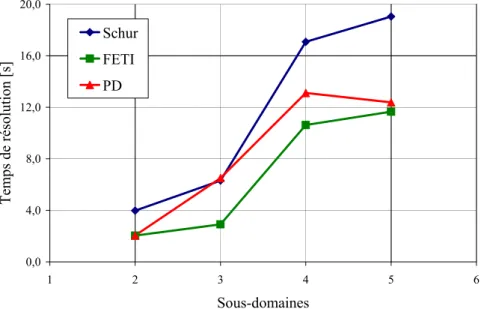
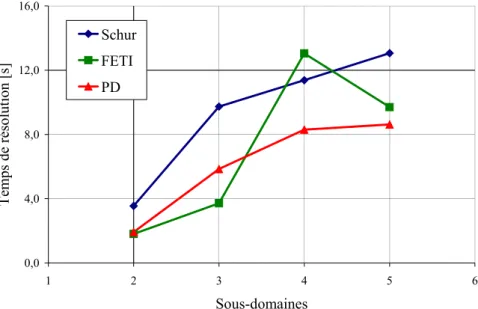
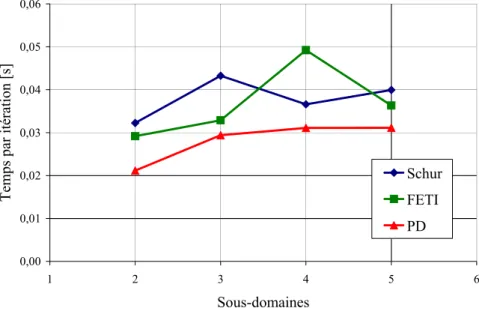
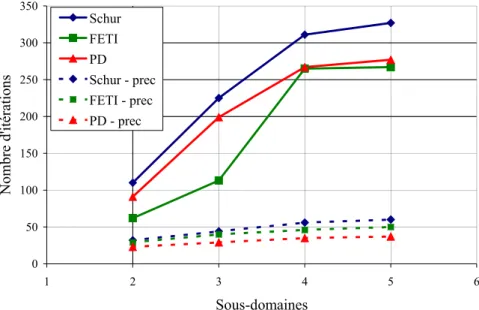
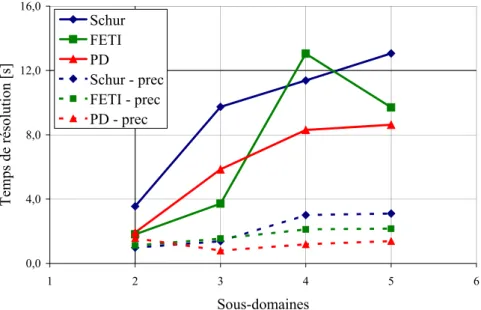
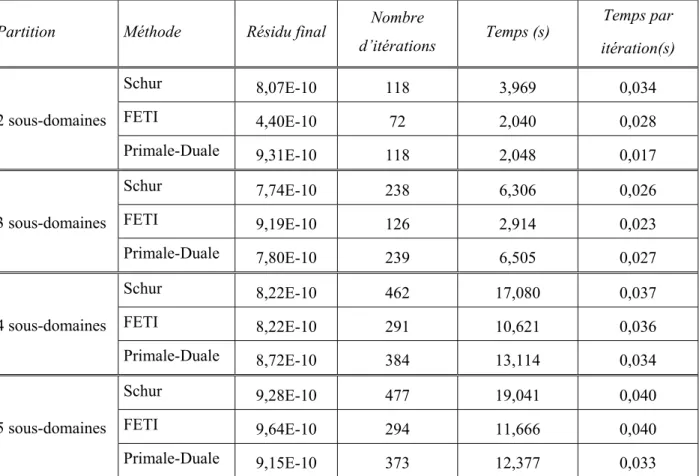
En revanche, pour atteindre une précision de 10−6 et pour plus de 3 sous-domaines, la méthode primal-dual s’avère plus rapide que FETI. De plus, sur plus de deux sous-domaines, le temps pour réaliser une itération est comparable pour les trois méthodes, avec toutefois un avantage pour la méthode hybride. Nous pouvons voir que le coût d’itération de la méthode primal-dual est inférieur à celui des deux autres méthodes.

C AS DU TRIAXE
Calcul sur 2 sous-domaines
En utilisant le préconditionneur de Dirichlet, on obtient 71% en nombre d'itérations par rapport au cas sans préconditionnement. Quant à la méthode primal-dual, l’utilisation du préconditionneur simple réduit le nombre d’itérations de 88 % sans augmenter la durée d’une itération. Non seulement le résidu final n’atteint pas le critère de convergence, mais en plus le nombre d’itérations augmente par rapport au simple préconditionneur.
Calcul sur 3 sous-domaines
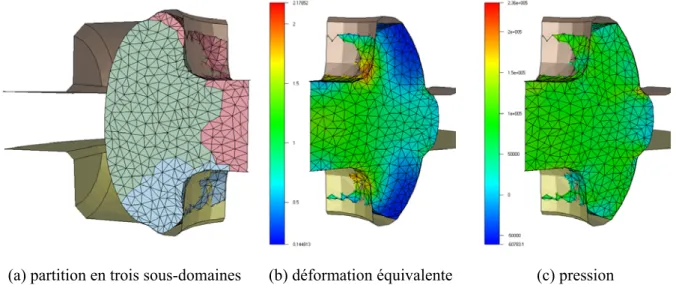
Dans la méthode du complément de Schur, l'utilisation de préconditionneurs diagonaux et de Neumann réduit le nombre d'itérations de 70 % et 90 %, respectivement, par rapport au calcul sans préconditionnement. Les performances du préconditionneur de Neumann, qui est le préconditionneur optimal de la méthode primitive, sont spectaculaires. Il convient de noter que la partition considérée comporte des points multiples, c'est-à-dire des nœuds partagés par les trois sous-domaines. a) divisé en trois sous-domaines (b) contrainte équivalente (c) pression Figure IV.12.
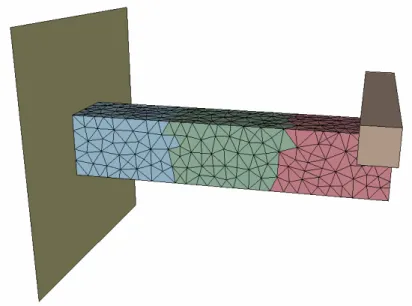
U NE POUTRE ENCASTRÉE
Pour la référence des deux méthodes, nous avons choisi la solution obtenue par la méthode FETI. En particulier, l'utilisation du préconditionneur de Neumann fournit le même nombre d'itérations que la méthode FETI sans préconditionnement. De plus, l’utilisation d’un préconditionneur complet pour la méthode primal-dual s’avère encore une fois inutile.
C ONCLUSION
Le comportement de la méthode primal-dual est très similaire à celui de la méthode FETI, notamment dans le cas sans préconditionnement et avec le préconditionnement léger. Des tests effectués sur la même tige, mais divisée pour produire des modes rigides et des points multiples, ont démontré la nécessité de ce traitement pour la méthode primal-dual. Ce n’est que pour la méthode du complément de Schur que le besoin d’un préconditionneur complet est apparu.
P RISE EN COMPTE DE LA RAIDEUR DE PRESSE
Cas Vaccari
Cas Vaccari : géométrie initiale (a) et forme finale de la pièce forgée obtenue sans grip. La forme finale prévue n'a pas été atteinte car la déformation élastique de la presse (ici exagérée) modifie la course de forgeage. Ils sont bien plus grands que dans la simulation sans tenir compte de la déformation de la presse, et correspondent également mieux à la réalité rapportée par les experts forgerons du projet.
Cas Smetek
Deux séries de mesures de déplacement le long de l'axe des x sont présentées à la figure V.5, ainsi que la courbe dérivée des données numériques. Les quatre déplacements de mesure expérimentale associés à la rotation autour de l'axe y sont représentés sur la figure V.6. Le cas Smetek : valeurs expérimentales et numériques du déplacement de la presse correspondant à la rotation autour de l'axe y.

Cas Iskra Avtoelektrika
Le modèle de presse est appliqué à l'outil inférieur avec les valeurs suivantes de la matrice de flexibilité, choisies arbitrairement faute de données expérimentales : k11=k22 =3,0⋅109N mm et. La figure V.8a montre les maillages en fin de simulation ainsi que les valeurs des isols de contact. La figure V.9 montre le déplacement le long de l'axe z dû aux déformations élastiques par compression. a) isovaleurs de contact (b) contrainte équivalente Figure V.8.
F ORGE 3 PARALLÈLE
Cas Vaccari
Les accélérations obtenues sur un cluster de 32 processeurs doubles Pentium-III (1 GHz, 512 Mo) sont indiquées dans le Tableau V.6. Les résultats sur 2 et 8 processeurs sont surprenants à première vue, mais cohérents avec les performances de Forge3 avec un préconditionnement Choleski incomplet [Marie 1997, Perchat 2000]. Cependant, même avec un rendement de seulement 60 %, le préconditionneur imparfait de Chloeski reste plus rapide que les préconditionneurs diagonaux.
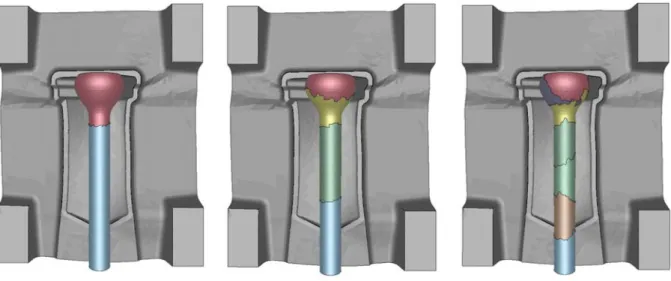
Cas Iskra Avtoelektrika
Cas Iskra : efficacité pour les trois mailles, en fonction du nombre de processeurs La simulation de ce cas de forge avec des calculs connectés dans l'outil a également été réalisée en parallèle sur deux processeurs. La figure V.13 présente la répartition de trois corps considérés au début de la simulation et la contrainte équivalente à la fin de la simulation. Cas Iskra parallèle : dimensions du maillage. a) répartition des corps sur deux processeurs (b) contrainte équivalente en fin de course Figure V.13.
C AS DU TRIAXE : CONFRONTATION F ORGE 3 VS . FETI
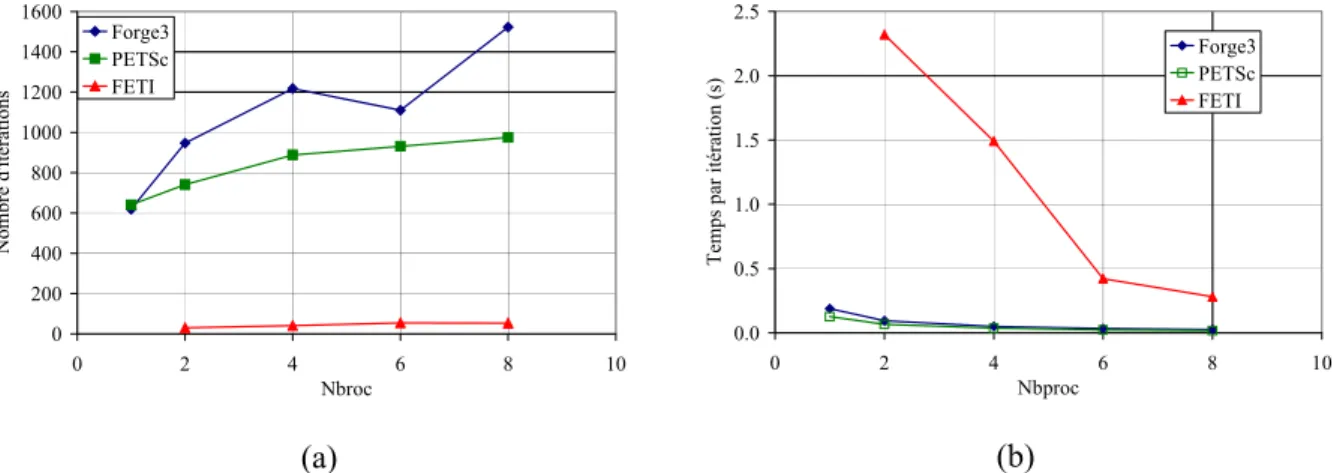
Cas à 10 602 nœuds
Le tableau B.1 en annexe B montre les résidus obtenus avec ces trois solveurs ainsi que les temps de solution correspondants. Il est alors clair que le solveur FETI atteint les meilleures performances lorsque le temps de factorisation est égal au temps de résolution itérative. Exemple de trios sur 10 602 nœuds : accélération (a) et efficacité (b) calculées avec le temps de calcul sur 2 processeurs comme référence.
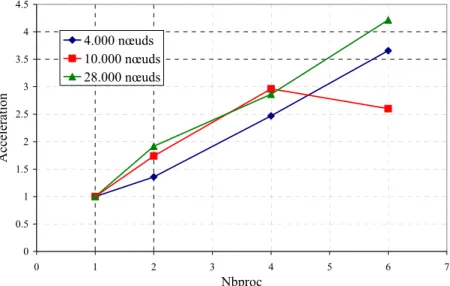
Cas à 58 626 nœuds
Par conséquent, dans ce cas, le nombre de sous-domaines devrait être plus élevé. Avec le partitionnement dynamique [Digonnet 2001] nous avons pu améliorer considérablement les partitions existantes et générer un partitionnement en 10 sous-domaines. Le cas triaxial à 58 628 nœuds : accélérations obtenues dans le cluster se référant au calcul sur 6 processeurs.
C ONCLUSION
Barboza 2004] Josué Barboza, Traitement du contact entre corps déformables et calcul parallèle pour la simulation 3D de forgeage multicorps, Thèse de Doctorat École des Mines de Paris, Sophia-Antipolis, (2004). Digonnet 2001] Hugues Digonnet, Distribution dynamique et réseau parallèle, thèse École des Mines de Paris, Sophia-Antipolis, (2001). Mocellin 1999] Katia Mocellin, Contribution à la simulation numérique tridimensionnelle du forgeage à chaud : étude contact et calcul multi-grille, Thèse de Doctorat École des Mines de Paris, Sophia-Antipolis, (1999).
6