fxng1n=0 dizisi r noktasına yakınsarsa ve g fonksiyonu r noktasında sürekliyse, o zaman r noktası sabit bir g noktasıdır. Belirli bir f fonksiyonunun sıfır konumunu bulmanın yaygın bir yöntemi, sıfır konumu problemini sabit nokta belirleme problemine dönüştürmektir. Böylece, f sıfır konumunu belirleme sorunu, karşılık gelen g fonksiyonu için sabit bir g noktası belirleme sorununa dönüşür;
Ancak bu fonksiyonların bir kısmı sıfır konumu için yakınsak iterasyon üretirken, diğer kısmı sıfır yerine başlangıç noktasının ne kadar yakın seçildiğine bakılmaksızın seçilir. farklı bir yineleme üretebilir. Belirli kriterleri kullanarak yakınsayan yinelemeler üreten yineleme fonksiyonlarını ayırt edebilir miyiz diye merak ediyorum. Aynı yineleme fonksiyonu aynı zamanda negatif sabit nokta için yakınsak yineleme de üretir çünkü .
Yineleme fonksiyonu tarafından üretilen dizinin, fonksiyonun sahip olduğu her sabit nokta için yakınsak yinelemeler üretmesi beklenmemelidir. Yakınsak yineleme genellikle yalnızca sabit noktaya yeterince yakın seçilen x0 başlangıç noktaları için elde edilebilir.
Iterasyon fonksiyonu seçimi ve · Newton - Raphson yöntemi
- Newton-Rapson yönteminin geometrik yorumu
- Newton-Rapson yönteminin yak¬nsakl¬¼ g¬
- Newton-Raphson yönteminde ba¸ slang¬ç noktas¬
- Newton-Rapson ve karma¸ s¬k kökler
- Katl¬kökler için Newton-Raphson yöntemi
- Say¬sal türev ile yakla¸ s¬m(Kiri¸ s yöntemi)
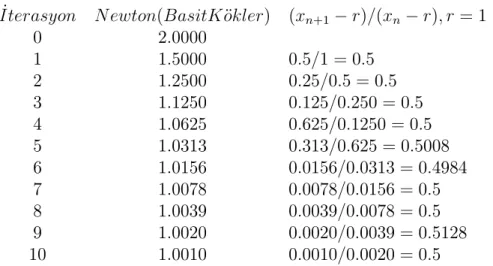
Yakınsak yineleme üretirken, farklı yineleme fonksiyonlarının farklı hızlarda yakınsayan diziler oluşturduğunu da gözlemledik. Bu fonksiyon yineleme fonksiyonu ve sıfıra yeterince yakın olan x0 başlangıç noktası ile üretilir. Her adımdaki virgülden sonraki doğru basamak sayısı, bir önceki adımın en az iki katıdır.
Benzer şekilde, x2 yaklaşım yöntemi, (x1; f(x1)) noktasından çizilen teğet x eksenini kesişim olarak alır. Bu yaklaşımlar bir noktaya yakınsarsa, yakınsadıkları nokta g fonksiyonunun sabit bir noktasıdır. Newton-Raphson yöntemi, sıfır noktasının küçük bir komşuluğunda ikinci dereceden (ikinci dereceden) yakınsak bir yöntemdir: noctasg fonksiyonunun sabit bir noktası, f0(r) 6 = 0 ve xn ve n'inci adımda elde edilen yaklaşım.
Bu sonuç, yöntemin yakınsaması durumunda ikinci dereceden yakınsadığını göstermektedir. Örnek 6.3'te elde edilen yaklaşımlar, yakınsaklığın ikinci dereceden olduğunu göstermektedir. Bu sonuç, yukarıdaki Newton yöntemi için elde edilen sonucun genel halidir ve benzer şekilde kanıtlanabilir. Dolayısıyla bu problemin başlangıç noktasının seçimi zor olmadı.
Her başlangıç noktası için elde edilen iterasyonlar yakınsaktır ancak yakınsama oranları çok farklıdır. Sonuç olarak örneğimizde başlangıç noktası seçiminin tekrarlanmasının yakınsama hızına etkisinin büyük olduğu görülmektedir. Bu sonuç özellikle Newton-Raphson yöntemi için de geçerlidir ancak bunun için başlangıç noktasının da karmaşık sayı olarak seçilmesi gerekir.
Bu sonuç, yöntemin en azından karesel olarak doğru başlangıç noktasına yakınsayacağını göstermektedir. Öte yandan, m = 2 için yukarıda verilen x0 = 2 başlangıç noktalarını aynı başlangıç değeriyle uyguladığımızda ilk adımda x1 = 1'in gerçek sıfırını elde ederiz.2 başlangıç noktası ve basit sıfırlar için Newton-Raphson yöntemi Örnek 4.1'de gösterildiği gibi 5 adımda yakınsar, m= 2 için ayarlanmış versiyon ise 2:0000 ile 1:3333 arasındadır ve dönüşümlü olarak salınım yapar (Alıştırma 14).
Bu durumda tek bir başlangıç değeri yerine x0 ve x1 başlangıç değerleri ile başlatılabilir. Newton-Raphson yönteminde olduğu gibi, teğetin (xi; f(xi)) noktasındaki kesişimi yerine, (xi 1; f(xi 1));(xi; f(xi))) ve.
Nonlineer sistemler için Newton yöntemi ve benzeri bir yöntem
Nonlineer sistemler için Newton benzeri uygu- lama
Yukarıdaki girişten görülebileceği gibi, skaler denklemlerde f fonksiyonunu ve f'nin türevini gerektiren Newton yöntemi, doğrusal olmayan cebirsel sistemler için de sistemin ve Jacobian matrisinin kullanıcı tarafından sağlanmasını gerektirir. Ancak paket yöntemini hatırlayarak f'nin türevi yerine türev için geri fark yaklaşımı kullanılarak türev bilgisi sağlama ihtiyacını ortadan kaldırmak mümkündü. Cebirsel sistemler için kısmi türevleri içeren Jacobian matrisi için benzer bir işlem gerçekleştirerek Jacobian'ı hesaplama ihtiyacını ortadan kaldırabiliriz.
Bir sonraki yinelemeye X(0) = X(1); X(1) = X(2) alarak devam ediyoruz ve uygun bir sonlandırma kriteri sağlanana kadar bu işleme devam ediyoruz. Newton-Raphson yöntemi Örnek 6.1'de gösterildiği gibi 5 adımda yakınsarken, 2 başlangıç noktası ve basit küreler için m = 2 ve katlanmış küreler için değiştirilen versiyon 2:0000 ve 1'dir. Şunlar arasında geçiş yaparsınız: 3333 değer. Eğer r noktası basit sıfır ve f fonksiyonunun dönüm noktası ise, bu casef tarafından oluşturulan Newton-Raphson yineleme fonksiyonu g'nin r noktasında bir ekstrema sahip olduğunu kanıtlayın.
Bu bölümde verilen Newton (Program 6.2) adlı programın Örnek 6.8'deki denklem sistemi ile çalıştırılması ve (x0; y0) = (2;1) ile elde edilen sonuçların doğruluğunu kontrol ediniz. Aşağıdaki doğrusal olmayan sistemlerin grafiklerini çizerek kaç tane gerçek çözüme sahip olduklarını tahmin edin. 17(b) numaralı sorunun doğrusal olmayan sistemi ve aşağıda verilen başlangıç değerlerinin her biri için (x1; y1) ve (x2; y2) yaklaşımları Newton'un yöntemine yardımcı olmaktadır. ile hesaplayın.
Yaklaşımlarınız şekildeki grafiklerin kesişme noktalarına yakınlaşıyor mu? Soru 19 ve Program 6.3'te verilen (x0; y0) orijinlerini kullanarak Soru 17(b)'deki doğrusal olmayan sistemin yaklaşık çözümünü elde edin. Uygun başlangıç değerleri ve Program 6.3 ile Soru 17(c)'nin her doğru çözümünü belirleyin.
Aral¬k üzerinde s¬f¬ryerleri
Vektörel ikiye bölme yöntemi
Yukarıda verilen alt serilere aynı anda ikiye bölme yöntemini uygulayarak her bir alt serideki sıfırı belirlemek istiyoruz. Yukarıdaki tabloda verilen sonuçlar gerçek değerlerle karşılaştırıldığında elde edilen yaklaşıkların virgülden sonraki on dört haneye kadar doğru olduğu anlaşılmaktadır. Yarıya indirme yönteminin tanıdık skaler versiyonu, fonksiyonun verilen aralığın uç noktalarında işaret değiştirmesini gerektirirken, yukarıda tartışılan vektör versiyonu da fonksiyonun işaret değiştirmesini gerektirir. İşlettiği alt serileri tanımlayarak her alt seride sıfırını bulur.
Öte yandan f(x) = x3 fonksiyonu da x=0'da üçlü sıfıra sahiptir ve aynı aralıkta işaret değiştirir. Bu amaçla aralık uç noktalarında işaret değişikliği gerektirmeyen yinelemeli yöntemlerin vektörel versiyonları gerçekleştirilebilir. A'nın boş küme olması ve X'in mevcut olması tesadüftür. değerleri varsayılan olarak döndürün. Uzak yay değişkeninin değerinin 1 olduğunu ve epsconclusion kriterinin değerinin 1 ila 5 olduğunu varsayalım. Farc değişkeni sonsuz normueps'ten büyük olduğu sürece aşağıdakileri tekrarlayın.
A ve C vektörlerinin jj ile gösterilen indislerini belirleyin. e) Eğer e=gerjj indeks seti boş değilse, A(jj) =C(jj) olarak değişir. f) f ark=jB Ajvector'ı tanımlayın. g) f arc <= eps veya jf(C)j< eps özelliğini sağlayan j0 yakınsak bölgesinin indislerini belirleyin. h) X=C(j0) ile elde edilen s¬f'leri X vektörüne atayın. i) f arc > eps özelliğini sağlayan henüz yakınlaşmamış alt bölgelerin j1 indekslerini belirleyin.
Vektörel Newton Yöntemi
Vektör ikiye bölme yönteminin Algoritma 6.2'sine uygun bir program hazırlayın ve aşağıda verilen fonksiyonlara göre verilen aralıklardaki sıfırları belirleyin. Proje (Polinomlar için Vektör Newton Yöntemi): Belirli bir radyo diskindeki tüm sıfırları, kullanıcıdan bir fonksiyon ve türevini alarak belirleyen Algoritma 6.3, verilen polinomun tüm sıfırlarını hesaplar. Bulmak için genişletin ve CVNewtonp olarak adlandırın. Öncelikle verilen bilgilere göre s¬f ¬rs içeren diskin yarıçapı bulunur. İlgili teoriyi keşfederek tahmin edin. Polinomun katsayılarının verilen vektörünü kullanarak, türev polinomunun katsayılarının vektörünü de belirleyin.).
Maksimum sayaç değerine ulaşılana kadar aşağıdakileri tekrarlayın;. d) jX1j< minörleri veren indisleri belirleyin. g) f ark eşitsizliğini veren j0 indekslerini belirleyiniz; h) f ark > esetsizlik veren indeksleri belirleyin;. k) X0 X1(j1); yakınsamayan bileşenleri geçerli başlangıç vektörü olarak alın; Xfr=yuvarlak(sazan*gerçek(Xf))/sazan; Yuvarlak %gerçek parçalar¬ Xfs=yuvarlak(sazan*resim(Xf))/sazan; Yuvarlak % sanal parçalar. OCTAVE (URL:aves.ktu.edu.tr/erhan/dokumanlar) ile dijital hesaplama ve kodlama.