No capítulo anterior, concluímos que é possível mapear um sistema de partículas interagentes para um sistema de exceções governado por uma estatística fracionária com um g bem definido. No caso de energyE, aparece a função dilogaritmo (o caso especial da função Lerch zeta), uma assinatura de um sistema governado por uma FES.
A função de partição no limite d → ∞
Partícula de massa m confinada em uma Caixa de tamanho L em D dimensões 15
Nesse limite, os argumentos da exponencial ficam muito pequenos e podemos aproximar a série por uma integral dada por.
Mecânica estatística do gás ideal governado por uma FES
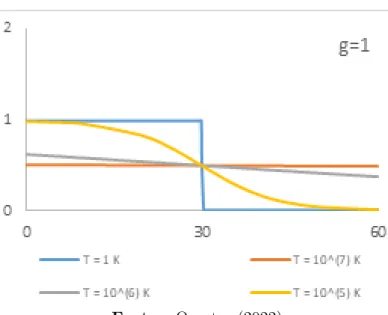
MECÂNICA ESTATÍSTICA DO GÁS IDEAL GOVERNADO POR UM FES18 válido quando o n-argumento do logaritmo é grande. 2.29). MECÂNICA ESTATÍSTICA DO GÁS IDEAL CONTROLADO POR UM FES20 Figura 1 – Curvas dos números de ocupação para g= 1.
Propriedades de um Gás Homogêneo
PROPRIEDADES DE UM GÁS HOMOGÊNEO 22 onde h é a constante de Planck e satisfaz o elemento de volume no espaço de momentos. Para manter a consistência da equação para N, ela não deveria depender explicitamente de g, apenas da energia de Fermi ϵF, definida na equação (2.35). Para generalizar o resultado acima, vamos usar a distribuição Wu para calcular a energia e o número de partículas no sistema para qualquer temperatura.
Na equação acima, a distribuição Wu, ni, é usada como peso, pois indica a degenerescência do estado de energia a uma dada temperatura. PROPRIEDADES DE UM GÁS HOMOGÊNEO 23 Observando que N é independente da temperatura (conservação do número de partículas), podemos dividir as equações (2.51) e (2.52) por (2.43), encontrando assim o conjunto de equações dos pares abaixo: 2.54) Ressaltamos que a energia acima foi normalizada pela energia de FermiϵF. A partir da equação acima, o potencial termodinâmico é separável e pode ser obtido resolvendo duas integrais, chamadas I1 e I2. 2.68) Primeiramente considerando I1, vamos alterar a variável:.
Gás homogêneo em bidimensional
Todos os tipos de integrais na equação acima já foram resolvidos em detalhes no caso fermiônico. A expressão acima revela um resultado muito importante: a energia adimensional por partícula para um sistema controlado por um FES é separável em uma parte fermiônica.
Problema de Wu: Gás Ideal Generalizado
PROBLEMA DE WU: GÁS IDEAL GENERALIZADO 29 nos aproximamos de sistemas físicos reais e ampliamos as possibilidades de mapeamento de sistemas em matéria condensada. A equação acima representa a variação dos estados disponíveis, ∆di, para a espécie i, dado que o número de partículas da espécie j variou de ∆Nj, cuja constante de proporcionalidade é αij. Além disso, entendemos {∆Nj} como um conjunto de mudanças permitidas no número de partículas do sistema.
Então, com base na definição acima (2.108), também podemos generalizar a equação (1.8), que determina o número total de configurações do sistema. Ni)!hGi−1−Pjαij(Nj−δij)i!, (2.109) onde δij é o delta de Kronecker (matriz de identidade) e Gi é o número de estados disponíveis para a espécie i quando não há partícula no sistema, ou isto é, a dimensão do espaço de Fock-Hilbert para as espécies. Para calcular a taxa de emprego média (mais provável) para cada espécie, precisamos minimizar a função de . PROBLEMA DE WU: GÁS IDEAL GENERALIZADO 31 Com essas equações em mãos, podemos determinar muitas outras propriedades termodinâmicas do sistema.
Para verificar a consistência do nosso formalismo, tentemos recuperar os resultados da seção (2.3), onde o gás ideal tinha apenas uma espécie. Mostraremos que este modelo pode ser mapeado em um gás ideal de três espécies não-interagentes, chamadas de exclusões, e obedece a uma estatística fracionária de exclusão [10].
O Modelo e suas Propriedades
O modelo mais simples que apresenta esse tipo de transição de fase é o modelo de Hubbard, que trata microscopicamente do comportamento dos elétrons em uma rede em interação. Neste modelo, a transição de Mott, na fase isolante, apresenta ordem antiferromagnética (girando em direções opostas). Como exemplo, temos o limite das dimensões infinitas [33], onde a fase metálica é solúvel e representa um líquido de Fermi renormalizado.
Ao contrário do gás de Fermi (não interativo), o líquido de Fermi introduz perturbativamente interações no sistema. Uma segunda versão, também solucionável, do modelo de Hubbard é a interação de curto alcance, que é resolvida exatamente no caso unidimensional [34]; entretanto, não possui transição metal-isolante no estado fundamental. Outro caso solucionável do modelo de Hubbard é a interação com séries infinitas [35], objeto de estudo neste capítulo.
Neste caso, a transição metal-isolante de Mott ocorre em um ponto crítico bem definido, onde a interação é igual à largura de faixa de energia: U = ∆ [35]. Notamos também que o termo cinético muda com o termo de interação no hamiltoniano, o que nos dá uma indicação da solubilidade do modelo.
Representação de Exclusão
Definindo o número médio de ocupação, nkα =Nkα/G0, podemos agora explicitar a condição para a maximização da grande função de partição (ou minimização da grande energia livre canônica), ∂n∂. De facto, apesar de ser uma escolha intuitiva, face aos resultados da secção anterior, sintetizados em (3.11), torna-se impossível obter a matriz de interação estatística para recuperar consistentemente a termodinâmica do modelo. O mesmo procedimento de minimização de energia livre pode ser usado para encontrar o conjunto de números médios de ocupação transformados, agora definidos por ˜nkα = N˜kα/G˜0.
De acordo com este fato, a energia livre do sistema é escrita em função das novas matrizes: Foi possível obter as seguintes matrizes para gkk';αα′ e Λkk';αα′, onde Λkk';αα′ corrige a matriz de interação estatística fornecida por Wu [14]:. A interpretação correta da matriz estatística foi dada na referência [10], onde foi identificada a verdadeira matriz de interação estatística dada por.
REPRESENTAÇÃO DE EXCLUSÃO 37 Esta matriz também se mostrou adequada para descrever outras variantes do modelo de Hubbard: o modelo atrativo [36], o modelo de interação ligação-carga [37] e o modelo Penson-Kolb-Hubbard [38].
Análise de Escala do Grande Potencial Ω
ANÁLISE DA ESCALA DE GRANDE POTENCIAL Ω 39 Portanto, é útil definir o parâmetro que controla a transição para a temperatura zero porg = (∆−U)/2. A teoria de escalonamento para uma transição controlada por T em g = 0 pode ser obtida de maneira totalmente análoga. Pela teoria do grupo de renormalização, a redução da proporçãob à escala do sistema (as magnitudes modificadas serão representadas por variáveis destacadas), o comprimento característico é alterado de forma que L′ = b−1L, e as variáveis termodinâmicas µ, U e T responda a esta mudança de escala na forma:. 3.43) Vamos definir o campo de temperatura, normalizado por U, como.
ANÁLISE EM GRANDE ESCALA DE POTENCIAL Ω 41 Figura 4 – Diagrama de fases em função de g e T, com linhas cruzadas. Com uma teoria de escala adequada para o nosso modelo em mãos, podemos analisar o grande potencial canônico e determinar os expoentes críticos do sistema. Agora, rearranjando a expressão obtida para a energia livre grand canônica do sistema (4.2), levando em conta o regime onde T → 0 (e−βU ≪0), obtemos. 3.57) As transições de fase quânticas são evidenciadas pela parte singular da energia livre, portanto os dois primeiros termos, que são regulares, não são úteis do ponto de vista da análise de escala.
ANÁLISE DE GRANDES POTENCIAIS Ω 43 Agora, analisando o regime quântico crítico (QC), T →0 eg = 0, façamos uma substituição de variável: y=−β(ε−U/2), que transforma a equação (3.58) em. ANÁLISE DE ESCALA DO GRANDE POTENCIAL Ω 44 que o módulo do parâmetro z nos dá o número médio de ocupações dos estados ocupados individualmente k.
Energia livre grâ-canônica no regime de spin incoerente
No capítulo anterior, o modelo de Hubbard foi mapeado para um gás ideal de três espécies sujeito a FES. Este capítulo discute os resultados originais que obtivemos no contexto de um regime especial do modelo de Hubbard de vão infinito: spin incoerente. Nesta seção, primeiro derivaremos a energia livre grande canônica no regime incoerente de spin e o limite de acoplamento rígido.
GRANDE ENERGIA LIVRE CANÔNICA NO REGIME DE SPIN INCOERENTE 47 Ressaltamos também que o regime de spin incoerente geralmente é estudado apenas em uma dimensão espacial, devido ao fácil tratamento matemático, embora em nosso estudo tenhamos feito uma extensão para dimensões arbitrárias no fortemente acoplado estado. Referindo-se a importantes trabalhos que abordaram este regime, temos: na referência [50] este regime foi estudado no contexto do estado fundamental de sistemas fortemente correlacionados; na referência [15], a “Teoria Fracionária de Landau” foi adicionalmente introduzida e utilizada no regime de spin incoerente do Líquido de Luttinger (LL) em cadeias de Hubbard. 4.7) Além disso, usando a condição de spin incoerente (4.1), podemos estender o limite superior da integração para ∞, de modo que a integral que precisamos resolver é.
ALTA ENERGIA LIVRE CANÔNICA NO REGIME DE REFLEXÃO COERENTE 48 Agora, pela expansão binomial, . A integral pode ser expressa pela série de potências abaixo: onde o sobrescrito "SI" significa rotação incoerente e os coeficientes de expansão, aSIm, são definidos por. 4.11). Mais importante, se usarmos a descrição de que o módulo dez associado à função Lerch é igual ao número médio de exceções de ocupação [10], nós o encontramos. um valor bastante notável [10], que exploraremos no contexto do comportamento termodinâmico do modelo na próxima seção.
Propriedades Termodinâmicas
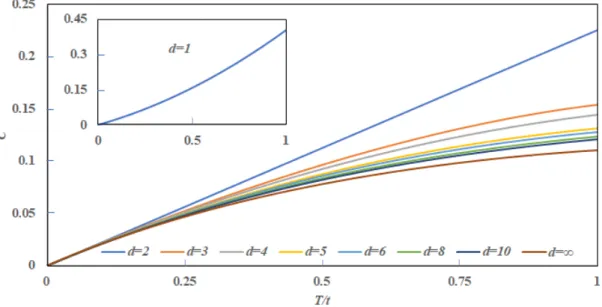
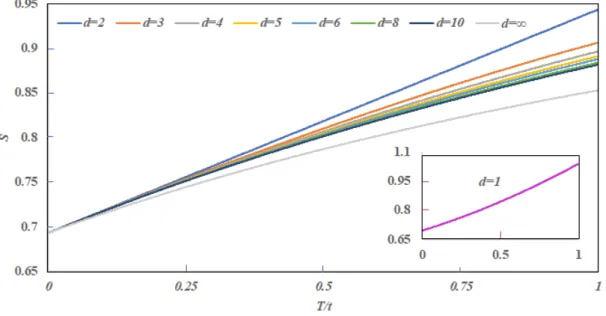
Nas tabelas 1 e 2 podemos ver que, para iguais dimensões, as séries que descrevem a entropia e o calor específico, (4.21) e (4.24), respectivamente, são finitas. Assim, para dimensões pares, temos funções polinomiais de ordem crescente com d, como podemos ver nas Figuras 5 e 6. Para dimensões ímpares, ambas as séries divergem no contexto das técnicas de soma de Borel, podendo assim classificar [51, 52 ] sua divergência assintótica como do tipo fatorial.
De fato, em três dimensões, os coeficientes de série para entropia e calor específico, respectivamente, satisfazem. Assim, podemos encurtar a série e considerar apenas os seis primeiros termos convergentes, no caso do calor específico. Em geral, as curvas aumentam continuamente em função da temperatura adimensional, T/t, com formas semelhantes para d≥3.
Além disso, usando a equação (4.29), podemos construir as últimas linhas das Tabelas 1 e 2, e também obter gráficos para propriedades termodinâmicas, conforme mostrado nas Figuras 5 e 6. Além disso, podemos enfatizar que a convergência das séries neste limite reafirma a consistência da soma de Borel para dimensões ímpares, pois neste caso a paridade é irrelevante.
Conclusões
Motivações para pesquisas futuras
Haldane, "Fractional quantization of the Hall effect: a hierarchy of incompressible quantum liquid states," Physical Review Letters, vol. Coutinho-Filho, "Metal-insulator transition with infinite-range coulomb coupling: Fractional statistics and quantum critical properties," Phys. Coutinho-Filho, “Fractional exclusion statistics and thermodynamics of the Hubbard chain in the spin-incoherent luttinger liquid regime,” Phys.
Coutinho-Filho, "Thermodynamics of the infinity-range hubbard model in the spin-incoherent regime", Journal of Physics A: Mathematical and Theoretical, vol. Aoyama, "Specific heat of the ideal gas satisfying general exclusion statistics", Eur.Phys B., vol. Wu, "Absence of mott transition in an exact solution of the short-range one-band model in one dimension", Phys.Rev.Lett., vol.
Coutinho-Filho, “Fractional statistics and quantum scaling properties of the Hubbard chain with bond-charge interaction,” Phys. Coutinho-Filho, “Fractional statistics and quantum scaling properties of the integrable penson-kolb-hubbard chain,” Phys.