Trabalho de Conclusão de Curso do Curso Superior de Matemática - Instituto Federal de Educação, Ciência e Tecnologia de. Ao meu namorado Marcos, que me auxiliou com várias sugestões e foi muito compreensivo com meu empenho no trabalho. Aos vários professores que me proporcionaram o conhecimento que tenho hoje, desde o ensino básico ao superior.
Considerando a riqueza de temas considerados pela curva ciclóide, este trabalho resgata o estudo da curva, tanto na educação básica quanto na educação superior. O objetivo principal deste trabalho é apresentar a importância do estudo da Ciclóide, mostrando sua interdisciplinaridade latente e sua relevância entre os mais diversos campos da ciência. Tendo em conta a vasta gama de temas abrangidos pela curva Cyclod, esta análise replica o exame da curva no ensino básico e superior.
No entanto, serão mostradas as equações paramétricas da curva cicloidal através da geometria analítica usando vetores. No final do meu 5º semestre de matemática, procurei professores que gostariam de estudar essa curva e apresentei os dados que já havia pesquisado sobre ela. Felizmente, iniciei uma iniciação científica com a professora Elisabete Guerato e pude continuar com a curiosidade que a curva cicloidal havia despertado em mim.
Comecei a me perguntar por que uma curva tão apropriada não havia sido estudada pelos graduandos de Matemática em nenhuma época, ou por que algo tão interessante não havia sequer sido mencionado na Educação Básica.
Afinal, o que é uma Cicloide?
Mas, para que serve a Curva Cicloide?
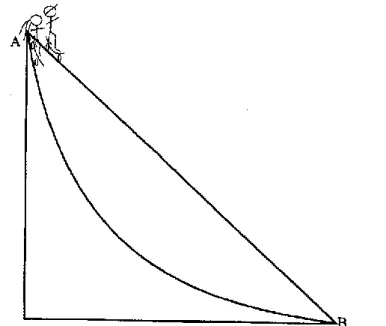
Para um melhor entendimento do leitor deste trabalho, é necessário entender o que é uma Curva Ciclóide, já que ela é desconhecida por muitos matemáticos. 1ª Questão: “Na Figura 2 há um desenho de dois patinadores descendo curvas radicais, um descendo um plano inclinado e o outro descendo uma curva. Suponha que os dois patinadores tenham o mesmo peso e, sob o efeito da gravidade, ambos partam simultaneamente do ponto superior A para o ponto inferior B.
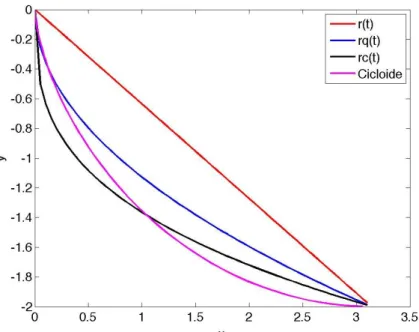
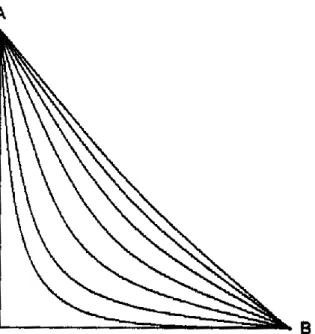
A questão é: quem chegará primeiro ao ponto B, ou seja, quem será mais rápido, quem descerá a ladeira ou quem irá pela cobertura?” (p. 16). Questão 2: “De acordo com o enunciado do problema anterior, dentre as infinitas curvas possíveis de descida do patinador do ponto A ao B (ver Figura 3) e sob a influência da gravidade, qual das curvas será a mais rápida. ?” (p. 17). Questão 3: “Em uma pista de skate conhecida como “metade”, cuja forma descreve a curva cicloidal invertida apresentada na Figura 4, dois patinadores praticam manobras radicais sob a influência da gravidade.
De todas as curvas infinitas que passam pelos pontos A e B, considerando a ação da gravidade, a Braquistócrona é a curva que permite o menor tempo de descida. Nos próximos capítulos veremos como derivar as equações paramétricas para a curva ciclóide e mostraremos a importância do estudo desta curva – ela está presente entre as mais diversas áreas do conhecimento.
Cicloide
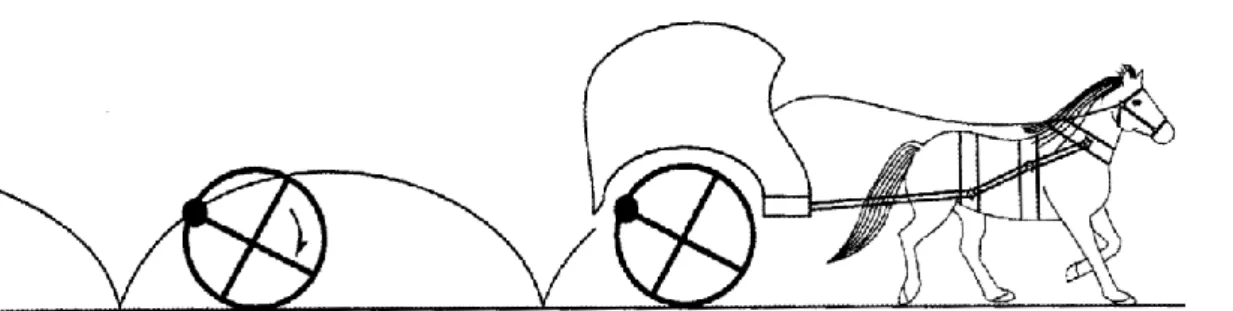
Aqui apresentamos como a curva ciclóide apareceu pela primeira vez na história da ciência, quem a nomeou assim e como seu estudo se desenvolveu ao longo dos anos. Como mencionado anteriormente, Galileu estava certo dia na janela, apenas observando o ambiente, quando começou a perceber o movimento de uma roda de carroça que passava (Figura 6). Interessado em descobrir qual curva esse movimento poderia gerar, Galileu primeiro usou placas de metal para demonstrá-lo.
Sem muito sucesso (BOYER, 1996), Galileu sugeriu que a curvatura poderia formar um belo arco de ponte. Ele também levantou a hipótese de que a área do arco da ciclóide é exatamente três vezes a área do círculo que ela gera. A "Helena da matemática" e o "Falo da discórdia" eram nomes que representavam a Curva Ciclóide no século XVI, tal era o debate que causava na época.
O irmão Marin Mersenne, colega de René Descartes, conhecido por sua famosa fórmula "Primos de Mersenne", também participou dessa história. Independentemente de Roberval, Evangelista Torricelli interessou-se pela ciclóide, por sugestão de Mersenne ou Galileu, ambos os quais muito admirava (EVES, 2011).
Tautócrona
Em 1644, Torricelle publicou sua obra intitulada De parabole, na qual incluía tanto a quadratura da ciclóide quanto a construção da tangente (Apêndice A) Roberval, que até então não havia publicado sua obra, acusou Torricelle de plágio, o que não é verdade (BUSTILLOS e SASSINE, 2011), pois seus trabalhos eram independentes, embora Roberval o tenha feito primeiro. Ele interpretou isso como um sinal de Deus, indicando que o estudo da matemática não O agradava (BOYER, 1996). Além de ser reconhecido como um grande físico de sua época, por sua teoria ondulatória da luz, o estudo do pêndulo, a invenção do relógio de pêndulo e as leis da queda dos corpos, Huygens demonstrou a importância do cálculo e fez contribuições para a geometria (COELHO, 2008).
A partir de seus estudos sobre o pêndulo, Huygens provou geometricamente que a tautocrona é uma curva cicloidal (sua demonstração segue no apêndice B). Conhecendo a propriedade do Tautochrone, Huygens chegou a construir um relógio mais preciso, o que contribuiu para a navegação - na localização dos navios em longitudes (COELHO, 2008). Ele então patenteou o relógio como sua criação, embora o relógio de pêndulo convencional tenha sido criado por Galileu (EVES, 2011).
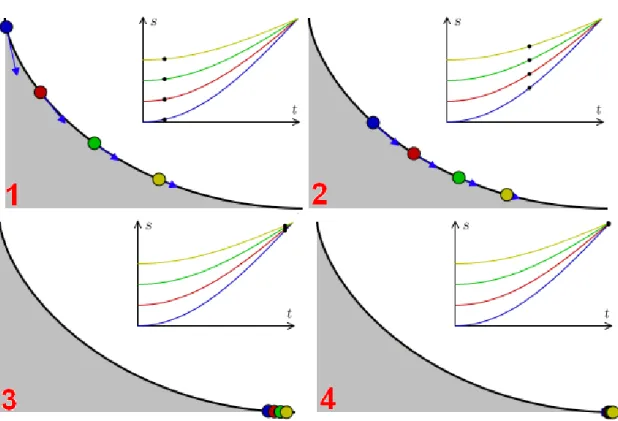
Braquistócrona
Newton apresentou sua resposta como um autor anônimo, mas quando Johan Bernoulli leu sua solução, ele disse. L'Hospital contratou Johan Bernoulli como seu tutor de matemática e, em troca, Johan poderia morar em seu castelo e receber comida e dinheiro. No entanto, tudo o que ele fez novamente em matemática teria o nome do Marquês L'Hospital.
Os irmãos Johan e Jackob levaram a disputa tão a sério para encontrar uma solução para Braquistócrona que a comunicação entre eles foi cortada. A resolução de Johan é muito interessante e diz-se que foi feita "usando o princípio da difusão de um feixe de luz através de uma densidade diferente, ou seja, calculando a curvatura do feixe em um meio não uniforme" (BUSTILLOS E SASSINE 2011 ). Por outro lado, Jakob Bernoulli resolveu de uma forma mais geral, usando máximos e mínimos como ferramentas7.
Graças à solução do problema da Braquistócrona surge o Cálculo Variacional8, que revolucionou a matemática e posteriormente a ótica devido aos trabalhos de Euler e Lagrange. 8 "O Cálculo Variacional visa fundamentalmente a investigação dos máximos e mínimos dos funcionais e é bastante semelhante à investigação dos máximos e mínimos das funções" (SOUZA JÚNIOR, 2010). Tomando Stewart (2011) e Bianchini (2011) como referência, aqui demonstraremos a curva ciclóide usando decomposição vetorial.
Para isso utilizamos o software Geogebra© como ferramenta para verificar o movimento da ciclóide com maior clareza. Agora que conhecemos a curva ciclóide e os principais problemas que a envolvem, vamos ver como podemos aplicá-la em sala de aula ao ensinar matemática. Neste capítulo apresentaremos três sugestões de atividades para o Ensino Fundamental II, Ensino Médio e Ensino Superior utilizando a curva ciclóide.
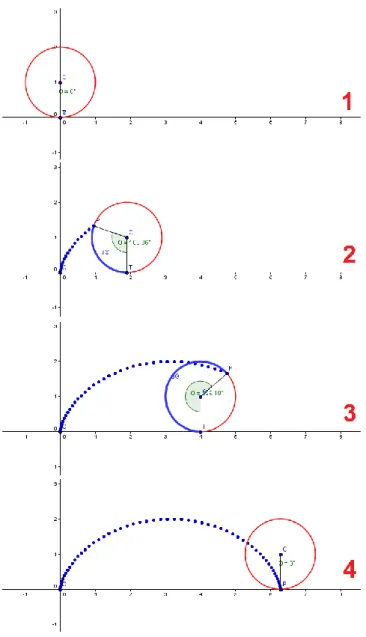
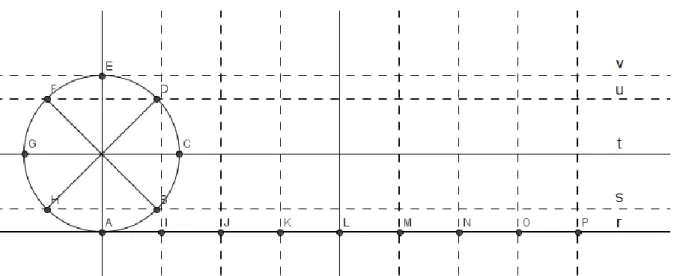
Construção da Curva Cicloide utilizando Desenho Geométrico
Agora desenhe uma linha s passando pelos pontos H e B; linha t passando pelos pontos G e C; a reta u passando pelos pontos F e D; e a linha v paralela à linha r passando pelo ponto E. Observe que quando a roda rolar sobre a linha r, o ponto B cairá no ponto I, o ponto C no ponto J e assim por diante” (MARMO e MARMO, 2008).
Comparação da Hipocicloide gerada pela Régua Espirógrafo com a
Curvas Derivadas da Curva Cicloide: Epicicloide e Hipocicloide
Régua Espirógrafo
Fases da Lua e Translação da Lua em Relação ao Sol
O problema da Braquistócrona
Como o espirógrafo gera hipociclóides, então, com a ajuda de uma régua, podemos dar aos alunos do ensino fundamental I e II e do ensino médio uma ideia mais ou menos concreta de como funciona o nosso Sistema Solar. Na ciência, cada vez mais trabalhos aparecem sobre a ciclóide, que é sempre uma "solução" para problemas. Podemos então verificar que “a partir de um problema proposto como desafio aos matemáticos da época, iniciou-se a busca por métodos de solução, culminando no que hoje conhecemos como cálculo de variações” (SOUZA JÚNIOR, 2010).
O cálculo das variações é um dos estudos que tem gerado o maior ramo da matemática aplicada, desde os estudos da economia até a mecânica quântica (BUSTILLOS e SASSINE, 2011). Com base na análise realizada, podemos dizer que a Cicloide aparece como tema autônomo em alguns materiais didáticos, que é apresentada com sua construção geométrica em materiais didáticos do Ensino Fundamental II e por meio de breves contextos históricos apresentando as equações paramétricas, no Ensino Superior. O Cicloide pode ser uma ferramenta interdisciplinar muito grande entre diferentes disciplinas atraindo assim o aluno para a educação matemática, mostrando que a matemática não é apenas fazer “notas” mas envolver o mundo em novos conceitos e soluções para os problemas presentes no dia a dia.
Assim como Bustillos e Sassine, também chegamos à conclusão de que a curva ciclóide pode ser chamada de curva mágica para quem percebe sua importância no desenvolvimento da filosofia da ciência” (BUSTILLOS e SASSINE, p. 191). Ainda há muito o que pesquisar e entender sobre o mundo, e a curva ciclóide pode ser a chave para várias questões na evolução da ciência. Disponível em:
Visões alternativas de alunos do ensino médio sobre o fenômeno da formação das fases da lua.