Um modelo discretizado da transformada de Radon é apresentado e são apresentados os métodos Algebraic Reconstruction Technique (ART), Filtered Back Projection (FBP) e Singular Value Decomposition (SVD), que são métodos de reconstrução de imagens. A tomografia computadorizada (TC) baseia-se nos mesmos princípios da radiografia convencional, segundo os quais tecidos com composições diferentes absorvem os raios X de maneira diferente. A base do problema de reconstrução de imagens médicas por meio de tomografia computadorizada é, sem dúvida, a matemática.
Este trabalho do curso está dividido da seguinte forma: O Capítulo 1 deriva o modelo matemático por trás da tomografia computadorizada, explicando e definindo propriedades em torno da operação de integração em hiperplanos para que possamos alcançar a transformada de Radon. Aplicando o método de separação de variáveis em (2.4) e integrando ao longo da reta ξ, obtemos.
Integra¸c˜ ao sobre Hiperplanos
O tipo de integral utilizado aqui será a integral de Lebesgue, que é uma generalização da integral de Riemann. A integral de Lebesgue apresenta diversas vantagens sobre a integral de Riemann, especialmente no que diz respeito aos processos limitantes. Além disso, a integral de Lebesgue é uma construção matemática generalizável para funções definidas num espaço de medidas, que assume valores reais ou complexos, ou mesmo num espaço General Banach¸co.
Abaixo apresentamos um exemplo de função de Lebesgue integrável que não é integrável de Riemann. Portanto, D(x) é uma função mensurável de Lebesgue e sua integral de Lebesgue é zero em qualquer conjunto mensurável. Se f é uma função integrável em Rn e se U é um conjunto aberto Rn, então.
Seja g uma função de Rn a Rn que possui uma primeira derivada parcial em todas as variáveis. Se f é uma função integrável em Rn, então a função que atribui x00 ∈Rn−ktoR. Uma consequência importante destes teoremas introduzidos é o uso de coordenadas polares: se é integrável no plano, então.
Como (cosα,sinα) é um vetor unitário de R2, podemos generalizar a Equação 1.16 realizando a integral sobre S1.
A Transformada de Radon
A transformação Radon é um operador R definido em L1(Rn) onde, para qualquer função integrável f em Rn, a função Rf é definida para θ ∈Sn−1 e s∈R per. No capítulo anterior definimos a transformada do Radon de uma forma geral, partindo de um caso específico que tem motivação física. Como C é uma matriz ortogonal, |det(C)|= 1 e isso prova que a integral sobre hiperplanos é independente da base ortonormal usada na definição.
Demonstração: Aplicando a definição de integração sobre hiperplanos (Definição 1.1.11), temos para o hiperplano hθ, xi=s,. 2.4) Fazendo a simples observação de que as equações (2.3) e (2.4) diferem apenas por uma translação e usando o fato de que a integral é invariante sob translações (coolário 1.1.9), completamos a demonstração. O próximo corolário nos diz que a transformada de Radon de uma função integrável existe como um número finito para quase todos, senão todos, s∈R. Além disso, isto mostra-nos que a transformada Radon de uma função integrável permanece integrável.
A definição integral Rf(θ, s) é independente da escolha da base usada na definição da transformada Radon. Neste exemplo apresentamos uma função f ∈ Rn que é quase sempre finita, e ainda assim existe um hiperplano no qual f não é integrável. Observe que ao definir θ o hiperplano hθ, xi = s simplesmente se torna xn=s e podemos aplicar o teorema da integração em hiperplanos para obter isso.
A restrição da variável x 0 à esfera unitária em Rn−1 é justificada pela definição da função f.
Propriedades da Transformada de Radon
O Teorema da Rotação (Teorema 2.2.4) pode ser generalizado para qualquer transformação linear não singular, mas para isso precisamos de algumas definições. Um resultado fundamental da teoria de Lebesgue é que esta equação quase sempre vale para funções integráveis. Pela definição de Es, esta última desigualdade será verdadeira se, e somente se, T x ∈ Es.
Diferenciando os dois lados desta equação em relação às variáveis e usando o lema 2.2.7, obtemos. Sef e g são funções integráveis em Rn, então definimos a convolução f∗g de f e g por. Usando o teorema de Fubini e o teorema da mudança de variáveis, podemos mostrar que a convolução de funções integráveis também é integrável.
Agora aplicamos o teorema de Fubini a Rn×Rn da seguinte forma: Sejam x0 e x00 elementos de Rn, então (x0, x00) é um elemento de Rn×Rn. Em seguida, usamos a definição da transformada e convolução de Radon para obter Observe que isso é possível devido ao Corolário 1.1.10, uma vez que a integração na integral interna de Lebesgue é integrável para quase tudo.
Além disso, como o integrando na equação (2.10) é integrável, podemos utilizar o teorema de Fubini para alterar a ordem da integração.
Injetividade da Transformada de Radon
O valor absoluto do integrando na definição da transformada de Fourier é |f(x)|, já que |exp−ihx,yi| = 1. Como sabemos que f é integrável, isso mostra que a transformada de Fourier de uma função integrável existe para todo y∈Rn. Precisamos apenas de uma propriedade da transformada de Fourier, sua injetividade: se Ff = 0, então f = 0 quase sempre.
Portanto, quando for necessário enfatizar a dimensão em que a transformada de Fourier é aplicada, utilizaremos a notação Fn. A relação entre a transformada de Radon e a transformada de Fourier é às vezes chamada de teorema da fatia de Fourier ou projeção da fatia. Demonstração: De acordo com a definição da transformada de Fourier, a integração sobre Rn pode ser realizada sobre qualquer conjunto de hiperplanos paralelos.
Uma função integrável é determinada exclusivamente por sua transformação Radon: se f e g são funções integráveis em Rn z.
Existˆ encia de uma F´ ormula de Invers˜ ao
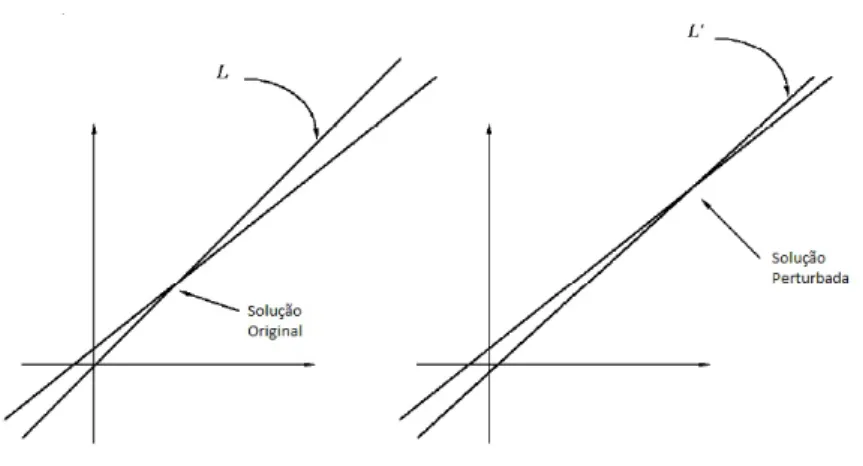
Rela¸c˜ ao entre a F´ ormula de Invers˜ ao e Problemas Mal-Postos
Em primeiro lugar, lembremos que os dados aos quais temos acesso no processo de tomografia são obtidos através da transformação Radon. Observe que quanto mais refinamos a aproximação (tomamos h mais próximo de zero), mais precisamente calculamos a derivada y0. Observe que em ambas as fórmulas de inversão obtidas na seção anterior, temos a diferenciação dos dados.
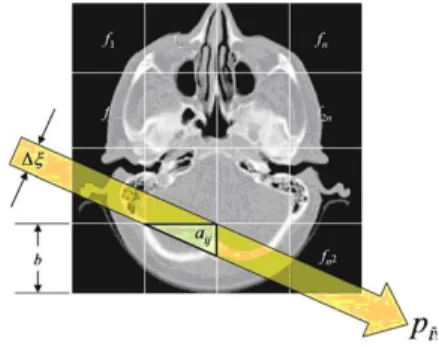
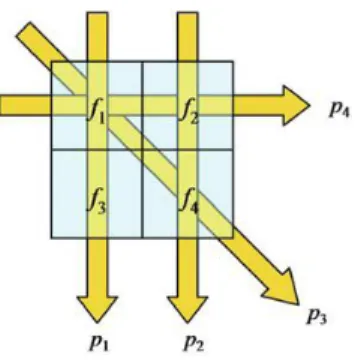
Nesta seção apresentamos a conexão entre a transformada de Radon derivada no capítulo 1 e uma versão discretizada do problema. Por exemplo, o processo mostrado na figura 4.4 gera um sistema de equações lineares da forma Quando o feixe de raios X passa pela região Ω, precisamos considerar quanto do pixel precisa ser reconstruído.
Para tanto, são introduzidos pesos que refletem a relação entre a área iluminada pelo feixe de raios X e a área total do pixel [6]. O valor de aij é determinado pela seguinte relação aij = área iluminada do pixel j no raio i. Porém, a inversão direta da matriz A, quando possível, não é bem-vinda devido aos seguintes fatores.
Além disso, em aplicações reais, a matrizA - por ser muito grande - provoca uma intensa demanda computacional em processos de inversão direta;
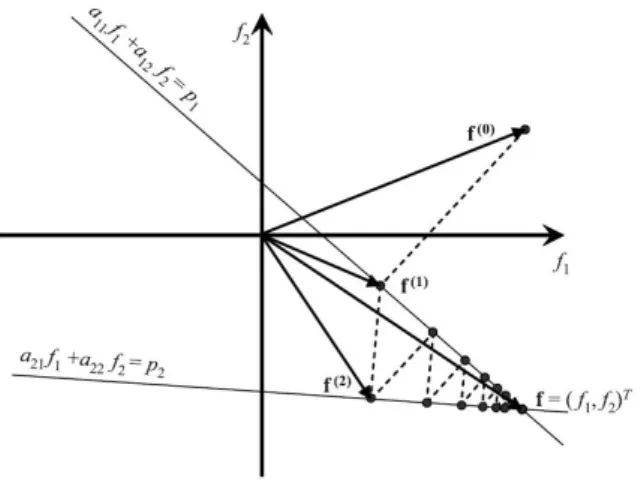
T´ ecnica de Reconstru¸c˜ ao Alg´ ebrica (ART)
Convergˆ encia do ART
Nesta decomposição em blocos de A, exigimos que cada bloco Aj tenha ordenação de linhas completa e defina uma aplicação sobrejetiva. Então, o algoritmo ART converge para a solução de norma mínima da equação Af =p, ou seja. Prova: Como esboço da prova, denotaremos a projeção ortogonal por Q.
Para relacionar as subprojeções Pj a Q, denotaremos a projeção ortogonal por Qj. Prova: A prova é fornecida por indução sobre o número de membros da projeção Qj. Demonstração: Como a decomposição do teorema anterior é válida para todos os operadores lineares contínuos, e não apenas para os operadores compactos, é suficiente mostrar que N(1−Q ) =N(1−Q∗).
Retroproje¸c˜ ao Filtrada (FBP)
Decomposi¸c˜ ao em Valores Singulares (SVD)
T´ ecnica de Reconstru¸c˜ ao Alg´ ebrica
A Técnica de Reconstrução Algébrica (ART) requer a solução através de projeção sequencial a partir de uma estimativa inicial, para o conjunto de soluções de equações seccionais lineares, onde cada um desses conjuntos é um hiperplano, conforme apresentado na seção 3.2. Abaixo apresentamos uma sequência de imagens criadas durante o processo de reconstrução pelo RTSH.
Retroproje¸c˜ ao Filtrada
As funções Matlab esradon e iradon foram utilizadas para reconstruir imagens usando o método FBP. Usando o resultado da última etapa, a função iradon, que é em si um método FBP, é aplicada.
Decomposi¸c˜ ao em Valores Singulares
Esta seção tem como objetivo analisar de forma simples a eficácia das implementações feitas na seção anterior. Para isso, fazemos comparações entre as imagens reconstruídas por cada método com as imagens Phantom e Phantom com ruído. Esta comparação é feita calculando a diferença entre as imagens original (Phantom) e original após implementação do ruído (Phantom com ruído) e as imagens reconstruídas fornecidas por cada método.
Para facilitar a visualização dessas diferenças entre as imagens, aplicamos um filtro de calor que destaca os pixels onde as imagens diferem. Na Figura 4.5 podemos ver que os três métodos produzem reconstruções razoavelmente próximas da imagem pretendida (Phantom). Vale ressaltar que o método FBP é o mais difundido na prática, pois possui baixo custo computacional e na grande maioria dos casos gera imagens razoáveis para análise qualitativa.
O método SVD não é amplamente utilizado em reconstruções de imagens devido à natureza mal condicionada do problema (Seção 2.5 e Exemplo 3.4.2). a) Diferença entre Fantasma e ART. b) Diferença entre Phantom com ruído e ART. c) Diferença entre Fantasma e FBP. d) Diferença entre fantasma com ruído e FBP. e) Diferença entre Fantasma e SVD. f) Diferença entre fantasma com ruído e SVD. 5] Antonio Carlos Pires Carvalho, História da Tomografia Computadorizada, 2007, online: http://www.sociedadeclementeferreira.org.br/images/Historia-da-Tomografia-Computadorizada.pdf. Travessini De Cezaro, Problemas inversos e a matemática da tomografia computadorizada, 2010, minicurso apresentado na 5ª Bienal da SBM.
11] Frank Natterer, The mathematics of computerized tomography (klassieke in toegepaste wiskunde), SIAM: Society for Industrial and Applied Mathematics, 2001.