In the diagonal case, the ordered Ramsey numbers R(S1,n;c) are equal to the Ramsey numbers R(K1,n−1;c) for every n and c, whether n is even or cis odd. Choudum and Ponnusamy [CP02] determined the ordered Ramsey numbers of all ordered star pairs according to the following recursive formulas. Furthermore, we give a lower bound for the ordered Ramsey numbers of ordered stars that have at least one edge collision to the central peak on each side.
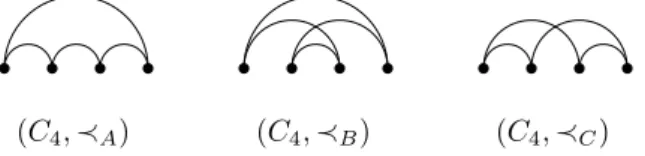
In contrast, we show a family of ordered paths whose ordered Ramsey numbers are linear in the number of vertices. We define the ordered Ramsey number of each of the three orders of C4 from Figure 2. We give a polynomial upper bound for the ordered Ramsey numbers of ordered graphs with bounded degeneracy and chromatic number of bounded interval.
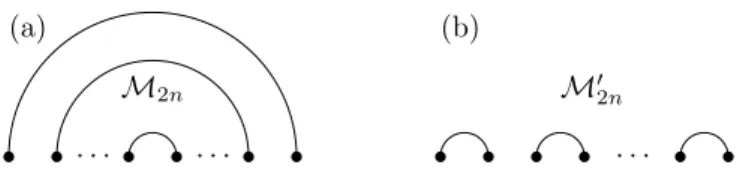
For example, it gives a quasipolynomial upper bound for ordered Ramsey numbers of k-degenerate ordered graphs. Since the intervalchromatic number of any ordered graph at n vertices is maximum, Theorem 15 immediately gives a quasipolynomial upper bound on the ordered Ramsey number of ordered graphs with bounded degeneracy. CFLS14] showed that ordered Ramsey numbers of almost all ordered matching onn vertices satisfy this lower bound.
In particular, we see that every n-vertex graph with maximum degree 1 admits an ordering with the ordered Ramsey number linear in n.
The Erd˝ os–Szekeres Lemma
The Erd˝ os–Szekeres Theorem
A conjecture of Peters and Szekeres
Let ES(k) be the maximum number of N such that there is a red-blue color of K3N with no-gon. If P is a set of points in the plane in general position, then k-tuples of points from P in convex position are in one-to-one correspondence with k-gons in the realizable coloring of K|P3 | taken from P. The proof is computer-aided and we use the Glucose SAT solver [AS13], the winner of the certified UNSAT category in the SAT 2013 competition [BBHJ13].
Although we have found counterexamples to the Peters–Szekeres conjecture for values of k= 7,8,9, we do not have a construction that provides counterexamples to this conjecture for arbitrarily large values of k.
Geometric Ramsey numbers
In a drawing D of a graph G in the plane, the vertices are represented by individual points and each edge is represented by a simple continuous arc connecting the images of the endpoints. The intersection number cr(G) of a graph G is the minimum of cr(D) taken over all drawings Dof G. It is well known and easy to see that any drawing of G that minimizes the intersection number is simple.
According to the well-known conjecture of Hill [Guy60, HH63] (also known as Guy's conjecture), the intersection number of the complete graph Kn at n vertices satisfies cr(Kn) =Z(n), where. By considering more limited classes of drawings, one can derive many variants of the intersection number. We mainly consider three specific classes of drawings and the corresponding variants of the intersection number in this chapter.
A drawing of a graph G in which every edge is represented by an x-monotone curve and no two vertices share the same x-coordinate is called x-monotone (or monotone, for short). The monotone crossing number mon-cr(G) of a graph G is the minimum of cr(D), taken over all monotone drawings Dof G. The rectilinear crossing number cr(G) of a graph G is the minimum number of crossings in a rectilinear drawing of G .
The pseudolinear intersection number cr(G)e of G is the minimum number of intersections in a pseudolinear drawing of G. Every rectilinear drawing of G is x-monotone and pseudolinear, but there are pseudolinear drawings of Kn that cannot be "stretched" into rectilinear drawings . The monotone crossing number was introduced by Valtr [Val05] and recently further studied by Pach and T´oth [PT12], who showed that mon-cr(G)<.
It is known that the pseudolinear number of intersections Kn is asymptotically greater than Z(n): this follows from the lower bound cr(Ke n n4. If we generalize the notion of a simple drawing, we call a drawing of a graph G semisimple if adjacent edges do not intersect, but independent edges can cross more than once. A monotone semisimple odd number of crossings of G (called monotone odd + by Schaefer [Sch14]), denoted by mon-ocr+(G), is the smallest number of pairs of edges that intersect an odd number of times in a monotone semisimple drawing G .
Monotone drawings of K n
Pseudolinear crossing number of K n
We recall that cr(G) and cr(G) denote the pseudolinear and rectilinear crossing numbers, respectively, of a graph G. Both the rectilinear and pseudolinear crossing numbers of Kn have attracted much attention; see the study by 'Abrego, Fern'andez-Merchant and Salazar [AFMS13]. For the pseudolinear crossing number for Kn, the best known lower limit is cr(Ke n)>0.379972 n4.
In his Rectilinear Intersection Number Project, Aichholzer [Aic] published a list of most famous rectilinear drawings of Kn forn≤100 (this list has been recently updated). We make small random changes in an initial pseudolinear drawing D of Kn for small n while keeping track of cr(D). In most of the cases (where n ≥ 42), we get a pseudolinear drawing of Kn with fewer crossings than the currently known upper bounds.
The improvement over the leading constant in cr(Ke n) is derived using a pseudolinear version of the 'Abrego and Fern'andez-Merchant construction [AFM07]. This applies to general graphs, see [HVLnS14] for a construction of graphs where the rectilinear intersection number is strictly larger than the pseudolinear number. In Discrete Probability and Algorithms, Volume 72 of The IMA Volumes in Mathematics and its Applications, pages 111–131, New York, 1995.
In Combinatorics and Computational Geometry, volume 52 of Publications of the Research Institute for Mathematical Sciences, pages 569–575, Cambridge, 2005. Proceedings of the 31st International Symposium on Computational Geometry (SoCG 2015, InternationaleforcedsLIizs.