Análise em conjunta de testes cosmológicos

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA

A

NÁLISE EM

C

ONJUNTA DE

T

ESTES

C

OSMOLÓGICOS

H

S

G

N

(

)

H

S

G

A

NÁLISE EM

C

ONJUNTA DE

T

ESTES

C

OSMOLÓGICOS

Dissertação de Mestrado apresentada ao Programa de

Pós-Graduação em Física do Departamento de Física Teórica e

Exper-imental da Universidade Federal do Rio Grande do Norte como

requisito parcial para a obtenção do grau deMestreem Física.

Orientador: Profa. Dra. Nilza Pires

N

(

)

Com muito carinho aos:

Meus Pais e Irmã

Agradecimentos

•Ao Departamento de Física Teórica e Experimental da Universidade Federal

do Rio Grande do Norte, pela oportunidade de realizar o curso de Mestrado.

•A Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - CAPES,

pelo apóio financeiro concedido.

• A professora Nilza Pires, pela oportunidade, paciência, ajuda, incentivo e

escolha do tema.

• Aos professores do programa da pós graduação em Física (UFRN), Janilo

Santos, Luciano Rodrigues da Silva, Madras Viswanathan Gandhi Mohan, Álvaro Fer-raz e Dory Hélio Aires de L. Anselmo, pelas aulas ministradas e principalmente pela paciência e ajuda.

•Ao professor Rodrigo Fernandes Lira de Holanda (UEPB), pela grande ajuda referente ao teste da fração de massa do gás, Muito Obrigado!

• Ao professor Raimundo Silva Júnior (UFRN), por aceitar em fazer parte da

banca examinadora.

•Aos meu amigos de curso Thiago Rafael da Silva Moura e Tiago de Medeiros

Vieira, pelo apoio e pelas grandes discussões científicas no decorrer dessa caminhada.

•A todos meus companheiros do curso em geral, pela ajuda com as dúvidas e

pelo incentivo.

•A Celina Pinheiro, por toda ajuda dada durante o curso.

Análise Conjunta de Testes Cosmológicos

por

Humberto Scalco Gimenes

Submetida ao Departamento de Física em 01 deAbril de2013, como requisito parcial à obtenção do grau deMestreem Física.

Resumo

Nesta dissertação, uma revisão sobre três modelos cosmológicos não-padrão do tipo Friedmann-Robertson-Walker são apresentados. O modeloωCDM, o gás de Chaplygin

generalizado e o modelo de brana de Dvali-Gabadadze-Porrati (DGP). Apresentamos também, três testes estatísticos utilizados em Cosmologia, cada um envolvendo uma vela padrão diferente. Estes testes têm como objetivo, vincular os diferentes parâme-tros de cada modelo e assim compará-los com os dados observacionais mais atuais. Efetuamos o teste do módulo de distância de Supernovas do tipo Ia, através de 580 Supernovas do Union Compilation 2.1 (2011) [1]. A Fração de massa de aglomerados

de galáxias, onde utilizamos um conjunto de 52 aglomerados observados pelo CHAN-DRA (2009) [2] e a razão CMB/BAO, onde foram utilizados um conjunto de 6 picos de BAO doWiggleZ Dark Energy Survey(2011) [3]. Esses testes foram aplicados para cada

um dos modelos apresentados. Verificamos que individualmente, os testes cosmológi-cos não são bons o suficiente para vincular modelos, criando espaços paramétricosmológi-cos degenerados, necessitando de uma análise em conjunta dos testes para vincular os pa-râmetros. Encontramos que, para o modeloωCDM os melhores ajustes dos parâmetros

são ω = ₋1.10+0−0..0604 eΩM = 0.31+0−0..0103. Enquanto que, para o gás de Chaplyigin gene-ralizado os melhores ajustes sãoα = ₋0.14−+0₀._.05₀₆ eAs = 0.74

+0.02

−_0.03. Para o modelo DGP curvo encontramos ΩRC = 0.15+0−0..0402 e ΩM = 0.25+0−0..0604, enquanto que para o modelo DGP plano encontramosΩM = 0.27+0−0..0802.

Palavras-chave:Análise Conjunta, testes cosmológicos, modelo brama DGP, gás de Chaplygin

generalizado, modeloωCDM, Supernova Ia, módulo de distância, fração de massa de

aglome-rados, razão CMB/BAO.

Global Analysis of Cosmological Tests

by

Humberto Scalco Gimenes

Submitted to theDepartment of PhysicsonApril 01,2013, in par-tial fulfillment of the requirements for the degree of Master in Physics.

Abstract

In this dissertation, a review about three non-standard cosmological models like Friedmann-Robertson-Walker are present. The ωCDM model, the generalized

Cha-plygin gas and the Dvali-Gabadadze-Porrati (DGP) brana model. Also present, three estatistical tests used in Cosmology, each one involving a different stardard candle, in order to link differents parameters for each model and compare them with more recent observational data. We made the Surpernova Ia distance modulus, via 580 Supernovas from Union Compilation 2.1 (2011) [1]. Also the cluster mass fraction test, where we use a set of 52 cluster from CHANDRA (2009) [2] and the CMB/BAO test, where we use a set of 6 BAO peaks from WiggleZ Dark Energy Survey (2011) [3]. We perform these tests for each present models. We found that individually, these cosmological tests are not good enough to link models, showing degenerate parametric spaces, re-quiring a global analysis to link these parameters. We found that for theωCDM model,

the best fit areω=₋1.10+0−0..0406andΩM = 0.31+0−0..0103. Whereas for the generalized Chaply-gin gas, the best fit areα =₋0.14−+0₀._.05₀₆and As = 0.74

+0.02

−_0.03. For curved DGP model, the best fit areΩRC = 0.15+0−0..0402andΩM = 0.25+0−0..0604, whereas for flat DGP model, the best fit areΩM = 0.27+0−0..0802.

Keywords: Global Analysis, cosmological tests, DGP brane Model, generalized Chaplygin

gas,ωCDM Model, Supernova Ia, distance modulus, cluster mass fraction, CMB/BAO ratio.

LISTA DE FIGURAS

4.1 Crista de luz emitida por uma fonte localizada emr1no tempot1e sendo observada por um telescópio na origem do sistema de coordenadas de F.R.W emr0 = 0num dado tempot0. . . 27

4.2 Esquema de um fluxo luminoso emitido por uma estrela na coordenada

r1no tempot1, sendo observado através de um telescópio de áreaAem

r= 0no tempot0. . . 29

5.1 Diagrama de Hubble para SN Ia relativamente próximas, log (V) vs o módulo de distância. . . 36

5.2 Curvas de luz na banda Azul de diferentes SN Ia. . . 37

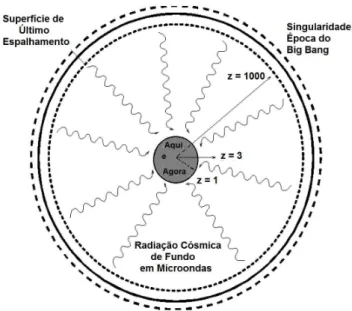
5.3 Esfera imaginária representando a última Superfície de Espalhamento e nossa posição no centro da mesma. . . 46

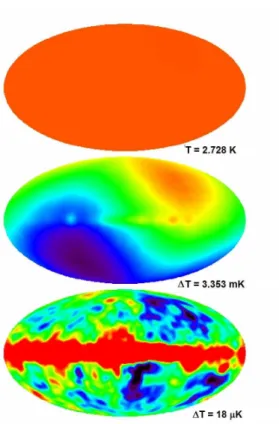
5.4 Anisotropias da RCF, de acordo com suas flutuações de temperatura. . . 47

5.5 Espectro de potências das anisotropias da RCF em termos da escala an-gular. . . 48

6.1 Gráfico mostrando o plano entre o módulo de distância µversus o

red-shiftz para o conjunto de 580 Supernovas do Union Compilation 2.1. . . 53

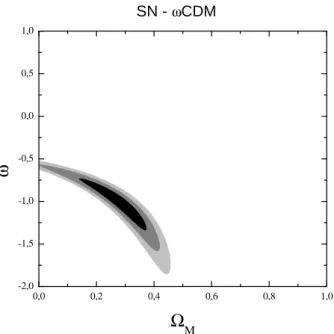
6.2 Plano paramétrico ω - ΩM referente ao teste de Supernova para o

mo-deloωCDM, para 578 graus de liberdade. Os contornos correspondem

as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoω =₋1.01eΩM = 0.28. . . 54

6.3 Plano mostrando a probabilidade P vsΩM para o modelo DGP Plano,

com 579 graus de liberdade, referentes ao teste de Supernovas. O melhor ajuste está localizado no pontoΩM = 0.179comP = 0.333. . . 55

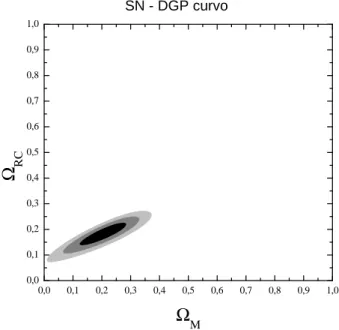
6.4 Plano paramétricoΩRC -ΩM referente ao teste de Supernovas o modelo

DGP curvo, com 578 graus de liberdade. Os contornos correspondem as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoΩRC = 0.18eΩM = 0.20. . . 55

6.5 Plano paramétrico α - As referente ao teste de Supernovas para o Gás

de Chaplygin Plano, com 578 graus de liberdade. Os contornos corres-pondem as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoAs= 0.76eα= 0.02. . . 56

6.6 Plano paramétrico ω - ΩM referente a fração de massa do gás para o

modeloωCDM, para 50 graus de liberdade. Os contornos correspondem

as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoω =₋2.0eΩM = 0.27. . . 61

6.7 Plano paramétrico ΩRC - ΩM referente a fração de massa do gás para o

modelo DGP, com 50 graus de liberdade. Os contornos correspondem as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoΩRC = 0.4eΩM = 0.26. . . 63

6.8 Plano mostrando a probabilidade P vsΩM para o modelo DGP Plano,

com 51 graus de liberdade, referentes ao teste da fração de massa do gás. O melhor ajuste está localizado no pontoΩM = 0.38comP = 0.592. . . . 64

6.9 Plano paramétricoα-Asreferente a fração de massa do gás para o gás de

Chaplygin Generalizado, com 50 graus de liberdade. Os contornos cor-respondem as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoα=₋1.0eAs = 0.93. . . 65

6.10 Plano paramétricoω -ΩM referente ao teste da razão CMB-BAO, para o

modeloωCDM com 4 graus de liberdade. Os contornos correspondem

as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoω =₋1.16eΩM = 0.29. . . 71

6.11 Plano paramétricoΩRC-ΩM referente ao teste da razão CMB-BAO, para

o modelo DGP com 4 graus de liberdade. Os contornos correspondem as curvas de confiança de 68%, 95% e 99% respectivamente. O melhor ajuste está localizado no pontoΩRC = 0.18eΩM = 0.19. . . 71

6.12 Plano mostrando a probabilidade P vsΩM para o modelo DGP Plano,

com 5 graus de liberdade, referentes ao teste da razão CMB-BAO. O melhor ajuste está localizado no pontoΩM = 0.29com1σ= 0.63. . . 72

6.13 Plano paramétrico α-Asreferente ao teste da razão CMB-BAO, para o

gás de Chaplygin Generalizado, com 4 graus de liberdade. Os contornos correspondem as curvas de confiança de 68% e 95% respectivamente. O melhor ajuste está localizado no pontoα= 0.31eAs = 0.83. . . 72

6.14 Plano paramétricoω₋ΩM referente ao teste conjunto de SN Ia (contorno

verde),fgas (contorno azul) e RCB (contorno vermelho), para 636 graus

de liberdade, para o modeloωCDM. Os contornos correspondem as

cur-vas de confiança de 68% 95% e 99% respectivamente. A análise conjunta é representada pelo contorno preto. O melhor ajuste está localizado no pontoω=₋1.10eΩM = 0.31. . . 75

6.15 Gráficos mostrando o desvio padrão de cada um dos parâmetros do mo-deloωCDM com 637 graus de liberdade, paraω (gráfico à esquerda) e

paraΩM (gráfico à direita) com respeito a 1σde confiança,χ2 _{= 616.3. . . 75}

6.16 Plano paramétricoα₋Asreferente ao teste conjunto de SN Ia (contorno

verde),fgas (contorno azul) e RCB (contorno vermelho), para 636 graus

de liberdade, para o gás de Chaplygin Generalizado. Os contornos cor-respondem as curvas de confiança de 68% 95% e 99% respectivamente. A análise conjunta é representada pelo contorno preto. O melhor ajuste está localizado no pontoα=₋0.14eAs = 0.74. . . 76

6.17 Gráficos mostrando o desvio padrão de cada um dos parâmetros do gás de Chaplygin generalizado com 637 graus de liberdade, paraα (gráfico

à esquerda) e paraAs(gráfico à direita) com respeito a 1σ de confiança,

χ2 _{= 612.167. . . 76}

6.18 Plano paramétricoΩRC₋ΩM referente ao teste conjunto de SN Ia

(con-torno verde),fgas (contorno azul) e RCB (contorno vermelho), para 636

graus de liberdade, para o modelo DGP curvo. Os contornos corres-pondem as curvas de confiança de 68% 95% e 99% respectivamente. A análise conjunta é representada pelo contorno preto. O melhor ajuste está localizado nos pontosΩRC = 0.15+0−0..0402eΩM = 0.25+0−0..0604. . . 77

6.19 Gráficos doχ2_{mínimo em função do parâmetroΩM (gráfico à direita) e} do parâmetroΩRC (gráfico à esquerda), para o modelo DGP. O melhor

ajuste foi,ΩM = 0.25+0−0..0604,ΩRC = 0.15+0−0..0402comχ2 = 664.4. . . 77

6.20 No gráfico à esquerda mostra a probabilidade P em função do parâmetroΩM, para o modelo DGP Plano. O melhor ajuste encontrado

foi ΩM = 0.27−+00..0802 com P = 0.797. Enquanto que no gráfico à direita, mostra o desvio padrão deΩM, comχ2 _{= 665.485. . . 78}

LISTA DE TABELAS

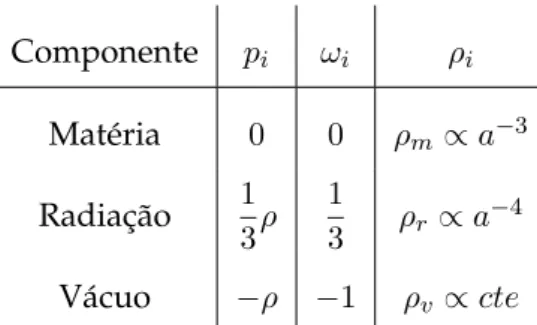
1.1 Tabela com os valores para pressão, parâmetro da equação de estado e densidade correspondentes para cada uma das componentes mais co-nhecidas. . . 9

6.1 Aglomerados com seus respectivos redshiftz, temperaturakTgase fração

de massa observada fgas referente ao modelo ΛCDM, dados obtido de

Ettori et. al (2009) [2]. . . 59

6.2 Tabela resumindo os 6 picos de BAO encontrados, assim como suas taxas do horizonte sonoro com a escala de dilataçãodz. . . 68

6.3 Tabela mostrando o resultado da razão CMB-BAO observada, através de propagação de erro, para cada pico acústico de BAO medidos pelo WiggleZ . . . 70

6.4 Tabela reunindo os resultados para todas as análises feitas referente ao modelo ωCDM. Na primeira coluna encontra-se o teste efetuado, na

segunda coluna encontra-se o χ2 _{mínimo, na terceira coluna tem-se o} número de graus de liberdadeν, na quarta coluna encontra-se oχ2 re-duzido, e nas duas últimas colunas, o best fit para os dois parâmetros do modelo. . . 78

6.5 Tabela reunindo os resultados para todas as análises feitas referente ao gás de Chaplygin generalizado. Na primeira coluna encontra-se o teste efetuado, na segunda coluna encontra-se oχ2_{mínimo, na terceira coluna} tem-se o número de graus de liberdadeν, na quarta coluna encontra-se

oχ2 _{reduzido, e nas duas últimas colunas, o best fit para os dois} parâ-metros do modelo. . . 79

6.6 Tabela reunindo os resultados para todas as análises feitas referente ao modelo DGP curvo. Na primeira coluna encontra-se o teste efetuado, na segunda coluna encontra-se oχ2 _{mínimo, na terceira coluna tem-se} o número de graus de liberdade ν, na quarta coluna encontra-se o χ2 reduzido, e nas duas últimas colunas, o best fit para os dois parâmetros do modelo. . . 79

6.7 Tabela reunindo os resultados para todas as análises feitas referente ao modelo DGP plano. Na primeira coluna encontra-se o teste efetuado, na segunda coluna encontra-se oχ2 _{mínimo, na terceira coluna tem-se} o número de graus de liberdade ν, na quarta coluna encontra-se o χ2 reduzido, e nas duas últimas colunas, o best fit para os dois parâmetros do modelo. . . 79

6.8 Tabela mostrando os valores do χ2 _{mínimo, o χ}2 _{reduzido, o número} de graus de liberdadeν, o número de parâmetros livres do modelod, o

número de amostrasn, a razão do número de amostras pelo número de

parâmetros livresn/d, o valor do AIC e BIC, assim como os valores do

∆AIC e∆BIC respectivamente, para a análise do módulo de distância

de SN. . . 81

6.9 Tabela mostrando os valores do χ2 _{mínimo, o χ}2 _{reduzido, o número} de graus de liberdadeν, o número de parâmetros livres do modelod, o

número de amostrasn, a razão do número de amostras pelo número de parâmetros livresn/d, o valor do AIC e BIC, assim como os valores do

∆AIC e∆BICrespectivamente, para a análise da fração de massa do gás. 81

6.10 Tabela mostrando os valores do χ2 _{mínimo, o χ}2 _{reduzido, o número} de graus de liberdadeν, o número de parâmetros livres do modelod, o

número de amostrasn, a razão do número de amostras pelo número de

parâmetros livresn/d, o valor do AIC e BIC, assim como os valores do

∆AIC e∆BICrespectivamente, para a análise da razão CMB/BAO. . . 82

6.11 Tabela mostrando os valores do χ2 _{mínimo, o χ}2 _{reduzido, o número} de graus de liberdadeν, o número de parâmetros livres do modelod, o

número de amostrasn, a razão do número de amostras pelo número de

parâmetros livresn/d, o valor do AIC e BIC, assim como os valores do

∆AIC e∆BICrespectivamente, para a análise conjunta. . . 82

CONTEÚDO

Introdução 1

1 O Modelo Cosmológico Padrão 4

1.0.1 O Modelo do Big-Bang . . . 6

1.0.2 Universos de Friedmann-Robertson-Walker . . . 7

1.0.3 As Equações de Friedmann . . . 8

2 O ModeloΛCDM 13

2.1 A Constante Cosmológica . . . 13

2.2 A Energia do Vácuo . . . 14

2.3 O Problema da Constante Cosmológica . . . 17

3 Modelos Alternativos aoΛCDM 19

3.1 Parametrizaçãoω . . . 19

3.2 Gás de Chaplygin Generalizado . . . 20

3.3 Branas - DGP . . . 23

4 Cosmologia Observacional 26

4.1 O Redshift Cosmológico . . . 26

4.2 Medidas de Distância . . . 28

4.2.1 A Magnitude Aparente . . . 28

4.2.2 Magnitude Absoluta . . . 30

4.2.3 Luminosidade, Distância Luminosidade e Distância Diâmetro Angular . . . 31

5 Observáveis Padrão 35 5.1 Supernovas do Tipo Ia . . . 35

5.2 Raios-X e a Fração de Massa de Agloremados de Galáxias . . . 37

5.2.1 Luminosidade de Raios-X de Aglomerados de Galáxias . . . 38

5.2.2 A Fração de Massa do Gás . . . 42

5.3 A Radiação Cósmica de Fundo - RCF . . . 45

5.4 Oscilações Acústicas de Bárions - BAO . . . 49

6 Testes Cosmológicos 51 6.1 Teste de Supernovas . . . 51

6.2 Teste da Fração de Massa do Gás . . . 57

6.3 Teste Razão CMB-BAO . . . 67

6.4 Análise Conjunta dos Testes Cosmológicos . . . 74

7 Conclusões e Perspectivas 84 APÊNDICE 87 A Propagação de Incertezas 87 A.1 Fórmula de propagação de incertezas . . . 87

A.2 Algumas fórmulas de propagação . . . 88

Bibliografia. 89

NOTAÇÃO E CONVENÇÕES

•Assinatura da métrica: (₋,+,+,+)

•Índices gregos variam de 0 a 3 e latinos de 1 a 3. Índices repetidos obedecem

a convenção de Einstein.

•Expressões em outros idiomas serão apresentados emitálico.

•A unidade de distância utilizada como padrão nesse trabalho é o megaparsec

(M pc): 1M pc= 3.26_×106 _{anos luz= 3.09×10}22_m.

•RCF é abreviação da Radiação Cósmica de Fundo, assim como CMB é a

abre-viação em inglês da mesma.

•BAO é a abreviação em inglês das Oscilações acústicas de bárions.

•A não ser que seja explicitado o contrário,c=~_{= 1}.

•Constante de Hubble fiducial:H70= 70km/s−1M pc−1

•Constante de Hubble utilizada: H0 = 72±8km/s−1M pc−1

•H0 = 100hkm/s−1M pc−1

•b= 0.874_±0.0023

•ΩB = 0.0437_±0.0098

INTRODUÇÃO

Uma das áreas que mais crescem na Física é a Cosmologia. Ao longo do século XX, foi estabelecida como uma importante área teórica e observacional.

O principal objeto de estudo da Cosmologia é o Universo. Questões como sua origem, sua composição e sua dinâmica formam a crescente base desse ramo da Física Contemporânea.

Entretanto, a cosmologia é ainda uma área em desenvolvimento. Grandes enigmas foram descobertos e ainda não foram respondidos, mas grandes avanços foram e estão sendo realizados na busca da solução desses enigmas.

Para descrever o Universo, modelos cosmológicos são criados. Sua criação é baseada a partir de leis e princípios básicos da Física os quais devem estar de acordo com as observações.

Os modelos cosmológicos mais bem sucedidos, têm como pré-requisito a Re-latividade Geral e o princípio cosmológico, conhecidos como modelos de Friedmann-Robertson-Walker (F.R.W). Estes modelos estão de acordo com a história de formação do Universo, através de dados da nucleossíntese primordial, Radiação Cósmica de Fundo (RCF), Oscilações Acústicas de Bárions (BAO), lentes gravitacionais, fração de bárions em aglomerados de galáxias, etc. Estas características, marcam os modelos chamados de Big-Bang.

2

Recentemente, o Universo começou a expandir aceleradamente. Embora esta aceleração cósmica esteja bem determinada, ninguém conhece ao certo sua natureza, criando uma das questões mais fundamentais a serem respondidas na Cosmologia.

Do ponto de vista relativístico, para o Universo estar acelerado, geralmente é atribuído a existência de uma componente exótica com pressão negativa conhecida como energia escura. Muitos modelos foram criados para tentar explicar essa expan-são, como modelo com constante cosmológicaΛ, modelo de quintessência, gás de

Cha-plygin, etc. Enquanto outros modelos tentam mudar a lei de gravitação, por exemplo, modelos de Brana, F(R).

O principal objetivo desse trabalho, é obter o modelo que mais se adeque às observações, através da análise estatística deχ2 _mínimo.

No primeiro capítulo dessa dissertação, é discutido um pouco da história e da métrica de Friedmann-Robertson-Walker (F.R.W), apresentando os principais funda-mentos de qualquer modelo cosmológico aceitável.

No segundo capítulo, é apresentado com detalhes o modelo padrão em Cos-mologia, o modeloΛCDM, ou modelo com constante cosmológica mais matéria escura

fria. Será apresentado toda a fundamentação desse modelo assim como seu grande problema, o problema da constante cosmológica.

No terceiro capítulo, são descritos três modelos alternativos aoΛCDM que

ten-tam explicar o Universo acelerado. A parametrizaçãoω ou modeloωCDM, o gás de

Chaplygin generalizado e o modelo de Branas DGP. Neste capítulo serão apresenta-dos as principais características de cada modelo, assim como as principais equações e relações que serão utilizadas no capítulo 6 para a execução dos testes.

No capítulo 4, são descritos os principais elementos observacionais, que são peça chave em Cosmologia, o redshift cosmológico e as medidas de distância. Elemen-tos essenciais para vincular modelos em testes cosmológicos.

3

No capítulo 6, são apresentados e analisados os resultados dos testes cos-mológicos de medida de distância de supernova, fração de massa do gás e razão CMB/BAO para cada um dos 3 modelos propostos. Também é feita a análise conjunta dos testes e análise desses resultados.

No capítulo 7, são apresentadas as conclusões e perspectivas desse trabalho.

CAPÍTULO

1

O MODELO COSMOLÓGICO PADRÃO

Desde o início do século passado, a Cosmologia passou por avanços significa-tivos tanto em questões teóricas quanto observacionais, sendo este último mais rele-vante nas últimas duas décadas contribuindo em muito o que conhecemos do universo atualmente.

O modelo padrão da Cosmologia é fundamentado teoricamente na Relativi-dade Geral e o primeiro modelo cosmológico baseado nesta teoria foi proposto por Einstein em 1917 [4]. Einstein, acreditava que o Universo deveria ser estático. Entre-tanto, como a matéria é atrativa, as suas equações de campo mostravam que o seu modelo de universo não seria estático. Assim, ele adicionou um novo termo, que ele chamou constante cosmológicaΛpara contrabalançar qualquer evolução.

No mesmo ano, em 1917, o astrônomo alemão W. de Sitter [5], propôs uma nova solução das equações de campo de Einstein, através de um modelo plano esta-cionário, ignorando a matéria ordinária, cuja a dinâmica é governada por uma cons-tante cosmológica.

Um pouco depois, em 1922, o matemático russo A. Friedmann [6], obteve um novo conjunto de soluções das equações de Einstein sem a necessidade de uma cons-tante cosmológica para sua expansão, este modelo tinha como principal característica ser dinâmico, em relação ao modelo de Einstein [4] que era estático.

Capítulo 1. O Modelo Cosmológico Padrão 5

O modelo padrão, chamado de “Big-Bang” se estabeleceu na primeira metade do século passado, baseado em descobertas observacionais que foram fundamentais.

E. Hubble, em 1929 [7], constatou que as galáxias estavam se distanciando com uma velocidade proporcional à sua distância em relação a nós, ou seja, o universo está em expansão.

Em seguida, em 1948, G. Gamow em colaboração com R. Alpher e H. Bethe [8] mostraram que a abundância dos elementos leves tais como, Hidrogênio e Hélio, podiam ser explicadas através de reações nucleares que ocorreram em um período da vida do universo quando ele deveria ser quente e denso. Essa teoria era coerente com a expansão e também, previa que hoje deveríamos ver os remanescentes dessa radiação térmica.

Mais de uma década depois, em 1965, A. Penzias e R. W. Wilson [9] detectaram uma radiação vinda de todas as direções do espaço equivalente a um espectro de corpo negro da ordem de3Kde temperatura, a chamada Radiação Cósmica de Fundo (RCF). Esta descoberta comprovou que o universo primordial deveria ser quente e denso.

Em 1992, o satélite COBE [10] detectou de maneira conclusiva que o espectro da RCF é de um perfeito corpo negro de temperatura na ordem de2.73K, com

peque-nas flutuações da ordem de10−5 _{que estão relacionadas com as flutuações na matéria,} as sementes das estruturas de matéria existentes no universo.

Em 1998, foi descoberto por dois grupos independentes, o Supernova Cosmo-logy Project[11] eHigh-zSupernova Search Team[12] através de medidas de distância de

Capítulo 1. O Modelo Cosmológico Padrão 6

1.0.1 O Modelo do Big-Bang

A Moderna Cosmologia e o modelo cosmológico nasceram com o advento da Relatividade Geral (RG). Nela, a geometria está relacionada com o conteúdo de matéria via equações de Einstein [13]

Rµν − 1

2gµνR= 8πGTµν , (1.1)

ondegµν é tensor métrico, Rµν é o tensor de Ricci, R o escalar de Ricci, Tµν o tensor

energia-momento,Ga constante gravitacional de Newton.

No Início do século XX, essas equações de campo (1.1) não eram nada triviais, pois, envolviam uma distribuição arbitrária de matéria.

Geralmente quando uma nova teoria é criada, argumentos de simetria são le-vados em consideração para diminuir o número de graus de libedade do sistema a ser estudado [14]. Na época da criação do primeiro modelo cosmológico relativístico, sabia-se pouco a respeito da composição e geometria do universo devido a enorme carência de dados observacionais.

Assim, esses modelos deveriam partir de algum princípio, hoje conhecido como Princípio Cosmológico.

O Princípio Cosmológico, diz que não existe nenhum observador especial, to-dos os pontos são equivalentes e não existem direções especiais. Entretanto, ele não tem fundamentação em qualquer modelo físico ou teoria em particular. Porém, tem sido comprovado como válido em grandes escalas (maiores que150 M pc) através de

Capítulo 1. O Modelo Cosmológico Padrão 7

1.0.2 Universos de Friedmann-Robertson-Walker

Em 1922, Friedmann apresentou uma métrica que, quando usada nas equações de campo de Einstein (1.1), resultaria em um universo homogêneo e isotrópico [6, 15].

dτ2 =₋c2dt2+a2(t)

dr2

1₋Kr2 +r

2_dΩ

. (1.2)

Nesta métrica vemos duas características importantes, a primeira vem do fatorK que

representa a curvatura do espaço. Vemos que independente do valor deK, seja

espa-cialmente fechado,K = +1, aberto,K =₋1, ou plano,K = 0, a curvatura permanece

espacialmente constante em qualquer região do universo fazendo com que toda infor-mação a respeito do campo gravitacional que está contida no tensor métricogµν, seja a

mesma em qualquer ponto, garantindo assim a homogeneidade.

Esta métrica é maximalmente simétrica, garantindo a isotropia. Essas carac-terísticas estão todas associadas às componentes espacias dessa métrica do espaço-tempo, a homogeneidade e a isotropia não ocorrem no eixo temporal. A dedução rigo-rosa da métrica de Friedmann pode ser encontrada em [15, 16].

Uma segunda característica vem do fator de escala a(t), responsável pela

dinâmica da componente espacial da métrica, constituindo uma métrica em coorde-nadas comóveis.

Podemos verificar isso, imaginando uma cadeia de galáxias comóveis, todas próximas, na mesma linha de visão entre nós, onde cada uma dessas galáxias distantes tem suas coordenadas r, θ, φ. Suponha que no mesmo tempo cosmológico t, os ob-servadores em cada galáxia medem a distância até a próxima galáxia, adicionando-se todas essas subdistânciasds=√grrdr, obtém-se,d(r, t).

Logo, a distância própria em um dado tempot, da origem até um objeto comóvel na

coordenada~r, é dada por

d(r, t) =

Z r

0

√_g

rrdr =a(t)

Z r

0

dr

√

Capítulo 1. O Modelo Cosmológico Padrão 8

onde a integral tem uma solução de maneira mais genérica dada por

Z r

0

dr

√

1₋Kr2 =

arc senh(√Kr)

√

K , (1.3)

ou seja,

d(~r, t) =a(t)

        

arc sen(r), K = 1

arc senh(r), K =₋1

r, K = 0

(1.4)

Vemos então que, a distância própria do objeto comóvel até um observador depende da escalaa(t). Isso é uma consequência do Princípio Cosmológico, pois, a

idéia de distância própria só ocorre dessa maneira devido aos observadores que fazem a medida de distância não possuírem um local e direção privilegiada do universo.

1.0.3 As Equações de Friedmann

Para entender toda a dinâmica do Universo, precisamos conhecer a sua métrica e o seu conteúdo energético, ou seja, precisamos encontrar o tensor energia-momento que se adeque ao princípio cosmológico. Supondo o Universo composto por um fluído perfeito, tem-se que o tensor energia-momento para esse fluído é dado por [15, 16]

Tµν = (p+ρ)UµUν+pgµν , (1.5)

onde p é a pressão, ρ é a densidade massa-energia do fluído e Uµ é o vetor

quadri-velocidade do fluído, onde em um referencial comóvel possui apenas componente temporalUµ= (1,0,0,0).

Substituindo a métrica de Friedmann (1.2) e o tensor energia-momento para um fluído perfeito (1.5), nas equações de campo de Einstein (1.1), encontramos as seguintes equações [15, 16]

−2_aK2 −

2 ˙a2

a2 −

¨

a

a =−4πG(ρ−p) (1.6)

3¨a

Capítulo 1. O Modelo Cosmológico Padrão 9

onde o ponto sobre a variável representa uma derivada temporal.

Substituindo a equação (1.7) na (1.6) também encontramos a seguinte relação

˙

a2

a2 +

K a2 =

8πGρ

3 . (1.8)

A equação (1.8) é chamada de equação de Friedmann [15], que dá a dinâmica do universo. Encontra-se também a lei da conservação do energia-momento,Tµν

;ν = 0,

˙

ρ+ 3H(ρ+p) = 0 , (1.9)

ondeHé o parâmetro de Hubble,H = a˙

a.

Para resolver estas equações, precisamos conhecer a equação de estado das diferentes componentes energéticas do universo [15, 17]. De um modo geral, ela é escrita como

pi =ωiρi , (1.10)

ondeωi é o parâmetro da equação de estado de determinada componente energética,

que levada à equação da conservação da energia (1.9) dá a lei de evolução da compo-nente energética. Para o caso deωi constante tem-se

ρi ∝a

−3(1+ωi)

i . (1.11)

Na tabela abaixo, são apresentados os parâmetros da equação de estado e as leis de evolução das componentes mais conhecidas, como, matéria, radiação e vácuo.

Componente pi ωi ρi

Matéria 0 0 ρm ∝a−3

Radiação 1

3ρ 1

3 ρr∝a

−4

Vácuo ₋ρ ₋1 ρv ∝cte

Capítulo 1. O Modelo Cosmológico Padrão 10

Dividindo a equação (1.8) porH2

0 e isolando o termo com curvatura, a equação (1.8) pode ser reescrita para o tempo atual como

K a2

0H02

= 8πG

3H0

ρ0−1 , (1.12)

onde o subíndice 0 indica os valores das componentes para o tempo atual. O termo8πG/3H0 tem dimensão do inverso da densidade, então

K a2

0H02

= ρ0

ρc −

1 , (1.13)

tal que se

K = 0, ρ0 =ρc

K <0, ρ0 < ρc (1.14)

K >0, ρ0 > ρc

Então,ρc é uma densidade crítica,

ρc =

3H2

0

8πG = 1.878×10

−29_h2_g/cm3 _{. (1.15)}

Reescrevendo a equação de Friedmann em termos da densidade crítica para o caso onde o universo possui uma mistura de vácuo, matéria e radiação com curvatura qualquerK, para o chamado modeloΛCDM (do qual falaremos com mais detalhes na

seção seguinte) temos:

˙

a2

a2 +

K a2 =H

2 0

"

ρv0

ρc

+ ρm0

ρc

a a0

−3

+ρr0

ρc

a a0

−4#

(1.16)

Fazendo

ρv0

ρc

= ΩV; ρm0

ρc

= ΩM; ρr0

ρc

= ΩR; ₋ K

a2 0H02

= ΩK

Capítulo 1. O Modelo Cosmológico Padrão 11

Então, em termos dos parâmetros de densidade e do redshift, a equação de Friedmann (1.16) fica

H2_(z)

H2 0

= [ΩV + ΩK(1 +z)2+ ΩM(1 +z)3+ ΩR(1 +z)4] . (1.17)

Para o tempo atual, z = 0, encontramos a relação de normalização entre os

parâmetros de densidade das componentes

1 = ΩV + ΩK+ ΩM + ΩR . (1.18)

De modo geral, a equação de Friedmann pode ser reescrita como

˙

a2

a2 =H 2

0E , (1.19)

ondeEé a soma dos parâmetros de densidade em um dado tempot.

Por exemplo, para o modelo ΛCDM com curvatura e radiação, o termoE da equação de Friedmann (1.19) é o termo entre os colchetes da equação (1.17).

A integração desta equação dá a idade do universo em um tempot,

Z t

0

dt=

Z a

0

da H0aE1/2

, (1.20)

dividindo o numerador e o denominador do lado direito pora0 (fator de escala hoje),

tem-se _Z

t

0

dt =

Z a

0

(da/a0)(a/a0H0E1/2) . (1.21)

Reescrevendo o integrando da direita em termos do redshiftz =a0/a+ 1, encontramos a idade do universo num dado redshift como,

t(z) =

Z ∞

z

dz H0(1 +z)E1/2

. (1.22)

Para o tempo atual,z = 0, tem-se a idade do universo hoje

t0 = Z ∞

0

dz H0(1 +z)E1/2

Capítulo 1. O Modelo Cosmológico Padrão 12

Como a matéria é atrativa, achava-se que o universo estava expandindo desacelerada-mente, e essa desaceleração era medida pelo parâmetro de desacaleração

q(a) =₋¨aa ˙

a2 ; (1.24)

em termos do redshift, o parâmetro de desaceleraçãoq(z)é dado por

q(z) = (1 +z)

H dH

dz −1 . (1.25)

O parâmetro de desaceleração pode ser relacionado com o conteúdo energético do Universo atual. Usando a equação (1.7), pode-se reescrever o parâmetro de desace-leração para o tempo presente como:

q0H02 =

4πG

3 (ρ0+ 3p0) , (1.26)

ou

q0 =

1 2

(ρ0+ 3p0)

ρc

CAPÍTULO

2

O MODELO

Λ

CDM

2.1 A Constante Cosmológica

A origem da constante cosmológica se deve a Albert Einstein em 1917. Eins-tein, aplicou sua equação de campo da Relatividade Geral ao seu modelo do Universo. Este modelo, era composto apenas por matéria gravitante, estático e fechado (ou seja, de simetria esférica) [4].

Devido a natureza atrativa da gravidade, pois a inércia do universo seria ge-rada pela matéria que a preenche, o universo o qual Einstein inicialmente imaginou colapsaria; para evitar esse colapso, Einstein, introduziu arbitrariamente uma cons-tante Λ atrelada ao tensor métrico no lado esquerdo da equação de campo. A esta

constante foi dada o nome de constante cosmológica

Rµν − 1

2Rgµν+ Λgµν = 8πGTµν. (2.1)

Mesmo com a adição dessa constante, cujo valor e a natureza física Einstein não sabia, o modelo do universo dele se mostrou instável [15].

Pouco depois, em 1922 e 1924, Friedmann apresentou em dois trabalhos fun-damentais [6, 18], uma métrica homogênea e isotrópica (obedecendo o princípio cos-mológico) que nas equações do campo de Einstein resultava em um universo dinâmico

Capítulo 2. O ModeloΛCDM 14

sem haver necessidade de uma constante cosmológica.

Apesar de ter sido abandonada por Einstein, outros cosmológos como Edding-ton, reivindicaram-na, pois ela resolveria o problema da idade do universo, quando a escala de tempo de Hubble dava aproximadamente 2 bilhões de anos (correspon-dente ao valor deH0 ≈ 500 km/s−1M pc−1 encontrados por Hubble naquela época). Esta idade era menor que a da própria Terra. Entretanto, logo depois devido a medi-das mais precisas da constante de Hubble, a constante cosmológica Λ novamente foi

descartada.

Em 1967, ela foi novamente revivida para explicar a aparente concentração de quasares em redshiftz _≈ 2; contudo, com o aumento de mais dados observacionais o

termoΛnovamente foi descartado [19].

Em 1968, Zel´dovich [20] trouxe mais uma vez ao cenário universal a constante cosmológica, dessa vez, associando-a a uma densidade de energia do vácuo, ou seja, agora, o termo cosmológico muda para o lado direito da equação de campo de Einstein e torna-se parte do tensor energia-momento. Interpretada como sendo a energia do campo de vácuo, ela hoje faz parte do chamado modeloΛCDM.

2.2 A Energia do Vácuo

Para entendermos como a constante cosmológica pode ser interpretada como sendo a energia do campo de vácuo, precisamos conhecer a equação de estado do vácuo.

A Relatividade Geral não indica o tamanho de Λ, enquanto que a física de

partículas permite considerar a escala de diferentes constituições durante a evolução do universo.

Um fluído perfeito é definido como um meio para qual em todos os pontos exista um sistema de referencial inercial cartesiano, sem viscosidade.

De acordo com a Relatividade Especial, o vácuo, deve ser invariante via trans-formação de Lorentz. Então, seja um referencialS′ com seu respectivo tensor energia-momento T′

Capítulo 2. O ModeloΛCDM 15

Temos que para o referencialS′_:

T′

µν = (ρ

′

+p′

)U′

µU

′

ν+p

′

ηµν , (2.2)

ondeU′

µ= (1,0,0,0).

Para o referencialS, fazendo a transformação de Lorentz temos

Tµν = (ρ+p)UµUν+pηµν , (2.3)

ondeηµν = (−1,1,1,1)é a métrica de Minkowski,ρep são a densidade de energia e

a pressão respectivamente, eUµo vetor quadri-velocidade do fluído perfeito

(transfor-mação de Lorentz para o observador que se move com velocidade~v com relação ao

referencialS′):

Uµ= (γ, γ~v); γ = 1

r

1₋ v

2

c2

. (2.4)

Com essa relação podemos encontrar a componente comóvel do tensor energia-momento, onde em um referencial sob Transformação de Lorentz temos

T00= (ρ+p)U0U0+pη00 (2.5)

T00 = (ρ+p)γ2−p

T00=

ρ+pv2_/c2

1₋v2_/c2 . (2.6)

Para ser invariante precisamos que a componente do tensor energia-momento correspondente não mude do referencial original S′ para o referencial sob transfor-mação de LorentzS,T′

00=T00:

T′ 00 = (ρ

′

+p′

)₋p′

=ρ′

, (2.7)

que igualada a equação (2.5),

T00=

ρ+pv2_/c2

1₋v2_/c2

ρ′

−ρ′v 2

c2 =ρ+p

v2

Capítulo 2. O ModeloΛCDM 16

Donde (tirando o índice ’ e pondo o subíndicevac, significando o vácuo):

pvac=−ρvac , (2.9)

ou seja, o tensor energia-momento do vácuo,Tµν

vac =ρvacηµν. Pela lei da conservação da

energia, o gradiente do tensor energia-momento do vácuo deve ser nuloTµν

;ν = 0,

∂ρvac

∂xν η µν_+ρ

vac

∂ηµν

∂xν = 0 .

Como a métrica de Minkoski não varia, a segunda derivada anula-se, restando então

∂ρ

∂xν = 0 ,

Logo,ρvacé constante (como já indicado na equação (2.8),ρ′ =ρ).

Considerando o tensor energia-momento Tµν composto por um termo do

vácuo e um termo de matéria, temos

Rµν − 1

2gµνR= 8πGT

M

µν + 8πGρVgµν , (2.10)

logo, o efeito de uma energia do vácuo é equivalente a equação (2.1)

Rµν − 1

2gµνR= 8πGTµν+ Λgµν ,

onde a densidade de energia do vácuo é escrita comoρvac = Λ

Capítulo 2. O ModeloΛCDM 17

2.3 O Problema da Constante Cosmológica

Na Relatividade Geral a constante cosmológica é um parâmetro livre, pos-suindo dimensão de comprimento L−2 _{(enquanto que a densidade ρ}

Λ tem unidade de energia por volume) ou seja, do ponto de vista relativístico,Λ, seria simplesmente uma constante da natureza que deveria ser determinada experimentalmente.

Como vimos na seção anterior, pode-se, relacionar a energia do vácuo com a constante cosmológica. Do ponto de vista da mecânia clássica, ou seja, física não-relativística, a energia do vácuo é ignorada, pois as partículas são tratadas classica-mente, possuindo energia total E = T +V, onde T é a energia cinética da partícula

envolta de uma energia potencialV. A força exercida em cada partícula é dada pelo

gradiente do potencialV. Logo, podemos adicionar uma constante arbitrária ao

po-tencial sem risco de alterar o movimento. Geralmente escolhemos esta constante para que o mínimo do potencialV seja nulo. Com esse raciocínio em mente, podemos dizer

que classicamente a energia de uma partícula em seu estado de vácuo é nula [21].

Se olharmos a energia do vácuo do ponto de vista quântico, ela passa a ser relevante. Considere um oscilador harmônico quântico simples de frequênciaω, ou

seja, uma partícula de massammovendo-se em um poço de potencial unidimensional

V(X) = 1/2ω2_x2_{. Nós não podemos escolher um potencial tal qualV(0) = 0, devido}

ao princípio da incerteza, que nos proíbe isolar uma partícula com energia cinética e potencial nula simultaneamente.

Para o oscilador a energia mínima é dada por E0 = 1/2~ω, donde para a mecânica quântica, a energia do vácuo seria a energia de ponto zero do oscilador. Pode-se imaginar, o universo como uma composição de infinitos osciladores quânti-cos contendo todas as frequências possíveis, onde as energias de ponto zero de cada oscilador estaria associada com as flutuações de vácuo (que em altas energias pode ser tornar cordas ou algo mais) [17].

Então, a energia do vácuo no estado fundamentalE0seria dada por

E0 = X

j 1

Capítulo 2. O ModeloΛCDM 18

onde a soma é sobre todos os modos possíveis do campo, isto é, sobre todos os vetores de onda~k. Podemos fazer a soma colocando os osciladores em uma caixa de volume

L3_{. Se impomos condições de contorno periódicas, forçando o comprimento de onda} (digamos, na i-ésima direção) para ser λi = L/ni, para algum inteiro ni, desde que

ki = 2π/λi, então existem dkiL/2π valores discretos de ki no intervalo (ki, ki +dki).

Portanto, a equação (2.11) torna-se

E0 =

1

2~L

3Z d3~k

(2π)3ωk , (2.12)

ondeωk=

p

k2_+m2_/~2_.

Tendendo L ao infinito, vemos que a energia resultante é infinita. Esta di-vergência surge através da combinação de infinitos modos de vibração com compri-mentos de onda muito pequeno, podendo gerar o erro, pois não se conhece o que real-mente acontece nessas escalas. Devido a isso, introduz-se um comprimento de onda mínimo, ou seja, uma energia de corte,kmax ≫ m/~. Ao substituir esse ponto de corte

na expressão (2.12) e dividindo ambos os lados porL3 _{encontramos que a densidade} de energia do vácuoρvacé dada por

ρvac ≡

E0

L3 =~

k4

max

16π2 . (2.13)

Portanto, considerando o comprimento de onda kmax contido na escala de

Planck, com energia da ordem de E0 ≈ 1019GeV encontramos o seguinte valor da densidade de energia do vácuoρvac[22, 17]

ρvac ≈10112erg/cm3 . (2.14)

Observacionalmente, o valor encontrado para a energia do vácuo ρobs

vac é dada

por

ρobs_vac≈10−8_erg/cm3 _{. (2.15)}

CAPÍTULO

3

MODELOS ALTERNATIVOS AO

Λ

CDM

Após a descoberta da expansão acelerada do univero, o modeloΛCDM passou a ter grande sucesso, baseado principalmente nas estimativas de medida de distância de Supernovas do tipo Ia, fração de massa de aglomerados de galáxias, oscilação acús-ticas de bárions, radiação cósmica de fundo, entre outros.

Porém, devido ao problema da constante cosmológica, vários outros modelos foram propostos para tentar explicar a expansão acelerada.

3.1 Parametrização

ω

O modelo mais simples além doΛCDM, é o modelo cuja equação de estado é

da forma:

p=ωρ , (3.1)

ondeωé um parâmetro constanteω <₋1/31[23, 24, 25, 26]. 1_{Substituindo a equação (3.1) na equação (1.7), temos3¨a/a=}

−4πG(3ω+ 1)ρque paraa >¨ 0, nos dá3ω+ 1<0

ouω <−1/3.

Capítulo 3. Modelos Alternativos aoΛCDM 20

Da equação da conservação da energia (1.9), encontramos a equação da evolução da componente de energia escuraρX,

˙

ρX + 3 ˙a

a (1 +ω)ρX = 0 , (3.2)

integrando,

ρX ∝a

−3(1+ω) _{. (3.3)}

Para um universo com energia escura parametrizada por ω, mais matéria

es-cura fria, curvatura e radiação, a equação de Friedmann (ou o pâmetro de Hubble) fica

H2(z) = H₀2[ΩX(1 +z)3(1+ω)+ ΩK(1 +z)2 + ΩM(1 +z)3+ ΩR(1 +z)4] . (3.4)

Escrevendo esta equação paraz = 0, encontramos a relação de normalização

1 = ΩX + ΩK + ΩM + ΩR , (3.5)

que mostra que um dos parâmetros é uma combinação linear dos outros. No caso em queω < ₋1, tem-se o regime chamadoPhantom Energyou Energia Fantasma [25].

Neste regime, o universo seria tão acelerado que em um dado futuro remoto, nem os átomos permaneceriam ligados, levando o universo ao chamadoBig-Rip[27].

3.2 Gás de Chaplygin Generalizado

Proposto inicialmente pelo físico russo Chaplygin em 1904 [28], para descrever um processo aerodinâmico adiabático. Este processo também é um meio alternativo em relação ao modeloΛCDM. Neste modelo, o setor escuro é representado por uma

única componente exótica, a qual tem a seguinte equação de estado [29]

pCg =−

A ρα Cg

, (3.6)

Capítulo 3. Modelos Alternativos aoΛCDM 21

Esta expressão é um caso mais generalizado do modelo proposto por Bilic´ et. al (2002) [30], onde originalmente seriaα = 1. Para α = 0 o modelo reduz-se aoΛCDM. Este

modelo é chamado de gás de Chaplygin generalizado.

Este gás tipo Chaplygin, apresenta dois comportamentos distintos de acordo com a época do universo. Em altos redshifts ele se comporta como matéria e em baixos redshifts se comporta como um fluído que acelera o universo. Vamos então, encontrar a equação da evolução de uma componente energética tipo gás de Chaplygin.

Pela lei da conservação da energia (1.9), temos a seguinte relação

˙

ρ+ 3a˙

a(p+ρ) = 0 .

Substituindo (3.6) na expressão acima, encontramos:

dρ dt + 3

˙

a a

−_ρAα +ρ

= 0 ,

Z ρ0

ρ

dρ

ρα

ρα+1_−A

=₋

Z a0

a

3da

a ,

logo

ρCg =

(ρα₀+1₋A)a0

a

3(α+1)

+A

1/1+α

,

Que pode ser reorganizada da seguinte forma:

ρCg =

A+Ba0 a

3(α+1)1/1+α

, (3.7)

ondeB = (ρα₀+1₋A). Podemos notar mais claramente as duas fases que o gás passa

ao longo da história temporal com o auxílio dessa última equação. Quando a _→ 0

encontramos que a densidade de energia do gás é proporcional à

ρCg(a →0)∝a−3 , (3.8)

ou seja, comportando-se como matéria não relativística, enquanto que para a _{→ ∞}

encontramos

ρCg(a_{→ ∞})_∝a−3(α+1)

Capítulo 3. Modelos Alternativos aoΛCDM 22

comportando-se como uma componente escura de pressão negativa.

Fazendo algumas manipulações algébricas, podemos encontrar uma expressão mais enxuta para a densidade de energia do gás de Chaplygin deixando em função de um novo termo

ρCg =ρ0Cg

"

As+

a a0

−3(1+α)

{1₋As}

#1/1+α

, (3.10)

ondeAs =A/ρα0Cg+1é uma quantidade relacionada com a velocidade adiabática atual do

som do gás de Chaplygin,v2

s =δP(z = 0)/δρc(z = 0) =αA/ρα0Cg+1.

Podemos encontrar a equação de Friedmann equivalente a este modelo, con-siderando o universo composto de matéria bariônica, radiação e esta componente exótica do gás de Chaplygin

˙

a2

a2 +

K a2 =

8πG

3 (ρB+ρr+ρCg) (3.11)

comρB =ρ0B

a a0

−3

;ρr =ρ0r

a a0

−4

;ρCg =ρ0Cg

"

As+

a a0

−3(1+α)

{1₋As}

#1/1+α

.

Substituindo estas expressões na equação (3.11), encontramos a equação de Friedmann para o modelo de gás de Chaplygin generalizado

H2 =H₀2

( ΩB a a0 −₃ + Ωr a a0 −₄ + ΩCg "

As+ (1−As)

a a0

−_3(1+α)#)1/1+α

.

(3.12)

Para o tempo atuala0 =a, encontramos a seguinte condição de normalização

Capítulo 3. Modelos Alternativos aoΛCDM 23

3.3 Branas - DGP

Outra alternativa para contornar os problemas associados ao modelo padrão, é considerar a mudança da teoria da gravidade, como por exemplo, o modelo de branas. Neste modelo, nosso universo 4-dimensional seria uma superfície ou uma brana, parametrizada pelas coordenadasxµ_{, imersa (definida pelas coordenadas X}A_(xµ_{) do}

volume da brana) num espaço-tempo (tipo Minkowski) de dimensão mais alta. No qual, somente a gravidade pode se propagar, enquanto as demais componentes ener-géticas ficam confinadas na brana. Neste trabalho, será abordado apenas um modelo de Brana em particular, o modelo Dvali-Gabadadze-Porrati, DGP (Dvali et al. 2000) [31].

O modelo DGP é caracterizado por uma brana 3D embutida em um espaço 5D plano do tipo Minkowski, cuja a ação de Einstein-HilbertSEH é dada por [31, 32]:

SEH =

M3 (5)

2

Z

d5X

q

|g(5)_|dR(5) _{, (3.14)}

ondeM(5) é a massa de Planck reduzida em 5D. A métrica 5D gab(5) induz através da

brana com coordenadasXA_(xµ_{)uma métricag}

µν, chamada de métrica induzida, cuja

definição é dada por

gµν =g(5)ab∂µXA∂νXB . (3.15)

Nas equações acima, o índice(5)está relacionado com quantidades em 5D, necessário

para diferenciar as quantidades análogas em 4D, que dependem somente da métrica induzida.

Para o modelo DGP, a ação gravitacional de Einstein-Hilbert (3.14), possui um termo adicionalSeh dado por [31]

Seh =

M2 (4)

2

Z

brana

d4Xp_|g_|R . (3.16)

Capítulo 3. Modelos Alternativos aoΛCDM 24

Para uma brana embutida nesse espaço 5D, com uma ação igual a soma das ações (3.14) com a (3.16) Dvali et. al [31] mostrou que, para fontes pontuais estáticas em pequenas distâncias na brana, são obedecidas a lei da gravitação de Newton usual, ou seja, evoluem com o inverso do quadrado da distância1/r2_{. Para distâncias maiores, a} influência do escoamento do campo gravitacional torna-se notável e as fontes pontuais na brana, obedecem uma evolução do inverso do cubo da distância1/r3_{. A escala que} separa esses dois regimes, é chamada de escala de cruzamentorc, dada por

rc =

M2 (4)

2M3

(5)

. (3.17)

A equação de Friedmman para este modelo de dimensão extra é dada por [33]

H2+ k

a2 = "s

ρ

3M2 +

1 4r2

c

+ 1

2rc

#2

, (3.18)

onde H = ˙a/a, M a massa de Planck (reduzida), M = p~_c/8πG, _rc é a escala de crossover definida por (3.17) ek = 0,_±1a constante de curvatura.

Dividindo ambos os lados da equação (3.18) porH2 0, H2 H2 0 + k a2 0H02

a2 0 a2 = "s ρ

3M2_H2

0

+ 1

4r2

cH02

+ 1

2rcH0 #2

. (3.19)

A massa de Planck (reduzida) é dada porM =p~_c/8πG, então

1

3M2_H2

0

= 8πG

3H2

0~c

= 1

ρc

, (3.20)

fazendo~_{=c= 1}, tem-se

H2

H2 0

+ k

a2 0H02

a2 0 a2 = "s ρ ρc + 1

4r2

cH02

+ 1

2rcH02 #2

, (3.21)

definindo os seguinte parâmetros de densidade,

ΩM ≡

ρ ρc

= ρm0

ρc ∝

(1 +z)3 , (3.22)

ΩK _{≡ −} K

H2 0a20

Capítulo 3. Modelos Alternativos aoΛCDM 25

Ωrc_≡ 1

4r2

cH02

. (3.24)

tem-se

H2(z) =H₀2

ΩK(1 +z)2+pΩrc+pΩrc+ ΩM(1 +z)32

, (3.25)

quanto que para o modelo planoK = 0temos

H2(z) =H₀2pΩrc+pΩrc+ ΩM(1 +z)32 _{. (3.26)}

Para o tempo prestentez = 0, encontramos a seguinte relação de normalização

1 = ΩK+ [pΩrc+pΩrc+ Ωm]2 . (3.27)

Enquanto que para o modelo plano a equação de normalização reduz-se a

Ωrc= (1−ΩM)

2

4 . (3.28)

CAPÍTULO

4

COSMOLOGIA OBSERVACIONAL

4.1 O Redshift Cosmológico

Como já foi comentado anteriormente, em 1929, Edwin P. Hubble descobriu que o Universo está em expansão. Ele observou que, exceto para um grupo de galáxias, o Grupo Local, as outras galáxias têm seu espectro deslocado para o vermelho, que usualmente é chamado deredshiftz [34], dado por

z = λ1−λ0

λ0

, (4.1)

ondeλ1 é o comprimento de onda dos fótons quando saem da fonte e λ0 é o compri-mento de onda observado desse fóton quando ele chega no telescópio. Caso, z < 0,

tem-se o deslocamento para o azul (blueshift).

O fator de escala a(t) vinda da métrica de FRW (1.2) está relacionado com o redshift.

Seja o observador (telescópio) na origem das coordenadas de F.R.W (r = 0), e

uma fonte luminosa distante, situada na coordenada radialr1. O raio de luz obedece a geodésica nula,

dτ2 = 0 =₋c2dt2+a2 dr

2

1₋kr2 , (4.2)

Capítulo 4. Cosmologia Observacional 27

ou seja,

cdt a =±

dr

√

1₋kr2 , (4.3)

como a luz vem em nossa direção (sentido contrário de crescimento da coordenadar),

devemos escolher um sinal negativo. Portanto, se uma crista de onda deixa a fonte na coordenada comóvelr1 no tempot1, e chega na origem (nós) emr = 0, no tempo posteriort0, conforme esquema mostrado na figura abaixo, tem-se:

Figura4.1: Crista de luz emitida por uma fonte localizada em r1 no tempo t1 e sendo

observada por um telescópio na origem do sistema de coordenadas de F.R.W emr0 = 0

num dado tempot0.

c

Z t0

t1 dt a(t) =−

Z 0

r1

dr

√

1₋Kr2 .

Façamos, _Z

r1

0

dr

√

1₋Kr2 =f(r1) . (4.4)

A próxima crista de onda deixa r1 no tempo t1 +δt1 e chega aqui no tempo

t0+δt0, ou seja,

c

Z t0+δt0

t1+δt1 dt

a(t) =f(r1) . (4.5)

Subtraindo equação (4.4) de (4.5) e observando que a(t) muda muito pouco durante

um intervalo de tempo (período) da ordem de 10−14_{s, típico de um sinal luminoso,} encontramos que:

Z t0

t1 dt a(t) −

Z t0+δt0

t1+δt1 dt

a(t) = 0 , (4.6)

ou

δt0

a(t0)

= δt1

a(t1)

Capítulo 4. Cosmologia Observacional 28

Como os intervalos de tempo estão relacionados com o envio de cristas de ondas subse-quentes temos que, a frequência emitida éν1 =

1

δt1

e a frequência observada éν0 =

1

δt0 , com isso temos:

δt0

δt1

= ν1

ν0

= a(t0)

a(t1)

, (4.8)

como

z = λ1−λ0

λ0

= ν1−ν0

ν0

= ν1

ν0 −

1 , (4.9)

então

1 +z = a(t0)

a(t1)

ou z = a(t0)

a(t1) −

1 . (4.10)

Logo, sea(t)aumenta, tem-se um redshiftz. Se, de modo contrário, a(t)estiver

dimi-nuindo, entãoz seria negativo.

4.2 Medidas de Distância

4.2.1 A Magnitude Aparente

A luminosidade absolutaL, é a quantidade total de energia radiante emitida

por uma estrela em cada segundo, ou seja, é a potência emitida pela estrela. A lu-minosidade absoluta, náo é um observável direto, sendo necessário relacioná-la com outras grandezas físicas.

Quando observamos uma estrela via um telescópio, conseguimos apenas ob-servar uma fração de toda a potência luminosa emitida. A quantidade de energia que atravessa cada metro quadrado, de uma esfera imaginária de raio igual à distância da estrela até o telescópio, estando a esfera centrada na estrela, é conhecida como lumi-nosidade aparentelou brilho aparente.

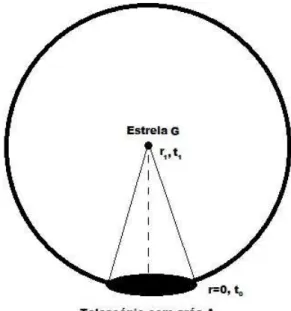
Suponha que uma fonte luminosa G (uma estrela, por exemplo), emita luz de forma isotrópica. Quando a luz dessa fonte nos alcança, estará distribuída uniformi-mente por uma esfera de raior1, centrada na estrela G, ver esquema na figura 4.2.

Capítulo 4. Cosmologia Observacional 29

Figura4.2: Esquema de um fluxo luminoso emitido por uma estrela na coordenadar1no

tempot1, sendo observado através de um telescópio de áreaAemr = 0no tempot0.

unidade de área é dada por

l = P

A = L

4πr2 1

, (4.11)

ondeLé a luminosidade absoluta.

No espaço euclideano, a luminosidade aparente de uma fonte em repouso à uma distânciadLé

l = L 4πd2

L

, (4.12)

ondedLé chamado de distância luminosidade.

Normalmente, o fluxo aparente F é expresso em termos de magnitude

aparentem, que por definição é dada por:

m =₋2.5log F +C , (4.13)

ondeCé uma constante.

Há 2000 anos, o grego Hiparcus (160-125 A.C), dividiu as estrelas visíveis a olho nú, de acordo com seu brilho aparente. Ele atribuiu magnitude 1 à mais brilhante e 6 às mais fracas.

Capítulo 4. Cosmologia Observacional 30

na percepção do olho humano, era logarítimico, e que o fluxoF1correspondente à uma estrela de primeira magnitude (m= 1), era 100 vezes mais brilhantes que o fluxoF6de uma estrela de magnitude (m= 6), tal que

F1 = 100F6, ∆m= 5 , (4.14)

onde

m1 =C log F1 , (4.15)

m6 =C log F6 , (4.16)

então temos

m6−m1 =C log

F6

F1

,

5 =C log F6

100F6

=C log10−2 _,

C =₋2.5 .

Logo, a diferença entre duas magnitudes quaisquer é dada por

m2 −m1 =−2.5log

F2

F1

. (4.17)

A constante C define o ponto zero da escala de magnitudes.

4.2.2 Magnitude Absoluta

Como vimos na seção anterior, podemos relacionar a magnitude aparente de um astro com seu brilho intríseco. O fluxo aparente é dado por,

F =l = L

4πr2 ,

onde L é a luminosidade absoluta, l a luminosidade aparente e r a

Capítulo 4. Cosmologia Observacional 31

m=₋2.5log L

4πr2 +C ,

vemos que a magnitude aparente depende da luminosidade da estrela e da sua distân-cia até nós. Então, a luminosidade pode ser expressa em termos de uma magnitude absoluta, M. A magnitude absoluta é a magnitude teórica que a estrela teria se

es-tivesse a10pcde nós

M =₋2.5log L

4π(102₎+C ,

ou

M =₋2.5log L

4π + 5 +C .

A magnitude aparentemé relacionada com a magnitude absolutaM, através do

Mó-dulo de distânciam₋M.

µ=m₋M =₋2.5log L

4πd2

L

+C+ 2.5log L

4π −5−C = 5log dL−5 . (4.18)

Esta última expressão mostra o módulo de distância, em escala depc. Também é

co-mum encontrar em distância deM pc, onde o módulo de distância é dado por

µ=m₋M = 5log dL+ 25 . (4.19)

4.2.3 Luminosidade, Distância Luminosidade e Distância Diâmetro Angular

Vimos a relação entre a luminosidade aparentelde uma fonte de luminosidade

absolutaL cuja sua distânciadL é dada pela equação (4.12) porém, para z > 0.1 esta

relação modifica-se devido a expansão.

No tempo t0 no qual a luz alcança o telescópio de área A, a área própria de uma esfera desenhada ao redor de um objeto luminoso, passando pelo telescópio é dada pela métrica de F.R.W como:

Atelesc= 4πr12a2(t0) . (4.20)

A fração de luz recebida por um telescópio é dada por:

F = A

Atelesc

= A

4πr2 1a2(t0)

Capítulo 4. Cosmologia Observacional 32

então, a equação (4.12) modifica-se, poisdLmuda:

l= L

4πr2 1a2(t0)

. (4.22)

A taxa de chegada dos fótons individualmente é menor que a taxa daqueles emitidos pela fonte por um fator que é igual ao redshift

a(t1)

a(t0)

= 1

1 +z , (4.23)

a energia dos fótons individuais recebidoshν0no telescópio, é menor que a energiahν1 quando eles são emitidos pelo mesmo fator de redshift (4.10).

Como a luminosidade aparente depende da potênciaP e da área temos que:

l = P

A =

1

A

∆ER

δt0

, (4.24)

onde ∆E é a energia emitida pela fonte que chega numa área A redshiftada, com a

anergia emitida pela fonte no intervaloδt1

∆ER=

A

4πa2_(t 0)r12

∆Ea(t1) a(t0)

, (4.25)

substituindo todas essas expressões na equação (4.24):

l = 1

A A

4πa2_(t 0)r21

∆E

δt0

a(t1)

a(t0)

,

l = 1

4πa2_(t 0)r21

Lδt1 δt0

a(t1)

a(t0)

,

como δt1

δt0

= a(t1)

a(t0)

temos:

l = L

4πa2_(t 0)r21

a(t1)

a(t0) 2

, (4.26)

l = L

4πa2_(t 0)r21

1

(1 +z)2 . (4.27)

Comparando com a expressão (4.12) temos que:

Capítulo 4. Cosmologia Observacional 33

esta distânciadLé a distância luminosidade não euclideana.

Partindo da geodésica da luz, ou

−

Z 0

r1

dr

√

1₋Kr2 =c

Z a0

a

dt

a , (4.29)

a integral do lado esquerdo é,

Z r1

0

dr

√

1₋Kr2 =

arc sen√Kr1

√

K (4.30)

e a integral do lado direito pode ser reescrita como

c

Z a0

a

dt a =c

Z z

0

dz a0H(z)

, (4.31)

ondez =a0/a+ 1eH(z)é o parâmetro de Hubble. Igualando (4.30) com (4.31)

arc sen√Kr1

√

K =c

Z z

0

dz a0H(z)

(4.32)

ou

r1 =

1 √ Ksen _√ Kc Z z 0 dz a0H(z)

, (4.33)

ondez é o redshift do objeto em r1. Substituindo a equação (4.33) na equação (4.28), usandoΩK = ₋K/(a2

0H02), temos a distância luminosidade em termos do parâmetro de Hubble

dL =

(1 +z)

H0

√

Ksenh

p

ΩKH0

Z z

0

dz H(z)

(4.34)

ou

dL =

(1 +z)

H0 √ Ksenh p ΩK Z z 0 dz E(z)

, (4.35)

ondeE(z) =H(z)/H0.

Enquanto a distância luminosidade é determinada para objetos pontuais (em particular para velas padrão), a distância diâmetro angular é usada para objetos exten-sos (em particular para réguas padrão), ou seja fontes subtendidas por um ângulo.

Capítulo 4. Cosmologia Observacional 34

ânguloθ. Então, o arcosformado é dado por:

s =a(t1)r1θ , (4.36)

a distância diâmetro angulardA é definida através do ângulo θ pela relação usual da

geometria,

dA=

s θ =

a(t1)r1θ

θ =a(t1)r1 , (4.37)

comparando com a equação (4.28), onde aqui levamos a expansão do universo em conta,

dA =

dL

(1 +z)2 (4.38)

ou para uma curvatura genérica

dA=

1

(1 +z)H0√ΩK

senhpΩK

Z z

0

dz E(z)

CAPÍTULO

5

OBSERVÁVEIS PADRÃO

5.1 Supernovas do Tipo Ia

As SN Ia, são excelentes velas padrão [11, 35, 12]. Elas são extremamente bri-lhantes, quase que rivalizando com o brilho da galáxia hospedeira. A explosão SN Ia ocorre numa anã branca pertecente a um sistema binário, quando sua massa excede o limite de Chandrasekhar (_∼1.4M⊙) ao absorver o gás da estrela companheira.

Supõe-se que apenas a metalicidade (proporção de elementos mais pesados que o Hélio) pode afetar a explosão.

É esperado que o processo de criação seja idêntico para todas as Supernovas do Tipo Ia, fazendo com que a luminosidade sempre seja a mesma. Para este caso, elas se tornariam excelentes velas padrão em virtude de sua alta luminosidade, fazendo com que ela seja detectada e examinada a grandes distâncias.

Porém, a SN Ia tem uma luminosidade que varia de objeto a objeto com uma dispersão de cerca de 0.4 mag na faixa do azul do espectro luminoso [36]. Se a

lu-minosidade fosse a mesma, teríamos um comportamento linear, respeitando a Lei de Hubble. Pela figura 5.1, vemos que existem desvios da lei de Hubble, que são sigini-ficativamente maiores que o erro da medição fotómetrico.

Isto se deve a uma forte correlação entre a luminosidade e o formato da curva

Capítulo 5. Observáveis Padrão 36

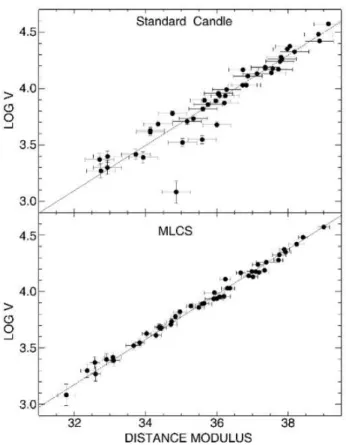
Figura5.1: Diagrama de Hubble para SN Ia relativamente próximas,log(V)vs o módulo

de distância. O diagrama acima é obtido pela suposição de que todas as SN Ia possuem a mesma luminosidade. Se essa previsão estivesse correta, todos os pontos estariam alin-hados ao longo de uma linha reta, conforme a lei de Hubble. Como se pode notar, existe um grande espalhamento na medição fotométrica na ordem de0.42mag. No diagrama

abaixo, encontramos o diagrama de Hubble para SN Ia que tiveram suas curvas de luz corrigidas, pelo filtro chamado MLCS, os desvios fotométricos caem drasticamente para ordem de0.15mag. Figura retirada de Schneider. P. (2006), pág 325, [36].

de luz emitida pela SN Ia. Aquelas com luminosidade máxima mais alta, mostram uma queda mais lenta na curva de luz. Outro fator que contribui com este problema é que, o fluxo observado seja possivelmente afetado pela extinção da galáxia hospedeira (algumas bandas são mais absorvidas e espalhadas do que outras), assim como tam-bém pela nossa própria galáxia. Este efeito (extinção) produz um avermelhamento na distribuição espectral.

É possível deduzir uma correção empírica para a luminosidade máxima das curvas de luz em alguns filtros, levando em consideração uma análise combinada da largura da curva de luz, com a extinção (avermelhamento).