Pontos notáveis de quadriláteros

Departamento de Matemátia - ICEx

Monograa da Espeialização

Pontos Notáveis de Quadriláteros

Carolina Silva Rezende

Orientador: Prof. Mihel Spira

AgradeçoaDeuspelaforçaparapersistirommuitaluznessaaminhada.

Aos meus pais, meu irmão e toda minha família pelo apoio e arinho. Ao

Luiz, peloinentivoe porestar sempreperto nas horas de diuldadese

de-sespero, pelo arinho, ompreensão e por me fazer areditar que sou apaz.

AomeuorientadorMihelSpira,aquemtantodesorientei,pelapaiênia,

de-diação,ensinamentos(portamparalgunsburaosdaminhaformação)epor

metrazerde voltaabelezadaMatemátia. AosprofessoresJussaraMoreira,

PauloAntnio,JorgeSabatui, FranisoDutenhefnerpelasorreções e

su-gestões apresentadas. A todos professores e funionários do departamento

de Matemátia da UFMG, emespeial Bernardo Lima, Fábio Enrique

Bro-hero Martinez,ElianeAndréaBarbosa eElianeKelliGaudênioquesempre

Introdução 4

1 Notação e Resultados Elementares 5

1.1 Pontos Notáveisde Triângulos . . . 7

1.2 Homotetias . . . 10

1.3 Círulode Nove Pontos . . . 13

1.4 Círulode Apolnio. . . 15

2 Quadriláteros 18 3 Quadriláteros Insritíveis 22 3.1 Preliminares . . . 22

3.2 Propriedades dos quadriláteros insritíveis . . . 24

3.3 Antientro . . . 30

3.4 Outras Propriedades . . . 33

Pretendo, om esse trabalho, apresentar algumas propriedades de

qua-driláteros de modoa torná-las mais onheidas e aessíveis a professores de

Geometria dos ensinos médio e superior que tenham passado por um urso

iniialdegeometriaplana. Abelezadessaspropriedadeseofatodeserem

de-monstradas pormétodos elementares tornam seu estudo relevante doponto

de vista ientío, didátio e estétio. Estas propriedades não são omuns

em livrosdidátios de língua portuguesa. Vamos disponibilizartambémum

CD om arquivos em GEOGEBRA que utilizamos nos estudos para a

pro-dução deste texto. Nosso trabalho é baseado no apítulo 4 do livro College

Geometry: An Introdutionto theModern Geometry of the Triangle andthe

Notação e Resultados

Elementares

Dado dois pontos

A

e

B

, denotaremos indistintamente por

AB

o seg-mento, o omprimento desse segmento, a reta ou a semirreta (de origem

A

) determinados por esses pontos; o ontexto tornará laro de qual objeto

se trata. Os símbolos

≡

e

∼

serão usados para denotar, respetivamente,

ongruênia e semelhança.

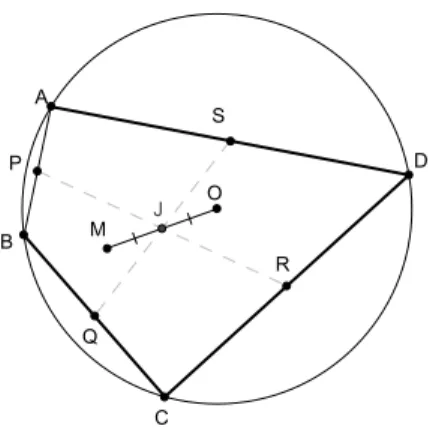
Figura1.1: Notação geral

CD

=

c

e

DA

=

d

; e por

P

,

Q

,

R

, e

S

os pontos médios destes lados,

respetivamente. As diagonais serão denotadas por

AC

=

f

e

BD

=

g

, e seus pontos médios por

V

e

U

, respetivamente; além disso, oloamos

UV

=

m

, omo na gura 1.1, que usaremos para xar notação ao longo do

trabalho.

A interseção de

P R

e

QS

, denotada por

J

, é dita o entróide (ver apítulo 2) do quadrilátero. Quando o quadrilátero for irunsritível,

de-notaremos por

O

o entro do írulo irunsrito. O ponto simétrio a

O

om relaçãoa

J

seráhamadode

M

(verseção3.3 )édito oantientro do quadrilátero irunsritível.

Figura 1.2: Notaçãopara quadriláteros insritíveis

No quadrilátero

ABCD

, o triângulo

ABC

é dito oposto ao ponto

D

; denotaremospor

D

′

seu inentro, eanalogamentedenimos

A

′

,

B

′

e

C

′

.

De-notaremos por

A

∗

o barientrodo triângulo

BCD

; analogamente, denimos

B

∗

,

C

∗

e

D

∗

Iniiaremosessa seçãoom osseguintes resultados elementares queserão

usados durante o texto; demonstrações não apresentadas podem ser

enon-tradas na referênia [1℄. Lembramos que, em um triângulo, apareem os

seguintes pontos notáveis:

Inentro: enontrodas três bissetrizes. Oinentroéoentrodoírulo

insrito.

Barientro: enontro das três medianas.

Cirunentro: enontrodas três mediatrizes. Oirunentroéoentro

do íruloirunsrito.

Ortoentro: enontro das três alturas.

Exentros: enontros de duas bissetrizes externas.

Dizemos também que um segmento de reta que liga o vértie de um

triângulo ao lado oposto ou ao seu prolongamento é uma omo eviana do

triângulo.

Proposição 1.1 (Base Média). Sejam

ABC

um triânguloe

M

,

N

pontos médios dos lados

AB

e

BC

, respetivamente. Então

MN//AC

e

MN

=

1

2

AC

.

✷

Proposição1.2 (Medianas). Sejam

ABC

um triângulo,

M

opontomédio do lado

AB

e

G

seu barientro. Então

AG

= 2

GM

; analogamente para os

outros lados.

✷

Proposição 1.3. Sejam

ABC

umtriângulo,

H

seuortoentro,

C

seuírulo irunsrito,

O

o entro de

C

. Sejam também

D, A

′

_∈

_BC

tais que

AD

e

OA

′

sejamperpendiulares a

BC

. Então

OA

′

₌

1

Demonstração. Temosque

COA

′

_∼

_CLB

earazãodesemelhançaéiguala

2

,

já que

OC

éraiodairunferêniae

CL

édiâmetro; logo

OA

′

₌

1

2

LB

. Além disso, oquadrilátero

LBHA

é um paralelogramo,poisomo

CL

é diâmetro então

AL

é perpendiular a

AC

e, omo

BE

é altura relativa ao lado

AC

do triângulo

ABC

, segue que

BE

é perpendiular a

AC

. Logo temos que

AL//BH

e segue que

BL

=

AH

, donde

OA

′

₌

1

2

AH

.

Apróxima proposição ésimples, mas nem sempreé abordadanos ursos

de geometria plana.

Proposição 1.4. Dado um triângulo retângulo

ABC

, o omprimento da medianarelativaà hipotenusa é iguala metade dahipotenusa.

Demonstração. Comootriângulo

ABC

éretângulo,ahipotenusa

AB

é tam-bémodiâmetrodoíruloirunsrito.Logoopontomédio

D

dahipotenusaé oentrodesseírulo.Segueque

AD

=

BD

=

CD

sãoraiosdesseírulo.

Proposição 1.5. (Relação de Stewart) Seja

ABC

um triânguloe onsi-dere a gura 1.5abaixo, então

b

2

_f

₊

_c

2

_e

₌

_a

₍

_ef

₊

_d

2

₎

_.

Figura1.5:

Demonstração. Pela lei dos ossenos, temos

b

2

₌

_d

2

₊

_e

2

₋

₂

_de

_cos

_β

e

c

2

₌

d

2

+

f

2

−

2

df

cos

α.

Multipliandoaprimeiraigualdadepor

f

,asegundapor

e

esomando temos

b

2

_f

₊

_c

2

_e

₋

_ad

2

₌

_aef

,ondelembramosque

cos

α

=

−

cos

β

uma vez que

α

+

β

= 180

o

.

Corolário1.1. Sejaotriângulo

ABC

e

d

amedianaemrelaçãoaBC.Então

b

2

₊

_c

2

_{= 2}

_d

2

_{+ 2}

a

2

2

.

✷

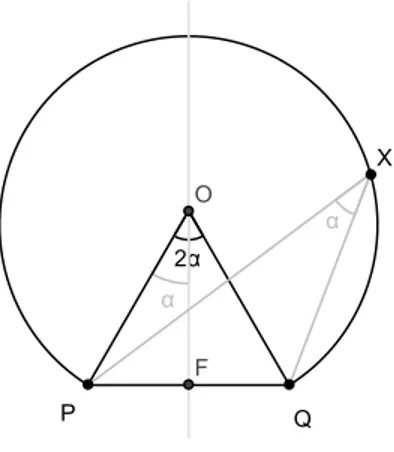
Denição 1.1. (Aro Capaz) Dados

P, Q

e

α

, o aro apaz de

P Q

om relação a

α

é o lugar geométrio dos pontos

X

tais que

P XQ

\

=

α

. Esse lugar é um aro de um írulo om extremos em

P

e

Q

, onforme gura abaixo, onde

O

éo entrodo írulo. Observamos que existem, na verdade, dois desses aros, simétriosom relação a AB.

✷

Figura 1.7: aro apaz

1.2 Homotetias

O termo homotetia é devido ao matemátio franês Mihel Chasles, em

1827eéderivadodogregoomoompostodehomo(similar)etetia(posição).

Denição 1.2. Sejam

O

um ponto e

k

6

= 0

. Uma homotetia de entro

O

e razão

k

é a transformação do plano no plano que leva um ponto

P

em um ponto

P

′

nareta

OP

talque

OP

′

OP

=

k

e 1)Se

k >

0

,

P

′

pertene à semirreta

OP

2)Se

k <

0

,

P

′

pertene à semirreta oposta a

OP

Observamos quese

k

= 1

então

ρ

O, k

é a identidade.

Para ahar o entro de uma homotetia dada, diferente da identidade,

basta traçar as retas determinadas por dois pontos distintos de uma gura

e os pontos orrespondentes da gura homotétia; o entro será o ponto de

interseção das retas.

Figura1.8:

Teorema 1.1. Sejam

α

e

β

homotetias de entro

A

e

B

e razões

a

6

= 1

e

b

6

= 1

,respetivamenteom

A

6

=

B

. Então

βα

éuma(i)translação,se

ab

= 1

ou (ii)uma homotetia de razão

ab

,se

ab

6

= 1

.

Demonstração. Sem perda de generalidade, onsideraremos

a, b >

0

(apenas para efeito de gura mais bonita).

Suponhamos primeiro

ab

= 1

; sem perda de generalidade, suponhamos também

a >

1

. Consideraremos agora agura 1.9a seguir.

Temos

AP

′

AP

=

a

e

BP

′′

BP

′

=

b

=

1

a

,ou seja,

BP

′

BP

′′

=

a

. Logo

AP

′

_B

_∼

_{P P}

′

_P

′′

,

donde

P P

′′

é paralelaa

AB

. Alémdisso,

P P

′

AP

′

=

AP

′

₋

_AP

AP

′

= 1

−

AP

AP

′

= 1

−

1

a

=

a

−

1

Figura1.9: aso

ab

= 1

Logo

−−→

P P

′′

éum vetor paralelo a

AB

de módulo

a

−

1

a

|AB

|

,que independe da

esolha de

P

; segue que

βα

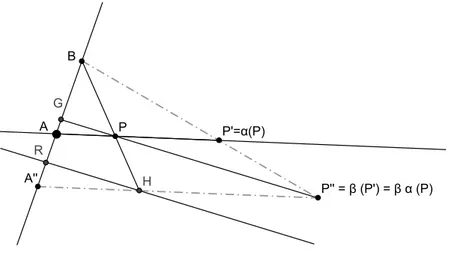
é uma translação.

Figura1.10: aso

ab

6

= 1

Suponhamos agora

ab

6

= 1

, om

a >

1

,

b >

1

e onsideraremos a gura 1.10, onde

P

é ponto qualquer,

P

′

₌

_α

₍

_P

₎

,

P

′′

₌

_β

₍

_P

′

_{) =}

_βα

₍

_P

₎

,

A

′

₌

α

(

A

) =

A

,

A

′′

₌

_β

₍

_A

′

_{) =}

_βα

₍

_A

₎

,

G

=

AB

∩

P P

′′

,

H

=

AB

∩

BP

e

R

∈

AB

é talque

HR//GP

′′

razão

ab

. Temos

BA

′′

BA

=

BP

′′

BP

′

=

b

ouseja,

BA

′′

_P

′′

_∼

_BAP

′

;empartiular,

AP

′

_//A

′′

_P

′′

e segue que

BH

BP

=

b.

Além disso, temos

AP

”

AH

=

AP

′

AP

=

a.

Da semelhança

A

′′

_GP

′′

_∼

_A

′′

_RH

temos que

GP

′′

RH

=

A

′′

_P

′′

A

′′

_H

=

a.

e da semelhança

BGP

∼

BRH

temos que

RH

GP

=

BH

BP

=

b.

Logo

GP

′′

GP

=

GP

′′

RH

RH

GP

=

ab

eonluímos que

βα

é uma homotetia de entro

G

erazão

ab

.

1.3 Círulo de Nove Pontos

Nesta seção vamos estudar um belo objeto da geometria: o írulo de

nove pontos.

Teorema1.2. Seja

ABC

umtriângulo,

K, M, N

ospontosmédiosdoslados,

P, Q, R

ospésdasalturase

U, V, W

ospontosmédiosdossegmentosqueligam

o ortoentro

H

aos vérties. Esses nove pontosestão em um mesmoírulo. O entrodeste íruloéo pontomédiodosegmento queligaoortoentroao

irunentrodotriângulo

ABC

. Alémdisso,oraiodoírulode novepontos valeametade doraiodo íruloirunsrito ao triângulo.

Demonstração. Vamos demonstrar primeiro que o írulo que passa pelos

Seja

C

o írulo determinado por

K, M, N

. Vamos mostrar que o qua-drilátero é

MKP N

é insritível. O triângulo

CP B

é retângulo e

P N

é a mediana referente a hipotenusa; pela proposição 1.4temos que

P N

=

BN

. Por outro lado, temos que

MK

é base média do triângulo

ABC

, então

MK

=

BN

. Assim

MK

=

P N

e nosso quadrilátero é um trapézio

isós-eles, que é insritível. Logo o írulo

C

passa por

P

; e analogamente, ele passa por

Q

e

R

.

Agora vamos provar que o írulo

C

passa também pelos pontos médios

dos segmentos determinados pelos vértiese pelo ortoentro dotriângulo.

Sejam

U

e

V

ospontosdeinterseçãodoírulo

C

om

AH

e

BH

, respe-tivamente. Temos que

MN

é base média dotriângulo

ABC

, logoé paralelo a

AB

e

MN

=

AB

2

. Temos, também, que

V RM

\

= 90

o

, logo

MV

é um diâmetro de

C

. Analogamente

UN

édiâmetro. Assim

MV

e

NU

são iguais e paralelos, isto implia que

MUV N

é um retângulo e

MN

=

AB

2

. Então

UV // AB

e

UV

=

AB

2

. Comissoonluímos que

UV

ébase média

△AHB

, em partiular

U

e

V

são pontos médios,respetivamente de

AH

e

BH

.

O írulo do teorema 1.2 é dito o írulo de nove pontos do triângulo

ABC

.

OCírulode novepontos eoíruloirunsritode um mesmotriângulo

estão relaionados de um modosurpreendete, omo vemos aseguir.

Teorema 1.3. O írulo de nove pontos e o írulo irunsrito de um

tri-ângulo

ABC

são homotétios por uma homotetia

ρ

de entro

H

e razão 2.

1.4 Círulo de Apolnio

Nesta seção vamos estudar um objeto maravilhoso e surpreendente: o

írulo de Apolnio

Lema 1.1. Dado um segmento

AB

e

1

=

6

k

≥

0

, existem e são únios os pontos

P

,

Q

na reta

AB

, om

P

interno e

Q

externo aosegmento

AB

, tais que

P A

P B

=

QA

QB

=

k

.

Demonstração. Seja

AC//BD

. Temos

ACQ

∼

BDQ

, logo

AC

BD

=

AQ

BQ

=

k

. Por outro lado, o triângulo

AEP

∼

BDP

, logo

AE

BD

=

AP

BP

=

k

. Então

AP

BP

=

AQ

QB

=

k

. Observação da gura do lema 1.1: Foi onstruída traçando paralelas a reta

AB

por

A

e

B

,

AC

=

AE

=

k

e

BD

= 1

, assim enontra-mos os onjugados harmnios

P Q

, tais que

P

=

AB

T

ED

e

Q

=

AB

T

CD

.Deixamos para o leitor a demonstração dauniidade de

P

e

Q

.

No lema anterior, o número

k

é dito a razão emque

P

e

Q

que dividem o segmento

AB

. Para uso posterior,observamos que se

X

e

Y

pertenem à reta

AB

, então

Y

está à direita de

X

se e somente se

Y A

Y B

>

XA

XB

. Ospontos

P

e

Q

são ditos osonjugados harmniosde

A

e

B

om relação a

k

.

Observamos quepontomédio

M

do segmento

AB

é oúnio ponto queo divide na razão

k

= 1

.

Teorema 1.4. Se

k >

0

e

P

,

Q

são os onjugados harmnios de

A

e

B

om relação a

k

então o lugar geométrio dos pontos

X

tais que

AX

BX

=

k

é a mediatrizde

AB

se

k

= 1

e é oírulo de apolnio

C

, de diâmetro

P Q

se

k

6

= 1

.

Demonstração. Para

k

= 1

éimediatoqueo lugardesrito peloponto

P

éa mediatrizdosegmento

AB

. Suponhamosagora

k

6

= 1

eseja

X

talque

AX

BX

=

k

. Temos

AP

BP

=

AX

BX

e o pelo teorema da bissetrizque diz:

AP

BP

=

AX

BX

=

AQ

BQ

, donde

AP

BP

=

AQ

BQ

=

k

, temos que

XP

é bissetriz de

AXB

. Analogamente

XQ

é bissetriz externa logo

P XQ

\

= 90

o

o que implia que

X

pertene ao írulo

C

de diâmetro

P Q

. Reiproamente, seja

X

pertenente ao írulo

C

, temos então que

P XQ

\

= 90

o

. Traçamos por

B

paralelas a

XP

e s

XQ

, que intereptam

AX

em

D

e

E

respetivamente. Então

AP

BP

=

AX

DX

e

AQ

BQ

=

AX

EX

; omo

AP

BP

=

AQ

BQ

obtemos

XD

=

XE

. Logo,

X

é o ponto médio da hipotenusa do triângulo retângulo

DBE

e obtemos

XD

=

XB

. Assim,

AX

BX

=

AX

DX

=

AP

BP

=

k

.

O írulo do teorema anterior é onheido omo írulo de Apolnio do

Quadriláteros

Nesteapítulo,tratamosdepropriedadesgeraisdequadriláterosonvexos

e introduzimosum pontoespeial, dito entróidede um quadrilátero.

Proposição 2.1. Os pontos médios dos lados de um quadrilátero (não

ne-essariamenteonvexo)são vérties de um paralelogramo.

Figura2.1:

Corolário 2.1. O perímetrodo quadrilátero

P QRS

é igual a

e

+

f

.

✷

Agora vamos apresentar oprimeiropontomágio deste trabalho.

Teorema 2.1. Seja

J

=

P R

T

QS

. Então

J

é ponto médio de

P R, QS

e

UV

.

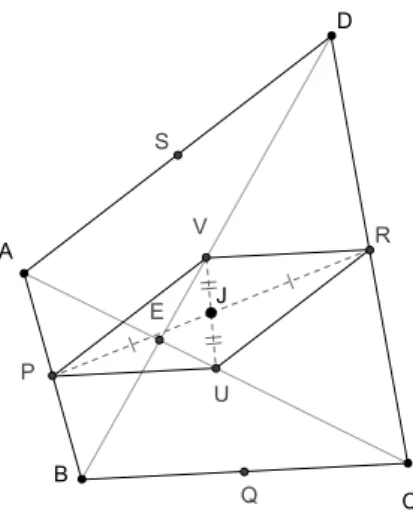
Figura 2.2: Centróide do quadrilátero,pontoJ

Demonstração. Como

P QRS

é paralelogramo,

J

é ponto médio das diago-nais

P R

e

QS

. Além disso,

P URV

também é paralelogramo, donde

J

é pontomédio das suas diagonais

P R

ee

UV

.

Denição 2.1. O ponto

J

doteorema 2.1édito oentróide de

ABCD.

✷

Paraoutraapresentaçãodoentróideindepedentedaanterior,lembramos

que

A

∗

denota o barientro do triânguloBCD, e analogamente para

B

∗

_{, C}

∗

e

D

∗

Teorema 2.2. As retas

AA

∗

,

BB

∗

,

CC

∗

e

DD

∗

onorrem em

J

.

Demonstração. No triângulo

ABD

, o segmento

DP

é mediana e

C

∗

é

ba-rientro. Pela proposição 1.2, segue que

P C

∗

P D

=

1

3

; analogamente,

P D

∗

P C

=

1

3

e pelo teorema de Tales segue que

C

∗

_D

∗

_{// CD}

e

C

∗

_D

∗

CD

=

1

3

. O raioínio

análogo paraos segmentos

A

∗

_B

∗

,

B

∗

_C

∗

e

D

∗

_A

∗

mostraque osquadriláteros

ABCD

e

A

∗

_B

∗

_C

∗

_D

∗

têm seuslados respetivamenteparaleloseemrazão

1

3

;

logo esses quadriláteros são homotétios. Vamos agora determinar o entro

dessa homotetia. Como

QS

é mediana no triângulo

AQD

e

A

∗

_D

∗

_{// AD}

,

QS

passa pelo ponto médio

S

′

de

A

∗

_D

∗

. Os pontos

S

e

S

′

são homotétios

nos dois quadriláteros;segue que areta

SQ

passa peloentrodahomotetia. Analogamente,

P R

passa pelo entro da homotetia; omo

P R

∩

QS

=

J

, segue que

J

é oentro dessa homotetia ea razão é

−

1

3

.

Figura2.3: Figura 2.4:

Agoraapresentaremosalgumaspropriedadesalgébriasdosquadriláteros.

Teorema 2.3. Seja

ABCD

um quadrilátero. Então

a

2

+

b

2

+

c

2

+

d

2

=

f

2

+

g

2

+ 4

m

2

.

Demonstração. No triângulo

ABD

,

V

é o ponto médio de

BD

=

g

. Pela relação de Stewart (proposição1.5), temos

2

AV

2

=

a

2

+

d

2

−

1

2

g

2

.

Analoga-mente, notriângulo

BCV

, temos

2

CV

2

₌

_b

2

₊

_c

2

₋

1

2

g

2

enotriângulo

ACV

temos

2

m

2

=

AV

2

+

CV

2

−

1

2

f

2

. Logo,

2

AV

2

+ 2

CV

2

=

a

2

+

d

2

+

b

2

+

c

2

−

g

2

e, substituindo,temos

a

2

+

b

2

+

c

2

+

d

2

=

f

2

+

g

2

+ 4

m

2

.

Lema 2.1. A soma do quadrados dos lados de um paralelogramo qualquer

P QRS

é igual àsoma dos quadrados de suas diagonais,istoé,

2(

p

2

+

q

2

) =

P R

2

+

QS

2

Demonstração. Apliandoaleidosossenosemadaumdostriângulos

P QR

e

P QS

,temos:

QS

2

=

p

2

+

q

2

−

2

pq

cos

α

e

P R

2

=

p

2

+

q

2

−

2

pq

cos

β

,somando

ambas, e observando que

α

e

β

são suplementares, segue que:

2(

p

2

+

q

2

) =

P R

2

+

QS

2

Corolário 2.2. A soma dos quadrados das diagonais de um quadrilátero é

igual aodobrodasomadoquadradodos doissegmentosqueligamospontos

médios dos lados opostos aos lados doquadrilátero, istoé:

g

2

+

f

2

= 2(

P R

2

+

QS

2

)

Quadriláteros Insritíveis

Nesse apítulo estudaremos propriedades espeiais de quadriláteros

ins-ritíveis. Observamos que essas propriedades deorrem da rigidez imposta

ao quadrilátero pelaondição da soma dos ângulos opostos ser igual a

180

◦

.

3.1 Preliminares

Denição 3.1. O quadrilátero quepossui seus vértiessobre uma

irunfe-rênia é hamadode quadrilátero insritível ouílio.

Teorema 3.1. As seguintes ondiçõessão equivalentes:

(a) O quadrilátero

ABCD

é insritível;

(b) Os ângulosopostos são suplementares;

() O ânguloentre um lado e umadiagonal éigual ao ânguloentre o lado

oposto e a outra diagonal.

Demonstração. (a)

⇒

(b). Como o ângulo

A

ˆ

éinsrito, temos que

A

ˆ

=

BCD

2

.

Como o ângulo

C

ˆ

é insrito,temos

C

ˆ

=

DAB

2

. Assim, segue que,

ˆ

A

+ ˆ

C

=

BCD

2

+

DAB

2

= 180

o

Analogamente,

B

ˆ

+ ˆ

D

= 180

o

.

(b)

⇒

(a). Seja

ABCD

um quadrilátero talque

A

ˆ

+ ˆ

C

= ˆ

B

+ ˆ

D

= 180

o

.

Suponha, porabsurdo, que

ABCD

não seja insritível. Seja

E

a interseção da irunferênia irunsrita ao triângulo

ABD

om o lado

BC

. No qua-drilátero

ABED

, temos, por hipótese, que

A

ˆ

+ ˆ

E

= 180

o

. Absurdo pela

propriedade doângulo externo. Logo, oquadrilátero

ABCD

é insritível. (a)

⇒

(). Os ângulos

D

AC

ˆ

e

D

BC

ˆ

enxergam o mesmo aro, logo, são iguais.

()

⇒

(a). Seja

ABCD

quadrilátero tal que

A

DB

ˆ

=

A

CB

ˆ

. Suponha, por absurdo, que

ABCD

não é insritível. Seja

E

a interseção da irunferên-ia irunsrita ao triângulo

ABD

e o lado

BC

. No quadrilátero

ABED

temos, por hipótese,

A

EB

ˆ

=

A

DB

ˆ

e,om isso, teremos

A

EB

ˆ

=

A

CB

ˆ

, on-tradizendo novamente a propriedade doângulo externo. Portanto

ABCD

é insritível.

Figura3.1:

Lembramos que

ABCD

é um quadrilátero,

A

′

o inentro do triângulo

BCD

; e analogamente, para

B

′

,

C

′

e

D

′

, omo naseção de notação.

Veremos a partir de agora uma série de resultados inesperados que

Teorema 3.2. Seja

ABCD

um quadrilátero. Então

A

′

_B

′

_C

′

_D

′

éum

quadri-látero insritível.

Figura3.2:

Demonstração. No triângulo

AA

′

_D

temos

AA

\

′

_D

=

180

o

−

A

ˆ

+ ˆ

D

2

.

Analoga-mente, para os triângulos

DB

′

_C

,

BC

′

_C

e

AD

′

_B

. Como

A

ˆ

′

e

C

ˆ

′

são ângulos

opostos, logo

A

ˆ

′

_{+ ˆ}

_C

′

_{= 180}

o

.

AA

\

′

_D

_{= 180}

₋

A

ˆ

+ ˆ

D

2

. Analogamente para

ˆ

B

′

_{+ ˆ}

_D

′

_{= 180}

o

3.2 Propriedades dos quadriláteros insritíveis

Teorema 3.3.

EG

e

F H

são perpendiulares.

Demonstração. Seja

S

a interseção de

BD

e

F H

. Temos

ALD

[

=

AD

+

BC

2

.

Como

HD

=

AD

2

e

BF

=

BC

2

, temos

\

HSD

=

HD

+

BF

2

=

\

ALD

2

. Logo

HF

é paralelo à bissetriz de

ALD

[

; analogamente,

EG

é paralelo à bissetriz de

[

ALB

esegue que

HF

e

EG

são perpendiulares.

Figura3.3:

Uma nota história para ontextualizar nosso próximo resultado.

Sabe-mosdegrandesmatemátiosdopassadoedesuasvariadasontribuiçõespara

os amposda álgebra, trigonometria,geometria e demais áreas da

matemá-tia, omo Pitágoras, Arquimedes, Pasal, Heron de Alexandria e outros.

ClaudiusPtolomeutambém foium desses grandesmatemátios,além de

as-trnomo e geógrafo. Ptolomeu naseu por volta do ano de 85 no Egito e

morreu,aproximadamente, noanode 165 emAlexandria,tambémnoEgito.

FoiPtolomeuquempropsateoriadogeoentrismo, queperdurouporera

eniouamatemátia (empartiular,a trigonometria)propondoum teorema

que leva seu nome: Teoremade Ptolomeu. Vejamoso que dizesse teorema.

Teorema 3.4. Emum quadrilátero insritíveltemos

ac

+

bd

=

f g

.

Figura3.4:

Demonstração. Sejam

r

areexãodasemirreta

AD

omrelaçãoàbissetrizde

B

AC

ˆ

e

Z

=

r

∩

BC

; notamosque

B

AZ

ˆ

=

C

AD

ˆ

. Como

ABCD

éinsritível,

temos

A

BZ

ˆ

=

A

DC

ˆ

e segue que

A

ZB

ˆ

=

A

CD

ˆ

; segue imediatamente que os triângulos

AZB

e

ACD

são semelhantes, donde

ZB

c

=

a

d

. Da semelhança

dos triângulos

AZC

e

ABD

segue que

ZC

g

=

f

d

. Logo

f

d

=

ZC

g

=

ZB

g

=

ac

d

+

b

g

=

ac

+

bd

dg

donde

ac

+

bd

=

f g

.

desigualdade triangular,

ZC < ZB

+

BC

e omo no aso anterior, temos que o triângulo

AZB

é semelhante ao triângulo

ACD

, o que implia que

AZ

AC

=

ZB

CD

=

AB

AD

−→

ZB

=

ac

d

,

ZC

=

ac

d

+

b

=

⇒

ZC < ac

+

bd

.

Comoapliaçãodoteoremade Ptolomeu, vamos mostraromo onstruir

um quadrilátero

ABCD

insritível, dados os lados

a

,

b

,

c

e

d

, nessa ordem, sendo

b

o maior lado. A ondição para essa onstrução é

b < a

+

c

+

d

, que é laramenteneessária, sendo verdadeira para qualquer quadrilátero.

Suponhamos agora

b < a

+

c

+

d

. Seja

Z

tal que

BZ

=

ac

d

, om

B

entre

Z

e

C

,

A

=

C

(

B, a

)

∩ A

(

ZC,

a

d

)

.

Figura3.5:

Finalmente, hamamos de

D

a interseção do írulo irsunsrito ao tri-ângulo

ABC

e

A

(

AC,

d

c

)

.

Devemos mostrar que as interseções aima, ou seja, os pontos

A

e

D

, existem. Começamos om

C

(

B, a

)

∪ A

(

ZC,

a

d

)

. Seja

P

=

ZC

∩ A

(

ZC,

a

d

)

.

Para mostrar que

P

está à direita de ou oinide om

B

, basta mostrar que

P Z

P C

≥

BZ

BC

. Como

P

∈ A

(

ZC,

a

d

)

, isto é o mesmo que

a

d

≥

ac

d

b

, ou seja,

b

≥

c

, o queé verdadepoissupomos que

b

éo maior lado doquadrilátero.

Vamos agora mostrar que

BP < a

. Para isso, seja

Q

∈

BC

tal que

BQ

=

a

; queremos mostrar que

P

está à esquerda de

Q

, o que é o mesmo

que

P Z

P C

<

QZ

QC

,ouseja,

a

d

<

a

+

ac

_d

b

−

a

. Esta desigualdadeequivalea

b < a

+

c

+

d

, queéaondição dada. Observamosagoraque,omo

A

(

ZC,

a

d

)

,temos

AZ

AC

=

Figura3.6:

a

d

, e segue a razão de semelhança dos triângulos

ABZ

e

ADC

é

a

d

. Logo

AD

=

d

a

AB

=

d

a

a

=

d

e

CD

=

d

a

BZ

=

d

a

ac

d

=

c

.

Observação 2. Na onstrução aima supomos que

d

era o lado oposto a

b

. Se

a

ou

c

são os lados opostos de

b

, obteremos possivelmente dois outros

quadriláteros insritos de lados

a, b, c

e

d

.

Apliando o teorema 3.4 aos quadriláteros

ABCD, ABCD

′

e

A

′

_BCD

temos:

yz

=

ab

=

cd

e obtemos

x

y

=

ad

+

bc

ab

+

cd

,

xy

=

ac

+

bd,

o que nos permite determinar asdiagonais doquadrilátero. Vemos também

que todos os quadriláteros insritos de lados

a, b, c

e

d

têm apenas três me-didas possíveispara asdiagonais. A gura 3.7é uma das três possibilidades

Nestaseçãovamosestudarumpontointeressantehamadode antientro,

o segundo pontomágio.

Teorema3.5. Emumquadrilátero

ABCD

insritível,ossegmentosderetas perpendiulares aos lados quepassam pelo pontomédio do lado oposto têm

um pontoem omum.

Figura3.8:

Demonstração. Sejam

O

o entro do írulo irunsrito ao quadrilátero,

J

seu entróide,

S

′

o pé da perpendiular traçada por

S

ao lado

BC

. A reta

OJ

interepta

SS

′

em um ponto

M

. Observamos que a reta

OQ

é paralela a reta

SS

′

Denição 3.2. O ponto

M

do teorema anterior, ou seja, o simétrio de

O

om respeito a

J

, será hamado de antientro doquadrilátero

ABCD

.

Teorema 3.6. Sejam

ABCD

um quadrilátero e

Ha

,

Hb

,

Hc

e

Hd

os orto-entros dostriângulos

BCD

,

ACD

,

ABD

,

ABC

, respetivamente. Entãoas retas

AHa

,

BHb

,

CHc

e

DHd

são onorrentes e seu ponto de enontro é o antientrode

ABCD

.

Figura3.9:

Demonstração. Pelolema 1.3, temos

AHd

= 2

OQ

=

DHa

; além disso,

AHd

e

DHa

são ambas perpendiulares a

BC

, donde

AHdDHa

é um paralelo-gramo. Seja

X

=

AHa

∩

DHd

; então

X

é oantientro. De fato a reta

SX

é paralela à reta

AHd

e, portanto,

SX

é perpendiular a

BC

. Logo

X

∈

SS

′

e, analogamente,

X

∈

P P

′

Observação 3. a demonstração mostraque

M

é tambémopontomédio de

AHa, BHb, CHc

e

DHd

.

Corolário 3.1. Seja

ABCD

insritível. Então ospontos

Ha, Hb

, Hc, Hd

for-mam um quadrilátero homotétio a

ABCD

, por uma homotetia de entro

M

e razão

−

1

.

Demonstração. Bastanotarque

AHaDHd

éumparalelogramoe

M

éoponto de enontro das diagonais, ou seja, é o ponto médio das diagonais

AHd

e

DHa

. Logo ahomotetia de entro

M

e razão

−

1

leva

A

em

Ha

e

D

em

Hd

;

analogamentepara

B

e

C

.

Figura3.10:

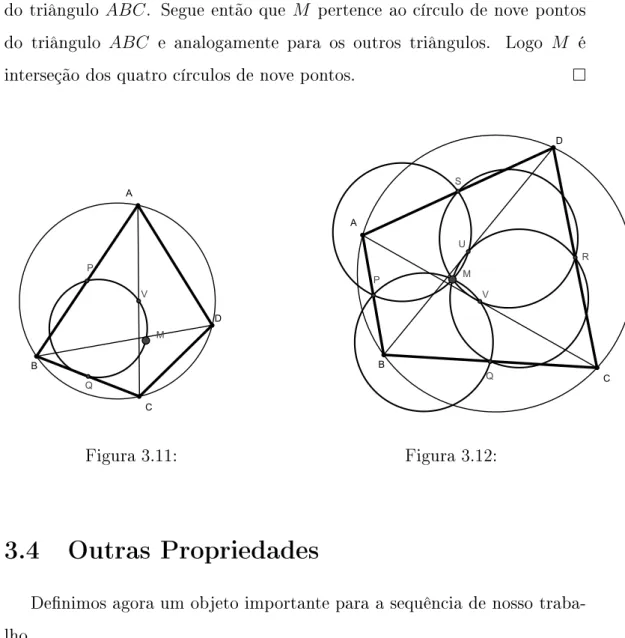
Teorema 3.7. Os írulos de nove pontos dos quatro triângulos

determi-nados pelos vérties de um quadrilátero ílio se intereptam noantientro

M

.

Demonstração. Seja

Hd

o ortoentro do triângulo

ABC

. Pelo teorema 3.6,

1

2

leva o írulo irunsrito do triângulo

ABC

no írulo de nove pontos do triângulo

ABC

. Segue então que

M

pertene ao írulo de nove pontos do triângulo

ABC

e analogamente para os outros triângulos. Logo

M

é interseção dos quatro írulos de nove pontos.

Figura 3.11: Figura3.12:

3.4 Outras Propriedades

Denimos agora um objeto importantepara a sequênia de nosso

traba-lho.

Denição 3.3. Seja

ABC

um triângulo,

C

seu írulo irunsrito,

D

′

seu

inentroe

Da

seu exentroopostoa

A

. Denotaremospor

CBD

′

C

oíruloque passa por

B

,

D

′

Lema 3.1. O entro de

CBD

′

C

é o ponto médio

F

do aro

BC

oposto a

A

no írulo

C

. Além disso,

D

′

_Da

é um diâmetro.

Demonstração. Vamos provar que

F

é o entro de

CBD

′

C

. Como

AD

′

é

bissetriz de

BAC

, ela passa por

F

, que é ponto médio do aro

BC

. Basta agora mostrarque o triângulo

D

′

_{F C}

éisóseles.

Figura3.13:

Temosque

\

F CB

=

BAF

[

=

α

,ambosessesângulosenxergamosegmento

BF

e

ACD

′

₌

_BCD

′

₌

_β

pois a reta

D

′

_C

é bissetriz. Então, pelo teorema

doângulo externo,temos que

CD

\

′

_F

₌

_α

₊

_β

e, omo

F CD

\

′

₌

_α

₊

_β,

temos

que o triângulo

D

′

_{F C}

Agora vamos provarque

D

′

_Da

édiâmetro. Como asbissetrizes internae

externa de umângulode um triângulosão perpendiulares,segue que

B

e

C

enxergam

D

′

_Da

por um ângulo reto. Logo

B

,

C

,

D

′

e

Da

pertenem a um írulo de diâmetro

D

′

_Da

.

Lema 3.2. Sejam

ABCD

um quadrilátero insritível,

E

,

F

,

G

e

H

pontos médios dos aros

AB

,

BC

,

CD

,

DA

, respetivamente. Então

F H

é perpen-diular a

EG

.

Demonstração. Observando a gura 3.14, temos que

GKF

\

=

GKH

\

pois subentendem aros de mesma medida; além disso,

GKF

\

+

GKF

\

= 180

o

;

omo

GKF

\

=

GKF

\

onluímos que

F H

éperpendiular a

EG

.

Figura3.14:

Teorema 3.8. Osinentrosdos quatro triângulosdeterminadospelos

vérti-es de um quadrilátero ílio são vérties de um retângulo.

Demonstração. Pelo lema anterior, temos que

A

′

_D

′

e

B

′

_C

′

são

perpendi-ulares a

HF

, logo

A

′

_D

′

e

B

′

_C

′

são paralelos; analogamente,

A

′

_B

′

_C

′

_D

′

um paralelogramo. Como

HF

e

EG

são perpendiulares, onluímos que

A

′

_B

′

_C

′

_D

′

é um retângulo.

No quadrilátero insritível

ABCD

, denotaremos por

Da

o exentro do triângulo

ABC

oposto aovértie

A

. Analogamente, deniremos

Da, Db

e

Dc

os exentros do triângulo

ABC

oposto, respetivamente, aos vérties

A, B

e

que feha esse trabalho, uja demonstração iniiamosom o lema aseguir.

Figura 3.17: 16 pontos, 4 a 4alinhadose perpendiulares

Lema 3.3. Sejam

Ba

,

Ca

e

Da

osexentros opostosaovértie

A

dos triângu-los

CDA

,

DAB

e

ABC

,respetivamente. Então

A

′

_D

′

_AdDa

éum retângulo.

Demonstração. Peloteorema

3

.

8

,

A

′

_B

′

_C

′

_D

′

éum retângulo. Temos

CBD

′

C

=

CBA

′

_C

; pelo lema 3.1, os pontos

A

′

e

Ad

são diametralmente opostos, bem omo

D

′

e

Da

. Logo

A

′

_D

′

_AdDa

é um retângulo e

Ad, D

′

_{, C}

′

e

Bc

estão alinhados.

Com raioínio análogo, temos as quadrúplas de pontosalinhados omo

Teorema 3.9. Os dezesseis exentros dos quatro triângulos formados pelos

vérties de um quadrilátero ilío formam dois grupos distintos de retas

organizadas quatro a quatro, perpendiulares ouparalelas.

Figura3.19:

Demonstração. Tendo em vista os teoremas 3.8 e o lema 3.3, basta

mos-trar queoquadrilátero

C

′

_AdCaAb

Figura3.20:

Para isso, basta mostrar que o írulo

CBC

′

D

passa por

Ad

. Observamos que

A

\

′

_AdB

₌

_A

\

′

_CB

_:=

_α

, pois ambos enxergam a orda

A

′

_B

em

C

(

BCD

)

. Como

CA

′

[1℄ Altshiler-Court, Nathan: College Geometry: An Introdution to the

Modern Geometryof the Triangleand the Cirle. Dover, 2007.

[2℄Elert, Glenn: Ptolemy'sTable ofChords: TrigonometryintheSeond

Century http://hypertextbook.om/eworld/hords.shtml.