Unicidade e discretização para problemas de valor inicial

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exatas e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Marcio Lemos do Nascimento

Unicidade e discretiza¸

c˜

ao para problemas de valor

inicial

(2)

Marcio Lemos do Nascimento

Unicidade e discretiza¸

c˜

ao para problemas de valor

inicial

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Modelagem Ma-tem´atica

Orientador:

Prof. Dr. Nir Cohen

(3)

(4)

(5)

Resumo

O presente trabalho tem dois objetivos: (i) a realiza¸cão de uma pesquisa bi-bliográfica sobre os critérios de unicidade de solu¸cão para problemas de valor inicial de equa¸cões diferenciais ordinárias. (ii) Introduzir uma modifica¸cão do método de Euler que parece ser capaz de convergir a uma das solu¸cões do problema, caso a solu¸cão não seja única.

(6)

Abstrat

This paper has two objectives: (i) conducting a literature search on the criteria of uniqueness of solution for initial value problems of ordinary differential equations. (ii) a modification of the method of Euler that seems to be able to converge to a solution of the problem, if the solution is not unique.

(7)

Lista de Figuras

2.1 infinite solutions translated. . . 6

2.2 gr´afico de ˙x em fun¸c˜ao de x . . . 7

2.3 gr´afico de x em fun¸c˜ao de t. . . 7

2.4 solu¸c˜ao do PVI - fun¸c˜ao cont´ınua passando pelo ponto inicial. . . 8

2.5 f =p_|x_| n˜ao ´e localmente lipschitziana no ponto (0,0). . . 12

4.1 linha poligonal composta por segmentos de reta . . . 39

4.2 Sequência de solu¸cões teóricas (xδ(t)) convergindo parax∗(t) . . . 45

4.3 cruzamento de solu¸c˜oes . . . 46

4.4 x_b(t) não é maior que a solu¸cão máxima x∗(t) . . . 47

4.5 Sanduiche em x∗(t) . . . 49

4.6 xδ =x(t+τh) . . . 53

4.7 Euler converge para a solu¸c˜ao constante x1(t)_≡0 . . . 54

4.8 convergˆencia para a primeira solu¸c˜ao positiva x∗(t) = t2. . . 55

4.9 Há paralelismo nas solu¸cões do PVI autônomo. . . 56

4.10 Não há paralelismo nas solu¸cões do PVI não autônomo. . . 57

4.11 Euler converge para a solu¸c˜ao constante x1(t)≡0 . . . 58

4.12 convergˆencia para a primeira solu¸c˜ao positiva x∗(t) = t4. . . 58

4.13 sequˆencia de aproxima¸c˜oes (xδ) . . . 59

B.1 Euler converge para a solu¸c˜ao m´ınima x(t)=t. . . 65

(8)

Sum´

ario

1 Introdu¸c˜ao 2

2 Conceitos preliminares 4

2.1 Equa¸c˜ao diferencial ordin´aria - EDO . . . 5

2.1.1 EDO autˆonoma . . . 5

2.2 Problema de valor inicial - PVI . . . 8

2.3 solu¸c˜ao do Problema de valor inicial . . . 8

2.3.1 Existência, Solu¸cões Máxima e M´ınima . . . 9

2.4 Fun¸c˜ao cont´ınua e lipschitziana . . . 11

2.5 Princ´ıpio da Contra¸c˜ao . . . 13

2.6 Teorema de Taylor . . . 14

2.7 Teorema da fun¸c˜ao inversa . . . 15

3 Existˆencia e Unicidade 16 3.1 Teorema da existˆencia de Peano . . . 16

3.2 Crit´erios de Unicidade . . . 18

3.2.1 Teorema de Picard . . . 18

3.2.2 A condi¸c˜ao Lipschitz com respeito `a t . . . 24

3.2.3 Caso não autônomo com f(t0, x0)₆= 0 e f não decrescente emt . 26 3.2.4 Condi¸cão Lipschitz unilateral . . . 26

3.2.5 Teorema de unicidade de Peano . . . 27

3.2.6 Condi¸c˜ao de Osgood . . . 28

3.2.7 Integral divergente . . . 34

(9)

1

3.2.9 Vari´aveis separ´aveis . . . 35

3.2.10Condi¸c˜ao de Majorana . . . 36

4 Métodos numéricos para resolu¸cão de EDO 38 4.1 O método de diferen¸cas finitas . . . 38

4.2 O m´etodo de Euler . . . 38

4.2.1 Erro local e erro global . . . 40

4.2.2 Covergência do método de Euler para o caso de não unicidade . . 43

4.2.3 O caso de vari´aveis separ´aveis . . . 50

4.2.4 caso autˆonomo . . . 52

4.3 Um exemplo . . . 53

4.3.1 Uma EDO autˆonoma . . . 54

4.3.2 Mudan¸ca de vari´avel . . . 55

4.3.3 Uma EDO n˜ao autˆonoma . . . 57

5 Conclus˜ao 60

A M´etodo de Euler no Matlab 63

B Um exemplo de PVI com mais de uma solu¸c˜ao e nenhuma delas ´e

a solu¸c˜ao constante 65

(10)

Cap´ıtulo 1

Introdu¸

c˜

ao

Considere o problema de valor inicial

˙

x=f(t, x)

x(t0) = x0 (1.1)

De acordo com a literatura, se a fun¸cãof é cont´ınua então existe solu¸cão para (1.1), enquanto que se a fun¸cão é localmente lipschitziana em rela¸cão à segunda variável segue-se que (1.1) possui solu¸cão única. Além disso, sob a mesma condi¸cão Lipschitz, é garantida a convergência dessa solu¸cão pelo método de Euler.

Podemos supor sempre a condi¸cão inicial na origem pois, “se o ponto inicial for outro, podemos sempre fazer uma mudan¸ca preliminar de variáveis, correspondente a uma transla¸cão dos eixos de coordenadas, e trazer o ponto dado (t0, x0) para a origem” [3].

Então, entenda-se este procedimento como uma forma de simplifica¸cão quando usarmos o ponto (0,0) ao invés de (t0, x0).

Neste trabalho contém duas contribui¸cões. Na primeira (Cap´ıtulo 3) Apresen-tamos uma pesquisa bibliográfica sobre várias extensões da condi¸cão Lipschitz que ainda garantem a unicidade da solu¸cão. Na segunda, consideramos o caso de falta de unicidade. Aqui, conforme [13] sempre existem uma solu¸cão local máxima x∗(t)

e uma solu¸cão local m´ınimax(t) tal que toda solu¸cão com a mesma condi¸cão inicial satisfaz

x(t)_≤x(t)_≤x∗(t). (1.2)

(11)

3

Este fato significa que não podemos esperar que o método de Euler, ou de maneira similar, métodos conhecidos de aproxima¸cão, como os métodos de Runge-Kutta, possam ser utilizados sem a garantia da unicidade.

“No entanto, a fim de aplicar um ou outro método de integra¸cão aproximada de uma equa¸cão diferencial, é necessário primeiro ter a certeza da existência da solu¸cão desejada e também da unicidade da solu¸cão, porque na ausência de unicidade não será clara qual solu¸cão a ser determinada” [8].

Um ex-aluno da Unicamp, Artur Gower, sugeriu um procedimento capaz de fazer o método de Euler convergir às outras solu¸cões. A idéia é, usando malha uni-forme h no algoritmo, come¸car com valor inicial perturbado ¯x0 =δ =chα _>_{0. Ele}

acreditava que, ao variar c _∈ (0,1] e α _≥ 1, ele conseguiria convergir a todas as solu¸c˜oes do PVI.

Porém, em várias simula¸cões que fizemos, usando o matlab, sempre houve con-vergência para x∗(t), independente dos c e α escolhidos. Se este fato for verdade,

então a estabilidade do algoritmo de Euler, que é garantida no caso Lipschitz, pode-ria ser estendida a casos bem mais gerais, no sentido de convergência do algoritmo com condi¸cão inicial modificada para a solu¸cão máximax∗(t). Assim pode-se formar

a seguinte afirma¸cão: qualquer método de aproxima¸cão do PVI (1.1) converge para a maior solu¸cão x∗(t), se ele for modificado usando uma condi¸cão inicial

infinitesi-malmente positiva.

Conseguimos provar teoricamente esta afirma¸cão, nos teoremas 4.2.3 e 4.2.5 onde mostram que as solu¸cões teóricas e núméricas do PVI

˙

x=f(t, x)

x(0) =δ (1.3)

(12)

Cap´ıtulo 2

Conceitos preliminares

A busca pelo entendimento f´ısico e matemático de diversos problemas da natu-reza tem sido de grande interesse por parte da comunidade cient´ıfica, dentre os quais estão os problemas técnicos e cient´ıficos descritos matematicamente por equa¸cões di-ferenciais as quais representam varia¸cões das quantidades f´ısicas que os descrevem.

A Teoria das Equa¸cões Diferenciais Ordinárias (equa¸cões que só apresentam derivadas ordinárias - em rela¸cão a uma variável) é objeto de intensa atividade de pesquisa por apresentar aspectos puramente matemáticos e um grande número de aplica¸cões provenientes da mecânica, qu´ımica, biologia, etc.

Muitos problemas encontrados em engenharia e outras ciências podem ser for-mulados em termos de equa¸cões diferenciais. Por exemplo, trajetórias bal´ısticas, trajetória dos satélites artificiais, estudo de redes elétricas, curvaturas das vigas, es-tabilidade de aviões, teoria das vibra¸cões, rea¸cões qu´ımicas e outras aplica¸cões estão relacionadas com equa¸cões diferenciais [11].

(13)

2.1 Equa¸c˜ao diferencial ordin´aria - EDO 5

dos métodos numéricos, no nosso caso o método de Euler, que converge para uma solu¸cão tão próxima da solu¸cão exata quanto menor for o passo da malha do dom´ınio temporal discretizado.

Tratamos de reunir neste cap´ıtulo alguns conceitos e defini¸cões importantes que serão necessários para o desenvlvimento e entendimento do nosso trabalho.

2.1 Equa¸

c˜

ao diferencial ordin´

aria - EDO

Uma equa¸cão diferencial ordinária é uma equa¸cão que contém uma única fun¸cão incógnita f, dependente de uma variável x e um número finito de deriva-das def [12].

Ela ´e dita de primeira ordem quando a primeira derivada, ˙x ´e a maior que ocorre.

2.1.1 EDO autˆ

onoma

Consideremos a equa¸c˜ao

˙

x=f(x), (2.1)

em que f : R_→R _{´e dita de classe} _C1_{. Quando} _f _{n˜ao depende explicitamente de} _t

´e dita autˆonoma.

Teorema 2.1.1. Se x é solu¸cão de (2.1) no intervalo (a, b) e t1 é um número real qualquer, então a fun¸cãox(t) =x(t+t1)é solu¸cão de (2.1) no intervalo(a−t1, b−t1).

Demonstra¸c˜ao:

Note que x(t) =x(t+t1)_⇒x˙(t) = ˙x(t+t1) =f(x(t+t1)) =f(x(t)).

Uma consequência imediata desse teorema é que, se x(t) é solu¸cão do PVI

˙

x=f(x)

x(t0) =x0 (2.2)

então, para qualquert0 _∈R, a fun¸cãox(t) = x(t₋t0) é solu¸cão do PVI (2.2). Exemplo 2.1.1.Considere o problema de valor inicial

˙

x= 2√x

(14)

As solu¸cões de (2.3) são x1(t) = t2 _e _x2₍_t₎_≡ _{0. Note que para qualquer transla¸cão} no eixot, i.e., x1(t) = (t₋c)2_{, t}_≥_c_{é também solu¸cão de (2.3), ver Teorema 2.1.1.} Portanto oP V I (2.3) possui infinitas solu¸cões. Veja que parat= 0 temos a solu¸cão que é diferente da contante e bifurca na origem, a essa solu¸cão chamaremos, no nosso trabalho, de primeira solu¸cão.

Figura 2.1 infinite solutions translated.

As equa¸cões diferenciais autônomas são bastante utilizadas nos modelos que governam a dinâmica populacional, entre outras aplica¸cões. E com elas podemos fazer uma análise qualitativa do comportamento de suas solu¸cões, através de uma análise geométrica das mesmas e em seguida esbo¸car fam´ılia de solu¸cões.

Exemplo 2.1.2.Considere a equa¸c˜ao autˆonoma

˙

x= (a₋bx)x (2.4)

que tem a forma

˙

x=f(x)

ondef ´e a fun¸c˜ao f(x) = (a₋bx)x. Ver figura 2.2.

Note que x1 = 0 e x2 = a_b são as ra´ızes da fun¸cão f e portanto solu¸cões cons-tantes da equa¸cão diferencial (2.4). Analisando o gráfico da figura 2.2, onde temos ˙x em fun¸cão dex, vamos esbo¸car o gráfico de x em fun¸cão det, que mostra a fam´ılia das solu¸cões de (2.4).

(15)

Figura 2.2 gr´afico de x˙ em fun¸c˜ao de x

0< x < a_b. Isto significa que no gráfico da figura 2.3, na faixa 0< x < a_b, as solu¸cões x são fun¸cões crescentes. Analogamente, para x > a

b, temos ˙x < 0. Logo, na faixa

x > a

b do gráfico da figura 2.3, as solu¸cões xsão decrescentes.

Na figura 2.3, esbo¸camos as solu¸c˜oes de 2.4 a partir dessas informa¸c˜oes.

Figura 2.3 gr´afico de x em fun¸c˜ao de t

Perceba que como mostra o gráfico da figura 2.2, ˙xé máximo quando x= ₂a_b. Portanto as solu¸cões têm máxima declividade quando x = a

2b. Conclu´ımos da´ı que

as solu¸c˜oes dentro da faixa 0< x < a

b tˆem ponto de inflex˜ao sobre a reta horizontal

(16)

2.2 Problema de valor inicial - PVI 8

2.2 Problema de valor inicial - PVI

Um problema de valor inicial é uma equa¸cão diferencial com a exigência de que a solu¸cão passe pelo ponto inicial (t0, x0).

Figura 2.4 solu¸c˜ao do PVI - fun¸c˜ao cont´ınua passando pelo ponto inicial.

2.3 solu¸

c˜

ao do Problema de valor inicial

Uma fun¸cão real x definida emI _⊂R _{é designada por solu¸cão do}_{P V I}

˙

x=f(t, x)

x(t0) = x0, t _∈ I (2.5)

se,

• x˙(t) existe para t_∈I;

• x˙(t) =f(t, x(t)), t_∈I e

(17)

2.3 solu¸c˜ao do Problema de valor inicial 9

2.3.1 Existˆ

encia, Solu¸

c˜

oes M´

axima e M´ınima

O pr´oximo resultado foi encontrado em [13].

Defini¸cão 2.3.1. Sejaf(t, x)uma fun¸cão cont´ınua em _ℜ. Por uma solu¸cão máxima x=x∗₍_t₎ _de

  

˙

x=f(t, x)

x(t0) =x0 (2.6)

entenda-se como uma solu¸cão de (2.6) em um intervalo máximo de existência tal que se x(t) é uma solu¸cão de (2.6), então

x(t)_≤x∗(t) (2.7)

mantém-se num intervalo comum de existência de x e x∗_{. A solu¸cão m´ınima é}

si-milarmente definida.

Teorema 2.3.1. Seja x, f _∈ R _e _f0₍_{t, x}₎_{, f1}₍_{t, x}₎_{, f2}₍_{t, x}₎_,_{· · ·} _{uma sequˆencia de}

fun¸c˜oes cont´ınuas no retˆangulo _ℜ:_{t0 _≤t _≤t0+a,_|x₋x0_{| ≤}b_} tal que

f0 = lim

n→∞fn unif ormemente em ℜ. (2.8)

Seja xn(t) uma solu¸c˜ao de

˙

x=fn(t, x), x(tn) =xn, (2.9)

em [t0, t0+a], onden = 1,2,· · · , e

(18)

2.3 solu¸c˜ao do Problema de valor inicial 10

Então existe uma subsequência xn1(t), xn2(t),· · · que é uniformemente convergente em [t0, t0+a]. E para qualquer tal subsequência o limite

x0(t) = lim

k→∞xnk(t) (2.11)

é uma solu¸cão de (2.9) em [t0, t0 +a]. Em particular, se (2.9) possui uma única solu¸cão x=x0(t) em [t0, t0+a], então

x0(t) = lim

n→∞xn(t) unif ormemente em [t0, t0+a]. (2.12)

Lema 2.3.2. Seja f(t, x) cont´ınua no retˆangulo

ℜ:_{t0 ≤t ≤t0+a, |x−x0| ≤b};

seja _|f(t, x)_{| ≤} M e α = min(a,_Mb ). Então (2.6) tem uma solu¸cão x = x0₍_t₎ _em [t0, t0+α] com a propriedade de que toda solu¸cãox=x(t)dex˙ =f(t, x), x(t0)_≤x0 satisfaz (2.7) em [t0, t0 +α].

Demonstra¸c˜ao: Seja 0< α′

< α. Ent˜ao, pelo Teorema ??,

˙

x=f(t, x) + _n1

x(t0) =x0 (2.13)

tem uma solu¸c˜aox=xn(t) em um intervalo [t0, t0+α

′

] sen´e suficientemente grande. Pelo Teorema 2.3.1, existe uma sequˆencia de n1 < n2 <_{· · ·} tal que

x0(t) = lim

k→∞unk(t) (2.14)

existe uniformemente em [t0, t0+α

′

] e ´e a solu¸c˜ao de (2.6).

Será verificado que (2.7) mantém em [t0, t0+α′]. Para isto é suficiente verificar que

x(t)_≤xn(t) em [t0, t0 +α

′

] (2.15)

(19)

2.4 Fun¸c˜ao cont´ınua e lipschitziana 11

t=t1, t0 < t1 < t0 +α

′

tal que x(t1)> xn(t1). Uma vez que existe um maior t2 em [t0, t1), ondex(t2) = xn(t2), de modo que x(t)> xn(t) em (t2, t1]. Mas (2.13) implica

que ˙xn(t2) = ˙x(t2) + _n1, de modo que xn(t)> x(t) para t > t2 pr´oximo de t2. Esta

contradi¸c˜ao prova (2.15). Uma vez queα′

< α ´e arbitr´ario, o lema segue.

2.4 Fun¸

c˜

ao cont´ınua e lipschitziana

A fun¸c˜ao f : X _→ R _{´e cont´ınua no ponto} _a _∈ _X _{quando, para todo} _{ǫ >} ₀

dado arbitrariamente, pudermos acharδ >0 tal quex_∈X e_|x₋a_|< δ impliquem

|f(x)₋f(a)_|< ǫ. Simbolicamente:

∀ǫ >0_∃ δ >0;x_∈X,0<_|x₋a_|< δ _{⇒ |}f(x)₋f(a)_|< ǫ.[15]

Em rela¸cão a escala de suavidade, toda fun¸cão lipschitziana é cont´ınua, dize-mos então que a condi¸cão de Lipshitz é mais forte do que a continuidade.

Teorema 2.4.1. Seja f :_{ℜ ⊂}R2_{. Diremos que} _f₍_{t, x}₎ _{´e lipschitziana relativamente}

a x em _ℜ se existir uma constante L >0 tal que

|f(t, x1)−f(t, x2)| ≤L|x1−x2|, ∀(t, x1),(t, x2)∈ ℜ (2.16)

Diremos quef(t, x) ´e localmente lipschitziana relativamente axquandof(t, x) for lipschitziana em uma vizinhan¸ca de cada (t0, x0)_{∈ ℜ}.

Exemplo 2.4.1.A fun¸c˜ao ˙x= 2xsen(t) ´e lipschitziana emR2 _pois

|f(t, x1)₋f(t, x2)_|= 2_|sen(t)_{| |}x1₋x2_{| ≤}2_|x1₋x2_|. (2.17)

Exemplo 2.4.2. A fun¸cão f(x) = p_|x_| não é lipschitziana no ponto x = 0, ver figura (2.5).

Para ver isto, escolha ǫ > 0, pegue x1 = ǫ2 _e _x2 _{= 4}_ǫ2 _{e suponha que} _f _´e Lipchitz. Como x1, x2 _{∈ ℜ}= [₋1,1] , deve existir uma constante L tal que

L_≥

f(x1)₋f(x2) x1−x2

=

ǫ₋2ǫ ǫ2₋₄_ǫ2 =

ǫ 3ǫ2 =

1

3ǫ → ∞ (2.18)

(20)

2.4 Fun¸c˜ao cont´ınua e lipschitziana 12

Figura 2.5 f =p_|x_|n˜ao ´e localmente lipschitziana no ponto (0,0).

x= 0.

Exemplo 2.4.3. A fun¸cão f(x) = x2_, _x _∈ _[₋₁_,_{1] é localmente lipschitziana mas} não globalmente. Esta fun¸cão é de classeC1_.

De fato, para todo x0 ∈R,

sup

x ∈ (x0−1,x0+1)

f′(x)= sup

x ∈ (x0−1,x0+1)

|2x_{| ≤}2(_|x0_|+ 1) (2.19)

Agora pegue dois pontos y, z _∈ (x0 ₋1, x0 + 1), segue-se pelo Teorema do valor m´edio que existe algumξ entre y ez, tal que

|f(z)₋f(y)_|=f˙(ξ)(z₋y)_≤ sup

θ ∈ (x0−1,x0+1)

f˙(θ)_|z₋x_| (2.20)

Usando (2.19) conclu´ımos que

|f(z)₋f(y)_{| ≤}(2_|x0_|+ 1)(z₋x), _∀ z, y _∈ (x0₋1, x0 + 1) (2.21)

Uma vez que a constante de Lipschitz def em (x0−1, x0+ 1) éL= 2|x0|+ 1 e a fun¸cão é localmente Lipschitz cont´ınua em todoR_.

Observe que a constante Lipschitz depende dex e sua vizinhan¸ca. Em particular se x0 → ∞ent˜ao L→ ∞.

(21)

2.5 Princ´ıpio da Contra¸c˜ao 13

|f(y)₋f(0)_|

|y₋0_| ≤ |y| → ∞, quando y→ ∞ (2.22)

N˜ao existeL que satisfa¸ca a condi¸c˜ao de Lipschitz global.

2.5 Princ´ıpio da Contra¸

c˜

ao

Um dos teoremas mais importantes em discussões de convergência e unicidade de algoritmos é o Teorema do ponto fixo de Banach ou princ´ıpio da contra¸cão, utili-zado na demonstra¸cão do Teorema de existência de solu¸cão para problema de valor inicial.

Sejam (M, d) e (N, d1) dois espa¸cos métricos. Uma aplica¸cão f : M → N é dita contra¸cão se existe 0_≤k <1 tal que

d1(f(x), f(y))≤kd(x, y), ∀x, y ∈ M. (2.23)

Teorema 2.5.1. Sejam (M, d) um espa¸co métrico completo e f : M _→ M uma contra¸cão. Então,f possui um único ponto fixo em M. Além disso, dado x0 _∈M a sequência definida por

x1 =f(x0), xn+1 =f(xn), n≥0. (2.24)

é uma sequência convergente e limn→∞xn =a é ponto fixo de f.

Demonstra¸c˜ao: Se a sequˆencia (xn) definida acima converge para a ∈ M,

ent˜ao como f ´e cont´ınua temos

f(a) =f(limxn) = limf(xn) = limf(xn+1) = a. (2.25)

Logo a´e ponto fixo de f.

Sef tem dois pontos fixos a e b, ent˜ao temos

d(a, b) =d(f(a), f(b))_≤kd(a, b), (2.26) o que ´e absurdo, a menos que a=b. Logo, a=b.

Resta provar que a sequˆencia (xn) converge. Notemos que d(x1, x2) ≤ kd(x0, x1) e

(22)

2.6 Teorema de Taylor 14

d(xn, xn+p)≤d(xn, xn+1) +· · ·+d(xn+p−1, xn+p) (2.27)

≤[kn+kn+1+_{· · ·}+kn+p−1_]_d₍_{x0, x1}₎ _(2.28) kn

1₋kd(x0, x1) (2.29)

Como o limkn _{= 0 segue que a sequˆencia ´e de Cauchy e portanto convergente, o que}

completa a prova do Teorema.

2.6 Teorema de Taylor

Teorema 2.6.1. Seja f : [a, b]_→R_{, onde} _fn _{´e cont´ınua, ou seja, uma fun¸c˜ao com}

n derivadas cont´ınuas e f(n+1) _{definida em todo} ₍_{a, b}_{). Sejam} _{x0, x} _∈ _[_{a, b}_] _ent˜ao existec_∈(x0, x) tal que

f(x) =

n

X

k=1

fk₍_x0₎

k! (x−x0)

k₊ fn+1(c)

(n+ 1)!(x−x0)

n+1 _(2.30)

O Teorema de Taylor é uma extensão do Teorema do Valor médio. Isto é, se considerarmos n= 1 teremos que

f(x) =f(x0) +f′(c)(x₋x0)_⇒ f(x)−f(x0) (x₋x0)

=f′(c). (2.31)

Demonstra¸c˜ao: Denotemos por

G(t) =f(x)₋f(t)₋

n

X

k=1

f(k)₍_t₎

k! (x−t)

k₊_A₍_x

−t)n+1 (2.32)

Onde A ´e de tal forma que G(x0) = 0. Portanto teremos que G(x) = G(x0) = 0. Pelo Teorema de Rolle existec_∈(x, x0) tal queG′

(c) = 0. DerivandoGencontramos

G′(t) =₋f′(t)₋

n X k=1 d dt

f(k)₍_t₎

k! (x−t)

k

−(n+ 1)A(x₋t)n (2.33)

Lembrando das f´ormulas das derivadas de um produto teremos que

G′(t) =₋f′(t)₋

n

X

k=1

f(k+1)₍_t₎

k! (x−t)

k

− f

(k)₍_t₎

(k₋1)!(x−t)

k−1

(23)

2.7 Teorema da fun¸c˜ao inversa 15

Note que o somatório anterior é telescópico, portanto

G′(t) = f

(n+1)₍_t₎

n! (x−t)

n

−(n+ 1)A(x₋t)n _⇒ f

(n+1)₍_c₎

(n!) (x−c)

n _{= (}_n_{+ 1)}_A₍_x

−c)n (2.35) Tomandot=c, segue-se que

A= f

(n+1)₍_c₎

(n+ 1)! (2.36)

Tomandot=x0 e aplicando o fato que G(x0) = 0 obtemos o resultado.

Lema 2.6.2. [4] Para todo x_{≥ −}1 e m positivo,

0_≤(1 +x)m _≤emx. (2.37)

2.7 Teorema da fun¸

c˜

ao inversa

Teorema 2.7.1. Seja f uma fun¸cão cujo dom´ınio é um intervalo aberto I, suponha quef é diferenciável emI, e suponha quef′

(c)₆= 0 para todo númerocem I. Então f tem uma inversa g, g é diferenciável, e

g′(x) = 1 f′

[g(x)] (2.38)

(24)

Cap´ıtulo 3

Existˆ

encia e Unicidade

Neste cap´ıtulo tratamos de reunir todas as informa¸c˜oes referente aos crit´erios de unicidade para Problemas de valor inicial para EDO´s de primeira ordem. Dado um PVI,

˙

x=f(t, x)

x(t0) = x0 (3.1)

se a fun¸cãof for cont´ınua o Teorema de Peano garante a existência de pelo menos uma solu¸cão, enquanto que se ela for localmente lipschitziana em rela¸cão a segunda variável, então o problema tem solu¸cão única. Mas, sob certas condi¸cões sobre f ou até mesmo no valor inicial podemos determinar a existência de unicidade para (3.1). “enquanto a unicidade do problema (3.1) tem sido investigado em muitos artigos, resultados tratando da não unicidade tem sido dado somente por poucos autores [16].”

Por solu¸cão do P V I (3.1), queremos dizer uma fun¸cão real diferenciável x(t) definida em algum intervalo [t0, t0+α], satisfazendo a condi¸cãox(t0) = x0 e tal que a derivada ˙x existe e é igual a f(t, x(t)) em cada pontox_∈[t0, t0+α].

3.1 Teorema da existˆ

encia de Peano

Teorema 3.1.1. Sejax, f _∈R_;_f₍_{t, x}₎_{cont´ınua no retˆangulo}_ℜ_:_{_t0 _≤_t_≤_t0₊_a,_|_x₋_x0_{| ≤}_b_}_;

|f(t, x)_{| ≤}M em _ℜ, α =min(a, b

M). Ent˜ao (2.6)

possui pelo menos uma solu¸c˜ao x=x(t) em [t0, t0+α], [13].

Exemplo 3.1.1.: Considere o problema de valor inicial

˙ x= 2x

t

(25)

3.1 Teorema da existˆencia de Peano 17

Se

• x(0) = 0, ent˜ao o P V I (3.2) tem infinitas solu¸c˜oes, i.e., x(t) =ct2_, _c_∈_R_.

• x(0) =x0 ₆= 0, então o P V I (3.2) não tem solu¸cão.

• x(t0) =x0, t0 ₆= 0, então o P V I (3.2) tem solu¸cão única.

Como já é bem conhecido a continuidade def(t, x) no retângulo_ℜé suficiente para a existência de pelo menos uma solu¸cão de (3.1) no intervalo Jα : |t−t0| ≤

α= min(a,_Mb ), ondeM = supℜ|f(t, x)|. No entanto, sef(t, x) ´e descont´ınua ent˜ao

a natureza das solu¸cões é arbitrária. Por exemplo, o problema de valor inicial

˙

x= 2(x_t−1)

x(0) = 0 (3.3)

n˜ao tem solu¸c˜ao; enquanto que o problema

˙

x= 2(x_t−1)

x(0) = 1 (3.4)

tem um número infinito de solu¸cõesx(t) = 1+ct2_{, onde}_c_{é uma constante arbitrária.}

Embora, continuidade de f(t, x) seja suficiente para a existência de solu¸cão de (3.1), isso não implica a unicidade de solu¸cões. Por exemplo, a fun¸cão f(t, x) = x23 é cont´ınua em R2_{, mas o problema}

˙ x=x23

x(0) = 0 (3.5)

tem um n´umero infinito de solu¸c˜oes x(t)_≡0, e

x(t) =

(

0, 0_≤t_≤c (t−c)3

27 , t≥c

onde cé uma constante arbitrária. No ano de 1995 Lavrentieff dar um exemplo de uma fun¸cão cont´ınua f(t, x) no retângulo aberto

N _{⊂ ℜ}:_{|t₋t0_{| ≤}a,_|x₋x0_{| ≤}b_}

(26)

3.2 Crit´erios de Unicidade 18

N, o problema de valor inicial (3.1) tem mais de uma solu¸cão em todo o intervalo [t0, t0+ǫ] e [t0₋ǫ, t0]. Além disso, no ano de 1963 [13] usou um método um pouco similar ao de Kampen e construiu uma outra fun¸cão cont´ınuaf(t, x)_∈R2 _{de modo} que o problema (3.1) tem a mesma propriedade de não unicidade. Por isso, para garantir a unicidade precisamos também, além da continuidade alguma condi¸cão adicional emf(t, x).

3.2 Crit´

erios de Unicidade

3.2.1 Teorema de Picard

Teorema 3.2.1. Seja o retângulo _ℜ uma vizinhan¸ca do ponto (t0, x0)_∈ R2 _{e seja} f : _{ℜ →} R cont´ınua em _ℜ. Se f satisfaz a condi¸cão de Lipschitz com respeito à segunda variável em _ℜ, i.e.,

∃ L >0 tal que (t, x1),(t, x2)_{∈ ℜ ⇒ |}f(t, x1)₋f(t, x2)_{| ≤}L_|x1₋x2_|, (3.6)

então o problema de valor inicial (3.1) tem uma única solu¸cão [6].

Note que para garantir a unicidade de solu¸cões de (3.1) come¸camos com a suposi¸cão de que a varia¸cão da fun¸cãof(t, x) relativa axpermanece limitada. para todo (t, x1),(t, x2) em _ℜ tendo o mesmo t. A constante L é chamada de constante Lipschitz.

A condi¸cão de Lipschitz está entre a continuidade e a diferenciabilidade de f com respeito ax. De fato, de (3.6) a continuidade def com respeito axé óbvia, e a fun¸cão cont´ınuaf(t, x) =x23 viola a condi¸cão de Lipschitz em qualquer dom´ınio que contenhax = 0. Entretanto, f(t, x) = _|x_|, x_∈R2 _{é Lipschitz mas não diferenciável} em x=0. Se a fun¸cão f é diferenciável com respeito a x, então é fácil calcular a constanteL. De fato, provaremos.

(27)

3.2 Crit´erios de Unicidade 19 sup ℜ

∂f_∂x(t, x)

≤L. (3.7)

Demonstra¸cão: Uma vez que f(t, x) é diferenciável com respeito a x e o dom´ınio N é convexo, para todo (t, x1),(t, x2) _∈ N o Teorema do valor médio for-nece

f(t, x1)₋f(t, x2) = ∂f(t, x

∗₎

∂x (x1−x2), (3.8)

ondemin_{x1, x2_}< x∗ _{< max}_{_{x1, x2}_}_{. Assim, usando (3}_._{7) em (3}_._{9), encontramos}

(3.6). Reciprocamente, de (3.6) temos

∂f_∂x(t, x)

= limx2→x1

f(t, x1₍_x)₁−₋_xf₂(₎t, x2)

≤L. (3.9)

Teorema 3.2.3. (Variante do Teorema de Picard, o caso C1_{) Seja} _f _:_{ℜ →}_R _uma fun¸cão cont´ınua em _ℜ. Suponhamos que a derivada parcial com rela¸cão à segunda variável, f′

: _{ℜ →} R_{, seja cont´ınua tamb´em. Ent˜ao, para cada} ₍_{t0, x0}₎ _{∈ ℜ}_{, existe}

um intervalo aberto I contendo t0 e uma única fun¸cão diferenciável x(t) : I → R com (t, x(t))_{∈ ℜ}, para todot _∈I, que é solu¸cão do problema de valor inicial (PVI)

˙

x=f(t, x)

x(t0) =x0 (3.10)

Demonstra¸cão: A fun¸cão x(t) : I _→ R _{é solu¸cão de (3}_._{10) se e somente se, for}

solu¸c˜ao da equa¸c˜ao integral

x(t) =x0+

Z t

t0

f(s, x(s))ds, t_∈I (3.11)

Para ver isto, note que ˙x(t) = f(t, x), ou seja, a derivada da equa¸cão inte-gral (3.11) é uma fun¸cão de t e x. E ainda que x(t0) = x0 +Rt0

(28)

Reciprocamente, se x(t) : I _∈ R _{é uma fun¸cão cont´ınua que é solu¸cão da equa¸cão}

integral (3.11), então, pelo Teorema Fundamental do Cálculo,x(t) é diferenciável e é também solu¸cão do problema de valor inicial (3.10).

Concentremo-nos, pois na resolu¸cão da equa¸cão integral (3.11). Dado (t0, x0)_{∈ ℜ}, tomemos a e b positivos tais que o retângulo

ℜ=(t, x)_∈R2_;_|_t₋_t₀_{| ≤}_{a e} _|_x₋_x₀_{| ≤}_b _(3.12)

Esteja inteiramente contido em _ℜ. Como f é cont´ınua e _ℜ é compacto , então f é limitada em_ℜ, Seja

M =max_{|f(t, x)_|; (t, x)_{∈ ℜ}}.

Tome

0_≤α_≤min

a, b M

e o intervalo

jα = [t0−α, t0+α].

Seja

C =_{g;g :jα → R continua, g(t0) =x0 e|g(t)−x0| ≤b}. (3.13)

Definimos em C a seguinte m´etrica:

d(g1, g2) =max_{|g1(t)₋g2(t)_|:t_∈jα}; (3.14)

é fácil verificar que (3.14) é de fato, uma métrica, isto é, tem-se as propriedades:

• i) d(g1, g2)_≥0, e d(g1, g2) = 0 se e s´o seg1 =g2;

• ii) d(g1, g2) =d(g2, g1) e

• iii) d(g1, g2)_≤d(g1, g3) +d(g3, g2).

Segue-se que (C, d) é um espa¸co métrico. Mais ainda, (C, d) é um espa¸co métrico completo, isto é, toda sequência de Cauchy é convergente.

(gn) ´e de Cauchy se dadoǫ >0 existirn0 tal que d(gn, gm)< ǫpara n, m > n0. Uma sucess˜ao (gn) converge parag ∈C se dadoǫ >0 existirn0 tal qued(gn, g)< ǫ,

(29)

O espa¸co métricoC definido no parágrafo anterior é completo, o que se prova simplesmente observando que a convergência na métricadé a convergência uniforme de fun¸cões e lembrando que o limite uniforme de fun¸cões cont´ınuas é uma fun¸cão cont´ınua.

De (3.11). observamos que toda solu¸c˜ao deve ser ponto fixo da aplica¸c˜ao dada porg _∈C _→φ(g) onde

φ(g)(t) =x0+

Z t

t0

f(s, x(s))ds. (3.15)

Note que φ(g) ´e cont´ınua em jα eφ(g)(t0) =x0. Al´em disso,

|φ(g)(t)₋x0_{| ≤}

Z t t0

f(s, g(s))ds

≤M|t−t0| ≤M α≤b (3.16)

e portantoφ(g)_∈C. Logo temos que

φ:C _→C. Por outro lado, se g1 e g2 pertencem a C temos que

|φ(g1)(t)₋φ(g2)(t)_{| ≤}

Z t

t0

|f(s, g1(s))₋f(s, g2(s))_|ds. (3.17)

Como f ´e lipschitziana na vari´avelx, existe uma constante positiva L tal que

|φ(g1)(t)₋φ(g2)(t)_{| ≤}

Z t

t0

L_|g1(s)₋g2(s)_|ds_≤Lαd(g1, g2). (3.18)

Segue que

d(φ(g1), φ(g2))_≤Lαd(g1, g2). (3.19)

Tomando α tal que Lα < 1 conclu´ımos que φ é uma contra¸cão. Pelo Te-orema da contra¸cão, φ tem um único ponto fixo e o teorema fica provado com

I = (t0 ₋α, t0+α).

Apenas a continuidade de f garante a existência de solu¸cão mas não a unici-dade. Para obtermos unicidade é preciso alguma condi¸cão adicional.

Agora vamos provar que se duas solu¸cões x1 e x2 coincidem em algum ponto t=t0 então elas coincidirão em todos os valores de t em que estiveram definidas.

(30)

I2, respectivamente. Suponha t0 ∈ I1 ∩I2 e x1(t0) = x2(t0) = x0. Ent˜ao, x1 e x2 coincidem em todos os valores de t _∈I1_∩I2.

Demonstra¸c˜ao: Sejam x1 =ϕ(t) e x2 =φ(t) duas solu¸c˜oes satisfazendo

ϕ(t0) =φ(to) =x0. (3.20)

SejaJ = (r1, r2) =I1_∩I2 o intervalo em queϕ(t) e φ(t) est˜ao definidas. Seja

W =_{t;t _∈J e ϕ(t) =φ(t)_}. (3.21) Note queW é não vazio poist0 _{∈ ℜ}. Mostraremos que_ℜé aberto e fechado em J e comoJ é conexo teremos que J =W.

Seja (tn) uma sequˆencia de elementos de W convergente parat ∈J.

Assim, ϕ(tn) = φ(tn). Como ϕ e φ s˜ao cont´ınuas temos que ϕ(t) = φ(t), segue que

t_∈W. Logo, W ´e fechado em J.

Seja t1 _∈W. Então, temos que ϕ(t1) = φ(t1) =x1. Resolvendo o problema de valor inicial com o par (t1, x1), o Teorema de existência e unicidade nos dá α eb tal queLα <1. Podemos escolher, usando a continuidade de ϕ eφ, α tal que

|ϕ(t)₋φ(t)_{| ≤}b, (3.22)

com _|t₋t1_|< α.

Como ϕ e φ s˜ao solu¸c˜oes temos que

ϕ(t) =x1 +

Z t

t1

f(s, ϕ(s))ds, (3.23)

φ(t) =x1 +

Z t

t1

f(s, φ(s))ds. (3.24)

Para _|t₋t1_|< α obtemos

|ϕ(t)₋φ(t)_|=L

Z t

t1

|ϕ(s)₋φ(s)_|ds_≤bLα. (3.25)

Voltando na desigualdade anterior obtemos

|ϕ(t)₋φ(t)_{| ≤}b(Lα)2. (3.26) Repetindo o argumento,segue-se que

(31)

Para todo n _≥ 1. Como Lα < 1 obtemos que ϕ(t) = φ(t) para todo _|t₋t1| < α. Logo, existe uma vizinhan¸ca de t1 onde ϕ(t) e φ(t) coincidem, isto é, W é aberto. ComoW é não vazio, aberto e fechado em J e J é conexo, segue que W =J.

Também pode-se provar unicidade para (3.10) usando a desigualdade de Gronwall, [14], usada por exemplo na demonstra¸cão da condi¸cão de unicidade de Osgood, que veremos mais adiante. Que é um dos resultados mais simples e útil envolvendo uma desigualdade integral [13].

Teorema 3.2.5. (Desigualdade de Gronwall) Sejamu(t)ev(t)fun¸c˜oes n˜ao-negativas e cont´ınuas em[a, b]; c > 0 uma constante; e

v(t)_≤c+

Z t

a

v(s)u(s)ds para a _≤t_≤b. (3.28)

Ent˜ao

v(t)_≤ceRatu(s)ds para a ≤t≤b; (3.29)

em particular, sec= 0, ent˜ao v(t) = 0.

Demonstra¸c˜ao: Caso (i), c >0. Denotamos V(t) o lado direito de (3.28), de modo que

v(t)_≤V(t), V(t)_≥c >0 em [a, b]. (3.30) Tamb´em,

˙

V(t) =u(t)v(t)_≤u(t)V(t). (3.31) Desde que V >0, V˙

V ≤u, eV(a) = c, uma integra¸c˜ao em [a, t] d´a

V(t)_≤ceRatu(s)ds. (3.32) Assim (3.29) resulta de v(t)_≤V(t).

(32)

3.2.2 A condi¸

c˜

ao Lipschitz com respeito `

a t

O próximo teorema encontrado em [6] estabelece equivalência entre unicidade de solu¸cão do problema de valor inicial (3.1) e unicidade para um problema rec´ıproco, duplicando assim, a aplicabilidade do Teorema de unicidade.

Teorema 3.2.6. Seja o retˆangulo _ℜ uma vizinhan¸ca do ponto (t0, x0) _∈ R2 _{e seja}

f :_{ℜ →}R2 _{cont´ınua em} _ℜ_.

Se f(t0, x0)₆= 0, então (3.1) tem uma única solu¸cão se, e somente se, o problema

  

˙

t= _f₍_t,x1 ₎

t(x0) = t0 (3.33)

tem uma ´unica solu¸c˜ao t(x).

Demonstra¸cão: Uma vez que f(t0, x0) ₆= 0 e f cont´ınua em (t0, x0), existe uma vizinhan¸ca de (t0, x0) ondef tem sinal constante e é limitada. Para simplificar, assumimos quef e _f1 têm sinal constante e são limitadas em _ℜ.

Para estabelecer o resultado vamos usar a seguinte afirma¸c˜ao que ´e interessante em si mesma:

Afirma¸cão: Se X é uma solu¸cão de (3.1) então X−1 _{é solu¸cão de (3.33) e,} in-versamente, seT é um solu¸cão de (3.33) então T−1 _{é uma solu¸cão de (3}_._1).

Seja X :I _→ R uma solu¸c˜ao de (3.1); para todo t _∈ I temos (t, X(t)) _∈N e ˙

X(t) =f(t, X(t)), assim ˙X tem sinal constante em I, em particular, ela tem uma inversa X−1 _: _X₍_I₎ _→ _R_{. vamos assim mostrar que} _T ₌ _X−1 _{resolve (3.33).} Pri-meiro,X(I) é um intervalo que contémx0 eT(x0) = t0; segundo, usamos o Teorema de diferencia¸cão de fun¸cões inversas para todo x_∈X(I) obtem-se que

˙

T(x) = (X)−1₍_x_{) =} 1 ˙

X(X−1₍_x₎₎ = 1 f(T(x), x).

A prova da inversa é análoga, assim a omitimos, e afirmamos está provada.

Finalmente, suponha que X é a única solu¸cão de (3.1) no intervalo I = [t0 −α, t0 +α], para algum α > 0. Vamos provar que X−1 é a única solu¸cão de (3.33) no intervalo J = [x0 ₋β, x0 +β] desde que β > 0 seja tão pequena que J _⊂ X(I) e se T é qualquer solu¸cão para (3.33) definida no intervalo ˜J _⊂ J então T( ˜J)_⊂I (tal escolha deβé poss´ıvel porque 1

(33)

de (3.33) no intervalo ˜j _⊂ j. Uma vez que T−1 _{é uma solu¸cão de (3.1) em} _T_{( ˜}_J_{) e} T( ˜J) _⊂I, concluimos que T−1 ₌_X _em _T_{( ˜}_J_{). Por isso} _T ₌_X−1 _{em ˜}_J_{. Argumento} análogo mostra que unicidade para (3.33) implica unicidade para (3.1).

Corolário 3.2.7. Seja ǫ > 0, f : (x0 ₋ǫ, x0 + ǫ) _→ R cont´ınua, e t0 _∈ R. Se f(x0)₆= 0 então o problema autônomo

  

˙

x=f(x)

x(t0) =x0 (3.34)

tem solu¸c˜ao ´unica.

Mostraremos em seguida, através de um exemplo, que para o caso não autônomo a condi¸cãof(t0, x0)6= 0 não é suficiente para unicidade.

Exemplo 3.2.1.: Considere

˙

x= 3(x₋t)23 + 1

z(0) = 0 (3.35)

com condi¸cão inicial f(0,0) = 1 ₆= 0 e seja f(t, x) cont´ınua. A escolha da variável x=z+t transforma o problema autônomo

_dz

dt = 3z

2 3

z(0) = 0 (3.36)

com solu¸c˜oes

z(t) = (t₋c)3_{, t} _≥_c

z(t) = 0, t_≤c (3.37)

em um problema não autônomo (3.35), cujas solu¸cões são:x1(t) =t ex2(t) = t3+t. Portanto (3.35) admite 2 solu¸cões diferentes.

Teorema 3.2.8. Seja a fun¸c˜ao g(x) cont´ınua em _|x₋x0_| < b. Al´em disso, seja o problema de valor inicial

  

˙

x=g(x) x(t0) =x0

(3.38)

(34)

Demonstra¸cão:Suponhax1(t) ex2(t) duas solu¸cões de (3.38) emU :|t−t0|< ǫ. Sejag(x0)₆= 0, então existe uma vizinhan¸caV dex0 em queg(x) é limitada longe de zero. Seja W : _|t₋t0_| < ǫ1 _≤ ǫ tal que x1(W) _⊂ V e x2(W) _⊂ V. Para t _∈W, definimos G(t) =Rx2(t)

x1(t)

dt

g(t). Obviamente, se x1(t) 6=x2(t) para algum t ∈W, ent˜ao G(t)₆= 0. Mas, para todo x_∈W

˙

G(t) = x2˙ (t) g(x2(t)) −

˙ x1(t) g(x1(t)) = 0.

Portanto, G(t) ´e constante emW. No entanto, uma vez que G(t0) = 0 segue-se que G(t) = 0, t_∈W. Esta contradi¸c˜ao completa a prova.

3.2.3 Caso n˜

ao autˆ

onomo com

f

(

t

0

, x

0

)

6 = 0

e

f

n˜

ao decrescente

em

t

Seja _ℜ uma vizinhan¸ca do ponto (t0, x0) _∈ R2 _{e seja} _f _: _{ℜ →} _R _cont´ınua em _ℜ. Se f(t0, x0) ₆= 0 e, além disso, f é não decrescente com rela¸cão à primeira variável (i.e., f(s, x)_≤ f(t, x)) para todo (s, x),(t, x) _∈ N e s _≤t, então (3.1) tem uma única solu¸cão [6].

3.2.4 Condi¸

c˜

ao Lipschitz unilateral

Teorema 3.2.9. Unicidade para frente no tempo para (3.1)se verifica se a condi¸cão de continuidade Lipschitz(2.16)no Teorema2.4.1é Substitu´ıda pela seguinte condi¸cão Lipschitz unilateral:

(f(t, x1)₋f(t, x2)).(x1₋x2)_≤K_|x1₋x2_|2 para todo(t, x1),(t, x2)_{∈ ℜ}, (3.39)

Por “para frente no tempo”, queremos dizer o seguinte: duas solu¸cões x1 e x2 para (3.1) que por defini¸cão satisfaz x1(t0) =x2(t0) =x0, coincide para t > t0. Ob-serve que a condi¸cão Lipschitz unilateral não garante unicidade para trás no tempo, uma vez que não é invariante sob uma inversão do sinal detna equa¸cão, que equivale a uma mudan¸ca de sinal de f [7].

(35)

a condi¸c˜ao Lipschitz unilateral podemos estimar

˙

r(t) = 2(x1(t)₋x2(t)).(f(t, x1(t))₋f(t, x2(t))) (3.40)

≤K_|x1(t)₋x2(t)_|2 =Kr(t). (3.41) Isto implica que

d dt[r(t)e

−Kt_{] =}_e−Kt_{[ ˙}_r₍_t₎

−Kr(t)]_≤0, (3.42)

assim que

0_≤r(t)e−Kt

≤r(t0)e−Kt0 _{= 0} _{para todo t}_≥_t0, _(3.43)

implicando quex1(t) = x2(t).

3.2.5 Teorema de unicidade de Peano

Discutiremos agora o Teorema de unicidade de Peano que assume uma condi¸c˜ao aparentemente diferente na f(t, x), tais como crescimento ou decrescimento no que diz respeito `ax.

Teorema 3.2.10. (Teorema de unicidade de Peano). Seja f(t, x) cont´ınua em_ℜ+: t0 _≤ t _≤ t0 +a,_|x₋x0_{| ≤} b e não crescente em x para cada t fixo em [t0, t0 +a]. Então, o problema de valor inicial (3.1)tem no máximo uma solu¸cão em [t0, t0+a]. [1]

Demonstra¸c˜ao:Suponhax1(t) ex2(t) duas solu¸c˜oes de (3.1) as quais diferem em algum lugar em [t0, t0+a]. Assumimos que,

x2(t)> x1(t) para algum t2 _∈ (t0, t0+a), (3.44) e sejat1 o maior ponto em em [t0, t2) tal que

x1(t) = x2(t) em t1. (3.45)

Assim, x2(t)> x1(t) em (t1, t2).

Assim, para todo t_∈(t1, t2), temos

(36)

e por isso

˙

x1(t)_≥x2˙ (t). (3.47)

Isto implica que a fun¸c˜ao

φ(t) =x2(t)₋x1(t) (3.48) é não crescente. Além disso, uma vez que φ(t1) = 0, temos φ(t) _≤ 0 em [t1, t2], O que contradiz o fato que φ(t) = x2(t)₋x1(t) > 0. Esta contradi¸cão prova que

x1(t) =x2(t) em [t0, t0+a].

O resultado acima ´e na verdade um caso particular do Teorema da condi¸c˜ao de Lipschitz unilateral quando a constante de Lipschitz for igual a zero.

O “não crescimento” def no teorema acima não pode ser substitu´ıda por “não decrescimento”.

3.2.6 Condi¸

c˜

ao de Osgood

Unicidade para (3.1) é garantida se a condi¸cão de continuidade Lipschitz (2.16) no Teorema 2.4.1 é Substitu´ıda pela seguinte condi¸cão de Osgood, na qual apre-sentaremos duas provas diferentes, mas antes demonstraremos o seguinte Teorema encontrado em [1].

Teorema 3.2.11.Sejawuma fun¸cão cont´ınua e não decrescente no intervalo[0,_∞) e w(0) = 0, w(z)>0 para z >0. Além disso,

limǫ→0+

Z α

ǫ

dz

w(z) =∞, α > 0. (3.49)

Seja φ(t) uma fun¸cão cont´ınua não negativa em [0, a]. Então,

φ(t)_≤

Z t

0

w(φ(τ))dτ, 0 < t _≤a (3.50)

implica queφ(t) = 0 em [0, a].

(37)

Φ(t) = max 0≤τ≤t φ(τ)

e assuma que Φ(t)>0 para 0< t_≤a. Ent˜ao,

φ(t)_≤Φ(t) e para cadat existe um t1 _≤t tal que

φ(t1) = Φ(t).

Da´ı, temos

Φ(t) =φ(t1)_≤

Z t1

0

w(φ(τ))dτ _≤

Z t

0

w(Φ(τ))dτ, (3.51)

i.e., a fun¸c˜ao crescente Φ(t) satisfaz a mesma desigualdade que φ(t). Vamos definir

¯ Φ(t) =

Z t

0

w(Φ(τ))dτ,

ent˜ao ¯Φ(0) = 0, Φ(t)_≤Φ(¯ t) e ¯

Φ′(t) =w(Φ(t))_≤w( ¯Φ(t)). Da´ı, para 0< δ < a, temos

Z a

δ

¯ Φ′

(t)

w( ¯Φ(t))dt ≤ a − δ < a. (3.52) No entanto de (3.49), segue-se que

Z a

δ

¯ Φ′(t) w( ¯Φ(t))dt=

Z α

ǫ

dz

w(z), Φ(¯ δ) = ǫ, Φ(¯ a) =α (3.53)

torna-se infinita quandoǫ_→0 (δ_→0). Esta contradi¸c˜ao mostra que Φ(t) n˜ao pode ser positiva e assim Φ(t)_≡0, e φ(t) = 0 em [0, a].

Teorema 3.2.12. (teorema de Osgood) Sejaf(t, x)cont´ınua em_ℜpara todo(t, x1),(t, x2)_∈

ℜ ela satisfaz a condi¸c˜ao de Osgood

|f(t, x1)−f(t, x2)| ≤w(|x1−x2|), (3.54)

(38)

no m´aximo uma solu¸c˜ao em [t₋t0]≤a.

Provemos este teorema de duas maneiras diferentes.

A Primeira demonstra¸c˜ao encontrada em [1]. Suponhax1(t) ex2(t) duas solu¸c˜oes de (3.1) em [t₋t0]_≤a. Devemos mostrar quex1(t) = x2(t) em [t0, t0+a]. De (3.54) segue-se que

|x1(t0+t)₋x2(t0+t)_{| ≤}

Z t0+t

t0

|f(t, x1(τ))₋f(t, x2(τ))_|dτ, (3.55)

≤

Z t0+t

t0

w(_|x1(τ)₋x2(τ)_|)dτ (3.56)

=

Z t

0

w(_|x1(z+t0)−x2(z+t0)|)dz. (3.57)

Parat em [0, a], vamos definirφ(t) =_|x1(t+t0)₋x2(t+t0)_|. Então, a fun¸cão cont´ınua não negativa φ(t) satisfaz a desigualdade (3.50), e portanto, o Teorema 3.2.11 implica queφ(t) = 0 em [0, a], i. e.,x1(t) = x2(t) em [t0, t0+a]. Se t está em [t0₋a, t0] então a prova permanece a mesma exceto que precisamos definir a fun¸cão φ(t) = _|x1(t0₋t)₋x2(t0₋t)_| em [0, a].

E a Segunda demonstra¸c˜ao encontrada em [7]. Consideremosr(t) =_|x1(t)₋x2(t)_|2. Temosr(t0) = 0 e assumimos por contradi¸c˜ao que r(t)>0 parat _∈(t0, t0+a) para alguma >0.

˙

r(t) = 2(x1(t)₋x2(t)).( ˙x1(t)₋x2˙ (t)) (3.58) = 2(x1(t)₋x2(t)).(f(t, x1(t))₋f(t, x2(t))). (3.59) Usando a condi¸c˜ao de Osgood e integrando em rela¸c˜ao a t obtemos

r(t)_≤2

Z t

t0

p

r(s)w(r(s))ds. (3.60)

Uma vez que estamos assumindo que pr(s) = _|x1(t)₋x2(t)_{| ∈} L1₍_{t0, t0} ₊_a_{) e} aplicamos uma extens˜ao do lema de Gronwall, segue-se o seguinte. Defina

R(t) = 2

Z t

t0

p

r(s)w(r(s))ds. (3.61)

(39)

˙

R(t) = pr(t)w(r(t))_≤pr(t)w(R(t)), (3.62)

onde a ´ultima desigualdade resulta de (3.60) da qual obtemos

˙ R(t) w(R(t)) ≤

p

r(t) t > t0. (3.63)

Vamos definir

Ω(z) =

Z 1

z

1

w(r)dr (3.64)

e observamos que Ω(z) est´a bem definida para z > 0, satisfaz ˙Ω(z) = −1

w(z) e Ω(z)↑ +_∞ quando z _↓0, devido a condi¸c˜ao de Osgood. Integrando (3.63) deduzimos que para todot0 < s < t temos

−Ω(R(t)) + Ω(R(s))_≤

Z t

s

p

r(τ)dτ, (3.65)

que, contudo, n˜ao se pode garantir para s muito perto de t. De fato, uma vez que R(s)_↓ 0 quandos _↓t0, neste caso ter´ıamos Ω(R(s))_↑+_∞ quando s_↓ t0 enquanto

a integral no lado direito permanece finita.

No Teorema 3.2.12 a condi¸cão de que a fun¸cão wé não decrescente é um fato supérfluo. Para mostrar isso veremos o seguinte resultado que de certo modo com-plementa o Teorema 3.2.14.

Teorema 3.2.13. Seja a fun¸c˜ao w(x) > 0 cont´ınua para x0 < x _≤ x0 +β para algum β > 0 e w(x0) = 0. Al´em disso, seja a integral R_xα

0+ǫ

dz

w(z) divergente quando ǫ_→0+_{. Ent˜ao, o problema de valor inicial}

  

˙

x=w(x)

x(t1) =x1 (3.66)

onde x0 < x1 _≤ x0 +β tem uma única solu¸cão. Esta solu¸cão x(t) é tal que x0 < x(t)_≤ x0+β e tende para x0 quando t _{→ −∞}. Além disso, se R_x₀₊_ǫ_wdz₍_z₎ converge quando ǫ_→0+_{, então existe um n´}_{umero infinito de solu¸cões de} ₍₃_._38).

(40)

Z x(t)

x1 dz

g(z) = (t−t1). (3.67)

Uma vez que w(x) está definida somente para x0 _≤ x _≤ x0 +β, é necessário que x0 _≤ x(t) _≤ x0 +β. De (3.67) e o fato de que w é cont´ınua e w(x) > 0 para x0 < x_≤ x0+β, encontramos que x(t) existe enquanto x0 < x(t)_≤x0+β. Já que a equa¸cão (3.67) define somente candidatos para uma solu¸cão (implicitamente), e uma vez que por substitui¸cão direta dá uma solu¸cão, segue-se que para (3.66), (3.67) define a solu¸cão única.

Para mostrar que limt→−∞x(t) =x0, onde

lim

ǫ→0+

Z x1

x0+ǫ dz

w(z) =∞ (3.68)

procedemos como segue. O lado esquerdo de (3.67) é finito, desde que x0 < x(t)_≤ x0+β. Como a integral (3.68) diverge, esta solu¸cão x(t) não pode tornar-sex0 para um valor finito det e ao mesmo tempo satisfazer (3.67). Assim, x0 < x(t)_≤x0+β para todo t < t1. Quando t _{→ −∞} o lado direito de (3.67) tende para _−∞, e por-tanto limt→−∞x(t) =x0.

Desde que w(x0) = 0, claramente x(t) _≡ x0 é uma solu¸cão de (3.38). Se existe uma outra solu¸cão φ(t) de (3.38) tal que x0 < φ(t) ≤ x0 +β para t 6= t0, então segue-se que

lim

ǫ→0+

Z φ(t)

x0+ǫ dz

w(z) = (t−t0). (3.69)

Se a integral em (3.68) diverge, então (3.69) não define uma fun¸cão. Se a integral em (3.68) converge, então a equa¸cão (3.69) define uma fun¸cão; de fato, então existe uma fam´ılia de solu¸cões φc(t) de (3.38) definida por

(

φc(t) =x0, t≤c

Rφc(t)

x0

dz

w(z) = (t−c), x > c

(3.70)

para todoc_≥t0. Aqui, entende-se que

Z φc(t)

x0

dz

w(z) = limǫ→0+

Z φc(t)

x0+ǫ dz

w(z), (3.71)

onde esta integral converge.

Exemplo 3.2.2.: Considere mais uma vez o problema de valor inicial

˙

x=x2/3

(41)

Exemplo 3.2.3.: Considere o problema de valor inicial

˙ x=Lx

x(0) = 0 (3.73)

OndeL >0. Para este problema escolhemosw(z) = Lz, que é claramente cont´ınua e não decrescente no intervalo [0,_∞). Além disso, uma vez que w(0) = 0, w(z)>0 para z > 0, e limǫ→0+Rα

ǫ dz w(z) =

1

Llimǫ→0+ln

1

ǫ = ∞. Esta fun¸c˜ao w(z) satisfaz as

condi¸c˜oes do Lema (3.2.11). Em seguida, para qualquer x1 e x2 temos

|f(t, x1)₋f(t, x2)_|=_|Lx1 ₋Lx2_|=w(_|x1₋x2_|) (3.74)

e da´ı a condi¸cão de Osgood (3.49) é também satisfeita. Portanto, do Teorema 3.2.12 o problema (3.73) tem uma única solu¸cão, a saber x(t)_≡0.

Exemplo 3.2.4.: Considere o problema de valor inicial ˙x=f(t, x), x(0) = 0 onde

f(t, x) =

−xlnx, 0< x_≤ 1

e

0, x= 0. (3.75)

Note que esta fun¸cão não satisfaz a condi¸cão de Lipschitz, logo o Teorema de unici-dade Lipschitz não é aplicável. Para este problema escolhemos

w(z) =

  

−zlnz, 0< z _≤ 1

e

0, z = 0 1

e, z >

1

e

.

Claramente, w(z) é cont´ınua e não decrescente em [0,_∞) com w(0) = 0, w(z) > 0 para z >0. Além disso, temos

lim

ǫ→0+

Z 1

ǫ

dz

g(z) = limǫ→0+

Z 1

ǫ

dz

−zlnz = limǫ→0+

Z 1

ǫ

ln(ln(1

ǫ)) =∞.

Assim, esta fun¸cão w(z) satisfaz as condi¸cões do lema (3.2.11). Agora, vamos veri-ficar a condi¸cão (3.54). Para isto notemos que

d2_f dx2 =−

1

x <0, 0< x≤ 1 e,

e portantof é côncava. Seja 0< x1−x2 < x2 < x1 ≤ 1_e, então segue-se que f(t, x1₋x2)₋f(t,0)

x1−x2 ≥

f(t, x1)₋f(t, x2) x1 −x2

,

(42)

−(x1₋x2) ln(x1₋x2)_{≥ −}x1lnx1+x2lnx2 e portanto

|f(t, x1)₋f(t, x2)_|=_|(₋x1lnx1)₋(₋x2lnx2)_{| ≤ − |}x1 ₋x2_|ln_|x1₋x2_|=w(_|x1₋x2_|). Assim, para o problema (3.75) o Teorema de unicidade de Osgood ´e aplic´avel.

3.2.7 Integral divergente

Teorema 3.2.14. Seja a fun¸c˜ao f(x)cont´ınua no intervalo_|x₋x0_{| ≤}b, ef(x0) = 0. Al´em disso, seja f(x)₆= 0 para x0 < x_≤x0+b e a integral

Z x0+b

x0

dz

f(z) (3.76)

é divergente. Então, não existe solu¸cão para o problema de valor inicial (3.77)

  

˙

x=f(x) x(t0) =x0

(3.77)

a n˜ao ser a solu¸c˜ao constantex(t) = x0 [1].

Demonstra¸cão: Assuma que existe uma solu¸cão x(t) ₆= x0 do problema de valor inicial (3.77). Então, seja (considerar um de quatro casos ) à direita de t0 um pontot1 comx0 < x(t1) =x1 < x0+b. Assim, pela equa¸cão diferencial segue-se por separa¸cão de variáveis que

Z x(t)

x1 dz

f(z) = (t−t1) (3.78)

pelo menos desde que x(t) satisfaz x0 < x(t) ≤ x0+b. Assume que ¯t é o primeiro ponto à esquerda det1 com x(¯t) =x0. Então, (3.78) leva a uma contradi¸cão, porque quando t _→ ¯t a integral no lado esquerdo de (3.78) tende para o infinito enquanto

que o lado direito permanece limitado. .

(43)

˙ x= 2x

x(0) = 0 (3.79)

tem uma ´unica solu¸c˜ao x(t)_≡0, e a integral R₀±αdz

z, (α > 0) deverge. Enquanto

que o problema

˙

x=x2/3

x(0) = 0 (3.80)

tem um n´umero infinito de solu¸c˜oes e a integral R₀±α_zdz2/3, (α > 0) converge.

3.2.8 f

autˆ

onoma, cont´ınua e positiva

Sef :R_→R+ _{é cont´ınua e positiva então a equa¸cão ˙}_x₌_f₍_x_{) tem unicidade} [17].

De fato a positividade de f é localmente equivalente à condi¸cão f(x0)>0.

Demonstra¸c˜ao: Fixe o ponto (a, b) _∈ R2_{, e suponha que} _x₍_a_{) =} _b _{e ˙}_x ₌ f(x(t)) para todo t no intervalo J, a _∈ J. E seja F a antiderivada de 1_f que tem F(b) =a. Pela regra da cadeia,

d

dtF(x(t)) = ˙F(x(t)) ˙x(t) = ˙ x(t)

f(x(t)) = 1. (3.81)

AssimF(x(t))₋té constante emJ. Uma vez queF(b) = aex(a) =b, esta constante é 0. ComoF é estritamente crescente, concluimos que x(t) = F−1₍_x_{) em} _J_.

3.2.9 Vari´

aveis separ´

aveis

Teorema 3.2.15. Seja a fun¸cãof(t, x) = u(t)v(x)cont´ınua no dom´ınio_ℜ, ev(x)₆= 0. Então, o problema de valor inicial (3.1) tem uma única solu¸cãox(t) =V−1₍_U₍_t_)), onde U(x) = R_tt

0u(τ)dτ e V(x) =

Rx x0

dt

v(t), desde que (t, U(t))∈ ℜ [1].

Demonstra¸c˜ao: Desde que v(x)₆= 0, x˙

v(x) =u(t), e segue-se que

V(x) =

Z x

x0 dz v(z) =

Z t

t0

(44)

Obviamente, a fun¸cão V(x) é estritamente monótona, e a conclusão segue pelo

Te-orema da fun¸c˜ao inversa .

3.2.10 Condi¸

c˜

ao de Majorana

[16] Estabelece uma condi¸cão necessária para a não unicidade do problema de valor inicial (3.1) e conseqüentemente um novo critério de unicidade que não requer nenhuma condi¸cão especial na diferen¸ca f(t, x1)₋f(t, x2).Pode-se tentar mostrar unicidade pela análise da equa¸cão algébrica 3.83

u₋x0 + (p−t0)f(p, u) = 0 (3.83)

e que depende só dos dados do problema original, onde u é uma icógnita e p um parâmetro cuja fun¸cão será especificada em seguida.

Assumimos o operadorf :_{ℜ →}R_{, onde}

ℜ=I_×R_, _I _{= [}_{t0, t0}₊_a_]_, _(3.84)

sendoa um n´umero positivo dado, e R_{denota a reta real.}

Teorema 3.2.16. Seja a fun¸cão f cont´ınua com respeito a t, e tal quef(t, x0) = 0 para todo t _∈ I. Assuma que o problema de valor inicial 3.1 admite duas solu¸cões diferentes, definidas em [t0, t0+a]. Então para todo ǫ > 0, existe p_∈]t0, t0+a] tal que(3.83) tem pelo menos duas ra´ızes diferentes u com _|u₋x0_|< ǫ .

Demonstra¸cão:E óbvio que (3´ .1) é satisfeito pelas constantesp=t0eu=x0; entretanto, assumimos que existe a solu¸cão z(t) de (3.1) diferente da solu¸cão cons-tantex0.

Seja ǫ >0 dado. Desde que u=x0 é uma solu¸cão de (3.1) para todo p_∈I, é suficiente para provar a existence de p_∈[t0, t0+a], para o qual (3.1) é stisfeito por algumu₆=x0, |u−x0|< ǫ.

Seja a fun¸cão real A definida em [t0, t0 +d] colocando A(t0) = 0 e A(t) = (z(t)₋x0)/(t₋t0) para t ₆= t0. Claramente a fun¸cão A é cont´ınua em [t0, t0 +a], diferenciável em ]t0, t0+a[, e temos

˙

A(t) = 1

(45)

para todot_∈]t0, t0+a[.

Agora, fixe um ponto t2 ∈]t0, t0 +a[ com z(t2) 6= x0, tal que |z(t)−x0| < ǫ para todot_∈[t0, t2], e denote

t1 =sup{x∈[t0, t2] :A(t) = 0}. (3.86) Notamos quez(t1) = x0 ez(t)₆=x0 para todot _∈]t1, t2[.

Neste ponto existem duas possibilidades.

Se existe p _∈]t1, t2[ tal que ˙A(t) = 0, então é claro a partir de (3.85) que, para um tal p, (3.1) é satisfeito por u =z(p). portanto, a prova é realizada apenas tomando estes pe u.

Caso contr´ario, se ˙A(t) ₆= 0 para todo t _∈]t1, t2] (uma vez que ˙A(t) tem sinal constante em ]t1, t2] ), ent˜ao colocamos u=z(t2)(₆=x0), e defina

g(t) = (t₋t0)f(t, u)₋u+x0 (3.87) para todot _∈[t0, t0+a]. Em seguida, notamos que se ˙A(t)>0 para todot∈]t1, t2[, ent˜ao A(t2)> A(t1) = 0, uma vez que u > x0 e conseq¨uentemente g(t0) = ₋u+x0. Por outro lado, temosg(t2) = (t2₋t0)2_A˙₍_t2₎_>_0.

(46)

Cap´ıtulo 4

M´

etodos num´

ericos para resolu¸

c˜

ao de

EDO

“A classe de equa¸cões diferenciais que são integráveis por quadratura é extre-mamente restrita; por esta razão, desde a época de Euler, métodos aproximados se tornaram muito importantes na teoria de equa¸cões diferenciais” [8].

Neste cap´ıtulo discutimos o m´etodo de Euler para aproxima¸c˜ao do P V I

˙

x=f(t, x)

x(0) = 0 (4.1)

4.1 O m´

etodo de diferen¸

cas finitas

O método de diferen¸cas finitas se baseia em transformar o problema de encon-trar a solu¸cão exata de uma equa¸cão diferencial em um problema de resolver um sistema onde as derivadas de suas equa¸cões são aproximadas por diferen¸cas entre va-lores da solu¸cão discretizada, usando a série de Taylor como ferramenta matemática principal.

4.2 O m´

etodo de Euler

(47)

co-4.2 O m´etodo de Euler 39

nhecemos.

Euler deduziu um processo iterativo que permitia determinar, de forma aproxi-mada, a solu¸cão de um problema de valor inicial num determinado ponto. A demons-tra¸cão rigorosa de que, de fato, o processo por ele apresentado conduzia à solu¸cão da equa¸cão só foi apresentada mais tarde, em 1824, por Augustine Cauchy (1789-1857) e melhorada por Rudolf Lipschitz (1832-1908). No entanto, nem assim, o processo apresentado por Euler se tornou popular. A t´ıtulo de exemplo, Karl Weierstrass (1815-1897), famoso matemático alemão do século XIX trabalhou nestes assuntos sem conhecer os trabalhos de Cauchy e Lipschitz [9].

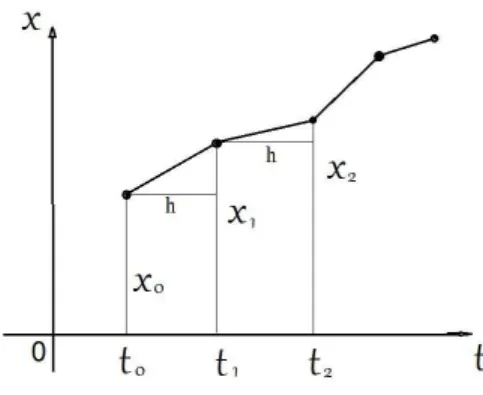
O método de integra¸cão aproximada de Euler, consiste no fato de que a curva integral desejada da equa¸cão diferencial ˙x = f(t, x) que passa através do ponto (t0, x0) é substitu´ıda por uma linha poligonal composta por segmentos de reta, ver figura (4.1), cada segmento dela é tangente a curva integral em um de seus pontos extremos. Onde aplicando este método de cálculo aproximado dos valores da solu¸cão desejadax(t) no ponto t=T, o segmento t0 _≤t _≤T (se T > t0) é subdividido em n partes iguais pelos pontos t0, t1, t2, ... , tn−1, tn, onde tn = T. O tamanho de

cada subdivis˜ao tn+1−tn=h ´e chamado de passo da malha. Denotamos por ¯xn os

valores aproximados da solu¸c˜ao desejada nos pontostn.

Figura 4.1 linha poligonal composta por segmentos de reta

Para calcular x1, no intervalo t0 _≤ t _≤ t1 substitua a curva integral desejada por um segmento tangente a ela no ponto (t0, x0). Uma vez que, x1 =x0+hx0˙ onde

˙

x0 =f(t0, x0) ver figura (4.1).

De forma similar, calculamos:

x2 =x1+hx1˙ onde x˙ =f(t1, x1); (4.2)

(48)

4.2 O m´etodo de Euler 40

...

xn=xn−1+hx˙n−1 onde x˙ =f(tn−1, xn−1); (4.4)

Se T < t0, o esquema de cálculo permanece o mesmo, mas o intervalo de calcula¸cãoh é negativo.

´

E natural esperar que quando o intervalo de integra¸cão decresse, i.e., h _→ 0, o método de Euler se torna cada vez mais preciso no cálculo da solu¸cão exata.

4.2.1 Erro local e erro global

Nesta se¸cão consideramos a solu¸cão exata x(t) com condi¸cão inicial x(0) e solu¸cão aproximada ¯xn(t) com condi¸cão inicial aproximada ¯x0, e calculamos o erro

cumulativo en = ¯xn−x(tn) no passo iterativo n´umero n. Como veremos, este erro

contém duas contribui¸cões: uma devido à discretiza¸cão, e a outra devido ao erro iniciale0 = ¯x0₋x(0).

O erro cometido ao se usar o método de Euler no cálculo dex1é obtido a partir do resto da fórmula de Taylor, ou seja, (t1−t0)2

2! x¨(ξ); t0 < ξ < t1. Como t1 −t0 =h, usa-se a seguinte nota¸c˜ao para o erro:e1 = h2

2!x¨(ξ). Numa etapande c´alculos tem-se analogamente

en=

h2

2!x¨(ξ), tn−1 < ξ < tn. (4.5) A expressão (4.5) é denominada erro local de truncamento [2]. A análise do erro é baseada na indu¸cão: para todo n _∈ N estudamos o erro ao se passar da etapa n para a etapan+ 1.

Seja en = ¯xn−x(tn) o erro total cometido na etapa n, onde ¯xn ´e a solu¸c˜ao

aproximada ex(tn) a solu¸c˜ao exata. O acr´escimo no erro total ao se passar da etapa

n `a etapan+ 1 ´e

en = ¯xn−x(tn) (4.6)

en+1 = ¯xn+1−x(tn+1) (4.7) en+1−en= ¯xn+1−x¯n

| {z }

hf(tn,x¯n)

− x(tn+1) +x(tn)

| {z }

hf(tn,x(tn))+h_2!2f˙(ξ,x(ξ)), tn<ξ<tn+1

(4.8)

segue-se que