Termodinâmica de um gás de fótons no contexto de eletrodinâmicas não-lineares

(1)

Universidade Federal do Rio Grande do Norte

DISSERTAC¸ ˜AO DE MESTRADO

Termodinˆ

amica de um G´

as de F´

otons no Contexto

de Eletrodinˆ

amicas N˜

ao-Lineares

Pierre Niau Akmansoy

Orientador

Prof. Dr. L´eo Gouvˆea Medeiros

(2)

Agradecimentos

Aos meus pais por me terem dado o apoio e a oportunidade de estudar, entre muitas outras coisas.

`

A Helena pela sua paciˆencia, companheirismo e presen¸ca em todos os momentos que precisei.

Ao pessoal da Lidia pelo seu companheirismo.

Ao meu orientador Prof. Léo Medeiros pela sua excelente orienta¸cão. Aos professores Gandhi e Jafelice pelo seu tempo, disposi¸cão e ajuda. Ao pessoal da sala Jayme Tiomno e ao das outras salas.

`

A CAPES, pelo apoio financeiro.

(3)

Resumo

Esta disserta¸cão tem como objetivo obter um formalismo geral para a análise das propriedades de um gás de fótons no contexto de teorias eletrodinâmicas não-lineares (NLED). Para isto obtemos, através da análise sistemática das propriedades do eletromagnetismo de Maxwell (EM), a dependência geral de uma Lagrangiana que descreve este tipo de teorias. A partir desta Lagrangiana deduzimos, no con-texto da teoria clássica de campos, a rela¸cão de dispersão que os fótons devem seguir em termos do campo eletromagnético de fundo e das propriedades que ca-raterizam uma NLED. É importante ressaltar que, para a obten¸cão da rela¸cão de dispersão, é adotada uma aproxima¸cão de tal maneira a permitir a separa¸cão do campo eletromagnético total em um campo de fundo forte e uma perturba¸cão. Uma vez que a rela¸cão de dispersão é obtida, é seguido o procedimento estat´ıstico de Bose-Einstein padrão levando às rela¸cões para a densidade de energia e pressão. É verificado que a equa¸cão de estado padrão de um gás de fótons no contexto do EM continua válida. Em seguida, são realizados dois exemplos onde são calculadas as propriedades termodinâmicas no contexto de duas NLED, a de Born-Infeld e uma aproxima¸cão quadrática. A primeira sendo escolhida devido à vasta literatura exis-tente ao seu respeito e, a segunda, devido a ser uma aproxima¸cão de primeira ordem de uma grande classe de NLED. Ademais, ambas são escolhidas por sua simplici-dade. Finalmente, os resultados obtidos a partir dos exemplos são comparados com o EM e interpretados, sugerindo possibilidades de testes de consistência interna das NLED e motivando o desenvolvimento da versão quântica do formalismo.

(4)

Abstract

(5)

Introdu¸c˜ao 1

1 Eletrodinˆamica N˜ao-Linear 6

1.1 Eletromagnetismo de Maxwell . . . 6

1.1.1 Equa¸c˜oes de Maxwell . . . 6

1.1.2 Deriva¸c˜oes em nota¸c˜ao vetorial . . . 7

1.1.3 Deriva¸c˜oes em nota¸c˜ao covariante . . . 11

1.1.4 Lagrangiana do eletromagnetismo de Maxwell . . . 15

1.2 Extens˜oes da eletrodinˆamica de Maxwell . . . 18

1.2.1 Lagrangiana geral para as NLED . . . 19

1.2.2 Equa¸c˜ao de movimento para uma NLED . . . 20

1.2.3 Rela¸cão de dispersão geral para o fóton . . . 21

2 Procedimento Estat´ıstico 24 2.1 Ensemble macrocanˆonico . . . 24

2.2 Estat´ıstica de Bose-Einstein . . . 27

3 Resultados e Discussão 31 3.1 Propriedades termodinâmicas para o gás de fótons em uma NLED arbitrária . . . 32

3.2 Lagrangiana de Born-Infeld e Lagrangiana quadr´atica . . . 34

3.2.1 Lagrangiana de Born-Infeld . . . 34

3.2.2 Lagrangiana quadr´atica . . . 36

3.2.3 Interpreta¸c˜ao dos resultados . . . 39

4 Conclus˜ao 42

A Deriva¸cão da Rela¸cão de Dispersão 44

B Base Linearmente Independente 52

C Rela¸c˜ao de Dispers˜ao Expl´ıcita 55

(6)

D Potencial Macrocanˆonico Incluindo Birrefringˆencia 58

E Obten¸c˜ao do Potencial Macrocanˆonico 60

F Grandezas Termodinˆamicas das NLED 65

(7)

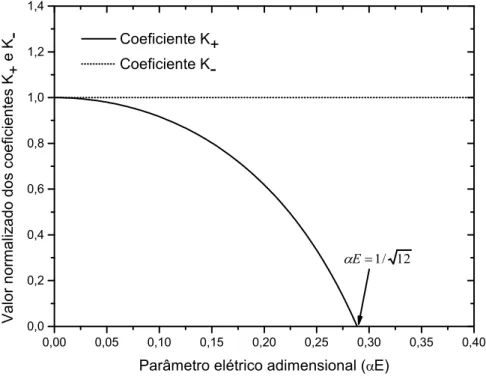
3.1 Gr´afico dos coeficientes K+ e K− do caso eletrost´atico do modelo

quadrático . . . 38 3.2 Gráfico da densidade de energia para caso eletrostático . . . 39 3.3 Gráfico da densidade de energia para caso magnetostático . . . 41

(8)

O eletromagnetismo de Maxwell (EM) é uma das teorias mais bem sucedidas da história da f´ısica. Classicamente, é capaz de descrever todos os fenômenos eletro-magnéticos conhecidos, incluindo a cria¸cão e propaga¸cão de ondas eletromagnéticas. Sua versão quântica, a QED, se revelou igualmente bem sucedida, obtendo resulta-dos com precisão de até dez partes em um bilhão [1]. Este modelo serviu como base para as atuais teorias que descrevem as intera¸cões fortes e fracas do modelo padrão. Mesmo assim, desde sua cria¸cão na metade do século XIX, uma série de extensões e formula¸cões alternativas come¸caram a surgir com motiva¸cões diversas, dentre os quais podemos citar: problema de divergência clássica para o potencial Coulombiano [2, 3, 4, 5], v´ınculos experimentais sobre a massa do fóton [6, 7, 8, 9], estudo clássico de efeitos de polariza¸cão do vácuo [10] e altera¸cões da eletrodinâmica no contexto de branas [11]. Além disto, o próprio estudo de extensões da eletrodinâmica nos ajuda a entender melhor o EM.

Do ponto de vista de teorias de calibre [12], o EM surge ao impor quatro condi¸cões à sua Lagrangiana: (i) a Lagrangiana deve ser invariante por transforma¸cões de Lorentz; (ii) deve ser invariante por transforma¸cões de calibre associadas ao grupo U(1); (iii) deve depender apenas do campo Aµ _{e da sua primeira derivada} _∂ν_Aµ_;

e (iv) estes termos apenas podem aparecer de forma quadrática. As extensões do EM geralmente surgem ao quebrar pelo menos uma das condi¸cões citadas acima. Violando a primeira destas condi¸cões aparecem termos tensoriais criando dire¸cões preferenciais e efeitos dependentes dos boosts [13, 14, 15, 16]. Por outro lado, a segunda condi¸cão é quebrada se introduzimos um termo de massa para o fóton, como é o caso da eletrodinâmica de Proca [17]. No caso da terceira condi¸cão ser quebrada surge uma extensão do EM conhecida como eletrodinâmica de Podolsky [18, 19, 20]. Finalmente, ao quebrar a quarta condi¸cão, surge uma fam´ılia de extensões chamadas de eletrodinamicas não-lineares (NLED) [21]. Estas são obtidas a partir de Lagrangianas do tipo _L = _L(F, G) onde F = ₋1

4F

µν_F

µν e G = −1₄F˜µνFµν.

Exemplos de NLED são as eletrodinâmicas de Born-Infeld [4, 5] e a eletrodinâmica de Heisenberg-Euler [22].

Modelos de NLED aparecem em diferentes ´areas da f´ısica. A partir da d´ecada

(9)

de 30, é sabido que pares virtuais de elétron-pósitron induzem a auto-intera¸cão do campo eletromagnético. De maneira geral esta auto-intera¸cão é complexa, porém para campos eletromagnéticos que variam lentamente, este efeito foi calculado e da sua interpreta¸cão clássica surgem as NLED [10, 22]. Outra área na qual surge este tipo de teoria é no contexto da teoria das cordas. Usando as propriedades da du-alidade T podemos mostrar que a eletrodinâmica nas D-branas é descrita por uma generaliza¸cão do modelo de Born-Infeld [23, 24, 25, 26]. Como terceiro exemplo, po-demos citar a descri¸cão da propaga¸cão de radia¸cão dentro de materiais. Neste caso, a abordagem não é feita pela formula¸cão Lagrangiana, mas os efeitos não-lineares surgem através de rela¸cões constitutivas não-constantes [27, 28, 29, 30]. Recente-mente, no contexto da double special relativity (DSR), alguns artigos têm estudado as consequências termodinâmicas da modifica¸cão da rela¸cão de dispersão relativ´ıstica [31, 32, 33, 34]. Estes trabalhos são geralmente motivados pela possibilidade de que-bra da simetria de Lorentz na escala de Planck [35, 36]. Uma das caracter´ısticas mais interessantes das NLED é o surgimento de rela¸cões de dispersão modificadas devido à intera¸cão da radia¸cão com um campo eletromagnético de fundo. Este efeito foi primeiramente obtido em [37] e [38] e mais recentemente por [39].

Neste trabalho, usamos o procedimento seguido em [40] para encontrar as rela¸cões de dispersão para o fóton. Assim, o campo eletromagnético fµν _{é separado em um}

campo eletromagn´etico forte de fundoFµν _{e uma perturba¸c˜ao fraca} _ϕµν _{que se}

pro-paga neste meio, ou sejafµν ₌_Fµν₊_ϕµν_{. A partir deste procedimento chegamos a}

uma rela¸cão de dispersão para a radia¸cão que depende do campo eletromagnético de fundo e das propriedades que caracterizam as NLED. Neste contexto, ainda existe a possibilidade, dependendo da forma da Lagrangiana, de surgirem duas rela¸cões de dispersão que estão associadas à polariza¸cão da radia¸cão. Este fenômeno é co-nhecido como birrefringência [46] e irá alterar as propriedades termodinâmicas da radia¸cão.

Encontrada a rela¸cão de dispersão (ou rela¸cões de dispersão) entramos no pro-cesso estat´ıstico que permite determinar as propriedades do gás de fóton. Por se tratar de fótons, usamos a estat´ıstica de Bose-Einstein para calcular a fun¸cão de parti¸cão da radia¸cão no contexto de uma NLED. Como mencionado acima, o efeito de birrefringência deve ser levado em conta neste cálculo. As propriedades termo-dinâmicas encontradas (pressãope densidade de energia ρ) dependem do campo de fundo e da forma da Lagrangiana, porém a equa¸cão de estado da radia¸cão (ρ = 3p) não se altera. Finalmente, aplicamos o procedimento às NLED de Born-Infeld e a uma aproxima¸cão quadrática e comparamos os resultados com a EM. Todos estes resultados podem ser encontrados em [42].

(10)

Eletrodinˆ

amica N˜

ao-Linear

Neste cap´ıtulo analizamos os principais resultados do eletromagnetismo de Maxwell (EM) em nota¸cão vetorial para depois obtê-los novamente em uma nota¸cão explicita-mente covariante. Este procedimento, além de permitir apreciar a simplicidade desta nova nota¸cão, leva naturalmente a uma formula¸cão de mais alto n´ıvel, a formula¸cão Lagrangiana do eletromagnetismo. Historicamente, o eletromagnetismo originou-se a partir de observa¸cões, levando à constru¸cão de leis de forma fenomenológica, como é o caso das leis de Coulomb e de Biot-Savart. Gra¸cas a cientistas como Oersted, Fa-raday, Ampère e Maxwell, entre muitos outros, os fenômenos elétricos e magnéticos foram melhor entendidos, entrela¸cando-os e levando a uma nova descri¸cão, a de cam-pos (em ocam-posi¸cão à de a¸cão a distância). Com a previsão das ondas eletromagnéticas, sua descoberta por Hertz e posteriormente o advento da relatividade restrita, houve um novo entendimento do espa¸co em que vivemos. Este deixou de ser euclidiano para dar lugar ao espa¸co minkowskiano (não levando em conta a curvatura devido a distribui¸cões de massa-energia).

Uma vez feita a análise do EM e a compara¸cão das duas nota¸cões, será proposta uma Lagrangiana a partir da qual veremos que os resultados do EM são obtidos em conjunto com a equa¸cão de Euler-Lagrange obtida da Teoria de Campos. Em seguida, é obtida a forma funcional das Lagrangianas que permitem descrever teorias não-lineares de eletrodinâmica. Com isto, e baseados nos procedimentos de [38], estaremos aptos a obter uma rela¸cão de dispersão geral para o fóton. Neste cap´ıtulo as unidades naturais não são usadas.

1.1 Eletromagnetismo de Maxwell

1.1.1 Equa¸c˜oes de Maxwell

O eletromagnetismo de Maxwell é uma teoria de campo clássico (naturalmente rela-tiv´ıstico) pois explica como distribui¸cões de cargas interagem através de campos, os

(11)

campos elétricos e de indu¸cão magnética. Estes são definidos pela for¸ca de Lorentz como a for¸ca por unidade de carga que um corpo carregado sente, pois esta indica como cargas em movimento interagem com os campos. A teoria é sintetizada nas chamadas equa¸cões de Maxwell (em unidades Gaussianas)†_,

⃗

∇ ·E⃗ (⃗r, t) = 4πρ(⃗r, t), (1.1) ⃗

∇ ×E⃗(⃗r, t) + 1 c

∂ ⃗B(⃗r, t)

∂t = 0, (1.2)

⃗

∇ ·B⃗ (⃗r, t) = 0, (1.3) ⃗

∇ ×B⃗(⃗r, t)₋ 1 c

∂ ⃗E(⃗r, t) ∂t =

4π

c ⃗j(⃗r, t), (1.4) onde E⃗ e B⃗ são, respectivamente, os campos elétrico e de indu¸cão magnética e, ρ e ⃗j as densidades de carga e de corrente que geram os campos. A partir destas conseguimos explicar todos os fenômenos de origem eletromagnética. Sua versão quântica, a eletrodinâmica quântica, desenvolvida por Dirac et al., explica com ex-trema precisão fenômenos quânticos como o desvio Lamb do hidrogênio e o momento magnético anômalo do elétron. Estes fatos fazem do eletromagnetismo um bom mo-delo padrão para o desenvolvimento de outras teorias de campo‡_.

1.1.2 Deriva¸c˜oes em nota¸c˜ao vetorial

A primeira vista, em regiões sem fontes, as equa¸cões de Maxwell possuem simetria dual, ou seja, a transforma¸cão dualE⃗ _→B⃗ eB⃗ _{→ −}E⃗ mantêm o grupo de equa¸cões inalteradas. A falta de simetria em regiões com fonte é devido a não existência de monopolos magnéticos.

No caso eletrodinâmico, a equa¸cão (1.3) permite a defini¸cão de um vetor potencial magnético,

⃗

B =_{∇ ×}⃗ A .⃗ (1.5)

Ao substituir esta rela¸c˜ao na equa¸c˜ao (1.2) obtemos,

⃗

∇ ×

(

⃗ E+ 1

c ∂ ⃗A

∂t

)

= 0.

Esta equa¸cão é sempre verdadeira se a grandeza entre parênteses for igual ao gra-diente de uma fun¸cão escalar. Por analogia com a eletrostática, identificamos este

†_{O poder das unidades Gaussianas vem do fato das unidades dos campos (e, consequentemente,}

dos potenciais) serem as mesmas. A vantagem disto é a simetria com a qual as equa¸cões são escritas.

(12)

campo escalar com o potencial elétrico. Com isto, o campo elétrico pode ser escrito em rela¸cão ao vetor potencial magnético e potencial elétrico,

⃗

E =₋_∇⃗ϕ₋ 1 c

∂ ⃗A

∂t. (1.6)

A vantagem imediata da defini¸cão dos potenciais é a redu¸cão da dependência de 6 componentes dos campos para apenas 4 componentes independentes. Há, porém, uma ambiguidade na defini¸cão dos potenciais pois, como é poss´ıvel ver pelas equa¸cões (1.5) e (1.6), o vetor A⃗ e o potencial elétrico ϕ não são definidos de maneira única. Vemos que pela sua defini¸cão o potencial vetor pode ser definido a menos de um gra-diente de uma fun¸cão arbitrária bem comportada, implicando que a transforma¸cão,

⃗

A(⃗r, t)_→A⃗′(⃗r, t) =A⃗(⃗r, t) +_∇⃗λ(⃗r, t),

não altera o campo de indu¸cão magnética. Para o campo elétrico não ser alterado pela transforma¸cão do potencial vetor, o potencial elétrico deve também sofrer uma transforma¸cão,

ϕ(⃗r, t)_→ϕ′(⃗r, t) =ϕ(⃗r, t) +V (⃗r, t),

onde V (⃗r, t), como veremos, está relacionado com λ(⃗r, t). A equa¸cão (1.6), após as transforma¸cões, gera o seguinte v´ınculo entre as novas fun¸cões,

⃗

∇

(

V (⃗r, t) + 1 c

∂λ(⃗r, t) ∂t

)

= 0,

que nos diz que o termo entre parˆenteses n˜ao depende do espa¸co, ou

V (⃗r, t) + 1 c

∂λ(⃗r, t)

∂t =k(t) ⇒ V (⃗r, t) =− 1 c

∂λ(⃗r, t) ∂t ,

onde a fun¸cão k(t) foi embutida na fun¸cão V (⃗r, t). Assim, obtemos a rela¸cão exis-tente entre as fun¸cõesV e λ, e as transforma¸cões se tornam

ϕ′(⃗r, t) =ϕ(⃗r, t)₋1 c

∂λ(⃗r, t)

∂t , (1.7)

⃗

A′(⃗r, t) =A⃗(⃗r, t) +_∇⃗λ(⃗r, t).

(13)

fun¸cãoλ de tal maneira que algumas rela¸cões se simplifiquem. Como exemplo disto, se reescrevemos a equa¸cão (1.4) em termos dos potenciais e obtemos

A⃗′₋_∇⃗

(

⃗

∇ ·A⃗′+ 1 c

∂ϕ′

∂t

)

=₋4π

c ⃗j, (1.8)

onde ´e o operador d’Alembertiano. Se fizermos uso das transforma¸c˜oes (1.7) obtemos

(A⃗+_∇⃗λ)₋_∇⃗

(

⃗

∇ ·A⃗+1 c

∂ϕ ∂t +λ

)

=₋4π c ⃗j,

não alterando a descri¸cão do sistema, porém ganhando um grau de liberdade. Po-demos escolher o parâmetro λ de tal maneira que

⃗

∇ ·A⃗+1 c

∂ϕ

∂t +λ= 0.

No referencial com linha, a escolha do parâmetro faz com que o termo entre parênteses da equa¸cão (1.8) se anule,

⃗

∇ ·A⃗′+1 c

∂ϕ′

∂t = 0, (1.9)

tornando-se

A⃗′ =₋4π

c ⃗j.

Esta escolha de calibre é chamada de calibre de Lorenz e permite deixar as equa¸cões mais simétricas e simples, dado que equa¸cão a análoga para o potencial elétrico é

ϕ′ =₋4πρ.

Esta escolha também permite obter uma das componentes do vetor potencial em termos das outras duas e, com isto, diminui o número de componentes independentes para 3. Porém, a condi¸cão (1.9) não define por completo o conjunto de potenciais

(

ϕ′_{, ⃗}_A′)_{, pois podemos novamente fazer uma transforma¸c˜ao de gauge do tipo}

ϕ′′(⃗r, t) =ϕ′(⃗r, t)₋ 1 c

∂λ′_{(⃗r, t)}

∂t , (1.10)

⃗

A′′(⃗r, t) =A⃗′(⃗r, t) +_∇⃗λ′(⃗r, t), (1.11) e obter a rela¸cão análoga à anterior a partir da equa¸cão (1.11),

⃗

∇ ·A⃗′′+1 c

∂ϕ′′

∂t =λ

′_,

(14)

conseguimos obter um grau de liberdade a mais. De fato, escolhendo λ′ _{na equa¸c˜ao}

(1.10) de tal forma que

ϕ′(⃗r, t)₋ 1 c

∂λ′_{(⃗r, t)}

∂t = 0, resulta em

ϕ′′ _{= 0,}

⃗

∇ ·A⃗′′ = 0.

Isto mostra que a aparente dependência inicial de 6 componentes (3 do campo elétrico e 3 do campo de indu¸cão magnética) se reduz a apenas 2 componentes independentes (2 componentes do potencial vetor magnético)! Este tratamento não é independente do referencial mas as fun¸cões λ e λ′ _{sempre podem ser escolhidas}

para obter estes resultados.

Uma rela¸cão importante é a conserva¸cão da carga elétrica. Ela é obtida mate-maticamente a partir das equa¸cões de Maxwell aplicando o divergente em (1.4) e substituindo o resultado em (1.1), ou seja,

∂ρ

∂t +∇ ·⃗ ⃗j = 0.

Foi poss´ıvel obter esta equa¸cão somente após a introdu¸cãoad hoc do termo 1

c ∂ ⃗E

∂t por

Maxwell na equa¸cão (1.4) que ao mesmo tempo permitiu que as equa¸cões fossem invariantes por transforma¸cões de gauge. Como veremos mais à frente, o fato das equa¸cões serem invariantes por transforma¸cões de gauge implica na conserva¸cão local da carga.

Analizamos agora como os campos se transformam pela mudan¸ca de referencial. Se em um dado referencial S um observador mede os campos E⃗ = (Ex, Ey, Ez) e

⃗

B = (Bx, By, Bz), ent˜ao um observador no referencial S′, que est´a em movimento

com velocidade v na dire¸c˜ao positiva do eixo x do referencialS medir´a os campos Ex′ =Ex, Bx′ =Bx,

E_y′ =γ(Ey−

v cBz

)

, B_y′ =γ(By+

v cEz

)

,

Ez′ =γ

(

Ez+

v cBy

)

, Bz′ =γ

(

Bz−

v cEy

)

.

(15)

1.1.3 Deriva¸c˜oes em nota¸c˜ao covariante

As equa¸cões de Maxwell são covariantes pelas transforma¸cões de Lorentz mesmo na presen¸ca de fontes, como demostrado por Einstein e Poincaré. Este último demos-trou (antes que Minkowski) que as transforma¸cões de Lorentz são nada mais que rota¸cões em um espa¸co quadridimensional unificando, assim, o espa¸co e o tempo.

´

E conveniente expressar as equa¸cões de Maxwell em uma nota¸cão que explicite a covariância e que permita observar propriedades com mais facilidades. Este processo trabalhoso tem o intuito de demostrar o poder e a elegância da nota¸cão covariante. As equa¸cões (1.5) e (1.6) em nota¸cão indicial†‡ _{são escritas como}

Bi ₌_ϵijk_∂ jAk,

e

Ei =₋∂0Ai₋∂iA0,

onde ϵijk _{é o s´ımbolo de Levi-Civita e} _A0 ₌_ϕ_{(x) é o potencial elétrico. Estes dois}

resultados podem ser condensados na seguinte express˜ao§

Fµν ₌_∂µ_Aν

−∂ν_Aµ_, _(1.12)

onde Aµ ₌ (_ϕ_(x)_{, ⃗}_A_(x)) _{´e o quadripotencial e} _∂ µ =

(

∂ ∂(ct), ⃗∇

)

´e o divergente quadridimensional.

O quadripotencial ´e dito contravariante pois, sob transforma¸c˜oes de Lorentz Λµ ν,

se transforma de maneira análoga às componentes xµ _{do vetor posi¸cão,}

x′µ = Λµνx ν

,

A′µ _{= Λ}µ νAν,

onde

Λµ ν =



   

γ ₋γv c 0 0

−γv

c γ 0 0

0 0 1 0

0 0 0 1



   

,

†_{Os ´ındices gregos s˜ao usados para definir componentes de quadrivetores e variam de 0 a 3. Os}

´ındices latinos indicam a parte espacial dos quadrivetores e variam de 1 a 3.

‡_{As grandezas que variam (contravariam) da mesma forma que o vetor de posi¸c˜ao s˜ao indicados}

com ´ındice superior e as entidades que variam (covariam) de maneira semelhante ao operador nabla são representados com ´ındice inferior. Tecnicamente o campo de indu¸cão magnética é um pseudovetor mas como não iremos considerar transforma¸cões de paridade este, para todos os efeitos, se comporta como um vetor.

§_{No espa¸co-tempo de Minkowski o espa¸co e o tempo est˜ao no mesmo n´ıvel hier´arquico. Por}

(16)

representa um boost na dire¸cão do eixox. O divergente quadridimensional se trans-forma de maneira análoga às 1-trans-formas,

x′µ = ¯Λ ν

µxν,

∂µ′ = ¯Λνµ∂ν,

de tal maneira que

¯ Λα

µΛ µ

β =δ α

β.

A rela¸cão entre as componentes do vetor e as componentes da sua 1-forma corres-pondente é dado por meio da métrica†_,

xµ =ηµνxν.

Pelas rela¸c˜oes

Ei =F0i e Bi = 1 2ϵ

i jkF

jk

,

identificamos as componentes do tensor campo eletromagn´etico,

Fµν =



   

0 E1 _E2 _E3

−E1 ₀ _B3 ₋_B2

−E2 ₋_B3 ₀ _B1

−E3 _B2 ₋_B1 ₀



   

. (1.13)

Este tensor é a unifica¸cão dos antigos campos elétrico e indu¸cão magnética em ape-nas uma grandeza chamada de campo eletromagnético. Existe um tensor análogo que contêm as mesmas propriedades denominado de tensor dual do campo eletro-magnético e é obtido através da transforma¸cão dual, definida por

˜

Fµν _≡ 1 2ϵ

µν αβF

αβ

⇒F˜µν =



   

0 B1 _B2 _B3

−B1 ₀ ₋_E3 _E2

−B2 _E3 ₀ ₋_E1

−B3 ₋_E2 _E1 ₀



   

. (1.14)

Nesta nota¸cão, o fato do EM ser invariante por transforma¸cão de gauge é expl´ıcito, pois dada a transforma¸cão

A′µ(x) =Aµ(x) +∂µλ(x),

(17)

onde λ(x) é uma fun¸cão arbitrária, e da defini¸cão deFµν _{dada pela equa¸cão (1.12),}

temos: †

F′µν ₌_∂µ_A′ν

−∂ν_A′µ_,

F′µν =∂µ(Aν +∂νλ)₋∂ν(Aµ+∂µλ), F′µν ₌_∂µ_Aν

−∂ν_Aµ₊_∂µ_∂ν_λ

−∂ν_∂µ_λ,

F′µν =∂µAν ₋∂νAµ, F′µν ₌_Fµν_.

Além disso, mostrar que o campo eletromagnético depende apenas de duas compo-nentes é direto. Dada, novamente, a transforma¸cão de gauge aplicamos o divergente quadridimensional,

∂µA′µ(x) =∂µAµ(x) +λ(x),

e escolhendo λ(x) convenientemente,

∂µA′µ(x) = 0.

Fazendo novamente uma transforma¸c˜ao de gauge,

A′′µ(x) = A′µ(x) +∂µλ′(x), ∂µA′′µ(x) = λ′(x),

e escolhendo λ′_{(x) de tal maneira que}_λ′_{(x) = 0 e}_∂0_λ′_{(x) =} ₋_A′0_{(x) obtemos as} condi¸c˜oes equivalentes,

A′′0(x) = 0 e ∂iA′′i(x) = 0.

O tensor campo eletromagnético tem existência independente da análise temática, é um ente f´ısico. Por isto, suas componentes se transformam de tal ma-neira que independa do sistema de referência. É poss´ıvel, através da equa¸cão (1.12), mostrar que o campo eletromagnético é realmente um tensor,

F′µν ₌_∂′µ_A′ν

−∂′ν_A′µ_,

F′µν = (Λµα∂ α

)(

ΛνβA β)

−(

Λνβ∂ β)

(ΛµαA α

), F′µν _{= Λ}µ

αΛ ν

β

(

∂α_Aβ

−∂β_Aα)

,

F′µν = ΛµαΛ ν

βF αβ

.

†_{A transforma¸cão de gauge é feita apenas no potencial} _Aµ_{, o operador de deriva¸cão não é}

(18)

Notamos que este desenvolvimento só é poss´ıvel em termos de derivadas ordinárias pelo fato do espa¸co ser plano†_{. Os tensores de transforma¸cão Λ}µ

αpodem representar

rota¸c˜oes ou boosts. Fazendo um boost ao longo do eixo x, para comparar com as rela¸c˜oes anteriores, obtemos, para as componentes F′01 _e_F′02_,

F′01= Λ0αΛ1βFαβ,

Ex′ =Ex,

e

F′02 = Λ0αΛ2βF αβ

,

Ey′ =γ

(

Ey−

v cBz

)

.

onde a matriz de transforma¸cão para um boost na dire¸cão de xé dada por

Λµα=



   

γ ₋γβ 0 0

−γβ γ 0 0

0 0 1 0

0 0 0 1



   

,

com β = v

c eγ = (1−β

2₎−12.

Nesta nota¸cão podemos reescrever as equa¸cões de Maxwell em uma nota¸cão simplificada e explicitamente covariante. As equa¸cões (1.1) e (1.4) são obtidas a partir da rela¸cão

∂νFµν =

4π c j

µ_, _(1.15)

onde jµ _{´e a quadricorrente definida como}

jµ₌(_cρ,⃗j)_.

As outras duas equa¸cões se originam da propriedade antissimétrica do tensor campo eletromagnético e são dadas a partir da rela¸cão,

∂αFβγ +∂βFγα+∂γFαβ = 0,

chamada de identidade de Bianchi. Esta rela¸cão pode ser reescrita em termos do tensor dual ˜Fµν_{, deixando o conjunto de equa¸cões mais simétrico,}

∂νF˜µν = 0. (1.16)

A conserva¸cão da carga nesta nota¸cão é obtida contraindo a equa¸cão (1.15) com o divergente quadridimensional que, devido à antissimetria de Fµν_{, resulta em}

∂µjµ= 0.

†_{No caso de espa¸cos curvos as derivadas ordin´arias devem ser substituidas por derivadas}

(19)

1.1.4 Lagrangiana do eletromagnetismo de Maxwell

As equa¸cões de Maxwell foram obtidas partindo de resultados mais fundamentais (resultados experimentais) e reformuladas através das ferramentas matemáticas que surgiram ao longo da história, obtiveram-se novas formula¸cões que permitiram uma melhor visualiza¸cão das propriedades do eletromagnetismo. Foi mostrado o poder, elegância e simplicidade da nota¸cão covariante. Estas equa¸cões, porém, podem ser obtidas fazendo uma liga¸cão com uma generaliza¸cão da formula¸cão Lagrangiana para a mecânica.

A formula¸cão Lagrangiana tem várias vantagens sobre a formula¸cão Newtoniana como tratar com grandezas escalares ao invés de tratar com grandezas vetoriais, ser independente do sistema de coordenadas utilizadas e abordar com simplicidade as simetrias e invariâncias de uma teoria. Além disso, a Lagrangiana é definida a menos do divergente quadridimensional de uma fun¸cão escalar arbitrária, e o funcional a¸cão contém todas as caracter´ısticas do sistema incluindo as condi¸cões de contorno.

O próximo passo é obter a equa¸cão que, a partir de uma Lagrangiana, resulta nas equa¸cões de movimento da teoria. Dado a a¸cão, definida como,

A =

∫

Ldx4,

o princ´ıpio de Hamilton diz que, para uma varia¸cão arbitrária dos graus de liberdade do sistema, a a¸cão se mantêm fixa, ou seja

δA= 0. (1.17)

A fun¸cão_L, chamada de densidade Lagrangiana, ou simplesmente Lagrangiana, é, de maneira geral, fun¸cão do pontox, do campoϕν(x) e da primeira derivada do campo

∂µϕν(x) (a extensão para segundas derivadas (e ordens maiores) é simples (mas não

muito comum na f´ısica) e, no caso do eletromagnetismo, leva à teorias como a de Podolsky. Ao calcular a varia¸cão da a¸cão (mantendo os extremos estacionários) e impondo (1.17) obtemos as equa¸cões de movimento de Euler-Lagrange para campos cont´ınuos,

∂µ

∂_L ∂(∂µϕν)

= ∂L ∂ϕν

. (1.18)

Esta é a equa¸cão que minimiza a a¸cão e, com isto, gera as equa¸cões de movimento certas.

(20)

as propriedades necessárias para restringir as poss´ıveis formas que a Lagrangiana pode ter. As propriedades óbvias das equa¸cões de Maxwell são sua covariancia pe-las transforma¸cões de Poincaré e por transforma¸cões de gauge do quadripotencial. Por este último fato é melhor expressar a equa¸cão (1.15) em termos do quadripo-tencial,

∂ν∂νAµ−∂µ∂νAν =−

4π c j

µ

, (1.19)

e tratar este como o campo fundamental do eletromagnetismo ao inv´es de Fµν_.

Po-demos ver diretamente que esta equa¸cão é linear nos potenciais e somente aparecem segundas derivadas dos potenciais e um termo de fonte. A Lagrangiana pode ser separada em um termo cinético, que descreverá a dinâmica dos campos, e um termo de fonte. Para obter uma equa¸cão deste tipo a partir de (1.18) o termo cinético da Lagrangiana deve

1. apenas depender dos potenciais e da sua primeira derivada, para gerar termos de at´e segunda ordem,

2. o campo e sua primeira derivada podem aparecer apenas de forma quadrática, pois as equa¸cões de campo são lineares.

Da primeira condi¸cão temos que a dependência da Lagrangiana é da forma _L =

L(A, ∂A). Já o fato das equa¸cões de Maxwell serem invariantes por transforma¸cões de gauge implica que a Lagrangiana deve ser invariante ao fazer o campo ir de Aµ

para Aµ₊_∂µ_{λ, i.e.} _δAµ₌_A′µ

−Aµ₌_∂µ_λ,

δ_L= ∂L ∂AµδA

µ₊ ∂L

∂(∂νAµ)

δ(∂νAµ) = 0.

O divergente quadridimensional e a varia¸c˜ao do campo comutam pelo fato deste ´

ultimo atuar no mesmo ponto do espa¸co-tempo, com isto obtemos ∂_L

∂Aµ∂ µ

λ+ ∂L ∂(∂νAµ)

∂ν∂µλ= 0.

A segunda derivada parcial é um tensor de segunda ordem e pode ser expresso em termos da sua parte simétrica e antissimétrica, para com isto aproveitar a simetria das derivadas deλ para eliminar o termo antissimétrico,

∂_L ∂Aµ∂

µ

λ+1 2

[(

∂_L ∂(∂νAµ)

+ ∂L ∂(∂µAν)

)

+

(

∂_L ∂(∂νAµ)−

∂_L ∂(∂µAν)

)]

∂ν∂µλ= 0,

∂_L ∂Aµ∂

µ_λ₊1

2

(

∂_L ∂(∂νAµ)

+ ∂L ∂(∂µAν)

)

(21)

Devido à arbitrariedade da fun¸cão λ, os dois termos devem anular-se de maneira independente. Com isto obtemos as seguintes restri¸cões,

∂_L

∂Aµ = 0 e

∂_L ∂(∂νAµ)

=₋ ∂L ∂(∂µAν)

.

A primeira condi¸cão implica que o termo cinético da Lagrangiana não pode depender explicitamente dos campos Aµ_{, a segunda diz que a dependência das primeiras}

deri-vadas deve ser do tipo antissimétrico. Conhecemos um objeto antissimétrico criado a partir das primeiras derivadas dos potenciais, o tensor campo eletromagnético, logo este é um candidato para a cria¸cão da Lagrangiana. Porém, esta deve ser invariante por transforma¸cões de Lorentz para gerar equa¸cões de movimento covariantes, isto implica que todos os ´ındices devem ser contra´ıdos. E, junto com a segunda condi¸cão, uma poss´ıvel Lagrangiana para descrever o EM no vácuo é

LM =−

1 4F

µν_F µν.

Efetivamente, se submetermos esta Lagrangiana à equa¸cão (1.18) obtemos a equa¸cão (1.19) sem o termo de fonte. Para obter este termo último, adicionamos um termo à Lagrangiana,

LM =−

1 4F

µν_F µν +

4π c jµA

µ_. _(1.20)

´

E interessante ver que a Lagrangiana com o termo de fonte continua mantendo as equa¸c˜oes de movimento invariantes por transforma¸c˜ao de gauge,

δ_LM =jµ∂µλ,

δ_LM =∂µ(jµλ)−λ(∂µjµ),

se e somente se o segundo termo do lado direito ´e identicamente nulo†_{. Como} _λ _´e

arbitr´ario temos a condi¸c˜ao,

∂µ_j µ= 0,

que nada mais é do que a equa¸cão da continuidade para a carga elétrica. Esta equa¸cão implica na conserva¸cão local da carga elétrica e foi obtida naturalmente impondo que a a¸cão de Maxwell seja invariante por transforma¸cão de gauge.

Em diversos casos ´e poss´ıvel obter a forma expl´ıcita da corrente: no caso de uma Lagrangiana de campo de mat´eria espinorial (e.g. QED), na qual foi imposto

†_{O primeiro termo não influencia na a¸cão pois esta é extremizada com os pontos iniciais e finais}

(22)

invariˆancia local de gauge, aplicamos o teorema de Noether e encontramos que esta corrente ´e dada por

jµ =

e cψγ¯ µψ, onde ψ ´e um campo de spin-1

2, e é a carga e γµ são as matrizes gama de Dirac. Vale enfatizar que (1.20) gera somente a rela¸cão (1.15). As equa¸cões (1.16) são naturalmente satisfeitas devido à forma antissimétrica de (1.12).

Rela¸cão de dispersão para o fóton na eletrodinâmica de Maxwell

Sabemos que a partir das equa¸cões de Maxwell podemos obter uma equa¸cão de onda que prevê e descreve a propaga¸cão de ondas eletromagnéticas. A partir das equa¸cões (1.15) e (1.16) no vácuo obtemos a rela¸cão,

ηαβ∂α∂βFµν = 0. (1.21)

Sabemos, também, que na teoria clássica de Maxwell não há termos de auto-intera¸cão, uma onda eletromagnética não vai ter sua energia alterada por um campo de fundo. Propomos então uma onda eletromagnética plana ϕµν _{se propagando na dire¸cão de}

⃗k e com amplitude constante εµν_,

ϕµν ₌_εµν_e−ikαxα_.

O resultado que a equa¸c˜ao de onda (1.21) gera quando aplicada a ϕµν _´e:

ηµνkµkν = 0, (1.22)

que é a rela¸cão clássica de dispersão para o fóton. Esta rela¸cão define o cone de luz que separa os eventos entre causal e não causal.

1.2 Extens˜

oes da eletrodinˆ

amica de Maxwell

Existem vários contextos nos quais aparecem extensões da eletrodinâmica de Maxwell, porém a grande maioria surge ao violar ao menos uma destas quatro condi¸cões,

1. Invariância pelo grupo de Poincaré, 2. Invariânia de gauge,

3. Dependˆencia apenas do campo e da sua primeira derivada, e

(23)

Exemplos de extensões são as eletrodinâmicas de Proca e de Podolsky que apa-recem quando a segunda e a terceira condi¸cões são quebradas respectivamente. Quando quebramos apenas a quarta condi¸cão, surge uma familia de extensões cha-madas de eletrodinâmicas não-lineares (NLED). Exemplos de NLED são as eletro-dinâmicas de Born-Infeld [3, 4] e de Heisenberg-Euler [22].

1.2.1 Lagrangiana geral para as NLED

Para obter uma Lagrangiana que descreva de forma geral as NLED devemos primeiro obter os objetos com os quais podemos constru´ı-la. Esta Lagrangiana ainda deve satisfazer as outras três condi¸cões, por isso o caminho é semelhante à dedu¸cão da Lagrangiana de Maxwell. É importante ressaltar que na deriva¸cão de (1.20) não levamos em conta todos os poss´ıveis objetos que podem entrar na constru¸cão de uma Lagrangiana para o eletromagnetismo, deduzimos a mais simples e, por compara¸cão com os resultados prévios, a rela¸cão se mostrou correta. Como o eletromagnetismo depende apenas do campo Aµ_{e as três primeiras condi¸cões ainda são obedecidas, os}

objetos dispon´ıveis para a constru¸c˜ao da Lagrangiana s˜ao Fµν

→tensor campo eletromagn´etico ηµν _→m´etrica de Minkowski

εαβγσ _→tensor de Levi-Civita

Os dois primeiros são tensores verdadeiros e o último é uma densidade tensorial de peso ₋1 pois sua transforma¸cão geral de coordenadas é dada por

εαβγσ ₌

∂x ∂x′

∂x′α

∂xµ

∂x′β

∂xν

∂x′γ

∂xδ

∂x′σ

∂xλε µνδλ_.

Com isto, os objetos relevantes para a constru¸c˜ao da Lagrangiana s˜ao o tensor Fµν

e a densidade tensorial ˜Fµν _{definida em (1.14)}†_{. Com estes, os ´}_{unicos escalares}

invariantes por transforma¸cões de Poincaré e de gauge são F =₋1

4F

µν_F µν =

1 2

(

E2₋B2)

, (1.23)

e

G=₋1 4F

µν_˜

Fµν =E⃗ ·B.⃗ (1.24)

Quaisquer outras contra¸cões resultam em combina¸cões dos escalares F e G ou em resultados nulos. É importante ressaltar que G é, devido ao tensor de Levi-Civita, uma densidade escalar e não se transforma “corretamente”quando a transforma¸cão

(24)

´e de paridade (o que pode ser visto explicitamente quando expresso em termos de ⃗

B),

G_{→ −}G.

Uma poss´ıvel solu¸cão é restringir a dependência da Lagrangiana aG2_{, porém existem} casos de sistemas f´ısicos nos quais há viola¸cão de paridade como é o caso da teoria que rege intera¸cão fraca no modelo padrão.

Devido a estes fatos, a Lagrangiana que descreve NLED no vácuo mais geral compat´ıvel com as teorias clássicas de campos é da forma

L=_L(F, G). (1.25)

No caso em que h´a fontes esta Lagrangiana se torna

LF =L(F, G) +

4π c jµA

µ

.

1.2.2 Equa¸c˜ao de movimento para uma NLED

O próximo passo é encontrar a equa¸cão de movimento para um sistema cuja La-grangiana é da forma (1.25), para isto usamos a equa¸cão de Euler-Lagrange (1.18),

∂µ

∂_L ∂(∂µAν)

= ∂L ∂Aν

.

Como (1.25) n˜ao tem termos de fonte e n˜ao depende explicitamente do campo Aν,

o lado direito desta equa¸cão é zero. A equa¸cão de movimento se torna, ∂µ

(

∂_L ∂F

∂F ∂(∂µAν)

+ ∂L ∂G

∂G ∂(∂µAν)

)

= 0,

onde a regra da cadeia foi usada. As derivadas de F e G podem ser explicitamente obtidas a partir de suas defini¸c˜oes,

∂F ∂(∂µAν)

= 4Fνµ e ∂G ∂(∂µAν)

= 4 ˜Fνµ, obtendo

∂µhµν = 0, (1.26)

com

hµν ₌ ∂L

∂FF

µν₊ ∂L

∂GF˜

µν_. _(1.27)

Como os tensores Fµν _{e ˜}_Fµν _{são antissimétricos o tensor}_hµν _{também o é e, por}

este fato, satisfaz a identidade de Bianchi,

(25)

que tamb´em pode ser expressa como

∂µh˜µν = 0,

onde ˜hµν ₌ 1 2ϵ

µν αβhαβ.

Nesta nota¸cão, este par de equa¸cões têm a mesma forma que o par de equa¸cões de Maxwell para o vácuo e, consequentemente, as mesmas técnicas usadas para encontrar Fµν _{podem ser usadas para encontrar} _hµν _{escrito como,}

hµν =



   

0 _E1 _E2 _E3

−E1 ₀ _B3 _−B2

−E2 _−B3 ₀ _B1

−E3 _B2 _−B1 ₀



   

,

onde a fonte estilizada foi utilizada para diferenciar os campos de hµν _e_Fµν_{, por´em}

explicitar a analogia. As componentes deste tensor s˜ao dados por (1.27).

1.2.3 Rela¸cão de dispersão geral para o fóton

Até agora estudamos as propriedades do campo eletromagnético, esta subse¸cão tem como objetivo estudar a propaga¸cão destes campos no contexto das NLED. As NLED se caracterizam por terem equa¸cões não-lineares nos campos o que torna a equa¸cão de onda igualmente não-linear. Por isso, consideramos o caso simplificado (porém bastante geral) em que uma perturba¸cão fraca se propaga em um meio em que existe um campo eletromagnético forte de fundo cuja varia¸cão é muito me-nor do que a da perturba¸cão. Com esta aproxima¸cão a equa¸cão de onda se torna linear mas os coeficientes continuam dependendo do campo de fundo. Estas con-sidera¸cões são baseadas em [38] e os procedimentos são desenvolvidos no apêndice A. Neste obtemos a rela¸cão de dispersão em fun¸cão dos módulos dos quadrivetores kµ _e _aµ

≡Fνµ_k

ν e das derivadas da Lagrangiana em termos dos invariantes F e G

dada por

k2 = −LF (LGG+LF F) + 2F (LF FLGG−L 2

F G)±

√

δ 2 [2LF(LGGF −LF GG) +G2(LF FLGG−L2F G)−L2F]

a2, (1.28)

onde

δ=[

2F (

LF FLGG−L2F G

)

+LF (LGG−LF F)

]2

+[

2G(

LF FLGG−L2F G

)

−2LFLF G

]2

(26)

e

LF =

∂_L

∂F, LG= ∂_L

∂G, LF F = ∂2_L ∂F2, LGG=

∂2_L

∂G2, LF G= ∂2_L ∂F ∂G.

A equa¸c˜ao (1.28) pode ser reescrita juntando todas as caracter´ısticas referentes `a NLED no termo z±,

k2 =z±a2. (1.29)

Nesta expressão fica evidente que existe a possibilidade de haver duas rela¸cões de dispersões, fenômeno chamado de birrefringência. Isto sempre acontece quando δ _̸= 0. Foi mostrado por G. Boillat [37] e independentemente por Plebanski [21] que os únicos casos† _{em que não ocorre este fenômeno são os das eletrodinâmicas de}

Maxwell‡ _{e de Born-Infeld.}

Abrindo a equa¸c˜ao (1.29) em componentes obtemos gµν_k

µkν = 0, (1.30)

com

gµν

≡ηµν₊_z

±FµβFβν, (1.31)

ondegµν _{pode ser interpretado como uma m´etrica efetiva que substitui a m´etrica de}

Minkowski e altera a estrutura de cone de luz. Um poss´ıvel uso desta equa¸cão seria para testar se ocorre desvio no percurso de um feixe de luz que passa por um campo eletromagnético forte de fundo Fµν_{. Multiplicando a equa¸cão (1.30) por um fator}

~2 _{para obter os vetores de quadrimomentos a partir dos quadrivetores de n´}_umero

de onda, podemos reexpressar explicitamente esta em termos do campo externo e da energia e momento do f´oton,§

pµηµνpν =z±pµFβµFβν, (1.32)

ε±=

z±⃗p·Sc⃗ 2+

√

δ 1 +z±E2c2

, (1.33)

com

δ =(z±⃗p·Sc⃗ 2

)2

−(

1 +z±E2c2

) {

z±

[ (

⃗p_×B⃗)2+(⃗p_·E⃗)2

]

c2₋_p2_c2

}

,

†_{Também não há occorencia de birrefringência no caso considerado não-f´ısico da Lagrangiana}

L= F

G.

(27)

onde S⃗ = E⃗ _× B. Esta é a equa¸cão que dá a energia do fóton em termos das⃗ propriedades da NLED em questãoz± e do campo de fundo. É importante ressaltar

que o campo de fundo pode depender do ponto do espa¸co-tempo, o que faz com que a energia do fóton também dependa do evento. Além disso, podemos ver que nos casos em quez± = 0 ou o campo de fundo é nulo recuperamos a rela¸cão de dispersão

(28)

Procedimento Estat´ıstico

Por se tratar de um gás de fótons é natural recorrer à f´ısica estat´ıstica para obter valores médios e, consequentemente, as propriedades do gás como um todo. Uma te-oria de eletrodinâmica não-linear irá apenas mudar a maneira com que os potenciais se comportam, ou seja, no contexto dos fótons, a sua energia e como estes interagem com os campos de fundo. A natureza da part´ıcula continua sendo quântica ou seja, por ter spin inteiro (múltiplo de ~_{) a fun¸cão de onda que descreve o sistema deve}

ser sim´etrica (o que implica na indistinguibilidade das part´ıculas ou, de maneira equivalente, na relevˆancia do princ´ıpio da incerteza) e, com isto, os procedimentos a serem seguidos continuam sendo os da estat´ıstica de Bose-Einstein.

´

E importante destacar que a escolha do sistema de referência não é arbitrário. Isto pode ser visto claramente na dependência da energiaε± dos fótons com o campo

eletromagnético de fundo. Como queremos que a distribui¸cão energética dos fótons seja isotrópica escolhemos o referencial comóvel ao material que gera os fótons.

´

E interessante ressaltar que, no caso relativ´ıstico, por mais que o volume dx3 _{e o} intervalo de momentodp3_{do espa¸co de fase não sejam invariantes por transforma¸cões} de Lorentz o produto dx3_dp3 _{o é [43]. No final deste cap´ıtulo, as unidades naturais} são usadas.

2.1 Ensemble macrocanˆ

onico

Queremos estudar um sistema caracterizado pelas grandezas: volume V, tempera-tura T e potencial qu´ımicoµ, sem energia nem número de part´ıculas fixas. A teoria de ensemble consiste em imaginar um número† _ℵ _{de cópias idênticas deste sistema}

†_{O n´}_{umero de sistemas que comp˜oe o ensemble pode ser interpretado como o espa¸co amostral}

do qual vamos tirar as informa¸cões. Nele encontraremos todas as poss´ıveis distribui¸cões de con-figura¸cões, até as que parecem mais absurdas. Como todo espa¸co amostral, quanto maior este é, mais fieis os dados obtidos. Este será o papel do limite termodinâmico.

(29)

que podem ser encontradas com qualquer número de part´ıculas e em qualquer auto-valor de energia acess´ıvel aos sistemas. Juntos compartilham a energia total_ℵE¯ e o número de part´ıculas_ℵN¯, onde ¯Ee ¯N são a energia e o número de part´ıculas médias que estão diretamente relacionados com a temperatura e o potencial qu´ımico, res-pectivamente. Podemos então definir nr,s como o número de sistemas com energia

Er e n´umero de part´ıculas Ns, com r, s = 0,1, ..., estes sistemas compartilham as

restri¸c˜oes

∑

r,s

nr,s=ℵ,

∑

r,s

nr,sNs =ℵN ,¯ (2.1)

∑

r,s

nr,sEr =ℵE.¯

Com isto, o conjunto _{nr,s}† indica um modo de distribui¸c˜ao que satisfaz (2.1).

Este, porém, não é o único pois poderiamos distribuir os sistemas de tal maneira a compor um conjunto diferente _{nr,s}que continue satisfazendo (2.1). É interessante

encontrar o modo de distribui¸cão mais provável, isto é, o evento que melhor descreve o espa¸co amostral, pois este nos permitirá obter previsões fieis (dentro de uma certa margem de erro ligada ao tamanho do espa¸co amostral) das medi¸cões que podem ser feitas do sistema.

Para encontrar este modo de distribui¸cão dito mais provável come¸camos por adotar o postulado da equiprobabilidade a priori (o mais simples e que obtêm resul-tados coerentes com as experiências). Este nos diz que o sistema estudado acessa com igual probabilidade todas as configura¸cões acess´ıveis a ele. Umaconfigura¸cão

é um modo de distribui¸cão no qual os sistemas estão distribuidos de maneira es-pec´ıfica. Se permutamos dois sistemas que estão em estados diferentes (um que está no estado (E1, N9) com outro que está no estado (E3, N2), por exemplo), em um dado modo de distribui¸cão, obtemos duas configura¸cões diferentes. De maneira geral, dado um modo de distribui¸cão_{nr,s}, este possui

W_{nr,s}= ℵ

!

∏

r,s

nr,s!

,

configura¸cões diferentes. Devido ao fato de todas as configura¸cões serem igualmente acess´ıveis, é razoável supor que o modo de distribui¸cão que proporciona o maior número de configura¸cões é o mais provável. Formalmente, a obten¸cão do modo mais provável de distribui¸cão (ou moda), que denotaremos por {

n∗

r,s

}

, ´e dada pela

(30)

maximiza¸cão de W_{nr,s} que é feita através do método de Lagrange levando em

conta as restri¸c˜oes (2.1)†_{. Com isto obtemos}

n∗

r,s

ℵ =

e−αNs−βEr

∑

r,se−αNs−βEr

. (2.2)

A raz˜aon∗

r,s/ℵindica a parcela dos ℵ sistemas que se encontram no estado (Er, Ns)

no modo de distribui¸cão mais provável. No limite, dito termodinâmico, em que_{ℵ →}

∞‡ _{(onde o n´}_{umero de part´ıculas total e a energia total tamb´em tendem ao infinito}

mas as suas m´edias permanecem constantes) a probabilidade pr,s de encontrar um

sistema no estado (Er, Ns), dado por ⟨nr,s⟩/ℵ, é idêntico à quantidade n∗r,s/ℵ pois,

devido a este limite, a flutua¸c˜ao estat´ıstica se torna nula§_{. Com isto, podemos definir}

pr,s=

e−αNs−βEr

∑

r,se−αNs−βEr

, (2.3)

como a probabilidade de encontrar um sistema no estado (Er, Ns).

A partir da equa¸cão (2.3) conseguimos obter a energia média e o número médio de part´ıculas do sistema,

¯ N =

∑

r,sNse−

αNs−βEr

∑

r,se−αNs−βEr

≡ − ∂

∂αln

(

∑

r,s

e−αNs−βEr

)

,

¯ E =

∑

r,sEre−αNs−βEr

∑

r,se−αNs−βEr

≡ −_∂β∂ ln

(

∑

r,s

e−αNs−βEr

)

.

Este resultado nos permite perceber a importância do denominador (coeficiente de normaliza¸cão) da densidade de probabilidade (2.3), este é chamado de fun¸cão de parti¸cão macrocanônica, que denotaremos por Ξ, e contêm todas as informa¸cões do sistema.

Analisando a grandeza

q= ln Ξ,

e fazendo a correspondˆencia com a primeira lei da termodinˆamica, conseguimos obter

†_{Ver [44] pp. 54 – 55.}

‡_{O limite termodinˆamico ´e aquele no qual o espa¸co amostral abrange cada vez mais elementos}

da popula¸cão até, no limite, abrangê-la completamente. É esperado que neste limite o espa¸co amostral caracterize perfeitamente a popula¸cão.

(31)

as seguintes interpreta¸c˜oes para q,α eβ†_,

α=₋ µ kT,

β = 1 kT,

q= pV

kT. (2.4)

Estes resultados nos fornecem a conexão entre a estat´ıstica e a termodinâmica. É interessante perceber que a terceira expressão implica no fato de q ser extensivo.

Como até agora não foi falado sobre as caracter´ısticas do sistema, este desenvol-vimento serve tanto para sistemas ditos clássicos quanto os quânticos.

2.2 Estat´ıstica de Bose-Einstein

O sistema estudado é quântico portanto o ensemble será caracterizado pelo Hamil-toniano ˆH. Cada sistema do ensemble será descrito pela fun¸cão de onda Ψk_(⃗r

i, t)

de tal maneira que

ˆ

HΨk(⃗ri, t) =i~Ψ˙k(⃗ri, t),

descreve a cinemática e dinâmica do k-ésimo sistema. Esta fun¸cão de onda pode ser decomposta em termos dos autovetores do Hamiltoniano. Estes abrangem o espa¸co de Hilbert e diagonalizam os operadores ˆH e ˆn (cujos autovalores indicam as energias accessveis e o número de part´ıculas do sistema). Com isto,

Ψk_(⃗r i, t) =

∑

r,s

ak

r,s(t)φr,s(⃗ri),

onde

ak r,s(t) =

∫

V

φ∗r,s(⃗ri) Ψk(⃗ri, t)dV,

nos dá, por meio do seu módulo quadrado, a probabilidade de encontrar o k-ésimo sistema no estado (Er, Ns). Um observável ˆG caracteriza, na forma de operador,

uma grandeza mensurável cuja média no k-ésimo sistema é dado por

⟨

ˆ G⟩k=

∫

Ψk∗GΨˆ kdV. (2.5)

Esta média é apenas espacial, ou seja, é uma média instantânea da grandeza. Ex-pandindo (2.5) em termos dos autovetores obtemos

⟨

ˆ

G⟩k= ∑

l,m,r,s

akl,m∗ a k

r,sGl,m,r,s,

(32)

onde

Gl,m,r,s =

∫

φ∗l,mGφˆ r,sdV.

Poderiamos tomar a média temporal de ⟨Gˆ⟩k feita em um per´ıodo suficiente-mente longo para que ok-ésimo sistema passe por todos os estados acess´ıveis e assim obter a média deste observável que caracterize o sistema estudado; este seria o pro-cedimento experimental. Como o sistema é composto por um grande número de part´ıculas (da ordem de 1023_{), levar em conta a dinâmica e cinemática de cada um} dos constituintes é trabalhoso e, até, imposs´ıvel. Por isso, conseguimos a média inde-pendente do tempo, que caracteriza o sistema estudado em seu estado de equil´ıbrio, por meio da média feita no ensemble macrocanônico [44]. Esta média deve ser feita sobre todos os estados acess´ıveis ao sistema dentro das restri¸cões (2.1),

⟨

ˆ G⟩= 1

ℵ

∑

k=1

⟨

ˆ

G⟩k. (2.6)

Reescrevendo esta m´edia obtemos

⟨

ˆ

G⟩= tr(ˆρG),ˆ

onde ˆρ´e chamado de operador densidade de probabilidade definido como

ρl,m,r,s =

1

ℵ

∑

k=1 akl,m∗ a

k r,s.

Este operador tem as mesmas informa¸c˜oes que (2.3) por isso fazemos a rela¸c˜ao ρr,s =

eµβNs−βEr

∑

r,seµβNs−βEr

,

onde ˆρ, na sua forma diagonalizada, ´e dado por

ρr,s=

1

ℵ

∑

k=1 ak∗

r,sa k r,s.

Feita esta rela¸cão, a conexão entre a estat´ıstica e a termodinâmica é dada pela rela¸cão (2.4), como visto na se¸cão anterior, através da qual podemos encontrar, entre outros, a pressão e a densidade de energia do sistema,

p(µ, V, T) = kT

V q e ρ(µ, V, T) =− 1 V

∂q

∂β. (2.7)

A fun¸cão de parti¸cão macrocanônica, Ξ =∑

r,s

(33)

pode ser desenvolvida levando em conta as intera¸cões e as caracter´ısticas quânticas das part´ıculas. Primeiro notamos que a somatória em s, pela qual obtemos todos os poss´ıveis estados de número de part´ıculas, pode ser reescrita como uma somatória do número de part´ıculas total do sistema (que pode ter qualquer valor inteiro entre 0 e_∞). Ainda mais, se levamos em conta que as part´ıculas não interagem entre si, e reescrevendo o número total de part´ıculasNsem termos do númeroni de part´ıculas

por estado de energia εi, podemos reescrever a energia total do estado Er como

Ns =

∞

∑

i=0

ni e Er=

∞

∑

i=0

niεi, (2.8)

obtendo

Ξ =

∞

∑

Ns=0

∑

{ni}r

˜ W_{ni}_r

∞

∏

i=0

(

ze−βεi)ni_, _(2.9)

onde z = eµβ _{´e chamado de fugacidade e a somat´oria sobre todos os estados} _r _foi

trocada pela somat´oria sobre o conjunto_{ni}_r que caracteriza o estador e que est´a

sujeito à primeira restri¸cão de (2.8). Para que a mudan¸ca na somatória esteja correta é necessário adicionar o termo ˜W_{ni}_r que indica o número de configura¸cões do

modo de distribui¸c˜ao_{ni}_r.† A avalia¸c˜ao deste coeficiente depende da natureza das

part´ıculas. Na mecância quântica, ao contrário da mecânica clássica, as part´ıculas são indistingu´ıveis‡ _{e podem se classificadas em dois grupos, férmions e bósons.}

Cada grupo tem suas próprias caracter´ısticas e a part´ıcula é classificada de acordo com seu spin (caso seja múltiplo inteiro de ~ _{é chamado bóson, caso contrário é}

dito férmion). O fóton por ter spin inteiro é de natureza bosônica e, ao contrário dos férmions, não segue o princ´ıpio de exclusão de Pauli, que implica que não há restri¸cão do número de part´ıculas por estado. Num sistema bosônico (e fermiônico) o conjunto de números_{ni}_r define por completo um estado do sistema. Isto é devido

ao fato da permuta¸cão entre duas part´ıculas em estados diferentes não gerarem uma nova configura¸cão (caso que no sistema clássico não é verdade). Este fato faz com que cada conjunto _{ni}_r tenha o mesmo peso, por isso fazemos ˜W{ni}= 1.

A dupla somat´oria, uma sobre todos os conjuntos _{ni}e sobre o n´umero total de

part´ıculas, é análoga à somar sobre cada ni independentemente. Com isto obtemos

Ξ =

∞

∏

i=0

[ _∞ ∑

ni=0

(

ze−βεi)ni

]g

,

†_{Seguimos a mesma linha de racioc´ınio da se¸c˜ao 2.1, contamos quantas part´ıculas est˜ao em cada}

autovalor de energiaεi e caracterizamos o sistema pelo conjunto{ni}.

‡_{Uma excessão é o caso de um sólido no qual as part´ıculas estão em posi¸cões fixas pois estas}

(34)

onde g leva em conta os graus internos de liberdade das part´ıculas. Na estat´ıstica de Bose-Einstein, a somat´oria pode ser avaliada caso µ < εi obtendo

Ξ =

∞

∏

i=0

[

1 1₋ze−βεi

]g

.

Finalmente, obtemos a fun¸cão de parti¸cão macrocanônica

q =₋g

∞

∑

i=0 ln(

1₋ze−βεi)_.

O potencial qu´ımico de um gás de fótons é nulo pois o número de fótons num volume arbitrário é indefinido. Isto pode ser visto melhor lembrando que o multi-plicador de Lagrange α em (2.2) surge da segunda restri¸cão (2.1) que nos diz que o número total de part´ıculas é conservado. Como este não é o caso para um gás de fótons, esta restri¸cão não é mais pertinente

.

O número de graus de liberdade internos do fóton é g = 2 devido às duas poss´ıveis polariza¸cões. Como a energia do fóton é uma fun¸cão cont´ınua do momento linear, fazemos a transi¸cão da soma discreta para a integral através da prescri¸cão

∑

ε →

1

h3

∫

d3_xd3_p,

q=₋ 2 (2π)3

∫

ln(

1₋e−βε)

d3xd3p,

(35)

Resultados e Discuss˜

ao

Obtivemos, nos dois cap´ıtulos anteriores, a rela¸cão de dispersão geral de um fóton e o potencial macrocanônico para um gás de fótons. Foi visto também que dependendo da NLED o fóton pode ter duas rela¸cões de dispersão que estão associadas às dire¸cões de polariza¸cão dos fótons. Este fato requer que o potencial macrocanônico seja reescrito de forma adequada para a levar em conta os casos em que há duas poss´ıveis rela¸cões de dispersão. Vimos que a forma do potencial para um gás de fótons é†

q=₋ 2 (2π)3

∫

ln(

1₋e−βε)

d3xd3p,

e lembramos que o fator 2, que foi propositalmente deixado expl´ıcito, provêm do fato do fóton ter dois graus de liberdade internos, as duas poss´ıveis dire¸cões de po-lariza¸cão. Pelo fato das ondas eletromagnéticas poderem ser decompostas em eixos arbitrários no plano, podemos interpretar o sistema como a superposi¸cão de dois sis-temas, cada um contendo ondas polarizadas apenas em uma dire¸cão. Isto é poss´ıvel pois, na aproxima¸cão usada para derivar a rela¸cão de dispersão [38], a equa¸cão de onda é linear e a perturba¸cão só interage com o campo externo. Foi observado que o potencial macrocanônico é extensivo, logo o potencial da superposi¸cão dos sistemas é a soma do potencial de cada um. Mas, como foi feita a decomposi¸cão, agora há apenas 1 grau de liberdade interno. Com isto temos que o potencial macrocanônico total é

qT =q++q−,

onde

q± =−

1 (2π)3

∫

ln(

1₋e−βε±)

d3xd3p. (3.1) Este resultado também pode ser obtido modificando a equa¸cão (2.9) para levar em conta duas part´ıculas com carcater´ısticas diferentes e depois reconhê-las como

†_{Neste cap´ıtulo s˜ao usadas as unidades naturais.}

(36)

sendo fótons com polariza¸cões diferentes†_{. A partir desta esqua¸cão, pode ser visto}

claramente que no caso em queε+=ε− a express˜ao para o potencial macrocanˆonico

recai na sua forma original.

Como a forma do potencial é a mesma para as duas poss´ıveis rela¸cões de dis-persão basta apenas resolver uma delas. A rela¸cão de disdis-persão obtida anteriormente independe do tempo, porém depende do ponto do espa¸co através do campo eletro-magnético de fundo.

Neste cap´ıtulo será obtido o potencial macrocanônico para o gás de fótons ape-nas no caso em que o campo eletromagnético de fundo é uniforme. Em seguida, estudaremos as propriedades termodinâmicas pressão e densidades de energia. Uma vez que estas expressões devem valer para qualquer NLED, serão feitos exemplos espec´ıficos usando duas Lagrangianas, a de Born-Infeld, e uma aproxima¸cão de se-gunda ordem de Lagrangianas que só dependem do invariante F. Por fim, será feita uma discussão dos casos eletrostáticos e magnetostáticos dos dois exemplos comparando-os com os resultados clássicos da EM.

3.1 Propriedades termodinˆ

amicas para o g´

as de f´

otons em

uma NLED arbitr´

aria

Como o campo de fundo é uniforme podemos escolher um sistema de coordenadas cartesianas de tal maneira que seu eixoxcoincida com a dire¸cão e sentido do campo elétrico e o campo magnético esteja no plano xy, ou seja,

⃗

E =E1ˆı, ⃗

B =B1ˆı+B2ȷ.ˆ

Neste sistema de coordenadas, podemos reescrever a rela¸c˜ao de dispers˜ao (1.33) deixando-a em uma forma mais simples,

ε±=

y±p3+

√

a±p21+b±p22+c±p23 +e±p1p2

x±

, (3.2)

(37)

onde os coeficientes s˜ao dados por

x±= 1 +z±E12, a±=

(

1 +z±E12−z±B22

)

x±,

b±=

(

1₋z±B12

)

x±,

c±=x±−x±z±B12−z±B22, e±= 2z±B1B2x±,

y±=z±E1B2.

(3.3)

O fato do campo de fundo ser uniforme também simplifica a forma de (3.1), pois a rela¸cão de dispersão não depende mais dos pontos do espa¸co tornando a integral em d3_x_{trivial. Com isto, juntando (3.1) e (3.2) obtemos,}

q± =−

V (2π)3

∫

ln

(

1₋e−β

y±p3 +√a±p21+b±p22+c±p23+e±p1p2

x±

)

d3p. (3.4) A resolu¸cão detalhada desta integral é feita no apêndice E, sendo sua solu¸cão dada por

q±=K±V (kT)3, (3.5)

onde

K±=

π2 90

|c±|

(

1₋z±B⃗2

)2. (3.6)

Observe que durante o processo de integra¸cão surgem os seguintes v´ınculos ne-cessários para que a integral não divirja,

x± >0 e |y±|<√c±. (3.7)

Com a forma expl´ıcita do potencial podemos encontrar as rela¸cões expl´ıcitas para a pressão e densidade de energia do sistema através das rela¸cões do cap´ıtulo anterior (2.7),

p= (K++K−) (kT)4 e ρ= 3 (K++K−) (kT)4.

Um resultado importante é, mesmo que as expressões para a pressão e a densidade de energia tenham mudado (pois agora dependem da NLED e do campo de fundo), a equa¸cão de estado,

p= ρ 3, ´e independente da NLED e permanece inalterada.

Como foi visto, no caso do EM z± = 0 implicando em K+ = K− = 1₂π

2

45. Com isto temos que a densidade de energia ´e independente do campo de fundo e dada por

ρEM =

π2 15(kT)

(38)

3.2 Lagrangiana de Born-Infeld e Lagrangiana quadr´

atica

Nesta se¸cão é feita a aplica¸cão do formalismo geral desenvolvido para o caso de duas Lagrangianas. Por questão de simplicidade, apenas os caso eletrostáticos e magnetostáticos são resolvidos. Logo em seguida uma compara¸cão dos resultados é feita com os do EM.

3.2.1 Lagrangiana de Born-Infeld

A partir da descoberta do elétron por J. J. Thomson em 1899, vários cientistas ten-taram desenvolver modelos que evitassem divergências do campo a curtas distâncias da part´ıcula. Uma poss´ıvel solu¸cão é o uso de uma teoria não-linear que, em analogia com as transforma¸cões de Lorentz, impusesse um limite superior para a intensidade do campo quando⃗r_→0 e que obtivesse os resultados clássicos a distâncias maiores. Uma formula¸cão feita por G. Mie [41] precedeu a formula¸cão de Born e Infeld, porém esta não era invariante por transforma¸cões de Lorentz nem por transforma¸cões de calibre como é esperado que o eletromagnetismo seja.

A Lagrangiana de Born-Infeld [4] ´e†

LBI =b2

[

1₋

√

1₋ 2F b2 −

G2 b4

]

, (3.8)

onde b‡ _{é o valor máximo que o módulo do campo elétrico pode atingir.}

As informa¸cões das NLED, como visto anteriormente, estão condensadas no co-eficiente z± que, para esta Lagrangiana, é dado por§

zBI =−

1

E2₋_B2₋_b2. (3.9)

Como esperado, há apenas uma rela¸cão parazpois na eletrodinâmica de Born-Infeld não há ocorrência de birrefringência.

Caso Eletrost´atico

No caso eletrost´atico os coeficientes (3.3) s˜ao dados por c=x e x= 1 +zBIE12,

†_{A forma da Lagrangiana varia na literatura pois depende da defini¸cão dos invariantes}_F _e_G_. ‡_{Este parâmetro não está associado ao coeficiente}_b _{em (3.3).}

(39)

onde zBI ´e dado por (3.9) com B2 = 0. Com isto, (3.6) ´e dado por

K = 1 2

π2 45

1 +zBIE₁2

,

K = 1 2

π2 45

(

1 1₋E21

b2

)

,

e, consequentemente, a densidade de energia ´e dada por

ρBI(E1, T) =

π2 15

(

1 1₋ E12

b2

)

(kT)4. (3.10)

Analisando as restri¸c˜oes (3.7) encontramos que E1 < b,

ou seja, a intensidade do campo deve ser sempre menor que o parâmetro b da Lagrangiana (3.8), este resultado concorda com a fun¸cão quebexerce na formula¸cão.

Caso Magnetost´atico

No caso magnetost´atico os coeficientes (3.3) s˜ao dados por†

c= 1₋zBIB12. Com isto, (3.6) ´e dado por

K = 1 2

π2 45

|1₋zBIB12| (1₋zBIB21) 2,

K = 1 2

π2 45

(

B2 1 b2 + 1

)

,

e a densidade de energia ´e dada por ρBI(B1, T) =

π2 15

(

B2 1 b2 + 1

)

(kT)4. (3.11)

Novamente analisamos (3.7) e notamos desta vez que as restri¸cões são naturalmente satisfeitas, ou seja o campo magnético pode assumir qualquer valor.

Devido ao fato da constante b não ser definida numericamente, analisaremos, posteriormente, o caso de Born-Infeld em termos dos parâmetros adimensionaisE/b e B/b para os casos eletrostáticos e magnetostáticos, respectivamente.

†_{Note que podemos alinhar o campo magn´etico com o eixo}_x_{, o que equivale a anular a}