Métodos de regiões de confiança para resolução do problema de quadrados mínimos: implementação e testes numéricos.

Uma Publiação daSoiedade BrasileiradeMatemátiaApliadaeComputaional.

Métodos de Regiões de Conança para Resolução

do Problema de Quadrados Mínimos:

Implementação e Testes Numérios

1

J.L.C. Gardenghi 2

, Departamento de Ciênia de Computação, IME - Instituto de

MatemátiaeEstatístia, USP-Universidade deSão Paulo,05508-090SãoPaulo,

SP,Brasil.

S.A. Santos 3

, Departamento de Matemátia Apliada, IMECC - Instituto de

Matemátia, Estatístia e Computação Cientía, UNICAMP - Universidade

EstadualdeCampinas,13083-859Campinas,SP, Brasil.

Resumo. Oproblemadequadradosmínimospossuiváriasapliaçõesnoampode

otimização. Nopresentetrabalho, abordamosduasestratégiasparasuaresolução:

Levenberg-MarquardteGradientesConjugados. Cadaumaexploraaraterístias

própriasdoproblema,eambasusamregiõesdeonançaparaaglobalização. Nossa

ontribuiçãoestá naimplementaçãode ambos os métodos noCAS Maxima e na

análiseomparativadodesempenhodessesmétodosnaresoluçãodeumafamíliade

problemasdequadradosmínimosdaliteratura.

Palavras-have. Quadradosmínimos,regiõesdeonança,implementação

om-putaional.

1. Introdução

Nestetrabalho,onsideramosoproblemadequadradosmínimos

min

x

∈

R

n

1

2

k

F

(

x

)

k

2

≡

f

(

x

)

,

(1.1)

sendo

F

:

R

n

→

R

m

a função residual, ao menos duas vezes ontinuamente

di-fereniável,

F

(

x

)

o resíduo do problema em

x

e

k · k

a norma Eulidiana. No ampodeotimização,quadradosmínimostemváriasapliações,destaando-seseu

usoparaajustarparâmetrosde modelosfrente aonjuntos dedadosoletadosem

experimentos, e neste ontexto

m

≫

n

. Para umreente panoramado estadoda

artedesteproblema,tantodopontodevistateórioquantoprátio,veja[14℄esuas

referênias.

1

EstetrabalhoontouomosapoiosdoCNPq(304032/2010-7,106731/2011-4e

151749/2011-6),FAPESP(2012/05725-0)ePRONEX-Otimização;TrabalhoapresentadonoXXXIVCNMAC.

2

johnime.usp.br

3

Na próxima seção, apresentamos dois métodos para resolução de (1.1): o

al-goritmo de Levenberg-Marquardt (LMA) e o método de Gradientes Conjugados

(MGC).Emseguida,destaamososdetalhesdaimplementaçãoeosresultadosdos

experimentos numériosque avalidam eilustram odesempenhoomparativodas

duasabordagensdistintas. Finalizamosotextoomumabreveonlusão.

2. Métodos de Regiões de Conança para

Quadra-dos Mínimos

Métodosderegiõesdeonançaparaminimizaçãoirrestrita,

min

f

(

x

)

s.a.

x

∈

R

n

,

sãoestratégiasiterativasbaseadasemmodelosquadrátiosparaafunçãoobjetivo

f

emtornodeumdadoponto[2℄. Emgeral,seja

xc

∈

R

n

oponto orrente,dene-se

ummodeloquadrátio

qc

para

f

emtornode

xc

eosubproblemaéformuladoomo

min

p

∈

R

n

qc

(

p

)

s.a.

k

p

k ≤

∆

c,

(2.1)

em que

0

<

∆

c

∈

R

é o raio da região de onança. A solução

pc

, exata ou aproximada,desteproblemaéusadaparaobterumpontoandidato

xn

=

xc

+

pc

. Obomdesempenhoderegiõesdeonançaestáligadoaoontroledotamanho

do raio, que determina a região em que o modelo é onável para se aproximar

a funçãoobjetivo. Nesta abordagem, vamos determinaro tamanho deste raio de

aordoom oderésimo quea soluçãode (2.1)ausou no problemaoriginal que

aproxima. Para isto, vamos avaliar a razão entre o derésimo no modelo e na

funçãoobjetivo,hamadoquoientedereduçãorelativa,dadopor

ρ

(

p

)

def

=

f

(

xc

)

−

f

(

xc

+

p

)

qc

(0)

−

qc

(

p

)

.

(2.2)

NoAlgoritmo1,página71,apresentamosoalgoritmobásioderegiõesde

on-ança. Osparâmetros

κ, η

1

e

η

2

sãodeterminadosexperimentalmente,emborahaja

algumasesolhaslássiasnaliteratura[2,11℄. Sobestaótia,esolhemos

κ

= 10

−

3

,

η

1

=

1

₄

e

η

2

=

3

4

. Para resolvero subproblema(linha 2), implementamosLMA e

MGC.Uma brevedesriçãodestes doismétodoséapresentadaaseguir.

2.1. Método de Levenberg-Marquardt

A prinipal araterístia deste método é ataar a estrutura partiular do

pro-blema (1.1). Originalmente,esta estratégiafoipropostaporLevenberg[6℄ e

Mar-quardt [8℄, e foi onsiderada preursora da ténia de regiões de onança (ver

também [7℄). Moré [9℄ props uma série departiularidades paraimplementação,

queforamexploradasnestetrabalho.

Dadoumponto

xc

∈

R

n

,LMAtrabalhaomaaproximação

qc

(

p

)

def

=

1

2

k

Jcp

+

Fc

k

2

emtornode

xc

,sendo

Fc

∈

R

m

oresíduoem

xc

e

Jc

∈

R

m

×

n

ajaobianadafunção

Algoritmo1:RegiõesdeConança

Entrada: Pontoiniial

x

0

∈

R

n

, raioiniialdaregiãodeonança

∆

0

, onstantes

κ

∈

[0

,

1

4

]

,

0

< η

1

≤

η

2

<

1

.

1 para

k

= 0

,

1

, . . .

haer

2 Enontre

pk

omosolução(aproximada)dosubproblema(2.1)

3

xk

+1

←

xk

+

pk

4 Avalieoquoiente dereduçãorelativa

ρ

(

pk

)

(2.2) 5 se

ρ

(

pk

)

> κ

então

6 Aeiteopontoandidato

xk

+1

eavalieritériosdeparada

senão

7 Desarteopontoandidatoeonsidere

xk

+1

=

xk

m

8 se

ρ

(

pk

)

≤

η

1

entãoObtenha

∆

k

+1

reduzindo

∆

k

9 senão

10 se

ρ

(

pk

)

≥

η

2

entãoObtenha

∆

k

+1

aumentando

∆

k

11 senão

∆

k

+1

←

∆

k

m

n

umproblemadequadradosmínimoslinearesompassorestrito,ujasondiçõesde

otimalidadesãodadaspor

(

J

T

c

Jc

+

λ

∗

I

)

p

∗

=

−

J

T

c

Fc

(2.3a)

λ

∗

₍

_k

_p

∗

_{k −}

_∆

c

) = 0

(2.3b)

λ

∗

_≥

₀

_,

_k

_p

∗

_{k ≤}

_∆

_c.

(2.3)

Osistema linear(2.3a) estábemdenido somentese

(

J

T

c

Jc

+

λ

∗

I

)

fordenida positiva. Como

J

T

c

Jc

é ao menos semidenida positiva, então

(

J

T

c

Jc

+

λ

∗

I

)

será denida positiva sempre que

λ

∗

_>

₀

. Em partiular, podemos ter diuldades

numérias,pormal ondiionamentoou porsingularidade, quando

λ

∗

_{= 0}

. Neste

aso,deaordoom(2.3b),temos queasoluçãode(2.1)podeserinterna,ouseja,

k

p

∗

_k

_<

_∆

c

. Oresultado aseguirestabelee ondiçõespara queasoluçãode(2.1)

sejainterioràregiãodeonança.

Proposição 2.1. O problema (2.1) não possui solução global na fronteira se, e

somente se,

J

T

c

Jc

é denida positiva e o passo de Newton é interior, ou seja,

k

(

J

T

c

Jc

)

−

1

J

c

T

Fc

k

<

∆

c

.

Demonstração. Ver[4,Corolário1℄.

Poroutrolado,asooproblemapossuasoluçãonafronteira,ésemprepossível

enontrar

λ

∗

quesatisfaça

k

p

∗

_k

_{= ∆}

c

. Assimsendo,onsideramos

p

(

λ

)

def

=

−

(

J

T

emque

†

éapseudoinversadeMoore-Penrose,equeremosenontrar

λ

∗

_≥

₀

talque

k

p

(

λ

∗

₎

_k

_{= ∆}

_c.

(2.4)

Aequação(2.4)éhamadadeequaçãoseular. Poronseguinte,nossoproblema

sereduzaenontrarumzerodeumaequaçãoemumavariável. Paratal,usaremos

oMétododeNewton,omalgumassalvaguardasqueserãoapresentadasnaSeção3.

Notemos que

λ

∗

atuaomo um regularizador,ou seja,ele ajusta osistema (2.3a)

paraquesempreexistaumasolução

p

∗

. Éjustamente essaaonexãodeLMAom

regiõesdeonança. Originalmente[6,8℄,oparâmetro

λ

∗

eraomputadodeforma

heurístia. Com regiões de onança, busamos o multipliador de Lagrange da

restriçãoquadrátia

λ

∗

_≥

₀

de talmaneiraque

k

p

∗

_k

_{= ∆}

c

, salvooasopartiular

emqueasoluçãosejainternaeentão

λ

∗

_{= 0}

.

2.2. Método de Gradientes Conjugados

Nestemétodo,vamosataaroproblema(1.1)omoumproblemageralde

minimiza-çãoirrestrita,eresolvê-lousandoaestratégiaderegiãodeonança,onsiderando,

aadaiteração,osubproblema deregião deonança(2.1),tomando

qc

(

p

)

def

=

1

2

p

T

_Hcp

₊

_g

T

c

p

+

fc

o modelo quadrátiode

f

em torno de um ponto orrente

xc

, om

Hc

∈

R

n

×

n

,

gc

∈

R

n

e

fc

∈

R

,respetivamente,amatrizhessiana, ovetorgradienteeafunção objetivo

f

,todosavaliadosem

xc

.

Para um estudo mais detalhado sobre a estratégia de gradientes onjugados,

veja[5,Seção3℄. Paraaresoluçãodosubproblema,aideiaéproduzirumasequênia

{

di

}

de direções onjugadas e enontrar a solução para (2.1) iterativamente, por

meiode

pi

+1

=

pi

+

αidi

. MGCseriaumaestratégianaturalse

Hc

fosseumamatriz denida positiva, mas, na prátia, nada sabemos sobre ela. É justamente neste

ponto queasregiõesdeonançatornam-seesseniais. Asondiçõesneessáriase

suientesdeotimalidadede(2.1)sãodadaspor

(

Hc

+

λ

∗

_I

₎

_p

∗

₌

₋

_gc,

(2.5a)

λ

∗

₍

_k

_p

∗

_{k −}

_∆

c

) = 0

,

(2.5b)

λ

∗

_≥

₀

_,

_k

_p

∗

_{k ≤}

_∆

_c,

(2.5)

(

Hc

+

λ

∗

_I

₎

ésemidenidapositiva

.

(2.5d)

Toint[13℄eSteihaug[12℄propuseramalgumasmodiaçõesnoMGCoriginaldetal

maneiraquese

k

gc

+

Hc

pi

k

formenorquedadatolerânia,entãotemosumasolução interna,pois

pi

satisfazaproximadamenteaondição(2.5a)om

λ

∗

_{= 0}

. Poroutro

lado,se

k

pi

+1

k

>

∆

c

,entãobastaenontrar

τ

deformaque

k

pi

+

τ dik

= ∆

c

. Por m,se

Hc

nãoédenida positiva,entãoexisteuma direçãode urvaturanegativa

ou nula apartir de

pi

. Assim sendo, se enontrarmos uma tal direção

di

, basta

denirumpassoqueatinjaabordadaregiãodeonança. Emoutraspalavras,se

d

T

Destemodo,MGCatuaomoGClássioquando

Hc

édenidapositiva. Caso

ontrário, se forenontradauma direção de urvatura negativa,determina-se um

passo queatinjaaborda daregião deonança. De qualquerforma, opassotem

seu tamanho restrito e essa também é uma ondição de parada do método. No

Algoritmo2desrevemosMGC.

Algoritmo2:GradientesConjugadosomRegiõesdeConança

Entrada: Pontoorrente

xc

∈

R

n

,amatriz hessiana

Hc

∈

R

n

×

n

eo

gradiente

gc

∈

R

n

dafunçãoobjetivoavaliadosem

xc

,

∆

c

oraio daregiãodeonança,

ε >

0

uma tolerâniaparaoerrode otimalidade.

Saída:

p

direçãoparaomputaronovopontoandidato

xn

=

xc

+

p

.

1

p

0

←

0

, r

0

←

gc, d

0

←

r

0

2 para

i

= 0

,

1

, . . .

haer 3 se

d

T

i

Hcdi

≤

0

então

4 Enontre

τ

tal que

k

pi

+

τ di

k

= ∆

c

5 retorna

pi

+

τ di

m

6

αi

←

(

r

T

i

ri

)

/

(

d

T

i

Hcdi

)

7

pi

+1

←

pi

+

αidi

8 se

k

pi

+1

k

>

∆

c

então

9 Enontre

τ

tal que

k

pi

+

τ dik

= ∆

c

10 retorna

pi

+

τ di

m

11

ri

+1

←

ri

+

αiHc

di

12 se

k

ri

+1

k ≤

ε

entãoretorna

pi

+1

13

βi

←

(

r

T

i

+1

ri

+1

)

/

(

r

i

T

ri

)

14

di

+1

←

ri

+1

+

βidi

n

3. Implementação Computaional

Nestaseção,apresentamososdetalhesdeimplementaçãodoLMAque,porexplorar

aspeuliaridadesdoproblema(1.1),possuimaispartiularidadesdeimplementação

queoAlgoritmo2,queéummétodopara resoluçãodosubproblema deregiõesde

onançanoasodeminimizaçãoirrestritageral.

3.1. Álgebramatriialempregadanasoluçãodosubproblema

A equação (2.3a) pode ser vista omo um sistema de equações normais para o

problemalineardequadradosmínimos:

Jc

√

λI

p

∼

=

−

Fc

0

Talequivalêniapermiteresolveroproblemasemavaliaroproduto

J

T

c

Jc

,reduzindo

pelametadeaquantidadedeoperações. Destemodo,sealularmosafatoração

QR

Jc

=

Q

Rc

0

teremos

Q

T

₀

0

I

Jc

√

λI

=





Rc

0

√

λI





.

(3.2)

Amatrizqueresultade(3.2)possuiumaestruturapartiular:

Rc

éumamatriz

triangular superior, enquanto

√

λI

é uma matriz esalar. Diante disto, é

possí-vel obter uma matriz triangular superior equivalente eliminando-se os

n

termos

não-nulos da matriz

√

λI

om uma sequênia de

n

(

n

+ 1)

/

2

rotações de Givens

apliadasemadalinha

i

de

√

λI

, simultaneamenteaadalinha

i

+

j

de

Rc

,para

j

= 0

, . . . ,

(

n

−

i

)

, omeçandoda linha

n

. Expressando tais rotaçõesem uma

matriz

Gλ

∈

R

(

m

+

n

)

×

(

m

+

n

)

pormeiode todosossuessivos

n

(

n

+ 1)

/

2

produtos, vemque

G

T

λ





Rc

0

√

λI





=





Rλ

0

0





.

(3.3)

Disto,obtemosamatriztriangularsuperior

Rλ

,demodoque

R

T

λ

Rλ

=

J

T

c

Jc

+

λ I

.

Poronseguinte,osistema (2.3a) torna-semenosustosodeserresolvidopara

di-ferentesvaloresde

λ

. Defato,afatoração

QR

de

Jc

éaluladaumaúniavez,no

iníioda iteraçãointerna,enquanto, paraadavalor de

λ

, obtém-se

Rλ

por(3.3),

queonsisteemumproedimento maisbaratoqueoálulodafatoração

QR

pro-priamentedita.

3.2. Raiz da equação seular

O problema(2.4) onsisteem enontrar

λ

∗

_≥

₀

tal que

k

p

(

λ

∗

₎

_k

_{= ∆}

c

. Então, se

denimos

δ

(

λ

)

def

=

p

(

λ

)

−

∆

c

,estamosinteressadosemenontrarumaraizpara

δ

(

λ

)

.

Todavia,umaanálise maisapurada [4, Seção3.2℄ nosmostraqueafunção

δ

pode

possuirpolosnosautovaloresdamatriz

J

T

c

Jc

+

λI

epodenãopossuirzerosnitos. Emvistadisto,umaestratégiamaisestáveléresolveraequaçãoseular

φ

(

λ

)

def

=

1

k

p

(

λ

)

k

−

1

∆

c

= 0

,

(3.4)

que, por serareíproa de

δ

, não possui polos nitosesuasraízesaonteemnos

valoresnegativosdosautovaloresdamatriz

J

T

c

Jc

+

λI

. Destemodo,paraenontrar

λ

∗

_≥

₀

que satisfaça(2.3a), avaliamos primeiro o asopartiular em que

λ

∗

_{= 0}

(solução interna). Se (2.3a) não possui solução neste aso, busamos uma raiz

positivaparaaequaçãoseularusandoométododeNewton.

OmétododeNewton apliado aoproblema(3.4) gerauma sequênia

{

λj

}

tal

que

λj

+1

=

λj

−

φ

(

λj

)

Emontrapartida,seriainteressantereduziroustodoálulode

λj

+1

eaindaobter

uma expressãonumeriamentemaisestável. Issoépossível,onformeestabeleeo

resultadoaseguir.

Teorema 3.1. Considere o problema (3.4) de enontrar a raiz da equação

seu-lar. Seja

Rλ

amatriz triangular alulada em (3.3), tal que

R

T

λ

Rλpj

=

−

J

T

c

Fc

e

R

T

λ

qj

=

pj

e seja

∆

c

o raio da região de onança orrente. A sequênia

{

λj

}

gerada pelo método de Newtondenidaem (3.5)éequivalentea:

λj

+1

=

λj

+

k

pj

k

k

qj

k

2

k

pj

k −

∆

c

∆

c

.

(3.6)

Demonstração. Ver[4,Lema1℄.

Porm, paraque ométodo deNewton não onvirjapara uma raizindesejada

de

φ

(

λ

)

(poisestamos interessadosem raízes positivas), usamosuma salvaguarda demodoque,aadaiteração,impomos

λj

∈

[

ℓj, uj

]

,sendo

ℓ

0

= 0

aestimativapara omenorautovalorde

J

T

c

Jc

+

λI

e

u

0

obtidopeloquoientedeRayleigh

(

µ

1

+

λ

)

2

≤

p

T

₍

_J

T

c

Jc

+

λI

)

T

(

J

c

T

Jc

+

λI

)

p

p

T

_p

≤

(

µn

+

λ

)

2

_,

sendo

µ

1

, µn

omenoreomaiorautovaloresde

J

T

c

Jc

,respetivamente. Como zero

éumlimitanteinferiorpara

µ

1

,eestamosprourando

k

p

k

= ∆

c

,vemque

λ

≤

k

J

T

c

Fc

k

∆

c

=

u

0

.

Ointervalodasalvaguardaéatualizadoaadaiteraçãodaseguintemaneira:

se

δ

(

λj

)

≥

0

,então

ℓj

+1

=

λj

+

k

qj

k

2

k

pj

k

,

asoontrário

uj

+1

=

λj

.

Paramaioresdetalhes,ver[4, Seção4.2.1℄.

3.3. Quoiente de redução relativa

Nestasubseção,nossoobjetivoéeliminaraoorrêniadeunderowseoverowsno

álulode(2.2). UsandoLMA,podemosalularoquoiente omo

ρ

(

p

) =

k

Fc

k

2

_{− k}

_Fn

_k

2

k

Fck

2

_{− k}

_Fc

₊

_Jcp

_k

2

,

(3.7)

emque

Fn

=

F

(

xc

+

p

)

. De(2.3a), temosque

J

T

c

Jcp

=

−

J

T

c

Fc

−

λp

(3.8a)

−

F

T

c

Jc

=

λp

T

+

p

T

J

c

T

Jc.

(3.8b)

Algumasmanipulaçõesom(3.8)em(3.7)impliamque

Portanto,podemosreesreveroquoiente(3.7)dividindotodosostermospor

k

Fc

k

2

eobtendoaseguinterelação:

ρ

(

p

) =

1

−

k

Fn

k

k

Fc

k

2

k

Jc

p

k

k

Fc

k

2

+ 2

λ

k

p

k

k

Fc

k

2

.

(3.9)

Destemodo, odenominadorde (3.9)serásempre não-negativoe não irágerar

overows. Por outrolado,onumeradorde(3.9)jamaisgeraráoverows anão ser

que

k

Fn

k ≫ k

Fc

k

. Nesteaso,temosqueomodelonãofoi reduzidoomrelaçãoà

funçãoobjetivo,portantonãoéneessárioalular

ρ

(

p

)

.

3.4. Atualização do raio da região de onança

Utilizamos a aproximação iniial

∆

0

=

k

J

T

0

F

0

k

/

10

, lássia da literatura [2℄. O

ontroledoraiodaregiãoonsisteemtrêsinstânias: manter,aumentaroureduzir.

OsasosemqueadaumaéadotadasãoexpostosnoAlgoritmo1. Paraaumentar

otamanho doraio,fazemos

∆

n

= 2

k

p

∗

_k

. Parareduzirotamanhodoraio,fazemos

∆

n

=

ϑ

∗

∆

c

. A m de denir um valor para

ϑ

∗

, seguimos Moré [9℄: denimos

γ

(

ϑ

)

def

= 1

/

2

k

F

(

xc

+

ϑp

∗

₎

_k

2

e enontramosominimizador

ϑ

∗

daparábola

interpo-lante

mq

(

ϑ

)

def

= [

γ

(1)

−

γ

(0)

−

γ

′

(0)]

ϑ

2

+

γ

′

(0)

ϑ

+

γ

(0)

.

Como

mq

ésuaveeonvexa,entãotemos que

m

′

q

(

ϑ

∗

) = 0

,ouseja,

ϑ

∗

₌

₋

γ

′

(0)

2[

γ

(1)

−

γ

(0)

−

γ

′

_(0)]

=

−

(

p

∗

₎

T

_J

T

c

Fc

k

Fn

k

2

_{− k}

_Fc

_k

2

₋

₂₍

_p

∗

₎

T

_J

T

c

Fc

.

(3.10)

Pré-multipliando(2.3a)avaliadoem

p

∗

por

(

p

∗

₎

T

,temos

−

(

p

∗

₎

T

₍

_J

T

c

Jc

+

λ

∗

I

)

p

∗

= (

p

∗

)

T

_J

T

c

Fc,

dondesegueque

(

p

∗

₎

T

_J

T

c

Fc

k

Fc

k

2

=

−

"

k

Jcp

∗

_k

k

Fc

k

2

+

λ

∗

k

p

∗

_k

k

Fc

k

2

#

.

(3.11)

Dividindo todos os termos de (3.10) por

k

Fc

k

2

, multipliando o numerador e o

denominadorpor

−

1

/

2

esubstituindo(3.11),quedenotamospor

α

,obtemos

ϑ

∗

=

1

2

α

α

+

1

2

"

1

−

k

Fn

k

k

Fc

k

2

#

.

(3.12)

Pelosmesmosmotivosexpostosnaseção anterior, (3.11)éumaexpressão

numeri-amente estável,e(3.12)éonávelebarataparaenontrar

ϑ

∗

4. Experimentos Numérios

Ambos osmétodos foram implementados no CAS Maxima [1, 15℄. O Maxima é

umsistemaalgébrioomputaionallivredeódigoaberto. Possuiumalinguagem

própria,interpretada,alémdeexeutarprogramasesritosemLisp. Esolhemos o

Maxima por serum sistema gratuito elivre, além de não possuir ferramentas de

otimização implementadas, omo é oaso doMatlab R

. Ostestes foram rodados

numomputadorIntelDual-CoreT34002.16GHzesistemaoperaionalWindows7

Professional64bits. Osproblemas-testeforamextraídosde[10℄eestãonumerados

de aordo om a referênia original, bem omo as dimensões e os pontos iniiais

adotados(verdetalhesem[4,5℄).

Comoritériosdeparada, adotamosasatisfaçãorelativadasondiçõesde

pri-meiraordem,istoé,

xk

ésoluçãoemLMAse

x

T

_k

J

_k

T

Fk

/

max

{k

Fk

k

,

1

}

≤

10

−

6

eem

MGC se

k

gk

k

/

k

g

0

k ≤

10

−

6

. Além disso,em LMAimpusemosparada seoresíduo

fossepequeno,ou seja,

k

Fk

k ≤

10

−

6

. Porm, usamosritériosque impliam

pa-radaseavariaçãoentreositerandosfossedaordemde

10

−

12

eseaquantidadede

iteraçõesultrapassasse200paraLMAe300paraMGC,todavianostestesefetuados

nenhumproblemaparouportaisritérios.

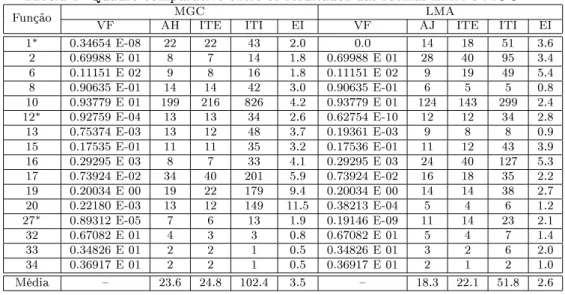
Osresultados dos experimentos são expostos na Tabela 1, enquanto os pers

dedesempenho[3℄naFigura1. Neles,onsideramosVFafunçãoobjetivoavaliada

nasolução,AHaquantidadede avaliaçõesdamatriz hessiana(para oMGC), AJa

quantidadedeavaliaçõesdamatrizJaobiana(paraoLMA),ITEaquantidadede

iteraçõesexternas, ITI a quantidade de iteraçõesinternas (isto é, para resolução

dos subproblemas de regiões de onança) e EI o esforço interno por problema,

dadopelarazãoentreaquantidadedeiteraçõesinternaseavaliaçõesmatriiais. A

quantidadede avaliaçõesdafunçãoobjetivoéigualàquantidadedeITEaresida

de um. Osproblemasmaradosom

∗

são aquelesquepararam pelo tamanhodo

resíduoemLMA;osdemaispararamporsatisfazerondiçõesdeprimeiraordem.

Asavaliaçõesmatriiaisrepresentamquantosdospontosgeradosforamaeitos.

Destemodo,onúmerodepontosrejeitados,paraadaproblema,édadopela

dife-rença entre aquantidadede avaliaçõesde funções ematriiais. Neste ontexto, o

esforçointernoporproblemarepresentaquantasiteraçõesinternasforam

despendi-das,emmédia,paraadapontoaeito.

Aeradosresultadosapresentados,notamosqueLMAémaiseienteem

ava-liaçõesdefunção,avaliaçõesmatriiaisequantidadedeiteraçõesinternas,enquanto

MGC,apenas emquantidadedeiteraçõesinternasdespendidas. Dopontodevista

derobustez,LMAsesobressainaquantidadedeiteraçõesinternas,enquantoMGC

emtermosdeavaliações,tantodefunçãoquantomatriiais,edeiteraçõesexternas.

Istosedeveaofato deque LMA,poraproveitarmelhor aestruturadoproblema,

trabalhamaisinternamente,onsumindomenositeraçõesinternasporémmais

ava-liações que MGC. Considerando-se, problema aproblema, onúmero de iterações

internas despendido para gerar a sequênia de pontos aeitos, o esforço interno

de LMA éinferior ao de MGC. Com relação ao número de pontos rejeitados, no

1

2

3

4

5

6

0

0.2

0.4

0.6

0.8

1

t

ρ

s

(t)

LMA

MGC

(a)AvaliaçõesdeFunção.

2

4

0

0.2

0.4

0.6

0.8

1

t

ρ

s

(t)

LMA

MGC

(b)AvaliaçõesMatriiais.

2

4

6

0

0.2

0.4

0.6

0.8

1

t

ρ

s

(t)

LMA

MGC

()IteraçõesExternas.

2

4

6

8

10

12

14

16

18

20

22

24

26

0

0.2

0.4

0.6

0.8

1

t

ρ

s

(t)

LMA

MGC

(d)IteraçõesInternas.

Figura1: PersdedesempenhodosalgoritmosLMA eMGC.

Tabela1: QuadroomparativoentreosresultadosdasrotinasLMAeMGC.

MGC LMA

Função

VF AH ITE ITI EI VF AJ ITE ITI EI

1

∗

0

.

34654

E-08 22 22 43 2.0

0

.

0

14 18 51 3.6

2

0

.

69988

E01 8 7 14 1.8

0

.

69988

E01 28 40 95 3.4

6

0

.

11151

E02 9 8 16 1.8

0

.

11151

E02 9 19 49 5.4

8

0

.

90635

E-01 14 14 42 3.0

0

.

90635

E-01 6 5 5 0.8

10

0

.

93779

E01 199 216 826 4.2

0

.

93779

E01 124 143 299 2.4

12

∗

0

.

92759

E-04 13 13 34 2.6

0

.

62754

E-10 12 12 34 2.8

13

0

.

75374

E-03 13 12 48 3.7

0

.

19361

E-03 9 8 8 0.9

15

0

.

17535

E-01 11 11 35 3.2

0

.

17536

E-01 11 12 43 3.9

16

0

.

29295

E03 8 7 33 4.1

0

.

29295

E03 24 40 127 5.3

17

0

.

73924

E-02 34 40 201 5.9

0

.

73924

E-02 16 18 35 2.2

19

0

.

20034

E00 19 22 179 9.4

0

.

20034

E00 14 14 38 2.7

20

0

.

22180

E-03 13 12 149 11.5

0

.

38213

E-04 5 4 6 1.2

27

∗

0

.

89312

E-05 7 6 13 1.9

0

.

19146

E-09 11 14 23 2.1

32

0

.

67082

E01 4 3 3 0.8

0

.

67082

E01 5 4 7 1.4

33

0

.

34826

E01 2 2 1 0.5

0

.

34826

E01 3 2 6 2.0

34

0

.

36917

E01 2 2 1 0.5

0

.

36917

E01 2 1 2 1.0

5. Conlusão

OalgoritmoLMA éuma propostaatraente para aresoluçãode (1.1), porserum

métodomaisbarato,seomparadoaométododeNewton. EmLMA,asinformações

desegundaordemdafunçãoresidualsãosubstituídaspelotermoregularizador

λI

.

Emontrapartida,ométodo perde desempenho em problemasextremamente não

linearesouseoresíduoformuitograndenasolução

x

∗

.

EmomparaçãoomMGC, LMAaproveitaaestruturadoproblema(2.3a) eé

maiseienteem algunsquesitos. Todavia,exigemuitasfatoraçõesdematrizes,e

trabalhamaisinternamente,oquepodeserruimem algunsasos. Emvistadisso,

MGCéummétodoompetitivo,mostrando-semaisrobustoqueLMAempartedos

quesitosanalisados. Gradientesonjugadosébemonheidoporserumaboa

estra-tégiapararesoluçãode sistemaslineares ommatrizesdenidaspositivas,todavia

aliado àestratégia de regiõesde onança pode ser uma alternativa interessante

tambémparaproblemasnãoonvexos.

Abstrat. Theleastsquares problem hasmanyappliations intheeld of

opti-mization. Inthepresentwork,weusetwostrategiesforitsresolution:

Levenberg-Marquardt and Conjugate Gradients. Eahone exploits some problem features,

and bothareglobalizedbythe trust-regionstrategy. Ourontributiononsistsin

theimplementationofbothmethodsusingtheCASMaximaandinthe

ompara-tiveanalysisofthesemethodsintheresolutionofafamilyofleastsquaresproblems

fromtheliterature.

Keywords. Leastsquares,trustregion,omputationalimplementation.

Referênias

[1℄ L.N.Andrade,Maxima: umompletoprogramadeomputaçãoalgébria,

Re-vistado Professorde Matemátia,n. 77,2012.

[2℄ A.R. Conn,N.I.L. Gould, Ph.L.Toint, Trust-region Methods. SIAM,

Phila-delphia,2000.

[3℄ E.D.Dolan,J.J.Moré,Benhmarkingoptimizationsoftwarewithperformane

proles,Mathematial Programming,v.91,pp.201-213,2002.

[4℄ J.L.C.Gardenghi,S.A.Santos,Sistemasnão-linearesviaregiãodeonança:

oalgoritmo de Levenberg-Marquardt.Relatório de Pesquisa, 2011.

Disponí-vel em http://www.ime.uniamp.br/sites/default/les/rel_pesq/rp03-11.pdf.

Aessoem05mar.2013.

[5℄ J.L.C.Gardenghi,S.A.Santos,Minimizaçãoirrestritausandogradientes

on-jugados e regiões de onança. Relatório de Pesquisa, 2012. Disponível em

http://www.ime.uniamp.br/sites/default/les/rel_pesq/rp04-12.pdf. Aesso

em05mar.2013.

[6℄ K.Levenberg,Amethodforthesolutionofertainnon-linearproblemsinleast

[7℄ K.Madsen,An algorithmfortheminimaxsolutionofoverdeterminedsystems

ofnonlinearequations.Journalof the Instituteof Mathematisand its

Appli-ations.v.16(3),pp.321-328,1975.

[8℄ D.W.Marquardt,Analgorithmforleast-squaresestimationofnonlinear

para-meters,SIAMJournalon AppliedMathematis 11,pp.431-441,1963.

[9℄ J.J.Moré, TheLevenberg-Marquardtalgorithm: implementationand theory.

LetureNotesinMathematis630: NumerialAnalysis,Springer-Verlag,New

York,pp.105-116,1978.

[10℄ J.J.Moré, B.S. Garbow,K.E. Hillstrom, Testing unonstrainedoptimization

software,ACM Transations onMathematial Software,v.7,pp.17-41,1981.

[11℄ J.Noedal, S.J.Wright,NumerialOptimization.Springer,NewYork,1999.

[12℄ T.Steihaug,Theonjugategradientmethodandtrustregioninlargesale

op-timization.SIAMJournalonNumerialAnalysis,v.20(3),pp.626-637,1983.

[13℄ Ph.L.Toint,TowardsaneientsparsityexploitingNewtonmethod for

mini-mization,em SparseMatrix andTheir Uses (I. Du, ed.), Aademi Press,

pp.57-88,1981.

[14℄ Y. Yuan, Reentadvanes in numerialmethods for nonlinearequations and

nonlinear least-squares. Numerial Algebra, Control and Optimization, v. 1,

n.1,pp.15-34,2011.